Abstract
Risk management in construction projects is a critical process aimed at identifying, evaluating, and mitigating potential risks that could impact project performance. Preventive measures play a central role in this process, serving as proactive strategies to minimize the likelihood and impact of risks on project outcomes. This study involved 37 experts from multidisciplinary fields related to road infrastructure, ensuring a diverse and comprehensive perspective on risk evaluation and prevention. The DELPHI method was employed to systematically define key risks and their corresponding preventive measures, providing a structured foundation for further analysis. The experts evaluated 302 preventive measures across 56 risks using 4 predefined criteria: implementation costs, time required for implementation, implementation complexity, and probability of success. A multi-criteria decision making (MCDM) approach was then applied to analyze these evaluations, enabling the prioritization of preventive measures and the allocation of resources toward the most effective strategies. Additionally, fuzzy logic was employed to analyze and validate the results, providing a complementary approach to the MCDM methodology. The results of this research provide a robust framework for risk management, offering practical guidance for decision makers in the construction industry. By integrating expert judgment, systematic evaluation, and advanced analytical methods, this study delivers actionable insights and establishes a reliable methodology for enhancing the effectiveness of risk mitigation in road infrastructure projects.
Keywords:
risk management; preventive measures; Delphi method; multi-criteria decision making; road infrastructure MSC:
90B06; 90B50
1. Introduction
Road infrastructure projects are crucial for economic growth, but they face numerous challenges due to risks and uncertainties, which may result in project delays and increased costs. This study bridges the gap in contemporary risk management practices by presenting a multi-criteria framework designed to prioritize targeted preventive measures effectively. In contrast with traditional models, our approach integrates expert judgment and empirical data to develop a practical and actionable framework. The main goal of this study is to reduce project inefficiencies by identifying and implementing the most impactful preventive measures.
Risk refers to the likelihood of an unfavorable event occurring, influenced by specific conditions. Risk management entails a structured process aimed at addressing these uncertainties, involving a sequence of decisions to ensure the project progresses safely and efficiently. Risks can emerge at any stage of project execution, and failing to assess and manage them properly can significantly impact the project’s overall performance [1,2,3].
The management of risks in construction projects is a critical component of project success due to the inherent complexity and uncertainty involved in such undertakings. Risks arise from various sources, including financial, environmental, technical, and operational factors, and they significantly impact project performance concerning time, cost, and quality objectives. The growing complexity and scale of road infrastructure projects, combined with risks associated with project delivery, inconsistent stakeholder requirements, and the dynamic nature of the construction process, create highly intricate challenges in project risk management [4]. These challenges are further exacerbated by the presence of vagueness, subjectivity, and uncertainty in decision making. To tackle these issues, researchers have developed and applied various advanced methodologies, including multi-criteria decision making (MCDM), simulation techniques, machine learning models, and optimization frameworks, to enhance the evaluation and prioritization of risks and preventive measures [5,6,7].
Risk management frameworks have evolved to incorporate advanced tools that facilitate the handling of incomplete, vague, or subjective data. For instance, the integration of fuzzy logic with MCDM methods, as discussed by Nguyen [4,8], has proven effective in addressing uncertainty and vagueness in construction engineering and management research. This hybrid approach allows for the prioritization and ranking of risks and preventive measures based on linguistic variables and expert opinions, thus enabling more precise decision making.
Effective risk management in infrastructure projects, particularly in the construction of transportation infrastructure, is crucial for ensuring timely project delivery and cost control. However, many projects in this domain face significant delays and cost overruns, indicating inadequacies in current risk management approaches. These challenges often stem from the complex nature of projects and the lack of advanced tools for identifying and prioritizing preventive measures.
Although numerous tools and models exist for risk management, most focus on the qualitative aspects of evaluation while neglecting quantitative analyses and the integration of multi-criteria decision-making methods. Additionally, the literature addressing infrastructure projects primarily relies on general approaches that fail to account for specific local factors such as regulatory frameworks, climatic conditions, and contractor capabilities. This creates a knowledge gap regarding the development of tailored models for transportation infrastructure projects.
The objectives of this study are as follows:
- To enhance the theoretical framework of risk management in infrastructure projects by integrating multi-criteria methods and empirical data from real projects.
- To develop a generic multi-criteria model that combines expert evaluations and quantitative analyses, enabling a more precise and objective ranking of preventive measures.
- To create a universal framework for assessing and ranking preventive measures that is adaptable to various sectors and geographic contexts while considering local specificities.
- To provide guidelines for formulating standards and policies in the construction industry, with a focus on effective risk management in infrastructure projects.
- To address a critical gap in the literature through the quantitative evaluation of prioritized preventive measures based on empirical data from transportation infrastructure projects.
This paper is structured as follows: Following the Section 1, which includes a general overview, a detailed literature review, and clearly defined research objectives, the Section 2 provides a comprehensive explanation of the data collection and processing methods, incorporating MCDM techniques and fuzzy logic for prioritizing preventive measures. The findings are presented in the Section 3, while the Section 4 analyzes the broader implications of these findings and identifies potential limitations. The paper concludes with key insights and specific recommendations for future research.
1.1. Literature Review
Road infrastructure projects face various risks that can significantly impact costs, timelines, and the quality of execution. Risk management in these projects is becoming increasingly complex, requiring advanced methodologies for assessment and prioritization. Multi-criteria decision making (MCDM) methods and fuzzy logic stand out as essential tools for addressing these challenges, enabling decision making under conditions of uncertainty and imprecise data.
Taylan et al. [9] applied a combination of fuzzy AHP and fuzzy TOPSIS methodologies for risk assessment in construction projects, enabling precise risk ranking based on criteria such as time, cost, and quality. This approach facilitates the transformation of qualitative data into quantitative values, ensuring improved decision making. Similarly, Zavadskas et al. [10] developed a model that combines COPRAS-G and TOPSIS–grey methods for multi-criteria risk analysis, providing efficient management of uncertainties in construction projects.
Fuzzy hierarchical models developed by Chan and Wang [11] have proven particularly useful for risk assessment in cases where data are incomplete or unclear, a common challenge in infrastructure projects. Similarly, Kuo and Lu [12] applied a fuzzy multi-criteria decision-making model for risk assessment in metropolitan construction projects, enabling precise risk ranking based on preferential relationships. A significant contribution also comes from the combination of SWOT analysis and multi-criteria decision making (MCDM) methods, as demonstrated by Zavadskas, Turskis, and Tamošaitienė [13]. Their model facilitates the identification of risk management strategies in construction enterprises tailored to the specificities of each project.
In recent research, methodologies such as fuzzy analytic hierarchy process (AHP) and multi-criteria decision making (MCDM) techniques have gained traction for their ability to incorporate expert judgment and address the inherent uncertainties in construction risk management [14,15,16,17]. For instance, Alvand et al. [18] utilized an integrated approach combining FMEA, SWARA, and WASPAS techniques within a fuzzy environment to identify, evaluate, and prioritize risks in construction projects more effectively. Similarly, many authors [11,19,20] demonstrate the applicability of a fuzzy hierarchical model for risk assessment.
A notable methodology, the TOPSIS-F model, employs fuzzy data to rank risks by their proximity to an ideal solution, providing a robust tool for dealing with the dynamic nature of construction projects, as desribed by Zavadskas and Turskis [7]. This method is particularly relevant for projects characterized by macro-, mezzo-, and micro-level risks, where conflicting criteria and constraints necessitate nuanced evaluation and strategic planning. In addition to the methodological advancements, the literature underscores the importance of expert judgment in risk evaluation. Biswas and Zaman [8] highlighted the role of epistemic uncertainty in construction risk management and pro-posed a fuzzy-based methodology to capture expert insights alongside limited historical data. This approach ensures a comprehensive understanding of risk factors and enables the formulation of effective response strategies. The integration of empirical data further enhances the strength of risk assessment models, as evidenced by the study conducted by Taylan et al. [9], which employed fuzzy TOPSIS alongside AHP to evaluate construction project risks based on real-world data. These approaches underline the necessity of incorporating both qualitative insights from experts and quantitative analyses to achieve comprehensive risk evaluations.
These studies highlight the importance of integrating advanced methodologies such as fuzzy logic and multi-criteria analysis to improve risk management processes in infrastructure projects. Such models enable better decision making, reducing the impact of risks on projects and enhancing their efficiency and sustainability. Table 1 presents a summary of key features and research findings from the literature review, highlighting advanced methodologies and their applications in managing the risks associated with infrastructure projects. The table emphasizes the use of modern analytical techniques, such as fuzzy logic and multi-criteria decision making, for effective decision making and prioritization of preventive measures.

Table 1.
Key features and research findings from the literature review: focus on infrastructure project management and modern analytical methods.
Our research builds on empirical data collected from experts to evaluate 302 preventive measures across 56 risks, providing a solid foundation for informed decision making in road infrastructure projects. By systematically integrating expert judgment with multi-criteria analysis and fuzzy logic alongside weighted scoring and normalization techniques, our study not only aligns with the established literature but also offers practical insights tailored to the context of road infrastructure projects. This empirical grounding ensures that the findings are directly applicable to real-world scenarios, providing a robust relationship between theoretical methodologies and practical implementation in risk management.
1.2. Research Objectives and Contributions
Road infrastructure projects play a critical role in economic growth but are often plagued by risks and uncertainties, leading to delays and cost overruns. This study addresses a specific research gap in risk management by developing a multi-criteria framework enhanced with fuzzy logic to prioritize and quantify the effectiveness of preventive measures. The existing literature often lacks robust methodologies for integrating expert judgment with quantitative analyses under uncertain conditions.
The primary objectives of this research are as follows:
1. To develop a practical and effective framework for prioritizing preventive measures that reduce inefficiencies in road infrastructure projects.
2. To quantitatively assess preventive measures using multi-criteria decision-making techniques combined with fuzzy logic, ensuring precise and actionable results.
This dual-layered methodology bridges the gap between theoretical advancements and practical implementation, offering a novel approach to risk management in road infrastructure. By combining advanced mathematical techniques with real-world insights, the study provides a reliable and applicable tool for improving decision making in complex risk scenarios.
2. Methodology
This study applies a comprehensive methodology to evaluate and rank preventive measures for mitigating risks in road infrastructure projects. The process begins with defining risk groups [4] and identifying specific risks and their associated preventive measures. Experts then evaluate these measures based on their effectiveness in reducing risks using clearly defined criteria. The aim is to prioritize measures that offer the greatest potential for risk mitigation, providing actionable insights for decision making in project management.
The methodology involves multiple phases, starting with the Delphi method to establish a robust foundation of risks and preventive measures. Experts then assess the measures according to selected criteria and determine the relative importance of these criteria in contributing to risk reduction. Consistency in the expert evaluations is analyzed to ensure the reliability of the data. In the process of data collection from experts, we implemented two approaches. First, the experts provided numerical values when assessing the importance of the considered criteria. Second, to investigate the fuzziness of the data in the expert evaluations, we added a control group of experts that gave the answers in a linguistic manner, which demands the use of fuzzy logic for further calculations. Finally, scores are aggregated using a weighted scoring method (WSM) to produce a single score for each measure, enabling their ranking and highlighting the most effective options for risk mitigation.
The study applies a weighted scoring method (WSM) to evaluate preventive measures across four criteria: implementation costs, time required, implementation complexity, and probability of success. The process involves the following steps:
- Identification of risks and grouping risks into categories [4].
- Evaluation of preventive measures by experts using two approaches, crisp values and fuzzy numbers.
- Weight assignment to criteria.
- Calculation of overall scores and ranking.
2.1. Delphi Method
As part of this research, the Delphi method [23,24,25] was applied as a structured technique for collecting and synthesizing expert opinions. The Delphi method [24,25] enables anonymous, iterative data collection from a selected panel of experts to reach a consensus on key aspects of risk analysis and proposed preventive measures. This approach is particularly suitable for complex issues in risk management, where a multidisciplinary approach and expert experience are required. The method is based on iterative rounds of data collection and feedback, allowing experts to revise their opinions and converge toward a consensus.
The selection of experts for the study was based on their qualifications and extensive experience in managing road infrastructure projects. The process, conducted in 2024 over 3 months, involved 37 professionals from diverse fields, such as civil and traffic engineering, law, economics, and management, ensuring a multidisciplinary approach. Each expert had a proven track record, with an average of 30 projects managed per individual and a minimum of 5 years of experience in road infrastructure projects. The average project value was approximately EUR 12,000,000, with a minimum threshold of EUR 3,000,000 for project experience. Additionally, the experts were selected to ensure demographic representativeness, with 65% male and 35% female participants, aligning with the gender structure of the profession. This diverse group brought a wealth of perspectives, with the multidisciplinary team providing a well-rounded evaluation of the study’s subject matter and enriching the overall quality of the analysis.
In the first phase of the research, the foundation for defining the groups of risks and specific risks was built on a thorough review of the literature from relevant studies in this field conducted over the past few years [26,27,28,29]. These studies provided a robust theoretical basis for understanding and categorizing the risks. Additionally, experts engaged in detailed discussions and deliberations to analyze and adopt well-grounded groups of risks and specific risks identified in the literature. This collaborative approach ensured a unified stance between the literature and the experts, resulting in comprehensive and consistent perspectives on the classification and selection of risks. As a result, 7 groups of risks were defined [4], encompassing a total of 56 specific risks, which served as the foundation for further steps in the research process. Based on the identified risks, the experts employed the Delphi method to propose and rank a total of 302 preventive measures. This structured methodology facilitated the systematic involvement of experts in defining effective and comprehensive preventive actions. After forming the list of risks, an expert panel discussion was organized to evaluate the risks and propose preventive measures. The proposals for preventive measures were derived based on the practical experiences of the experts, the analysis of completed projects, the scientific literature, and case studies. Based on this assessment, the experts collaboratively formulated a set of preliminary preventive measures. The aim was to ensure that the proposals were realistic, applicable, and tailored to the specific characteristics of the identified risks. The preliminary measures, therefore, represented a synthesis of theoretical knowledge and practical feasibility. Once developed, these measures were incorporated into the questionnaires to facilitate broader data collection and validation. Through iterative rounds of feedback, discussion, and refinement, the experts analyzed the results and exchanged insights to achieve consensus. This application of the Delphi method ensured that the preventive measures were thoroughly evaluated, well founded, and aligned with the expertise of the participants.
2.2. Evaluation Methodology for Preventive Measures
In this study, each of the 302 preventive measures was evaluated according to four key criteria: implementation costs, time required for implementation, implementation complexity, and probability of success. In the first phase, the evaluation process was carried out with the involvement of 37 experts from the fields of engineering (civil, electrical, traffic, environmental protection, architecture, and spatial planning), law, economics, and management, ensuring the expertise and reliability of the collected data. In the second phase, where the control group of experts was involved, we interviewed an additional five experts, implementing a fuzzy logic approach.
In the first phase, each preventive measure was assessed using a 1-to-10 scale, where 1 represented the lowest level (e.g., highest costs, longest time, greatest complexity, lowest probability of success), and 10 represented the highest level (e.g., lowest costs, shortest time, lowest complexity, highest probability of success) [30,31,32,33]. The 1-to-10 scale was chosen due to its intuitiveness and wide applicability in multi-criteria decision-making research. This scale enables precise differentiation between options while remaining simple to apply, avoiding complications associated with broader or less intuitive scales. According to the literature [1,34,35], this scale is a standard for quantifying subjective evaluations within the context of multi-criteria decision-making methods.
The 1-to-10 scale was chosen for its flexibility, simplicity, and widespread application in multi-criteria decision making (MCDM) analyses. This scale allows experts to express nuanced evaluations, providing greater flexibility compared with binary or smaller scales. For instance, it enables fine differentiation between similar options, making it particularly suitable for prioritizing preventive measures.
The simplicity of the 1-to-10 scale ensures its accessibility to experts with varying levels of experience, facilitating faster and more reliable evaluations. Furthermore, this scale is widely accepted in decision-making methodologies, ensuring compatibility with the weighting and ranking techniques commonly used in risk management.
In addition to its flexibility, the scale allows for detailed numerical analysis and validation of expert assessments. The numerical values simplify statistical processing and enhance the credibility of the results by providing a clear structure for comparisons. While the standard 1-to-10 scale was used in this study, the model can adapt to alternative scales based on specific project requirements.
A total of 37 experts participated in this study who were selected based on the following professional criteria: a minimum of 5 years of work experience in the field, involvement in at least 5 completed infrastructure projects, experience with at least 1 international FIDIC contract, and predominantly working on international contracts throughout their careers. The roles of the experts varied, including supervision (7 experts), construction execution (5), design (9), technical consultancy (2), project management (6), public procurement (2), legal consultancy (2), finance (3), and environmental protection (1). The average age of the experts was 46 years, with an average of 19 years of work experience and participation in an average of 30 projects. All experts had experience in international projects, with 30 experts primarily engaged in international projects and 7 in regional ones. The evaluation process involved initial discussions of proposed preventive measures until a consensus was reached, followed by a single round of scoring. The results were further validated through consistency analysis and additional discussions among experts, ensuring the reliability and credibility of the findings.
Experts evaluated the preventive measures individually, and the process was organized to ensure participant anonymity, reducing bias and the influence of group dynamics. For each preventive measure, a total of 4 scores was collected, one for each criterion, generating a dataset of 1204 evaluations per expert.
The consistency of the results among the experts was assessed using Cohen’s kappa coefficient, a statistical measure widely recognized for evaluating inter-rater reliability. The calculated kappa value of 0.834 indicates a very high level of agreement among the experts, significantly above the threshold for substantial agreement (0.61–0.80). This demonstrates the reliability of the evaluations and the robustness of the scoring process. The analysis was conducted using the SPSS v.30 statistical software, which ensured precise computation and facilitated the validation process. By employing this methodological approach, the study reinforced the credibility of the findings and provided a solid foundation for further analysis.
This methodology enables a comprehensive and scientifically validated approach to analyzing preventive measures, addressing key aspects of their implementation. By employing well-defined criteria and a standardized scale, the evaluation results provide a solid foundation for decision making and ranking measures. This evaluation process also ensures practical applicability, as it facilitates the quantification of the complexity and effectiveness of measures in real-world risk management conditions within road infrastructure projects.
In the second phase, we interviewed an additional five experts to serve as a control group. In addition, in this phase, the methodological approach was different. The experts expressed their evaluations in a linguistic manner, and for calculation purposes, fuzzy logic was used. In continuation, some basic definitions of fuzzy sets and numbers are provided [36].
Definition 1.
A fuzzy set in a universe of discourse X is characterized by a membership function (x), which associates with each element x in X, a real number in the interval . The function value
(x) represents the grade of membership of x in
.
Definition 2.
A fuzzy set
of the universe of discourse X is convex if and only if for all in X,
where .
Definition 3.
A fuzzy set
of the universe of discourse X is called a normal fuzzy set, implying that X, () = 1.
Definition 4.

A fuzzy number is a fuzzy subset in the universe of discourse X that is both convex and normal. An example of a triangular fuzzy number is given in Figure 1.

Figure 1.
A triangular fuzzy number .
Definition 5.
A triangular fuzzy number
can be defined by a triplet (, , ) shown in Figure 1. The membership function is defined as:
To evaluate the criteria, the experts gave the linguistic answers. These linguistic answers can be expressed as triangular fuzzy numbers. The scale used is provided in Table 2.

Table 2.
A relation between linguistic answers and fuzzy numbers.
If there are K experts that perform the evaluations, and each of the evaluations is considered as fuzzy number , then the ratings can be calculated as follows:
As a defuzzification method for triangular fuzzy numbers, we use the following:
2.3. Evaluation Methodology for Weighting Evaluation Criteria
In this study, an evaluation of the significance of the defined criteria was conducted to establish a baseline weighting distribution that reflects their relative importance in the assessment of preventive measures. This step is essential in multi-criteria decision making (MCDM) as it allows priorities to be clearly defined and integrated into the decision-making process. Experts assessed the importance of each criterion using a proportional scale, where the total value for all criteria was predefined as 100%. This approach ensured that the evaluations were relatively comparable and that the key factors influencing the selection of optimal measures were identified.
The justification for this approach lies in the fact that each criterion contributes differently to the evaluation of the effectiveness and practical feasibility of preventive measures. For example, criteria such as cost or implementation time may have a direct impact on the practical application of a measure, while others, such as complexity or probability of success, provide insights into the long-term sustainability and efficiency of the measure. Weighting distribution enables these differences in importance to be expressed quantitatively, ensuring that the final evaluation results align with real-world priorities in risk management.
Furthermore, this methodology is grounded in the scientific foundations of MCDM, which emphasize the importance of integrating expert opinions when shaping weight coefficients. The theoretical and practical validity of this approach is well documented in the relevant literature [31,34,35], where weighting evaluation is used to balance the often conflicting impacts of various criteria. This ensures that the evaluation process is based on objective and scientifically validated principles, while also maintaining the practical applicability of the results.
Normalization of Criteria Weights
To ensure that the sum of the average weights for the four criteria (implementation costs, time required for implementation, implementation complexity, and probability of success) equals 100, the following steps are applied:
Collecting expert evaluations:
Each expert assigns weights to the four criteria (C1, C2, C3, C4) such that:
for each expert i (I = 1, 2, …, n), where n is the number of experts.
C1i + C2i + C3i + C4i = 100
Calculating the average weight for each criterion:
The arithmetic mean of the weights for each criterion is computed across all experts, as follows:
where
Cji is the weight assigned to criterion jj by expert ii.
Normalizing the average weights:
The average weights are normalized to ensure their sum equals 100, using the following equation:
where is the normalized weight for criterion j and is the sum of the unnormalized average weights.
This procedure ensures that the final weights are proportional to the experts’ evaluations while maintaining a total sum of 100, making them suitable for use in further analyses.
2.4. Methodology for Aggregating Scores and Ranking Preventive Measures
In this study, the weighted scoring method (WSM) was applied to derive a single overall score for each preventive measure and enable their ranking according to efficiency. This method integrates evaluations across multiple criteria into a composite value, accounting for the relative importance of each criterion. The methodology was developed to ensure scientifically grounded and practically applicable results, facilitating the prioritization of measures in the context of risk management in road infrastructure projects.
Each preventive measure was evaluated based on four defined criteria:
- Costs,
- Time required,
- Complexity,
- Probability of success.
Each measure was rated on a scale from 1 to 10, where 1 represents the lowest and 10 is the highest performance level within the specific criterion. The weights of the criteria were determined through a weighting process by experts and represented the proportional contribution of each criterion to the overall score. The total weight of all criteria was 100%, expressed in decimal form for computational purposes (e.g., 25% = 0.25).
The overall score for each preventive measure (Si) was calculated as a weighted sum of scores for the criteria using the following equation:
where:
Si is the overall weighted score for the i-th preventive measure,
Wj is the weight of the j-th criterion,
Xij is the score of the i-th preventive measure for the j-th criterion (scale 1–10),
n is the total number of criteria (n = 4).
Based on the overall scores (Si), preventive measures were ranked in descending order, with the highest-ranked measure representing the best balance among the defined criteria. This ranking facilitates decision making regarding the priorities for implementing measures, particularly in scenarios with limited resources.
The weighted scoring method ensures that evaluations across multiple criteria are integrated into a single overall score while appropriately reflecting the relative importance of each criterion. By incorporating expert-determined weights, this approach guarantees that criteria with higher significance exert greater influence on the final evaluation. Furthermore, the method is straightforward and suitable for practical applications, offering a clear framework for evaluating and prioritizing preventive measures. Its scientific validity is widely recognized in the literature on multi-criteria decision making [31,34,35], where it is regarded as an effective tool for addressing complex datasets and supporting decision-making processes.
The use of MCDM in this study was justified by the need to systematically evaluate and prioritize a large number of preventive measures (302) across multiple criteria, including implementation costs, time required for implementation, implementation complexity, and probability of success. The complex and interdependent nature of risks in road infrastructure projects necessitates a methodology capable of accommodating subjective expert judgments and integrating them into a coherent, quantitative framework. MCDM offered the flexibility to handle uncertainties and variability in expert evaluations across these criteria, ensuring strong and actionable results. By facilitating a nuanced analysis of the relative importance of each criterion and the effectiveness of individual measures, MCDM enabled the identification of the most impactful preventive measures, directly supporting decision-making processes in real-world infrastructure risk management.
Calculating the Combined Probability of Risk Reduction
When considering multiple preventive measures that operate independently of one another, the total probability of risk reduction (Ptotal) can be calculated using the following formula:
where:
Ptotal represents the total probability of reducing the risk,
Pi is the probability that the i-th preventive measure successfully reduces the risk,
n is the total number of considered preventive measures.
This formula is based on the principle of independence of events, where the probability of failure for each measure (1 − Pi) is accounted for, and the total probability of success complements the probability that all measures fail collectively. This approach allows for assessing the effectiveness of combined measures, providing insight into their contribution to overall risk reduction.
The results of this methodology have significant practical value for risk management projects in road infrastructure. Identified and ranked preventive measures can serve as the basis for strategic decision making, resource allocation, and implementation planning. This methodology is adaptable and can be applied in future projects, ensuring a consistent and transparent evaluation process aligned with the priorities and goals of stakeholders and infrastructure managers. This approach provides a clear framework for decision making under real-world conditions, contributing to the improvement of risk management processes and enhancing the efficiency of preventive measure implementation.
The scores assigned to each preventive measure (ranging from 1 to 10) represent expert evaluations based on defined criteria, including the probability of success. To derive the probability of risk reduction (Ptotal) for each measure, the scores corresponding to the probability of success (Pi) are normalized by dividing each score by the maximum possible value (10). This process scales the scores to a range between 0 and 1, ensuring consistency and interpretability within a probabilistic framework. For example, a score of 7.6 is normalized to 0.76, while a score of 6.4 is normalized to 0.64.
This normalization allows the expert evaluations to be directly linked to probabilistic values, providing a clear and quantitative basis for assessing the effectiveness of individual preventive measures. By integrating these normalized probabilities, the methodology ensures a comprehensive approach to evaluating and prioritizing risk reduction strategies in infrastructure projects.
2.5. Consistency of Expert Evaluations
During the evaluation process, the consistency of expert assessments was carefully analyzed to ensure the reliability and validity of the collected data. The majority of the experts provided consistent evaluations across the four criteria for all preventive measures. Consistency was assessed using a statistical approach, analyzing the variance and correlation of scores within each expert’s dataset, as well as comparing them with the collective average of all participants. This approach ensured that individual evaluations aligned with the expected patterns of logical reasoning inherent to the defined criteria.
Out of the 37 experts, 2 experts exhibited significant inconsistency in their assessments, with evaluations deviating markedly from both their internal patterns and the group consensus. Specifically, their scores demonstrated high variance without a clear justification, such as extreme values that did not correspond to the provided definitions of the scoring scale (e.g., rating measures with contradictory extremes across criteria, such as assigning high complexity alongside low costs). This lack of internal coherence suggested either a misunderstanding of the criteria or insufficient adherence to the evaluation guidelines.
To maintain the integrity of the dataset, the results from these two experts were excluded from the final analysis. This decision was supported by established practices in multi-criteria decision-making research [31,37,38], where inconsistent evaluations can disproportionately skew aggregated results and compromise the validity of the conclusions [1,35,39]. The exclusion was further justified by the fact that the remaining 35 experts provided a representative sample, ensuring that the final results retained their statistical reliability.
The process of excluding inconsistent evaluations aligns with best practices in expert-based research. By removing outliers, the analysis focused on capturing the collective expertise of the group while minimizing the impact of potential anomalies. The final dataset, consisting of evaluations from 35 experts, demonstrated high internal consistency and strong alignment with the expected logical patterns, thereby providing a sound foundation for further analysis and interpretation.
This rigorous approach to evaluating and validating expert assessments underscores the strength of the methodology and enhances the credibility of the results. By addressing inconsistencies transparently and methodologically, the research ensures that the findings accurately reflect the collective expertise and provide a reliable basis for decision making in risk management within road infrastructure projects.
2.6. Ethical Considerations
This study was conducted in full compliance with established ethical standards to ensure the integrity and transparency of the research process. The anonymity of all experts involved in the evaluation was strictly maintained throughout the study. At no point were individual identities disclosed, and the data were processed and analyzed in a manner that prevented the identification of individual contributions, thereby safeguarding their privacy and encouraging unbiased participation.
All experts were thoroughly briefed on the study’s objectives and methodology prior to their involvement. A detailed presentation was organized to explain the purpose of the research, the role of the experts, and the specific tasks they would be undertaking. Experts were given the opportunity to ask questions and provide feedback during this initial session.
Written informed consent was obtained from all experts before the study commenced. This consent ensured that participants were fully aware of their involvement in the study, the scope of their contributions, and the measures in place to protect their confidentiality. Furthermore, regular meetings and discussions were organized to provide a platform for experts to share insights, clarify uncertainties, and contribute to a collaborative and informed evaluation process.
By adhering to these ethical measures, the study ensured a transparent, respectful, and inclusive research environment. This approach not only upheld the highest standards of ethical research but also fostered a sense of trust and engagement among the participating experts, contributing to the reliability and validity of the results.
2.7. Software and Tools Used
The analysis in this study was conducted using a combination of statistical and computational tools to ensure accurate data processing, evaluation, and presentation of the results. For statistical analysis, SPSS Statistics (version 28.0) was used to perform descriptive statistics, consistency checks, and reliability tests for the expert evaluations. This software facilitated the processing of large datasets, ensuring precision and efficiency in analyzing the consistency and reliability of the collected data.
To implement the weighted scoring method (WSM) and aggregate scores, as well as to automate computations, Python (version 3.10) was utilized. Python’s flexibility and wide range of libraries, such as Pandas for data manipulation and NumPy for numerical computations, enabled efficient processing and clear presentation of the results.
The integration of these tools ensured a strong and transparent workflow, combining statistical rigor with computational efficiency and enabling a comprehensive evaluation of preventive measures.
3. Results
In this section, the results of the study are presented and organized by the seven identified groups of risks. Each subsection focuses on one group of risks and provides a detailed overview of its findings. For each group, the defined risks are introduced, followed by the corresponding preventive measures identified to address these risks.
The evaluation results for each preventive measure are presented based on the four predefined criteria: implementation costs (ICs), time required for implementation (TRI), implementation complexity (ICO), and probability of success (PS). The values of the coefficients of the four weighting criteria are shown in Table 3. The scores assigned to each preventive measure for these criteria are detailed, and their aggregation into a single overall score (Si) is highlighted. This comprehensive presentation allows for a clear understanding of the effectiveness and prioritization of preventive measures within each risk group, providing actionable insights for decision making in risk management.

Table 3.
Coefficient of the four weighting criteria.
3.1. Evaluation of Preventive Measures in the Design Group
Table 4 presents the identified risks within the Design group along with the evaluation scores for each associated preventive measure. A total of 11 risks have been identified in this group, with corresponding preventive measures tailored to mitigate each risk. The table includes the assessment of these measures based on four predefined criteria. These scores provide a comprehensive overview of the relative performance of the preventive measures, enabling their prioritization based on their effectiveness in reducing design-related risks in road infrastructure.

Table 4.
Risks and evaluation of preventive measures in the Design group.
The results of the statistical analysis showed no statistically significant differences between the mean values of Si and the Si fuzzy scores. The independent samples t-test indicated the absence of a statistically significant difference between the groups (t = −0.082, p = 0.935). These findings suggest that the Si and Si fuzzy scores are practically equivalent in the context of the analysis.
3.2. Evaluation of Preventive Measures in the External Group
Table 5 highlights the risks categorized under the External group along with the evaluation results for the associated preventive measures. This group encompasses a total of 10 risks, each of which is addressed through specifically defined measures aimed at mitigating their impact. These evaluations serve as a foundation for comparing the effectiveness of preventive measures within this group, facilitating their prioritization and strategic application in managing external risks in road infrastructure projects.

Table 5.
Risks and evaluation of preventive measures in the External group.
The results of the statistical analysis showed no statistically significant difference between the mean values of the Si and Si fuzzy scores for this dataset. The independent samples t-test indicated the absence of a statistically significant difference between the groups (t = 0.408, p = 0.684). These findings suggest that the Si and Si fuzzy scores are practically equivalent for this group as well.
3.3. Evaluation of Preventive Measures in the Resource Group
The risks associated with the Resource group are presented in Table 6 along with the evaluation of their corresponding preventive measures. This category includes six identified risks, each addressed through specific measures designed to minimize their impact.

Table 6.
Risks and evaluation of preventive measures in the Resource group.
The results of the statistical analysis showed no statistically significant difference between the mean values of the Si and Si fuzzy scores for the third group of preventive measures. The independent samples t-test indicated the absence of a statistically significant difference between the groups (t = 0.408, p = 0.685). These findings suggest that the Si and Si fuzzy scores are practically equivalent for this group as well.
3.4. Evaluation of Preventive Measures in the Employer Group
Table 7 provides an overview of the risks identified within the Employer group and the associated preventive measures developed to address them. This group includes a total of seven risks, each linked to specific measures aimed at reducing their potential impact.

Table 7.
Risks and evaluation of preventive measures in the Employer group.
The results of the statistical analysis showed no statistically significant difference between the mean values of the Si and Si fuzzy scores for this group of preventive measures. The independent samples t-test indicated the absence of a statistically significant difference between the groups (t = −0.566, p = 0.573). These findings suggest that the Si and Si fuzzy scores are practically equivalent for this group as well.
3.5. Evaluation of Preventive Measures in the Contractor Group
The Contractor group encompasses six distinct risks, each addressed by tailored preventive measures designed to minimize their impact on road infrastructure projects. Table 8 presents a detailed analysis of these risks, including the evaluation of their corresponding measures across four key criteria. These scores provide a structured comparison of the proposed measures, highlighting their strengths and areas for improvement. The results aim to guide the prioritization of actions to effectively manage contractor-related risks and ensure smoother project execution.

Table 8.
Risks and evaluation of preventive measures in the Contractor group.
The analysis of the mean Si and Si fuzzy scores for this group of preventive measures did not reveal any statistically significant differences. The independent samples t-test indicated no significant differences between the mean values (t = 0.572, p = 0.570). These findings suggest a similarity between the Si and Si fuzzy scores within this group of measures.
3.6. Evaluation of Preventive Measures in the Engineer Group
The Engineer group consists of six identified risks, each of which is addressed through specific preventive strategies aimed at mitigating their effects on project outcomes. Table 9 outlines these risks alongside the evaluation of their corresponding measures, which have been assessed based on four criteria.

Table 9.
Risks and evaluation of preventive measures in the Engineer group.
The results of the analysis for the penultimate group of preventive measures showed no statistically significant difference between the mean values of the Si and Si fuzzy scores. The independent samples t-test did not identify a statistically significant difference between the mean scores (t = −0.591, p = 0.557). The mean difference between the scores was −0.36371, with a 95% confidence interval ranging from −1.59185 to 0.86442. Based on these findings, it can be concluded that the Si and Si fuzzy scores are practically the same for this group.
3.7. Evaluation of Preventive Measures in the Project Group
The Project group encompasses 10 critical risks, reflecting challenges that impact the overall management and execution of road infrastructure projects. Table 10 provides an in-depth analysis of these risks and the associated preventive measures.

Table 10.
Risks and evaluation of preventive measures in the Project group.
For the last group of preventive measures, the statistical analysis results indicated no statistically significant difference between the mean values of the Si and Si fuzzy scores. The independent samples t-test showed t = 1.004, p = 0.317, and was not statistically significant. These results clearly suggest that the Si and Si fuzzy scores are consistent for this group as well.
4. Discussion
The dataset presents a detailed evaluation of the preventive measures across defined risk groups, capturing their scores for four key criteria: implementation costs, time required for application, complexity of application, and probability of success. Each measure is accompanied by its aggregated score (Si), calculated using the weighted coefficients assigned to each criterion. These coefficients reflect the relative importance of each criterion, ensuring a balanced and prioritized assessment.
The analysis revealed the most impactful preventive measures across different risk groups. Figure 2 highlights the top-ranked measures based on their weighted scores.
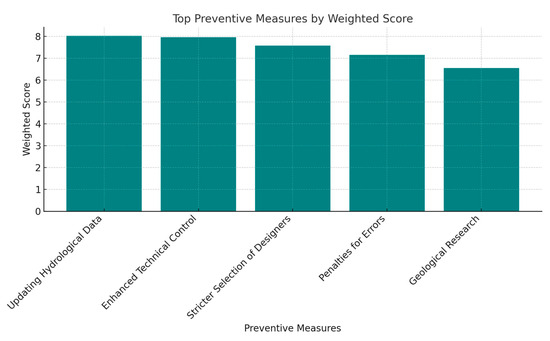
Figure 2.
Top preventive measures by weighted score.
This study demonstrates the application of a robust multi-criteria approach to prioritizing preventive measures in road infrastructure projects. The findings emphasize the importance of updating hydrological data, enhancing technical control, and using stricter selection processes for designers and contractors. By addressing critical risks, the model ensures better allocation of resources and reduces project inefficiencies.
However, the study is limited by the availability of data on small-scale projects and the representativeness of the expert panel. Future research could explore the application of this model to other types of infrastructure, such as pipelines and railways, and include a broader range of experts to validate findings. The established and selected preventive measures should be implemented in future projects, with continuous monitoring to evaluate how well these statistical insights align with real-world outcomes. While the identified risks are meticulously observed in actual projects, and the proposed measures are based on the expertise of highly experienced professionals, strategic implementation has not been carried out. Moreover, the impact of certain measures that were implemented has neither been systematically tracked nor assessed in real-world scenarios.
The proposed multi-criteria framework provides a practical tool for prioritizing preventive measures in road infrastructure projects. Key recommendations include integrating this model into the early planning phases, validating results through expert workshops, and expanding its use to other infrastructure domains. This approach not only improves risk management but also contributes to sustainable and efficient project execution.
The variations in scores across the different measures and criteria underscore the diversity in their practical and theoretical implications for risk management. Measures with high Si values generally combine moderate to high success probabilities with balanced costs, time, and complexity ratings, reflecting their overall feasibility and effectiveness. However, measures with lower Si values often indicate challenges in one or more criteria, such as high costs or extended implementation time, which may hinder their practical application despite their potential effectiveness.
Measures with disproportionately high costs or complexity may still be worth considering if their probability of success justifies the investment, particularly in critical risk scenarios.
The results also reveal insights into group-specific trends. For example, measures addressing risks in the Design and Resource groups often exhibit higher complexity and cost scores, reflecting the technical and resource-intensive nature of these areas. In contrast, measures in the External and Employer groups tend to prioritize faster and simpler implementation, aligning with the dynamic and organizational challenges in these domains.
4.1. Results and Industry Implications
The obtained results highlight the importance of ranking preventive measures based on criteria such as probability of success and implementation costs. For instance, measures like updating hydrometeorological data received high scores due to their direct link with reducing uncertainties in planning. Similarly, stricter selection of designers and contractors ensures better performance in later phases of the project.
The proposed model provides a clear decision-making framework that can benefit not only project managers but also policymakers. By integrating this model in the early planning phases, organizations can achieve significant savings by minimizing risks before they escalate. For example, in large-scale projects such as highways and bridges, prioritizing investments in highly ranked measures can reduce costs by 15–20%.
These findings also align with global trends in risk management, where quantitative decision-making methods are increasingly emphasized. The construction industry is progressively adopting multi-criteria analyses as a standard for evaluating complex problems, further underscoring the importance of the proposed model.
The application of high-ranked measures such as enhanced technical control can significantly contribute to medium-sized projects. For instance, in the construction of local roads, additional technical reviews before the start of construction reduce the likelihood of design errors, avoiding costly rework and delays.
Overall, implementing this model not only improves risk management processes but also contributes to the sustainability of infrastructure projects. A focus on prevention rather than remediation enables better planning and long-term savings, which is particularly critical in public projects with constrained budgets.
This study developed a multi-criteria framework for ranking preventive measures in infrastructure projects, specifically in the domain of transportation infrastructure. The findings highlight the importance of careful planning and decision making based on quantitative data. Top-ranked measures, such as updating hydrometeorological data and stricter technical controls, provide clear guidelines for enhancing efficiency and reducing risks.
4.2. Challenges to Implementing the Proposed Risk Management Practices
Road infrastructure projects play a crucial role in the economy of any country [40], but in practice, they face numerous diverse risks [41,42]. While the proposed risk management framework offers a comprehensive methodology for identifying, evaluating, and ranking preventive measures, its implementation in real-world projects may face several challenges. A key issue is aligning the diverse interests of stakeholders such as contractors, investors, regulatory bodies, and local communities, who often have conflicting priorities. The lack of consensus among these groups can delay decision making and hinder the execution of measures. Additionally, regulatory frameworks and legal requirements can vary significantly between countries or even regions within the same country. These requirements often necessitate adjustments to the proposed practices, potentially increasing implementation costs and timelines. For instance, legislative changes during a project’s lifecycle may require revisiting and revising selected measures, further complicating risk management efforts.
Resource limitations, including of financial, human, and material resources, also pose significant challenges. In projects with constrained budgets, implementing all proposed measures may not be feasible, necessitating further prioritization of actions that provide the highest cost–benefit ratio. Resistance to change within organizations accustomed to traditional project management approaches can also slow the adoption of innovative methods such as multi-criteria analyses. Insufficient training and a lack of understanding of the advantages of new approaches among key decision makers can further limit their application. Lastly, the quality and availability of qualitative and quantitative data, which are critical for the success of a multi-criteria framework, may be inconsistent, incomplete, or unavailable. This issue is particularly pronounced in projects implemented in regions with underdeveloped systems for data collection and processing. To overcome these challenges, it is recommended to establish clear communication channels among all stakeholders, ensure flexibility in adapting the methodology to local conditions, and provide continuous education and training for key actors. Additionally, developing more advanced systems for data collection and analysis can enhance the efficiency and reliability of the proposed practices.
4.3. Practical Recommendations
1. Implement the framework in planning phases: Organizations should integrate the multi-criteria framework into the initial planning stages to identify key preventive measures. High-ranking measures should be included in project specifications and contracts.
2. Prioritize investments in high-ranking measures: Stakeholders, including employers and project managers, should allocate resources according to the framework’s results. For instance, investing in stricter technical controls can directly reduce the likelihood of design errors.
3. Use the model for strategic decision making: The framework can be utilized to assess the impact of various strategies on projects of different sizes and complexities. Smaller projects can focus on quick and low-cost measures, while large infrastructure projects may rely on long-term strategies.
4. Develop training programs and standardize practices: Workshops and training sessions for engineers and managers are recommended to ensure proper implementation of the framework. Standardizing procedures for ranking preventive measures can improve consistency and efficiency across projects.
5. Monitor and evaluate implementation: Introducing a system to track the effects of the implemented preventive measures will enable continuous improvement in risk management processes. Regular updates to the framework’s input data will ensure its relevance and reliability over time.
The preventive measures evaluated by the experts yielded relatively similar overall scores, reflecting a high level of consensus in their assessments. This similarity arises from the shared criteria used in the evaluation process—implementation costs, time required for implementation, implementation complexity, and probability of success—which are universally relevant to decision making in project management. Despite the similarity in overall scores, the breakdown of evaluations by individual criteria provides significant added value. Such a detailed data structure will enable future project managers to go beyond aggregate scores and gain a nuanced view of each measure, allowing them to prioritize based on specific project needs. For instance, a manager with limited resources might focus on measures with lower implementation costs, while one working under time constraints could prioritize faster-to-implement solutions.
This study demonstrates the effectiveness of integrating MCDM and fuzzy logic as complementary approaches for evaluating and prioritizing preventive measures in road infrastructure projects. The combined methodology provides a robust and systematic framework, ensuring accurate analysis and validation of expert assessments. By offering practical insights and actionable strategies, this approach enhances decision making in risk management and supports the efficient allocation of resources. The findings of this research are highly applicable in both academic and practical contexts, contributing to the advancement of methodologies for mitigating risks in the construction industry.
Such a detailed data structure will enable future project managers to go beyond aggregate scores and gain a nuanced view of each measure, allowing them to prioritize based on specific project needs. For instance, a manager with limited resources might focus on measures with lower implementation costs, while one working under time constraints could prioritize faster-to-implement solutions. This flexibility ensures that the evaluation framework remains adaptable and practical for diverse project scenarios.
This granularity ensures that the evaluation system remains flexible and adaptable, enabling tailored decision making even when the overall scores do not show significant variation. Furthermore, the similarity in scores underscores the balance and feasibility of the measures, a testament to the rigorous consensus achieved through the Delphi method. By facilitating a detailed understanding of the strengths and trade-offs of each measure, this approach ensures that decision makers can align preventive strategies with the specific requirements of their projects. The result is a robust ranking system that not only reflects expert judgment but also empowers practical, context-sensitive applications in risk mitigation and resource allocation.
4.4. Specific Recommendations for Changes in Local Laws and Enforcement
To address regulatory gaps in road infrastructure projects, we recommend amendments to the law on planning and construction to obligate designers to correct project documentation defects within a clearly defined timeframe, with financial penalties for non-compliance. Additionally, the scope of professional liability insurance should be expanded to cover damage caused by delays or non-compliance in correcting these defects. Furthermore, safety standards for tunnels should be updated to align with modern fire protection requirements, distinguishing between new and existing infrastructure to ensure cost-effective implementation. Enforcement mechanisms should include stronger oversight by regulatory bodies, integration with public procurement eligibility, and targeted training programs to ensure compliance and capacity building among stakeholders.
4.5. Phased Technical Control During the Design Process
To address inefficiencies in the current practice, where technical control occurs only after the design phase, we propose integrating technical control into the design process itself through incremental reviews. This phased approach includes monthly reviews of completed project segments, providing early feedback to ensure compliance and reduce rework. Key benefits include improved quality, harmonization of project documentation, and faster approval timelines. By the final stage, project documentation has already been reviewed iteratively, streamlining the building permit process and fostering a collaborative relationship between designers and technical control teams.
5. Conclusions
The objectives outlined in this study have been successfully addressed through the development and application of a robust multi-criteria framework. This research contributes to both theoretical advancements and practical implementations, providing a universal and adaptable tool for risk management in infrastructure projects.
This study has systematically identified and prioritized preventive measures to mitigate risks in road infrastructure projects. By evaluating 302 preventive measures across 56 identified risks using a multi-criteria approach, we have highlighted key strategies that significantly contribute to reducing project delays and budget overruns. The highest-ranked measures, such as updating hydrometeorological and climate data, enforcing stricter selection criteria for designers, and ensuring thorough technical control of project documentation, offer practical solutions that can directly enhance the planning and execution phases of infrastructure projects.
Integrating these top-ranked preventive measures into standard risk management procedures is essential, particularly during the initial planning stages. Allocating resources based on the priorities established in this research can substantially improve project outcomes, especially in environments with constrained budgets. Implementing these measures will not only mitigate risks but also enhance the overall efficiency and success rate of infrastructure projects.
Training and educating project teams on the application of these high-impact preventive measures is crucial for consistent implementation. Such capacity-building efforts will ensure that the project teams are well equipped to apply the recommended strategies effectively, leading to long-term benefits for the infrastructure sector.
Future research should focus on applying this evaluation model to other types of infrastructure projects such as pipelines, railway systems, and energy infrastructure to validate its applicability and effectiveness across different contexts. Additionally, exploring the integration of advanced statistical methods and decision-making tools can further refine the prioritization process, providing even more robust frameworks for risk management in infrastructure development.
Future studies could also investigate the role of emerging technologies, such as Building Information Modeling (BIM), Artificial Intelligence (AI), and the Internet of Things (IoT), in enhancing real-time risk identification and mitigation strategies across various project phases. For instance, AI-driven models could predict risks based on historical data, while IoT-enabled monitoring could detect on-site hazards in real time. Moreover, these technologies can provide dynamic frameworks that adapt to changing project conditions, offering a more flexible and proactive approach to risk management.
Also, future research directions could focus on enhancing the predictive accuracy and applicability of risk models in road infrastructure projects. This includes refining methodologies for quantifying risks associated with cost overruns (ICP) and time extensions (EoT), incorporating dynamic factors such as changing economic conditions and other impacts. Additionally, developing hybrid models by combining advanced statistical techniques, machine learning algorithms, and fuzzy logic to improve risk assessment and cluster analysis could provide deeper insights into the interdependencies among risks and their impacts on project outcomes [43,44]. Such approaches would not only enhance risk prioritization but also enable tailored mitigation strategies for specific risk clusters. Moreover, investigating innovative strategies for risk mitigation and management, including early identification and proactive measures for high-priority risk clusters, could significantly enhance project efficiency and sustainability in real-world infrastructure development scenarios.
In conclusion, the adoption of the prioritized preventive measures identified in this study can significantly enhance risk mitigation efforts in road infrastructure projects. By systematically integrating these strategies into project planning and execution, stakeholders can achieve more reliable, timely, and cost-effective outcomes, thereby contributing to sustainable infrastructure development.
The consistency of the results among the experts was assessed using Cohen’s kappa coefficient, a statistical measure widely recognized for evaluating inter-rater reliability. The calculated kappa value of 0.834 indicates a very high level of agreement among the experts, significantly above the threshold for substantial agreement (0.61–0.80). This demonstrates the reliability of the evaluations and the robustness of the scoring process. The analysis was conducted using the SPSS statistical software, which ensured precise computation and facilitated the validation process. By employing this methodological approach, the study reinforced the credibility of the findings and provided a solid foundation for further analysis.
By addressing both theoretical gaps and practical challenges, the study establishes a foundation for future research and offers guidelines for standardizing risk management practices in the construction industry.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, M.D., M.I. and Z.S.; validation, A.S. and Z.S.; formal analysis, A.S., M.I. and M.D.; investigation, A.S.; resources, A.S.; data curation, A.S.; writing—original draft preparation, A.S., Z.S. and M.I., writing—review and editing, A.S., M.D., Z.S., M.I. and M.D.; visualization, M.D.; supervision, Z.S.; project administration, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting the reported results are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thomas, A.V.; Kalidindi, S.N.; Ganesh, L.S. Modelling and Assessment of Critical Risks in BOT Road Projects. Constr. Manag. Econ. 2006, 24, 407–424. [Google Scholar] [CrossRef]
- Dikmen, I.; Birgonul, M.T.; Han, S. Using Fuzzy Risk Assessment to Rate Cost Overrun Risk in International Construction Projects. Int. J. Proj. Manag. 2007, 25, 494–505. [Google Scholar] [CrossRef]
- Pehlivan, S.; Öztemir, A.E. Integrated Risk of Progress-Based Costs and Schedule Delays in Construction Projects. Eng. Manag. J. 2018, 30, 108–116. [Google Scholar] [CrossRef]
- Nguyen, P.H.D.; Robinson Fayek, A. Applications of Fuzzy Hybrid Techniques in Construction Engineering and Management Research. Autom. Constr. 2022, 134, 104064. [Google Scholar] [CrossRef]
- Chatterjee, K.; Zavadskas, E.K.; Tamošaitiene, J.; Adhikary, K.; Kar, S. A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry 2018, 10, 46. [Google Scholar] [CrossRef]
- Tan, T.; Mills, G.; Papadonikolaki, E.; Liu, Z. Combining Multi-Criteria Decision Making (MCDM) Methods with Building Information Modelling (BIM): A Review. Autom. Constr. 2021, 121, 103451. [Google Scholar] [CrossRef]
- Zavadskas, E.; Turskis, Z. Multi-Criteria Complex for Construction Profitability Analysis of Construction Projects; Technologija: Kaunas, Lithuania, 2011. [Google Scholar]
- Lee, J.; Jung, D.; Baek, C.; Hu, Y.-C.; Lin, M.-H.; Tsai, J.-F.; Nguyen, P.-H.; Lu, M.-T.; Lee, J.; Jung, D.; et al. An Analytical Study Predicting Future Conditions and Application Strategies of Concrete Bridge Pavement Based on Pavement Management System Database. Sustainability 2023, 15, 16680. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.S.; Kabli, M.R. Construction Projects Selection and Risk Assessment by Fuzzy AHP and Fuzzy TOPSIS Methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Tamošaitiene, J. Risk Assessment of Construction Projects. J. Civ. Eng. Manag. 2010, 16, 33–46. [Google Scholar] [CrossRef]
- Chan, H.K.; Wang, X. Fuzzy Hierarchical Model for Risk Assessment. In Fuzzy Hierarchical Model Risk Assess; Springer: London, UK, 2013. [Google Scholar] [CrossRef]
- Kuo, Y.C.; Lu, S.T. Using Fuzzy Multiple Criteria Decision Making Approach to Enhance Risk Assessment for Metropolitan Construction Projects. Int. J. Proj. Manag. 2013, 31, 602–614. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Tamosaitiene, J. Selection of Construction Enterprises Management Strategy Based on the SWOT and Multi-Criteria Analysis. Arch. Civ. Mech. Eng. 2011, 11, 1063–1082. [Google Scholar] [CrossRef]
- Chen, W.T.; Huang, Y.-H.; Wang, H.-H.; Abreu, A.; Topal, S.; Atasoylu, E. A Fuzzy Risk Assessment Model for Small Scale Construction Work. Sustainability 2022, 14, 4442. [Google Scholar] [CrossRef]
- Qi, Y.; Bai, M.; Song, L.; Wang, Q.; Tian, G.; Wang, C. Research on Risk Assessment Method for Land Subsidence in Tangshan Based on Vulnerability Zoning. Appl. Sci. 2023, 13, 12678. [Google Scholar] [CrossRef]
- Razi, P.Z.; Ali, M.I.; Ramli, N.I. AHP-based analysis of the risk assessment delay case study of public road construction project: An empirical study. J. Eng. Sci. Technol. 2019, 14, 875–891. [Google Scholar]
- Seresht, N.G.; Lourenzutti, R.; Salah, A.; Fayek, A.R. Overview of Fuzzy Hybrid Techniques in Construction Engineering and Management. In Fuzzy Hybrid Computing in Construction Engineering and Management: Theory and Applications; Emerald Publishing Limited: Leeds, UK, 2018; pp. 37–107. [Google Scholar] [CrossRef]
- Alvand, A.; Mirhosseini, S.M.; Ehsanifar, M.; Zeighami, E.; Mohammadi, A. Identification and Assessment of Risk in Construction Projects Using the Integrated FMEA-SWARA-WASPAS Model under Fuzzy Environment: A Case Study of a Construction Project in Iran. Int. J. Constr. Manag. 2023, 23, 392–404. [Google Scholar] [CrossRef]
- Tah, J.H.M.; Carr, V. A Proposal for Construction Project Risk Assessment Using Fuzzy Logic. Constr. Manag. Econ. 2000, 18, 491–500. [Google Scholar] [CrossRef]
- Shahbodaghlou, F.; Samani, B.A. A Fuzzy Systematic Approach to Construction Risk Analysis. J. Risk Anal. Cris. Response 2012, 2, 275–284. [Google Scholar] [CrossRef]
- Li, H.X.; Al-Hussein, M.; Lei, Z.; Ajweh, Z. Risk Identification and Assessment of Modular Construction Utilizing Fuzzy Analytic Hierarchy Process (AHP) and Simulation. Can. J. Civ. Eng. 2013, 40, 1184–1195. [Google Scholar] [CrossRef]
- Zhang, X.; Mohandes, S.R. Occupational Health and Safety in Green Building Construction Projects: A Holistic Z-Numbers-Based Risk Management Framework. J. Clean. Prod. 2020, 275, 122788. [Google Scholar] [CrossRef]
- Mahajan, V. The Delphi Method: Techniques and Applications; Enhanced Reader; SAGE Publications Sage CA: Los Angeles, CA, USA, 1976. [Google Scholar]
- Ameyaw, E.E.; Hu, Y.; Shan, M.; Chan, A.P.C.; Le, Y. Application of Delphi Method in Construction Engineering and Management Research: A Quantitative Perspective. J. Civ. Eng. Manag. 2016, 22, 991–1000. [Google Scholar] [CrossRef]
- Sourani, A.; Sohail, M. The Delphi Method: Review and Use in Construction Management Research. Int. J. Constr. Educ. Res. 2015, 11, 54–76. [Google Scholar] [CrossRef]
- Simić, N.; Ivanišević, N.; Nedeljković, Ð.; Senić, A.; Stojadinović, Z.; Ivanović, M. Early Highway Construction Cost Estimation: Selection of Key Cost Drivers. Sustainability 2023, 15, 5584. [Google Scholar] [CrossRef]
- Senić, A.; Dobrodolac, M.; Stojadinović, Z. Predicting Extension of Time and Increasing Contract Price in Road Infrastructure Projects Using a Sugeno Fuzzy Logic Model. Mathematics 2024, 12, 2852. [Google Scholar] [CrossRef]
- Senić, A.; Dobrodolac, M.; Stojadinović, Z. Development of Risk Quantification Models in Road Infrastructure Projects. Sustainability 2024, 16, 7694. [Google Scholar] [CrossRef]
- Dandage, R.; Mantha, S.S.; Rane, S.B. Ranking the Risk Categories in International Projects Using the TOPSIS Method. Int. J. Manag. Proj. Bus. 2018, 11, 317–331. [Google Scholar] [CrossRef]
- Dunn-Rankin, P.; Knezek, G.A.; Wallace, S.R.; Zhang, S. Scaling Methods, 2nd ed.; Psychology Press: London, UK, 2014; ISBN 9781135692940. [Google Scholar]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; O’Bryan, C.; Ni, Y.; Morley, C.D.; Taylor, C.R.; Angelini, T.E. Hydrogel Compression and Polymer Osmotic Pressure. Biotribology 2020, 22, 100125. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Ge, W.; Liu, X. Multi-Scale Methodology for Complex Systems. Chem. Eng. Sci. 2004, 59, 1687–1700. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Decision Making with the Analytic Network Process; Springer: Berlin/Heidelberg, Germany, 2013; p. 195. [Google Scholar] [CrossRef]
- Čubranić-Dobrodolac, M.; Jovčić, S.; Bošković, S.; Babić, D. A Decision-Making Model for Professional Drivers Selection: A Hybridized Fuzzy–AROMAN–Fuller Approach. Mathematics 2023, 11, 2831. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic Hierarchy Process: An Overview of Applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistics Notes: Cronbach’s Alpha. BMJ 1997, 314, 572. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Wang, G.; Li, G.; Pesce, G. Transport Infrastructure Connectivity and Conflict Resolution: A Machine Learning Analysis. Neural Comput. Appl. 2022, 34, 6585–6601. [Google Scholar] [CrossRef]
- Pešić, A.; Stephens, A.N.; Newnam, S.; Čičević, S.; Pešić, D.; Trifunović, A. Youth Perceptions and Attitudes towards Road Safety in Serbia. Systems 2022, 10, 191. [Google Scholar] [CrossRef]
- Trifunović, A.; Cicevic, S.; Pesic, D.; Samčović, A.; Markovic, V. Surveying Disadvantaged Children’s Traffic Safety Education in a Comparison between Paper and Electronic Methods: A Case Example for the Expanded Use of Educational Technology. Transp. Res. Rec. 2022, 2677, 401–417. [Google Scholar] [CrossRef]
- Kapatsa, C.; Kavishe, N.; Maro, G.; Zulu, S. The Identification of Sustainability Assessment Indicators for Road Infrastructure Projects in Tanzania. Sustainability 2023, 15, 14840. [Google Scholar] [CrossRef]
- Picardo, A.; Soltero, V.M.; Peralta, E. Life Cycle Assessment of Sustainable Road Networks: Current State and Future Directions. Buildings 2023, 13, 2648. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).