Abstract
A linear functional is classical if there exist polynomials and with and such that , where is a certain differential, or difference, operator. The polynomials orthogonal with respect to the linear functional are called classical orthogonal polynomials. In the theory of orthogonal polynomials, a correct characterization of the classical families is of great interest. In this work, on the one hand, we present the Laguerre constellation, which is formed by all the classical families for which , obtaining for all of them new algebraic identities such as structure formulas and orthogonality properties, as well as new Rodrigues formulas; on the other hand, we present a theorem that characterizes the classical families belonging to the Laguerre constellation.
Keywords:
recurrence relation; characterization theorem; classical orthogonal polynomials; Laguerre constellation MSC:
42C05; 33C45; 33D45
1. Introduction
Orthogonal polynomials associated with a measure on the real line, i.e.,
satisfy a three-term recurrence equation
where , and, according to the Favard theorem (cf. [1] (p. 21)), if for all , this recurrence completely characterizes such a polynomial sequence.
Due to the property of orthogonality of such a polynomial sequence, the following relation between the recurrence coefficients is well known:
where is the squared norm of .
Such a polynomial sequence is said to be classical if it is orthogonal with respect to a linear functional which fulfills the Pearson-type equation
where is a polynomial of degree at most 2, is a polynomial of degree 1, and is the differential operator in the continuous case, the forward or backward difference operator in the discrete case, and the Hahn operator in the q-discrete case.
Remark 1.
Note that if a linear functional fulfills (3), then it also fulfills the Pearson-type equation [2]
where we have the following:
- In the continuous case , so and .
- In the discrete case , , , .
- In the q-discrete case, , , and .
Definition 1.
The polynomial sequence belongs to the Laguerre constellation (in short, LC) if it is a classical orthogonal polynomial sequence and or .
The so-called characterization theorems play a fundamental role, i.e., the theorems which collect those properties that completely define and characterize the classical orthogonal polynomials. One of the many ways to characterize a family of continuous classical polynomials (Hermite, Laguerre, Jacobi, and Bessel), which was first posed by R. Askey and proved by W. A. Al-Salam and T. S. Chihara [3] (see also [4]), is the structure relation
where .
A. G. Garcia et al. proved in [5] that the relation (4) also characterizes the discrete classical orthogonal polynomials (Hahn, Krawtchouk, Meixner, and Charlier polynomials) when the forward replaces the derivative difference operator .
Later on, J. C. Medem et al. [6] characterized the orthogonal polynomials which belong to the q-Hahn class by a structure relation obtained from (4), replacing the derivative by the q-difference operator (see also [7,8,9]). One of the most general characterization theorems for the q-polynomials in the q-quadratic lattice was given in [10].
The structure of this work is the following: in Section 2, we introduce some notations and definitions used throughout the paper. In Section 3 we present the main results of the polynomials that belongs to the Laguerre constellation and the algebraic properties supporting the presented results. In Section 4, we present the specific identities about the different families of the Laguerre constellation. In Appendix A several Wolfram Mathematica® codes used to obtain the different expressions presented in this work are included.
2. Preliminaries
In this section, we give a brief survey of the operational calculus that we will use as well as some basic notations that we will need in the rest of this work.
2.1. Basic Concepts and Results
We adopt the following set notations: , and we use the sets , , , which represents the integers, real numbers, and complex numbers, respectively. Let be the linear space of polynomial functions in (in the following, we will refer to them as polynomials) with complex coefficients, and be its algebraic dual space, i.e., is the linear space of all linear maps . In the following, we will call the elements of functionals. In general, we represent the action of a linear functional over a polynomial by
Therefore, a functional is completely determined by a sequence of complex numbers , , the so-called moments of the functional.
Definition 2.
Let be a linear functional. We say that is a quasi-definite functional if there exists a polynomial sequence which is orthogonal with respect to , i.e.,
where is the Kronecker delta.
In order to obtain our derived identities, we rely on properties of the shifted factorial, or Pochhammer symbol, , and the q-shifted factorial, or q-Pochhammer symbol, . For any , a, , the shifted factorial is defined as
and the q-shifted factorial is defined as
We also use the following common notational product conventions:
The hypergeometric series , where , is defined by the series ([11], (1.4.1))
and the basic hypergeometric series is defined by the series as ([11], (1.10.1))
Observe that both hypergeometric and basic hypergeometric series are entire functions of z if , are convergent for for , and are divergent if and unless it terminates.
Note that when we refer to a hypergeometric or basic hypergeometric function with arbitrary argument z, we mean that the argument does not necessarily depend on the other parameters, namely, the ’s, ’s. However, for the arbitrary argument z, it very well may be that the domain of the argument is restricted, such as for .
The next theorem [1] (p. 8) is useful if one works with linear functionals.
Theorem 1.
Let be a linear functional with moments . is quasi-definite if and only if the Hankel determinants ,
2.2. Definition of the Operators in and
Next, we will define the backward and forward difference operators as well the so-called q-derivative operator, or Hahn operator:
Since the polynomial sequences depend on n, x and their parameters, and we are going to focus more on the variable n along this work (n as a discrete variable) than in the variable x, we need to also consider in the paper the operators and that are defined analogously as the operators and ∇, i.e.
Definition 3.
Let and , and let , and be the linear functionals defined by
Notice that we use the same notation for the operators on and . Whenever it is not specified the linear space where an operator acts, it is understood that it acts on the polynomial space .
3. The Laguerre Constellation
In this section, we present several identities that the polynomials belonging to LC fulfill. First, we show some theoretical aspects and the results related to them.
Lemma 1.
Let be a quasi-definite classical functional, and let be the polynomial sequence orthogonal with respect to . If belong to the LC, then there exists a numerical sequence so that fulfills the recurrence relation (1) for which and for all , where c is a root of , or .
Proof.

To prove this result, it is enough to consider all the families of the hypergeometric orthogonal polynomials scheme and the basic hypergeometric orthogonal polynomials scheme (see [6,11,12]) that are of the Laguerre type, i.e., or . These families are the Laguerre (L), Charlier (C), Meixner (M), big q-Laguerre (bqL), q-Meixner (qM), little q-Laguerre (lqL), q-Laguerre (qL), q-Charlier (qC), Stieltjes–Wigert (SW), and the 0-Laguerre/Bessel (0LB) polynomials
Once we obtain all the families belonging to LC, it is enough to verify that the conditions established for each of the families (see Table 1) are satisfied. Observe that the value of , where c is a zero of or , is known (see [13,14]), and these values are non-zero, so one can define as . □

Table 1.
Essential data of the families belonging to the Laguerre constellation.
Remark 2.
Note that Lemma 1 is not a characterization theorem since other families of the basic hypergeometric orthogonal polynomials scheme fulfill the condition about the recurrence coefficients (RCs), i.e., is a constant; however, they do not belong to the LC, for example, the Askey–Wilson polynomials (see [11] (14.1.4)).
In the next result, we write the recurrence relation as a structure-type relation on n.
Lemma 2.
Let be a polynomial sequence that belongs to the Laguerre constellation. For any , the recurrence relation (1) can be written as
if , and
if .
Proof.
Let us assume that , i.e., , then by Lemma 1, we have that the coefficients of the recurrence relation (1) fulfill , then, rewriting the recurrence assuming this relation, the result holds. The case is analogous. □
Remark 3.
For the sake of convenience, we replace by assuming that . In the case that and , then one must replace ϕ by in the further results since such identities and results hold similarly.
We write the recurrence relation in the next result as a Sturm–Liouville form difference equation on n.
Lemma 3.
Let be a polynomial sequence that belongs to the Laguerre constellation. For any , the recurrence relation (1) can be written as
Proof.
Theorem 2.
Let be a polynomial sequence that belongs to the Laguerre constellation. For any , the sequence is orthogonal with respect to , and the sequence is orthogonal with respect to .
Proof.
Let us fix such that . By Korovkin’s Theorem (see [15] or [16] (Theorem 2.1)), we have the following closure relation:
where is the weight function and both the left- and right-hand sides should be treated as distributions. From this expression, using (13) and Abel’s lemma on partial sums [17] (p. 313) for , we obtain
Moreover,
The proof for the sequence is analogous. Hence, the result follows. □
Remark 4.
Since we have the data for all the families which belong to the LC, it is a straightforward calculation to check that (since ) and
Remark 5.
Observe that the previous result does not characterize families belonging to LC since, for example, for the Jacobi polynomials, the following identity holds:
and in such a case .
Theorem 3
(Characterization Theorem). Let be an orthogonal polynomial sequence with respect to ω such that . For any such that , the following statements are equivalent:
- 1.
- belongs to the Laguerre constellation.
- 2.
- The polynomial sequence fulfills the second-order difference equationwhich is equal to its discrete structure-type relation.
- 3.
- The polynomial sequence satisfies the Sturm–Liouville difference equations
Proof.
since the 2nd item is the recurrence relation in such a case. is a consequence of Lemma 3. □
4. The Families
In this section, we present several identities related to the different families that belong to LC. Since there are some relation among them (see Figure 1), we present such identities only for some of the families in order to avoid duplicates. We consider the Laguerre, Meixner, Charlier, big q-Laguerre, little q-Laguerre and Stieltjes–Wigert cases.
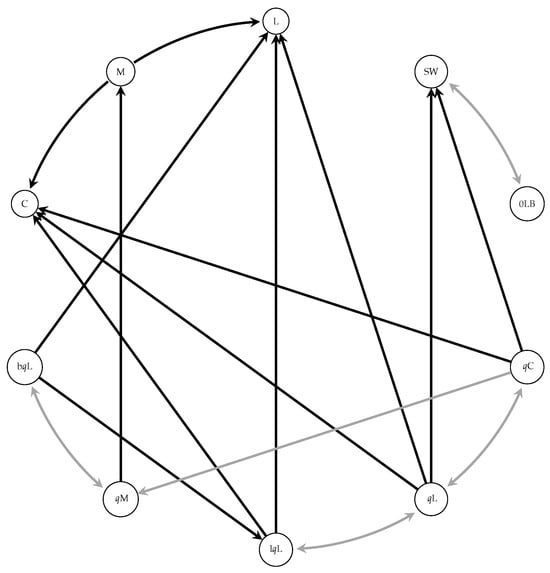
Figure 1.
Relations between the families in the Laguerre constellation. The gray lines are the particular cases. The black lines are the limiting cases.
Before presenting the main results, let us show the relations between the families we are going to consider with respect to the rest of the families that belong to LC (see [18] (p. 20), [11] remark (p. 526)):
where denote the 0-Laguerre/Bessel polynomials (see [12,19] (p. 244)).
4.1. The Laguerre Poynomials
The Laguerre polynomials can be written in terms of hypergeometric series as [11] (§9.12)
In this case, , i.e., this family belongs to the Laguerre constellation where the zero of is , and . Taking this into account, we can state the following result.
Lemma 4.
For any and any , the following identities hold:
where , and .
Proof.
These identities can be checked by identifying the polynomial coefficients on the left- and right-hand sides of each identity. Hence, the results follow. □
A direct consequence of the former result is stated as follows.
Theorem 4.
For any , any , , and any , the polynomial sequence is orthogonal with respect to the certain moment functional.
Proof.
By combining (21)–(23), we have the following second-order difference equations:
which is connected with the Charlier polynomials case (see [11], (9.14.5)). Using the theory of discrete Sturm–Liouville and assuming that for any , in this case, is variable, and the rest of the elements are fixed, the result holds. □
Remark 6.
Observe that one can construct, under certain condition on α and x, certain integral representation for such a moment functional.
From Lemma 4, we can deduce some new identities related to the Laguerre polynomials.
Theorem 5.
For any , and any , the following Rodrigues-type identities hold:
Proof.
The first identity holds by mathematical induction on k after a straightforward simplification and using (20) written in the following way:
The second identity holds by mathematical induction on k after a straightforward simplification and using (22) written in the following way:
The third identity holds by mathematical induction on k after a straightforward simplification and using (23) written in the following way:
The fourth and the fifth relations hold from (18) and (21). □
The last result, but not least interesting, concerning the operators associated with the Laguerre polynomials is as follows.
Proposition 1.
The Laguerre polynomials fulfill the following identity:
Proof.
The identity follows using the identities:
applying the first twice, and later the second one once, mapping . □
4.2. The Charlier Polynomials
The Charlier polynomials can be written in terms of hypergeometric series as [11] (§9.14)
In this case, and , i.e., , and . Taking this into account, we can state the following result.
Lemma 5.
For any and any , the following identities hold:
Proof.
(34) is a direct consequence of the identity presented in Remark in [11] (p. 249)
The other identities can be checked by identifying the polynomial coefficients on the left- and right-hand sides of each identity. Hence, the results follow. □
From Lemma 5, we can deduce some new identities related to the Charlier polynomials.
Theorem 6.
For any , and any , the following Rodrigues-type identities hold:
Proof.
The first identity is a direct consequence of (33), and the second is due to the following identity:
□
4.3. The Meixner Polynomials
The Meixner polynomials can be written in terms of hypergeometric series as [11] (§9.10)
In this case, and , and therefore we must consider two cases, , and , for which we have , and . Taking into account Lemma 1, we can state the next result.
Lemma 6.
The polynomial sequence fulfills the recurrence relation
with initial condition ,
and fulfills the second-order difference equation
As in the Laguerre polynomial case, the next result follows.
Lemma 7.
For any , , , and any , the following identities hold:
Proof.
These identities can be checked by identifying the polynomial coefficients on the left- and right-hand sides of each identity and with the help of Wolfram Mathematica 13®. □
A direct consequence is the fact that this polynomial sequence is orthogonal with respect to the parameter .
Theorem 7.
For any , with , any , , and any , the polynomial sequence is orthogonal with respect to a certain moment functional.
Proof.
By combining (42)–(44), we have the following second-order difference equations:
which is connected with the continuous-Hahn-polynomials case (see [11] (9.4.5)). Using the theory of discrete Sturm–Liouville and assuming that for any , in this case, is variable, and the rest of the elements are fixed, the result holds. □
Remark 7.
Note that in [20], the authors extend the orthogonality relations for the Meixner polynomials through the orthogonality relations of the continuous Hahn polynomials.
Observe that one can construct, under certain conditions for the parameters n and x, a certain integral representation for such a moment functional.
From Lemma 7, we can deduce some new identities related to the Meixner polynomials.
Theorem 8.
For any , and any , the following Rodrigues-type identities hold:
Proof.
The first identity holds by mathematical induction on k after a straightforward simplification and using (39). The second identity holds by mathematical induction on k after a straightforward simplification and using (41) written in the following way:
The third identity holds by mathematical induction on k after a straightforward simplification and using (42). The fourth and the fifth relations hold from (45). □
The last result concerning the operators associated with the Meixner polynomials is as follows.
Proposition 2.
The following identity holds:
Proof.
The proof follows after using an algorithm written in Wolfram Mathematica13®. □
4.4. The Big q-Laguerre Polynomials
The big q-Laguerre polynomials can be written in terms of basic hypergeometric series as [11] (§14.11)
In this case, and , i.e., , and . Observe that these polynomials are symmetric in the parameters a and b. Taking this into account, we can state the following result.
Lemma 8.
For any , and any , the following identities hold:
where and are the big q-Laguerre recurrence relation coefficients (see Table 1), and
Proof.
These identities can be checked by identifying the polynomial coefficients on the left- and right-hand sides of each identity and with the help of Wolfram Mathematica 13®. □
A direct consequence is the fact that this polynomial sequence is orthogonal with respect to the parameters a and b.
Theorem 9.
For any , any , , and any , the polynomial sequences and are orthogonal with respect to a certain moment functional.
Proof.
By combining (55)–(57), we have the following second-order difference equations:
where , and , which is connected with the big q-Jacobi polynomials case (see [11] (14.5.5)). By using the theory of Sturm–Liouville, the result holds. The result also holds for the parameter b by symmetry. □
From Lemma 8, we can deduce some new identities related to the big q-Laguerre polynomials.
Theorem 10.
For any , and any , the following Rodrigues-type identities hold:
Proof.
The identities hold by mathematical induction on k after a straightforward simplification and using (52) and (55). □
The last result concerning the operators associated with the big q-Laguerre polynomials is as follows.
Proposition 3.
The following identity holds:
where the polynomial coefficients are
Proof.
The proof follows after using an algorithm written in Wolfram Mathematica 13®. □
4.5. The Little q-Laguerre/Wall Polynomials
The little q-Laguerre polynomials can be written in terms of basic hypergeometric series as [11] (§14.20)
In this case, and , i.e., , and . Taking this into account, we can state the following result.
Lemma 9.
For any , and any , the following identities hold:
Proof.
These identities can be checked by identifying the polynomial coefficients on the left- and right-hand sides of each identity and with the help of Wolfram Mathematica 13®. □
A direct consequence is the fact that this polynomial sequence is orthogonal with respect to the parameter a.
Theorem 11.
For any , any , , and any , the polynomial sequence is orthogonal with respect to a certain moment functional.
Proof.
By combining (55)–(57), we have the following second-order difference equations:
where , and , which is connected with the big q-Laguerre polynomials case (see [11] (14.11.5)). Using the theory of discrete Sturm–Liouville and assuming that for any , in this case, a is variable, and the rest of the elements are fixed, the result holds. □
The last result concerning the operators associated with the little q-Laguerre polynomials is as follows.
Proposition 4.
The following identity holds:
where the polynomial coefficients are
Proof.
The proof follows after using an algorithm written in Wolfram Mathematica 13®. □
4.6. The Stieltjes–Wigert Polynomials
These polynomials can be written in terms of basic hypergeometric series as [11] (§14.21)
In this case, and , i.e., , and . Taking this into account, we can state the following result.
Lemma 10.
For any , the following identities hold:
From Lemma 10, we can deduce some a new identities related to the Stieltjes–Wigert polynomials.
Theorem 12.
For any , the following Rodrigues-type identities hold:
Proof.
The first identity holds by mathematical induction on k after a straightforward simplification and using (71).
The second identity holds by mathematical induction on k after a straightforward simplification and using (72) written in the following way:
□
The last result concerning the operators associated with the Stieltjes–Wigert polynomials is as follows.
Proposition 5.
The following identity holds:
Proof.
The proof follows after using an algorithm written in Wolfram Mathematica 13®. □
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Code in Wolfram Mathematica® to Check the Identities
We present the different codes we can use to check all the identities presented in this work. Let us start with expression (18):
- 1
- Table[LaguerreL[n,a,x]-LaguerreL[n-1,a,x]-LaguerreL[n,a-1,x],{n,1,6}]//Factor
One can check this for all the terms as one desires; using similar expressions, one can check (22) and (23) and the rest of the expressions where one uses the operators or .
In an analogous way, one can check, for instance, (42):
- 1
- mep[n_,b_,c_,x_]:=Hypergeometric2F1[-n,-x,b,1-1/c];Table[mep[n,b,c,x]-mep[n,b-1,c,x]-x n(c-1)/(b-b^2)/c mep[n-1,b+1,c,x-1],{n,1,6}]//Factor
One can check identity used in the proof of Theorem 6:
- 1
- chp[n_,a_,x_]:=HypergeometricPFQ[{-n,-x},{},-1/a];Table[a^{n+1}/(n+1)! chp[n+1,a,x]-a^n/n! chp[n,a,x]-a^{n+1}/(n+1)! chp[n+1,a,x+1],{n,1,6}]//Factor
We also use different codes to know what kind of expression we expect
- 1
- m:=4; Solve[CoefficientList[mep[m+1,b,c,x]-mep[m, b, c, x]-(Ax+B)mep[m,bb,c,x-dd],x]==Table[0,{i,1,m+2}],{A,B,bb,dd}]
obtaining in such a case
- 1
- {{A ->(-1+c)/(bc), B->0, bb->1+b, dd->1}}
Let us finish this sequence of expressions with the only challenging one related to the big q-Laguerre polynomial expression, Proposition 3:
- 1
- dfqu[k_,f_]:=If[k==0,f,If[k==1,Return[((f/.{x->q x})-f)/(qx-x)],Return[dfqu[k-1,dfqu[1,f]]]]];
- 2
- bqLp[n_,a_,b_,x_]:=QHypergeometricPFQ[{q^{-n},0,x},{a q,b q},q,q];
- 3
- AAbqL[k_,a_,b_,x_]:=A[k]bqLp[k+1,aq,bq,Bx]-Sum[AAbqL[l,a,b,x]dfqu[l,bqLp[k,a,b,x]],{l,0,k-1}])/dfqu[k,bqLp[k,a,b,x]]//FunctionExpand// Factor
By using the Solve and coefficientList former algorithm modified to be used for the big q-Laguerre polynomials one used previously, one can obtain the leading term , and assuming the expression should be finite, it is not hard to obtain .
References
- Chihara, T.S. An Introduction to Orthogonal Polynomials; Mathematics and its Applications; Mathematics and its Applications, Reprinted by Dover Publications; Gordon and Breach Science Publishers: New York, NY, USA; London, UK; Paris, France, 1978; Volume 13. [Google Scholar]
- Costas-Santos, R.S.; Moreno-Balcázar, J.J. The semiclassical Sobolev orthogonal polynomials: A general approach. J. Approx. Theory 2011, 163, 65–83. [Google Scholar] [CrossRef]
- Al-Salam, W.A.; Chihara, T.S. Another characterization of the classical orthogonal polynomials. SIAM J. Math. Anal. 1972, 3, 65–70. [Google Scholar] [CrossRef]
- Marcellán, F.; Branquinho, A.; Petronilho, J. Classical orthogonal polynomials: A functional approach. Acta Appl. Math. 1994, 34, 283–303. [Google Scholar] [CrossRef]
- García, A.G.; Marcellán, F.; Salto, L. A distributional study of discrete classical orthogonal polynomials. In Proceedings of the Fourth International Symposium on Orthogonal Polynomials and Their Applications, Evian-Les-Bains, France, 19–23 October 1992; Volume 57, pp. 147–162. [Google Scholar] [CrossRef]
- Medem, J.C.; Nodarse, R.Á.; Marcellán, F. On the q-polynomials: A distributional study. J. Comput. Appl. Math. 2001, 135, 157–196. [Google Scholar] [CrossRef]
- Alfaro, M.; Nodarse, R.Á. A characterization of the classical orthogonal discrete and q-polynomials. J. Comput. Appl. Math. 2007, 201, 48–54. [Google Scholar] [CrossRef]
- Nodarse, R.Á. On characterizations of classical polynomials. J. Comput. Appl. Math. 2006, 196, 320–337. [Google Scholar] [CrossRef]
- Nodarse, R.Á.; Arvesú, J. On the q-polynomials in the exponential lattice x(s)=c1qs+c3. Integral Transform. Spec. Funct. 1999, 8, 299–324. [Google Scholar] [CrossRef]
- Costas-Santos, R.S.; Marcellan, F. q-classical orthogonal polynomials: A general difference calculus approach. Acta Appl. Math. 2010, 111, 107–128. [Google Scholar] [CrossRef]
- Koekoek, R.; Lesky, P.A.; Swarttouw, R.F. Hypergeometric Orthogonal Polynomials and Their q-Analogues; With a foreword by Tom H. Koornwinder; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Nikiforov, A.F.; Uvarov, V.B. Polynomial solutions of hypergeometric type difference equations and their classification. Integral Transform. Spec. Funct. 1993, 1, 223–249. [Google Scholar] [CrossRef]
- Koepf, W.; Masjed-Jamei, M. A generic formula for the values at the boundary points of monic classical orthogonal polynomials. J. Comput. Appl. Math. 2006, 191, 98–105. [Google Scholar] [CrossRef][Green Version]
- Petronilho, J. Generic formulas for the values at the singular points of some special monic classical Hq,ω-orthogonal polynomials. J. Comput. Appl. Math. 2007, 205, 314–324. [Google Scholar] [CrossRef][Green Version]
- Korovkin, P.P. Linear Operators and Approximation Theory; Russian Monographs and Texts on Advanced Mathematics and Physics; (Translated from the Russian ed. (1959)); Gordon and Breach Publishers, Inc.: New York, NY, USA; Hindustan Publishing Corp.: Delhi, India, 1960; Volume III. [Google Scholar]
- Ismail, M.E.H.; Zhang, R.; Zhou, K. q-fractional Askey-Wilson integrals and related semigroups of operators. Phys. D Nonlinear Phenom. 2022, 442, 133534. [Google Scholar] [CrossRef]
- Knopp, K. Theory and Application of Infinite Series; Blackie & Sons: London, UK, 1928; Volume XII, 571p. [Google Scholar]
- Christiansen, J.S. Indeterminate Moment Problems Within the Askey-Scheme. Master’s Thesis, University of Copenhagen, Copenhagen, Denmark, 2004. [Google Scholar]
- Álvarez Nodarse, R.; Medem, J.C. q-classical polynomials and the q-Askey and Nikiforov-Uvarov tableaus. J. Comput. Appl. Math. 2001, 135, 197–223. [Google Scholar] [CrossRef]
- Costas-Santos, R.S.; Sánchez-Lara, J.F. Extensions of discrete classical orthogonal polynomials beyond the orthogonality. J. Comput. Appl. Math. 2009, 225, 440–451. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).