Application of Evolutionary Game to Analyze Dual-Channel Decisions: Taking Consumer Loss Aversion into Consideration
Abstract
1. Introduction
2. Literature Review
3. Research Methods
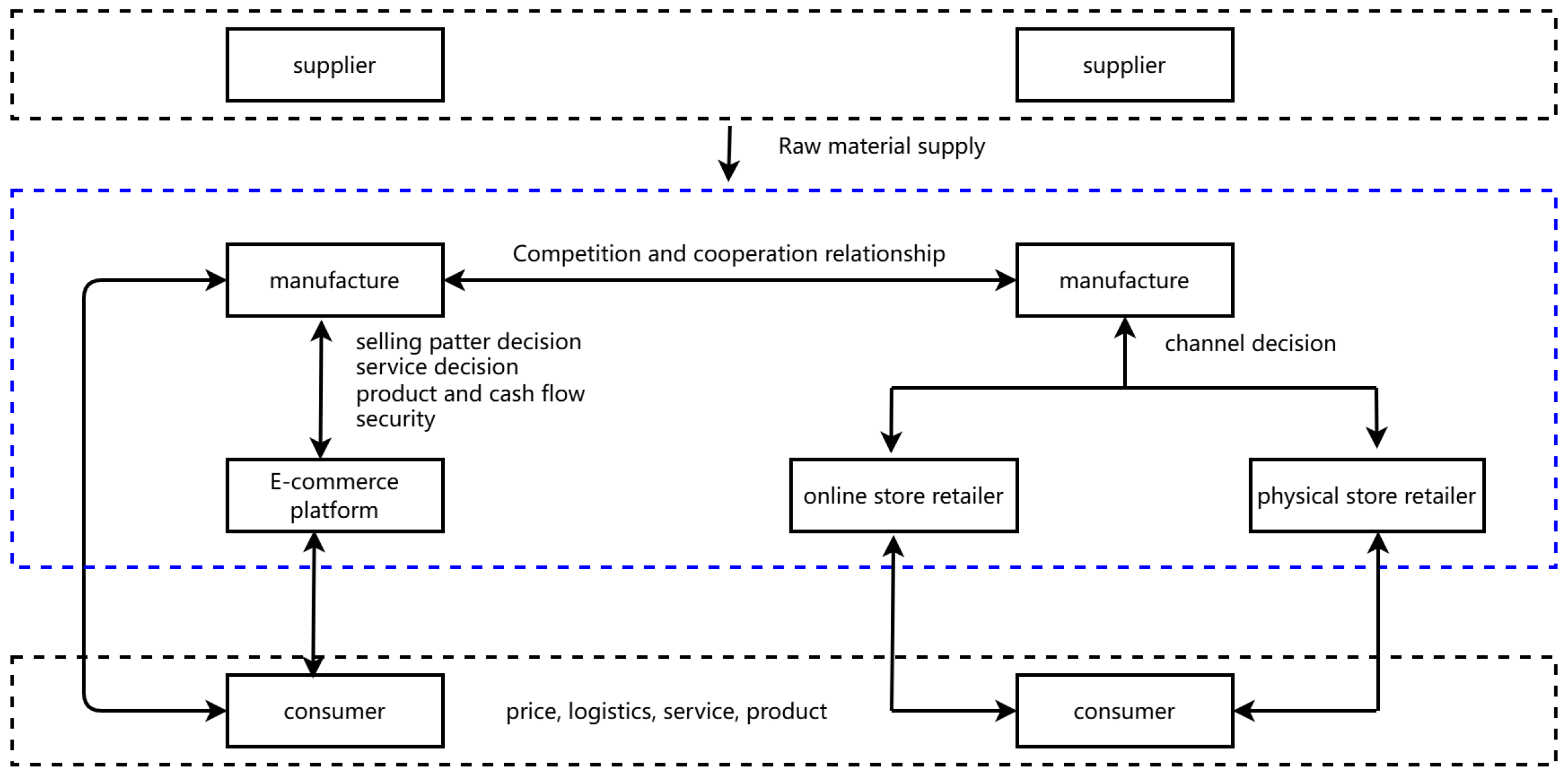
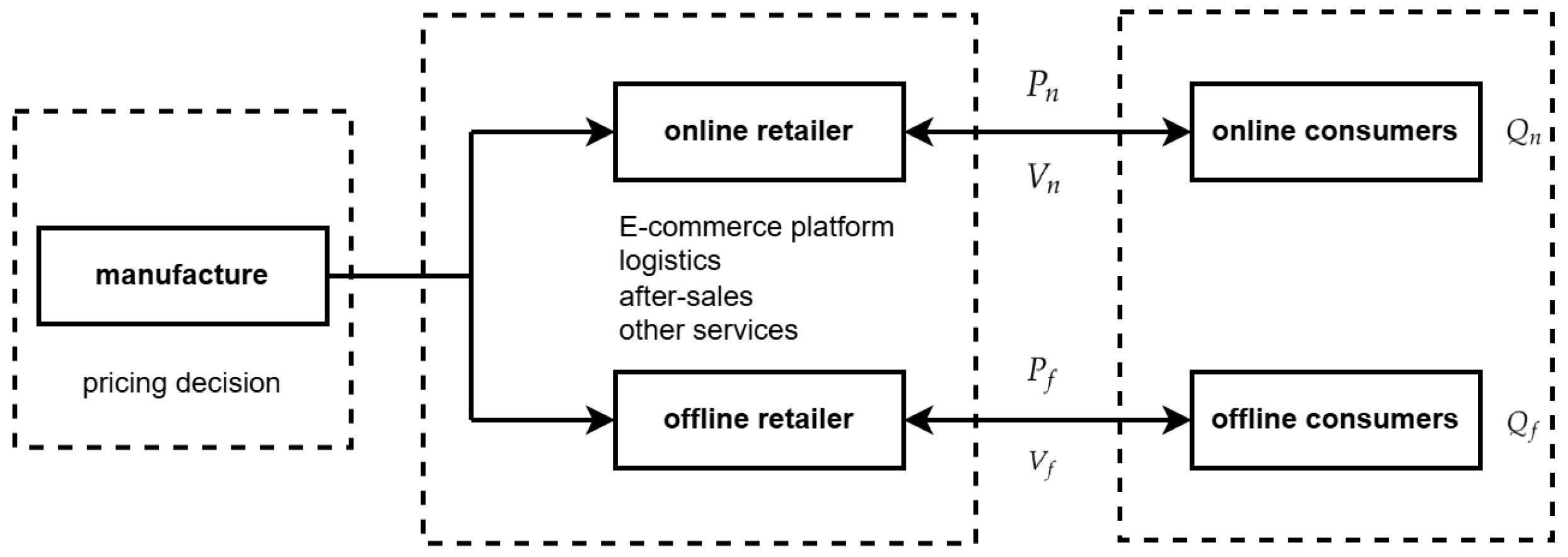
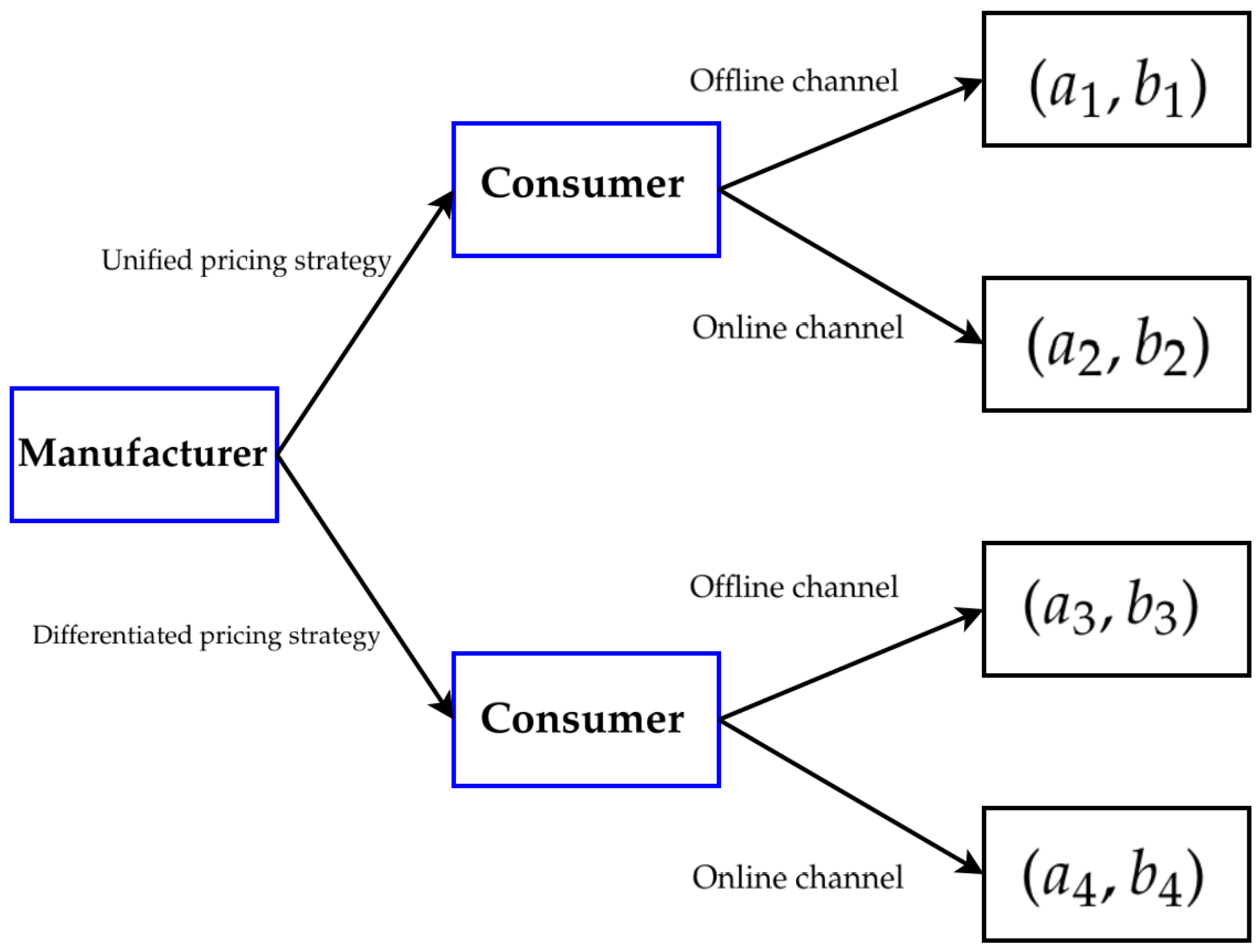
3.1. Model Descriptions and Assumptions
3.2. The Payoff for Each Player
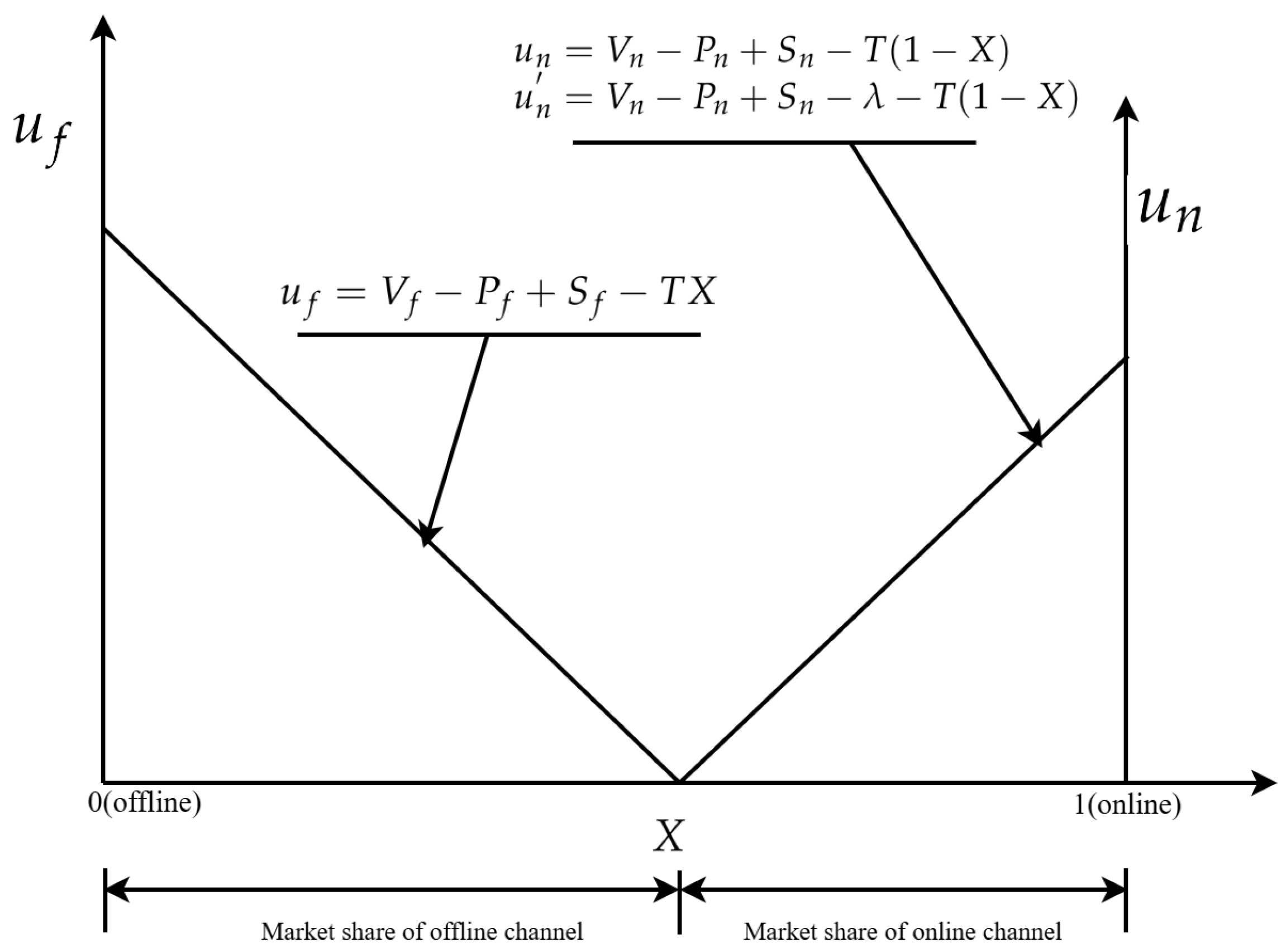
3.2.1. Market Share and Profit Calculation Based on Consumer Loss Aversion and the Hotelling Model
3.2.2. The Payoff of the Evolutionary Game Between Manufacturers and Consumers
3.3. Solutions and Analysis of the Evolutionary Game
4. Results and Discussion
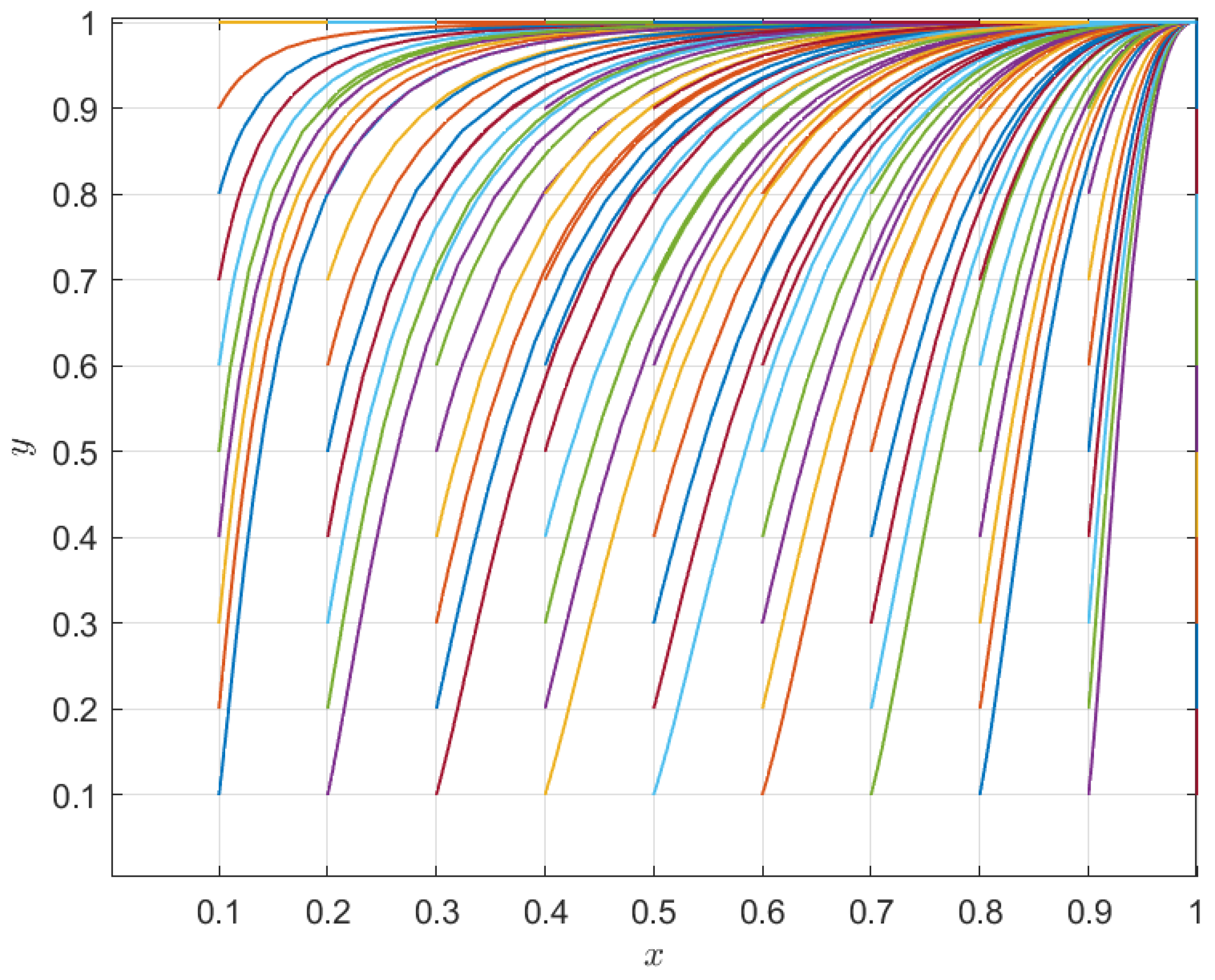
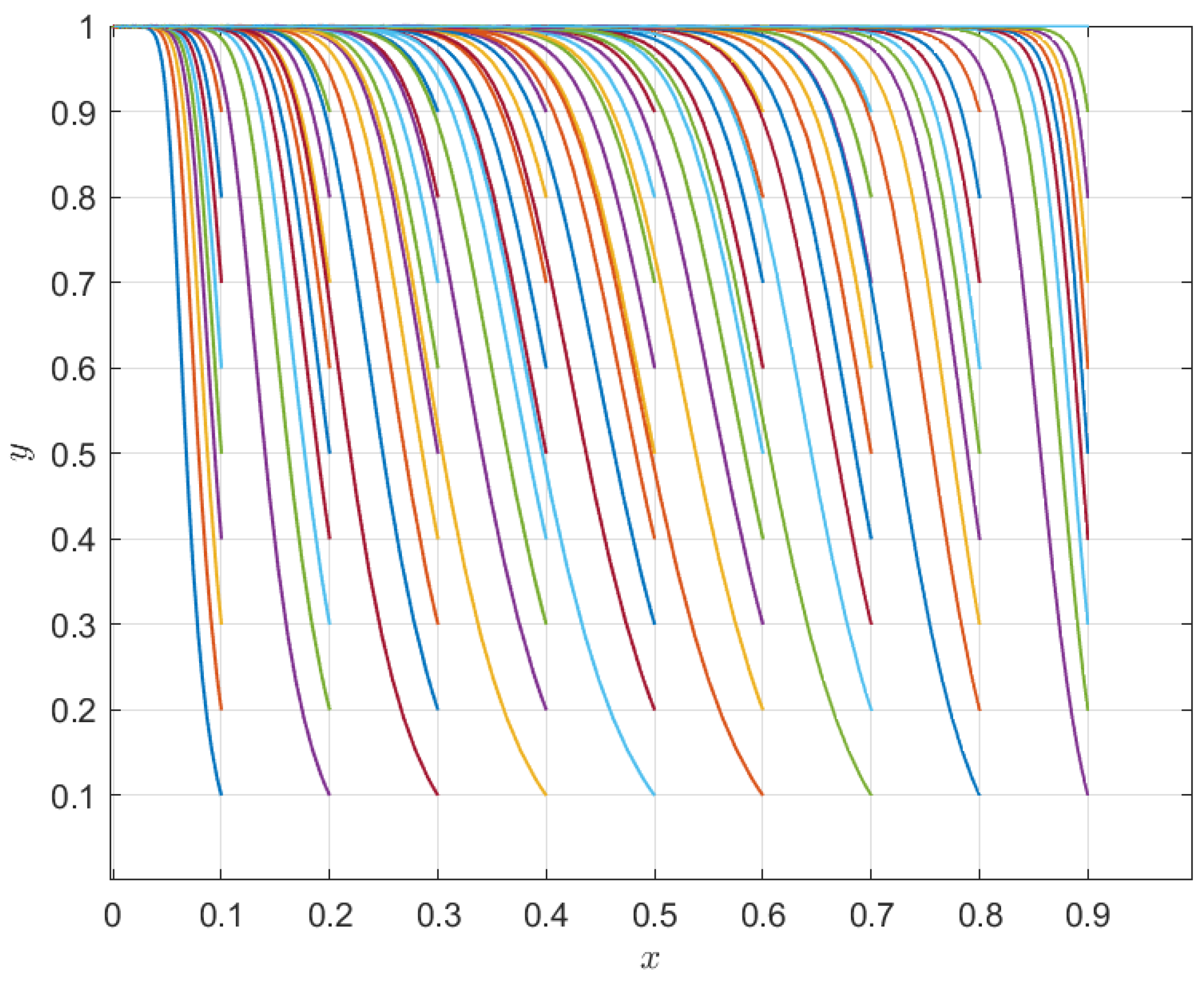
4.1. Simulation
4.2. Parameter Sensitivity Analysis
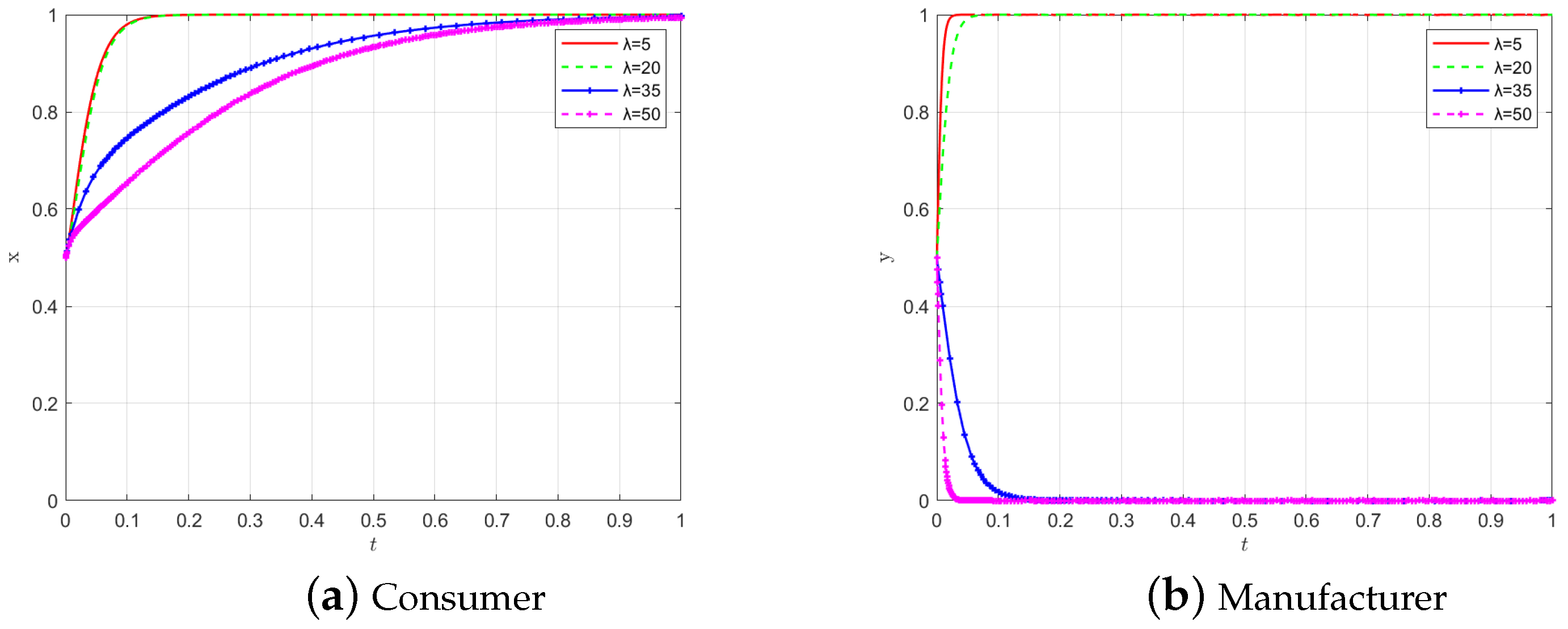
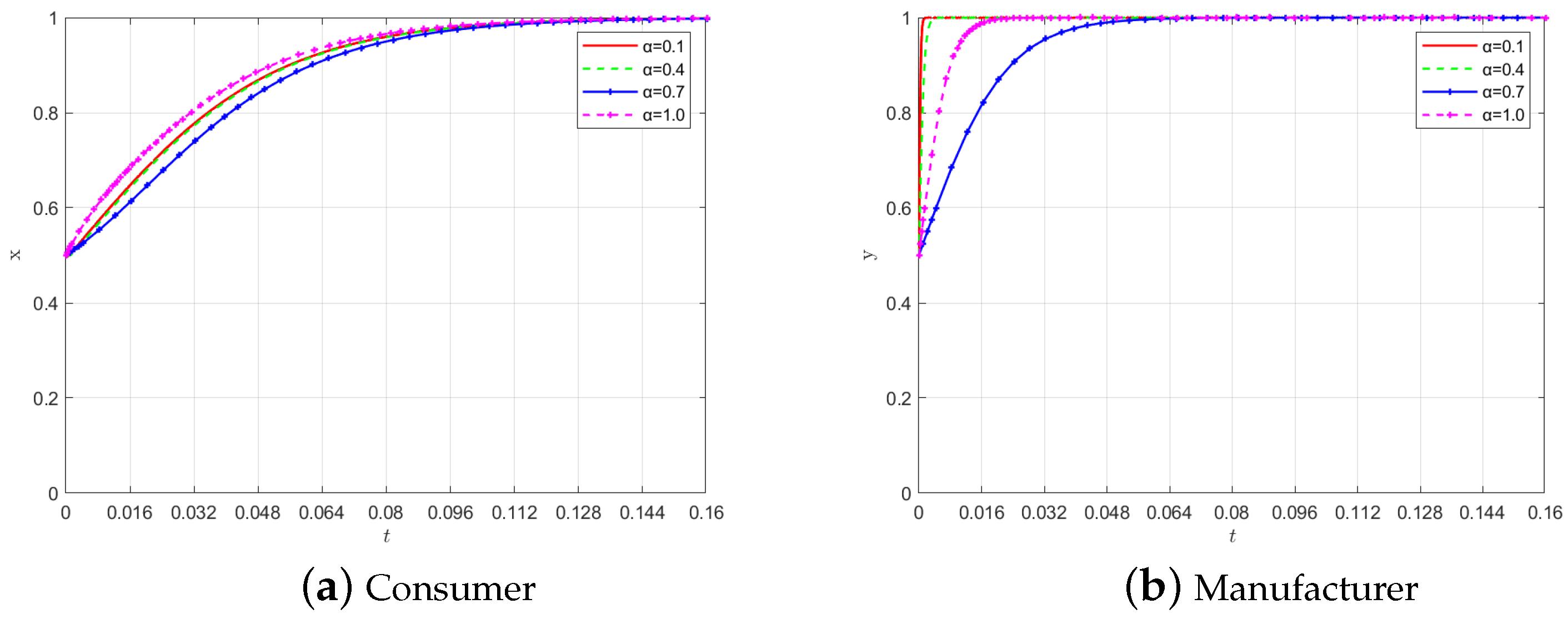
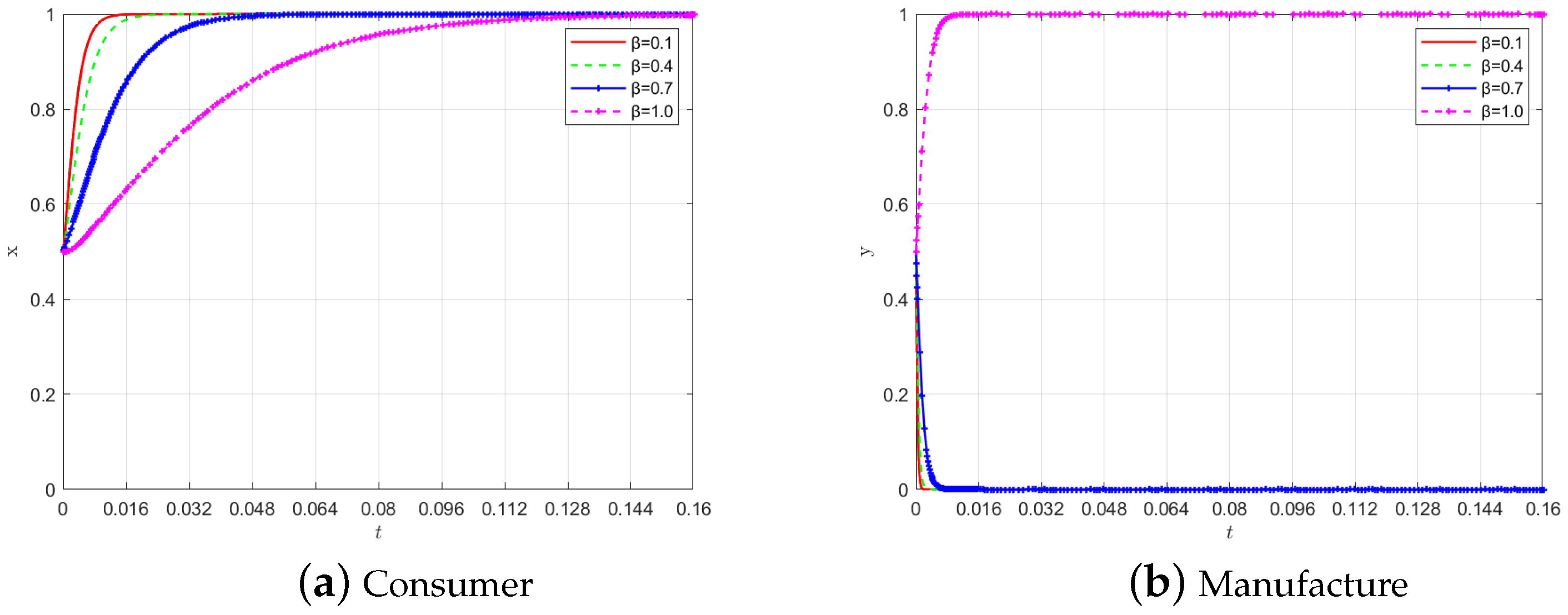
4.2.1. The Effect of Consumer Loss Aversion on Evolution
4.2.2. The Impact of Other Parameters on Evolution
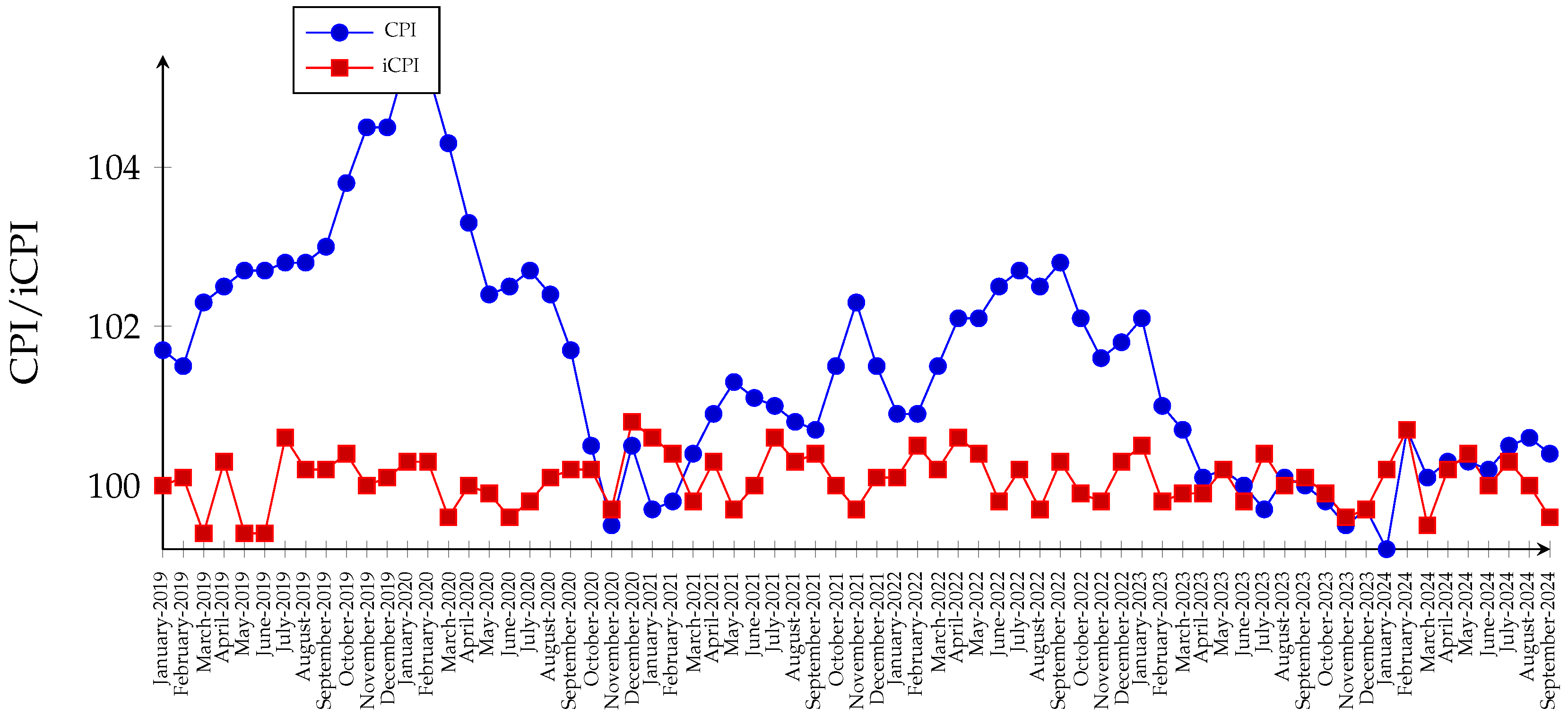
4.3. Model Validation and Verification
5. Conclusions
5.1. Main Findings
5.2. Implications and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chiang, W. Multi-Channel Supply Chain Management in the E-Business Era. Ph.D. Thesis, University of Illinois at Urbana, Champaign, IL, USA, April 2002. [Google Scholar]
- Statista. Available online: https://www.statista.com/topics/2443/us-ecommerce (accessed on 23 October 2024).
- Asante, I.O.; Jiang, Y.S.; Luo, X. Does it matter how I stream? Comparative analysis of livestreaming marketing formats on Amazon Live. Humanit. Soc. Sci. Commun. 2023, 10, 403. [Google Scholar] [CrossRef]
- Sun, Y.; Shao, X.; Li, X.T.; Guo, Y.; Nie, K. How live streaming influences purchase intentions in social commerce: An IT affordance perspective. Electron. Commer. Res. Appl. 2019, 37, 100886. [Google Scholar] [CrossRef]
- Ballerini, J.; Yahiaoui, D.; Giovando, G.; Ferraris, A. E-commerce channel management on the manufacturers’ side: Ongoing debates and future research pathways. Rev. Manag. Sci. 2024, 18, 413–447. [Google Scholar] [CrossRef]
- Chen, W.; Katehakis, M.; Tang, Q. Dynamic inventory system with pricing adjustment for price-comparison shoppers. Appl. Stoch. Model. Bus. Ind. 2023, 39, 413–447. [Google Scholar] [CrossRef]
- Chen, Y.X.; Dai, Y.; Zhang, Z.; Zhang, K. Managing multirooming: Why uniform price can be optimal for a monopoly retailer and can be uniformly lower. Manag. Sci. 2023, 70, 3102–3122. [Google Scholar] [CrossRef]
- Yang, R.; Yang, Y.Z.; Shafi, M.; Song, X.T. Do customers really get tired of Double Eleven Global Carnival? An exploration of negative influences on consumer attitudes toward online shopping website. In Proceedings of the Thirteenth International Conference on Management Science and Engineering Management, St. Catharines, ON, Canada, 5–8 August 2019; Volume 1002, pp. 189–200. [Google Scholar]
- Jaejung, K.; Kim, J. A solution of channel conflict and chowrooming in culti channel—Application of thinking process and TRIZ’. J. Internet Electron. Commer. Res. 2018, 18, 395–408. [Google Scholar]
- Bucklin, C.B. Channel conflict: When is it dangerous? Mckinsey Q. 1997, 3, 36–43. [Google Scholar]
- Wang, L.; He, Z.; He, S.G. Quality differentiation and e-tailer’s choice between reselling and agency selling. Manag. Decis. Econ. 2023, 44, 3518–3536. [Google Scholar] [CrossRef]
- Zhang, Q.K.; Mantin, B.; Chen, H.Z. On selling format choice and quality differentiation in dual-channel supply chains. Manag. Decis. Econ. 2023, 44, 3308–3324. [Google Scholar] [CrossRef]
- Zhou, L.X.; Fan, T.J.; Zhang, L.H.; Chang, L.Y. Quality differentiation with manufacturer encroachment: Is first mover always an advantage for retail platform? Ind. Manag. Data Syst. 2023, 123, 762–793. [Google Scholar] [CrossRef]
- Chen, Y.J.; Ho, W.H.; Kuo, H.W.; Kao, T.W. Repositioning conflicting partners under inventory risks. IEEE Trans. Eng. Manag. 2020, 67, 454–465. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Akhavizadegan, F.; Ansarifar, J. Pricing and quality level decisions of substitutable products in online and traditional selling channels: Game-theoretical approaches. Int. Trans. Oper. Res. 2019, 26, 1718–1751. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Cheng, T.C.E. Channel selection in a supply chain with a multi-channel retailer: The role of channel operating costs. Int. J. Prod. Econ. 2016, 173, 54–65. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.X.; Cai, Z.G. Hybrid channel structure and product quality distribution strategy for online retail platform. PLoS ONE 2023, 18, e0285860. [Google Scholar] [CrossRef]
- Brynjolfsson, E.; Hu, Y.J.; Rahman, M.S. Competing in the age of omnichannel retailing. MIT Sloan Manag. Rev. 2013, 54, 23–29. [Google Scholar]
- Gao, F.; Su, X.M. Omnichannel retail operations with buy-online-and-pick-up-in-store. Manag. Sci. 2017, 63, 2478–2492. [Google Scholar] [CrossRef]
- Yu, D.D.; Wan, M.Y.; Luo, C.L. Dynamic pricing and dual-channel choice in the presence of strategic consumers. Manag. Decis. Econ. 2022, 43, 2392–2408. [Google Scholar] [CrossRef]
- Liu, C.L.; Lee, C.; Zhang, L.L. Pricing strategy in a dual-channel supply chain with overconfident consumers. Comput. Ind. Eng. 2022, 172, 108515. [Google Scholar] [CrossRef]
- Radhi, M.; Zhang, G.Q. Pricing policies for a dual-channel retailer with cross-channel returns. Comput. Ind. Eng. 2018, 119, 63–75. [Google Scholar] [CrossRef]
- Deng, Z.H.; Zheng, B.R.; Jin, L. Dual-channel supply chain coordination with online reviews. Electron. Commer. Res. Appl. 2023, 60, 101281. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Y.X.; Chen, X.F.; Liang, J.Y. Pricing decision models of manufacturer-led dual-channel supply chain with free-rider problem. Sustainability 2023, 15, 4087. [Google Scholar] [CrossRef]
- Frambach, R.T.; Roest, H.C.A.; Krishnan, T.V. The impact of consumer internet experience on channel preference and usage intentions across the different stages of the buying process. J. Interact. Mark. 2007, 21, 26–41. [Google Scholar] [CrossRef]
- Hu, Y.S.; Zeng, L.H.; Huang, Z.L.; Cheng, Q. Optimal channel decision of retailers in the dual-channel supply chain considering consumer preference for delivery lead time. Adv. Prod. Eng. Manag. 2020, 15, 453–466. [Google Scholar] [CrossRef]
- Kang, Y.; Chen, J.H.; Wu, D. Research on pricing and service level strategies of dual-channel reverse supply chain considering consumer creference in multi-regional situations. Int. J. Environ. Res. Public Health 2020, 17, 9143. [Google Scholar] [CrossRef]
- Florenthal, B.; Shoham, A. Four-mode channel interactivity concept and channel preferences. J. Serv. Mark. 2010, 24, 29–41. [Google Scholar] [CrossRef]
- Flavián, C.; Gurrea, R.; Orús, C. The influence influence of online product presentation videos on persuasion and purchase channel preference: The role of imagery fluency and need for touch. Telemat. Inform. 2017, 34, 1544–1556. [Google Scholar] [CrossRef]
- Chiou, J.S.; Chou, S.Y.; Shen, G.C.C. Consumer choice of multichannel shopping The effects of relationship investment and online store preference. Internet Res. 2017, 27, 2–20. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Z.; Li, X. Robust optimization of a closed-loop supply chain network based on an improved genetic algorithm in an uncertain environment. Comput. Ind. Eng. 2024, 189, 109997. [Google Scholar] [CrossRef]
- Lai, H.; Zhou, Y.; Chen, X.; Li, G. Physical stores versus physical showrooms: Channel structures of online retailers. Electron. Commer. Res. Appl. 2024, 68, 101458. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, C.; Cai, D. Delivery arrangement in online distribution channels under different power structures. Omega 2024, 126, 103070. [Google Scholar] [CrossRef]
- Wan, N.; Fan, J. Platform service decision and selling mode selection under different power structures. Ind. Manag. Data Syst. 2024, 124, 1991–2020. [Google Scholar] [CrossRef]
- Pei, F.; Xia, X.; Qian, X.; Yan, A. Extended warranty strategy analysis for online platform marketplace considering product reliability transparency. Comput. Ind. Eng. 2025, 199, 110642. [Google Scholar] [CrossRef]
- Mao, Z.; Yuan, R.; Shen, Z.M. Strategic interactions between manufacturer channel choice and platform entry in a dual-market system. Int. J. Prod. Econ. 2024, 199, 110642. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, B. Securing the network in e-retailing and manufacturing: A balanced decision analysis under competition and cooperation modes. Int. J. Syst. Sci. Oper. Logist. 2024, 11, 2357079. [Google Scholar] [CrossRef]
- Jafar, C.; Ozgun, C.D. Effects of consumer loyalty and product web compatibility on cooperative advertising and pricing policies in a dual-channel supply chain. RAIRO—Oper. Res. 2022, 56, 2557–2580. [Google Scholar]
- Baldi, B.; Ilenia, C.; Ivan, R.; Barbara, G. Consumer-Centric Supply Chain Management: A Literature Review, Framework, and Research Agenda. J. Bus. Logist. 2024, 45, e12399. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Friedman, D. On economic applications of evolutionary game theory. J. Evol. Econ. 1998, 8, 15–43. [Google Scholar] [CrossRef]
| Parameters | Descriptions |
|---|---|
| The product price for offline retail. | |
| The product price for online retail. | |
| The proportion of online consumers lost due to a price increase. | |
| The product utility for offline retail. | |
| The product utility for online retail. | |
| The price discount for the online product, . | |
| The quality discount for the online product, . | |
| The consumer loss aversion coefficient. Consumers are more loss-averse when is larger. | |
| T | The unit mismatch cost caused by choice. |
| The service utility of offline retail. | |
| The service utility of online retail. | |
| R | Benefits to manufacturers caused by simplifying management, preventing price erosion issues, improving brand positioning, etc., when manufacturers choose a dual-channel unified pricing strategy and consumers tend to prefer an offline purchasing channel. |
| M | Benefits to manufacturers caused by simplifying management, preventing price erosion issues, improving brand positioning, etc., when manufacturers choose a dual-channel unified pricing strategy and consumers tend to prefer an online purchasing channel. |
| F | The increased cost to manufacturers caused by increased management for price erosion problems, the free-riding effect, etc., when manufacturers choose a dual-channel differential pricing strategy and consumers tend to prefer an offline purchasing channel. |
| N | The increased cost to manufacturers caused by increased management for price erosion problems, the free-riding effect, etc., when manufacturers choose a dual-channel differential pricing strategy and consumers tend to prefer an online purchasing channel. |
| x | The proportion of consumers choosing a dual-channel unified pricing strategy. |
| y | The proportion of manufacturers choosing offline channels for purchase. |
| The market share of offline retail. | |
| The market share of online retail. | |
| The total utility for consumers by buying the product offline. | |
| The total utility for consumers by buying the product online. | |
| The manufacturer’s profit when consumers buy the product offline. | |
| The manufacturer’s profit when consumers buy the product online. | |
| X | The marginal consumer with the same evaluations in the two channels. |
| Manufacturer | Unified Pricing Strategy | Differentiated Pricing Strategy | |
|---|---|---|---|
| Consumer | y | ||
| Offline channel | , | , | |
| x | |||
| Online channel | |||
| Local Equilibrium Point | Sign of | Sign of | Results |
|---|---|---|---|
| ESS ➀ | |||
| ESS ➁ | |||
| ESS ➂ | |||
| ESS ➃ | |||
| 0 | 0 | Saddle point |
| Product Registration Number | Brand | Prices on Taobao | Sales on Taobao | Counter Prices in Shopping Malls |
|---|---|---|---|---|
| 2024004383 | Lancome | 1120 | 60,000+ | 1120 |
| 2023001769 | LA MER | 1060 | 70,000+ | 1060 |
| 2022006890 | Clarins | 1030 | 20,000+ | 1030 |
| 2020003600 | Estee Lauder | 990 | 100,000+ | 990 |
| 2023000066 | Guerlain | 780 | 50,000+ | 780 |
| 2020007702 | SK-II | 610 | 100,000+ | 610 |
| 2024005718 | Lancome | 500 | 100,000+ | 500 |
| 2023006081 | Elizabeth Arden | 410 | 10,000+ | 410 |
| 2023009305 | Kiehl’s | 395 | 100,000+ | 395 |
| 2024000651 | Origins | 380 | 30,000+ | 380 |
| 2023005172 | L’oreal | 359 | 100,000+ | 370 |
| 2023001147 | PROYA | 349 | 500,000+ | 349 |
| OLAY | 339 | 400,000+ | 339 | |
| 2022000473 | Winona | 338 | 100,000+ | 338 |
| 2023001593 | Clinique | 310 | 20,000+ | 310 |
| Product Registration Number | Brand | Prices on Taobao | Sales on Taobao | Tag Price |
|---|---|---|---|---|
| N23101A01007 | NEELY | 339 | 16 | 339 |
| BDS1MD1184 | broadcast | 798 | 5 | 798 |
| JLFGM253 | jessie | 671 | 7 | 1499 |
| JWCD31302 | JZ | 394 | 34 | 1580 |
| 5P1113980 | JNBY | 695 | 87 | 695 |
| A3EEE3422 | PEACEBIRD | 599 | 1 | 599 |
| 1EA332241 | Eifini | 596 | 8 | 596 |
| 89124370104 | HOPESHOW | 449 | 9 | 449 |
| 3F8331781 | SEIFINI | 539 | 33 | 598 |
| 124420TC348 | LILY | 719 | 0 | 719 |
| FR470034043 | FeiNiao&XinJiu | 899 | 0 | 899 |
| LWT009177C0B | Lee | 629 | 26 | 629 |
| S23483523 | sdeer | 549 | 6 | 599 |
| C2EEE420439 | LEDiN | 499 | 17 | 499 |
| 112401102049 | H’s | 614 | 4 | 614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Du, Y. Application of Evolutionary Game to Analyze Dual-Channel Decisions: Taking Consumer Loss Aversion into Consideration. Mathematics 2025, 13, 234. https://doi.org/10.3390/math13020234
Zhang S, Du Y. Application of Evolutionary Game to Analyze Dual-Channel Decisions: Taking Consumer Loss Aversion into Consideration. Mathematics. 2025; 13(2):234. https://doi.org/10.3390/math13020234
Chicago/Turabian StyleZhang, Shuang, and Yueping Du. 2025. "Application of Evolutionary Game to Analyze Dual-Channel Decisions: Taking Consumer Loss Aversion into Consideration" Mathematics 13, no. 2: 234. https://doi.org/10.3390/math13020234
APA StyleZhang, S., & Du, Y. (2025). Application of Evolutionary Game to Analyze Dual-Channel Decisions: Taking Consumer Loss Aversion into Consideration. Mathematics, 13(2), 234. https://doi.org/10.3390/math13020234






