One More Thing on the Subject: Generating Chaos via x|x|^a−1, Melnikov’s Approach Using Simulations

Abstract

In this article, we propose a new hypothetical differential model with many free parameters, which makes it attractive to users. The motivation is as follows: an extended model is proposed that allows us to investigate classical and newer models appearing in the literature at a “higher energy level”, as well as the generation of high–order Melnikov polynomials (corresponding to the proposed extended model) with possible applications in the field of antenna feeder technology. We present a few specific modules for examining these oscillators’ behavior. A much broader Web-based application for scientific computing will incorporate this as a key component.

1. Introduction

The freedom of a potential well may be guaranteed by a number of oscillatory natural phenomena that arise in a wide range of fields, including engineering, quantum optics, acoustics, hydrodynamics, electronics, and mechanics. These phenomena are represented by a general escape nonlinear oscillator model. The equation of movement for the sinusoidal-driven escape oscillator is examined by Sanjuan [1], who incorporates nonlinear damping conditions as a power series on the speed reads:

$$\ddot{x}+{\displaystyle \sum _{p=1}^n}\beta \dot{x}{\left|\dot{x}\right|}^{p-1}+x-x^2=F\sin \omega t,$$

(1)

where F and $\omega$ represent the forcing amplitude and frequency of the outer disturbance, respectively, $\beta$ represents the damping level, and p represents the damping exponent. The following is a representation of the nonlinearly damped general escape oscillator and nonlinear vessel trundling reply:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -{\displaystyle \sum _{j=1}^m}{a}_j{x}^j+{\displaystyle \sum _{p=1}^n}{c}_{p}y{\left|y\right|}^{p-1}+F\cos \omega t\hfill \end{array}\right.$$

(2)

with the initial conditions $x\left(t_0\right)=x_0;y\left(t_0\right)=y_0$. In [2], the authors have thoroughly examined the effects of the damping level on the escape oscillator’s basin bifurcation models and the rational response of steady-state decisions. The amount and diversity of the literature on this topic are noteworthy. To find more similar studies, we refer the reader to [2,3,4,5,6,7]. Some extended differential models can be found in [8,9].

The character of the equation $x\left|x\right|$ as a chaos producer in a non-self-governing differential model is examined in the work by Tang, Man, Zhong, and Chen [10]. More specifically, the following model is taken:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& ax-bx\left|x\right|-ϵ\left(\xi y-c\sin \left(\omega t\right)\right)\hfill \end{array}\right.$$

(3)

with initial conditions $x\left(t_0\right)=x_0;y\left(t_0\right)=y_0$.

In [11], the generalized Duffing-type model with fractional-order nonlinear term is considered

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& x-{x\left|x\right|}^{a-1}+ϵ\left(\gamma \cos \left(\omega t\right)-\delta y\right)\hfill \end{array}\right.$$

(4)

with initial conditions $x\left(t_0\right)=x_0;y\left(t_0\right)=y_0$, where $a>1$ is an integer or a fraction. For $ϵ\le 1$, the coefficients $ϵ\gamma$ and $ϵ\delta$ are small parameters. Equation (4) represents the oscillatory motion of a buckled beam with simply supported or hinged ends for modal displacement $x\left(t\right)$ (see [12,13,14]).

In [15], the authors propose several control strategies to stabilize the chaotic behavior a fractional piecewise-smooth oscillator.

In this paper, we suggest a new extended model based on (4). Investigations in the light of Melnikov’s approach [16] are considered. Several simulations are composed. Additionally, we present a few specialized modules for examining the dynamics of these artificial oscillators. The obtained results can be included into a much broader scientific computing application; see [17] for additional information.

The following is this paper’s plan. In Section 2, we provide a description of our model. Section 3 examines investigations in the context of Melnikov’s methodology. Section 4 presents a few simulations. Section 5 brings us to a close. The modeling and synthesis of radiating antenna designs is also explored as a potential use case for Melnikov functions.

2. The Model

We consider the following new class of extended oscillators:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& x-{x\left|x\right|}^{a-1}+ϵ\left({\displaystyle \sum _{j=1}^N}{a}_j\cos \left(j\omega t\right)-Ay\right),\hfill \end{array}\right.$$

(5)

where $0\le ϵ<1$, $A>0$, $a_i\ge 0,i=1,2,\dots ,N$, and N is integer.

The level set ${\displaystyle \frac{1}{2}}{y}^2-{\displaystyle \frac{1}{2}}{y}^2+{\displaystyle \frac{x^2{\left|x\right|}^{a-1}}{a+1}}=0$ is composed of two homoclinic orbits, ${\Gamma }_{+}\left(t\right)=(x_0\left(t\right),y_0\left(t\right))$ and ${\Gamma }_{-}\left(t\right)=-{\Gamma }_{+}\left(t\right)$. We consider the orbit

$$\begin{array}{c}{x}_0\left(t\right)={\left({\displaystyle \frac{a+1}{2}}\right)}^{{\displaystyle \frac{1}{a-1}}}{\left(\mathrm{sech}\left({\displaystyle \frac{a-1}{2}}t\right)\right)}^{{\displaystyle \frac{2}{a-1}}},\hfill \\ y_0\left(t\right)=-{\left({\displaystyle \frac{a+1}{2}}\right)}^{{\displaystyle \frac{1}{a-1}}}{\left(\mathrm{sech}\left({\displaystyle \frac{a-1}{2}}t\right)\right)}^{{\displaystyle \frac{2}{a-1}}}\tanh \left({\displaystyle \frac{a-1}{2}}t\right)\hfill \end{array}$$

(6)

(some details can be found in [11]).

3. Considerations in the Light of Melnikov’s Approach

Where the stable and unstable manifolds cross transversely can be determined using the Melnikov function, which provides a measure of the leading-order distance between them when $ϵ\ne 0$. The Melnikov integral is defined as follows:

$$M\left(t_0\right)={\displaystyle {\int }_{-\infty }^{\infty }}{y}_0\left(t\right)\left({\displaystyle \sum _{j=1}^N}{a}_j\cos \left(j\omega (t+t_0)\right)-A{y}_0\left(t\right)\right)dt,$$

(7)

where Equation (6) define the functions $x_0\left(t\right)$ and $y_0\left(t\right)$. The task of determining the root of $M\left(t_0\right)$ is more intriguing from a numerical perspective since the parameters that appear in the suggested differential model are subject to certain practical and physical constraints.

We can prove the following propositions.

Proposition 1.

If $a=2$, $N=1$ and $\left|\mathrm{Im}\right(\omega \left)\right|<1$, then the roots of the Melnikov function $M\left(t_0\right)$ are given as solutions of the equation

$$M\left(t_0\right)=-{\displaystyle \frac{6A}{5}}+6a_1\pi {\omega }^2\mathrm{csch}\left(\pi \omega \right)\sin \left(t_0\omega \right)=0.$$

(8)

Proposition 2.

If $a=2$, $N=2$ and $\left|\mathrm{Im}\left(\omega \right)\right|<{\displaystyle \frac{1}{2}}$, then the roots of the Melnikov function $M\left(t_0\right)$ are given as solutions of the equation

$$M\left(t_0\right)=-{\displaystyle \frac{6A}{5}}+6\pi {\omega }^2\mathrm{csch}\left(\pi \omega \right)\left(a_1\sin \left(t_0\omega \right)+2a_2\mathrm{sech}\left(\pi \omega \right)\sin \left(2t_0\omega \right)\right)=0.$$

(9)

Proposition 3.

If $a=4$, $N=2$ and $\left|\mathrm{Im}\left(\omega \right)\right|<{\displaystyle \frac{1}{2}}$, then the roots of the Melnikov function $M\left(t_0\right)$ are given as solutions of the equation given in Figure 1.

In this case, the explicit representation of $M\left(t_0\right)$ (as well as that for large values of the parameter N) is laborious, because it is expressed in terms of the Euler gamma function and hypergeometric function—$\mathrm{Hypergeometric}2\mathrm{F}1[.,.,.,.]$, and it requires the user to perform a number of operations (for example, the operator $\mathrm{Simplify}[\%]$). Figure 1 illustrates the calculation of $M\left(t_0\right)$ using CAS Mathematica. It is known that if $M\left(t_0\right)=0$ and ${\displaystyle \frac{\mathrm{d}M\left(t_0\right)}{\mathrm{d}{t}_0}}\ne 0$ for some $t_0$ and some sets of parameters, then chaos occurs. From Propositions 1–3, the reader may formulate Melnikov’s criterion for the appearance of the intersection between perturbed and unperturbed separatrixes.

Example 1.

The equation $M\left(t_0\right)=0$ for $a=4;N=2;A=0.008;\omega =0.35;a_1=0.2;$$a_2=0.6$ is depicted in Figure 2.

Example 2.

The equation $M\left(t_0\right)=0$ for $a=4;N=2;A=0.55;\omega =0.25;a_1=0.1;a_2=0.4$ is depicted in Figure 3.

Example 3.

The equation $M\left(t_0\right)=0$ for $a=4;N=2;A=0.1;\omega =0.25;a_1=0.6;a_2=0.3$ is depicted in Figure 4.

Proposition 4.

If $a=4$, $N=4$ and $\left|\mathrm{Im}\left(\omega \right)\right|<{\displaystyle \frac{1}{4}}$, then the roots of the Melnikov function $M\left(t_0\right)$ are given as solutions of the equation given in Figure 5.

Example 4.

The equation $M\left(t_0\right)=0$ for $a=4;N=4;A=0.12;\omega =0.93;a_1=0.1;$$a_2=0.3;a_3=0.1;a_4=0.15$ is depicted in Figure 6.

Example 5.

The equation $M\left(t_0\right)=0$ for $a=4;N=4;A=0.005;\omega =0.83;a_1=0.1;$$a_2=0.1;a_3=0.1;a_4=0.15$ is depicted in Figure 7.

Melnikov functions could be used, for example, in radiating antenna pattern modeling and synthesis.

We will now concentrate on $M\left(t\right)$. We provide the following definition for the hypothetical normalized antenna factor:

$$M^{*}\left(\theta \right)={\displaystyle \frac{1}{D}}\left|M(K\cos \theta +k_1)\right|,$$

where $\theta$ is the azimuth angle; $K=kd;k={\displaystyle \frac{2\pi }{\lambda }};\lambda$ is the wave length; d is the distance between emitters; $k_1$ is the phase difference.

The analogous approximation issue for randomly selected a and N might be examined by the reader.

For the purposes of our research, the user does not need to have an explicit representation of Melnikov’s polynomials corresponding to our differential model (for large values of the parameters), because the output of the first module used becomes the input for the second and most important module used, designed to generate and visualize the corresponding diagrams of radiating antenna array.

We will illustrate what was said with suitable examples.

Example 6.

For fixed $a={\displaystyle \frac{9}{2}};N=5;A=0.005;\omega =0.41;a_1=0.4;a_2=0.1;a_3=0.5;$$a_4=0.2;a_5=0.6;k=3.9;k_1=0$, the equation $M\left(t_0\right)=0$ and normalized antenna factor $M^{*}\left(\theta \right)$ are depicted in Figure 8.

If $a={\displaystyle \frac{11}{2}}$, $N=7$ and $\left|\mathrm{Im}\left(\omega \right)\right|<{\displaystyle \frac{1}{7}}$, then the roots of the Melnikov function $M\left(t_0\right)$ are given as solutions of the equation given in Figure 9.

Example 7.

For fixed $a={\displaystyle \frac{11}{2}};N=7;A=0.005;\omega =0.23;a_1=0.4;a_2=0.1;$$a_3=0.5;a_4=0.2;a_5=0.6;a_7=0.7k=4.9;k_1=0$, the equation $M\left(t_0\right)=0$ and normalized antenna factor $M^{*}\left(\theta \right)$ are depicted in Figure 10.

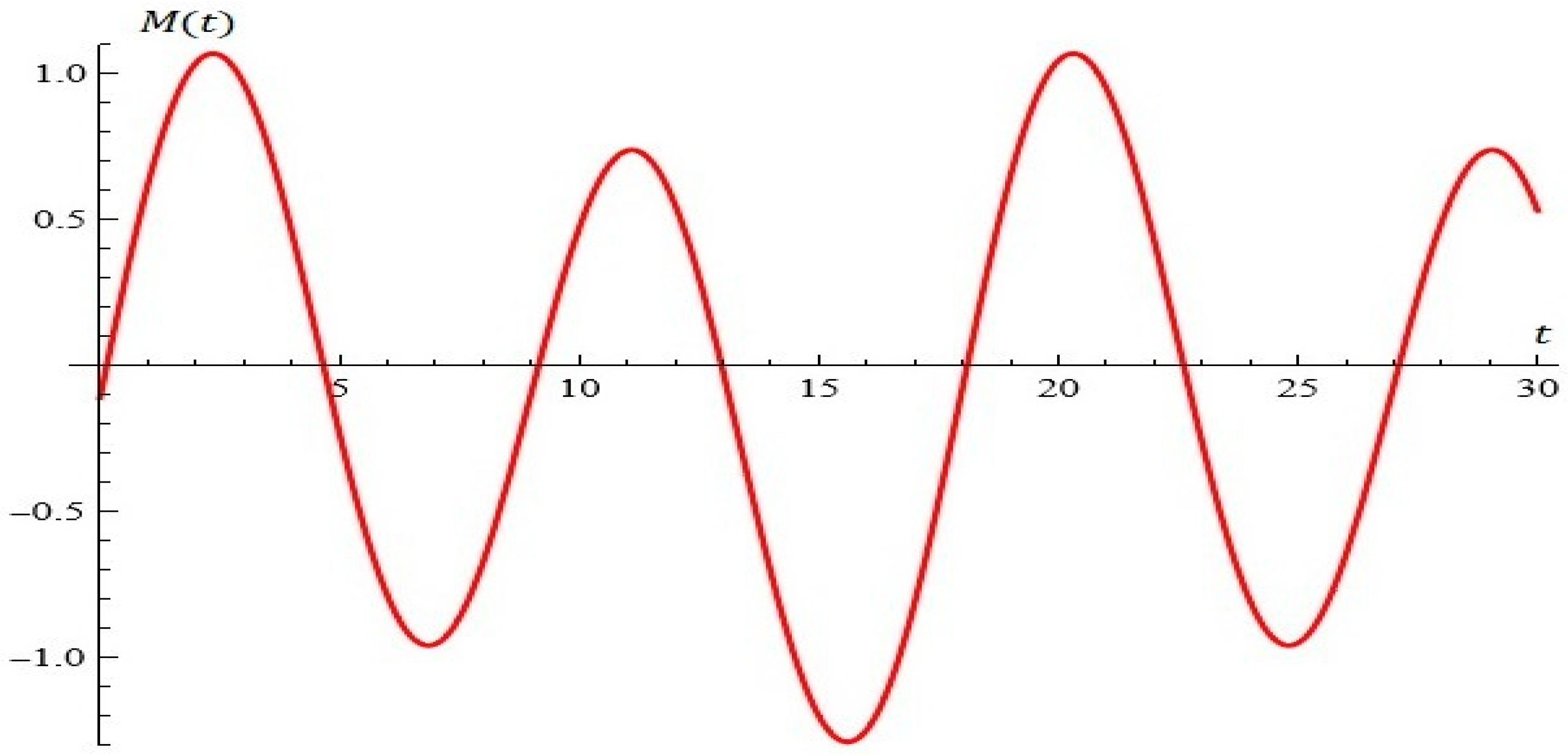
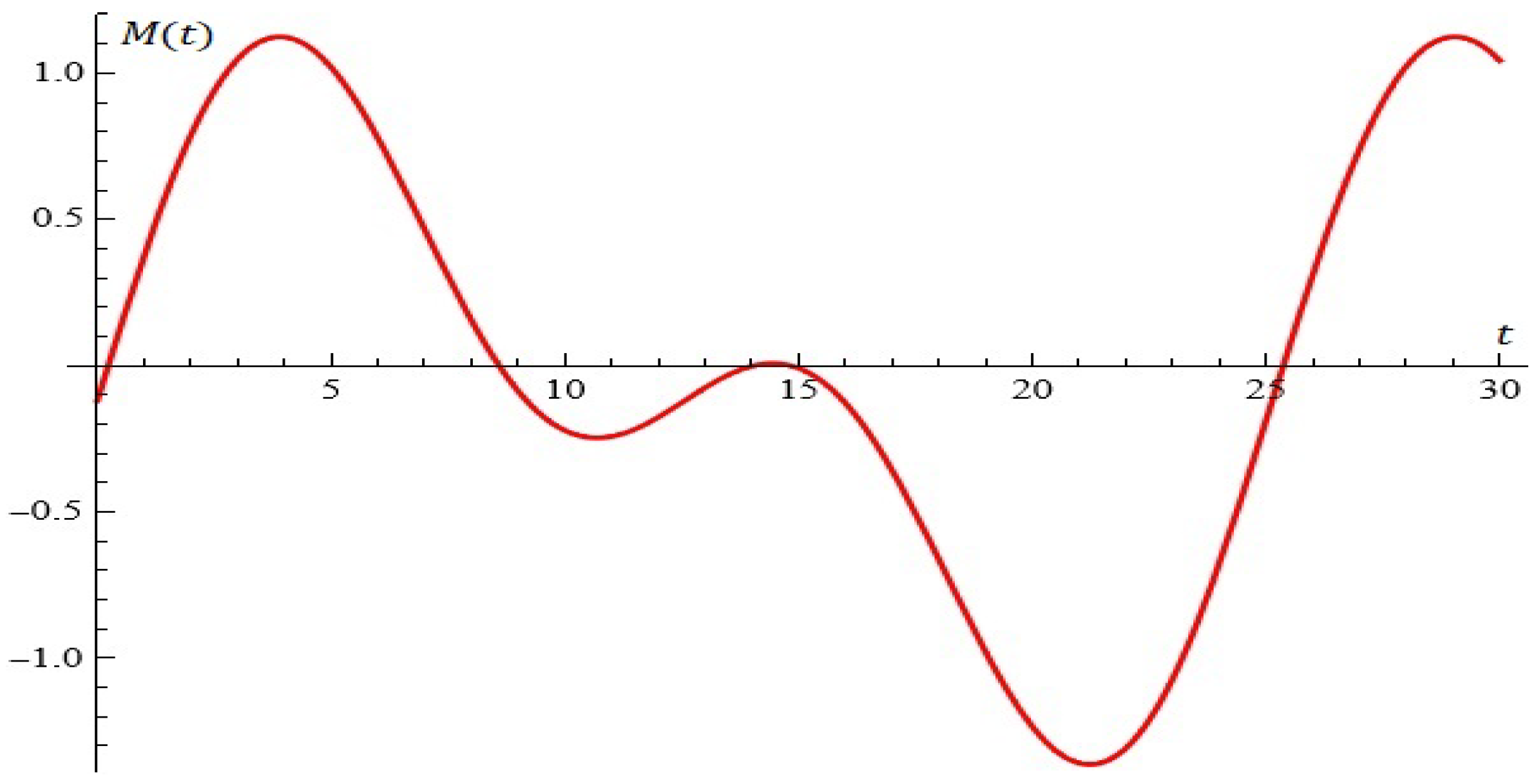
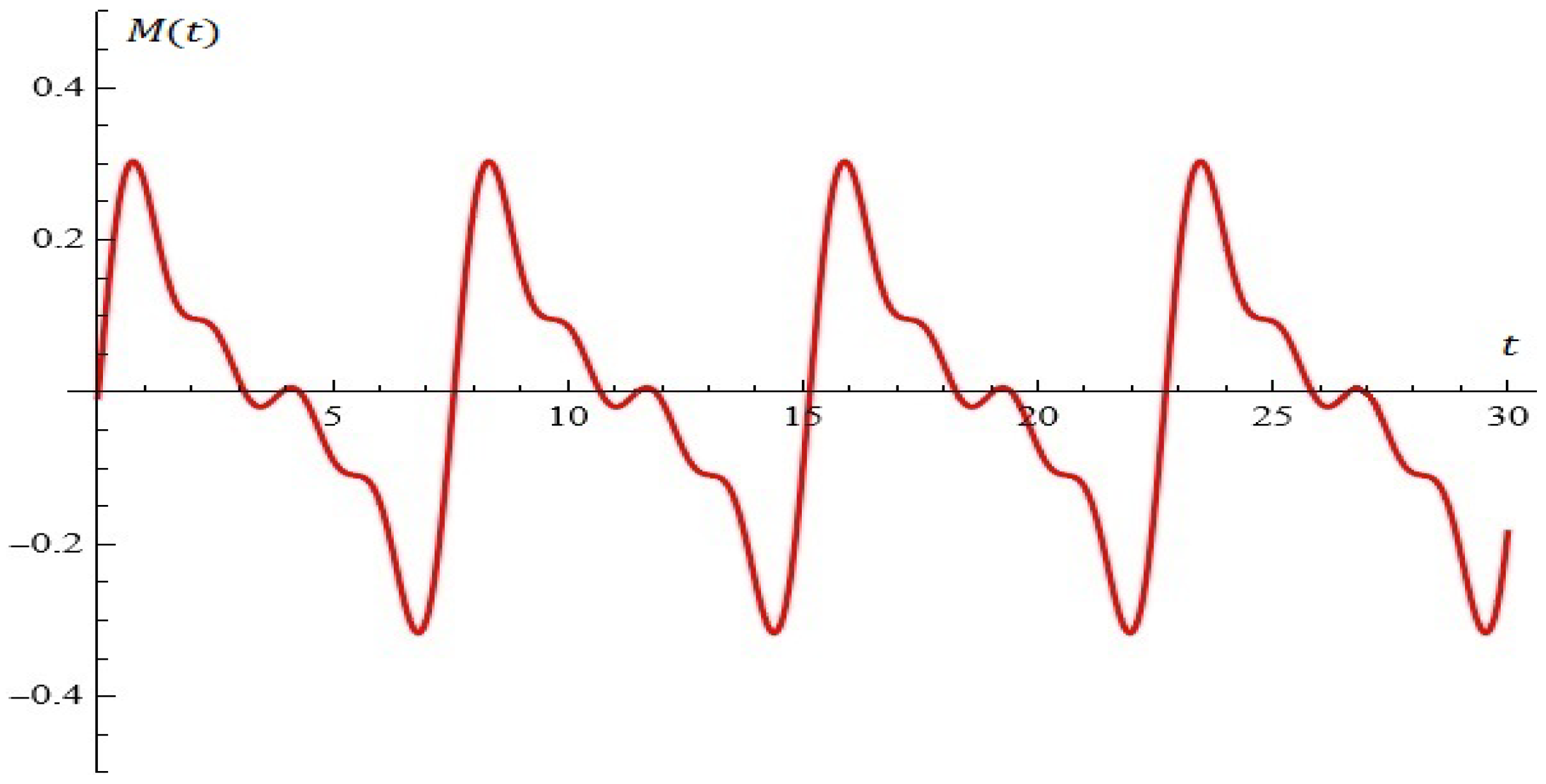
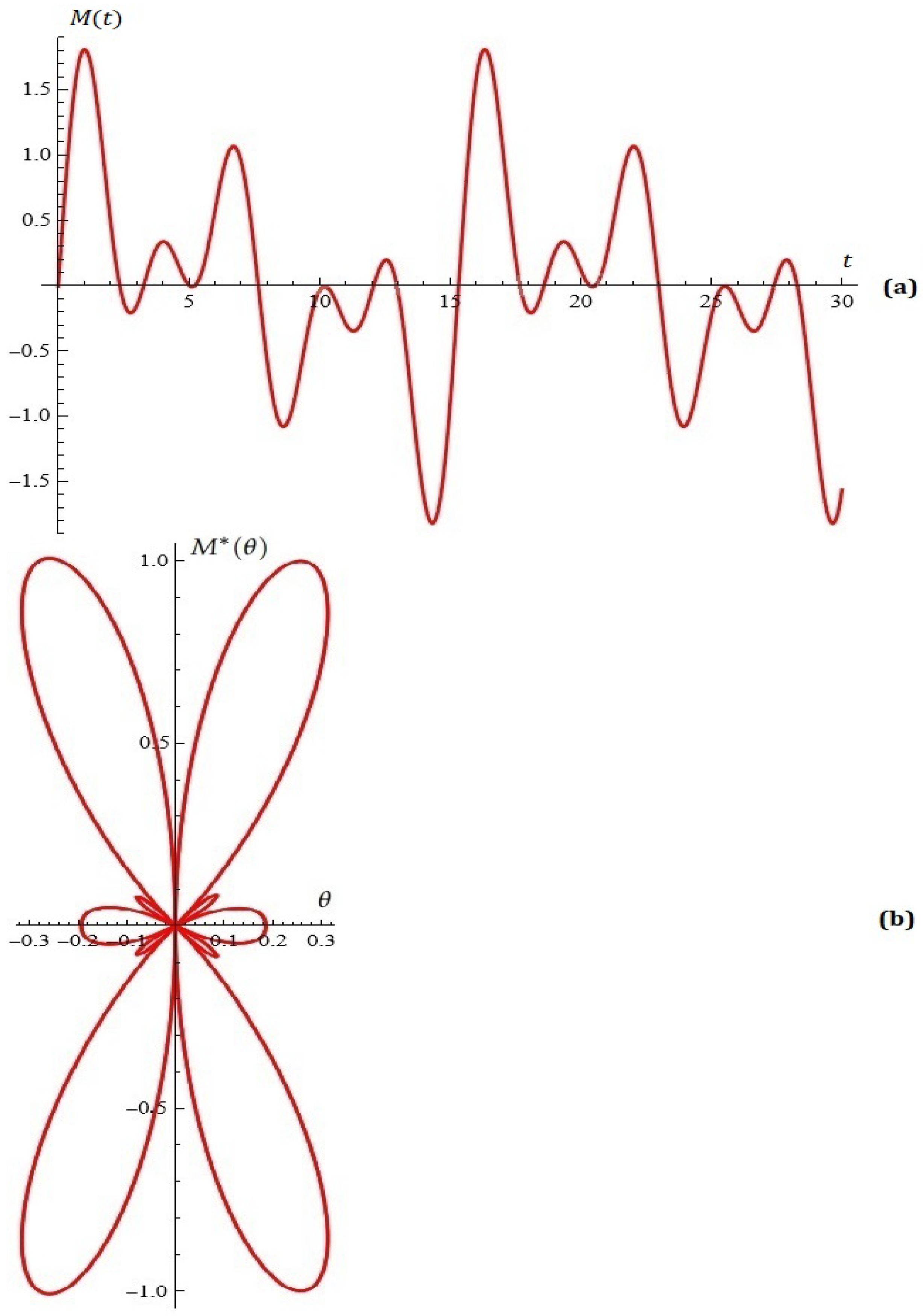
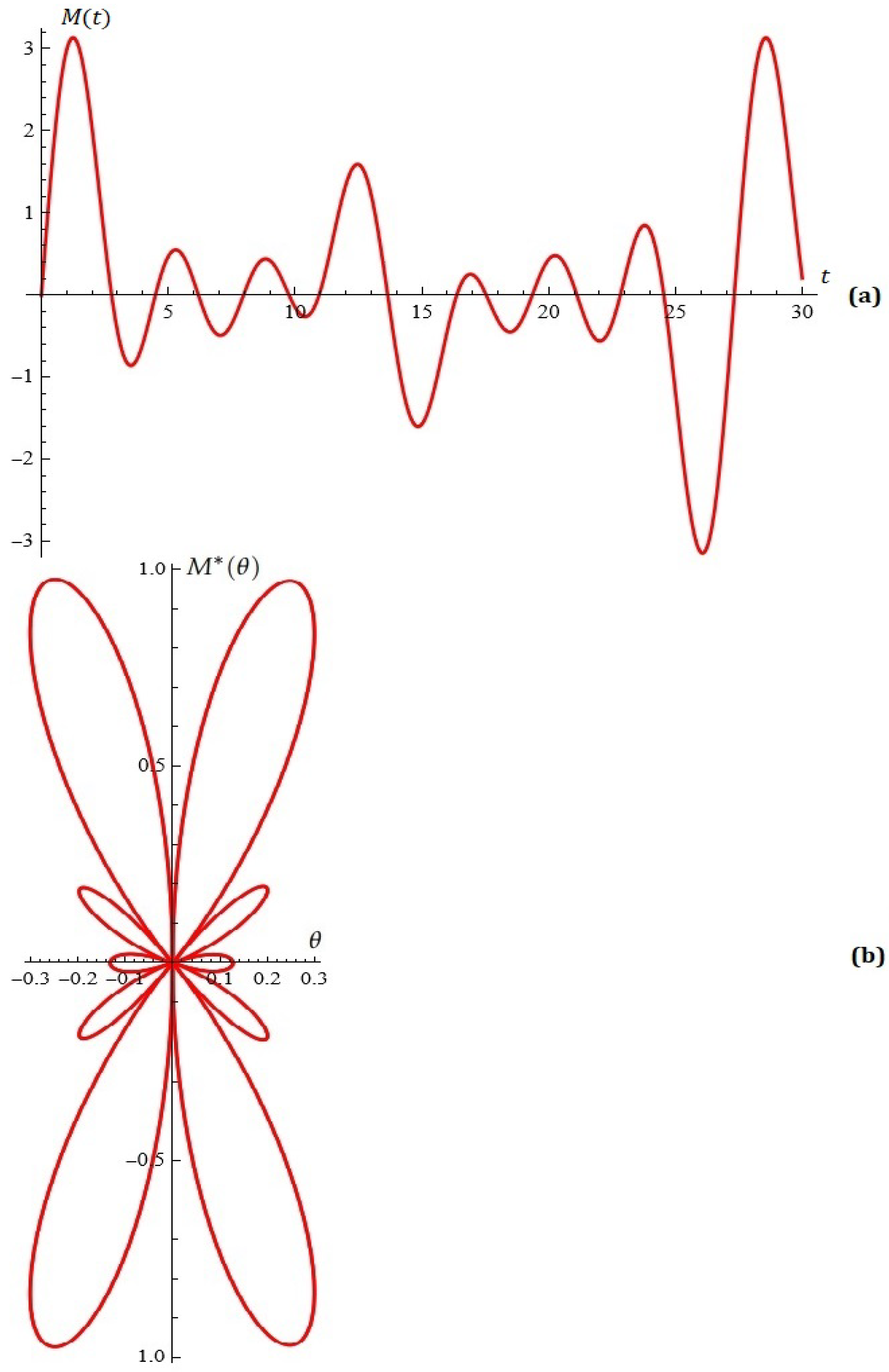
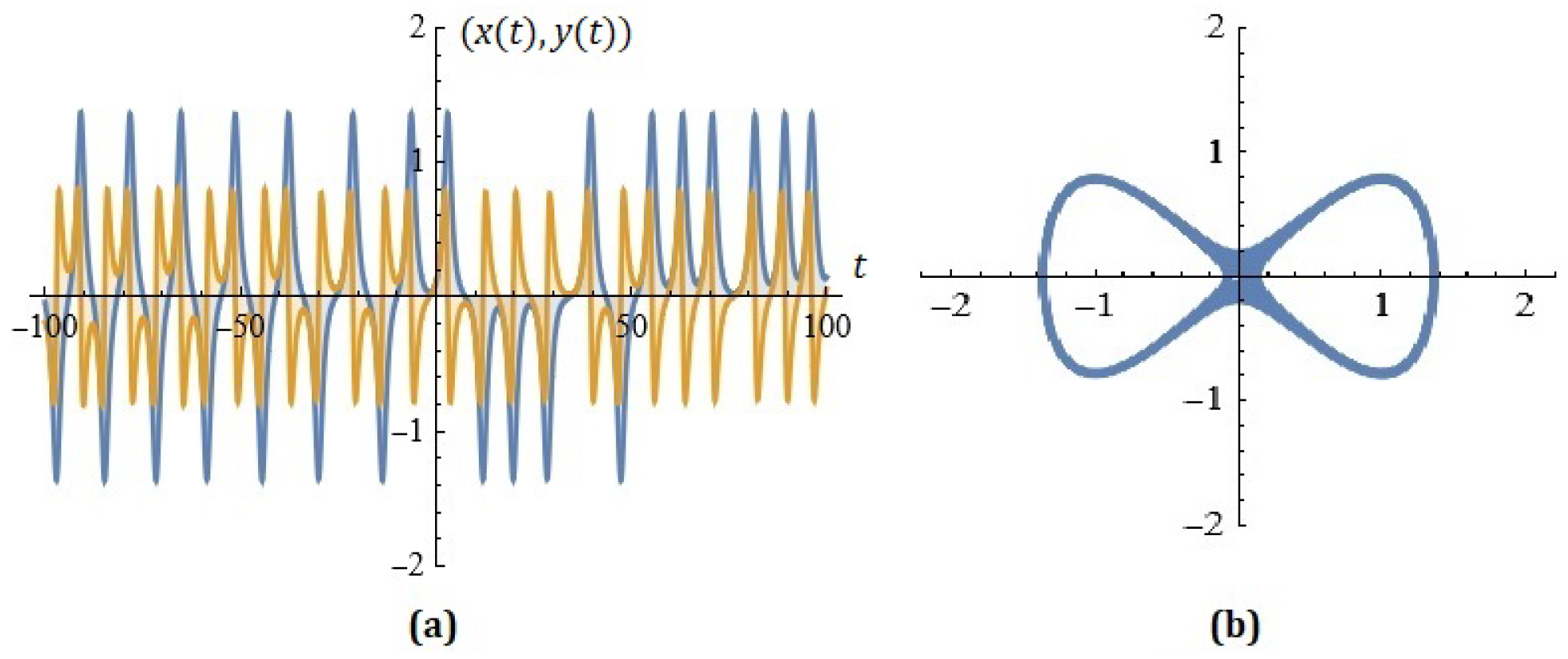
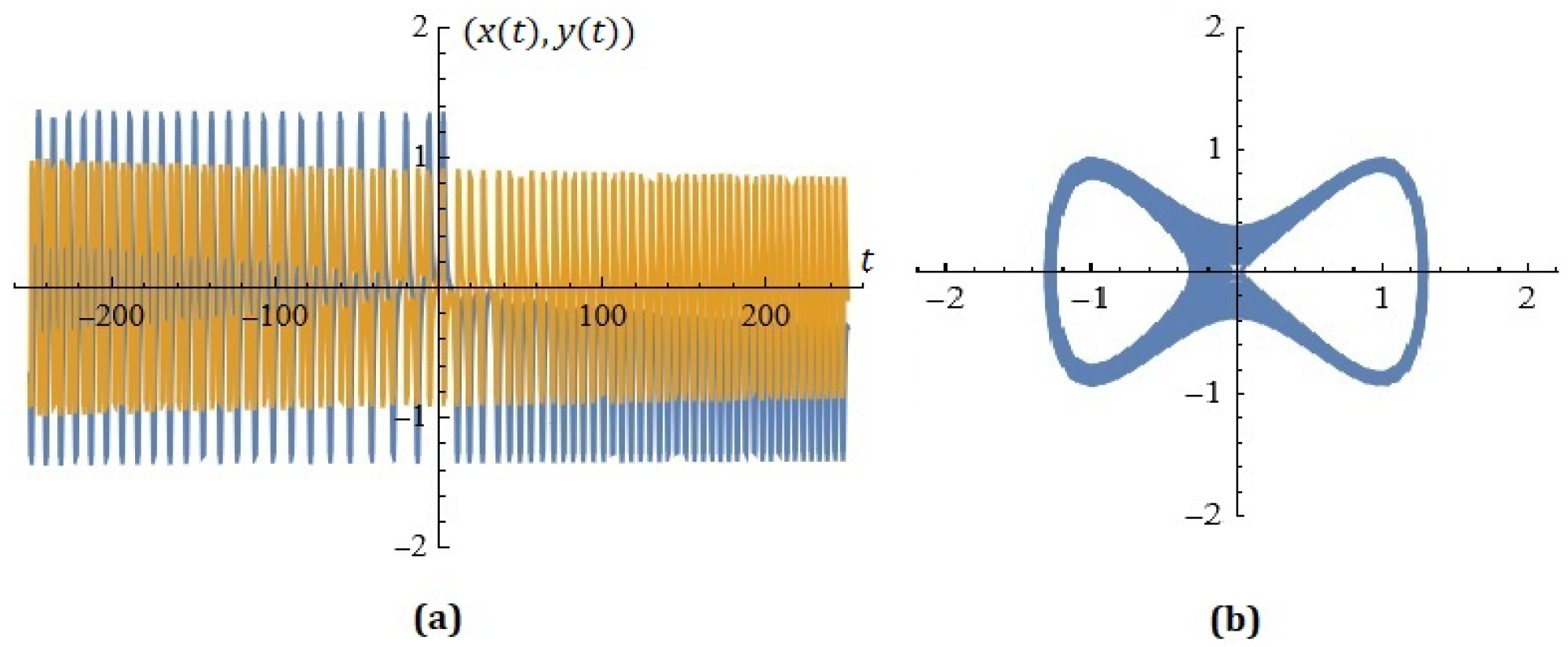
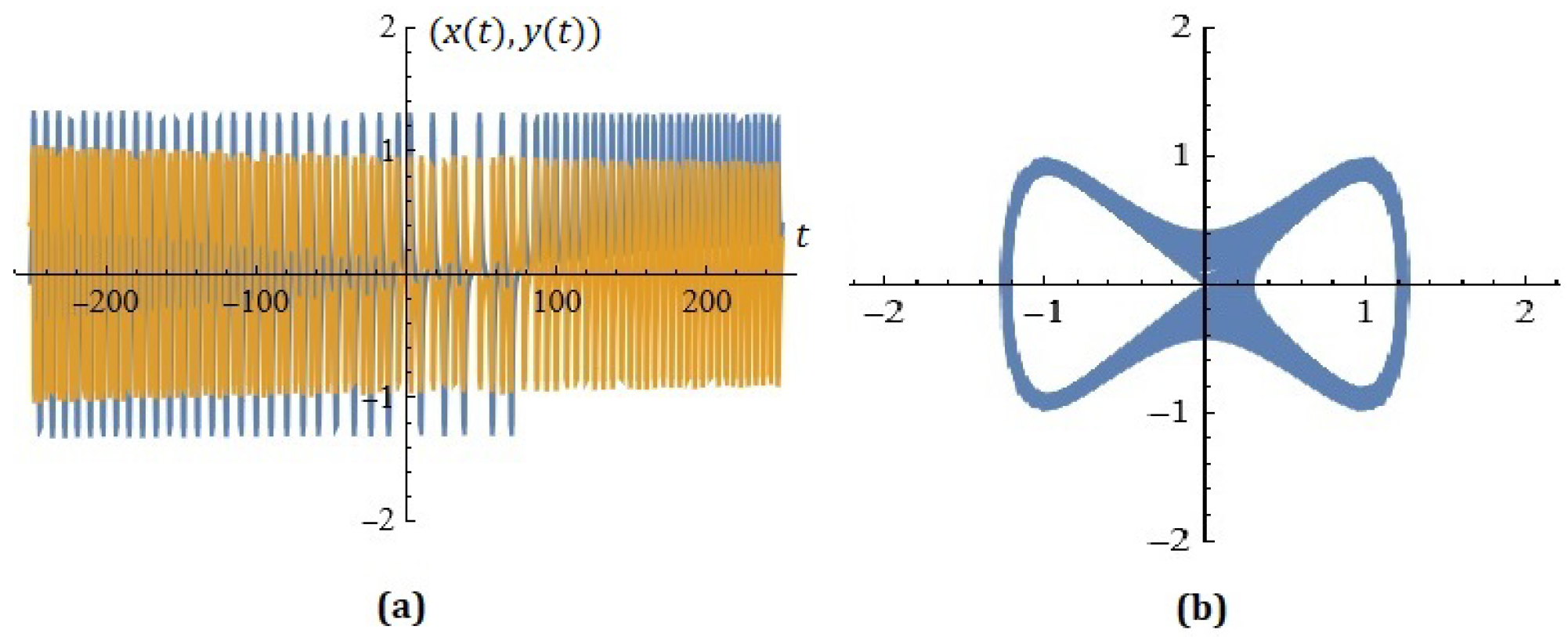
4. Some Simulations

Here, we will focus on some interesting simulations:

Example 8.

For given $a=4;N=2;A=0.1;ϵ=0.0095;\omega =0.1;a_1=0.07;a_2=0.8$, the simulations on System (5) for $x_0=0.1$; $y_0=0.1$ are depicted in Figure 11.

Example 9.

For given $a=6;N=3;A=0.1;ϵ=0.0095;\omega =0.1;a_1=0.07;a_2=0.8;$$a_3=0.09$, the simulations on System (5) for $x_0=0.1$; $y_0=0.1$ are depicted in Figure 12.

Example 10.

For given $a=8;N=4;A=0.1;ϵ=0.0095;\omega =0.1;a_1=0.07;a_2=0.8;$$a_3=0.09;a_4=0.5$, the simulations on System (5) for $x_0=0.1$; $y_0=0.1$ are depicted in Figure 13.

5. Concluding Remarks

In this research, we have examined a novel hypothetical differential model that has a large number of free parameters, which makes it appealing to users. We present a few specific modules for examining these oscillators’ behavior. For some of them, a cloud version is available that just needs a browser and an internet connection. This will be an essential component of a much broader Web-based program for scientific computing that is in the works. The task of determining the roots of $M\left(t_0\right)=0$ is more intriguing from a numerical perspective since the parameters that appear in the suggested differential model are subject to certain practical and physical constraints. [18] contains numerical techniques for resolving nonlinear equations. Naturally, the hypothetical Melnikov array that we provided can be viewed as an addition to the Array Antenna Theory following a careful evaluation by experts in this field of study.

Some notes:

• Diverting homoclinic chaos in a class of piecewise smooth oscillators to stable periodic orbits using small parametrical perturbations is considered in [19]. The authors consider the model

  $$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& ax-{bx\left|x\right|}^{\alpha -1}+ϵ\left(\gamma \cos \left(\omega t\right)-\left(\delta +F\sin (\omega t+\mathrm{\Psi })\right)y\right),\hfill \end{array}\right.$$

  where F is the amplitude, $\omega$ is the angular frequency, and $\mathrm{\Psi }$ is the phase position of the sinusoidal control signal. Other interesting results can be found in [20,21,22]. In a number of cases, in the process of calculating Melnikov’s functions, researchers find that their expressions cannot be solved analytically because homoclinic orbits are very complex. For this purpose, numerical algorithms are usually proposed and used in practice. Following the considerations in this article, the reader can successfully formulate and investigate the dynamics of the following new class of extended mixed oscillators:

  $$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& ax-{bx\left|x\right|}^{\alpha -1}+ϵ\left({\displaystyle \sum _{j=1}^N}{a}_j\cos \left(j\omega t\right)-Ay{\left|y\right|}^{p-1}\right).\hfill \end{array}\right.$$
  The detailed study of the dynamic model, as well as the role of the $a_i,i=1,2,\dots ,N$ coefficients in generating a probabilistic construction for controlling oscillations, will be the subject of our future research.
• Obviously, Melnikov polynomials can be used to approximate arbitrary point sets in the plane about a uniform metric. Such tasks are relevant to the general theory of synthesis and analysis of digital filters and radiation diagrams. The general N-element linear phased array factor used to find $A_k$ coefficients is

  $$AF\left(\theta \right)={\displaystyle \sum _{k=1}^{\frac{N}{2}}}{A}_k\cos \left((2k-1)u\right)=M\left(x\right),$$

  where $u={\displaystyle \frac{\pi d}{\lambda }}\cos \theta$, d is element separation, $\theta$ is polar angle, and $x=x_0\cos u$, where $x_0$ is a design parameter. This idea was borrowed from Soltis [23], where new Gegenbauer–like and Jacobi–like antenna arrays were generated. Of course, this relatively new idea of justification and right to exist is subject to serious research by specialists working in this scientific field. The issue related to noise minimization (in decibels) also remains to be investigated.