Abstract
An edge-coloring of a connected graph G is called rainbow if there exists a rainbow path connecting any pair of vertices. In contrast, is monochromatic if there is a monochromatic path between any two vertices. Some graphs can admit a coloring which is simultaneously rainbow and monochromatic; for instance, any coloring of is rainbow and monochromatic. This paper refers to such a coloring as dual coloring. We investigate dual coloring on various graphs and raise some questions about the sufficient conditions for connected graphs to be dual connected.
MSC:
05C15
1. Introduction
The edge coloring of graphs is a fundamental topic of graph theory that includes various interesting concepts. Recent studies have concentrated on modifying or extending the concept of coloring to special kinds of graphs. For instance, the proper coloring of graphs is a well-studied concept referring to the assignment of colors to the edges such that no two adjacent edges share the same color. Recently, Richard Behr [1] and Zhang et al. [2] independently extended the proper coloring to signed graphs. Similarly, the Ramsey number is an extensively studied concept of the well-known Ramsey theory, which asks about the smallest positive integer r such that edge 2-colored contains either a monochromatic of color 0 or of color 1. Recently, Mutar et al. [3] modified this concept to signed graphs in which is the smallest positive integer r, such that signed contains or .
Let G be a simple undirected connected graph of order n and size m. Let denote the set of non-negative integers up to . An edge k-coloring is a function that assigns colors to the edges of G with no restrictions in the way adjacent edges are allowed to have the same color. The coloring is called rainbow if, for any pair of vertices, there exists a rainbow path joining that pair (that is, a path in which all the edges are colored with distinct colors). The concept of edge rainbow coloring was introduced by Chartrand et al. [4]. Later, Caro et al. in [5] introduced monochromatic coloring as the opposite concept of rainbow coloring. That is, the coloring is monochromatic if, for any pair of vertices, there exists a monochromatic path joining the pair. By simply assigning distinct colors or exactly one color to the edges of any connected graph, one always ends up with a rainbow or monochromatic coloring. Although such colorings might seem trivial for some graphs, like trees, these assignments are the only possible option. The minimum number of colors required for ensuring rainbow coloring is called the rainbow connection number and is denoted by . Correspondingly, denotes the monochromatic connection number, which is the maximum number of colors required for obtaining a monochromatic coloring. We refer to [6,7,8,9] for their significant contributions to both concepts, as well as to the well-established surveys [10,11].
Both concepts have been extensively studied over the years. A total coloring refers to assigning colors to both the vertices and edges of a graph. In 2015, Yuefang Sun [12] introduced total rainbow coloring, which requires the existence of a path between every pair of vertices such that the edges and the internal vertices of the path all have distinct colors. The total rainbow connection number of G is then automatically defined and denoted as . Recently, Zhang et al. [13] studied this concept on families of connected graphs. In contrast, Hui Jiang et al. [14] introduced the so-called total monochromatic coloring where every pair of vertices is connected by a path whose vertices and edges are assigned the same color. The total monochromatic connection number is denoted by .
Some graphs can admit a coloring that is simultaneously rainbow and monochromatic. This observation motivated us to investigate connected graphs admitting such a coloring. In this paper, we call this coloring dual. That is, for any pair of vertices, there exist both rainbow and monochromatic paths connecting this pair. If G admits dual coloring, then the minimum number of colors needed to obtain a dual coloring will be denoted and called the lower dual connection number. Moreover, the inequality holds. Note that any coloring of complete graphs is simultaneously rainbow and monochromatic. However, it turns out that a tree T of order does not admit dual coloring, because of the next two results.
Theorem 1
([5]). If G is -free, then .
Proposition 1
([4]). Let G be a connected graph.
- If G is a cycle on vertices, then .
- If G is a tree, then .
2. A Discussion on Necessary and Sufficient Conditions
An obvious necessary condition for G to admit dual coloring is that . For instance, if is a cycle with vertices, then does not admit dual coloring. Theorem 1 shows that , while Proposition 1 assures that .
However, this condition is not enough, as we will see shortly. Let us consider the generalized Petersen graph, denoted by , which is a class of graphs characterized by the positive integers and . This graph is a 3-regular connected graph on vertices, which are divided into two sets: an outer set and an inner set . The construction of this graph is as follows: each vertex in the outer set is adjacent to and (with indices taken modulo n). In other words, the outer vertices induce a cycle. In addition, every vertex in the inner set is adjacent to the corresponding vertex in the outer set as well as to the vertex in the inner set (with indices taken modulo n). The graph is called a prism; it consists of an outer cycle and an inner cycle connected by the edges .
Figure 1 exhibits three examples of dual colorings of prisms with . For , the graph is Hamiltonian and -free with edges. Thus, . However, Theorem 2 shows that is not dual connected.
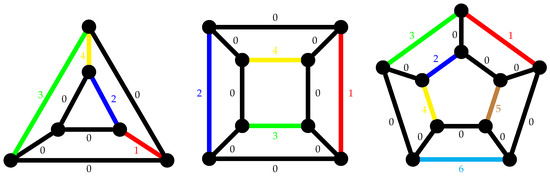
Figure 1.
Dual coloring of prisms with . The colors black, red, blue, green, yellow, brown, and cyan correspond the numbers 0, 1, 2, 3, 4, 5, and 6, respectively.
Theorem 2.
For , the graph is not dual connected.
The proof of Theorem 2 will follow from the following several intermediate claims.
Lemma 1.
The vertices of can be partitioned into n pairs such that the distance between the vertices in each pair is .
Proof.
Let and be the sets of vertices in that form the outer and inner cycles, respectively. For , define as where . This is a bijection where the distance between and is for all . □
Claim 1.
For a fixed , a monochromatically colored has a monochromatic spanning tree.
Proof.
If the incident edges at some vertex v are assigned same color, then monochromatic connectivity implies that the graph must have a monochromatic spanning tree rooted at v. Thus, assume that a monochromatically colored has no vertex v whose incident edges are identically colored. We will show that has a monochromatic path of length .
Let P be the longest monochromatic path with length l. First, we claim that . Otherwise, the longest monochromatic path will be of length . By Lemma 1, let denote the monochromatic path connecting to for all and . Clearly, for any , the paths and cannot share edges. If they do, it would either result in a vertex with its incident edges assigned the same color, or one of the paths would not remain monochromatic. Hence, they are pairwise edge-disjoint. This yields that the total edges are at least , contradicting the fact that has only edges. Therefore, .
Now, we will prove that . Suppose, by contradiction, that . Then, there exists a vertex that is not on the path P, which contains at least four internal vertices . Let , and be four monochromatic paths connecting and to , respectively. Since has no vertex with its incident edges identically colored, each path is colored differently from P. Moreover, since each vertex has degree 3, the paths , and must emanate from , and , respectively. This implies that either some of the paths , and share edges, or has degree 4, which is a contradiction. □
Claim 2.
A coloring σ of is not rainbow if the colored contains a monochromatic spanning tree having degree 3.
Proof.
Let be a coloring of . Suppose that H is a monochromatic spanning tree of the colored . That is, at least edges of are assigned a color i. Let v be a vertex which has degree 3 in H, or equivalently, the incident edges to v in have the same color i. Since v is not adjacent to vertices in , it follows that, in order for v to be rainbow connected to all other vertices, there must be at least edges of colors different to i. This is impossible because the size of is . Thus, is not rainbow. □
Claim 3.
A coloring σ of is not rainbow if the colored contains a monochromatic path of length , where .
Proof.


Let P be a monochromatic path of length given as , and , a spanning subgraph obtained by removing from the edges of P. Clearly, the subgraph H has vertices, each of degree 1 except and , which are of degree 2. Moreover, H consists of components because it has only edges.
If and are not adjacent, then for some distinct vertices and , the paths and are the only components consisting of more than one edge in H; see Figure 2. Recall from Lemma 1 that the vertices can be partitioned into n pairs of vertices, such that the distance between the vertices of each pair is . That is, there are at least 6 such pairs, each with a distance of at least 4. Therefore, either is at a distance at least 4 from a vertex in , and consequently, there exists a pair of distinct vertices and at a distance of at least 4, belonging to two distinct single-edge components and , respectively. As a result, any path connecting to cannot be rainbow, as it must traverse at least two edges of P. Or is at a distance of at least 4 from the vertex in a single-edge component . Now, since any path connecting to will use, at most, either the edge or , such a path cannot be rainbow as well.

Figure 2.
Dashed edges represent the edges of P while the solid ones represent those of H.
Otherwise, and are adjacent, see Figure 3. Then for some distinct vertices and , the path is the only component with more than one edge in H. This leaves a pair of vertices in two distinct single-edge components, where the distance between the vertices of that pair is at least 4. Therefore, they cannot be rainbow connected, as we wanted to prove. □

Figure 3.
Dashed edges represent the edges of P while the solid ones represent those of H.
Claim 1 shows that any monochromatic coloring of will always result in a monochromatic spanning tree. Claims 2 and 3 together show the coloring will not be rainbow as long it has a monochromatic spanning tree. Thus, no coloring of can be monochromatic and rainbow at the same time, which proves the statement of Theorem 2. This raises the following natural questions.
Question 1.
Let G be a connected -free graph. Does every monochromatic coloring of G induce a monochromatic spanning tree?
Question 2.
Does every connected graph G with and admit dual coloring?
Question 3.
Is dual connected when ?
3. Lower Dual Connection Number of Some Graphs
In this section, we will focus on the lower dual connection number of wheels and complete bipartite graphs.
Theorem 3.
Let be a wheel where ; then,
Proof.
For , let be the vertices of the wheel , where the vertices induce a cycle C and is adjacent to every vertex in C. If , then and a single color is sufficient to ensure dual connectivity. Thus, .
For , is not a complete graph. In this case, there exists a pair of vertices at distance 2. Therefore, . For , consider the coloring below:
This coloring is monochromatic since the subgraph induced by the edges of color 1 is a connected spanning subgraph. Consider two non-adjacent vertices and on the cycle C. If i and j have a different parity, then they are connected by a rainbow path through the vertex because . If i and j have the same parity, then, since the cycle C has length , and must be at a distance of 2 on the cycle. Thus, there exists a vertex in C between and such that k has a different parity from i and j. Consequently, the path is rainbow. Therefore, the coloring is rainbow and, consequently, is dual.
For , we claim that . Suppose that is any 2-coloring of . Then, at least of the edges incident to will receive the color x for some . Equivalently, at least vertices of the cycle C will be the endpoints of edges colored by x. With respect to C, two of these vertices, say, u and v, will be at distance greater than 2 because for . Therefore, there is no rainbow path connecting u to v which either goes through or is completely contained within the cycle C. Hence, .
It remains to be shown that . To this end, consider the 3-coloring , defined as follows:
This coloring is monochromatic because all edges of C are assigned color 2 and all vertices of C are adjacent to . Additionally, let and be a pair of non-adjacent vertices on the cycle C. If i and j have a different parity, then and are connected by a rainbow path through the vertex because . Otherwise, i and j have the same parity. Without the loss of generality, suppose . Then, the path is rainbow. Therefore, is dual, which finishes the proof. □
Example 1.
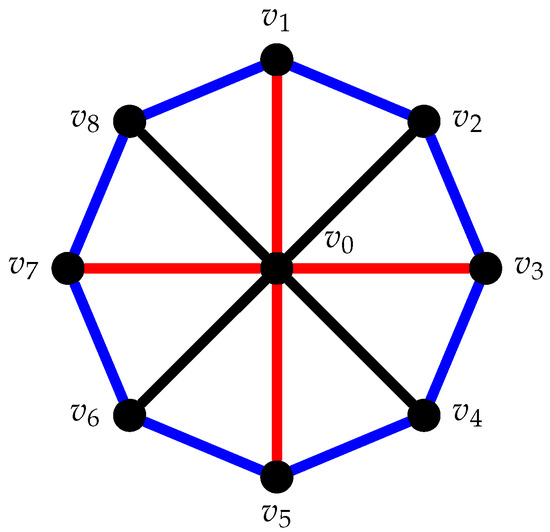
Figure 4 illustrates the coloring used in Theorem 3.

Figure 4.
Dual coloring of wheel graph , where black, red, and blue represent 0, 1, and 2, respectively.
Theorem 4.
Let be a complete bipartite graph with and and . If , then . Otherwise,
The proof of Theorem 4 will be presented later, after the establishment of several necessary concepts and results.
Definition 1.
An matrix Σ over is called transitive if the following conditions hold:
- The columns of Σ are distinct.
- For any pair of columns v and u, there exists an element and a sequence of vectors , such that for each consecutive pair and , there exists at least one position where and have the value x.
Example 2.
For , the identity matrix over is transitive.
Lemma 2.
For and , there exists an matrix Σ over such that both Σ and are transitive.
Proof.
Let be an matrix consisting of all r-dimensional column vectors over , where each vector contains at least one 0 entry. Consequently, has columns, including the identity matrix as a block. Suppose u and v are two distinct columns of with 0 entries in non-corresponding positions i and j, respectively. Then, there exists a standard basis vector w in that has 0 at positions i and j, allowing for a sequence for every such pair of columns. Therefore, is transitive, and so is its transpose , thanks to the existence of the block in . Furthermore, any submatrix obtained by removing columns from other than those in , along with its transpose, will also be transitive. □
Lemma 3.
For and , there exists a transitive matrix over .
Proof.
Aside from the all-zeros column vector, let be an matrix consisting of all r-dimensional column vectors over where each vector contains at least one 0 entry. That is, consists of distinct columns, including the identity matrix as a block. In a manner similar to the argument made in the proof of Lemma 2, for any , there exists an matrix that is transitive, and its transpose is also transitive.
For , let be a matrix consisting of distinct column vectors from such that includes as a block but no vector like for all . Thus, the transpose is transitive because includes . Now, let u and v be two columns. Then, u and v contain a same entry y (not necessarily in corresponding positions, say, in position i and j, respectively). This implies that there exists a standard vector w having y as entry at both positions i and j. Therefore, is transitive. □
Proof of Theorem 4.
Let the vertices of be partitioned into two independent sets and . For a k-coloring , let be an matrix and denote the transpose of , where .
First of all, let us note that is dual if and are transitive. To verify this statement, suppose that v and u are two column vectors of . Then, v and u must differ in at least one coordinate, say, at coordinate c. This implies that the corresponding vertices and are connected by a rainbow path of length 2 through the vertex . Additionally, the transitivity guarantees the existence of a vector sequence such that for some , two consecutive vectors and agree in at least one coordinate by the element x. In other words, for , both and have x at a coordinate . Consequently, there is a monochromatic path of color x connecting to , given as . A similar argument applies to , leading to the same conclusion. That is, there exist rainbow and monochromatic paths between any pair of vertices in the same partition. Hence, is a dual coloring.
If , then is a dual coloring if and only if is transitive and contains a column vector for some . To prove this claim, suppose that is a dual coloring. Since all paths between and are of lengths 2, there is a monochromatic path joining to through a vertex . Hence, and such a vector v exists. Now suppose that there is a column vector u which does not coincide with the vector v at any coordinate. Then, there exists no monochromatic path joining to since the two incident edges at share no common color with the incident edges at . This is a contradiction. Therefore, all column vectors must coincide in at least a coordinate with v. Furthermore, if for some column vectors u and w, then there is no rainbow path joining to . To verify this point, suppose without the loss of generality that u and w coincide with v in their first position. That is, and . One can see immediately that there is no rainbow path of length 2 passing through or . Moreover, assuming that there is a rainbow path of length at least 4, yielding that this path must start with color and end with color . Therefore, there must be a vertex on the path with a column vector l not coinciding with v in any of its coordinates. This is a contradiction.
Conversely, suppose that is transitive and contains a column vector for some . Since the columns of are distinct and have x at one of their two coordinates, the two columns of are also distinct but coincide with x at one coordinate. Thus, the matrix is also transitive.
Now, the maximum number of two-dimensional columns that a transitive matrix over , containing a vector like , can have is given by . Therefore, the lower dual connection number of must be the smallest positive integer k satisfying the following inequality.
Basic simplifications of inequality (2) yields
Therefore, , the smallest positive integer greater or equal . Lastly, we will address the cases when , as follows:
- Case 1
- Suppose that . This implies that . By Lemma 2, there exists an matrix over , such that both and are transitive. The 2-coloring induced by is dual; thus, . In general, because the distance between any two vertices in the same partition is 2. Therefore, .
- Case 2
- If and , then . Lemma 3 guarantees the existence of an matrix over , such that both and are transitive. Thus, . It remains to be shown that . Since , using the elements of to color the edges of results in having either two identical columns or the columns share no entry. Assume that and are two identical columns in . Then, the corresponding vertices and cannot be connected by a rainbow path of length 2 because every path of length 2 will be monochromatic. In addition, if and share no entry, then the corresponding vertices and will not be connected by any monochromatic path. Thus, .
- Case 3
- If , then . In a manner similar to the argument presented in Case 2, using the elements of would result in two identical columns or columns sharing no common entry. Thus, .Consider the 4-coloring given as follows: for or , , and for and ,Note that the incident edges at and are colored with 0, making monochromatic. Furthermore, for and , the vertices and are connected to and through the rainbow paths and , respectively. Additionally, let and , where and . If and have different a parity, and similarly, and have different parity, then the paths and are also rainbow. Otherwise, the paths and are rainbow. Therefore, the coloring is dual, and .
□
Example 3.
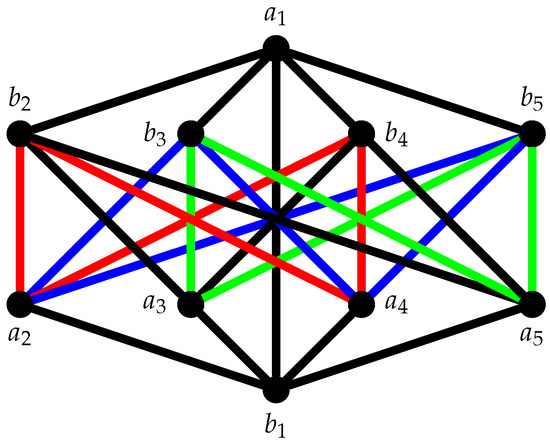
Figure 5 illustrates the dual coloring proposed in case 3 of Theorem 4.

Figure 5.
Dual coloring of , where black, red, blue, and green represent 0, 1, 2, and 3, respectively.
4. Conclusions
An edge coloring of a complete graph will always be rainbow and monochromatic, while a tree does not enjoy this property. This observation motivated us to study dual connectivity on some graphs. Clearly, if a connected graph can be decomposed into two disjoint spanning trees, it is dual connected. This condition is sufficient but not necessary. For instance, the prism on 10 vertices is dual connected, but it cannot be decomposed into two spanning trees. Furthermore, one might conjecture that dense graphs are more likely to admit dual coloring. However, this claim is not always true. Consider the graph formed by the union of a path with vertices and a complete graph with vertices . This graph G is not dual connected because the segment exists in every path connecting to the vertices of ; see Figure 6. Moreover, we showed that the prism , where is not dual connected neither. This naturally poses questions mentioned in Section 2.
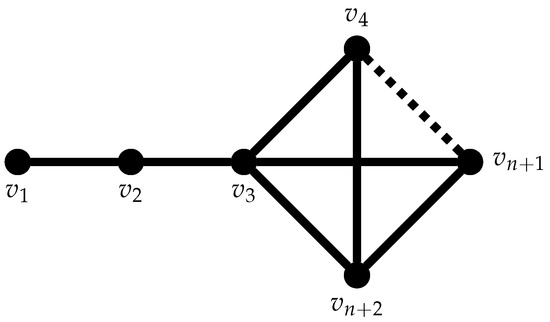
Figure 6.
An example of a dense graph that is not dual connected.
As a correspondence to the rainbow connection number, we defined the lower dual connection number of a dual connected graph G, denoted by , as the minimum number of colors needed to obtain a dual coloring. We then investigated this number in some graphs that admit dual colorings. We can also define the upper dual connection number of a dual connected graph G, denoted as , as the maximum number of colors required for G to obtain a dual coloring. Clearly, the inequality . For future work, two questions need to be investigated:
- What is the upper dual connection number of a complete graph , i.e, ?
- Are there graphs where ?
A biorientation of G is the process of replacing each undirected edge e connecting vertices u to v with the two directed edges and . Wang et al. most recently investigated the rainbow connection number of bioriented graphs; see [15]. In contrast, a bidirection of graph refers to assigning two directional arrows to every edge in the graph. This concept was introduced by Edmonds and Johnson [16] and recently studied by Busch et al. [17]. Directed, bioriented, and bidirected graphs offer a framework for investigating dual connectivity in future research.
Author Contributions
Conceptualization, M.A.M.; Methodology, M.A.M., D.E.O. and H.A.K.; Validation, D.E.O.; Investigation, M.A.M. and H.A.K.; Supervision, D.E.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors thank the referees for the comments and the suggestions provided.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Behr, R. Edge Coloring Signed Graphs. Discrete Math. 2020, 343, 111654. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Y.; Luo, R.; Ye, D.; Zhang, S. Edge coloring of signed graphs. Discret. Appl. Math. 2020, 282, 234–242. [Google Scholar] [CrossRef]
- Mutar, M.A.; Sivaraman, V.; Slilaty, D. Signed Ramsey Numbers. Graphs Comb. 2024, 40, 9. [Google Scholar] [CrossRef]
- Chartrand, G.; Johns, G.L.; McKeon, K.A.; Zhang, P. Rainbow connection in graphs. Math. Bohem. 2008, 133, 85–98. [Google Scholar] [CrossRef]
- Caro, Y.; Yuster, R. Colorful monochromatic connectivity. Discret. Math. 2011, 311, 1786–1792. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Liu, S.; Chandran, L.S.; Mathew, R.; Rajendraprasad, D. Rainbow Connection Number and Connectivity. Electron. J. Comb. 2012, 19, P17. [Google Scholar] [CrossRef]
- Caro, Y.; Lev, A.; Roditty, Y.; Tuza, Z.; Yuster, R. On Rainbow Connection. Electron. J. Comb. 2008, 15, R26. [Google Scholar] [CrossRef] [PubMed]
- Chartrand, G.; Johns, G.L.; McKeon, K.A.; Zhang, P. The Rainbow Connectivity of a Graph. Networks 2009, 54, 75–81. [Google Scholar] [CrossRef]
- Gu, R.; Li, X.; Qin, Z.; Zhao, Y. More on the Colorful Monochromatic Connectivity. Bull. Malays. Math. Sci. Soc. 2015, 40, 1769–1779. [Google Scholar] [CrossRef]
- Li, X.; Wu, D. A Survey on Monochromatic Connections of Graphs. Theory Appl. Graphs 2018, 4. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Shi, Y.; Sun, Y. Rainbow Connections of Graphs: A Survey. Graphs Comb. 2012, 29, 1–38. [Google Scholar] [CrossRef]
- Sun, Y. On Rainbow Total-Coloring of a Graph. Discret. Appl. Math. 2015, 194, 171–177. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, H.; Li, W. Total-Rainbow Connection and Forbidden Subgraphs. Discret. Appl. Math. 2024, 359, 364–370. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Zhang, Y. Total monochromatic connection of graphs. Discret. Math. 2017, 340, 175–180. [Google Scholar] [CrossRef][Green Version]
- Wang, L.; Liu, S.; Jiang, H. Rainbow connections of bioriented graphs. Heliyon 2024, 10, e31426. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, J.; Johnson, E.L. Matching: A well-solved class of integer linear programs. In Combinatorial Structures and Their Applications (Proceedings of the Calgary International Conference on Combinatorial Structures and Their Applications held at the University of Calgary. June 1969); Gordon and Breach: New York, NY, USA, 1970; pp. 89–92, MR 0267898. [Google Scholar]
- Busch, A.; Mutar, M.; Slilaty, D. Hamilton cycles in bidirected complete graphs. Contrib. Discrete Math. 2022, 17, 137–149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).