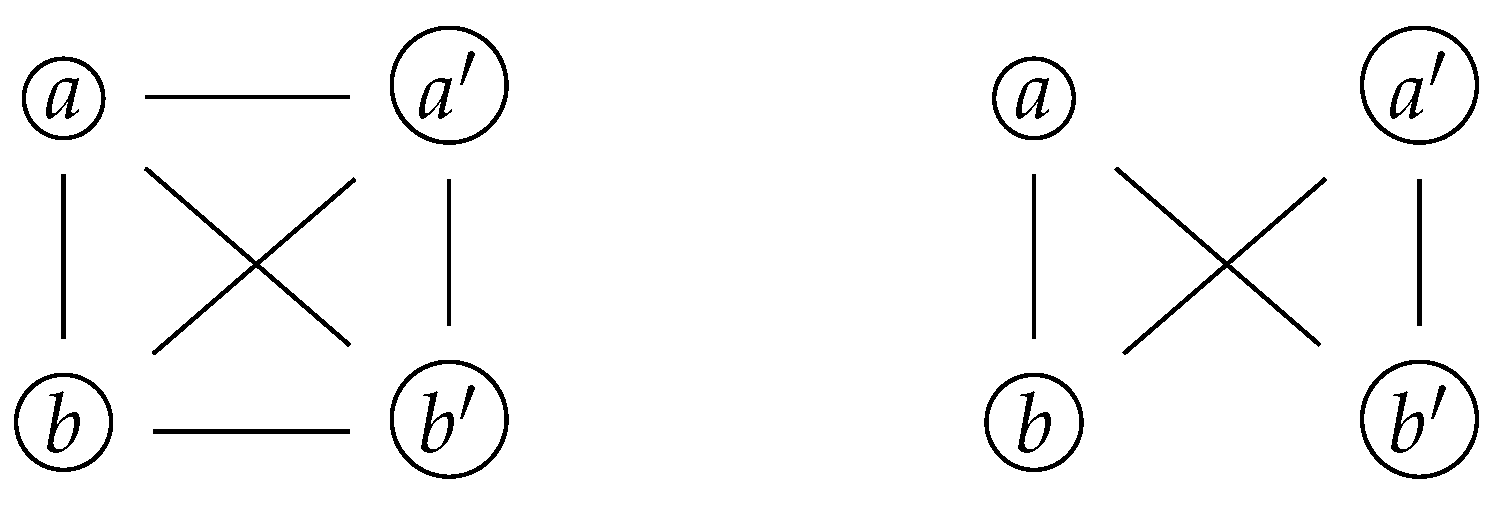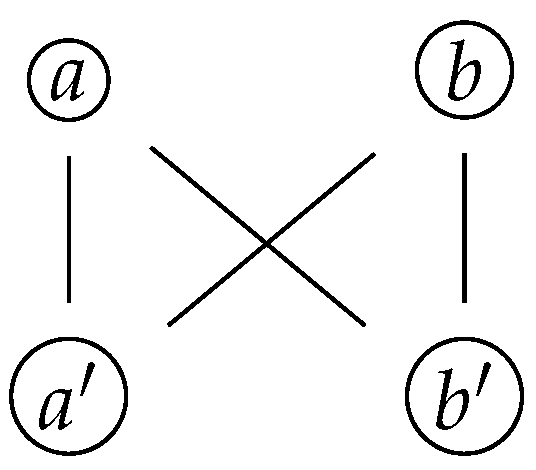On the Graph Isomorphism Completeness of Directed and Multidirected Graphs

Abstract

The category of directed graphs is isomorphic to a particular category whose objects are labeled undirected bipartite graphs and whose morphisms are undirected graph morphisms that respect the labeling. Based on this isomorphism, we begin by showing that the class of all directed graphs is a Graph Isomorphism Complete class. Afterwards, by extending this categorical framework to weighted prime graphs, we prove that the categories of multidirected graphs with and without self-loops are each isomorphic to a particular category of weighted prime graphs. Consequently, we prove that these classes of multidirected graphs are also Graph Isomorphism Complete.

1. Introduction

The Graph Isomorphism (GI) problem is a fundamental challenge in computer science and graph theory. It seeks to determine whether two finite graphs, G and H, are isomorphic. Recall that an isomorphism is a bijective function $f:V\left(G\right)⟶V\left(H\right)$ that preserves the graph structure. This means that if two vertices are connected by an edge in G, their corresponding vertices in H must also be connected by an edge. If such a function exists, then the graphs G and H are said to be isomorphic.

The complexity of the Graph Isomorphism problem is unique compared to many other problems in graph theory. It does not fit neatly into the categories of P or $NP$-complete. Recall that a problem is in P if it can be solved in polynomial time by a deterministic Turing machine, while an $NP$-complete problem is one that is both in $NP$ and $NP$-hard; the latter means that a solution to the problem can be verified in polynomial time and every other problem in $NP$ can be reduced to this problem in polynomial time. Within this context, it is known that the Graph Isomorphism problem lies in class $NP$, meaning that if a proposed isomorphism is given, its correctness can be verified in polynomial time. However, it has not been proven that the problem can be solved in polynomial time, nor has it been shown to be $NP$-complete.

Significant progress has been made in addressing the Graph Isomorphism problem (see [1,2,3,4,5,6,7,8,9,10,11,12,13,14]). For instance, Babai [1] introduced a quasi-polynomial time algorithm, marking a major advancement that bridges the gap between polynomial and exponential time complexity. While this algorithm does not classify the problem as being in P, it does lower the upper bounds of its complexity, providing new avenues for research.

Several methods solve the GI problem for specific classes of graphs in polynomial time. Surveys have identified many additional classes of graphs for which the GI problem is equivalent to that of arbitrary graphs. Here, “equivalence” means that the GI problem for a specific class can be transformed into the GI problem for arbitrary (undirected) graphs in polynomial time, and vice versa (see for instance [4,10,14]). This relationship is what defines a class C of graphs to be GI-complete.

Recently, the class of GI-complete graphs has expanded to include chordal bipartite graphs and strongly chordal graphs [13], geometric graphs [12], and perfect graphs [5]. Although the class of directed graphs was proved to be GI-complete in [10], to our knowledge, there is no formal proof that the class of multidirected graphs is GI-complete. Here, we approach this using concepts and notions from Category Theory. Specifically, we utilize a categorical framework that connects directed graphs with a specific type of undirected graph known as a prime graph [15]. These prime graphs are undirected bipartite graphs that have a prime labeling, which encodes directional information. Using this connection, we demonstrate that the class of directed graphs is GI-complete. However, our main contribution relies on extending this result first to the class of multidirected graphs without self-loops, and later to the class of multidirected graphs with self-loops.

From a categorical perspective, these findings illustrate how the GI-complete class encapsulates the complexity of the Graph Isomorphism problem within a broader context of similarly structured problems. The reductions and equivalences we establish indicate that the inherent difficulty of the Graph Isomorphism problem is shared across these classes, despite their structural differences. Thus, the GI-complete classes serve as a valuable framework for understanding the boundaries and relationships within computational complexity.

The rest of this paper is organized as follows: Section 2 gives some preliminary definitions and facts about the category of prime graphs. In Section 3, we present our theoretical results. We first prove that the class of prime graphs is isomorphic complete. This is considered to prove that the class of directed graphs is isomorphic complete as well. Later, we show that the category of multidirected graphs and the category of weighted prime graphs are isomorphic. This result, in turn, is used to proof that the class of multidirected graphs is isomorphic complete. Finally, Section 4 gives some concluding arguments and future lines of research.

2. Preliminaries

Mathematically, a graph is a pair $G=(V,E)$, where V is a set whose elements are called vertices (or nodes), and E is a set consisting of two-element subsets of V, called edges (or connections). A graph is undirected if its set of edges consists of connections without directionality. In this case, we will denote an edge between the nodes u and v as an unordered pair $(u,v)=(v,u)$, since the two-element subsets $\{u,v\}$ and $\{v,u\}$ represent the same unordered set. In contrast, a graph is directed if all its edges are connections with a direction. In this case, we will denote an edge from node u to node v as an ordered pair $(u,v)$. Note that the order in the two-element subsets is now significant, meaning $\{u,v\}\ne \{v,u\}$ for directed graphs. Conceptually, we can think of an edge $(u,v)$ as an arrow with initial node u and target node v. In general, given a vertex v in G, we call u a neighbor of v if u and v are connected by an edge in G. Throughout this work, we will consider simple directed graphs, that is, directed graphs with no multiple edges and no self-loops.

Here, we think of a graph morphism as a function between the vertex sets that preserves the structure or topology of the graphs; that is, it preserves the edges under transformation. Formally,

Definition 1.

Let $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ be two undirected graphs. An undirected graph morphism is a function $f:V_1⟶V_2$ that maps adjacent vertices in $G_1$ into adjacent vertices in $G_2$.

Algebraically, an undirected graph morphism f is a function that satisfies that, for any pair of vertices $u,v\in V_1$ with $(u,v)\in E_1$, we have $(f\left(u\right),f\left(v\right))\in E_2$. For the case of directed graphs $G_1$ and $G_2$, we say that a function $V_1\stackrel{f}{⟶}{V}_2$ is a directed graph morphism if f maps initial nodes into initial nodes, and terminal nodes into terminal nodes. In this work, we focus on particular graph morphisms known as graph isomorphisms. Formally,

Definition 2.

Let $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ be two graphs. We say that a graph morphism $f:V_1⟶V_2$ is a graph isomorphism if f is a bijection between the vertex sets.

One can verify that, in both undirected and directed case, the composition of two graph morphisms always yields another graph morphism. Further, the composition is an associative operation that has a neutral element, called the identity morphism (which coincides with the identity map). These properties constitute the definition of a category.

Definition 3.

A category $\mathcal{C}$ consists of a collection of objects $X,Y,Z,\cdots$, a collection of morphisms $f:X⟶Y$ between the objects, and a composition operation by which two morphisms $f:X⟶Y$ and $g:Y⟶Z$ can be combined to produce another morphism $h:X⟶Z$. Also, for each object, there is an identity morphism, and the composition is an associative operation.

Considering the above, the collection of all undirected graphs with all undirected graph morphisms form a category denoted by UndGraph. Likewise, the collection of all simple directed graphs with all directed graph morphisms form a category, denoted by DGraph. In this work, we will consider the category PGraphs, described in [15], whose objects are prime graphs.

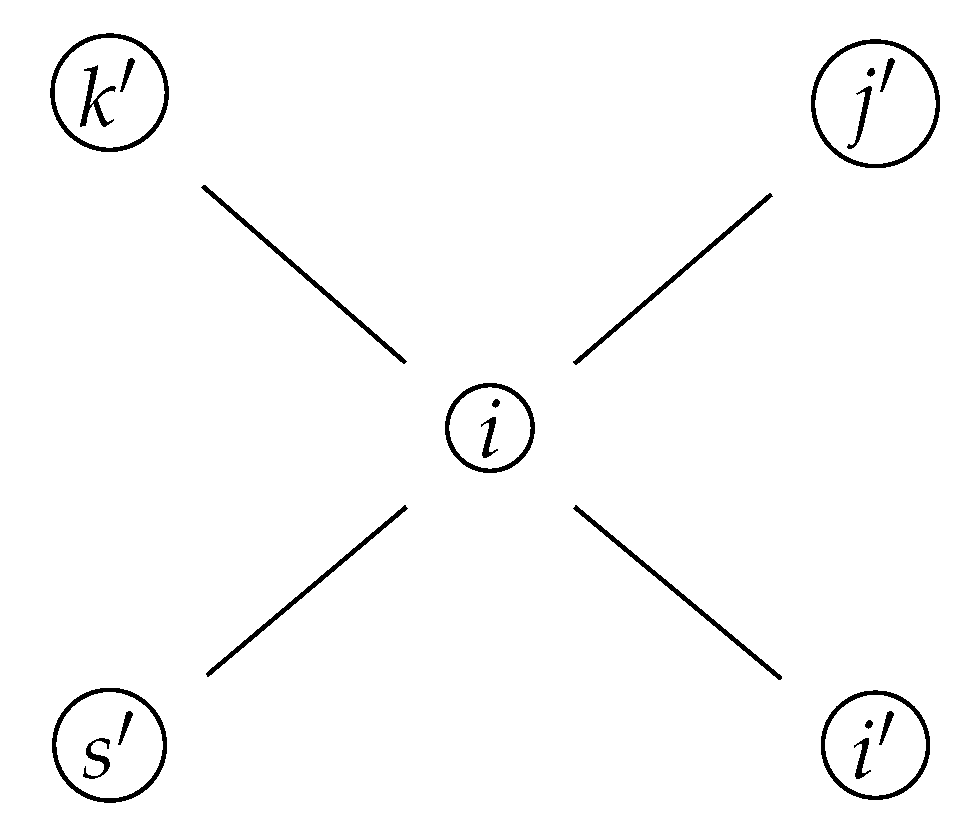
Definition 4.

Let $G_u=\left(V_u,E_u\right)$ be an undirected graph with $2n$ vertices, and let the sets $I=\{1,2,\cdots ,n\}$ and $I^{\prime }=\{1^{\prime },2^{\prime },\cdots ,n^{\prime }\}$. We say that $G_u$ admits a  prime labeling  if there exists a bijective function $\phi :V_u⟶I\cup I^{\prime }$ such that for $v\in V_u$ one has the following three cases:

(i) 

If $\phi \left(v\right)=i$ and $i\in I$, then for each neighbor u of v, $\phi \left(u\right)=k^{\prime }$ for some $k^{\prime }\in I^{\prime }$. (We visualize this in Figure 1).

(ii) 

If $\phi \left(v\right)=i^{\prime }$ and $i^{\prime }\in I^{\prime }$, then for each neighbor u of v, $\phi \left(u\right)=k$ for some $k\in I$. (We visualize this in Figure 2).

(iii) 

If $\phi \left(v\right)=i$ and $i\in I$, then there exists a neighbor w of v such that $\phi \left(w\right)=i^{\prime }$ and $i^{\prime }\in I^{\prime }$. (We visualize this in Figure 3).

For instance, the following graphs (Figure 4)

are not prime graphs, as the prime-labeled nodes are connected to each other. However, the graph on the right becomes a prime graph if we endow it with the following prime labeling (Figure 5).

One important property of prime graphs is that these can be visualized as undirected bipartite graphs (Figure 6). This is a consequence of the definition of a prime labeling, as prime-labeled nodes only have non-prime-labeled nodes as neighbors, and vice versa.

In [15], it is proved that the category DGraphs and the category PGraphs are isomorphic. This means that the objects and morphisms of these two categories are in a one-to-one correspondence. Grounded on this isomorphism, we prove in the next section that the class of directed graphs is isomorphic complete, which paves the way to generalize the result to the case of multidirected graphs.

Moreover, by extending this isomorphism to the category of weighted prime graphs and the category of multidirected graphs, we show in Section 3.2 that the class of multidirected graphs is isomorphic complete.

3. Results

This section contains our main theoretical results. First, we show a polynomial time reduction between prime graphs and undirected graphs, which leads us to prove that the class of directed graphs is isomorphic complete. Then, we extend the isomorphism between DGraphs and PGraphs to consider multidirected graphs and weighted prime graphs. This last isomorphism, in turn, is used for the polynomial time reduction between multidirected graphs and undirected graphs.

3.1. Directed Graphs Are GI-Complete

Broadly speaking, we say that a class $\mathcal{C}$ of graphs is isomorphism complete if one can reduce its isomorphism problem to that of undirected graphs in polynomial time. This reduction is in both directions; that is, it comprises a map that relates undirected graphs to graphs in $\mathcal{C}$, and another map relating graphs in $\mathcal{C}$ with undirected graphs. Each of these transformations is subject to three main properties as described in [4] (Section 3.2). For instance, if T assigns undirected graphs to graphs in $\mathcal{C}$, then the following hold:

• $T\left(G\right)$ is in $\mathcal{C}$ for each undirected graph G;
• G is isomorphic to H if, and only if, $T\left(G\right)$ is isomorphic to $T\left(H\right)$;
• $T\left(G\right)$ can be computed in polynomial time from the number of vertices of G.

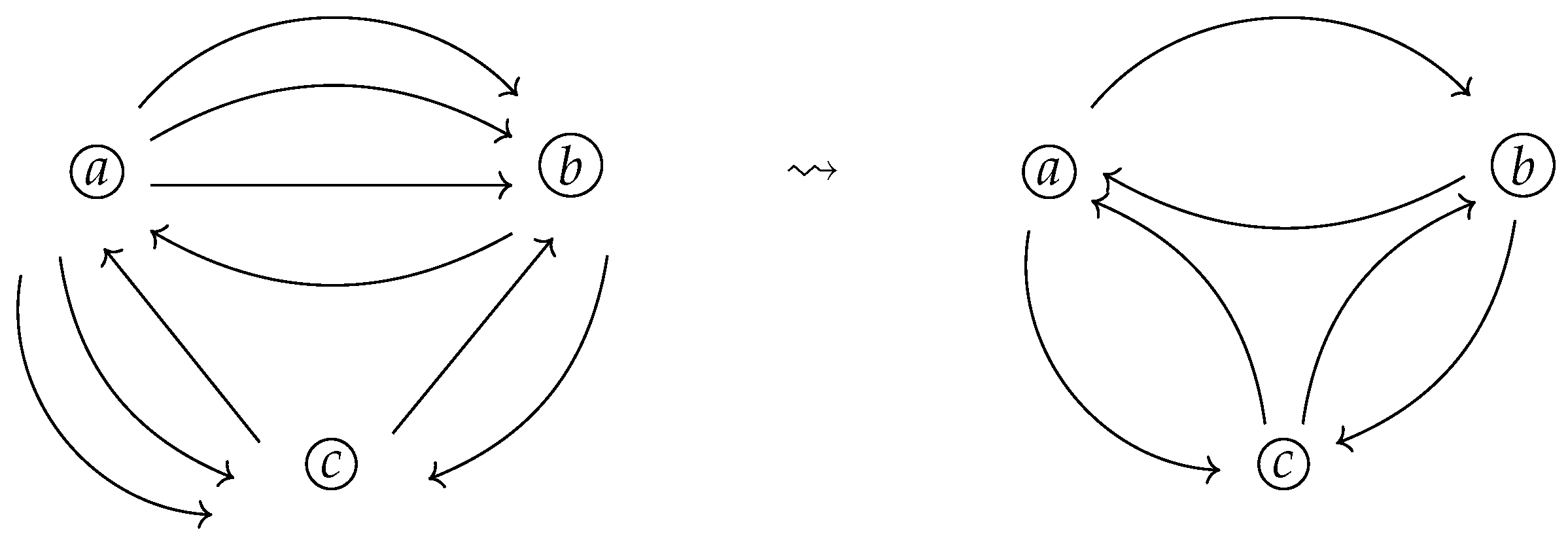
Example 1.

Any undirected graph can be turned into a bipartite graph by splitting each edge into two edges and inserting a new vertex between them. This process preserves isomorphisms and is carried out in polynomial time. The reverse transformation is trivial, as each bipartite graph is an undirected graph. Thus, the class of bipartite graphs is isomorphic complete.

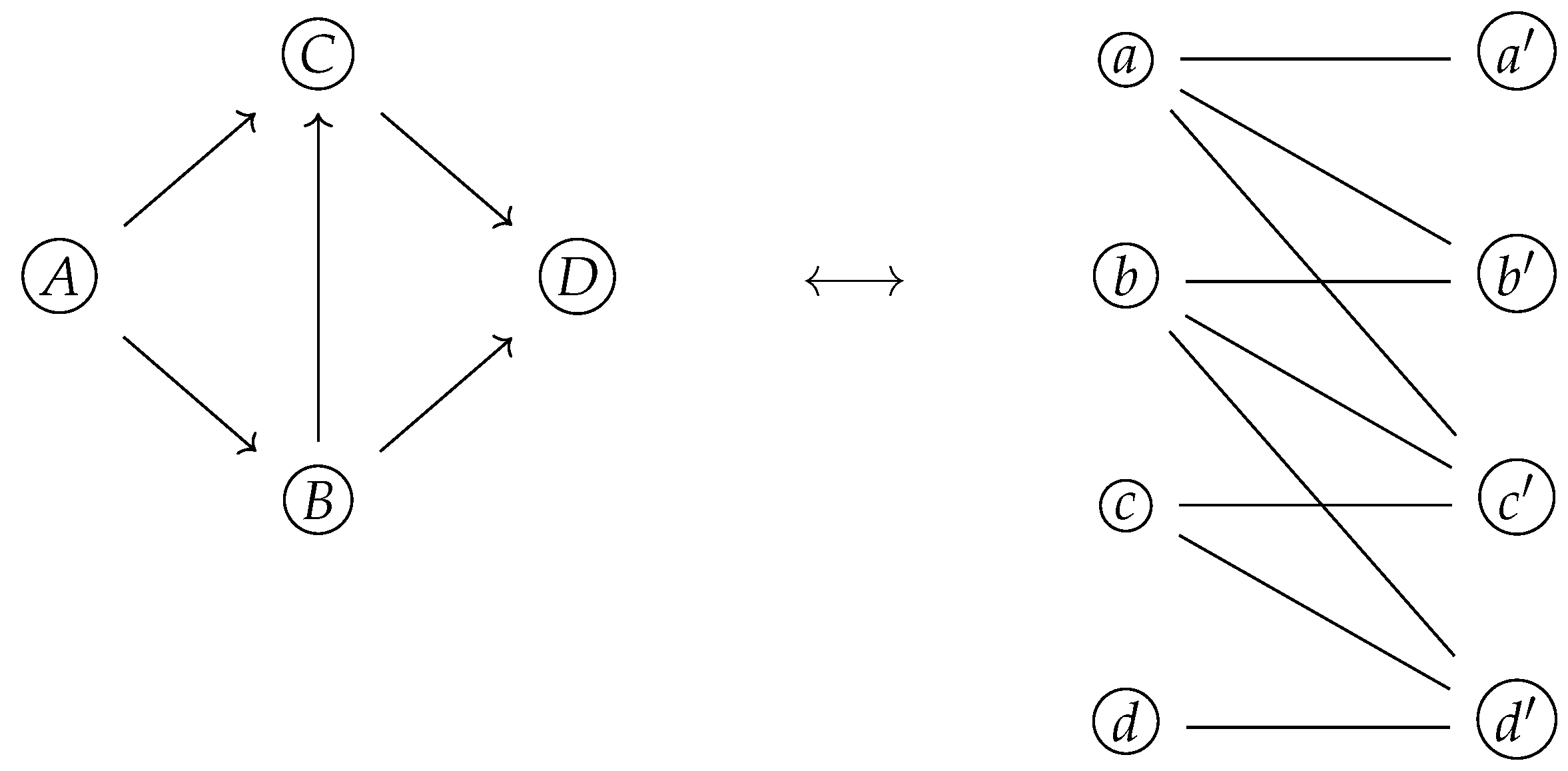
In [15], the authors introduce the category of prime graphs and prime graph morphisms. Essentially, a prime graph is an undirected graph that allows a prime labeling function. Here, the prime labeling function endows a notion of direction in the corresponding prime graphs. Further, the authors prove that the category of prime graphs and the category of simple directed graphs are isomorphic; that is, there exists a bijective correspondence between the objects and the morphisms that respects the composition operation. As an example, Figure 7 shows a simple directed graph and its corresponding prime graph under this isomorphism.

Moreover, the time complexity of transforming a directed graph into a prime graph is $O\left(n\right)$, where n is the number of nodes. One consequence of the prime labeling function defined on prime graphs is that the adjacency matrix for any prime graphs has the form

$$\left(\begin{array}{cc}0& A\\ A^T& 0\end{array}\right)$$

where A is a square matrix, $A^T$ is its transpose matrix, and 0 is a zero matrix of the same size as A. In this context, matrix A contains all the adjacencies between prime and non-prime nodes. As we see next, the class of all prime graphs is isomorphic complete.

Remark 1.

Two graphs G and H are isomorphic if, and only if, their adjacency matrices are similar. This means that, if $A_G$ and $A_H$ denote the adjacency matrices of G and H, respectively, then there exist an invertible matrix P such that $A_G=P{A}_H{P}^{-1}$. Moreover, as graph isomorphism involves permutations of the vertices, it follows that P is a permutation matrix of the identity matrix and, hence, it is an orthogonal matrix. This way, we see that $P^{-1}=P^T$.

Proposition 1.

There exists a transformation that reduces undirected graphs to prime graphs in polynomial time.

Proof. 

Let $G_u$ be an undirected graph with n vertices, and let $A_u$ be its adjacency matrix. Let us define the matrix $\overline{A_u}=A_u+I_n$, where $I_n$ is the identity matrix of $n\times n$. Thus, by considering the matrix

$$\left(\begin{array}{cc}0& \overline{A_u}\\ {\overline{A_u}}^T& 0\end{array}\right),$$

we obtain a prime graph $G_p$ that contains the adjacencies of the undirected graph $G_u$ in the non-diagonal entries of the matrix $\overline{A_u}$. Note that this process is carried out in polynomial time. Now, if $G_{u_1}$ is isomorphic to $G_{u_2}$, by Remark 1, $A_{u_1}=P{A}_{u_2}{P}^T$ for a permutation matrix P. This way, we obtain that

$$P\overline{A_{u_2}}{P}^T=P\left(A_{u_2}+I_n\right)P^T=P{A}_{u_2}{P}^T+P{P}^T=A_{u_1}+I_n=\overline{A_{u_1}}.$$

Hence, the matrices $\overline{A_{u_1}}$ and $\overline{A_{u_2}}$ are similar. With this in mind, we claim that the adjacency matrices

$$\left(\begin{array}{cc}0& \overline{A_{u_1}}\\ {\overline{A_{u_1}}}^T& 0\end{array}\right)\mathrm{and}\left(\begin{array}{cc}0& \overline{A_{u_2}}\\ {\overline{A_{u_2}}}^T& 0\end{array}\right)$$

of the corresponding prime graphs $G_{p_1}$ and $G_{p_2}$, respectively, are similar. Indeed, the matrices

$$\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\mathrm{and}\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right)$$

are inverse to each other and satisfy that

$$\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\left(\begin{array}{cc}0& \overline{A_{u_2}}\\ {\overline{A_{u_2}}}^T& 0\end{array}\right)\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right)=\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\left(\begin{array}{cc}0& \overline{A_{u_2}}{P}^T\\ {\overline{A_{u_2}}}^T{P}^T& 0\end{array}\right)$$

$$=\left(\begin{array}{cc}0& P\overline{A_{u_2}}{P}^T\\ P{\overline{A_{u_2}}}^T{P}^T& 0\end{array}\right)=\left(\begin{array}{cc}0& \overline{A_{u_1}}\\ {\overline{A_{u_1}}}^T& 0\end{array}\right)$$

The last equality follows because $P\overline{A_{u_2}}{P}^T=\overline{A_{u_1}}$, and so,

$$\overline{A_{u_2}}=I_n\overline{A_{u_2}}{I}_n=\left(P^{T}P\right)\overline{A_{u_2}}\left(P^{T}P\right)=P^T\left(P\overline{A_{u_2}}{P}^T\right)P=P^T\overline{A_{u_1}}P.$$

In turn, we get that ${\left(\overline{A_{u_2}}\right)}^T=P^T{\left(\overline{A_{u_1}}\right)}^{T}P$. Consequently,

$$P{\left(\overline{A_{u_2}}\right)}^T{P}^T=P{P}^T{\left(\overline{A_{u_1}}\right)}^{T}P{P}^T=I_n{\left(\overline{A_{u_1}}\right)}^T{I}_n={\left(\overline{A_{u_1}}\right)}^T.$$

Assume now that $G_{u_1}$ and $G_{u_2}$ are two undirected graphs such that their corresponding prime graphs $G_{p_1}$ and $G_{p_2}$ are isomorphic. Then, by Remark 1, it follows that the adjacency matrices

$$\left(\begin{array}{cc}0& \overline{A_{u_1}}\\ {\left(\overline{A_{u_1}}\right)}^T& 0\end{array}\right)\mathrm{and}\left(\begin{array}{cc}0& \overline{A_{u_2}}\\ {\left(\overline{A_{u_2}}\right)}^T& 0\end{array}\right)$$

are similar. In this case, by the way prime graph morphisms are defined, the invertible matrix corresponding to the permutation of the vertices must preserve the labelings. In other words, it must send prime-labeled nodes to prime-labeled nodes, as well as non-prime-labeled nodes to non-prime-labeled nodes. Additionally, it must be compatible with the prime and non-prime label for each node in the following sense: if $a\in V\left(G_{p_1}\right)$ and $b\in V\left(G_{p_2}\right)$ are two non-prime-labeled nodes that correspond to each other under the prime graph isomorphism, then their prime-labeled nodes $a^{\prime }\in V\left(G_{p_1}\right)$ and $b^{\prime }\in V\left(G_{p_2}\right)$ also correspond to each other. Thus, the invertible matrix must have the form

$$\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)$$

and, further, its inverse coincides with the matrix $\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right)$, due to orthogonality. Taking the above into consideration, one obtains that

$$\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\left(\begin{array}{cc}0& \overline{A_{u_1}}\\ {\overline{A_{u_1}}}^T& 0\end{array}\right)\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right)=\left(\begin{array}{cc}0& \overline{A_{u_2}}\\ {\overline{A_{u_2}}}^T& 0\end{array}\right),$$

from which it follows that $\overline{A_{u_2}}=P\overline{A_{u_1}}{P}^T$. Hence, $\overline{A_{u_1}}$ and $\overline{A_{u_2}}$ are similar matrices through the permutation matrix P. Consequently, by Remark 1, the undirected graphs $G_{u_1}$ and $G_{u_2}$ are isomorphic. □

Example 2.

On the left of Figure 8, we have the undirected graph $G_u$, and on the right, we have its corresponding prime graph $G_p$.

Notice that, for the undirected edge $(a,d)$ in $G_u$, we constructed two edges in $G_p$: one is $(a,d^{\prime })$ and the other is $(d,a^{\prime })$.

Remark 2.

The Proposition 1 might also be argued as follows: Any undirected graph $G_u$ can be transformed into a directed graph $G_d$ by considering two directed edges $(a,b)$ and $(b,a)$, for each undirected edge $(a,b)$ in $G_u$. Then, by applying [15] (Theorem 4), one obtains a prime graph whose adjacency matrix has the form

$$\left(\begin{array}{cc}0& \overline{A_u}\\ {\overline{A_u}}^T& 0\end{array}\right),$$

with $\overline{A_u}=A_u+I_n$. Here, $A_u$ corresponds to the adjacency matrix of the undirected graph $G_u$, and $I_n$ is the identity matrix of $n\times n$. The above process is verified in Example 2, where for the undirected edge $(a,d)$ in $G_u$, we defined the edges $(a,d^{\prime })$ and $(d,a^{\prime })$ in $G_p$, which correspond to the directed edges $(a,d)$ and $(d,a)$ in $G_d$. It is also worth noticing that the identity matrix $I_n$ is responsible for all edges of the form $(a,a^{\prime })$ in $G_p$.

To prove the converse of Proposition 1, we will associate wth each prime graph an undirected graph that reflects the essence of the prime labeling. For illustrative purposes, consider the following.

Example 3.

On the left of Figure 9, we have the prime graph $G_p$, and on the right, we have its corresponding undirected graph $G_u$.

Observe that the edges in $G_p$ of the form $(x,y^{\prime })$, with $x\ne y$, are the ones that generate the edges of the undirected graph $G_u$.

Proposition 2.

There exists a transformation that reduces prime graphs to undirected graphs in polynomial time.

Proof. 

Let $G_p$ be a prime graph with $2n$ nodes. Then, its adjacency matrix has the form

$$\left(\begin{array}{cc}0& A\\ A^T& 0\end{array}\right)$$

where A is a square matrix of size $n\times n$. Moreover, by the way prime graphs are defined, matrix $A=A_u+I_n$, with $A_u$ being an $n\times n$ matrix with 0 in the diagonal. Considering this, we define the undirected graph $G_u$ as the graph with $A_u$ as its adjacency matrix. Note that this process is carried out in polynomial time.

Now, let $G_{p_1}$ and $G_{p_2}$ be two isomorphic prime graphs whose adjacency matrices are given by $A_1$ and $A_2$, respectively. Then, by Remark 1, $A_1$ and $A_2$ are similar matrices. Moreover, as described in Proposition 1, the invertible matrix must be a permutation matrix of the form

$$\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)$$

with the inverse given by $\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right)$. This way, we have that

$$\left(\begin{array}{cc}0& A_1\\ A_1^T& 0\end{array}\right)=\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\left(\begin{array}{cc}0& A_2\\ A_2^T& 0\end{array}\right)\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right),$$

which implies that $A_1=P{A}_2{P}^T$. Furthermore, as $A_1=A_{u_1}+I_n$ and $A_2=A_{u_2}+I_n$, we obtain that

$$A_{u_1}+I_n=A_1=P{A}_2{P}^T=P\left(A_{u_2}+I_n\right)P^T$$

$$=P{A}_{u_2}{P}^T+P{I}_n{P}^T=P{A}_{u_2}{P}^T+P{P}^T=P{A}_{u_2}{P}^T+I_n.$$

Consequently, we obtain that $A_{u_1}$ and $A_{u_2}$ are similar matrices, thus showing that $G_{u_1}$ and $G_{u_2}$ are isomorphic.

Assume now that the undirected graphs $G_{u_1}$ and $G_{u_2}$, corresponding to the prime graphs $G_{p_1}$ and $G_{p_2}$, are isomorphic. Then, by Remark 1, their adjacency matrices $A_{u_1}$ and $A_{u_2}$ are similar. Hence, $A_{u_1}=P{A}_{u_2}{P}^T$, with P being a permutation matrix. Considering this, we have that

$$A_1=A_{u_1}+I_n=P{A}_{u_2}{P}^T+P{I}_n{P}^T$$

$$=P\left(A_{u_2}+I_n\right)P^T=P{A}_2{P}^T.$$

Moreover, it follows that $A_1^T={\left(P^T\right)}^T{A}_2^T{P}^T=P{A}_2^T{P}^T$. Taking this into consideration, we can see that

$$\left(\begin{array}{cc}0& A_1\\ A_1^T& 0\end{array}\right)=\left(\begin{array}{cc}P& 0\\ 0& P\end{array}\right)\left(\begin{array}{cc}0& A_2\\ A_2^T& 0\end{array}\right)\left(\begin{array}{cc}{P}^T& 0\\ 0& P^T\end{array}\right).$$

Thus, $G_{p_1}$ and $G_{p_2}$ are isomorphic. □

As a consequence of Proposition 1 and Proposition 2, we have the following:

Theorem 1.

The class of prime graphs is isomorphic complete.

Moreover, since the transformation between prime graphs and simple directed graphs shown in [15] is polynomial in time, we have the following.

Theorem 2.

The class of directed graphs is isomorphic complete.

3.2. Multidirected Graphs Are GI-Complete

In this section, we show that the class of multidirected graphs is GI-complete. To this end, we start by considering the category MGraph, whose objects are multidirected graphs with no self-loops, and whose morphisms are multidirected graph morphisms. We first show that MGraph is isomorphic to a category WPGraph, whose objects are weighted prime graphs and whose morphisms are given by prime graph morphisms that respect the edges’ multiplicity. This isomorphism, in turn, leads us to prove that the class of multidirected graphs with no self-loops is GI-complete. After, by modifying the weight values on the weighted prime graphs, we show that the class of multidirected graphs, now with self-loops allowed, is also GI-complete.

3.2.1. Multidirected Graphs and Weighted Prime Graphs Are Isomorphic

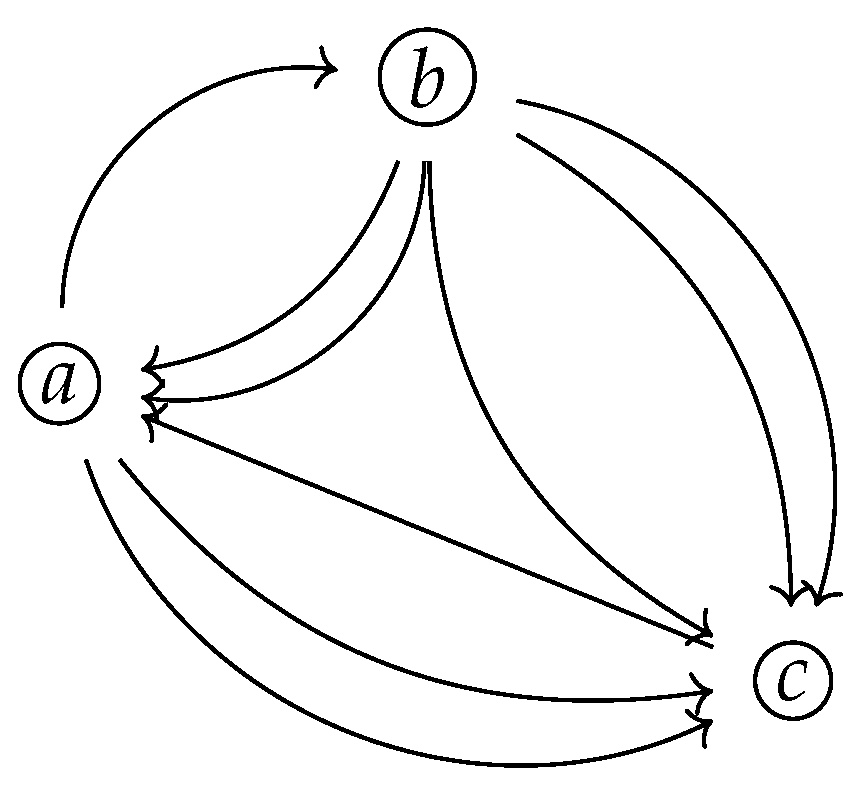
We start considering multidirected graphs as directed graphs without self-loops, and where multiple directed edges between two nodes are allowed. This multiplicity can be represented as a weight value taken from the positive integers ${\mathbb{Z}}^{+}$. For instance, for the multidirected graph in Figure 10,

the edge multiplicity of the arrow with tail a and head c is 2, while the edge multiplicity of the arrow with tail c and head a is 1. From what follows, we will denote the edge multiplicity of a directed edge $(a,b)$ by $m(a,b)$.

Definition 5.

Let $M_1$ and $M_2$ be two multidirected graphs. We say that the function $f:V\left(M_1\right)⟶V\left(M_2\right)$ is a multidirected graph morphism if the following conditions hold:

1. 

For any $(u,v)\in E_{M_1}$, $(f\left(u\right),f\left(v\right))\in E_{M_2}$;

2. 

$m(u,v)\le m\left(f\right(u),f(v\left)\right)$ for any $(u,v)\in E_{M_1}$.

The above definition can be rephrased by saying that a multidirected graph morphism is a directed graph morphism—between the underlying directed graphs—-that respects the edge multiplicity. With this in mind, it follows that the composition of multidirected graph morphisms is an associative operation. Moreover, for each multidirected graph, the identity morphism coincides with the identity map. Hence, one obtains that the collection of multidirected graphs along with the collection of multidirected graph morphisms forms a category we denote by MGraph.

Now, on the other hand, we have weighted prime graphs. Here, the weight values are also taken from the set of all positive integers ${\mathbb{Z}}^{+}$, with one constraint: the weight of any edge of the form $(v_i,v_i^{\prime })$ will always be 1 (see Figure 11). From now on, we will call these type of graphs weighted prime graphs; these will comprise the class of objects of a category we denote by WPGraph.

With regard to morphisms, these are given by functions between the underlying prime graphs that respect the topology, as well as the weight values on the corresponding edges. In other words,

Definition 6.

Let $G_{p_1}$ and $G_{p_2}$ be two weighted prime graphs. We say that the function $f:V\left(G_{p_1}\right)⟶V\left(G_{p_2}\right)$ is a weighted prime graph morphism if the following hold:

1. 

f is a prime graph morphism between the underlying prime graphs;

2. 

if $w(v_i,v_j^{\prime })$ is the weight of the edge $(v_i,v_j^{\prime })$ in $G_{p_1}$, then, $w(v_i,v_j^{\prime })\le w(f\left(v_i\right),f{\left(v_j\right)}^{\prime })$.

Notice that weighted prime graph morphisms are essentially prime graph morphisms that respect multiplicity. Thus, their composition is an associative operation. Further, the identity morphism coincides with the identity map for each weighted prime graph. Hence, one obtains that the class WPGraph of weighted prime graphs becomes a category whose morphisms are given by weighted prime graph morphisms.

We will now show that the categories MGraph and WPGraph are isomorphic. First, note that each multidirected graph has a unique underlying structure of a directed graph, obtained by compressing all multiple edges.

Example 4.

On the left of Figure 12, we have a multidirected graph, and on the right, we have its underlying structure as a directed graph.

Let us consider a multidirected graph morphism $f_m:G_{m_1}⟶G_{m_2}$. Notice that, by definition, $f_m$ is a directed graph morphism that respects multiplicities on the edges. Thus, by [15] (Theorem 4), $f_m$ is in correspondence with a prime graph morphism $f_p:G_{p_1}⟶G_{p_2}$. Here, the prime graphs $G_{p_1}$ and $G_{p_2}$ are obtained by applying [15] (Theorem 4) to the directed graphs given by the underlying structure of $G_{m_1}$ and $G_{m_2}$, respectively. Bearing this in mind, one can define the weights on the prime graphs based on the weights of the multidirected graphs. For instance, for the prime graph $G_{p_1}$, one obtains the weighted prime graph $G_{w{p}_1}$, whose weight values are given by the following:

• If $(v_i,v_j^{\prime })$ is a non-prime prime edge in $G_{p_1}$, we set $w(v_i,v_j^{\prime })=m(v_i,v_j)$, that is, the multiplicity of the directed edge $(v_i,v_j)$ in $G_{m_1}$.
• For any edge of the form $(v_i,v_i^{\prime })\in E_{p_1}$, we set $w(v_i,v_i)=1$.

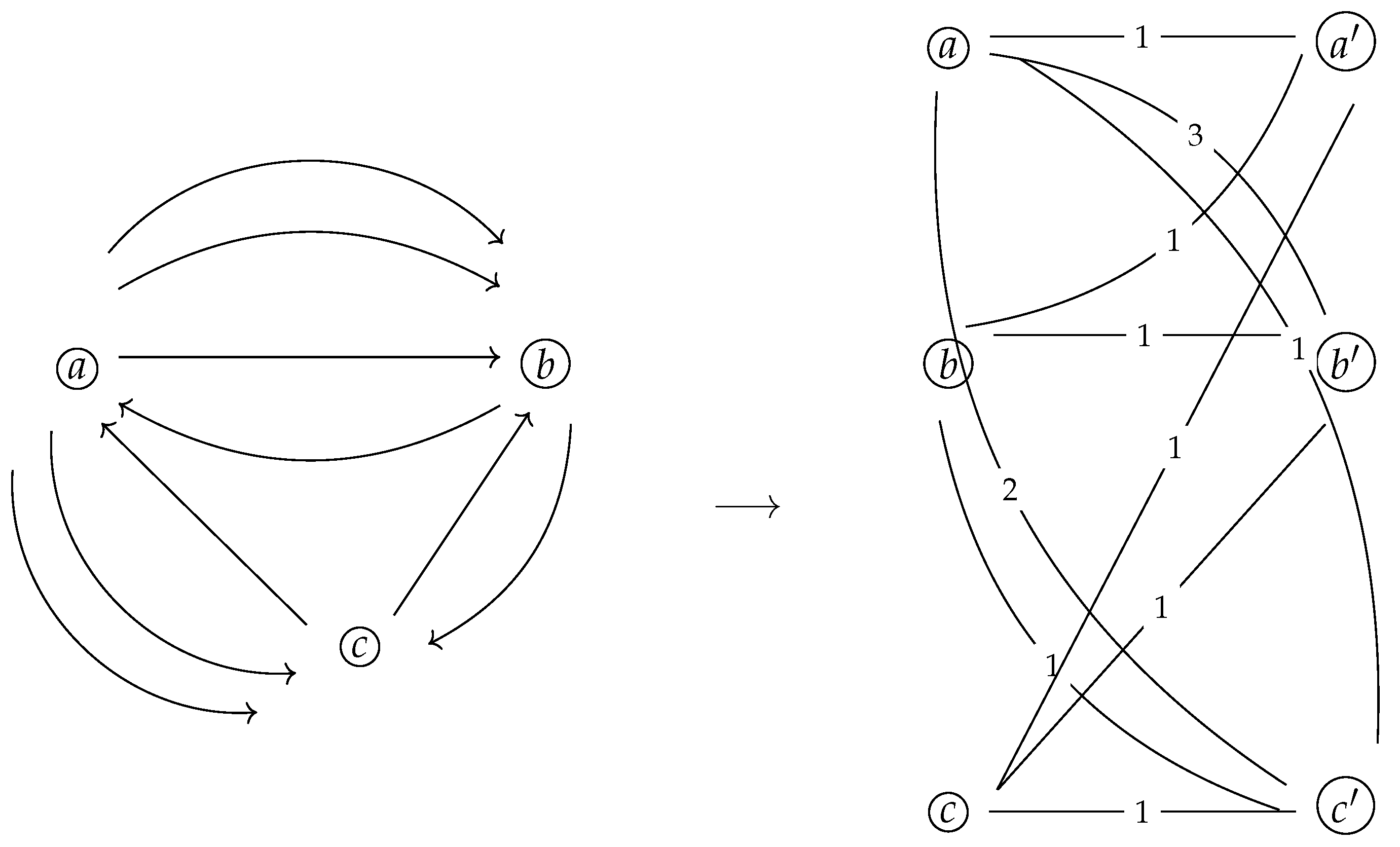
Example 5.

For the multidirected graph in Example 4, one obtains the weighted prime graph in Figure 13.

Observe that the correspondence in Example 5 is reversible. Indeed, each weighted prime graph $G_{wp}$ gives rise to a unique multidirected graph $G_m$, where the multiplicities are induced by the weights of the non-prime edges of $G_{wp}$. Furthermore, as multidirected graph morphisms are essentially directed graph morphisms that respect multiplicity, and weighted prime graph morphisms are basically prime graph morphisms that respect the weight values, then the isomorphism in [15] (Theorem 4) yields to the following.

Theorem 3.

The categories MGraph and WPGraph are isomorphic.

3.2.2. The Class of Multidirected Graphs Without Self-Loops Is GI-Complete

We now prove that the class of all multidirected graphs without self-loops is GI-complete. To this end, we start by showing that there exists a polynomial time reduction from multidirected graphs to undirected graphs that encodes edge multiplicity as the number of ascending chains within the structure of the undirected graphs. In fact, this construction generalizes the one in [10], where the author considers a “gadget” to convert a directed graph into an undirected graph. After this, using Proposition 1, we provide a polynomial time reduction from undirected graphs to multidirected graphs based on prime graphs.

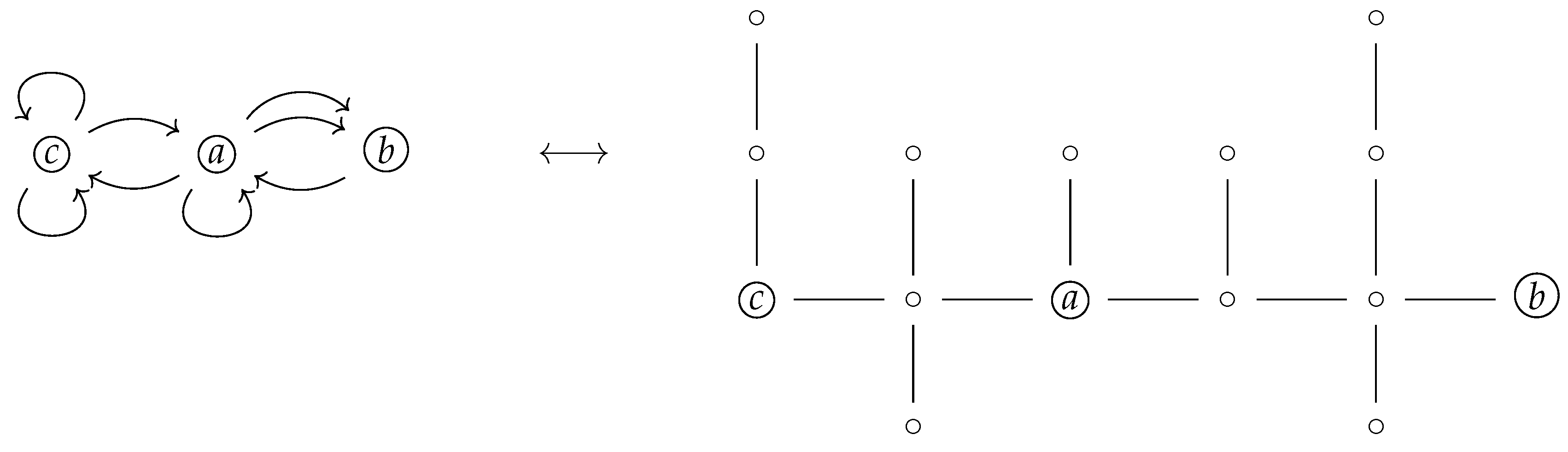
Let us consider a multidirected graph $G_m$, and two nodes $a,b\in V\left(G_m\right)$. Then, in the corresponding undirected graph, we will have two nodes $a,b\in G_u$, with as many chains in between as the sum of the multiplicities of the directed edges $(a,b)$ and $(b,a)$ in $G_m$.

Example 6.

In Figure 14, the multidirected graph on the left has $m(a,b)=3$ and $m(b,a)=2$. Thus, its corresponding undirected graph has three ascending chains from node a to node b, while it has two ascending chains from node b to node a.

While performing the above transformation for each edge of the multidirected graph, one preserves the connectivity and, further, it encodes the notion of edge multiplicity as the number of ascending chains. Note that the above transformation T is carried out in polynomial time. To check the isomorphism properties for T, observe that if $G_{m_1}$ and $G_{m_2}$ are two isomorphic multidirected graphs, then their corresponding undirected graphs $T\left(G_{m_1}\right)$ and $T\left(G_{m_2}\right)$ will be isomorphic. Indeed, while preserving connectivity and transforming multiplicities into ascending chains, T transforms the same underlying topologies and multiplicities into the same underlying topologies and number of ascending chains. Conversely, suppose that $T\left(G_{m_1}\right)$ is isomorphic to $T\left(G_{m_2}\right)$ for two multidirected graphs $G_{m_1}$ and $G_{m_2}$. Since $T\left(G_{m_1}\right)\cong T\left(G_{m_2}\right)$, these have the same underlying topology, implying that $G_{m_1}$ and $G_{m_2}$ do as well. Further, as T encodes the multiplicities as the number of ascending chains, we see that the multidirected graphs will have the same edge multiplicity between each pair of vertices. Hence, $G_{m_1}$ and $G_{m_2}$ are isomorphic.

Let us now consider an undirected graph $G_u$. Then, it induces a unique prime graph $G_p$, as described in Proposition 1. This unique prime graph, in turn, can be considered as a weighted prime graph $G_{pw}$ whose weight values are all 1. Thus, by Theorem 3, the graph $G_{pw}$ corresponds to a multidirected graph $T^{\prime }\left(G_u\right)=G_m$ whose edge multiplicities are all 1 as well. Note that the whole transformation is carried out in polynomial time due to Proposition 1. To verify the isomorphism properties, let us consider $G_{u_1}$ and $G_{u_2}$, two isomorphic undirected graphs. Then, by Proposition 1, the graphs $G_{p_1}$ and $G_{p_2}$ are isomorphic. If we now conceive these two graphs as weighted prime graphs $G_{w{p}_1}$ and $G_{w{p}_2}$, with weight values 1, then, by Theorem 3, these graphs give rise to two isomorphic multidirected graphs $T^{\prime }\left(G_{u_1}\right)=G_{m_1}$ and $T^{\prime }\left(G_{u_2}\right)=G_{m_2}$.

$$G_{u_1}\cong G_{u_2}\stackrel{Prop.1}{⟹}{G}_{p_1}\cong G_{p_2}\stackrel{asweightedprimegraphs}{⟶}{G}_{w{p}_1}\cong G_{w{p}_2}\stackrel{Theo.3}{⟹}{T}^{\prime }\left(G_{u_1}\right)\cong T^{\prime }\left(G_{u_2}\right).$$

Conversely, let us assume that $T^{\prime }\left(G_{u_1}\right)=G_{m_1}$ and $T^{\prime }\left(G_{u_2}\right)=G_{m_2}$ are two isomorphic graphs, coming from the undirected graphs $G_{u_1}$ and $G_{u_2}$ under the transformation $T^{\prime }$. Then, by Theorem 3, their weighted prime graph counterparts, $G_{w{p}_1}$ and $G_{w{p}_2}$, have the same underlying structure as prime graphs. Thus, by Proposition 2, their corresponding undirected graphs have the same underlying structure. Hence, $G_{u_1}$ and $G_{u_2}$ are isomorphic.

$$G_{u_1}\cong G_{u_2}\stackrel{Prop.2}{⟸}{G}_{p_1}\cong G_{p_2}\stackrel{sameunderlyingstructure}{⟵}{G}_{w{p}_1}\cong G_{w{p}_2}\stackrel{Theo.3}{⟸}{G}_{m_1}\cong G_{m_2}.$$

Therefore, we have the following.

Theorem 4.

The class of multidirected graphs with no self-loops is a GI-complete class.

3.3. Multidirected Graphs with Self-Loops Are GI-Complete

Finally, as a result of the above construction, we show that the class of multidirected graphs where self-loops are allowed is isomorphic complete. This will follow from loosing the restriction on the weight values for all edges of the form $(v_i,v_i^{\prime })$ in the weighted prime graph. In fact, this time $w(v_i,v_i^{\prime })$ will take the value 1 if there is no self-loop, and will take the value $n+1$ if there is a self-loop with multiplicity n.

Example 7.

The multidirected graph on the left of Figure 15 has a simple self-loop at node a, no self-loop at node b, and a self-loop of multiplicity 2 at node c. Thus, in its corresponding weighted prime graph, we have that $w(a,a^{\prime })=2$, $w(b,b^{\prime })=1$, and $w(c,c^{\prime })=3$.

The above construction shows that the class of multidirected graphs with self-loops is in a one-to-one correspondence with a broader class of weighted prime graphs, where now the edge weight values $w(v_i,v_i^{\prime })$ can take any positive integer. We denote this broader class of weighted prime graphs by WePGraph.

Remark 3.

The class WPGraph is a proper subclass of WePGraph.

In terms of the transformation $\mathcal{T}$ mapping of multidirected graphs with self-loops to undirected graphs, this is defined similarly as in Section 3.2.2, with the additional condition of adding an n-chain link at any vertex that corresponds to a vertex of the directed graph with a self-loop with multiplicity n.

Example 8.

In Figure 16, the multidirected graph on the left has a simple self-loop at node a and a self-loop of multiplicity two at node c. The graph on the right corresponds to its undirected graph under the transformation $\mathcal{T}$.

Notice that in the undirected graph, node a has a single chain link that corresponds to the simple self-loop, while node c has a chain link of length two, corresponding to the self-loop of multiplicity 2.

We also observe that the map $\mathcal{T}$ from multidrected graphs with self-loops to undirected graphs is a polynomial time reduction because it only adds a finite number of chain links for each vertex that corresponds to a vertex of the directed graph with a self-loop.

Lastly, regarding the transformation ${\mathcal{T}}^{\prime }$ that maps undirected graphs into multidirected graphs with self-loops, this remains the same as in Section 3.2.2, since the class of weighted prime graphs WPGraph is contained in the broader class of weighted prime graphs WePGraph. Therefore, we obtain the following.

Theorem 5.

The class of multidirected graphs with self-loops is GI-complete.

4. Conclusions

This work addresses and formally resolves the open question concerning the Isomorphic Completeness problem for directed graphs, as well as its more general extension to multidirected graphs. To this end, we utilize Category Theory to establish an isomorphism with a category whose isomorphism problem can be reduced to that of undirected graphs in polynomial time.

Our findings open the door to explore the time complexity of directed graph techniques, many of which are known to be NP-hard. By leveraging our framework, these techniques can be translated into a more suitable framework, where the problem is solvable in polynomial time. This methodology reinterprets time complexity in terms of the objects and morphisms of the categories we are working with, allowing us to relativize and simplify the problem through isomorphic categories.

These results highlight the utility of Category Theory as a unifying framework for addressing complex graph-theoretic problems, offering both theoretical insights and practical strategies for computational efficiency.