Interaction Between Two Rigid Hydrophobic Spheres Oscillating in an Infinite Brinkman–Stokes Fluid
Abstract
1. Introduction
2. Brinkman–Stokes Fluid Field Equations
3. Axisymmetric Oscillating Solutions of Brinkman Viscous Fluid
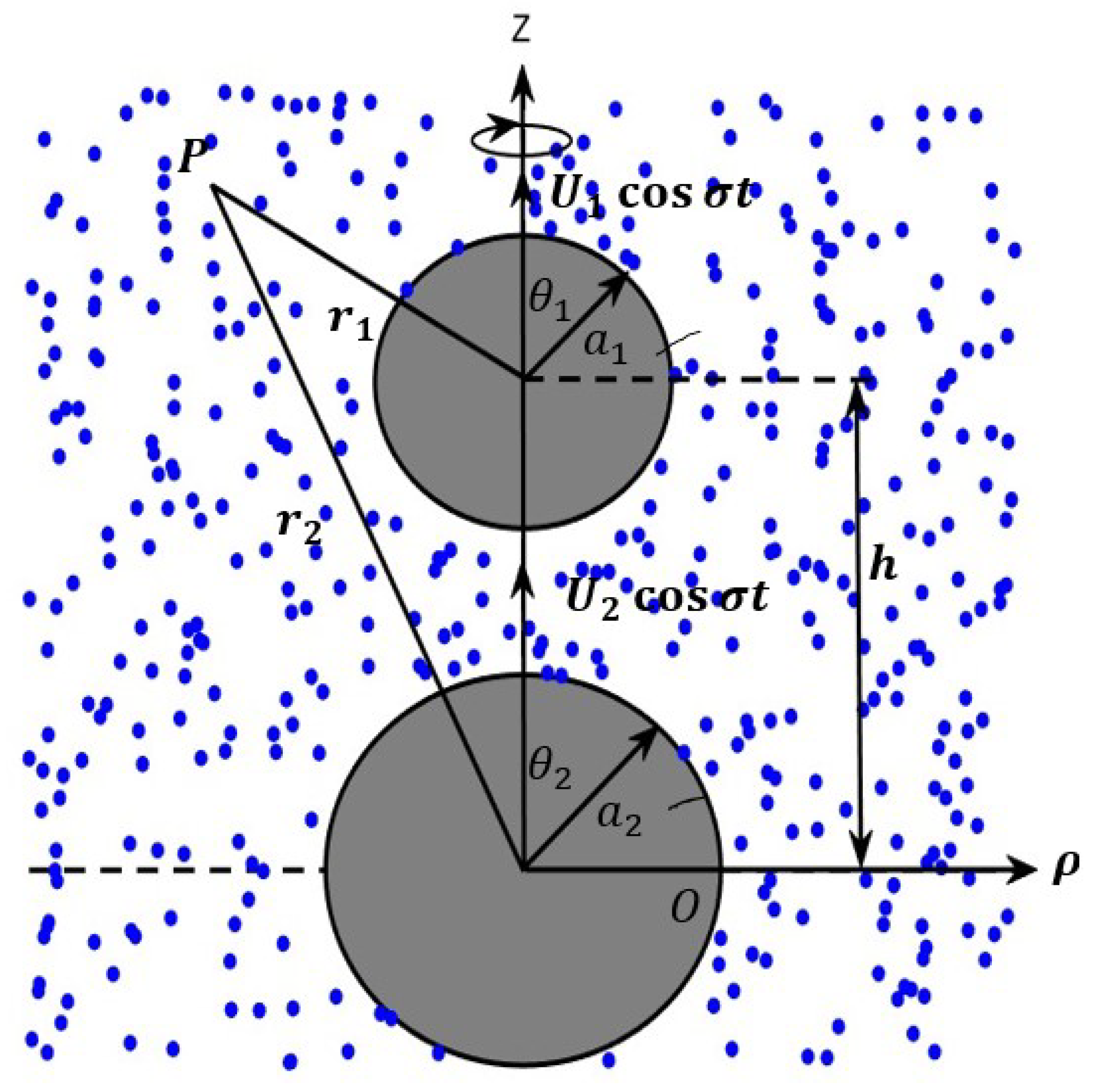
4. Interaction of Two Oscillating Spheres in a Porous Medium
5. Numerical Method for the Problem Undertaken
- Method of Distributed Internal Singularities: This method involves distributing a set of Sampson spherical singularities along the axis of revolution within a prolate particle or on the fundamental plane within an oblate particle. This approach helps in finding the general solution for the fluid velocity field that satisfies the boundary conditions at infinity.
- Boundary-Collocation Technique: After obtaining the general solution for the fluid velocity field, the boundary-collocation technique is applied to satisfy the slip condition on the surface of the translating particle. This technique is used to determine the unknown coefficients in the solution, ensuring that the boundary conditions are met accurately.
- Convergence Behavior: The method demonstrates good convergence behavior for various cases, allowing for reliable calculations of the drag force exerted on the particle by the fluid. The results obtained using this method show excellent agreement with exact solutions for special cases, such as a sphere and a no-slip spheroid, as well as with approximate analytical solutions for slip spheroids.
6. Effect of Slip Coefficient
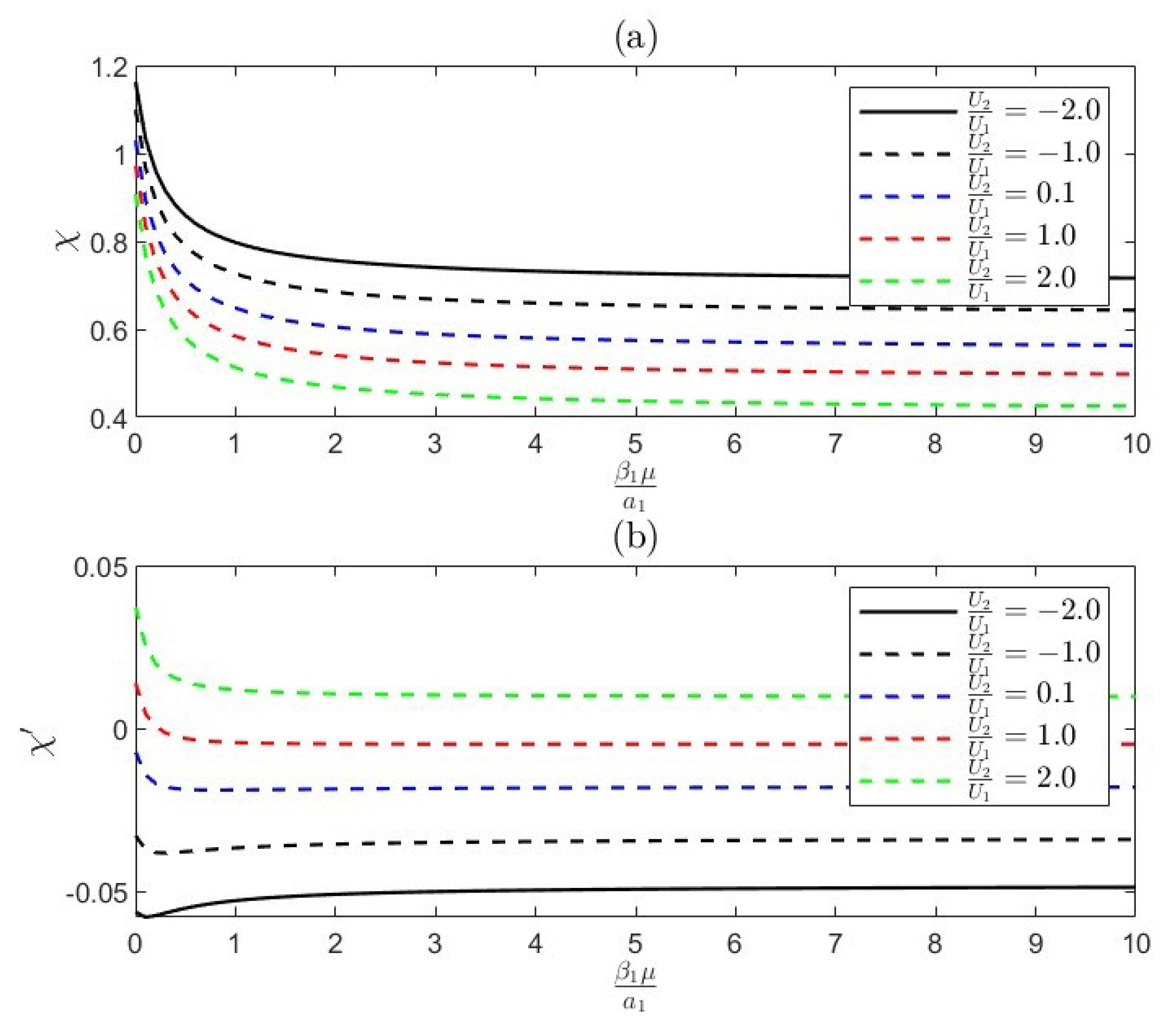
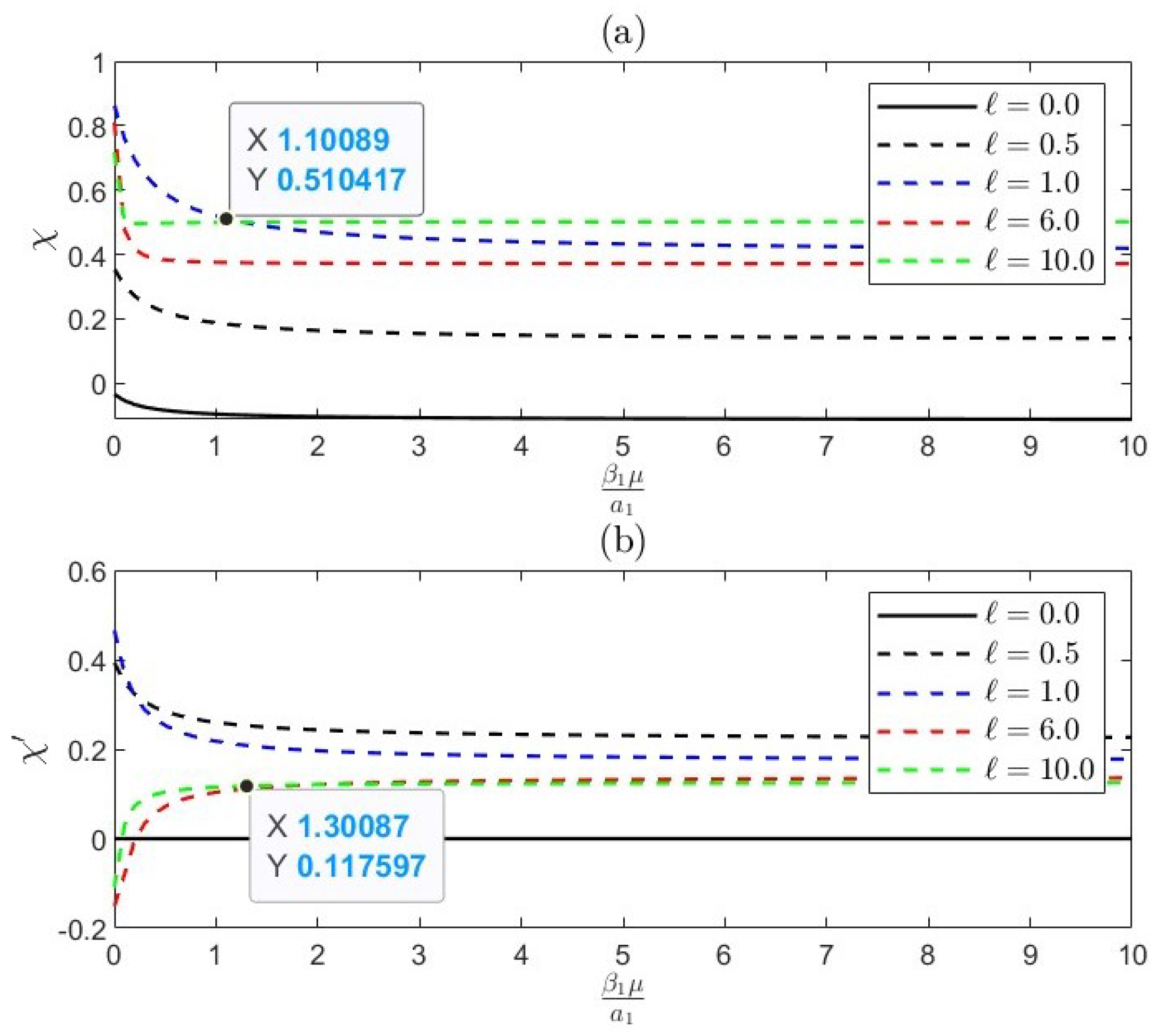
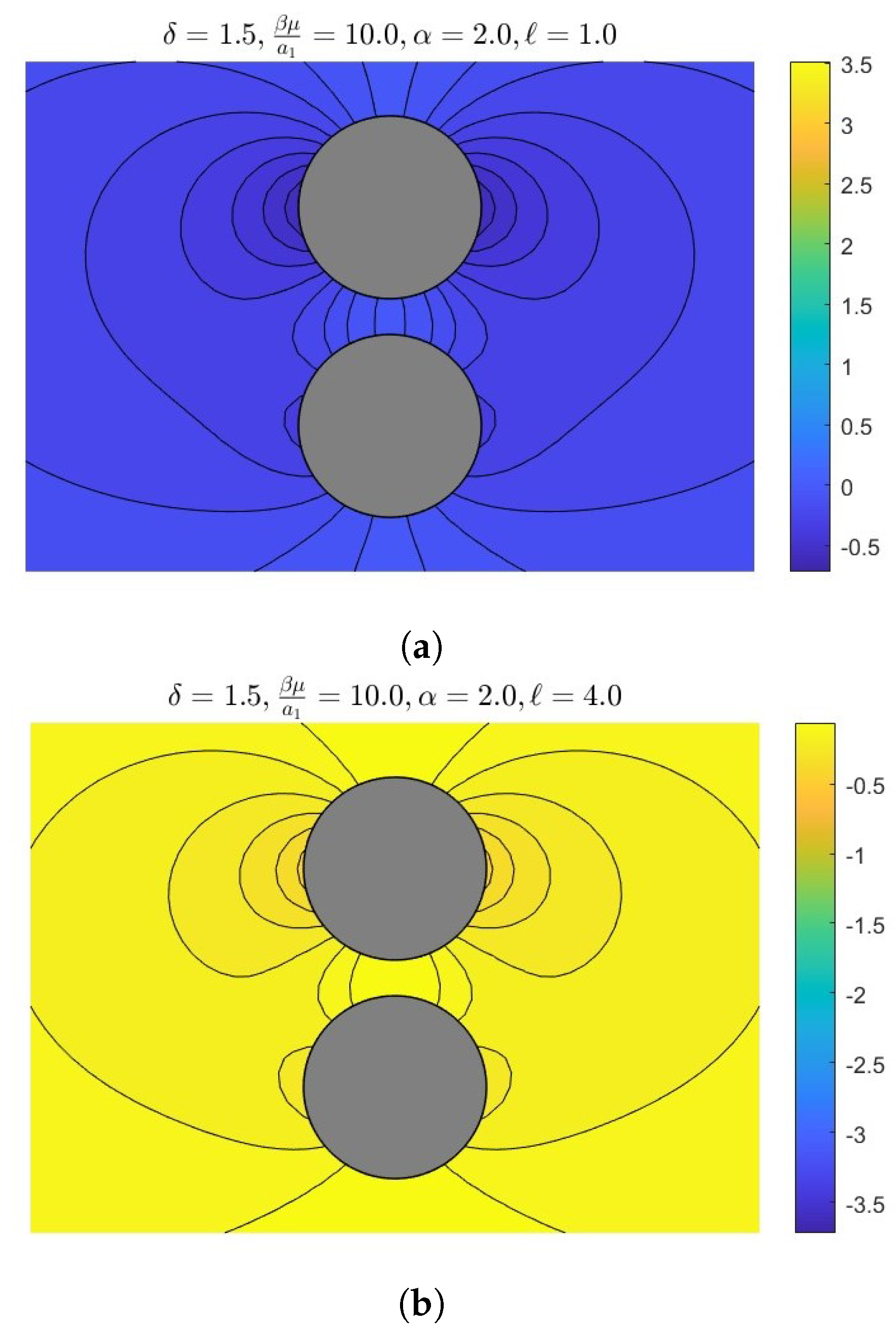
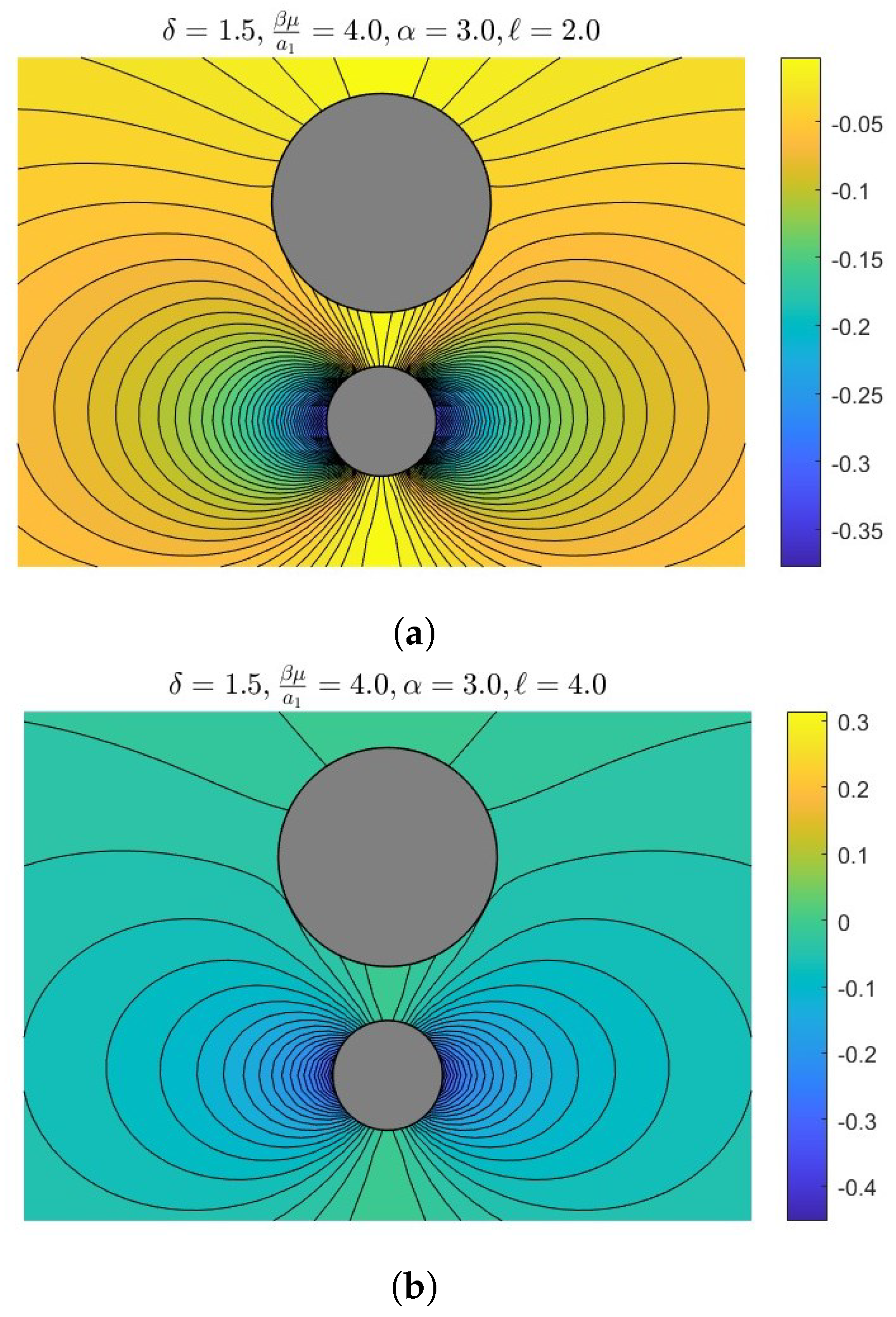
7. Results and Numerical Discussion
8. Conclusions
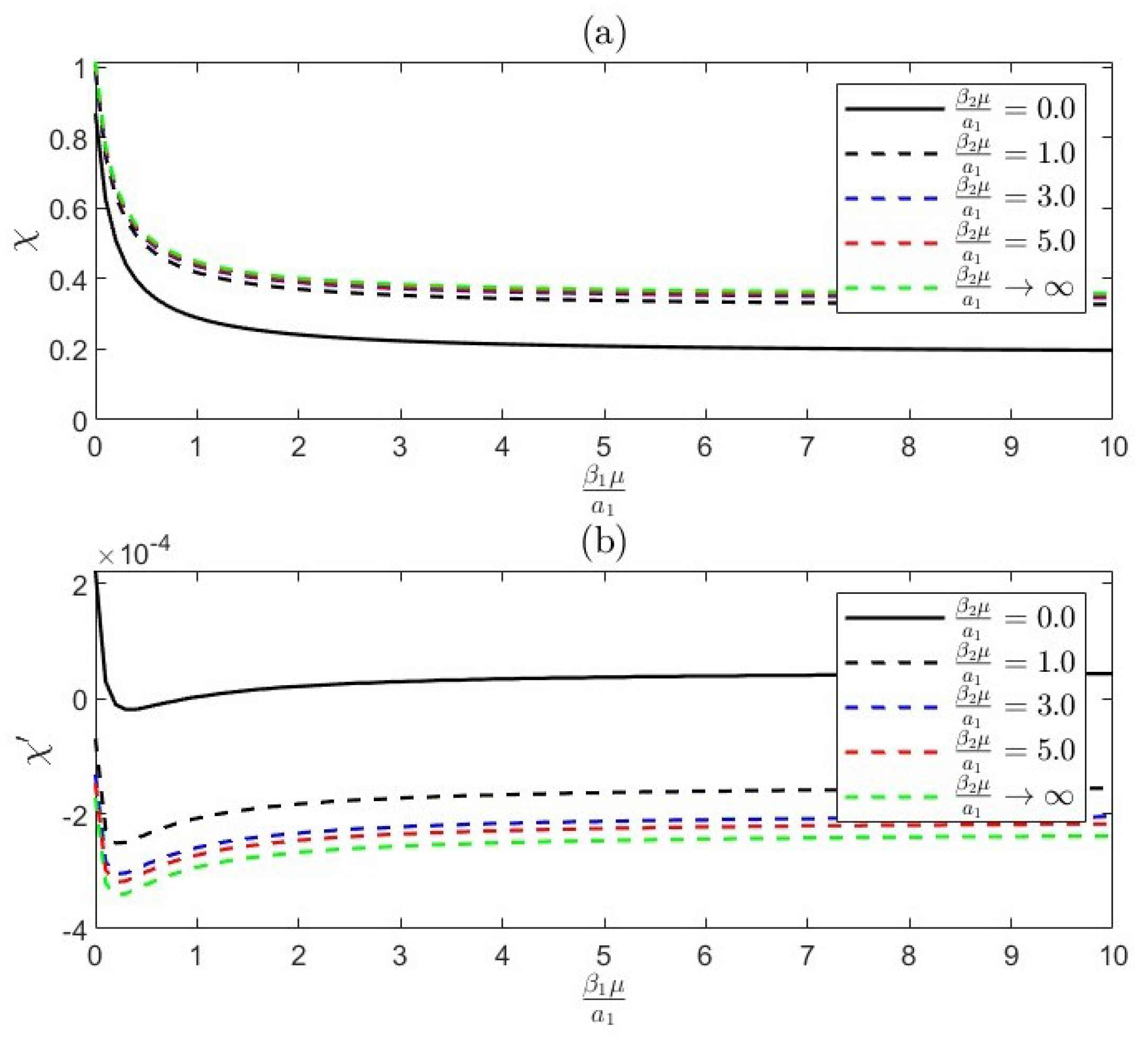
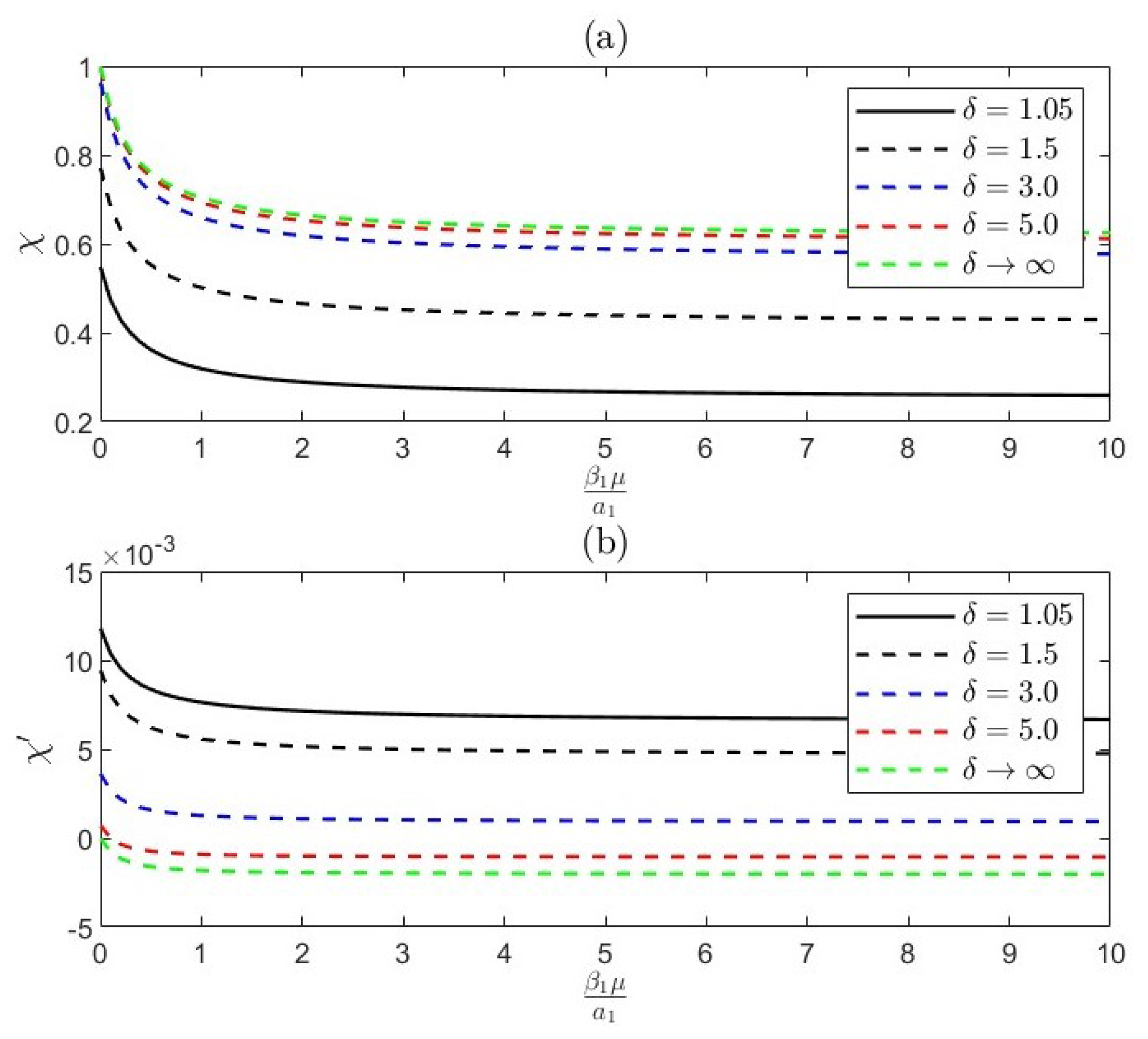
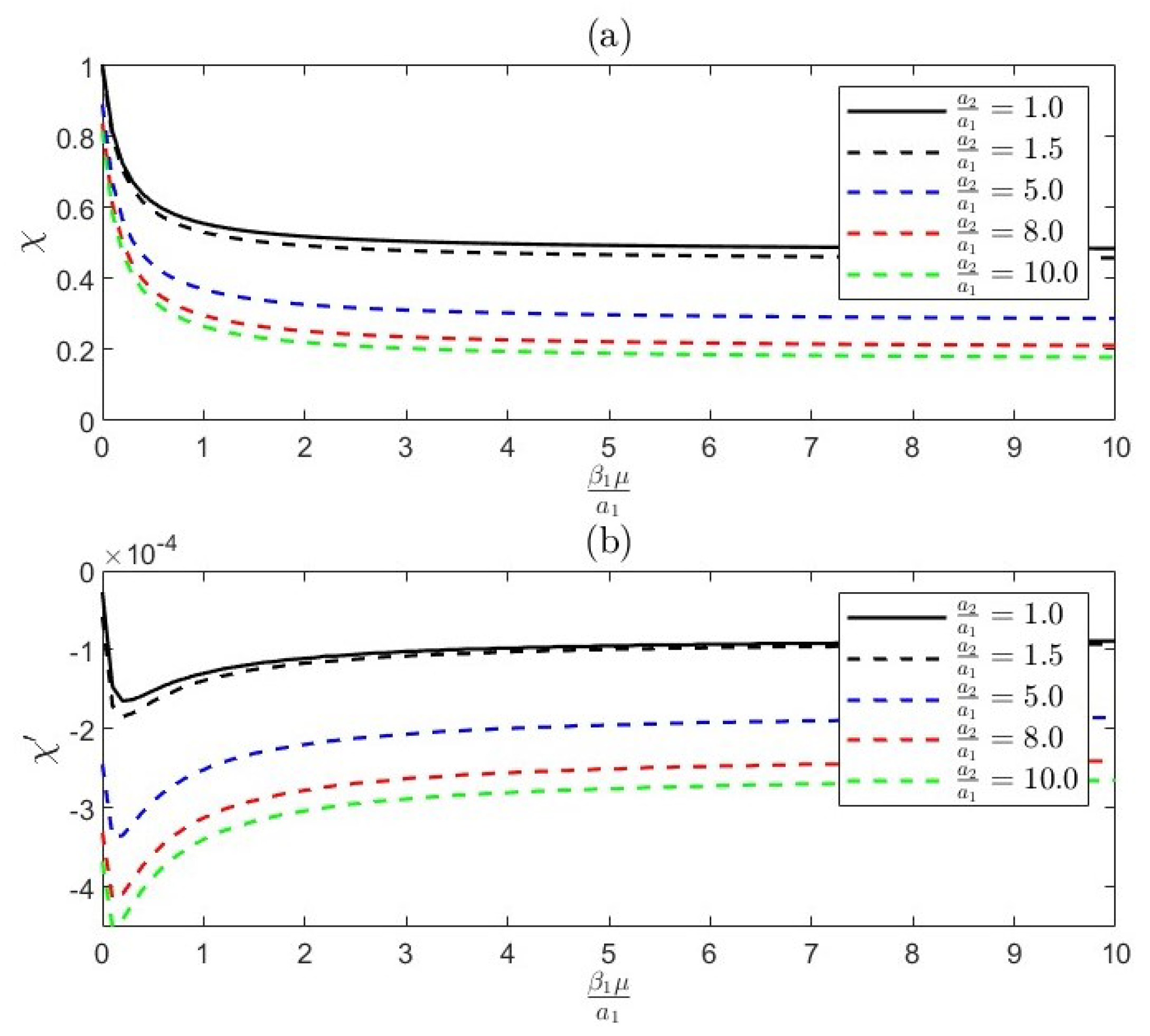
- The radius ratio influences flow dynamics, with smaller ratios leading to stronger interactions and increased drag due to closer proximity. Larger ratios result in weaker interactions, allowing flow to bypass the smaller body.
- Permeability is a property of materials that determines how much fluid can flow through them, which influences drag forces. Higher permeability can reduce drag by allowing fluid to pass through a body, leading to complex interactions.
- The distance between bodies is critical for interaction dynamics, with decreased separation enhancing hydrodynamic coupling. This can result in in-phase interactions that increase drag or out-of-phase interactions that reduce it.
- In-phase interactions occur when bodies move together, amplifying drag through constructive interference. Out-of-phase interactions happen when they move oppositely, leading to destructive interference and reduced drag, influenced by radius ratio, permeability, and separation distance.
- Slippage length refers to the distance over which fluid can slide past a surface without sticking. Increased slippage can reduce drag by allowing smoother fluid flow around the bodies, altering the interaction dynamics, and potentially leading to different coupling behaviors based on the extent of slippage.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Sapa, S.; Alhejaili, W. On the hydrodynamic interaction of two coaxial spheres oscillating in a viscous fluid with a slip regime. Zamm J. Appl. Math. Mech. 2023, 103, e20210050. [Google Scholar] [CrossRef]
- El-Sapa, S. The force on a magneto-spherical particle oscillating in a viscous fluid perpendicular to an impermeable planar wall with slippage. Eur. J. Pure Appl. Math. 2022, 15, 1376–1401. [Google Scholar] [CrossRef]
- Chaudhary, R.C.; Jain, A. Combined heat and mass transfer effects on MHD free convection flow past an oscillating plate embedded in a porous medium. Rom. J. Phys. 2007, 52, 505–524. [Google Scholar]
- Teng, B.; Luo, W.; Chen, Z.; Kang, B.; Chen, L.; Wang, T. A comprehensive study of the effect of Brinkman flow on the performance of hydraulically fractured wells. J. Pet. Sci. Eng. 2022, 213, 110355. [Google Scholar] [CrossRef]
- Albalawi, W.; Taha, H.H.; El-Sapa, S. Effect of the permeability on the interaction between two spheres oscillating through Stokes-Brinkman medium. Heliyon 2023, 9, e14396. [Google Scholar] [CrossRef]
- Faltas, M.S.; El-Sapa, S. Rectilinear oscillations of two spherical particles embedded in an unbounded viscous fluid. Microsyst. Technol. 2019, 25, 39–49. [Google Scholar] [CrossRef]
- Keh, H.J.; Huang, C.H. Slow motion of axisymmetric slip particles along their axes of revolution. Int. J. Eng. Sci. 2004, 42, 1621–1644. [Google Scholar] [CrossRef]
- Felderhof, B.U. Hydrodynamic force on a particle oscillating in a viscous fluid near a wall with dynamic partial-slip boundary condition. Phys. Rev. 2012, 85, 046303. [Google Scholar] [CrossRef]
- Lawrence, C.; Weinbaum, S. The force on an axisymmetric body in linearized, time-dependent motion: A new memory term. J. Fluid Mech. 1986, 171, 209–218. [Google Scholar] [CrossRef]
- Ardekani, A.M.; Range, R.H. Unsteady motion of two solid spheres in Stokes flow. Phys. Fluids 2006, 18, 103306. [Google Scholar] [CrossRef]
- Basak, S.; Raman, A. Hydrodynamic coupling between micromechanical beams oscillating in viscous fluids. Phys. Fluids 2007, 19, 017105. [Google Scholar] [CrossRef]
- Brenner, H. The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Eng. Sci. 1961, 16, 242–251. [Google Scholar] [CrossRef]
- Chadwick, R.S.; Liaot, Z. High-frequency oscillations of a sphere in a viscous fluid near a rigid plane. Siam Rev. 2008, 50, 313–322. [Google Scholar] [CrossRef]
- Chen, S.H.; Keh, H.J. Axisymmetric motion of two spherical particles with slip surfaces. J. Colloid Interface Sci. 1995, 171, 63–72. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Springer Science and Business Media: Berlin, Germany, 2012; p. 1. [Google Scholar]
- Jeffrey, D.J.; Onishi, Y. Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 1984, 139, 261–290. [Google Scholar] [CrossRef]
- Faltas, M.S.; Nashwan, M.G.; Ahmed, B.A.; Hamdy, P. Axisymmetric motion of two spherical particles in a Brinkman medium with slip surfaces. Chin. J. Phys. 2024, 89, 1377–1399. [Google Scholar] [CrossRef]
- Yadav, P.K.; Yadav, N. A study on the flow of couple stress fluid in a porous curved channel. Comput. Math. Appl. 2023, 152, 1–15. [Google Scholar] [CrossRef]
- Ramesh, K. Effects of slip and convective conditions on the peristaltic flow of couple stress fluid in an asymmetric channel through porous medium. Comput. Methods Programs Biomed. 2016, 135, 1–14. [Google Scholar] [CrossRef]
- Madasu, K.P.; Sarkar, P. Couple stress fluid past a sphere embedded in a porous medium. Arch. Mech. Eng. 2022, 69, 5–19. [Google Scholar] [CrossRef]
- Khan, N.A.; Mahmood, A.; Ara, A. Approximate solution of couple stress fluid with expanding or contracting porous channel. Eng. Comput. Int. J. Comput. Aided Eng. Softw. 2013, 30, 399–408. [Google Scholar]
- Maurya, P.K.; Deo, S.; Maurya, D.K. Couple stress fluid flow enclosing a solid sphere in a porous medium: Effect of magnetic field. Phys. Fluids 2023, 35, 072006. [Google Scholar] [CrossRef]
- El-Sapa, S.; Alsudais, N.S. Effect of magnetic field on the motion of two rigid spheres embedded in porous media with slip surfaces. Eur. Phys. J. 2021, 44, 68. [Google Scholar] [CrossRef] [PubMed]
- Ochoa-Tapia, J.A.; Whitaker, S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid—ii. comparison with experiment. Int. J. Heat Mass Transf. 1995, 38, 2647–2655. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; Whitaker, S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid—i. theoretical development. Int. J. Heat Mass Transf. 1995, 38, 2635–2646. [Google Scholar] [CrossRef]
- Breugem, W.-P. The effective viscosity of a channel-type porous medium. Phys. Fluids 2007, 19, 103104. [Google Scholar] [CrossRef]
- Kishore, N. Flow and drag phenomena of tandem spheroid particles at finite Reynolds numbers. Ind. Eng. Chem. Res. 2012, 51, 553–554. [Google Scholar] [CrossRef]
- Kishore, N. Numerical investigation of interaction between spheroid particles in tandem arrangement at moderate Reynolds numbers. Ind. Eng. Chem. Res. 2012, 51, 555–556. [Google Scholar] [CrossRef]
- Prathiksha, P.; Manjunatha, G.; Choudhari, R.; Vaidya, H.; Prasad, K.V. Impact of Variable Fluid Properties on the Peristaltic Flow of Eyring-powell Fluid through Porous Medium: Applications to Hemodynamics. CFD Lett. 2025, 17, 114–139. [Google Scholar] [CrossRef]


| = 0.0 | = 1.0 | = 0.0 | = 1.0 | ||||
|---|---|---|---|---|---|---|---|
| 1.01 | 0.771117 | 0.733521 | 0.778314 | 0.008599 | −0.000364 | 0.298957 | |
| 2.0 | 0.838207 | 0.674175 | 0.589401 | 0.016392 | 0.004380 | 0.009223 | |
| 3.0 | 0.882201 | 0.690110 | 0.621292 | 0.019938 | 0.006023 | 0.009225 | |
| 4.0 | 0.910087 | 0.702168 | 0.629555 | 0.021612 | 0.006641 | 0.002462 | |
| 0.0 | 5.0 | 0.929053 | 0.711002 | 0.637173 | 0.022329 | 0.006803 | 0.004330 |
| (Ref. [1]) | 6.0 | 0.942750 | 0.717641 | 0.641179 | 0.022495 | 0.006715 | 0.003821 |
| 7.0 | 0.953103 | 0.722783 | 0.644794 | 0.022315 | 0.006477 | 0.001978 | |
| 8.0 | 0.961201 | 0.726871 | 0.648514 | 0.021909 | 0.006143 | 0.004035 | |
| 9.0 | 0.967704 | 0.730190 | 0.649641 | 0.021347 | 0.005744 | 0.003694 | |
| 10.0 | 0.973033 | 0.732932 | 0.651254 | 0.020678 | 0.005303 | 0.001248 | |
| 1.01 | 0.931430 | 0.675753 | 0.601945 | 0.000731 | −0.000469 | −0.000600 | |
| 2.0 | 0.996931 | 0.626133 | 0.532315 | 0.000152 | −0.000590 | −0.000592 | |
| 3.0 | 1.000098 | 0.622496 | 0.527872 | 0.000003 | −0.000615 | −0.000598 | |
| 4.0 | 0.999869 | 0.621368 | 0.526677 | −0.000009 | −0.000605 | −0.000585 | |
| 1.0 | 5.0 | 0.999786 | 0.621070 | 0.526366 | −0.000006 | −0.000599 | −0.000579 |
| 6.0 | 0.999802 | 0.620998 | 0.526285 | −0.000003 | −0.000596 | −0.000576 | |
| 7.0 | 0.999839 | 0.620987 | 0.526268 | −0.000002 | −0.000594 | −0.000575 | |
| 8.0 | 0.999873 | 0.620992 | 0.526268 | −0.000001 | −0.000593 | −0.000574 | |
| 9.0 | 0.999900 | 0.621000 | 0.526273 | −0.000001 | −0.000593 | −0.000574 | |
| 10.0 | 0.999921 | 0.621009 | 0.526279 | 0.000000 | −0.000593 | −0.000573 | |
| 1.01 | 1.035134 | 0.600139 | 0.557121 | −0.000002 | 0.000035 | 0.000052 | |
| 2.0 | 0.991689 | 0.561543 | 0.518993 | −0.000002 | 0.000040 | 0.000057 | |
| 3.0 | 0.995804 | 0.565268 | 0.522658 | −0.000001 | 0.000042 | 0.000059 | |
| 4.0 | 0.997829 | 0.566921 | 0.524271 | 0.000000 | 0.000042 | 0.000059 | |
| 4.0 | 5.0 | 0.998759 | 0.567661 | 0.524991 | 0.000000 | 0.000042 | 0.000060 |
| 6.0 | 0.999230 | 0.568031 | 0.525352 | 0.000000 | 0.000042 | 0.000060 | |
| 7.0 | 0.999492 | 0.568236 | 0.525550 | 0.000000 | 0.000042 | 0.000060 | |
| 8.0 | 0.999647 | 0.568357 | 0.525668 | 0.000000 | 0.000042 | 0.000060 | |
| 9.0 | 0.999745 | 0.568433 | 0.525742 | 0.000000 | 0.000042 | 0.000060 | |
| 10.0 | 0.999810 | 0.568483 | 0.525790 | 0.000000 | 0.000042 | 0.000060 | |
| 1.01 | 1.028299 | 0.783802 | 0.775381 | 0.000000 | 0.000011 | 0.000012 | |
| 2.0 | 0.985974 | 0.748445 | 0.740244 | 0.000000 | 0.000011 | 0.000012 | |
| 3.0 | 0.993709 | 0.755927 | 0.747715 | 0.000000 | 0.000011 | 0.000012 | |
| 4.0 | 0.996857 | 0.758862 | 0.750642 | 0.000000 | 0.000011 | 0.000012 | |
| 10.0 | 5.0 | 0.998233 | 0.760131 | 0.751908 | 0.000000 | 0.000011 | 0.000012 |
| 6.0 | 0.998914 | 0.760756 | 0.752531 | 0.000000 | 0.000011 | 0.000012 | |
| 7.0 | 0.999287 | 0.761097 | 0.752871 | 0.000000 | 0.000011 | 0.000012 | |
| 8.0 | 0.999508 | 0.761299 | 0.753072 | 0.000000 | 0.000011 | 0.000012 | |
| 9.0 | 0.999646 | 0.761425 | 0.753197 | 0.000000 | 0.000011 | 0.000012 | |
| 10.0 | 0.999737 | 0.761508 | 0.753280 | 0.000000 | 0.000011 | 0.000012 |
| = 0.0 | = 1.0 | = 4.0 | |||
|---|---|---|---|---|---|
| 1.05 | 0.557132 | 0.637036 | 0.735240 | 0.768777 | |
| 2.0 | 0.586619 | 0.650153 | 0.782240 | 0.838207 | |
| 3.0 | 0.594137 | 0.668675 | 0.817160 | 0.882200 | |
| 4.0 | 0.606071 | 0.684018 | 0.840725 | 0.910086 | |
| 0.1 | 5.0 | 0.617348 | 0.695440 | 0.857141 | 0.929052 |
| 6.0 | 0.624814 | 0.704061 | 0.869143 | 0.942749 | |
| 7.0 | 0.630466 | 0.710745 | 0.878281 | 0.953102 | |
| 8.0 | 0.636299 | 0.716063 | 0.885463 | 0.961200 | |
| 9.0 | 0.638650 | 0.720386 | 0.891251 | 0.967703 | |
| 10.0 | 0.640430 | 0.723965 | 0.896008 | 0.973032 | |
| 1.05 | 0.435825 | 0.467591 | 0.705044 | 1.018732 | |
| 2.0 | 0.421562 | 0.452922 | 0.686774 | 0.990985 | |
| 3.0 | 0.425687 | 0.457121 | 0.691428 | 0.995700 | |
| 4.0 | 0.427306 | 0.458779 | 0.693337 | 0.997810 | |
| 4.0 | 5.0 | 0.428006 | 0.459496 | 0.694172 | 0.998756 |
| 6.0 | 0.428351 | 0.459850 | 0.694587 | 0.999230 | |
| 7.0 | 0.428539 | 0.460043 | 0.694813 | 0.999491 | |
| 8.0 | 0.428650 | 0.460157 | 0.694947 | 0.999646 | |
| 9.0 | 0.428720 | 0.460228 | 0.695031 | 0.999744 | |
| 10.0 | 0.428765 | 0.460275 | 0.695087 | 0.999808 | |
| 1.05 | 0.809721 | 0.807464 | 0.810099 | 1.010685 | |
| 2.0 | 0.787792 | 0.785581 | 0.788172 | 0.984705 | |
| 3.0 | 0.796068 | 0.793858 | 0.796472 | 0.993234 | |
| 4.0 | 0.799276 | 0.797064 | 0.799687 | 0.996631 | |
| 10.0 | 5.0 | 0.800658 | 0.798445 | 0.801073 | 0.998107 |
| 6.0 | 0.801337 | 0.799125 | 0.801754 | 0.998836 | |
| 7.0 | 0.801708 | 0.799495 | 0.802126 | 0.999234 | |
| 8.0 | 0.801926 | 0.799713 | 0.802344 | 0.999469 | |
| 9.0 | 0.802063 | 0.799850 | 0.802481 | 0.999616 | |
| 10.0 | 0.802153 | 0.799940 | 0.802572 | 0.999713 | |
| 1.05 | 1.003035 | 1.003024 | 1.002920 | 1.009203 | |
| 2.0 | 0.975924 | 0.975912 | 0.975811 | 0.981947 | |
| 3.0 | 0.986121 | 0.986109 | 0.986007 | 0.992150 | |
| 4.0 | 0.990078 | 0.990067 | 0.989965 | 0.996113 | |
| ∞ | 5.0 | 0.991784 | 0.991773 | 0.991671 | 0.997821 |
| 6.0 | 0.992624 | 0.992612 | 0.992510 | 0.998662 | |
| 7.0 | 0.993081 | 0.993070 | 0.992968 | 0.999120 | |
| 8.0 | 0.993351 | 0.993339 | 0.993237 | 0.999391 | |
| 9.0 | 0.993520 | 0.993508 | 0.993406 | 0.999560 | |
| 10.0 | 0.993631 | 0.993619 | 0.993517 | 0.999671 |
| = 0.0 | = 1.0 | = 4.0 | |||
|---|---|---|---|---|---|
| 1.05 | 0.015649 | −0.001063 | 0.005687 | 0.008883 | |
| 2.0 | 0.009284 | 0.003918 | 0.012056 | 0.016392 | |
| 3.0 | 0.008586 | 0.005625 | 0.014894 | 0.019938 | |
| 4.0 | 0.002031 | 0.006409 | 0.016230 | 0.021612 | |
| 0.1 | 5.0 | 0.003990 | 0.006748 | 0.016802 | 0.022329 |
| 6.0 | 0.003010 | 0.006832 | 0.016930 | 0.022494 | |
| 7.0 | 0.003570 | 0.006756 | 0.016782 | 0.022315 | |
| 8.0 | 0.004158 | 0.006574 | 0.016450 | 0.021909 | |
| 9.0 | 0.006280 | 0.006319 | 0.015992 | 0.021347 | |
| 10.0 | 0.002680 | 0.006013 | 0.015447 | 0.020678 | |
| 1.05 | 0.189126 | 0.133284 | −0.040952 | −0.014563 | |
| 2.0 | 0.183009 | 0.128790 | −0.038289 | −0.006118 | |
| 3.0 | 0.185964 | 0.131726 | −0.035146 | −0.002223 | |
| 4.0 | 0.187000 | 0.132731 | −0.034174 | −0.001029 | |
| 4.0 | 5.0 | 0.187435 | 0.133148 | −0.033788 | −0.000557 |
| 6.0 | 0.187645 | 0.133350 | −0.033605 | −0.000335 | |
| 7.0 | 0.187759 | 0.133458 | −0.033508 | −0.000217 | |
| 8.0 | 0.187826 | 0.133522 | −0.033451 | −0.000149 | |
| 9.0 | 0.187867 | 0.133561 | −0.033417 | −0.000107 | |
| 10.0 | 0.187895 | 0.133587 | −0.033394 | −0.000079 | |
| 1.05 | 0.207764 | 0.197606 | 0.121689 | −0.002832 | |
| 2.0 | 0.202356 | 0.192411 | 0.118075 | −0.003537 | |
| 3.0 | 0.204611 | 0.194656 | 0.120249 | −0.001363 | |
| 4.0 | 0.205471 | 0.195507 | 0.121037 | −0.000647 | |
| 10.0 | 5.0 | 0.205840 | 0.195872 | 0.121370 | −0.000355 |
| 6.0 | 0.206021 | 0.196051 | 0.121532 | −0.000215 | |
| 7.0 | 0.206119 | 0.196148 | 0.121620 | −0.000140 | |
| 8.0 | 0.206177 | 0.196205 | 0.121671 | −0.000097 | |
| 9.0 | 0.206214 | 0.196241 | 0.121704 | −0.000069 | |
| 10.0 | 0.206238 | 0.196265 | 0.121725 | −0.000052 | |
| 1.05 | 0.011920 | 0.011904 | 0.011758 | −0.000139 | |
| 2.0 | 0.011598 | 0.011582 | 0.011440 | −0.000180 | |
| 3.0 | 0.011720 | 0.011704 | 0.011561 | −0.000070 | |
| 4.0 | 0.011767 | 0.011751 | 0.011608 | −0.000033 | |
| ∞ | 5.0 | 0.011787 | 0.011771 | 0.011628 | −0.000018 |
| 6.0 | 0.011797 | 0.011781 | 0.011638 | −0.000011 | |
| 7.0 | 0.011802 | 0.011787 | 0.011644 | −0.000007 | |
| 8.0 | 0.011806 | 0.011790 | 0.011647 | −0.000005 | |
| 9.0 | 0.011808 | 0.011792 | 0.011649 | −0.000004 | |
| 10.0 | 0.011809 | 0.011793 | 0.011650 | −0.000003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algatheem, A.M.; Taha, H.H.; El-Sapa, S. Interaction Between Two Rigid Hydrophobic Spheres Oscillating in an Infinite Brinkman–Stokes Fluid. Mathematics 2025, 13, 218. https://doi.org/10.3390/math13020218
Algatheem AM, Taha HH, El-Sapa S. Interaction Between Two Rigid Hydrophobic Spheres Oscillating in an Infinite Brinkman–Stokes Fluid. Mathematics. 2025; 13(2):218. https://doi.org/10.3390/math13020218
Chicago/Turabian StyleAlgatheem, Azza M., Hala H. Taha, and Shreen El-Sapa. 2025. "Interaction Between Two Rigid Hydrophobic Spheres Oscillating in an Infinite Brinkman–Stokes Fluid" Mathematics 13, no. 2: 218. https://doi.org/10.3390/math13020218
APA StyleAlgatheem, A. M., Taha, H. H., & El-Sapa, S. (2025). Interaction Between Two Rigid Hydrophobic Spheres Oscillating in an Infinite Brinkman–Stokes Fluid. Mathematics, 13(2), 218. https://doi.org/10.3390/math13020218






