Abstract
A resolution of a Steiner triple system of order v (STS(v)) is point-cyclic if it has an automorphism permuting the points in one cycle. An STS(v) is cyclically resolvable if it has at least one point-cyclic resolution. Cyclically resolvable STS(v)s have important applications in Coding Theory. They have been classified up to and before the present work was the first open case. There are 2,353,310 cyclic STS(57)s. We establish that 155,966 of them are cyclically resolvable yielding 3,638,984 point-cyclic resolutions which we classify with respect to their automorphism groups and to the availability of some configurations.
Keywords:
Steiner triple system; cyclically resolvable; automorphism; point-cyclic resolution; anti-Pasch; anti-mitre; 5-sparse MSC:
05B07; 05B30; 94B60
1. Introduction
Definition 1.
A Steiner triple system of order v (STS(v)) is a pair where V is a set of v elements called points and B a family of 3-element subsets (triples) of V called blocks, such that each pair of elements of V is contained in exactly one block of B.
An STS(v) has blocks and each of its points is in blocks. Its incidence matrix has v rows and b columns and the element in the i-th row and j-th column is 1 if point i is in block j, or 0 otherwise. An STS(v) is a 2- block design. That is why we will further talk either of STS(57)s, or of 2- designs. Two STS(v)s are isomorphic if there is a bijection of the point sets such that blocks are mapped to blocks. An automorphism of an STS(v) is an isomorphism to itself. All the automorphisms of an STS(v) form its full automorphism group.
A parallel class of an STS(v) is a set of blocks, such that each point is in exactly one block. A resolution of an STS(v) is a partition of the collection of blocks to parallel classes. Two resolutions R and are isomorphic if there exists an automorphism of the underlying STS(v) which maps each parallel class of R to a parallel class of . An automorphism of the resolution R is an automorphism of the STS(v) which maps each parallel class of R to a parallel class of R. An STS(v) together with a resolution of its blocks is called a Kirkman triple system (KTS(v)). For the basic knowledge on STS(v)s and KTS(v)s refer, for instance, to [1,2]. KTS(v)s are related to error correcting codes in many different ways [3]. It is well known that a KTS(v) is equivalent to an optimal equidistant code (length r, v codewords, distance , alphabet of elements) [4].
An STS(v) is cyclic if it has an automorphism of order v permuting its points in one cycle. A cyclic STS(v) corresponds to a cyclic difference family. A resolution is point-cyclic if it has an automorphism permuting the points in one cycle. An STS(v) is resolvable if it has at least one resolution, and it is cyclically resolvable if at least one of its resolutions is point-cyclic.
Example 1.

A cyclic STS(15) is presented in Figure 1. It is invariant under an automorphism of order 15 which permutes the points in one cycle. It generates a cyclic group of order 15 which partitions the blocks to three orbits, namely one short orbit of length 5 and two full orbits of length 15. The full automorphism group of this design is of order 20,160. One of its resolutions is presented in the figure too. It has seven parallel classes, the short block orbit being one of them. This resolution is invariant under an automorphism group of order 168 which is transitive on the parallel classes, but it is not invariant under the cyclic group of order 15 and is therefore not point-cyclic.

Figure 1.
Cyclic 2- design = cyclic STS(15), points, blocks, .
The incidence matrix of an STS(v) can be used as a parity-check matrix of a binary ()-regular Low-Density Parity-Check (LDPC) code with v parity-check equations, b codeword bits, row weight r and column weight 3 [5]. If the STS(v) is cyclic, the parity-check matrix is quasi-cyclic (contains circulant submatrices) and therefore allows linear-complexity encoding with simple feedback shift registers [6,7,8]. KTS(v)s are useful when the row weight of such an LDPC code has to be reduced by removing some columns of the parity-check matrix in such a way that the same number of ones are cut off from each row (true if one or several parallel classes are removed) to obtain a lower rate code without changing the other code properties [5,6,9,10]. If the KTS(v) is point-cyclic, fast encoding might be possible too by using the quasi-cyclic structure of the remaining matrix.
A KTS(v) exists if and only if (mod , [11]. KTS(v)s are classified up to [12,13]. The full classification of KTS(21)s is out of reach now. One of the most recent results on KTS(21)s presents over 13 million KTS(21)s with subsystems STS(7)s and STS(9)s [14]. Constructions of KTS(v)s for have been considered by many authors [14,15,16,17,18,19,20,21,22,23]. General constructions of point-cyclic KTS(v)s are considered in [24,25] and point-cyclic KTS(v)s with small parameters have been classified up to (Table 1). Before the present work was the smallest open case. The big number of cyclic STS(v)s and possible parallel classes make it much more difficult to consider than any smaller v. The present paper solves this problem (Table 1).

Table 1.
Point-cyclic KTS(v)s with small parameters.
A KTS(57) with sub-STS(27) can be obtained from the infinite class of Dukes and Lamken of KTS() with sub-STS(u) [16]. The existence of a KTS(57) with sub-KTS(15) is proved in [20]. There are 2,353,310 cyclic STS(57)s [2,26]. Using them we construct all point-cyclic KTS(57)s and study their automorphism groups and some important configurations. Our investigation is computer-aided. We use two different construction algorithms implemented respectively by the two authors in C++.
The paper consists of 5 sections. The action of the cyclic automorphism group of order v on a point-cyclic resolution of an STS(57) is considered in Section 2 and the construction methods are explained in Section 3. Section 4 presents the main results, and a discussion on their impact follows in Section 5.
2. The Action of the Automorphism Group of a Cyclic STS(57)
2.1. The Full Automorphism Groups of the Cyclic STS(57)s
We have in advance all the 2,353,310 cyclic STS(57)s [27] and first find their automorphism groups (Table 2). Most of the groups are easy to obtain by our own software written in C++ 14.20 but the calculations were too slow on four of the designs (three with 513 automorphisms and one with 1026). That is why to find their automorphisms we used the software described in [28].

Table 2.
The number of automorphisms of the cyclic STS(57)s.
All full automorphism groups contain a subgroup (we denote it ) isomorphic to the cyclic group of order 57, namely , where .
2.2. Block Orbits Under
A point-cyclic resolution must be invariant under all subgroups of , namely under the subgroup of order 3, and the subgroup of order 19. Their action on the blocks of an STS(57) is presented in Table 3. An STS(57) has 532 blocks. Under there are 9 full block orbits of length 57 and one short block orbit of length 19 which is a parallel class. Under the action of there are 28 block orbits of length 19. One of them is the short block orbit under . Under the action of there are 19 block orbits of length 1 and 171 of length 3. The 19 blocks which fixes are the blocks of the short block orbit under .

Table 3.
Block orbits of a cyclic STS(57) under and its subgroups.
2.3. Point-Cyclic Resolutions of STS(57)s and Their Parallel Class Orbits Under
According to Mishima and Jimbo [29] there are three types of point-cyclic KTS(v)s:
- —the short block orbit under is a parallel class of the resolution;
- —each block from the short block orbit is in a different parallel class of the resolution;
- —the resolution has parallel classes with more than one block from the short block orbit.
Lemma 1.
Under the cyclic STS(57)s can have at most 19 block orbits which are parallel classes.
Proof.
is generated by which acts on the points as
i.e., under there are three point orbits , , and . If a block B of the STS(57) has two points a and b from one and the same orbit , there is an automorphism from mapping a to b and B to . Therefore the point b is in two blocks B and of the corresponding block orbit and that is why this block orbit is not a parallel class. If a block orbit under is a parallel class, all its blocks contain one point from each point orbit under .
In each block orbit which is a parallel class there is a block containing point 0, a point a from , and a point b from . There are 19 different ways to choose the point a from . Since the pair of points should be in exactly one block of the Steiner triple system, there can be at most 19 blocks containing point 0 and a point a from and therefore there can be not more than 19 block orbits under which are parallel classes. □
Theorem 1.
All the point-cyclic resolutions of a cyclic STS(57) are of type and under their parallel classes are in 1 orbit of length 19 and 3 orbits of length 3.
Proof.
The number of parallel classes is 28. That is why a class orbit of length 57 is not possible, class orbits should be of lengths 1 (the classes are fixed by ), 3 (the classes are fixed by ) or 19 (the classes are fixed by ).
There is only one parallel class which is fixed by , namely the short block orbit. That is why there can be at most one parallel class orbit of length 1. Therefore there are only two possibilities for the parallel class orbits of a point-cyclic KTS(57), namely either 9 class orbits of length 3 and one of length 1, or 3 class orbits of length 3 and one of length 19.
A resolution of type should consist of one class orbit of length 1 and nine class orbits of length 3. In this case should fix each parallel class, namely each parallel class should consist of the blocks of one block orbit under , and therefore all the 28 block orbits under should be parallel classes. That is why by Lemma 1 a resolution of type is not possible.
A resolution of type or should consist of one class orbit of length 19 and three class orbits of length 3. In this case should fix the parallel classes from the orbit of length 19. Since a parallel class has 19 blocks, can only fix it if it contains at least one block which is fixed by . Since fixes exactly 19 blocks (the blocks of the short orbit) each class of the class orbit of length 19 should contain exactly one of the 19 blocks of the short block orbit. Therefore all point-cyclic resolutions of STS(57)s are of type . □
Corollary 1.
A cyclically resolvable STS(57) has at least 10 (out of all 28) block orbits under which are parallel classes.
Proof.
fixes the short block orbit under . By Theorem 1 the blocks of the short orbit are in the parallel classes of the class orbit of length 19 of a point-cyclic resolution. The remaining 9 parallel classes make three class orbits of length 3, so fixes these 9 parallel classes too. That is why at least block orbits under should be parallel classes. □
3. Construction
To double-check the results, we obtain them in parallel by two different algorithms. For each design we start with sorting its blocks in a lexicographic order defined by the points they contain. We further work with the successive numbers of the blocks in the sorted array.
The first algorithm () uses substantially the results from Section 2.3. We first construct the block orbits under and establish that there are 368,486, 1,828,784 and 156,040 cyclic STS(57)s with respectively 1, 7, and 13 block orbits under which are parallel classes. By Corollary 1 we further test for cyclic resolvability only the 156,040 designs that have 13 block orbits under which are parallel classes. Their full automorphism groups are presented in Table 4. It further turns out that only 74 of the 156,040 designs are not cyclically resolvable.

Table 4.
The number of automorphisms of the cyclic with 13 parallel classes that are block orbits under .
constructs only resolutions with the structure from Theorem 1. We denote by the lexicographically smallest parallel class (base class) from the class orbit of length 19 and by , , and the lexicographically smallest parallel classes (base classes) from the three class orbits of length 3. We shall illustrate the construction by several code segments. The first of them presents the function PCres57 in which ReadDes reads each cyclic STS(57) and initializes the variables that will be used further.
The block orbits under the subgroups of are found by Orb19PCEnough. This function returns true if at least 10 of the orbits under are parallel classes and the computation goes on only for the designs for which this is true. This way using Corollary 1 we consider a number of designs which is 16 times smaller than the initial one. Since Orb19PCEnough is very fast, this practically reduces the computation time about 16 times. We start constructing by calling PutBlock19 to add the first block of the short block orbit and then P19Constr.
void PCres57(void)
{
for(int i=1; i<=2353310; i++)
{
ReadDes();
if(Orb19PCEnough()) //true for only 156040 of all 2353310 designs
{
PutBlock19(1,1);
P19Constr(2);
}
}
}
The function P19Constr is presented below. It performs exhaustive backtrack search to choose the blocks of , , , and . If a block is in , all the blocks from its orbit under are in the class too, and no other block from its orbit under is in the class. Two global arrays are used in the function. TakenOrb19 is one-dimensional and TakenOrb19[i] is true if a block from the i-th orbit under has already been added to . Using it we ensure that contains at most one block from each block orbit under . The array O19 is two-dimensional and O19[i][j] is the number of the j-th block from the i-th orbit under .
Block19OK(j,n) checks if block j is disjoint with the already chosen blocks of . PutBlock19(j,n) (TakeBlock19(j,n)) adds to (removes from) block j and the two blocks from its orbit under and makes the corresponding changes in TakenOrb19. Since not only one, but three blocks are added, P19Constr(n+3) is called next.
void P19Constr(int n) //choose the n-th block of P19 { for(int i=1; i<=28; i++)if(!TakenOrb19[i]) //at most 1 block from orbit { for(int j=1; j<=19; j++) //19 blocks in an orbit { if(Block19OK(O19[i][j],n)) { PutBlock19(O19[i][j],n); if(n==17) //P19 is completed { //construct classes from class orbits of length 3: if(OKP19()) if(NewRes(1)) P3Constr(20); } else P19Constr(n+3); //choose the n+3rd block of P19 TakeBlock19(O19[i][j],n); } } } }
If the class is ready after PutBlock19 has added the last three blocks. In this case 19 out of all 28 parallel classes have already been constructed. Then OKP19 checks if the constructed contains exactly 4 blocks from orbits under which are parallel classes. If this is true, NewRes establishes if the current solution for is not equivalent to a previously obtained lexicographically smaller one. If the solution is new, P3Constr(20) is called.
void P3Constr(int nn)
{
int n=nn;
for(int i=1; i<=28; i++) if(!TakenOrb19[i])
{
if(OKOrb19(i,n))
{
PutOrb19(i,n);
n+=3;
}
}
if(n!=28) ErrorStop();
WriteRes();
}
P3Constr chooses the remaining base parallel classes , and (with class orbits of length 3). Each of them contains the blocks of one orbit under . That is why having constructed , the remaining 9 classes of the resolution are defined, i.e. these are the 9 block orbits under which do not have blocks in the constructed . That is why P3Constr uses TakenOrb19 to see which these 9 orbits are, checks once again by OKOrb19 if they are parallel classes and by PutOrb19 adds them to the resolution together with the other two parallel classes of their class orbits and makes changes to TakenOrb19. Finally WriteRes is called to write the resolution in a file. This way the construction of all point-cyclic KTS(57)s is completed in 5 h on a 3.2 GHz Intel-i9 PC.
The second algorithm () constructs one by one the 28 parallel classes of the resolution, without taking in account the results from Section 2.3, but using only the more general fact that a parallel class contains either whole block orbits under , or whole block orbits under . The current parallel class is constructed from orbits under one of these subgroups in all possible ways, and all parallel classes from its class orbit are added to the resolution before the construction of the next parallel class starts. In particular, the construction is organized by the function ResConstr which does not use Corollary 1 to reduce the number of the considered designs. After reading the design, initializing the necessary variables and finding the necessary block orbits, it calls ChooseBlock to look for possible point-cyclic resolutions.
void ResConstr(void)
{
for(int s=1; s<=2353310; s++)
{
ReadDes();
FindOrbits();
ChooseBlock(1,1,1);
}
}
Two global arrays are used in ChooseBlock. TakenBlock is one-dimensional and TakenBlock[i] is true if block i has already been added to the resolution. The array clLen contains all possible lengths of parallel class orbits, namely and , and .
void ChooseBlock(int n, int cl, int lencl)
{
for(int j=1; j<=532; j++) if (!TakenBlock[j]) //all blocks are 532
{
if(BlockOK(j, n, cl, clLen[lencl]))
{
all=PutBlock(j,n,cl,clLen[lencl]);
if(all==19) if(NewRes(cl))
{
PutClassOrb();
if(cl+clLen[lencl]-1==28) WriteRes(); //all parallel classes are 28
else ChooseBlock(1, cl+clLen[lencl], 1);
TakeClassOrb();
}
else ChooseBlock(all+1, cl, lencl);
TakeBlock(j,n,cl,clLen[lencl]);
}
}
if(n==1) if(lencl<maxlencl) ChooseBlock(1,cl,lencl+1);//next class length
}
ChooseBlock(n,cl,lencl) chooses in all possible ways the n-th block of the -th parallel class with class orbit of length . If and after finishing the search, ChooseBlock(n,cl,lencl+1) is called. BlockOK(j,n,cl,len) checks if block j and the blocks from its orbit under are mutually disjoint among themselves and disjoint with the already chosen blocks of class . PutBlock(j,n,cl,len) (TakeBlock(j,n,cl,len)) adds to (removes from) class block j and the blocks from its orbit under and makes the corresponding changes in TakenBlock. PutBlock returns the number of all the constructed blocks of class and assigns it to the variable all. If not all the blocks are constructed, ChooseBlock is called to choose the st block of the class.
If the class is ready and NewRes checks if this partial solution is not isomorphic to a previously constructed one. If the solution is new, all parallel classes from the class orbit of the last class are added to the solution by PutClassOrb, and ChooseBlock is called to start constructing the next parallel class, or if all parallel classes have been constructed WriteRes is called to write the resolution in a file.
By the algorithm it would take more than a month to complete the job on a PC. That is why we used the high-performance computer Avitohol of the Bulgarian Academy of Sciences (see the acknowledgment), where a parallel implementation of the program ran on 96 cores and completed the job in 12 h.
Advantages and disadvantages of the two algorithms:
- Both algorithms are based on exhaustive backtrack search and therefore their complexity is exponential. This is a serious disadvantage which makes backtrack search usable only for classification of combinatorial structures with relatively small parameters. Such an algorithm can be made applicable for definite parameters by the rejection of isomorphic partial solutions of some sizes, and by the implementation of suitable restrictions which are true for the considered objects and parameters.
- For the rejection of isomorphic solutions a minimality test is used in both algorithms in the function NewRes. This test is applied to some of the partial solutions and rejects partial solutions for which there exists an automorphism of the considered STS(57) that maps the current partial solution to a lexicographically smaller one. The rejection of partial solutions cuts off big branches of the search tree and makes the computation feasible.
- is applied on all the STS(57)s, while considers only those 156,040 designs which remain after using Corollary 1 and is therefore much faster.
- tries to construct resolutions of all possible types and structure, not only with the structure from Theorem 1 which is considered by . This makes faster too.
- also constructs parallel classes with more than one block which is fixed under . By Theorem 1 there are no such parallel classes in a point-cyclic resolution of an STS(57) and does not construct them. This way saves a lot of time, while obtains a lot of partial solutions which are not extendable to point-cyclic resolutions.
Although is much faster, we implemented the more general algorithm too as a partial check of the correctness of the obtained results, and in particular to check that no solutions were lost by possible errors in the theoretical restrictions, or in the C++ implementations of the algorithms. Each author has implemented in C++ one of the two algorithms. The same results were obtained.
4. Results and Open Problems
We construct all point-cyclic KTS(57)s. The number of automorphisms of the cyclically resolvable STS(57)s and of their resolutions is presented in Table 5, where the abbreviation D stands for designs (STS(57)s), R for point-cyclic resolution, AutD denotes the number of automorphisms of the designs, and AutR of the resolutions.

Table 5.
Automorphisms of the cyclically resolvable STS(57)s and their resolutions.
It can be seen that less than 7% of all cyclic STS(57)s are cyclically resolvable and most of their resolutions possess no automorphisms except those from the constructive automorphism group . There are 1592 point-cyclic KTS(57)s with a full automorphism group of order 171 and 2 with a full automorphism group of order 513.
Some of the point-cyclic KTS(57)s with a full automorphism group of order 171 have only two parallel class orbits under their full automorphism group (Table 6). In this case there is an automorphism of order three which maps to one-another the parallel class orbits of length 3 under , and this way these 9 classes form one class orbit under the full automorphism group of the resolution.

Table 6.
Parallel class orbits of point-cyclic KTS(57)s with a full automorphism group of order 171.
Each cyclically resolvable STS(57) has between 1 and 154 resolutions. The distribution of the number of point-cyclic resolutions of an STS(57) is presented in Figure 2. The maximal number 154 of point-cyclic KTS(57)s of one cyclic STS(57) is achieved by an STS(57) with a full automorphism group . There are STS(57)s with 21 point-cyclic resolutions.
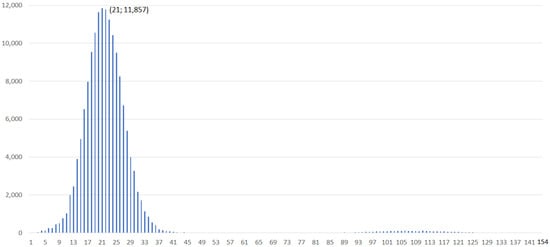
Figure 2.
STS(57)s with a given number of point-cyclic resolutions.
A full m-configuration in an STS(v) is a set of m blocks which cover points. Each point is in at least two blocks. Full configurations on 4 and 5 blocks are unique and also known as the Pasch and the mitre configurations. The absence of these configurations in a cyclically resolvable cyclic STS(v) is a desirable property with respect to coding applications [6,7,10,30].
The minimum distance of an LDPC code is equal to the minimum nonzero number of columns in its parity-check matrix for which a nontrivial linear combination sums to zero (mod 2) [31]. For an LDPC code from an STS(v) the minimum distance constructively is settled to at least 4 (each column has weight 3 and two columns share no more than one point). The 4 blocks of a Pasch configuration sum to zero (mod 2), while the 5 blocks of a mitre configuration do not. In anti-Pasch STS(v)s no four triples are isomorphic to the Pasch configuration. That is why an LDPC code from an anti-Pasch STS(v) has minimum distance at least 6 [5].
In anti-mitre STS(v)s no five triples are isomorphic to the mitre configuration. If an STS(v) is without any Pasch or mitre configuration it is 5-sparse. 5-sparse KTS(v)s are of major importance not only for the constructions of LDPC codes, but for some other applications in Coding Theory too. One of them is the application of KTS(v)s to optimal erasure-resilient codes for large disk arrays [32].
The number of anti-Pasch, anti-mitre and 5-sparse cyclic STS(57)s is presented in [26]. There are 843 5-sparse cyclic STS(57)s [26]. We establish that only 63 of them are cyclically resolvable, one of them has 171, one 342 automorphisms and all the remaining 61 cyclically resolvable 5-sparse STS(57)s have 57 automorphisms. The number of the resolutions of 5-sparse cyclic STS(57)s is presented in Table 7. All these resolutions possess only .

Table 7.
5-sparse cyclic STS(57)s with a given number of point-cyclic resolutions.
All the constructed in this paper point-cyclic resolutions are available online at http://www.moi.math.bas.bg/moiuser/~stela/SRSTS(57).htm (accessed on 6 January 2025). They can be useful both in possible applications, as well as in future research on the topic.
The classification of the point-cyclic resolutions of STS(63)s is the next open problem, which at the moment is very difficult to attack by our methods because
- The nonisomorphic cyclic STS(63)s are 21 times more than the cyclic STS(57)s.
- The cyclic group of order 57 has two proper subgroups and a parallel class of a point-cyclic resolution is always fixed by one of the two subgroups, while the cyclic group of order 63 has 4 proper subgroups, and this leads to much more complicated considerations.
- The structure of all point-cyclic resolutions of STS(57)s is the same (Theorem 1), while there are several types of point-cyclic resolutions of STS(63)s.
- An STS(63) has 1.1 times more points and 1.22 times more blocks than an STS(57). Such a difference in the considered parameters affects several times the speed of an exponential backtrack search algorithm even if it rejects effectively equivalent partial solutions.
5. Discussion on the Obtained Results
Only a few KTS(57)s were known before the present work, while their number is at least 3,638,984 now. The obtained resolutions have a quasi-cyclic structure that makes them particularly interesting for the construction of LDPC codes with useful structural properties and code rate [5,6,7,9,10]. In addition the anti-Pasch KTS(v)s can produce ()-regular LDPC codes with minimum distance at least 6, and those of them which are 5-sparse yield optimal erasure-resilient codes [32]. The availability online of all the obtained resolutions and their automorphisms can be of use for choosing the best of them for certain applications, or for further investigations.
Our computer-aided results have been double-checked by two different algorithms, each of them implemented by one of the two authors. They also comply with previous theoretical results, namely the parameters meet the necessary conditions for the existence of resolutions of type [25] and we obtain resolutions of type .
Our investigation shows that:
- There are 155,966 cyclically resolvable STS(57)s with 3,638,984 point-cyclic resolutions.
- The point-cyclic resolutions of STS(57)s have full automorphism groups of orders 57, 171, and 513.
- There are 63 cyclically resolvable 5-sparse STS(57)s with 109 point-cyclic resolutions which are of particular interest for applications in Coding Theory.
We believe this computer-aided investigation will aid further research on these fascinating objects and their applications.
Author Contributions
Conceptualization, S.T. and S.Z.; methodology, S.T. and S.Z.; software, S.T. and S.Z.; validation, S.T.; formal analysis, S.T. and S.Z.; investigation, S.Z.; resources, S.T.; data curation, S.Z.; writing—original draft preparation, S.T. and S.Z.; writing—review and editing, S.T. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
S.T. was partially supported by the Bulgarian National Science Fund under Contract No KP-06-H62/2/13.12.2022, and S.Z. was partially supported by the Bulgarian National Science Fund under Contract No. KP-06-H62/2/13.12.2022.
Data Availability Statement
The data obtained and presented in this study is openly available at http://www.moi.math.bas.bg/moiuser/~stela/SRSTS(57).htm (accessed on 6 January 2025).
Acknowledgments
We are grateful to the anonymous referees for their careful reading of the text, and for the valuable suggestions which have improved the presentation of the results. The research that led to these results was carried out using the infrastructure purchased under the National Roadmap for RI, financially coordinated by the MES of the Republic of Bulgaria (grant No. D01-325/01.12.2023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and notations are used in this manuscript:
| STS(v) | a Steiner triple system of order v, a 2- design |
| KTS(v) | a Kirkman triple system of order v is a resolution of an STS(v) |
| the constructive cyclic group of automorphisms of order 57 | |
| the subgroup of order 19 of | |
| the subgroup of order 3 of |
References
- Colbourn, C.J.; Dinitz, J.H. (Eds.) Handbook of Combinatorial Designs, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Colbourn, C.J.; Rosa, A. Triple Systems; Clarendon Press: Oxford, UK, 1999. [Google Scholar]
- Colbourn, C.J.; Dinitz, J.H.; Stinson, D.R. Applications of Combinatorial Designs to Communications, Cryptography, and Networking. In Surveys in Combinatorics; Lamb, J.D., Preece, D.A., Eds.; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1999; pp. 37–100. [Google Scholar] [CrossRef]
- Semakov, N.V.; Zinovev, V.A. Equidistant q-ary codes with maximal distance and resolvable balanced incomplete block designs. Probl. Peredachi Inform. 1968, 4, 3–10. English translation in Probl. Inform. Transm. 1968, 4, 1–7. (In Russian) [Google Scholar]
- Johnson, S.J.; Weller, S.R. Construction of low-density parity-check codes from Kirkman triple systems. In Proceedings of the GLOBECOM’01. IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001; pp. 970–974. [Google Scholar] [CrossRef]
- Gruner, A.; Huber, M. New Combinatorial Construction Techniques for Low-Density Parity-Check Codes and Systematic Repeat-Accumulate Codes. IEEE Trans. Commun. 2012, 60, 2387–2395. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.; Park, H.; No, J.-S. Design of Protograph LDPC Codes Using Resolvable Block Designs for Block Fading Channel. IEEE Wirel. Commun. Lett. 2022, 11, 1970–1974. [Google Scholar] [CrossRef]
- Townsend, R.; Weldon, E.J. Self-orthogonal quasi-cyclic codes. IEEE Trans. Inf. Theory 1967, 13, 183–195. [Google Scholar] [CrossRef]
- Johnson, S.J.; Weller, S.R. Resolvable 2-designs for regular low-density parity-check codes. IEEE Trans. Commun. 2003, 51, 1413–1419. [Google Scholar] [CrossRef]
- Vasic, B.; Milenkovic, O. Combinatorial constructions of low-density parity-check codes for iterative decoding. IEEE Trans. Inf. Theory 2004, 50, 1156–1176. [Google Scholar] [CrossRef]
- Ray-Chaudhuri, D.K.; Wilson, R.M. Solution of Kirkman’s school-girl problem. Proc. Sympos. Pure Math. Comb. 1971, 19, 187–203. [Google Scholar]
- Cole, F.N. Kirkman parades. Bull. Am. Math. Soc. 1922, 28, 435–437. [Google Scholar] [CrossRef]
- Mulder, P. Kirkman-Systemen. Ph.D. Thesis, Rijksuniversiteit Groningen, Groningen, The Netherlands, 1917. [Google Scholar]
- Kokkala, J.I.; Östergård, P.R.J. Kirkman triple systems with subsystems. Discrete Math. 2020, 343, 1111960. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Magliveras, S.S.; Mathon, R.A. Transitive Steiner and Kirkman triple systems of order 27. Math. Comput. 1992, 58, 441–449. [Google Scholar] [CrossRef]
- Dukes, P.J.; Lamken, E.R. An update on the existence of Kirkman triple systems with Steiner triple systems as subdesigns. J. Comb. Des. 2022, 30, 581–608. [Google Scholar] [CrossRef]
- Lam, C.W.H.; Miao, Y. Cyclically resolvable cyclic Steiner triple systems of order 21 and 39. Discrete Math. 2000, 219, 173–185. [Google Scholar] [CrossRef]
- Li, X.-Y.; Xu, Z.-D.; Chou, W.-X. A new method of constructing Kirkman triple system. In Proceedings of the 2011 Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 4237–4242. [Google Scholar] [CrossRef]
- Mathon, R.A.; Phelps, K.T.; Rosa, A. A class of Steiner triple systems of order 21 and associated Kirkman systems. Math. Comput. 1981, 37, 209–222. [Google Scholar] [CrossRef]
- Rees, R.; Stinson, D.R. On the existence of Kirkman triple systems containing Kirkman subsystems. Ars Comb. 1988, 26, 3–16. [Google Scholar]
- Stinson, D.R. A survey of Kirkman triple systems and related designs. Discrete Math. 1991, 92, 371–393. [Google Scholar] [CrossRef]
- Topalova, S.; Zhelezova, S. Point-cyclic KTS(45). In Advanced Computing in Industrial Mathematics; Lilkova, E., Datcheva, M., Alexandrova, T., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Tonchev, V.D.; Vanstone, S.A. On Kirkman triple systems of order 33. Discrete Math. 1992, 106/107, 493–496. [Google Scholar] [CrossRef]
- Genma, M.; Mishima, M.; Jimbo, M. Cyclic resolvability of cyclic Steiner 2-designs. J. Comb. Des. 1997, 5, 177–187. [Google Scholar] [CrossRef]
- Mishima, M.; Jimbo, M. Recursive constructions for cyclic quasiframes and cyclically resolvable cyclic Steiner 2-designs. Discrete Math. 2000, 211, 135–152. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Mendelsohn, E.; Rosa, A.; Siran, J. Anti-Mitre Steiner Triple Systems. Graph. Combinator. 1994, 10, 215–224. [Google Scholar] [CrossRef]
- Baicheva, T.; Topalova, S. Classification results for (v, k, 1) cyclic difference families with small parameters. In International Book Series: Information Science and Computing; Deza, M., Petitjean, M., Markov, K., Eds.; Book 25; ITHEA: Sofia, Bulgaria, 2012; pp. 24–30. [Google Scholar]
- Bouyuklieva, S.; Bouyukliev, I. How to Find the Equivalence Classes in a Set of Linear Codes in Practice? Mathematics 2024, 12, 328. [Google Scholar] [CrossRef]
- Mishima, M.; Jimbo, M. Some types of cyclically resolvable cyclic Steiner 2-designs. Congr. Numer. 1997, 123, 193–203. [Google Scholar]
- Park, H.; Hong, S.; No, J.-S.; Shin, D.-J. Design of Multiple-Edge Protographs for QC LDPC Codes Avoiding Short Inevitable Cycles. IEEE Trans. Inform. Theory 2013, 59, 4598–4614. [Google Scholar] [CrossRef]
- Wicker, S.B. Error Control Systems for Digital Communication and Storage; Prentice-Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Chee, Y.M.; Colbourn, C.J.; Ling, A.C.H. Asymptotically optimal erasure-resilient codes for large disk arrays. Discrete Appl. Math. 2000, 102, 3–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).