Metric Morphological Interpretation of 3D Structures by Gray–Scott Model Simulation Utilising 2D Multifractal Analysis
Abstract
1. Introduction
2. Methods
2.1. Multifractal Theory
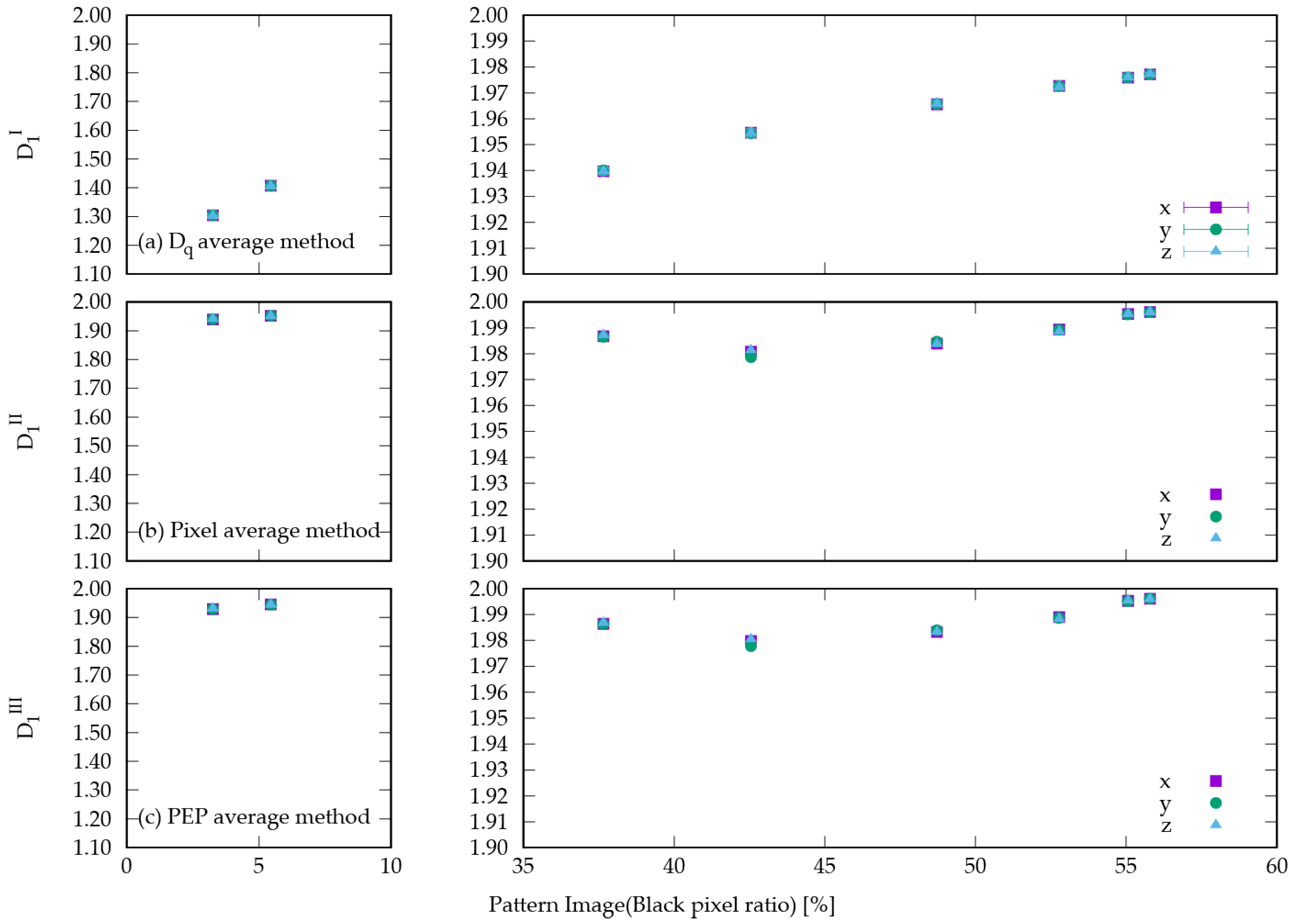
2.2. Proposal 1: Average Method
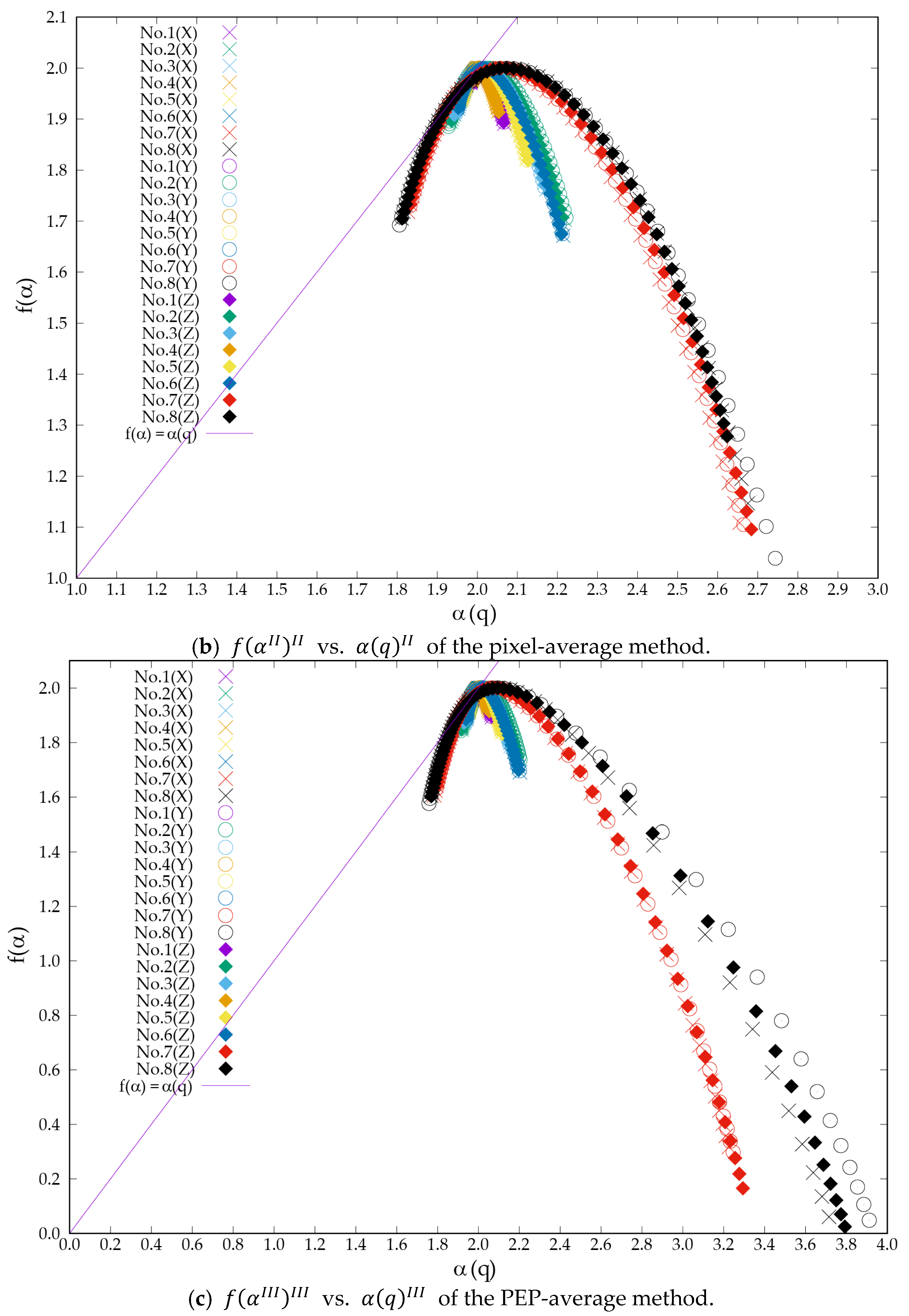
2.3. Proposal 2: Pixel-Average Method
2.4. Proposal 3: PEP Average Method (PEP: Pixel-Existence Probability)
3. Valuation and Verification of Dispersion in the Slice Direction
3.1. Method of Distributed Image Simulation
3.1.1. Pattern A: Simulation with Equal Dispersion
3.1.2. Pattern B: Simulation with Unequal Dispersion
3.2. Results and Methodology Verification
4. Three-Dimensional Structure Evaluation by Self-Assembly
4.1. Theory of the Gray–Scott Model
4.2. Generation of Gray–Scott Model Simulation Images
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Number of Trials | Entropy ∆S | |||
|---|---|---|---|---|
| 1 | 1.2935960 | 0.6726074 | 0.9999534 | 1.0653261 |
| 2 | 1.3752910 | 1.7281945 | 0.9999534 | 1.0791908 |
| 3 | 1.1777972 | 1.7000611 | 0.9999534 | 1.0448574 |
| 4 | 1.3469162 | 0.9697403 | 0.9999534 | 1.0758888 |
| 5 | 1.1887294 | 1.5154851 | 0.9999534 | 1.0483877 |
| 6 | 1.1972921 | 1.1820644 | 0.9999534 | 1.0488341 |
| 7 | 1.3286980 | 0.8784778 | 0.9999534 | 1.0726144 |
| 8 | 1.3266124 | 1.6755119 | 0.9999534 | 1.0709015 |
| 9 | 1.2025691 | 1.7942907 | 0.9999534 | 1.0498063 |
| 10 | 1.1520390 | 0.7323597 | 0.9999534 | 1.0375790 |
| 11 | 1.0635399 | 1.3355127 | 0.9999534 | 1.0176194 |
| 12 | 1.3047466 | 0.7999125 | 0.9999534 | 1.0691615 |
| 13 | 1.1934109 | 1.5645343 | 0.9999534 | 1.0483230 |
| 14 | 1.0943972 | 1.0658812 | 0.9999534 | 1.0246358 |
| 15 | 1.3055950 | 1.7990874 | 0.9999534 | 1.0678811 |
| 16 | 1.0703669 | 1.0709745 | 0.9999534 | 1.0180825 |
| 17 | 1.3685292 | 1.2540443 | 0.9999534 | 1.0762876 |
| 18 | 1.0314567 | 1.0221169 | 0.9999534 | 1.0076374 |
| 19 | 1.1356704 | 1.0978999 | 0.9999534 | 1.0350160 |
| 20 | 1.2839586 | 1.2035429 | 0.9999534 | 1.0640828 |
| 21 | 1.3461463 | 1.2642253 | 0.9999534 | 1.0758348 |
| 22 | 1.2597768 | 1.1959571 | 0.9999534 | 1.0583868 |
| 23 | 1.2236903 | 1.1685399 | 0.9999534 | 1.0536964 |
| 24 | 1.0924876 | 1.0954151 | 0.9999534 | 1.0238992 |
| 25 | 1.1392720 | 1.1093918 | 0.9999534 | 1.0348228 |
| 26 | 1.1781465 | 1.1810969 | 0.9999534 | 1.0445545 |
| 27 | 1.2619710 | 1.1887206 | 0.9999534 | 1.0623428 |
| 28 | 1.1739030 | 1.1390590 | 0.9999534 | 1.0443692 |
| 29 | 1.2739621 | 1.3090071 | 0.9999534 | 1.0611155 |
| 30 | 1.1855635 | 1.1555629 | 0.9999534 | 1.0457690 |
Appendix B

References
- Vaz, C.; Pascoal, R.; Sebastião, H. Price appreciation and roughness duality in bitcoin: A multifractal analysis. Mathematics 2021, 9, 2088. [Google Scholar] [CrossRef]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed]
- Hirabayashi, T.; Ito, K.; Yoshii, T. Multifractal analysis of earthquakes. Pure Appl. Geophys. 1992, 138, 591–610. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Farhidzadeh, A.; Salamone, S. Multifractal analysis of crack patterns in reinforced concrete shear walls. Struct. Health Monit. 2016, 15, 81–92. [Google Scholar] [CrossRef]
- López-Lambraño, A.A.; Fuentes, C.; Serpa-Usta, Y.; Tejada, G.; López-Ramos, A. Multifractal Measures and Singularity Analysis of Rainfall Time Series in the Semi-Arid Central Mexican Plateau. Atmosphere 2025, 16, 639. [Google Scholar] [CrossRef]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal Methodology. Phys. A Stat. Mech. Appl. 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Wu, J.; Jin, X.; Mi, S.; Tang, J. An Effective Method to Compute the Box-Counting Dimension Based on the Mathematical Definition and Intervals. Results Eng. 2020, 6, 100106. [Google Scholar] [CrossRef]
- Rajković, N.; Krstonošić, B.; Milošević, N. Box-Counting Method of 2D Neuronal Image: Method Modification and Quantitative Analysis Demonstrated on Images from the Monkey and Human Brain. Comput. Math. Methods Med. 2017, 2017, 8967902. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Y. A Three-Dimensional Box-Counting Method to Study the Fractal Characteristics of Urban Areas in Shenyang, Northeast China. Buildings 2022, 12, 299. [Google Scholar] [CrossRef]
- Sato, Y.; Munakata, F. Morphological characteristics of self-assembled aggregate textures using multifractal analysis: Interpretation of multifractal τ(q) using simulations. Phys. A Stat. Mech. Appl. 2022, 603, 127771. [Google Scholar] [CrossRef]
- Munakata, F.; Ogiya, T.; Sato, Y. Thermal conductivities and complex network properties of fractal self-assembled/self-organized texture in binary composite materials. Appl. Phys. A 2024, 130, 522. [Google Scholar] [CrossRef]
- Breki, C.-M.; Dimitrakopoulou-Strauss, A.; Hassel, J.; Theoharis, T.; Sachpekidis, C.; Pan, L.; Provata, A. Fractal and multifractal analysis of PET/CT images of metastatic melanoma before and after treatment with ipilimumab. EJNMMI Res. 2016, 6, 61. [Google Scholar] [CrossRef] [PubMed]
- Horstmann, H.; Körber, C.; Sätzler, K.; Aydin, D.; Kuner, T. Serial section scanning electron microscopy (S3EM) on silicon wafers for ultra-structural volume imaging of cells and tissues. PLoS ONE 2012, 7, e35172. [Google Scholar] [CrossRef]
- Phaneuf, M.W. FIB for Materials Science Applications—A Review; Springer: Boston, MA, USA, 2005; Volume 30, pp. 277–288. ISBN 9780387231167. [Google Scholar]
- Fiske, L.D.; Aalders, M.C.G.; Almasian, M.; van Leeuwen, T.G.; Katsaggelos, A.K.; Cossairt, O.; Faber, D.J. Bayesian analysis of depth resolved OCT attenuation coefficients. Sci. Rep. 2021, 11, 2263. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A Gen. Phys. 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Kermouni Serradj, N.; Messadi, M.; Lazzouni, S. Classification of mammographic ROI for microcalcification detection using multifractal approach. J. Digit. Imaging 2022, 35, 1544–1559. [Google Scholar] [CrossRef]
- Yadav, R.P.; Dwivedi, S.; Mittal, A.K.; Kumar, M.; Pander, A.C. Fractal and multifractal analysis of LiF thin film surface. Appl. Surf. Sci. 2012, 261, 547–553. [Google Scholar] [CrossRef]
- Xiong, G.; Yu, W.; Xia, W.; Zhang, S. Multifractal signal reconstruction based on singularity power spectrum. Chaos Solitons Fractals 2016, 91, 25–32. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Multifractal characterization of urban form and growth: The case of Beijing Environ. Plan. B Plan. Des. 2013, 40, 884–904. [Google Scholar] [CrossRef]
- Wang, F.; Liao, D.W.; Li, J.W.; Liao, G.P. Two-dimensional multifractal detrended fluctuation analysis for plant identification. Plant Methods 2015, 11, 12. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Boeing, G. Visual analysis of nonlinear dynamical systems: Chaos, fractals, self-similarity and the limits of prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Gray, P.; Scott, S.K. Autocatalytic reactions in the isothermal, continuous stirred tank reactor. Chem. Eng. Sci. 1983, 38, 29–43. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Jin, Z.; Lu, B.; Xin, Z.X.; Kang, C.K.; Kim, J.K. Effect of Flame Retardants on Mechanical Properties, Flammability and Foamability of PP/Wood–Fiber Composites. Compos. Part B Eng. 2012, 43, 150–158. [Google Scholar] [CrossRef]
- Lee, C.H.; Salit, M.S.; Hassan, M.R. A Review of the Flammability Factors of Kenaf and Allied Fibre Reinforced Polymer Composites. Adv. Mater. Sci. Eng. 2014, 2014, 514036. [Google Scholar] [CrossRef]
- Garfinkel, A.; Tintut, Y.; Petrasek, D.; Boström, K.; Demer, L.L. Pattern Formation by Vascular Mesenchymal Cells. Proc. Natl. Acad. Sci. USA 2004, 101, 9247–9250. [Google Scholar] [CrossRef]
- Chen, T.-H.; Hsu, J.J.; Zhao, X.; Guo, C.; Wong, M.N.; Huang, Y.; Li, Z.; Garfinkel, A.; Ho, C.-M.; Tintut, Y.; et al. Left-Right Symmetry Breaking in Tissue Morphogenesis via Cytoskeletal Mechanics. Circ. Res. 2012, 110, 551–559. [Google Scholar] [CrossRef]


| Pattern No. | F | K | Black Pixel Ratio | Fractal Dimension | Structure Type | Image | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.08 | 0.035 | 0.03 | 0.05554 | 55.06475 | 2.95768 | Network pattern |  |
| 2 | 0.08 | 0.035 | 0.03 | 0.05540 | 55.79173 | 2.90277 | Network pattern |  |
| 3 | 0.08 | 0.035 | 0.03 | 0.05600 | 52.77910 | 2.90932 | Network pattern |  |
| 4 | 0.08 | 0.035 | 0.03 | 0.05710 | 48.72027 | 2.96180 | Network pattern |  |
| 5 | 0.08 | 0.035 | 0.03 | 0.05880 | 42.54765 | 2.93311 | Network pattern |  |
| 6 | 0.08 | 0.035 | 0.03 | 0.06000 | 37.65502 | 2.89795 | Mix (Network/Spot) pattern |  |
| 7 | 0.08 | 0.035 | 0.03 | 0.06000 | 5.446016 | 2.41616 | Spot pattern |  |
| 8 | 0.08 | 0.035 | 0.03 | 0.06000 | 3.261236 | 2.28930 | Spot pattern |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahara, A.; Sato, Y. Metric Morphological Interpretation of 3D Structures by Gray–Scott Model Simulation Utilising 2D Multifractal Analysis. Mathematics 2025, 13, 3234. https://doi.org/10.3390/math13193234
Takahara A, Sato Y. Metric Morphological Interpretation of 3D Structures by Gray–Scott Model Simulation Utilising 2D Multifractal Analysis. Mathematics. 2025; 13(19):3234. https://doi.org/10.3390/math13193234
Chicago/Turabian StyleTakahara, Akira, and Yoshihiro Sato. 2025. "Metric Morphological Interpretation of 3D Structures by Gray–Scott Model Simulation Utilising 2D Multifractal Analysis" Mathematics 13, no. 19: 3234. https://doi.org/10.3390/math13193234
APA StyleTakahara, A., & Sato, Y. (2025). Metric Morphological Interpretation of 3D Structures by Gray–Scott Model Simulation Utilising 2D Multifractal Analysis. Mathematics, 13(19), 3234. https://doi.org/10.3390/math13193234







