Mathematical Modeling and Intensive Simulations Assess Chances for Recovery of the Collapsed Azov Pikeperch Population
Abstract
1. Introduction
2. Data and Methods
2.1. The Model
2.2. Sensitivity Analysis to the Model’s Structural Assumptions
2.3. Identification and Validation of the Model
2.3.1. Sources of Input Data
2.3.2. Identification Procedure
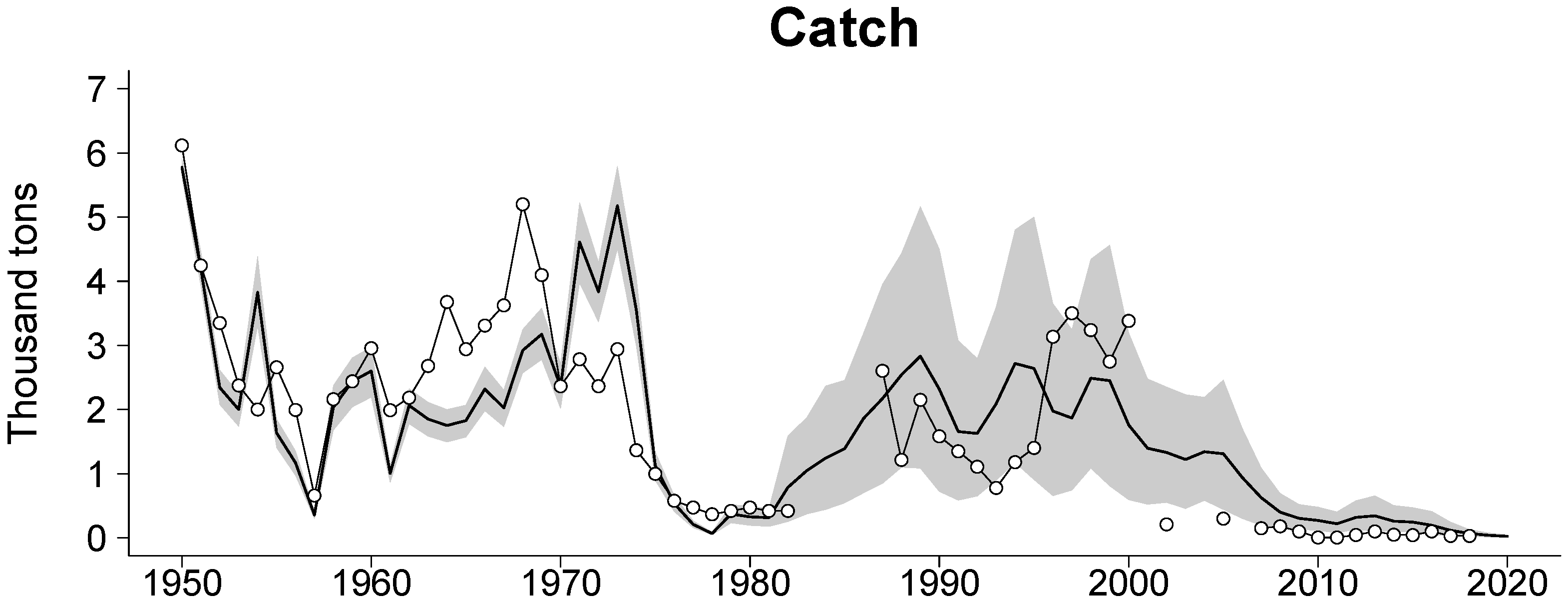
2.3.3. Validation
2.4. Scenarios of Monte Carlo Simulations
3. Simulation Results for the Projection Period
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Coefficient | Value | SE | t-Stat | p-Value |
|---|---|---|---|---|
| C | 3.9689 | 0.34739 | 11.425 | 8.5758 |
| A | −0.47112 | 0.1293 | −3.6435 | 0.00062093 |
| B | −0.38966 | 0.075378 | −5.1694 | 3.7966 |
| Number of observations: 55, Error degrees of freedom: 52 | ||||
| Root Mean Squared Error: 1.42 | ||||
| R-squared: 0.414, Adjusted R-Squared: 0.391 | ||||
| F-statistic vs. constant model: 18.4, p-value = 9.25 | ||||
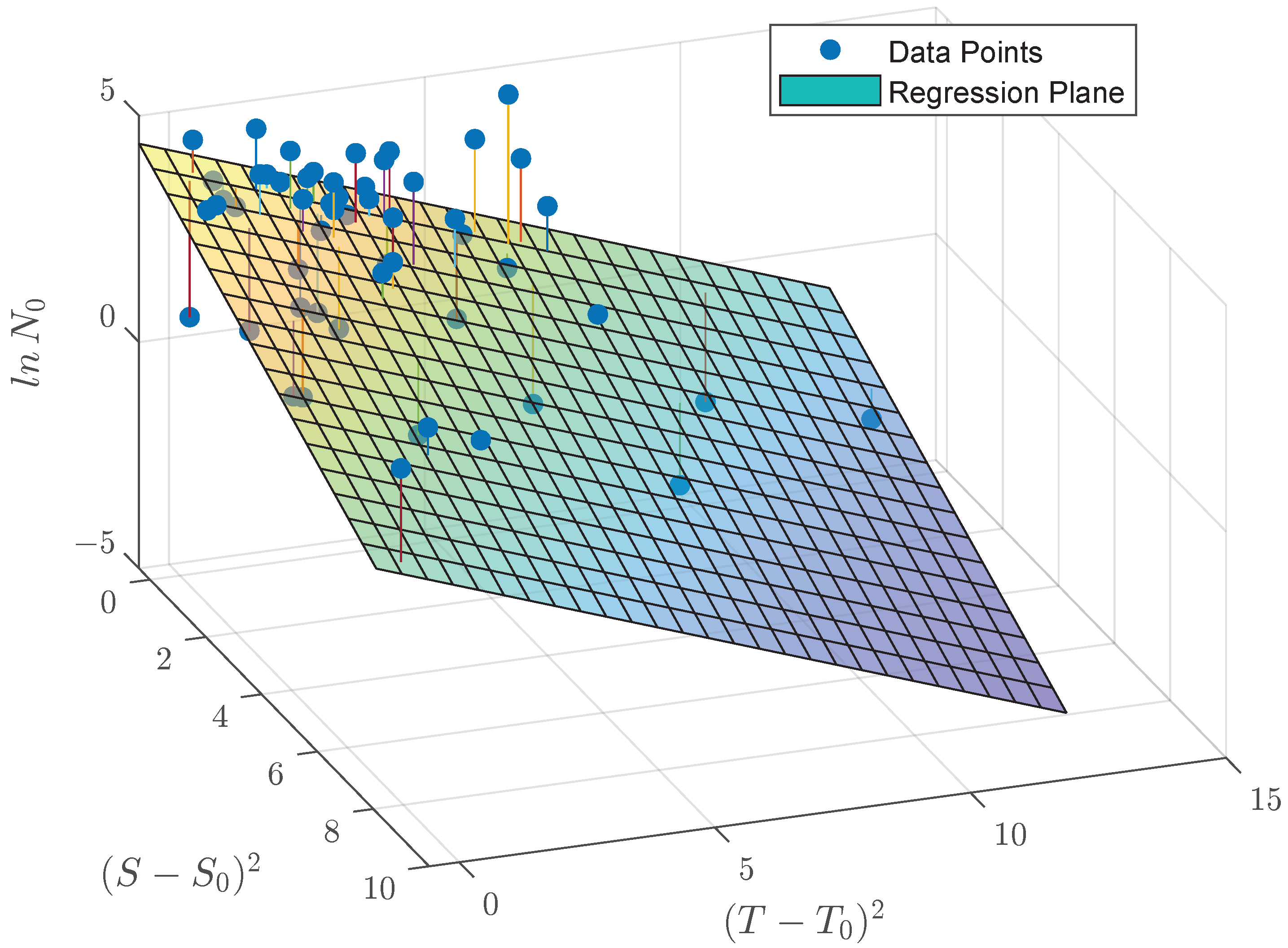
References
- Tyutyunov, Y.; Senina, I.; Jost, C.; Arditi, R. Risk assessment of the harvested pike-perch population of the Azov Sea. Ecol. Modell. 2002, 149, 297–311. [Google Scholar] [CrossRef]
- Dudkin, S.I.; Leontiev, S.Y.; Mirzoyan, A.V. The state of stocks and catches of commercial fish species of the Azov and Black Seas for the period 2000–2020: Dynamics and trends. Trudy VNIRO 2024, 195, 35–44. (In Russian) [Google Scholar] [CrossRef]
- Zhivoglyadov, A.A.; Luk’yanov, S.V. Stock assessment of the current state of the zander Sander lucioperca population in the Azov Sea basin. Probl. Fish. 2018, 19, 405–415. (In Russian) [Google Scholar]
- Podoinitsyn, D.A. Modern ecological state of pike perch population in the Azov Sea. Izv. Vuzov Sev.-Kavkaz. Region, Ser. Estestv. Nauki 2010, 4, 111–112. (In Russian) [Google Scholar]
- Balykin, P.A.; Ponomareva, E.N.; Sorokina, M.N.; Startsev, A.V. Changes in the size and composition of catches in the Taganrog Bay in the 21st century. Nauka Yuga Rossii 2022, 18, 55–61. [Google Scholar] [CrossRef]
- Ponomareva, E.; Balykin, P.; Startsev, A.; Savitskaya, S.; Sorokina, M.; Korchunov, A. Current state of the Sea of Azov main commercial fishery resources and ways to restore them. E3S Web Conf. 2023, 431, 01055. [Google Scholar] [CrossRef]
- Tyutyunov, Y.V.; Senina, I.N.; Titova, L.I.; Dashkevich, L.V. Long-range prediction of the risk of extinction faced by the pikeperch in the Azov Sea: Was the prediction correct? Biophysics 2020, 65, 338–348. [Google Scholar] [CrossRef]
- Berdnikov, S.V.; Dashkevich, L.V.; Kulygin, V.V. A new state in the hydrological regime of the Sea of Azov in the 21th century. Dokl. Earth Sci. 2022, 503, 123–128. [Google Scholar] [CrossRef]
- Berdnikov, S.V.; Sorokina, V.V.; Kleshchenkov, A.V.; Tyutyunov, Y.V.; Kulygin, V.V.; Kovaleva, G.V.; Bulysheva, N.I. Marine indicators of climate change in the Azov Sea ecosystem. J. Sea Res. 2023, 193, 102373. [Google Scholar] [CrossRef]
- Balykin, P.A.; Kutsyn, D.N.; Orlov, A.M. Changes in salinity and species composition of ichthyofauna in the Sea of Azov. Oceanology 2019, 59, 358–366. [Google Scholar] [CrossRef]
- Kjellman, J.; Lappalainen, J.; Urho, L. Influence of temperature on size and abundance dynamics of age-0 perch and pikeperch. Fish. Res. 2001, 53, 47–56. [Google Scholar] [CrossRef]
- Ložys, L. The growth of pikeperch (Sander lucioperca L.) and perch (Perca fluviatilis L.) under different water temperature and salinity conditions in the Curonian Lagoon and Lithuanian coastal waters of the Baltic Sea. Hydrobiologia 2004, 514, 105–113. [Google Scholar] [CrossRef]
- Gröger, J.P.; Winkler, H.; Rountree, R.A. Population dynamics of pikeperch (Sander lucioperca) and its linkage to fishery driven and climatic influences in a southern Baltic lagoon of the Darss-Zingst Bodden Chain. Fish. Res. 2007, 84, 189–201. [Google Scholar] [CrossRef]
- Heikinheimo, O.; Pekcan-Hekim, Z.; Raitaniemi, J. Spawning stock–recruitment relationship in pikeperch Sander lucioperca (L.) in the Baltic Sea, with temperature as an environmental effect. Fish. Res. 2014, 155, 1–9. [Google Scholar] [CrossRef]
- Olin, M.; Heikinheimo, O.; Lehtonen, T.K.; Raitaniemi, J. Long-term monitoring of pikeperch (Sander lucioperca) populations under increasing temperatures and predator abundances in the Finnish coastal waters of the Baltic Sea. Ecol. Freshw. Fish. 2023, 32, 750–764. [Google Scholar] [CrossRef]
- Goptarev, N.P.; Simonov, A.I.; Zatuchnaya, B.M.; Gershanovich, D.E. Hydrometeorology and Hydrochemistry of Seas of the USSR. Vol. 5. The Sea of Azov; Gidrometeoizdat: St. Petersburg, Russia, 1991; 236p. (In Russian) [Google Scholar]
- Lund, I.; Rodríguez, C.; Izquierdo, M.S.; El Kertaoui, N.; Kestemont, P.; Reis, D.B.; Dominguez, D.; Pérez, J.A. Influence of salinity and linoleic or α-linolenic acid based diets on ontogenetic development and metabolism of unsaturated fatty acids in pike perch larvae (Sander lucioperca). Aquaculture 2019, 500, 550–561. [Google Scholar] [CrossRef]
- Chernichko, J.I.; Demchenko, V.A.; Podorozhny, S.N.; Zhmud, M.Y.; Suchkov, S.I. Possible impact of different scenarios of climate change on the formation of some ecosystem services in the Azov-Black Sea region. IOP Conf. Ser. Earth Environ. Sci. 2022, 1049, 012065. [Google Scholar] [CrossRef]
- Shelford, V.E. Animal Communities in Temperate America as Illustrated in the Chicago Region: A Study in Animal Ecology; Univ. of Chicago Press: Chicago, IL, USA, 1913; 362p. [Google Scholar]
- Shelford, V.E. Some concepts of bioecology. Ecology 1931, 12, 455–467. [Google Scholar] [CrossRef]
- Lynch, M.; Gabriel, W. Environmental tolerance. Am. Nat. 1987, 129, 283–303. [Google Scholar] [CrossRef]
- Erofeeva, E.A. Plant hormesis and Shelford’s tolerance law curve. J. For. Res. 2021, 32, 1789–1802. [Google Scholar] [CrossRef]
- Senina, I.; Tyutyunov, Y.; Arditi, R. Extinction risk assessment and optimal harvesting of anchovy and sprat in the Azov Sea. J. Appl. Ecol. 1999, 36, 297–306. [Google Scholar] [CrossRef]
- Senina, I.N.; Lehodey, P.; Hampton, J.; Sibert, J. Quantitative modelling of the spatial dynamics of South Pacific and Atlantic albacore tuna populations. Deep-Sea Res. II Top. Stud. Oceanogr. 2020, 175, 104667. [Google Scholar] [CrossRef]
- Gabriel, W.; Lynch, M. The selective advantage of reaction norms for environmental tolerance. J. Evol. Biol. 1992, 5, 41–59. [Google Scholar] [CrossRef]
- Skagen, D.W.; Skern-Mauritzen, M.; Dankel, D.; Enberg, K.; Kjesbu, O.S.; Nash, R.D.M. A simulation framework for evaluating fisheries management decisions using environmental information. ICES J. Mar. Sci. 2013, 70, 743–754. [Google Scholar] [CrossRef]
- Senina, I. innasenina/pikeperch-model: v3.0-pikeperch-model-with-cc (v3.0). Zenodo 2025, 15625329. [Google Scholar] [CrossRef]
- Ricker, W.E. Stock and recruitment. J. Fish. Res. Board Can. 1954, 11, 559–623. [Google Scholar] [CrossRef]
- Elaydi, S.N. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005; 546p. [Google Scholar] [CrossRef]
- Beverton, R.J.H.; Holt, S.J. On the Dynamics of Exploited Fish Populations; Springer: Cham, The Netherlands, 1957; 538p. [Google Scholar] [CrossRef]
- Belousov, V.N. History of harvesting pikeperch Stizostedion lucioperca (Linnaeus, 1758) in the Azov Sea. Izv. Vuzov Sev.-Kavkaz. Reg. Ser. Estestv. Nauki 2004, 5, 47–65. (In Russian) [Google Scholar]
- Belousov, V.N. The Formation and Use of the Stock of Semi-Anadromous Pikeperch Stizostedion lucioperca (Linnaeus, 1758) in Conditions of Varying Regime of the Azov Sea; Extended Abstract of Candidate’s Dissertation in Biology; Kuban State Agrarian University: Krasnodar, Russia, 2004; 34p. (In Russian) [Google Scholar]
- Luk’yanov, S.V.; Zhivoglyadov, A.A. Environmental problems of formation of the stock of pike-perch Stizostedion lucioperca (Linnaeus, 1758) in the Azov Sea. In Ecological, Industrial and Energy Safety; Lukina, L.I., Bezhina, N.A., Lyamina, N.V., Eds.; Sevastopol State University: Sevastopol, Crimea, 2018; pp. 739–743. (In Russian) [Google Scholar]
- Luk’yanov, S.V.; Zhivoglyadov, A.A. Catadromous pike perch of the Azov Sea Stizostedion lucioperca (Linnaeus, 1758) in the conditions of salinity increase. In The Wildlife Management Conflict: A Role in Noosphere Evolution; Shuvaev, N.S., Kolchin, E.A., Eds.; Astrakhan State University: Astrakhan, Russia, 2019; pp. 78–83. (In Russian) [Google Scholar]
- Boiko, E.G. Evaluating natural mortality in the Azov zander (Stizostedion lucioperca). In Translation Series No. 541; Ricker, W.E., Ed.; Fisheries Research Board of Canada, Biological Station: Nanaimo, BC, Canada, 1964; Available online: https://waves-vagues.dfo-mpo.gc.ca/Library/29894.pdf (accessed on 10 August 2025).
- Bronfman, A.M.; Dubinina, V.G.; Makarova, G.D. Hydrological and Hydrochemical Bases of Productivity of the Sea of Azov; Pishchevaya Promyshlennost: Moscow, Russia, 1979; 288p. (In Russian) [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: London, UK, 1994; 456p. [Google Scholar]
- Gribanova, S.E.; Zaydiner, Y.I.; Landar, E.A.; Popova, L.V.; Filchagina, I.N. (Eds.) Catches of Fish and Non-Fish Objects by Fishery Organizations of the Azov-Black Sea Basin (1995–2000). Statistical Collection; Everest: Rostov-on-Don, Russia, 2003; 90p. (In Russian) [Google Scholar]
- Zaydiner, Y.I.; Popova, L.V. (Eds.) Catches of Fish and Non-Fish Objects by Fishery Organizations of the Azov-Black Sea Basin (1990–1995). Statistical Collection; Molot: Rostov-on-Don, Russia, 1997; 100p. (In Russian) [Google Scholar]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the coupled model Intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Bronfman, A.M.; Surkov, F.A. A statistical model of salinity in the Azov Sea. Trudy VNIRO 1976, 118, 62–69. (In Russian) [Google Scholar]
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Abakumov, A.; Izrailsky, Y. Optimal harvest problem for fish population—Structural stabilization. Mathematics 2022, 10, 986. [Google Scholar] [CrossRef]
- Danilov, M.B.; Kriksunov, E.A.; Bobyrev, A.E.; Sheremet’ev, A.D.; Mel’nik, M.M.; Severin, S.O. Dynamics of the Sander lucioperca population in lake Peipsi-Pihkva. J. Ichthyol. 2018, 58, 531–544. [Google Scholar] [CrossRef]
- Il’ichev, V.G.; Rokhlin, D.B. Internal prices and optimal exploitation of natural resources. Mathematics 2022, 10, 1860. [Google Scholar] [CrossRef]
- Medvinsky, A.B.; Bobyrev, A.E.; Burmensky, V.A.; Kriksunov, E.A.; Nurieva, N.I.; Rusakov, A.V. Modelling aquatic communities: Trophic interactions and the body mass-and-age structure of fish populations give rise to long-period variations in fish population size. Russ. J. Numer. Anal. Math. Model. 2015, 30, 55–70. [Google Scholar] [CrossRef]
- Neverova, G.P.; Abakumov, A.I.; Yarovenko, I.P.; Frisman, E.Y. Mode change in the dynamics of exploited limited population with age structure. Nonlinear Dyn. 2018, 94, 827–844. [Google Scholar] [CrossRef]
- Revutskaya, O.; Neverova, G.; Frisman, E. Fluctuations in real population sizes: Mathematical modeling and estimation of demographic parameters. Ecol. Model. 2025, 507, 111175. [Google Scholar] [CrossRef]
- Tyutyunov, Y.; Arditi, R.; Büttiker, B.; Dombrovsky, Y.; Staub, E. Modelling fluctuations and optimal harvesting in perch populations. Ecol. Model. 1993, 69, 19–42. [Google Scholar] [CrossRef]
- Mirzoyan, A.V.; Belousov, V.N.; Shevchenko, V.N.; Polin, A.A.; Rybalchenko, A.D.; Poroshina, E.A. Artificial reproduction of semi-anadromous fish species under different development scenarios of hydrological situation in the Azov Sea. Aquat. Bioresour. Environ. 2023, 6, 91–108. (In Russian) [Google Scholar] [CrossRef]
- Zherdev, N.A.; Luk’yanov, S.V. Status of the Azov Sea populations of roach and zander at the present time. Proc. AzNIIRKH 2021, 3, 31–41. (In Russian) [Google Scholar]
- Jacobs, B.; Tobi, H.; Hengeveld, G.M. Linking error measures to model questions. Ecol. Modell. 2024, 487, 110562. [Google Scholar] [CrossRef]
- Kamilov, B. The use of irrigation systems for sustainable fish production: Uzbekistan. In Fisheries in Irrigation Systems of Arid Asia. FAO Fisheries Technical Paper 430; Petr, T., Ed.; FAO: Rome, Italy, 2003; pp. 115–126. Available online: https://www.fao.org/4/y5082e/y5082e0e.htm (accessed on 9 April 2025).
- Ermakhanov, Z.K.; Plotnikov, I.S.; Aladin, N.V.; Micklin, P. Changes in the Aral Sea ichthyofauna and fishery during the period of ecological crisis. Lakes Reserv. Res. Manag. 2012, 17, 3–9. [Google Scholar] [CrossRef]
- Berdiakhmetkyzy, S.; Assylbekova, S.Z.; Abdybekova, A.; Barakbaev, T. Current state of populations of the main commercial fish species of the Small Aral Sea. Exp. Biol. 2021, 88, 120–129. [Google Scholar] [CrossRef]
- Lehodey, P.; Senina, I.; Nicol, S.; Hampton, J. Modelling the impact of climate change on South Pacific albacore tuna. Deep-Sea Res. II Top. Stud. Oceanogr. 2015, 113, 246–259. [Google Scholar] [CrossRef]
- Neverova, G.P.; Frisman, E.Y. Dynamic modes of population size and its genetic structure for species with nonoverlapping generations and stage development. Commun. Nonlinear Sci. 2021, 94, 105554. [Google Scholar] [CrossRef]
- Lamarins, A.; Carlson, S.M.; Prévost, E.; Satterthwaite, W.H.; Buoro, M. Eco-evolutionary consequences of selective exploitation on metapopulations illustrated with Atlantic Salmon. Fish Fish. 2025, 26, 291–305. [Google Scholar] [CrossRef]
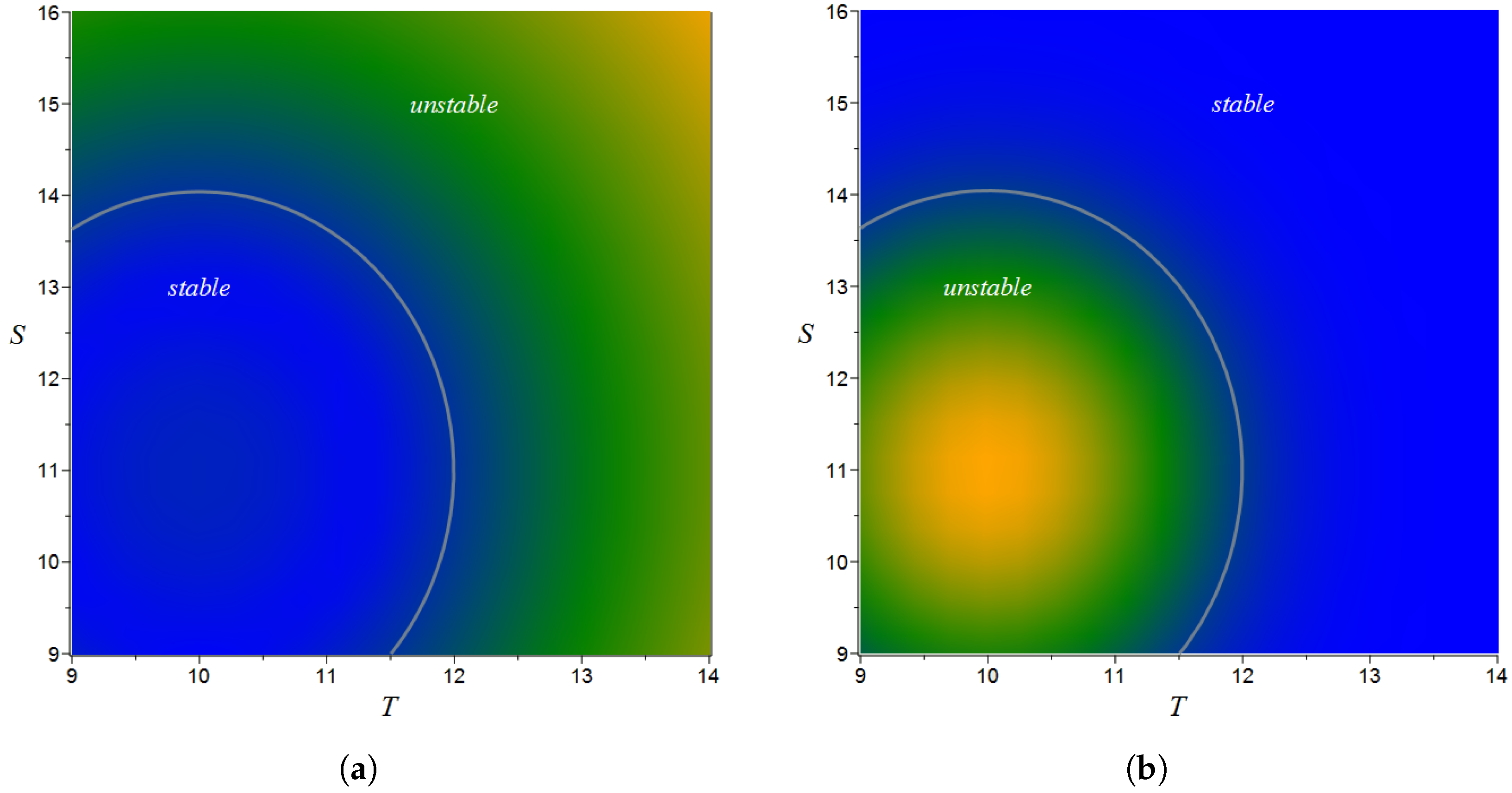
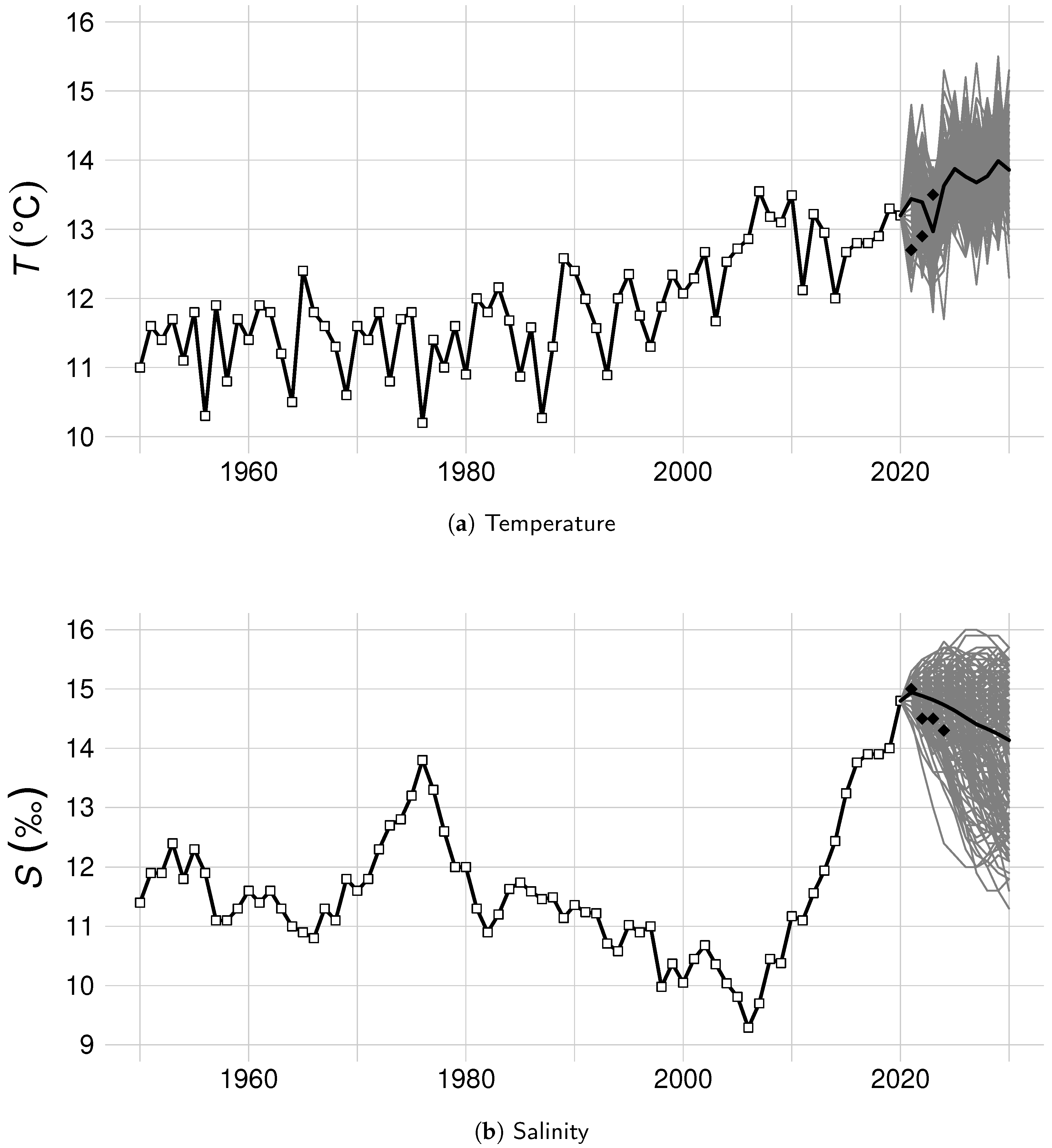
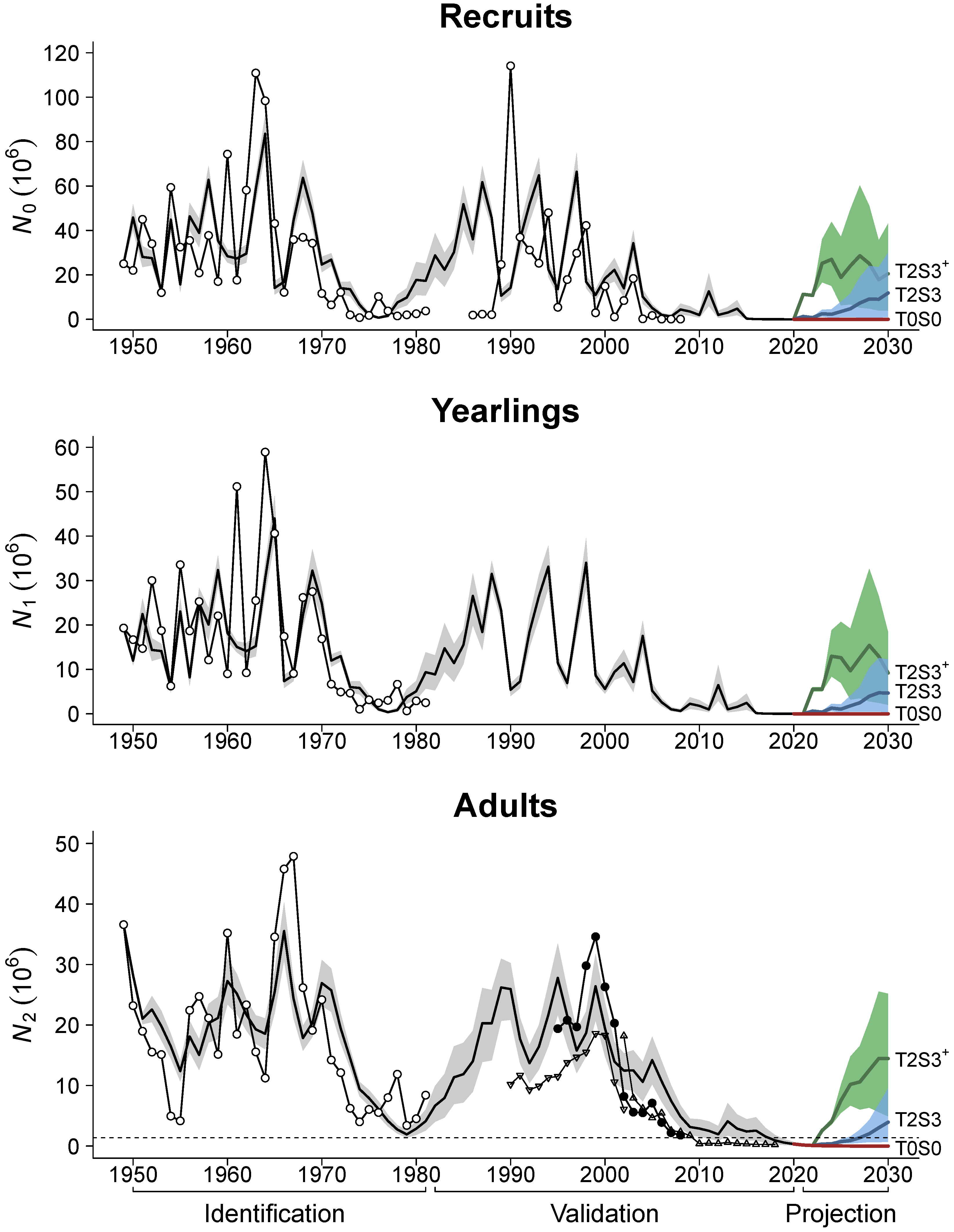
| Notation | Parameter | Estimate | Bootstrap Mean ± SE |
|---|---|---|---|
| Yearling reproduction | 6.77 | ||
| Adult reproduction | 12.59 | ||
| b | Intraspecific competition | 0.039 | — |
| Survival of recruits | 0.55 | ||
| Survival of yearlings | 0.47 | ||
| Survival of adults | 0.62 | — | |
| Temperature tolerance | 1.26 | ||
| Salinity tolerance | 1.92 | ||
| Optimal temperature, °C | 10 | — | |
| Optimal salinity, ‰ | 11 | — |
| Salinity | Temperature Scenario | Temperature Scenario | Temperature Scenario | Temperature Scenario | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | T0 | T1 | T2 | T3 | T0 | T1 | T2 | T3 | T0 | T1 | T2 | T3 | T0 | T1 | T2 | T3 |
| S0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.09 | 0.12 | 0.05 | 0.13 | 0.21 | 0.25 | 0.80 | 0.83 | 0.84 | 0.86 |
| S1 | 0.00 | 0.00 | 0.00 | 0.02 | 0.01 | 0.15 | 0.28 | 0.37 | 0.19 | 0.40 | 0.60 | 0.71 | 0.86 | 0.93 | 0.96 | 0.98 |
| S2 | 0.00 | 0.00 | 0.06 | 0.24 | 0.07 | 0.52 | 0.87 | 0.94 | 0.58 | 0.94 | 0.99 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 |
| S3 | 0.00 | 0.00 | 0.87 | 0.97 | 0.31 | 0.98 | 1.00 | 1.00 | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Stocking | Without restocking | 10 mln released recruits | 20 mln released recruits | 25 mln released recruits | ||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyutyunov, Y.V.; Senina, I. Mathematical Modeling and Intensive Simulations Assess Chances for Recovery of the Collapsed Azov Pikeperch Population. Mathematics 2025, 13, 3232. https://doi.org/10.3390/math13193232
Tyutyunov YV, Senina I. Mathematical Modeling and Intensive Simulations Assess Chances for Recovery of the Collapsed Azov Pikeperch Population. Mathematics. 2025; 13(19):3232. https://doi.org/10.3390/math13193232
Chicago/Turabian StyleTyutyunov, Yuri V., and Inna Senina. 2025. "Mathematical Modeling and Intensive Simulations Assess Chances for Recovery of the Collapsed Azov Pikeperch Population" Mathematics 13, no. 19: 3232. https://doi.org/10.3390/math13193232
APA StyleTyutyunov, Y. V., & Senina, I. (2025). Mathematical Modeling and Intensive Simulations Assess Chances for Recovery of the Collapsed Azov Pikeperch Population. Mathematics, 13(19), 3232. https://doi.org/10.3390/math13193232








