Abstract
We propose a GPU-parallelized collision-detection and response framework for rigid-body dynamics, designed to efficiently handle densely populated 3D simulations in real time. The method combines explicit Euler time integration with a hierarchical Octree–AABB collision-detection scheme, enabling early pruning and localized refinement of contact checks. To resolve collisions, we employ a two-step response algorithm that integrates non-penetration correction and impulse-based velocity updates, stabilized through smoothing, clamping, and bias mechanisms. The framework is fully implemented within Unity3D using compute shaders and optimized GPU kernels. Experiments across multiple mesh models and increasing object counts demonstrate that the proposed hierarchical configuration significantly improves scalability and frame stability compared to conventional flat AABB methods. In particular, a two-level hierarchy achieves the best trade-off between spatial resolution and computational cost, maintaining interactive frame rates (≥30 fps) under high-density scenarios. These results suggest the practical applicability of our method to real-time simulation systems involving complex collision dynamics.
Keywords:
rigid-body simulation; real-time collision detection; collision response; GPU-parallel processing MSC:
08A70
1. Introduction
We propose a GPU-parallelized collision detection and response framework for rigid-body dynamics, designed to efficiently handle densely populated 3D simulations in real time. The method combines explicit Euler time integration with a hierarchical Octree–AABB collision detection scheme, enabling early pruning and localized refinement of contact checks. To resolve collisions, we employ a two-step response algorithm that integrates non-penetration correction and impulse-based velocity updates, stabilized through smoothing, clamping, and bias mechanisms. The framework is fully implemented within Unity3D version 2020.3.26f1 using compute shaders [1] and optimized GPU kernels [2]. Experiments across multiple mesh models and increasing object counts demonstrate that the proposed hierarchical configuration significantly improves scalability and frame stability compared to conventional flat AABB methods. In particular, a two-level hierarchy achieves the best trade-off between spatial resolution and computational cost, maintaining interactive frame rates (≥30 fps) [3,4] under high-density scenarios. These results suggest the practical applicability of our method to real-time simulation systems involving complex collision dynamics. Among these two stages, collision response poses a particular computational bottleneck due to its strict requirements on physical correctness and numerical stability. Collision response then determines how intersecting objects should be separated and how their velocities and positions are updated. Physically accurate response mechanisms often rely on constraints derived from Newton’s laws of motion and restitution principles, ensuring that energy and momentum are preserved or damped appropriately. However, achieving high-fidelity collision handling introduces substantial computational challenges [5]. In particular, enforcing the non-penetration condition, which requires maintaining strict separation between interacting bodies throughout the simulation, demands accurate contact resolution and often involves iterative correction procedures [6]. As the number of objects increases, especially in densely populated scenes, brute-force pairwise collision checks incur quadratic computational complexity [7], rendering the approach impractical even on highly parallel GPU architectures. This inherent scalability limitation highlights the necessity of employing spatial acceleration structures that can reduce redundant computations while preserving the physical accuracy of the simulation [8,9].
To address this challenge, we design a hierarchical Octree–AABB space subdivision scheme that enables scalable and real-time collision handling [10,11]. At the heart of our approach lies an explicit non-penetration constraint, which is enforced through a two-step process involving both geometric position correction and velocity impulse updates. This formulation guarantees physically plausible separation between objects, even in densely populated simulation environments. The core mechanism operates by recursively partitioning the simulation domain using an octree, a hierarchical data structure where each node represents an axis-aligned cubic cell that is subdivided into eight equally sized children. Each rigid object is inserted into the Octree according to the spatial extent of its Axis-Aligned Bounding Box (AABB), enabling a structured and localized organization of the simulation space. In the broad phase of collision detection, comparisons begin at higher levels of the tree, where large bounding volumes are used to efficiently eliminate distant or irrelevant object pairs. As the algorithm traverses deeper into the hierarchy, spatial granularity increases and finer tests are applied only to those regions where bounding boxes intersect. This hierarchical top-down pruning dramatically reduces the number of narrow-phase checks, as collision tests are confined to localized clusters of potentially interacting objects.
By reducing unnecessary pairwise distance calculations, our Octree-AABB framework reclaims significant computational budget, which can then be reallocated to enforce more accurate and aggressive non-penetration constraints in the response phase. This design not only improves scalability across a wide range of scene complexities but also ensures robust physical realism suitable for real-time GPU simulation. Unlike traditional force-based methods or post-collision corrections, our system treats collision handling as a proactive and integrated process. Contact resolution is invoked at the earliest possible moment—as soon as bounding volumes overlap—and relies on both positional and velocity-based adjustments derived from collision normals and relative motion. This design prevents error accumulation, reduces interpenetration artifacts, and supports stable stacking interactions in real time.
Previous work has explored diverse collision-detection strategies, including Signed Distance Functions (SDFs) for arbitrary object shapes [12], Bounding Volume Hierarchies (BVH) for mesh acceleration, and Continuous Collision Detection (CCD) for preventing tunneling effects during fast motion [13]. However, few frameworks explicitly integrate these ideas with GPU-optimized hierarchical space partitioning and real-time non-penetration constraints.
Our contributions in this paper are as follows:
- We propose a GPU-accelerated Octree–AABB collision-detection algorithm, supporting broad-to-narrow pruning and vertex-level filtering, implemented entirely in compute shaders.
- We formulate an explicit non-penetration constraint enforced via both positional correction and Newtonian impulse, ensuring stable contact and separation.
- We introduce a velocity constraint mechanism that suppresses high-frequency oscillation and improves the visual fidelity of rigid-body stacking and sliding.
- We evaluate the proposed system using a diverse set of high-resolution 3D models (Bunny, Armadillo, and Dragon), and demonstrate stable real-time performance above 30 frames per second (fps) in scenes with up to 400 interacting objects and multi-level octree hierarchies.
2. Related Work
2.1. Time Integration Method
Time integration plays a central role in physically based simulation by advancing the dynamic state of rigid bodies over discrete time steps. Several numerical schemes have been proposed to solve Newton’s second law, each offering different trade-offs between accuracy, stability, and computational cost. The explicit Euler method remains the most widely adopted in interactive and real-time environments due to its simplicity and low computational overhead. Despite its known limitations in stiff or high-frequency systems, its forward stepping scheme allows for easy integration into GPU-based pipelines and real-time simulation engines [14,15]. In contrast, the implicit Euler method (also called backward Euler) improves stability by incorporating the next state into the update equation. This allows larger time steps and better handling of stiff constraints but requires solving nonlinear systems, which can be computationally intensive [16]. Higher-order methods such as the Runge–Kutta (RK) (e.g., RK2, RK4) offer improved accuracy and better energy conservation in some cases [17], but their computational demands often limit their applicability in real-time applications. Hybrid schemes, such as those used in Position-Based Dynamics (PBD) [15,18], combine explicit prediction with constraint-based corrections and are widely used for character animation and cloth simulation.
In this work, we adopt the explicit Euler integration scheme to propagate rigid-body states across time steps. This choice reflects the need for computational efficiency and parallelizability within large-scale GPU simulations, where the ability to process thousands of objects per frame outweighs the benefits of higher-order accuracy.
2.2. Collision Detection
Collision detection is a fundamental component of rigid-body simulation, responsible for identifying potential contacts between moving objects. Due to its quadratic complexity in naïve pairwise comparisons, most modern approaches adopt a two-stage pipeline consisting of a broad phase and a narrow phase [19]. In the broad phase, computationally inexpensive bounding volumes are used to eliminate non-intersecting object pairs, while the narrow phase performs fine-grained geometric checks to confirm actual collisions. One of the most widely used bounding volumes is the Axis-Aligned Bounding Box (AABB), which encloses each object in a rectangular box aligned to the coordinate axes. Overlap tests between AABBs can be performed using simple min–max comparisons on each axis, making them particularly suitable for GPU-parallel execution [20]. Several hybrid approaches extend this idea by integrating Oriented Bounding Boxes (OBB) or sphere trees to better conform to object geometry and reduce false positives [21]. To further improve scalability in complex scenes, spatial partitioning techniques such as the Octree have been extensively employed [22]. An octree recursively subdivides the 3D simulation space into eight octants, forming a hierarchical structure in which objects are inserted based on their spatial location. When combined with AABBs at each level, the Octree–AABB hierarchy allows efficient pruning of distant or non-overlapping objects, significantly reducing the number of narrow-phase tests required. This hierarchical scheme is especially effective in simulations with non-uniform object distributions or sparse interactions. Recent studies have explored GPU acceleration of octree traversal and bounding volume queries by leveraging data-parallel operations. Techniques such as non-recursive tree search [23] or GPU-accelerated bounding volume hierarchies [24] allow real-time traversal and intersection tests across thousands of objects. Extensions such as probabilistic volumetric mapping (PVM) further improve memory utilization while maintaining interactive frame rates in dynamic environments [25]. In our framework, we adopt a hierarchical Octree–AABB structure to efficiently manage broad-phase collision detection. Objects are inserted into spatial cells based on their AABB extent, and overlap queries are performed hierarchically to eliminate redundant checks. This structure aligns well with GPU compute pipelines, enabling coarse-to-fine pruning and scalable parallelism even in densely populated scenes.
2.3. Collision Response
While collision detection identifies when and where objects intersect, collision response governs how objects should react once contact is confirmed. The primary objective of collision response is to ensure physically plausible behavior by enforcing conservation principles, such as the conservation of momentum, while also preventing interpenetration and preserving numerical stability. A common approach is to formulate the response according to Newton’s third law, which stipulates that every force exerted by one object on another is met with an equal and opposite force. Westhofen et al. [26] developed an IPC-based contact potential within incremental potential-based time integration, achieving interpenetration-free and bounce-free collision response through a distance-strengthened cubic penalty and energy-based coupling with magnetic forces. Ferguson et al. [27] modeled collisions using a barrier function and friction potential, resolving contact implicitly by minimizing the total energy in the rigid-body incremental potential. Modern collision response techniques typically incorporate both geometric and dynamic constraints. Geometric constraints, such as non-penetration conditions, ensure that objects remain separated following contact. Dynamic constraints, such as velocity adjustments through impulses, enable restitution behavior and energy exchange modeling. When these constraints are integrated within a unified solver, the system can achieve robust, stable interactions even in highly cluttered or densely populated simulations. For real-time GPU-based simulations, computational efficiency and parallelism are critical. By combining geometric correction and impulse-based velocity adjustment in a data-parallel fashion, the proposed approach maintains physically consistent responses while avoiding divergence across thousands of simultaneously updated objects.
2.4. GPU-Parallel Processing
Recent advances have demonstrated the effectiveness of GPU acceleration in physics-based simulation, particularly through compute shaders in frameworks such as Unity3D using DirectX. GPUs enable massive parallelism and high-throughput memory access, which are well suited for collision detection and response computations. One class of applications is cloth simulation, where GPU-based implementations commonly rely on Verlet integration to enforce position constraints and elastic behavior in cloth models [28]. These methods leverage compute shaders to process large numbers of particles or mesh vertices simultaneously, achieving real-time performance without compromising visual fidelity. Another relevant area is GPU-accelerated collision detection using hierarchical spatial structures. For instance, Hor et al. [29] presented an Octree–AABB algorithm that significantly reduces the number of triangle–primitive checks by spatially slicing the scene for Unity3D. Their GPU implementation enabled efficient culling across octree levels and achieved real-time performance in dense environments. In prior implementations, however, many Octree–AABB hierarchies were only partially GPU-accelerated or optimized for CPU execution. Moreover, they often targeted simple models rather than scaling to high object counts or complex meshes. In contrast, our framework fully integrates the Octree–AABB structure into GPU compute shaders within Unity3D. This allows highly parallel execution and direct use of GPU memory, enabling simulation of complex models such as Bunny, Armadillo, and Dragon with tens of thousands of vertices and triangles—even when multiplied across concurrent instances. Furthermore, our evaluation emphasizes scalability: instead of solely measuring algorithmic efficiency, we quantify the maximum number of rigid-body instances that can be simulated at interactive frame rates (≥30 fps). This practical focus on large-scale, real-time performance sets our work apart from earlier implementations and reveals the true potential of GPU-accelerated Octree–AABB collision handling.
3. Method
Our method consists of four stages: (i) explicit Euler integration, (ii) hierarchical broad-phase collision detection, (iii) narrow-phase response with friction and stabilizers, and (iv) a GPU-based parallel implementation, with concise pseudocode illustrating each kernel.
3.1. Explicit Euler Time Integration for Rigid-Body Dynamics
The most popular approaches for dynamic physically based simulation in computer graphics are force-based, particularly for use in interactive environments. External forces (such as gravity, wind, or interaction forces between nodes) are accumulated and applied according to Newton’s second law, . For time integration, we employ the explicit Euler method to update the predicted velocities and positions of objects at each time step during the dynamic simulation of rigid bodies. Each node i is associated with three attributes, namely mass, velocity, and position.
Starting from Newton’s second law, the acceleration of node i is defined as
where is the external force and the mass of the node.
The explicit Euler integration scheme then updates velocity and position sequentially as:
By applying this scheme, the subsequent position of each node is predicted from the accumulated force contributions in a simple yet robust manner. This enables efficient estimation of potential collisions, simplifying intersection checks in large-scale simulations. While higher-order integration schemes such as Runge–Kutta (RK4) can improve numerical accuracy, they introduce significant computational overhead and are not energy-preserving, which limits their suitability for real-time GPU-based rigid-body simulation [30].
Stability of the Explicit Euler Scheme
Although the explicit Euler method is simple and efficient, its stability requires a restriction on the step size. For a linearized rigid body with damping,
the discrete update in Equations (2) and (3) is
A standard eigenvalue analysis of this recurrence shows that the solution remains bounded provided
Choosing below this limit prevents divergence and preserves the stability of the simulation.
3.2. Hierarchical Octree–AABB Collision-Detection Framework
To perform efficient and scalable collision detection for large-scale 3D simulations, we employ a hierarchical approach based on Axis-Aligned Bounding Boxes (AABBs) integrated with an octree spatial partitioning structure. Our method consists of two main phases: (1) a broad-phase filtering using AABB intersection tests and octree traversal, and (2) a narrow-phase refinement using vertex-level proximity checks.
AABB Representation
Each 3D object is enclosed in an AABB defined by the minimum and maximum coordinates of its geometry, aligned with the global coordinate axes. The bounding region R of an object is defined as:
Broad-Phase Collision Detection: Two objects are considered to potentially collide if their AABBs intersect. This condition is satisfied when their bounding intervals overlap along all three coordinate axes:
Traditional AABB methods check every object pair in a brute-force manner, which becomes computationally intractable for large N. To address this, we utilize an octree structure that recursively subdivides the simulation domain into axis-aligned subregions.
Octree Construction: Starting from the root (Level 0), the domain is recursively partitioned into eight child nodes per level. Each object is inserted into the lowest-level node that completely contains its AABB. This hierarchical spatial indexing accelerates collision checks by pruning non-overlapping regions early.
Figure 1 illustrates our octree-based collision-detection framework. AABBs are used at different levels to coarsely identify regions of interest, and the number of colliding candidates significantly decreases with deeper levels due to improved spatial filtering.
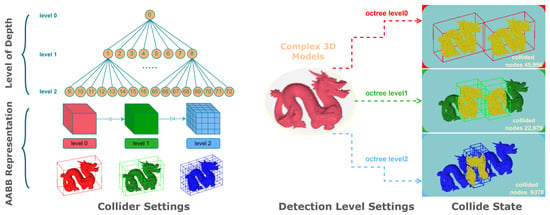
Figure 1.
Hierarchical Octree–AABB collision-detection framework. (Left): Octree depth levels and AABB colliders. (Right): collision states of a complex 3D model at different octree depths, showing progressively reduced collision candidates.
Narrow-Phase Collision Refinement: Once a potential collision is identified in the broad phase, vertex-level proximity is tested to confirm actual contact. Let and be vertices from two objects. A collision is confirmed if their Euclidean distance is less than a predefined threshold :
The full collision-detection pipeline can thus be summarized as:
Here, the threshold is calibrated based on the mesh resolution and the scale of simulation objects. It enables flexible contact detection even under mesh discretization errors.
From a complexity viewpoint, building the octree for N objects with depth L costs , while broad-phase pruning requires under a uniform distribution assumption. Thus, increasing L reduces the number of candidate pairs from toward linear complexity.
In our implementation, each frame updates the AABBs based on new positions computed by the physics solver. As demonstrated in our results, this hierarchical strategy leads to significant performance gains, especially in densely populated scenes.
3.3. Enhanced Collision Response Algorithm
The collision response stage combines mass-weighted penetration correction with an impulse-based velocity update, extended with Coulomb friction and several stabilizers to ensure robustness in stacking and dense contact scenarios.
- (1)
- Position correction for non-penetration
When two AABBs overlap, penetration depths along the three axes are:
If any , the pair is discarded. Otherwise, the axis of smallest penetration defines the normal n and the depth :
Penetration is resolved by a Baumgarte-style correction:
where controls correction strength and is a small bias (“slop”) to ignore negligible overlaps.
The displacement is split by inverse masses:
Optionally, smoothing can be applied:
3.3.1. Non-Penetration Guarantee
Let denote the penetration depth at step k. After applying the correction,
with , the sequence is monotonic and converges to a gap not larger than , ensuring that configurations remain non-penetrating.
Optionally, smoothing can be applied:
- (2)
- Impulse-based velocity update
After correction, the relative velocity is decomposed:
If , the bodies are separating. Otherwise, restitution with a velocity threshold is used:
A minimum magnitude is enforced:
Velocities are updated:
3.3.2. Friction (Coulomb Model)
If , define . The ideal tangential impulse is
Friction is then
Apply to velocities:
With the Coulomb law, the tangential impulse satisfies , hence , and friction cannot increase kinetic energy.
- (3)
- Stability safeguards
To maintain robustness:
- Substitute n with a fixed axis if .
- Bias prevents tiny overlaps from accumulating.
- disables restitution at low speeds, improving stacking.
- avoids sticking from numerical noise.
- A velocity clamp enforces
This unified formulation integrates penetration correction, restitution-aware normal impulses, and Coulomb friction under a single set of parameters, ensuring non-penetration, bounded energy, and smooth sliding in real-time simulations.
3.3.3. Parameter Constraints
For monotone non-penetration and bounded energy, we require , , , , and a finite . The penetration correction contracts as , so the effective rate is governed by . Restitution is suppressed at low speeds via for .
- (4)
- Parameter summary
Table 1 summarizes the parameters used in the collision response stage. Each term originates from standard impulse-based contact models and is selected to ensure non-penetration, bounded restitution, stable frictional response, and numerical robustness.

Table 1.
Parameters for the collision response algorithm.
3.4. GPU-Based Parallel Processing
With the benefit of GPGPU programming via the Unity engine and HLSL, collision detection and response can be implemented as parallel algorithms. These kernels leverage direct GPU memory access for efficient execution within compute shaders. Each shader can be organized into one or more kernel programs, invoked from C# scripts, and may share a limited number of buffers per kernel. This design allows the GPU to process many independent tasks concurrently, taking advantage of parallelism while minimizing memory latency through optimized hardware and data transfer mechanisms.
Moreover, GPU-based kernels can be utilized for a wide variety of tasks, such as physically based graphical simulation pipelines, general-purpose parallel processing on graphics processing units (GPGPU), and numerical calculations involving large datasets. Each block consists of threads that are synchronized within the GPU cores, with a maximum of 1024 threads per block. This enables the simultaneous execution of multiple threads in parallel.
Additionally, several essential kernels are utilized to implement random movement in rigid-body simulation. Solving collision detection involves many kernels, as described in Table 2.

Table 2.
List of essential GPU kernels in collision detection and response.
In addition, we also require the ability to store or transfer vertex-based data to the GPU compute buffers. Table 3 lists the compute buffers used in this study. This design allows configuring compute buffer values of multiple types, such as int and float3. For instance, a compute buffer of type int is used to store a one-dimensional array of integers, while a float3 buffer stores a three-dimensional array of floating-point values.

Table 3.
List of GPU compute buffers in collision detection and response.
To execute the complete simulation on the GPU, both computational tasks and rendering processes are integrated to solve collision detection and response in real time. The overall pipeline is illustrated in Figure 2.
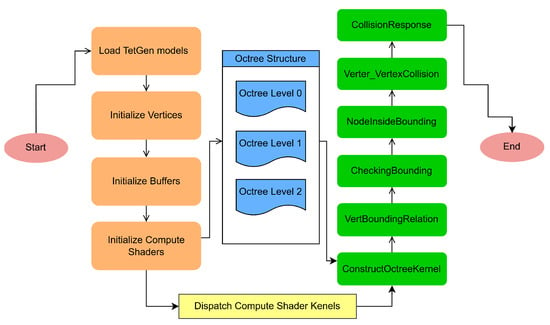
Figure 2.
Flowchart of collision detection and response in the simulation of a randomly moving rigid body.
3.5. GPU Kernel Implementation
We implement three core GPU kernels and two auxiliary GPU kernels that form the backbone of our hierarchical collision detection and response framework. Each kernel is parallelized using compute shaders and executed across multiple threads on the GPU. The detailed implementations of two auxiliary GPU kernels are provided in the Appendix A.
3.5.1. Hierarchical Octree Construction
This kernel initializes the hierarchical spatial subdivision by constructing an Octree bounding structure up to level 2. Starting from the root node (level 0), each cell is recursively subdivided into eight children, forming level 1 and level 2 regions. For each node, the algorithm calculates the minimum, maximum, and center coordinates, which are used to define local AABBs for collision filtering. Algorithm 1 shows the detail hierarchical octree construction process.
| Algorithm 1: Hierarchical Octree Construction |
 |
3.5.2. Broad-Phase Collision Candidate Detection
This algorithm performs the broad-phase collision pruning by comparing the Octree node indices of all objects. It discards non-overlapping pairs early based on their AABB locations in the spatial hierarchy. Only object pairs sharing the same parent node (i.e., spatially close) are passed to the next stage as collision candidates. Algorithm 2 shows the detail broad-phase collision candidate detection process.
| Algorithm 2: Broad-Phase Collision Candidate Detection |
 |
3.5.3. Narrow-Phase Collision Response
This algorithm handles narrow-phase contacts by combining mass-weighted penetration correction and impulse-based velocity updates, with Coulomb friction and several stabilizers for stacked or densely interacting rigid bodies.
First, overlaps along the x, y, and z axes of the two AABBs are tested. If no positive depth is found, the pair is discarded; otherwise, the axis of minimum penetration defines the contact normal n and depth .
To remove interpenetration, a symmetric position correction
is applied.
(Baumgarte factor) controls how fast penetration is resolved, and (“slop”) avoids jitter from negligible overlaps. The stability of the Baumgarte position correction depends on the choice of and the allowable penetration . While we adopt values suggested by (Table 1), we additionally provide an ablation study of and parameters and their effect on penetration depth in Appendix A.3.
Next, the relative velocity is split into normal and tangential components. A normal impulse as
is applied only when the approach speed exceeds a threshold ( otherwise), with a floor to keep resting contacts stable. Coulomb friction is then applied along the tangential direction: if the ideal impulse is below (static limit) the tangential velocity is removed; otherwise, a kinetic impulse of size opposes sliding.
Finally, velocities are clamped to and the states of both bodies are written back, refreshing AABBs for subsequent contacts. Typical values—–, a small fraction of body size, tied to minimal stacking energy, and from material data—balance fast convergence, low energy drift, and minimal penetration.
The combination of these parameters provides: (i) penetration suppression without oscillation (), (ii) bounded restitution (), (iii) stable frictional response (), and (iv) robustness against numerical drift (), yielding reliable stacks and smooth sliding without global constraints. Algorithm 3 shows the detail narrow-phase collision response process.
| Algorithm 3: Narrow-Phase Collision Response |
 |
4. Experiments
We implemented rigid-body dynamics simulations in the Unity3D engine, with a particular emphasis on collision detection and response for randomly moving objects. The hardware and software configurations of the experimental workstation are provided in Table 4.

Table 4.
Hardware and software environments for simulations.
To evaluate the scalability and robustness of the proposed framework, we selected four representative benchmark models with varying geometric complexities, as shown in Figure 3. The Bunny model consists of 2527 vertices and 4968 triangles, representing a relatively simple mesh suitable for lightweight simulations; it serves as a baseline to test performance under low complexity and minimal collision conditions. The Armadillo model includes 41,787 vertices and 15,580 triangles, introducing moderate complexity due to its compact yet articulated form. Its structure, featuring a detailed torso and limbs, provides a balanced challenge for both broad-phase culling and narrow-phase refinement. The Dragon model is composed of 50,000 vertices and 100,000 triangles, offering a dense surface and elongated limbs that stress-test the collision pipeline at higher resolution. Finally, the Asian Dragon, with 360,947 vertices and 721,902 triangles, represents the most challenging case in our benchmarks. Its intricate surface details and large number of elongated features make it an ideal target for evaluating the scalability and performance ceiling of the GPU-accelerated framework. Together, these models span a wide range of mesh densities, topology, and structural intricacies, thereby enabling a comprehensive assessment of collision-detection efficiency, response stability, and the scalability of the GPU-based implementation across increasing geometric complexity.

Figure 3.
3D models used for scalability and performance evaluation in collision-heavy simulation environments.
To evaluate the performance of our proposed framework, we conducted a series of experiments using complex 3D models with a large number of nodes. Each experiment was averaged over 3000 frames in the compute shader, which primarily leveraged the GPU’s parallel processing capability and, in particular, its VRAM capacity. A high-VRAM GPU can efficiently manage large-scale simulations while simultaneously processing extensive data, and our results suggest that simulation performance can be further improved by deploying more powerful GPU devices capable of handling increasingly complex scenarios. The Unity engine provides a V-Sync option that synchronizes the frame rate with the monitor’s refresh rate; however, this feature was disabled so that the maximum fps was determined solely by the underlying GPU performance.
Building on this setup, we designed two experiments to assess different aspects of the collision framework. In the first, we conducted an ablation study to evaluate which culling configurations in a hierarchical Octree–AABB structure most improve performance. In the second, we examined whether the Octree–AABB structure outperforms Spatial Hashing, a widely used collision-detection method, within our simulation scenario.
4.1. Scalability Analysis of Hierarchical Octree–AABB Collision Detection
In order to systematically analyze scalability and performance limits, each experiment was conducted with three representative models (Bunny, Armadillo, and Dragon) while progressively increasing the number of object instances within the simulation scene. This setup allowed us to identify the performance threshold, i.e., the maximum number of objects that can be simulated before the frame rate drops below real-time requirements. In addition, a critical evaluation criterion was to determine the minimal simulation conditions under which the system consistently maintains interactive frame rates (≥30 fps). We considered three different configurations of the proposed hierarchical collision handling algorithm:
- Experiment A (Level 2 only): A flat configuration in which all collisions are processed at the finest granularity using level 2 bounding boxes exclusively. This setup provides a baseline for the effectiveness of a single-level spatial subdivision.
- Experiment B (Level 1 → Level 2): A two-level hierarchical configuration where broad-phase pruning occurs at level 1 and narrow-phase collision handling is refined at level 2. This configuration is designed to balance detection accuracy and computational efficiency.
- Experiment C (Level 0 → Level 1 → Level 2): A full hierarchical configuration in which collision handling is performed across all octree levels. This setting exploits the complete spatial subdivision hierarchy to maximize pruning efficiency and reduce unnecessary vertex-level checks.
Figure 4 illustrates the performance trade-offs introduced by varying the depth of the Octree hierarchy in real-time collision handling. The table in the upper right corner of each figure shows the performance results profiled in the Unity3D. When only a shallow hierarchy (Level 1) is applied, broader bounding regions result in fewer collision checks but may also increase false positives, leading to redundant processing and reduced accuracy. In contrast, a deeper configuration (Level 2) achieves more selective pruning by subdividing the space into finer regions, yet incurs additional overhead due to increased tree traversal and box management. The fps values clearly reflect this shift: although the shallower setup achieves higher raw performance, the deeper configuration provides finer control over densely packed collisions. This experiment highlights the need to balance spatial resolution with computational efficiency, depending on the simulation complexity and collision density. Table 5 summarizes the experimental results, reporting the average fps (mean ± standard deviation over five runs) achieved under different configurations and varying object counts for each model. These results highlight the progressive improvements obtained through hierarchical collision handling and confirm the effectiveness of the proposed approach in achieving real-time performance even under high-complexity scenarios.
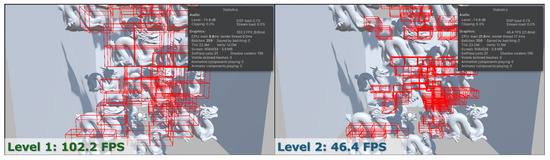
Figure 4.
Performance comparison between Octree depth levels in dense collision scenarios using 50 Dragon models. (Left): Level 1 configuration achieves 102.2 fps with a shallower hierarchy. (Right): Level 2 introduces deeper spatial subdivision, resulting in increased collision checks and reduced performance (46.4 fps). Red boxes denote AABB collision bounds. This illustrates the trade−off between spatial resolution and computational cost in hierarchical collision detection.

Table 5.
FPS (mean ± std over 5 runs) for Octree configurations: A (Level 2), B (Level 1→2), and C (Level 0→1→2). Deeper hierarchies (C) provide better scalability and frame rates than shallower ones.
Furthermore, to rigorously assess the impact of our hierarchical approach, we performed an ablation study by comparing the results against the conventional Level 0 only setting, which corresponds to the traditional AABB-based collision-detection method without octree partitioning. This comparison isolates the contribution of hierarchical collision handling and quantifies its benefit in terms of scalability and sustained performance. As summarized in Table 6, the ablation study highlights a clear trade-off between raw frame rate and simulation robustness. While the traditional Level 0 AABB configuration achieves higher fps values at lower object counts, its performance rapidly deteriorates in terms of stability and scalability when handling more complex models. In contrast, the hierarchical Octree configurations (B and C) maintain stable operation even under dense collision scenarios, demonstrating the necessity of multi-level pruning for practical large-scale rigid-body simulation. This comparison highlights that our proposed method prioritizes consistent real-time performance over raw throughput, thereby offering a more reliable foundation for complex interactive applications. Table 6’s relative change ratio field is calculated by
where is the value from the hierarchical configuration (C) and is the corresponding Level 0 (AABB only) result.

Table 6.
Ablation study comparing the flat AABB baseline (Level 0) with the hierarchical Octree method (Experiment C). The table reports mean FPS (±std over 5 runs) as object count increases, showing that the Octree maintains scalability and stability in dense scenes.
4.2. Comparison of Broad-Phase Collision-Detection Methods
To further investigate the efficiency of our broad-phase design, we compared the proposed hierarchical Octree–AABB strategy with a Spatial Hashing approach, which partitions space into uniform cells of size h (here ). Both methods were implemented with identical data structures for the narrow phase, with the only difference lying in the broad-phase mechanism. As in the previous experiment, we conducted a free-fall stacking test with 50 instances of four 3D models (Bunny, Armadillo, Dragon, and Asian Dragon). Two primary metrics were measured: (i) average frame rate (FPS) over five runs, and (ii) runtime memory footprint. This setup isolates the impact of the broad-phase algorithm on scalability and resource usage.
To obtain reliable measurements, collision detection was executed for up to 3000 frames to ensure a sufficient number of contacts. Metrics were recorded every 100 frames, and running averages were computed to smooth out short-term fluctuations caused by transient contacts or garbage collection. This sampling strategy provides a clear view of long-term performance as stacking becomes denser.
The FPS traces reveal two distinct stages. During the initial free-fall phase, Spatial Hashing performs better due to its expected insertion and query cost. As stacking progresses and object density increases, the Octree–AABB approach maintains higher throughput and stability because its hierarchical culling reduces unnecessary candidate checks. Figure 5 shows the FPS evolution with error bands for both methods across the four models, highlighting how Spatial Hashing dominates in sparse scenes while Octree–AABB offers improved stability under dense collisions.
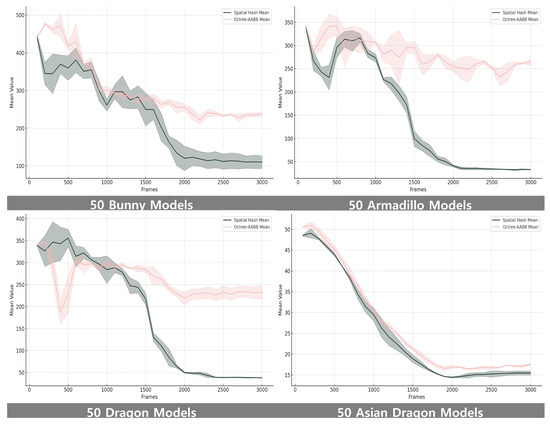
Figure 5.
Performance comparison of Spatial Hash and Octree–AABB for 50 instances of each dataset (Bunny, Armadillo, Dragon, and Asian Dragon). Mean FPS values with error bands are plotted over 3000 frames. Spatial Hash maintains higher speed in the early sparse phase, while Octree–AABB shows greater stability and throughput once stacking increases collision density.
Spatial Hashing achieves constant-time insertion and query on average, but may produce redundant candidate pairs when objects span multiple cells, especially for elongated meshes or crowded scenes. By contrast, the Octree–AABB method scales as for tree construction, with culling cost
under a uniform distribution. This complexity enables more selective filtering at the cost of additional hierarchy management, which becomes advantageous as collisions grow denser.
To quantify the observed trends, we divided the simulation into an early phase (≤1500 frames) and a late phase (1500–3000 frames) and computed the mean FPS for each method. During the early phase, Octree–AABB achieved FPS vs. FPS for Bunny (+10.08%), vs. for Armadillo (+17.75%), vs. for Dragon (–4.31%), and vs. for Asian Dragon (+4.88%). In the late phase, the advantages of hierarchical culling became more pronounced: FPS vs. (+45.14%) for Bunny, vs. (+83.26%) for Armadillo, vs. (+75.85%) for Dragon, and vs. (+10.81%) for Asian Dragon. These results, summarized in Table A1 in Appendix A, confirm that hierarchical Octree–AABB sustains significantly higher throughput in dense state, while the performance of Spatial Hashing tends to fluctuate for models with extended appendages (e.g., Armadillo, Dragon) that map to multiple cells, increasing candidate checks and degrading efficiency in the late phase.
In terms of memory usage, both methods remained stable over the entire simulation. Octree–AABB consumed slightly more memory (about 5–10% on average) but exhibited smaller variance, indicating more predictable behavior in dense stacking scenarios. For example, average memory footprints were MB vs. MB for Bunny, MB vs. MB for Armadillo, MB vs. MB for Dragon, and MB vs. MB for Asian Dragon. Overall, Octree–AABB offers slightly higher but more consistent memory usage, while Spatial Hashing trades lower memory for less predictable performance under high-density conditions.
5. Discussion
5.1. Effectiveness of Hierarchical Collision Handling Compared to Flat AABB
The ablation study comparing the baseline flat AABB method (Level 0 only) with the proposed hierarchical Octree-based configurations revealed clear differences in scalability, frame stability, and robustness under dense collision scenarios. Flat AABB collision detection performs bounding box checks between all object pairs without spatial filtering. While this method yields high frame rates in low-density environments, its performance quickly degrades as the number of objects increases.
For example, with 300 instances of the Dragon model, the flat AABB method achieved only 17.04 fps, well below the real-time threshold of 30 fps. This drop is due to the quadratic growth in pairwise comparisons and the absence of spatial pruning. In contrast, the hierarchical Octree configuration (Level 0 to 2) reduced unnecessary checks by leveraging spatial partitioning. Although the absolute frame rate was lower in some cases (13.16 fps for Dragon 300), it provided better frame stability and fewer performance spikes. Among the configurations, the two-level hierarchy (Level 1 to 2) achieved the best balance. For instance, with 250 Dragon models, it recorded 40.35 fps, significantly outperforming both the flat and full-depth hierarchical methods. These results demonstrate that hierarchical collision handling improves not only detection efficiency but also enables more stable simulation in complex and crowded scenes.
5.2. Hierarchy Depth Configuration and Trade-Offs
The performance of hierarchical collision detection is highly sensitive to the depth of the Octree. Increasing the number of levels improves spatial resolution, but it also introduces additional computation for tree traversal and bounding volume updates. The configuration using Level 2 only applies fine-grained bounding boxes to all objects without prior filtering. While this provides high precision, it also generates significant computational overhead due to the lack of early rejection. In contrast, the two-level approach (Level 1 to 2) filters candidates at a coarse level before performing detailed checks, resulting in better performance across various models and object counts.
Adding an extra Level 0 node at the top of the hierarchy further reduces collision candidates but introduces overhead in GPU memory access and kernel logic. In some scenarios, the full hierarchy (Level 0 to 2) performed slightly worse than the two-level configuration, indicating diminishing returns from deeper hierarchies. These findings suggest that the optimal depth configuration depends on the complexity of the 3D model and the object distribution within the scene. For scenes with medium to high complexity, a two-level hierarchy provides the most efficient balance between spatial filtering and computational cost.
5.3. Simulation Scalability and Frame Rate Stability
To maintain real-time responsiveness in interactive applications, the simulation must sustain a minimum of 30 fps. This constraint was used to assess scalability across three representative models: Bunny, Armadillo, and Dragon. The experiments showed a clear relationship between model complexity and the number of objects that can be simulated while preserving the real-time threshold. The Bunny model maintained over 30 fps up to 400 instances. The Armadillo model sustained real-time performance up to around 250 instances, while the Dragon model fell below 30 fps at approximately 200 instances. These trends reflect the increasing cost of collision detection and response as mesh resolution and vertex count rise.
Hierarchical configurations significantly improved the ability to maintain real-time performance under increasing load. In the Dragon 250 case, the flat AABB method dropped to 12.55 fps, whereas the two-level hierarchy achieved 40.35 fps. Even in scenarios where real-time thresholds were not fully met, the hierarchical approach showed greater consistency, lower frame variance, and improved physical stability. All measurements were taken with V-Sync disabled in the Unity engine to ensure that frame rates were determined solely by GPU compute capacity. This setup allowed us to isolate the algorithmic performance from display-related limitations and provided a reliable basis for assessing simulation scalability under hardware constraints.
6. Limitations and Future Work
While the proposed hierarchical collision detection and response framework demonstrates strong scalability and stability in GPU-based rigid-body simulations, several limitations remain that warrant further investigation.
First, the current method is optimized for axis-aligned bounding volumes and static spatial hierarchies. Although the Octree structure provides effective pruning in scenes with relatively stable object distributions, it must be rebuilt or updated entirely whenever objects undergo large-scale displacements or transformations. This limitation can lead to inefficiencies in highly dynamic environments, such as particle explosions or deformable object interactions. To mitigate this cost, future work could adopt dynamic spatial data structures, such as GPU-friendly bounding volume hierarchies (BVH) or ray-tracing-based optimization [31]. Exploring hybrid or wide-branching BVH schemes, or leveraging neural intersection functions for secondary rays, could further accelerate query performance in large or highly dynamic scenes. Future work may also consider stackless traversal and GPU-parallel construction algorithms, enabling real-time updates of the hierarchy as objects or viewpoints change.
Second, the framework assumes uniform thresholds for collision resolution, such as proximity distance and impulse floor values, across all models and scales. While these parameters were empirically tuned to balance stability and responsiveness, they may not generalize across different simulation contexts or mesh resolutions. An adaptive strategy could be introduced, where thresholds such as , , or are scaled by local object size, collision density, or recent energy drift. Learning-based meta-controllers could predict parameter values, balancing stability and responsiveness across heterogeneous scenes.
Third, all experiments were conducted using triangular mesh models without considering topological deformation or articulated joints. As a result, the current system does not support soft body dynamics or skeleton-based character simulations. One avenue is to extend the solver with constraint-based formulations(e.g., eXtended Position-based Dynamics, Vertex Block Descent), so that joint limits, angular momentum conservation, and compliance can be incorporated alongside the current impulse solver. This would enable articulated or deformable models while retaining GPU parallelism.
Finally, from a GPU compute perspective, the kernel logic was designed to be simple and parallelizable, but it does not yet take advantage of advanced features such as warp-level primitives, shared memory optimization, or persistent thread blocks. These features could reduce memory latency and improve performance under extreme object densities, especially on newer architectures.
In future work, we plan to explore hybrid approaches that combine Octree and BVH structures to support both static and dynamic object groups more efficiently. Additionally, integrating learning-based components to predict collision-prone regions or to adapt parameter settings in real time could further enhance system robustness and generalizability. Finally, extending the method to support continuous collision detection (CCD) will be necessary for applications involving fast-moving objects where discrete-time approximations are insufficient. Implementing these enhancements constitutes our next research goal, with the broader aim of establishing a simulation specification suitable for XR environments, where high fidelity, responsiveness, and scalability are critical for immersive interaction.
7. Conclusions
We presented a GPU-accelerated hierarchical collision detection and response framework for large-scale rigid-body simulation. By integrating multi-level Octree spatial subdivision with parallel compute kernels, the proposed method achieved scalable and stable performance across various model complexities and object densities. Experimental results demonstrated that the hierarchical configuration significantly reduced unnecessary collision checks and maintained interactive frame rates under dense conditions, while preserving physical plausibility and numerical stability. These findings suggest that the proposed approach provides an effective foundation for real-time physics-based simulation in graphics and engineering applications.
Author Contributions
Conceptualization, N.-J.S.; Methodology, N.-J.S.; Software, N.-J.S.; Validation, N.-J.S.; Writing—original draft, N.-J.S.; Writing—review and editing, N.-J.S. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education under Grant NRF-2022R1I1A3069371, was funded by the BK21 FOUR (Fostering Outstanding Universities for Research) No. 5199990914048, and supported by the Soonchunhyang University Research Fund.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Visualization
Figure A1 provides a qualitative visualization of the hierarchical collision-detection framework applied under varying Octree depth configurations. The figure consists of three rows, each corresponding to a specific depth level of the Octree (Level 0, Level 1, and Level 2 from top to bottom), and three columns representing different 3D mesh models—Bunny, Armadillo, and Dragon, arranged from left to right. Red wireframe boxes denote the Axis-Aligned Bounding Boxes (AABBs) used to encapsulate geometry for broad-phase collision detection. At Level 0, the bounding regions are coarse and large, resulting in fewer initial collision checks but a higher chance of false positives due to low spatial selectivity. As the depth increases, particularly at Level 2, the simulation space is subdivided into finer partitions, enabling more precise localization of collision candidates and effectively reducing the number of unnecessary checks. However, this comes at the cost of increased computational overhead for tree traversal and bounding volume management. The visual comparison clearly demonstrates the spatial filtering effect introduced by deeper Octree hierarchies. In densely populated regions such as those represented by the Dragon model, the Level 2 configuration produces significantly tighter bounding volumes, thereby enhancing the effectiveness of spatial pruning. This observation aligns with the quantitative results discussed in Section 4, further validating the trade-off between spatial resolution and performance in hierarchical collision-detection schemes.

Figure A1.
Visual comparison of hierarchical collision-bounding volumes across Octree depth levels in dense simulation scenarios. Each row corresponds to a different Octree depth configuration ((top): Level 0, (middle): Level 1, (bottom): Level 2), and each column shows a different model. Red boxes indicate axis-aligned bounding boxes (AABBs) used in collision detection. As the hierarchy deepens, the bounding volumes become more spatially localized, reducing the number of unnecessary collision checks. This figure illustrates the trade-off between coarse-level pruning and fine-grained spatial resolution in hierarchical collision handling.
Appendix A.2. Supplementary GPU Kernels
For completeness, we provide pseudocode descriptions of two auxiliary GPU kernels used in the preprocessing stage of the collision-detection pipeline. These functions support the mapping between vertices and spatial regions, and prepare the data structures used in the narrow-phase stage.
Appendix A.2.1. Vertex-Bounding Box Relation
This kernel builds the mapping between each vertex and the axis-aligned bounding box (AABB) it belongs to inside the Octree. It runs in parallel over all vertices and stores, for each vertex , the identifier of the leaf cell that contains it, or a sentinel if none is found. This information is used by later stages to restrict collision checks to relevant spatial partitions.
| Algorithm A1: Vertex-Bounding Box Relation |
 |
Appendix A.2.2. Check Node Inside Bounding Box
This kernel links the set of candidate octree boxes flagged during the broad phase with the vertices that reside inside them. It scans the list of active boxes and, for each, collects the indices of vertices previously mapped by Algorithm A1. Atomic increments are used to append valid indices into a compact buffer.
| Algorithm A2: Check Node Inside Bounding Box |
 |
Appendix A.3. Penetration-Depth Ablation
To assess the influence of stability parameters on contact quality, we measured the penetration depth between colliding objects during simulation. Given two bodies A and B with axis-aligned bounding boxes (AABBs), we define the overlap along each axis as
and the penetration depth as whenever all . The corresponding contact normal n is aligned with the axis that achieves , with its sign determined by the relative centers of the two AABBs. This quantity feeds directly into the Baumgarte correction term and guarantees non-penetration under the contraction bound in Equation (A1).
In practice, we log for each frame the average and maximum over all colliding pairs, together with the ratio of cases exceeding the slop . These statistics are written every 100 frames, together with FPS, memory, and collision counts, and later visualized as heatmaps versus parameters such as and .
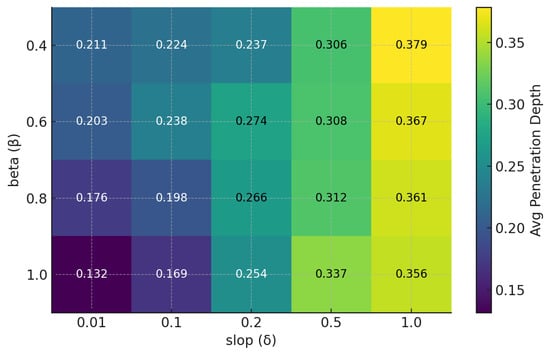
Figure A2.
Average penetration depth for combinations of Baumgarte factor and slop (time step ). Lower values (darker) indicate reduced interpenetration.
Appendix A.4. Comparison Between Spatial Hash and Hierarchical Octree–AABB Method
Table A1 summarizes the measured FPS in the early and late phases of the stacking experiment for each dataset. Positive gains indicate cases where the hierarchical Octree–AABB strategy outperforms Spatial Hashing.

Table A1.
Mean FPS of Spatial Hash and Hierarchical Octree–AABB in early (≤1500) and late (1500–3000) phases of the simulation. The rightmost column reports the relative improvement of Hierarchical Octree–AABB over Spatial Hash. SH: Spatial Hash, O-A: Octree–AABB, RCR: Relative Change Ratio.
Table A1.
Mean FPS of Spatial Hash and Hierarchical Octree–AABB in early (≤1500) and late (1500–3000) phases of the simulation. The rightmost column reports the relative improvement of Hierarchical Octree–AABB over Spatial Hash. SH: Spatial Hash, O-A: Octree–AABB, RCR: Relative Change Ratio.
| Model | Early Phase (≤1500 Frames) | Late Phase (1500–3000 Frames) | ||||
|---|---|---|---|---|---|---|
| SH | O-A | RCR [%] | SH | O-A | RCR [%] | |
| Bunny | 327.20 | 363.87 | +10.08 | 134.20 | 244.63 | +45.14 |
| Armadillo | 252.50 | 306.98 | +17.75 | 43.10 | 257.55 | +83.26 |
| Dragon | 300.64 | 288.23 | −4.31 | 56.86 | 235.44 | +75.85 |
| Asian Dragon | 34.79 | 36.58 | +4.88 | 15.36 | 17.22 | +10.81 |
References
- Schütz, M.; Kerbl, B.; Wimmer, M. Rendering Point Clouds with Compute Shaders and Vertex Order Optimization. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2021; Volume 40, pp. 115–126. [Google Scholar] [CrossRef]
- Unity Technologies. Compute Shaders; Unity Technologies: San Francisco, CA, USA, 2025. [Google Scholar]
- Spjut, J.; Madhusudan, A.; Watson, B.; Boudaoud, B.; Kim, J. The Esports Frontier: Rendering for Competitive Games. arXiv 2022, arXiv:2208.11774. [Google Scholar] [CrossRef]
- Akenine-Moller, T.; Haines, E.; Hoffman, N. Real-Time Rendering; AK Peters/CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chung, M.; Kwon, T.; Kim, Y. Fast Simulation of Soft-body Deformation using Connected Rigid Objects. Comput. Graph. 2025, 128, 104202. [Google Scholar] [CrossRef]
- Sui, S.; Sentis, L.; Bylard, A. Hardware-accelerated Ray Tracing for Discrete and Continuous Collision Detection on Gpus. In Proceedings of the 2025 IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 19–23 May 2025. [Google Scholar] [CrossRef]
- Yu, C.; Du, W.; Zong, Z.; Castro, A.; Jiang, C.; Han, X. A Convex Formulation of Material Points and Rigid Bodies with GPU-Accelerated Async-Coupling for Interactive Simulation. arXiv 2025, arXiv:2503.05046. [Google Scholar] [CrossRef]
- Mandarapu, D.K.; James, N.; Kulkarni, M. Mochi: Fast & Exact Collision Detection. arXiv 2024, arXiv:2402.14801. [Google Scholar] [CrossRef]
- Hor, K.; Kim, T.; Hong, M. Fast Collision Detection Method with Octree-Based Parallel Processing in Unity3D. Eng. Proc. 2025, 89, 37. [Google Scholar] [CrossRef]
- Wong, T.H.; Leach, G.; Zambetta, F. An Adaptive Octree Grid for GPU-based Collision Detection of Deformable Objects. Vis. Comput. 2014, 30, 729–738. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X. Application and Prospect of Virtual Reality Technology in Dentistry in the Internet Era. Appl. Math. Nonlinear Sci. 2024, 9. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Y.; Wang, H.; Yip, M.K.; Liu, E.S.; Jin, X. Real-time Collision Detection between General SDFs. Comput. Aided Geom. Des. 2024, 111, 102305. [Google Scholar] [CrossRef]
- Yuan, X.; Xiang, F.; Yang, Y.; Su, H. C5D: Sequential Continuous Convex Collision Detection Using Cone Casting. Acm Trans. Graph. (TOG) 2025, 44, 1–14. [Google Scholar] [CrossRef]
- Müller, M.; Heidelberger, B.; Teschner, M.; Gross, M. Interactive Collision Detection for Deformable Objects. Comput. Graph. Forum 2004, 23, 567–576. [Google Scholar] [CrossRef]
- Bender, J.; Müller, M.; Macklin, M. A Survey on Position-Based Simulation Methods in Computer Graphics. Comput. Graph. Forum 2014, 33, 228–251. [Google Scholar] [CrossRef]
- Baraff, D.; Witkin, A. Large Steps in Cloth Simulation. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 24 July 1998; ACM: New York, NY, USA, 1998; pp. 43–54. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinarv Differential Equations. Comput. Math. Appl. 2003, 45, 1782–1784. [Google Scholar] [CrossRef][Green Version]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position Based Dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef]
- Mirtich, B. Efficient Algorithms for Two-phase Collision Detection. In Practical Motion Planning in Robotics: Current Approaches and Future Directions; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997; pp. 203–223. [Google Scholar]
- Gottschalk, S.; Lin, M.C.; Manocha, D. OBBTree: A Hierarchical Structure for Rapid Interference Detection. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; ACM: New York, NY, USA, 1996; pp. 171–180. [Google Scholar] [CrossRef]
- Larsson, T.; Akenine-Möller, T. Collision Detection for Continuously Deforming Bodies. Eurographics 2001, 20, 325–333. [Google Scholar]
- Samet, H. The Quadtree and Related Hierarchical Data Structures. Acm Comput. Surv. (CSUR) 1984, 16, 187–260. [Google Scholar] [CrossRef]
- Frisken, S.F.; Perry, R.N. Simple and Efficient Traversal Methods for Quadtrees and Octrees. J. Graph. Tools 2002, 7, 1–11. [Google Scholar] [CrossRef]
- Garanzha, K.; Loop, C. Fast Ray Sorting and Breadth-First Packet Traversal for GPU Ray Tracing. Comput. Graph. Forum 2010, 30, 289–298. [Google Scholar] [CrossRef]
- Min, H.; Han, K.M.; Kim, Y.J. OctoMap-RT: Fast probabilistic volumetric mapping using ray-tracing GPUs. IEEE Robot. Autom. Lett. 2023, 8, 5696–5703. [Google Scholar] [CrossRef]
- Westhofen, L.; Fernández-Fernández, J.A.; Jeske, S.R.; Bender, J. Strongly Coupled Simulation of Magnetic Rigid Bodies. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2024; Volume 43, p. e15185. [Google Scholar] [CrossRef]
- Ferguson, Z.; Li, M.; Schneider, T.; Gil-Ureta, F.; Langlois, T.; Jiang, C.; Zorin, D.; Kaufman, D.M.; Panozzo, D. Intersection-free rigid body dynamics. Acm Trans. Graph. 2021, 40, 1–16. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, R. Real-time Cloth Simulation based on Improved Verlet Algorithm. In Proceedings of the 2010 IEEE 11th International Conference on Computer-Aided Industrial Design &Conceptual Design, Yiwu, China, 17–19 November 2010; Volume 1, pp. 443–446. [Google Scholar] [CrossRef]
- Hor, K.; Sung, N.; Ma, J.; Choi, M.; Hong, M. A Fast Parallel Processing Algorithm for Triangle Collision Detection based on AABB and Octree Space Slicing in Unity3D. IEEE Access 2025, 13, 4759–4773. [Google Scholar] [CrossRef]
- Hou, S.; Lu, X.; Gao, W.; Jiang, S.; Zhang, X. Interactive Physically based Simulation of Roadheader Robot. Arab. J. Sci. Eng. 2023, 48, 2441–2454. [Google Scholar] [CrossRef]
- Weier, P.; Rath, A.; Michel, E.; Georgiev, I.; Slusallek, P.; Boubekeur, T. N-BVH: Neural Ray Queries with Bounding Volume Hierarchies. In Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers, Denver, CO, USA, 27 July–1 August 2024; ACM: New York, NY, USA, 2024; pp. 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).