Theoretical Modeling of Light-Fueled Self-Harvesting in Piezoelectric Beams Actuated by Liquid Crystal Elastomer Fibers
Abstract
1. Introduction
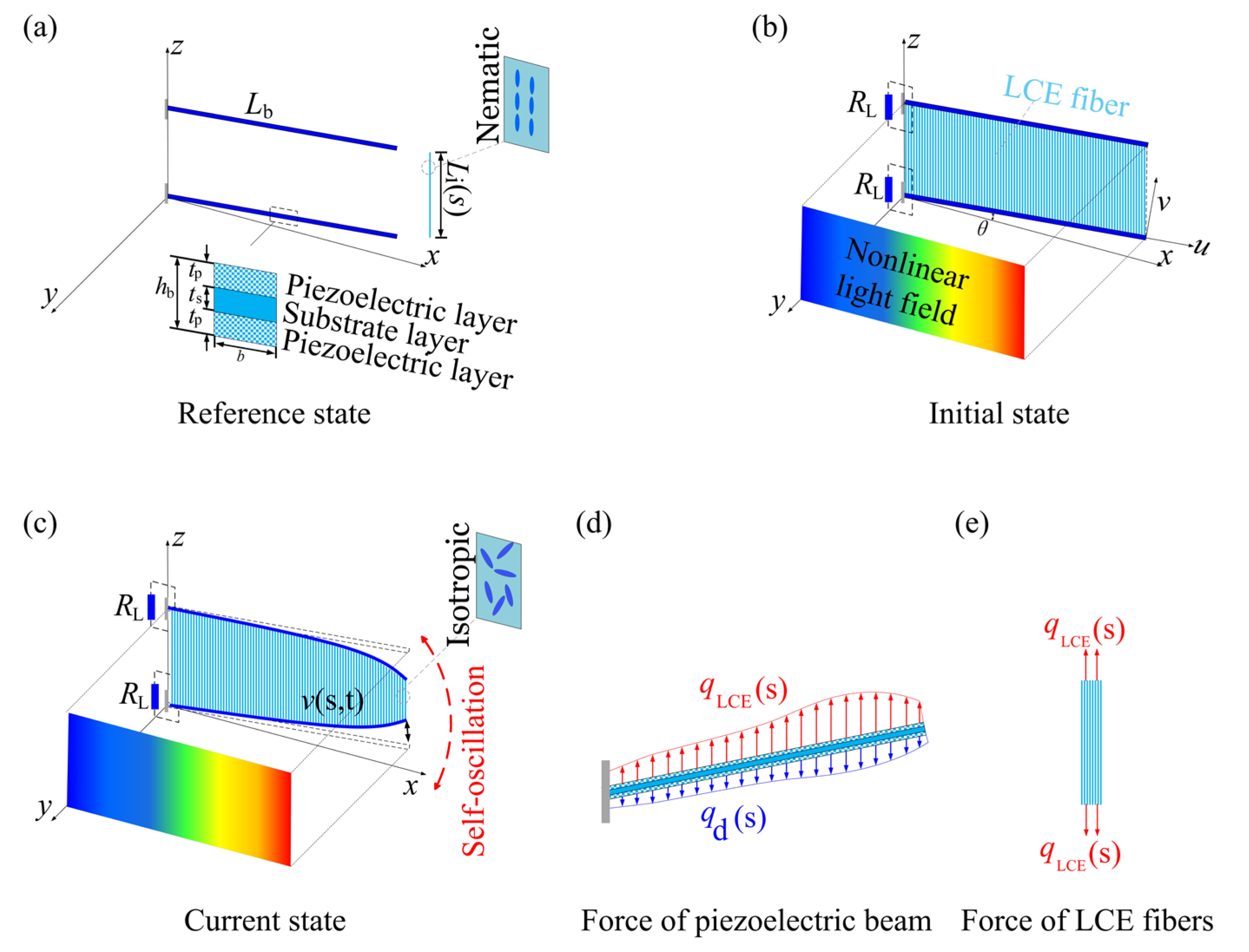
2. Theoretical Model and Formulation
2.1. The Temperature Field of the LCE Fiber
2.2. The Energy and Work Analysis of the LCE Fiber–Piezoelectric Beam System
2.3. Dimensionless Formulation
2.4. Galerkin Method
3. Motion States and Their Mechanisms
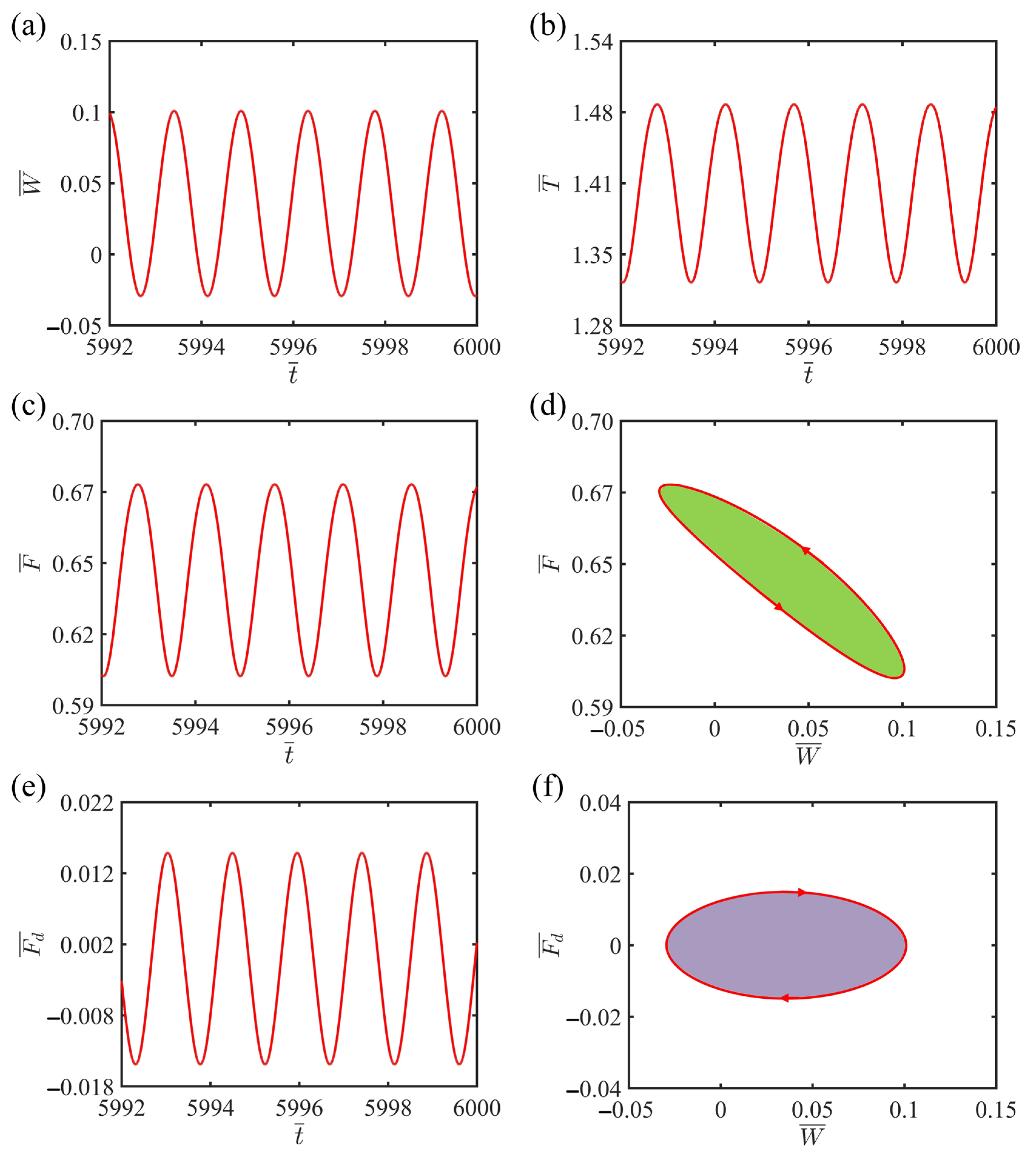
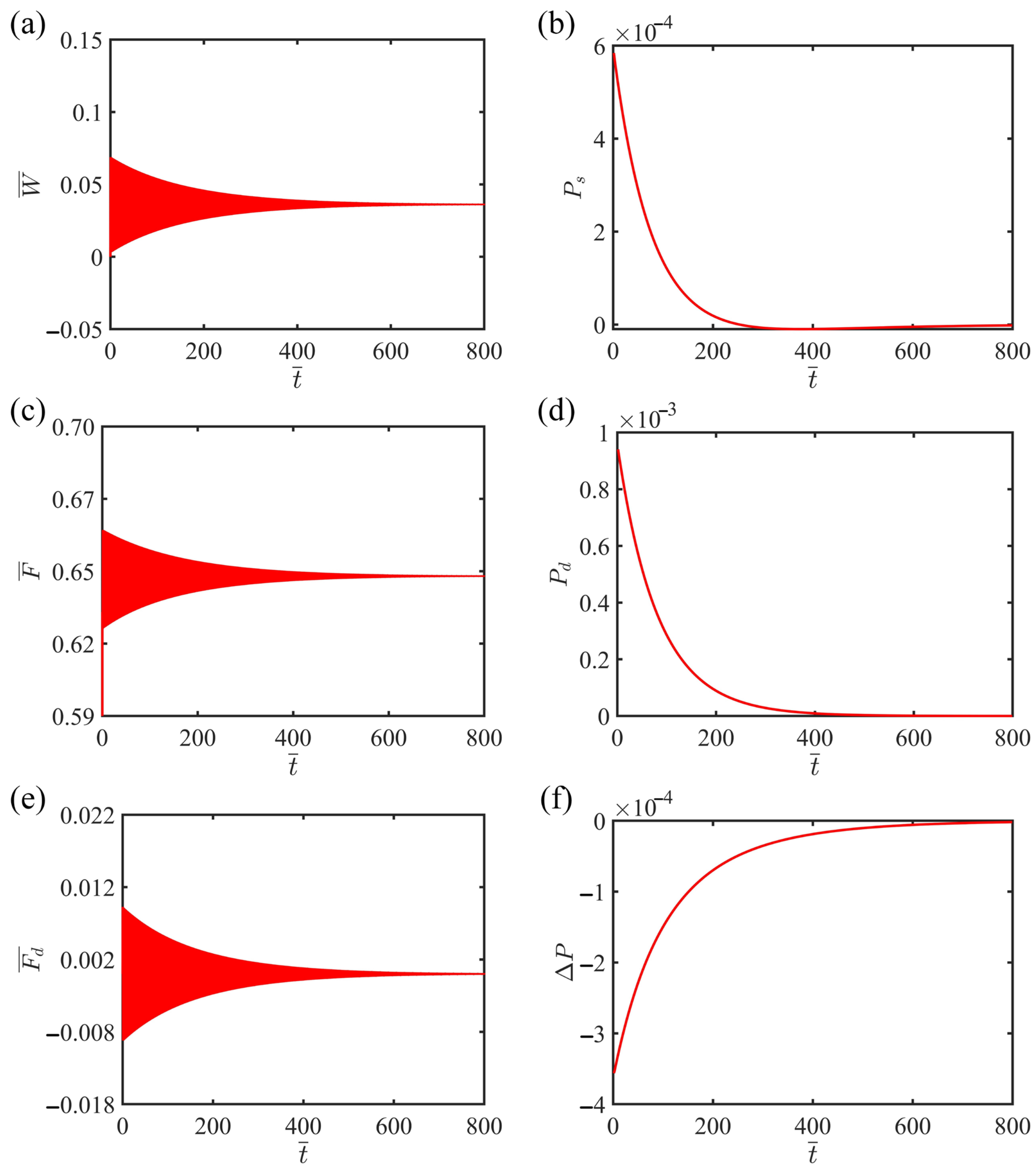
3.1. Two Motion States
3.2. Mechanism of the Self-Harvesting State
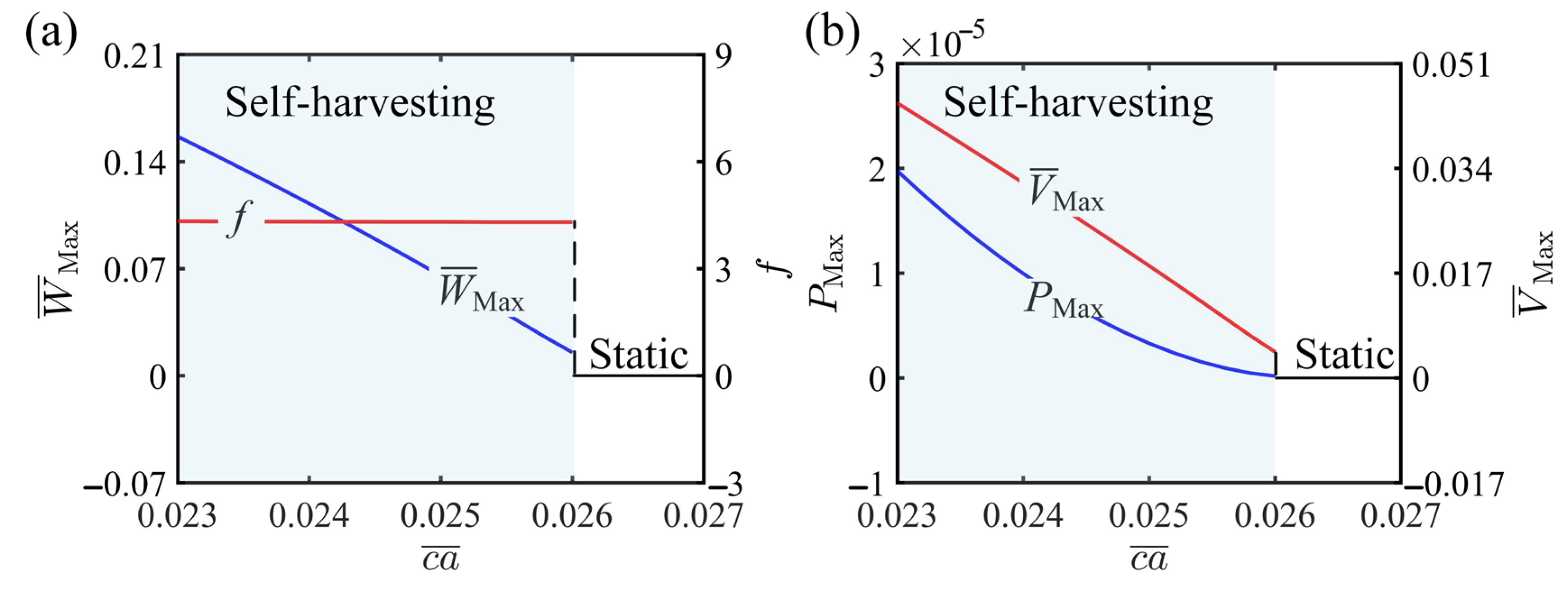
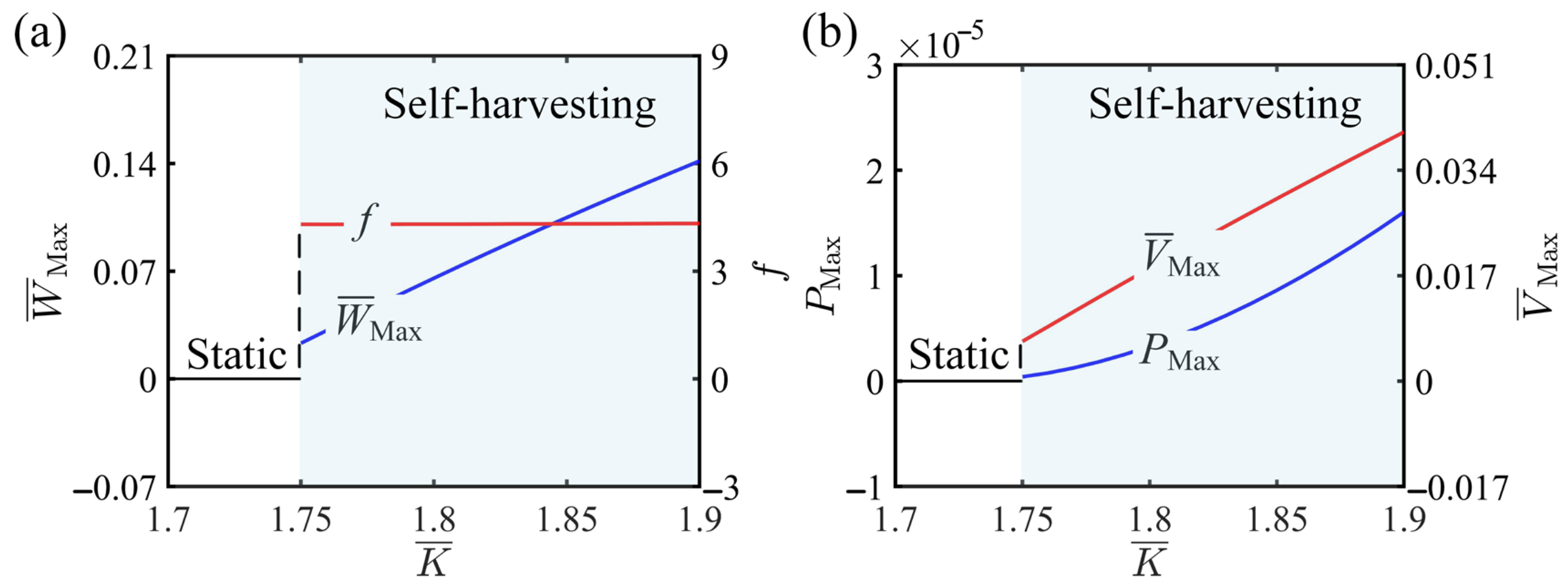
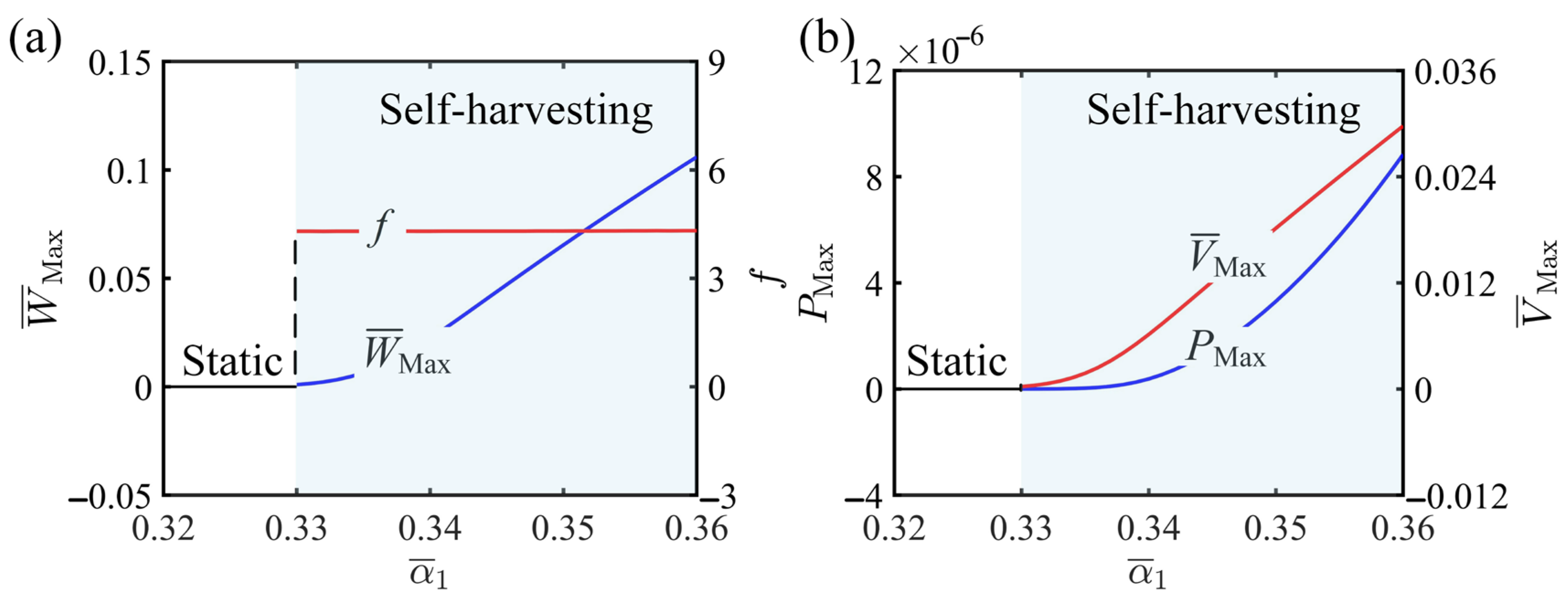
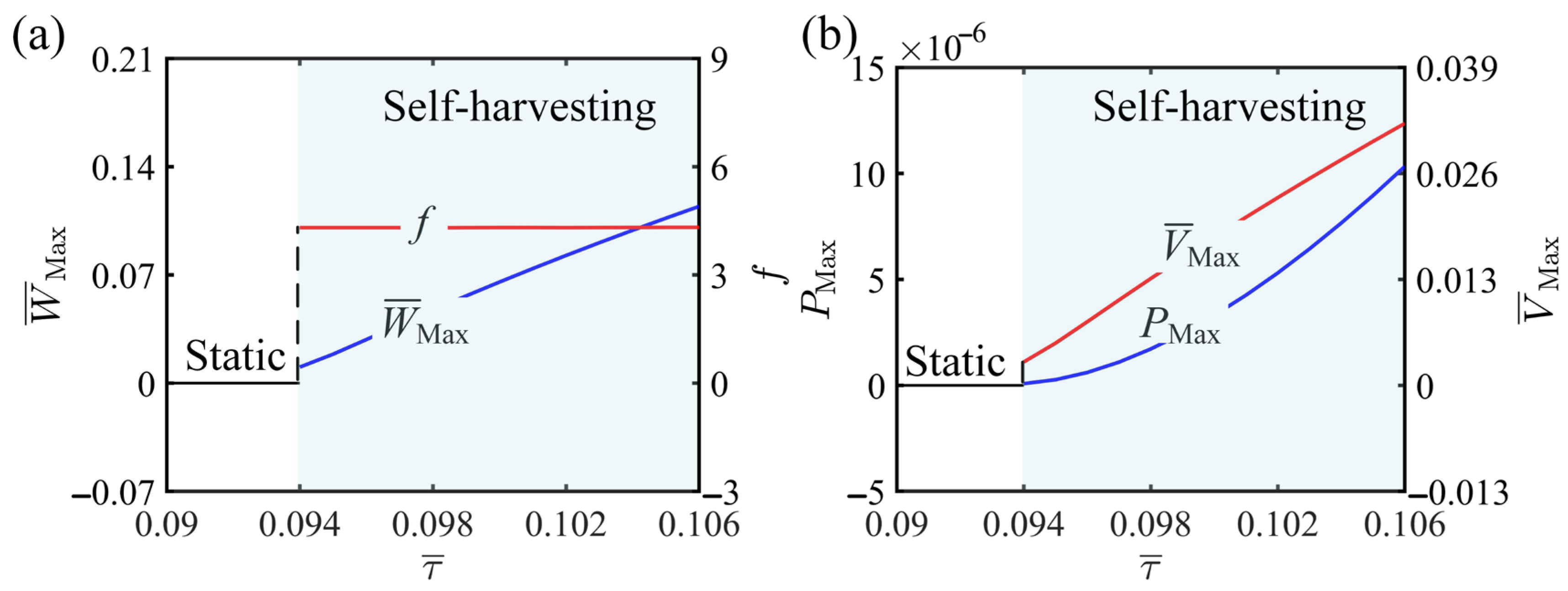
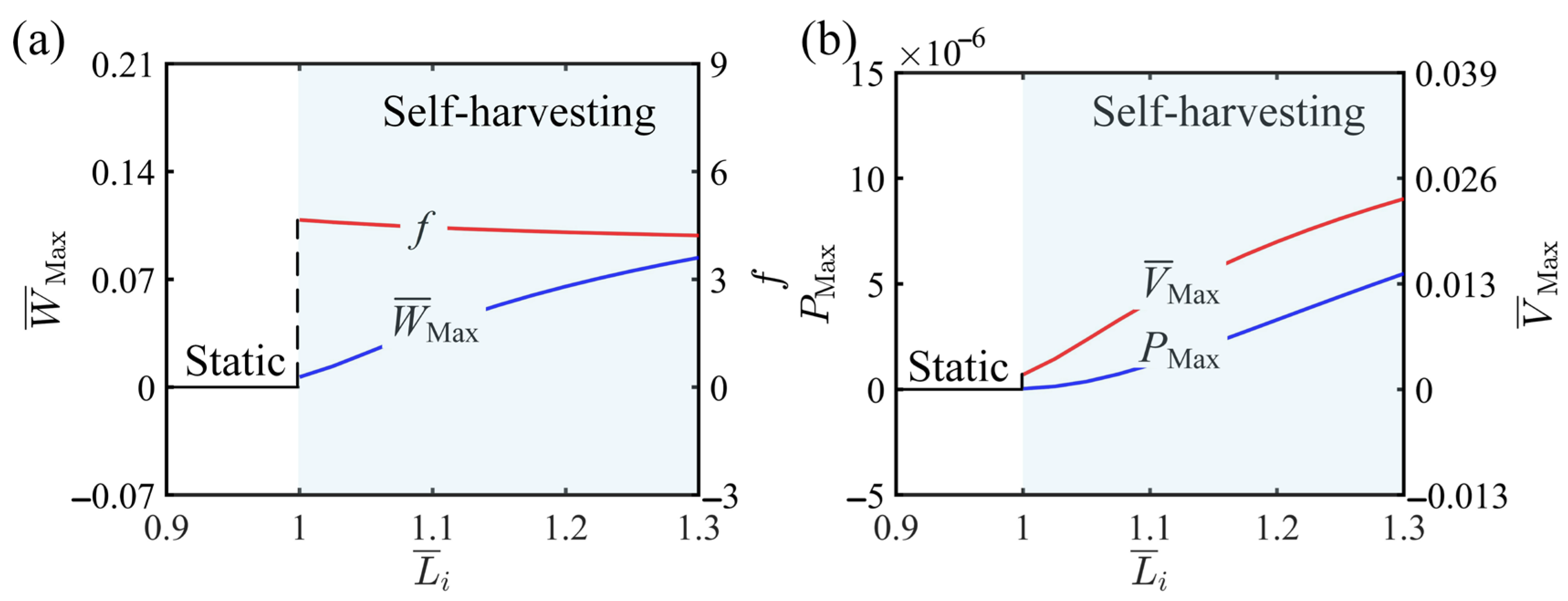
4. Performance of Self-Harvesting
4.1. Parameters Inhibiting Self-Harvesting
4.2. Parameters Promoting Self-Harvesting
4.3. Parameters Non-Monotonically Affecting Self-Harvesting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Kang, X.; Ji, L.; Zhang, A.; Xia, G. Low frequency vibration energy harvesting of bio-inspired multi-stable piezoelectric vibration system with an adjustable device. Chaos Solitons Fractals 2025, 192, 116026. [Google Scholar] [CrossRef]
- Lv, H.; Liang, L.; Zhang, Y.; Deng, L.; Chen, Z.; Liu, Z.; Wang, H.; Chen, G. A flexible spring-shaped architecture with optimized thermal design for wearable thermoelectric energy harvesting. Nano Energy 2021, 88, 106260. [Google Scholar] [CrossRef]
- Zhang, X.; Shiu, B.C.; Li, T.; Liu, X.; Ren, H.; Wang, Y.; Lou, C.; Lin, J. Photo-thermoelectric nanofiber film based on the synergy of conjugated polymer and light traps for the solar-energy harvesting of textile solar panel. Sol. Energy Mater. Sol. Cells 2021, 232, 111353. [Google Scholar] [CrossRef]
- Sandelic, M.; Peyghami, S.; Sangwongwanich, A.; Blaabjerg, F. Reliability aspects in microgrid design and planning: Status and power electronics-induced challenges. Renew. Sustain. Energy Rev. 2022, 159, 112127. [Google Scholar] [CrossRef]
- Beniwal, R.; Kalra, S.; Beniwal, N.S.; Mazumdar, H.; Singhal, A.K.; Singh, S.K. Walk-to-charge technology: Exploring efficient energy harvesting solutions for smart electronics. J. Sens. 2023, 2023, 6614658. [Google Scholar] [CrossRef]
- Kumar, M.; Suhaib, M.; Sharma, N.; Kumar, S.; Kumar, M.; Choudhary, S. Energy harvesting technologies in mechanical systems: A comprehensive review. Int. J. Res. Public Rev. 2024, 5, 2782–2787. [Google Scholar] [CrossRef]
- Zhou, W.; Du, D.; Cui, Q.; Lu, C.; Wang, Y.; He, Q. Recent research progress in piezoelectric vibration energy harvesting technology. Energies 2022, 15, 947. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, P.; Li, S.; Gao, M.; Ouyang, H.; He, Q.; Wang, P. An electromagnetic vibration energy harvester using a magnet-array-based vibration-to-rotation conversion mechanism. Energy Convers. Manag. 2022, 253, 115146. [Google Scholar] [CrossRef]
- Li, M.; Luo, A.; Luo, W.; Liu, X.; Wang, F. Electrostatic vibration energy harvester with a self-rechargeable electret. IEEE Electron. Device Lett. 2023, 44, 540–543. [Google Scholar] [CrossRef]
- Ge, D.; Bao, W.; Chen, H.; Li, K. A liquid crystal elastomer-based generator using light-powered self-oscillations. Chaos Solitons Fractals 2025, 199, 116690. [Google Scholar] [CrossRef]
- Asadi Jafari, M.H.; Zarastvand, M.; Zhou, J. Doubly curved truss core composite shell system for broadband diffuse acoustic insulation. Vib. Control 2024, 30, 4035–4051. [Google Scholar] [CrossRef]
- Kang, X.; Wang, X.; Xia, G. Ultra-low frequency vibration energy harvesting of piezoelectric vibration systems with an adjustable device. Alex. Eng. J. 2024, 100, 92–110. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Zheng, R.; Nakano, K.; Cartmell, M. A piezoelectric cantilever-asymmetric-conical-pendulum-based energy harvesting under multi-directional excitation. J. Sound Vib. 2024, 569, 118080. [Google Scholar] [CrossRef]
- Abdelkefi, A. Aeroelastic energy harvesting: A review. Int. J. Eng. Sci. 2016, 100, 112–135. [Google Scholar] [CrossRef]
- Zhou, S.; Lallart, M.; Erturk, A. Multistable vibration energy harvesters: Principle, progress, and perspectives. J. Sound Vib. 2022, 528, 116886. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, G.; Jin, B.; Feng, H.; Chen, Z.; Fang, M.; Yang, B.; Xiao, R.; Xie, T.; Zheng, N. Multimodal autonomous locomotion of liquid crystal elastomer soft robot. Adv. Sci. 2024, 11, 2402358. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Jiang, X.; Qiu, Y.; Li, K. Stepwise self-oscillation of a photo-oscillator via time delay. Int. J. Mech. Sci. 2025, 288, 110046. [Google Scholar] [CrossRef]
- Dai, L.; Xu, J.; Xiao, R. Modeling the stimulus-responsive behaviors of fiber-reinforced soft materials. Int. J. Appl. Mech. 2024, 16, 2450041. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z.; Sun, X.; Zuo, W.; Li, K. Multi-modal self-sustained motions of a silicone oil paper disc on a surface driven by hot steam. Chaos Solitons Fractals 2025, 191, 115898. [Google Scholar] [CrossRef]
- Ge, D.; Bao, W.; Li, K.; Liang, H. Self-oscillation-driven locomotion in a liquid crystal elastomer-based robot under constant illumination. Commun. Nonlinear Sci. Numer. 2025, 145, 108706. [Google Scholar] [CrossRef]
- Wang, X.; Ho, G.W. Design of untethered soft material micromachine for life-like locomotion. Mater. Today 2022, 53, 197–216. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Ji, Q.; Chang, L.; Hu, Y.; Peng, Q.; He, X. A MXene-based light-driven actuator and motor with self-sustained oscillation for versatile applications. Adv. Funct. Mater. 2024, 34, 2310955. [Google Scholar] [CrossRef]
- He, Q.; Yin, R.; Hua, Y.; Jiao, W.; Mo, C.; Shu, H.; Raney, J.R. A modular strategy for distributed, embodied control of electronics-free soft robots. Sci. Adv. 2023, 9, eade9247. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Yin, X.; Zhang, C.; Chen, B.; Sun, P.; Xu, Y. Weaving liquid crystal elastomer fiber actuators for multifunctional soft robotics. Sci. Adv. 2025, 11, eads3058. [Google Scholar] [CrossRef] [PubMed]
- Liao, W.; Yang, Z. The integration of sensing and actuating based on a simple design fiber actuator towards intelligent soft robots. Adv. Mater. Technol. 2022, 7, 2101260. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Liao, W.; Yang, Z. Ultrafast, high-contractile electrothermal-driven liquid crystal elastomer fibers towards artificial muscles. Small 2021, 17, 2103700. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, K.; Xu, P. Chaotic self-beating of left ventricle modeled by liquid crystal elastomer. Thin-Walled Struct. 2024, 205, 112540. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, R.; Jin, L.; Liu, M.; Gao, Y.; Raney, J.; Yang, S. 3D-Printed photoresponsive liquid crystal elastomer composites for free-form actuation. Adv. Funct. Mater. 2023, 33, 2210614. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Z.; Xu, Z.; Yu, Q.; Wu, Z.; Wang, Z.; Qian, J.; Xiao, R. Shape morphing of 3d printed liquid crystal elastomer structures with precuts. ACS Appl. Polym. Mater. 2023, 5, 7477–7484. [Google Scholar] [CrossRef]
- Lu, D.; Wang, L.; Chen, B.; Xu, Z.; Wang, Z.; Xiao, R. Shape memory behaviors of 3D printed liquid crystal elastomers. Soft Sci. 2023, 3, 5. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Zhu, L.; Ge, Q.; Wu, Z.L.; Qu, S.; Xiao, R. Tailored helix morphing of 3D-printed liquid crystal elastomer bilayers. Cell Rep. Phys. Sci. 2025, 6, 102835. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, A.; Zhang, Z.; Yin, R.; Gao, Y.; Feng, L.; Yang, S. Repeatable and reprogrammable shape morphing from photoresponsive gold nanorod/liquid crystal elastomers. Adv. Mater. 2020, 32, 2004270. [Google Scholar] [CrossRef]
- Wang, X.; Shao, H.; Tang, J.; Chen, J.; Huang, Y.; Pan, J.; Zhang, Y.; Wang, W.; Jiang, J.; Chen, N. Braided liquid crystal elastomer fiber actuator with programmable deformation for artificial muscles. Adv. Mater. Technol. 2023, 8, 2300814. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, Y.; Luo, D. Polarization dependent light-driven liquid crystal elastomer actuators based on photothermal effect. Adv. Opt. Mater. 2021, 9, 2001861. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, K. Light-powered self-striking liquid crystal elastomer hammers inspired by mantis shrimp. Commun. Nonlinear Sci. Numer. 2025, 146, 108802. [Google Scholar] [CrossRef]
- Huang, C.; Yang, F.; Li, K.; Dai, Y.; Yu, Y. Modeling and analysis of self-sustaining oscillation behavior of liquid crystal elastomer fiber/baffle system under stable full-field illumination. Chaos Solitons Fractals 2025, 194, 116259. [Google Scholar] [CrossRef]
- Zhu, L.; He, M.; Chen, B.; Qian, J.; Xiao, R.; Solids, P. Inflation of a polydomain nematic elastomeric membrane. J. Mech. Phys. Solids 2025, 198, 106075. [Google Scholar] [CrossRef]
- Bai, C.; Kang, J.; Wang, Y. Kirigami-inspired light-responsive conical spiral actuators with large contraction ratio using liquid crystal elastomer fiber. ACS Appl. Mater. Interfaces 2025, 17, 14488–14498. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, C.; Dai, Y.; Li, K. Light-fueled self-fluttering aircraft with a liquid crystal elastomer-based engine. Commun. Nonlinear Sci. Numer. 2024, 132, 107942. [Google Scholar] [CrossRef]
- Liu, J.; Qian, G.; Dai, Y.; Yuan, Z.; Song, W.; Li, K. Nonlinear dynamics modeling of a light-powered liquid crystal elastomer-based perpetual motion machine. Chaos Solitons Fractals 2024, 184, 114957. [Google Scholar] [CrossRef]
- Rešetič, A.; Milavec, J.; Domenici, V.; Zupančič, B.; Bubnov, A.; Zalar, B. Deuteron NMR investigation on orientational order parameter in polymer dispersed liquid crystal elastomers. Phys. Chem. Chem. Phys. 2020, 22, 23064–23072. [Google Scholar] [CrossRef]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Li, C. Design of mxene composites with biomimetic rapid and self-oscillating actuation under ambient circumstances. ACS Appl. Mater. Interfaces 2021, 13, 31978–31985. [Google Scholar] [CrossRef]
- Dai, Y.; Jiang, X.; Wang, K.; Li, K. A phototunable self-oscillatory bistable seesaw via liquid crystal elastomer fibers. Chaos Solitons Fractals 2025, 200, 117041. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, C.; Liu, C.; Wang, Z.; Ma, H.; Xu, P. Heat-driven self-wobbling of a liquid crystal elastomer double-wheel linkage. Thin-Walled Struct. 2025, 217, 113829. [Google Scholar] [CrossRef]
- Bai, C.; Kang, J.; Wang, Y. Light-induced motion of three-dimensional pendulum with liquid crystal elastomeric fiber. Int. J. Mech. Sci. 2024, 266, 108911. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Qiu, Y.; Chen, H.; Li, K. Light-powered self-swing of a bistable magnetic pendulum utilizing liquid crystal elastomer fibers. Chaos Solitons Fractals 2025, 198, 116565. [Google Scholar] [CrossRef]
- Li, K.; Zhao, C.; Qiu, Y.; Dai, Y. Light-powered self-rolling of a liquid crystal elastomer-based dicycle. Appl. Math. Mech-Engl. 2025, 46, 253–268. [Google Scholar] [CrossRef]
- Wu, H.; Ge, D.; Qiu, Y.; Li, K.; Xu, P. Mechanics of light-fueled bidirectional self-rolling in a liquid crystal elastomer rod on a track. Chaos Solitons Fractals 2025, 191, 115901. [Google Scholar] [CrossRef]
- Bai, C.; Kang, J.; Wang, Y. Light-induced wrinkling in annulus anisotropic liquid crystal elastomer films. Phys. Rev. E 2025, 111, 015421. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, Y.; Li, K. Light-fueled self-ejecting liquid crystal elastomer launcher inspired by lizard tail autotomy. Chaos Solitons Fractals 2025, 194, 116265. [Google Scholar] [CrossRef]
- Yu, Y.; Dai, Z.; Li, T.; Wang, Z.; Ma, H.; Li, K. Self-tapping of a liquid crystal elastomer thin beam above a hot plate. Chaos Solitons Fractals 2025, 199, 116904. [Google Scholar] [CrossRef]
- Fang, X.; Lou, J.; Wang, J.; Chuang, K.; Wu, H.; Huang, Z. A self-excited bistable oscillator with a light-powered liquid crystal elastomer. Int. J. Mech. Sci. 2024, 271, 109124. [Google Scholar] [CrossRef]
- Wu, H.; Lou, J.; Dai, Y.; Zhang, B.; Li, K. Multi-scale analysis of the self-vibration of a liquid crystal elastomer fiber-spring system exposed to constant-gradient light. J. Zhejiang Univ.-Sci. A 2025, 26, 652–665. [Google Scholar] [CrossRef]
- Sun, X.; Ge, D.; Li, K.; Xu, P. Chaotic self-oscillation of liquid crystal elastomer double-line pendulum under a linear temperature field. Chaos Solitons Fractals 2024, 189, 115653. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, K.; Chen, Y.; Gao, J.; Xu, P. Self-oscillation chaotic motion of a liquid crystal elastomer pendulum under gradient-stabilized illumination. Chaos Solitons Fractals 2025, 193, 116128. [Google Scholar] [CrossRef]
- Kang, W.; Cheng, Q.; Liu, C.; Wang, Z.; Li, D.; Liang, X. A constitutive model of monodomain liquid crystal elastomers with the thermal-mechanical-nematic order coupling. J. Mech. Phys. Solids 2025, 196, 105995. [Google Scholar] [CrossRef]
- Verma, R. Energy harvesting techniques for self-powered electronics: State-of-the-art and challenges. J. Adv. Res. Electron. Eng. Technol. 2023, 10, 6. [Google Scholar]
- Wu, N.; Bao, B.; Wang, Q. Review on engineering structural designs for efficient piezoelectric energy harvesting to obtain high power output. Eng. Struct. 2021, 235, 112068. [Google Scholar] [CrossRef]
- Zhang, W.; Nan, Y.; Wu, Z.; Shen, Y.; Luo, D.J.M. Photothermal-driven liquid crystal elastomers: Materials, alignment and applications. Molecules 2022, 27, 4330. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Global nonlinear distributed-parameter model of parametrically excited piezoelectric energy harvesters. Nonlinear Dyn. 2012, 67, 1147–1160. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: London, UK, 2003. [Google Scholar]
- Ahn, C.; Liang, X.; Cai, S. Bioinspired design of light-powered crawling, squeezing, and jumping untethered soft robot. Adv. Mater. Technol. 2019, 4, 6004. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Wang, Q.; Cross, L. Constitutive equations of symmetrical triple layer piezoelectric benders. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1999, 46, 1343–1351. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodi, S.; Jalili, N. Non-linear vibrations and frequency response analysis of piezoelectrically driven microcantilevers. Int. J. Non-Linear Mech. 2007, 42, 577–587. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, S.; Kang, X.; Han, T.; Chen, L.; Lim, C.W. Performance analysis of nonlinear piezoelectric energy harvesting system under bidirectional excitations. Compos. Struct. 2023, 324, 117529. [Google Scholar] [CrossRef]
- Sadeghian, H.; Rezazadeh, G. Comparison of generalized differential quadrature and Galerkin methods for the analysis of micro-electro-mechanical coupled systems. Commun. Nonlinear Sci. Numer. 2009, 14, 2807–2816. [Google Scholar] [CrossRef]
- William, T. Theory of Vibration with Applications; Prentice-Hall Inc.: Saddle River, NJ, USA, 1988. [Google Scholar]
- Li, K.; Cai, S. Modeling of light-driven bending vibration of a liquid crystal elastomer beam. J. Appl. Mech. 2016, 83, 031009. [Google Scholar] [CrossRef]
- Azimi, M. Stability and bifurcation of Mathieu–Duffing equation. Int. J. Nonlinear Mech. 2022, 144, 104049. [Google Scholar] [CrossRef]
- Braun, L.; Hessberger, T.; Pütz, E.; Mueller, C.; Giesselmann, F.; Serra, C.; Zentel, R. Actuating thermo- and photo-responsive tubes from liquid crystalline elastomers. J. Mater. Chem. C 2018, 6, 9093–9101. [Google Scholar] [CrossRef]
- Li, H.; Sun, H.; Song, B.; Zhang, D.; Shang, X.; Liu, D. Nonlinear dynamic response of an L-shaped beam-mass piezoelectric energy harvester. J. Sound Vib. 2021, 499, 116004. [Google Scholar] [CrossRef]


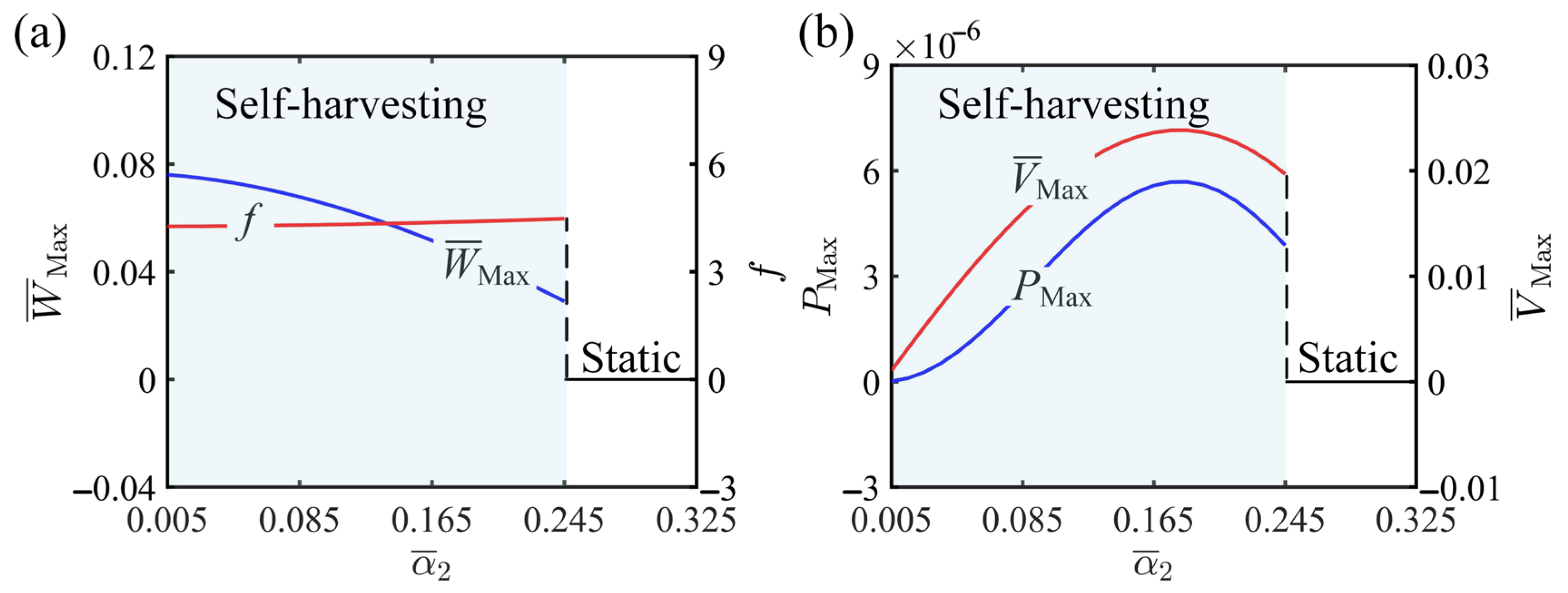
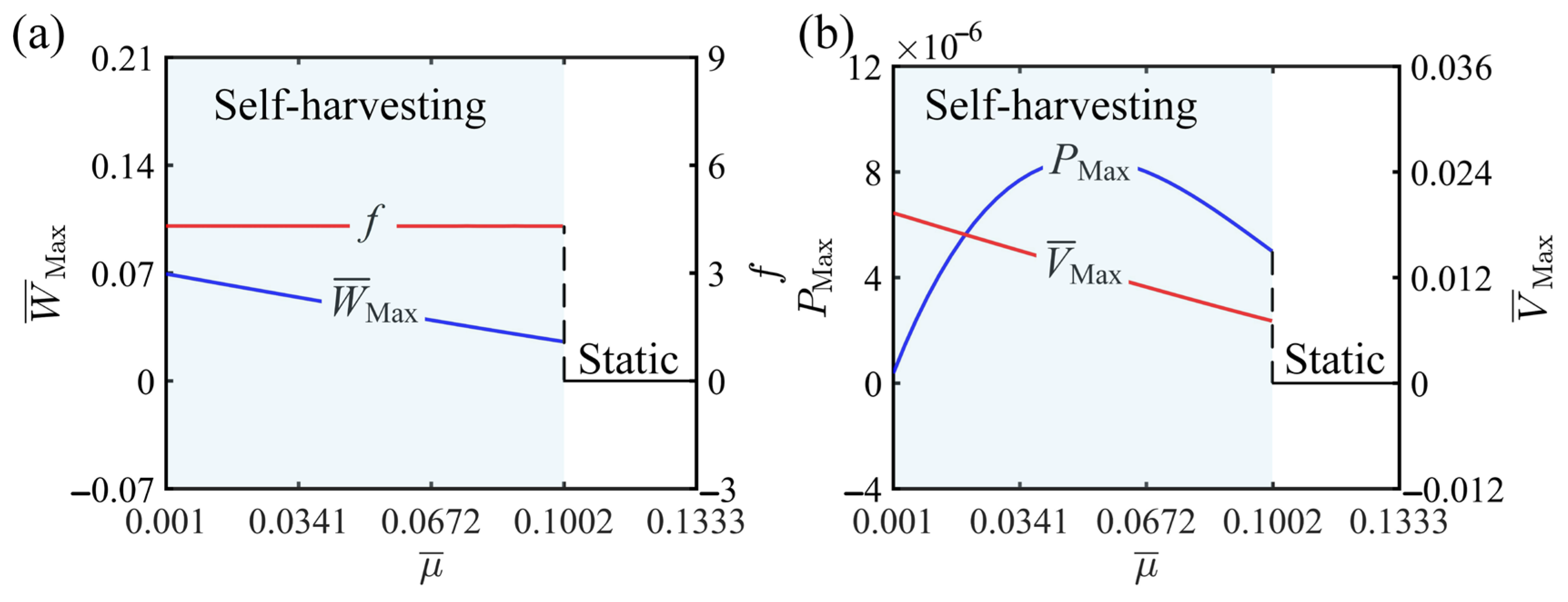
| Parameter | Definition | Value | Units |
|---|---|---|---|
| Length of the cantilever beam | |||
| Initial length of LCE fiber | |||
| Contraction coefficient | |||
| Thermal relaxation time | |||
| Photothermal intensity | |||
| Light gradient | |||
| Inclined angle | |||
| Elastic coefficient of LCE fiber | |||
| First-order damping coefficient | |||
| Second-order damping coefficient | |||
| Width of the cantilever | |||
| Mass per unit length of the cantilever | |||
| Thickness of substrate layer | |||
| Young’s modulus of substrate layer | |||
| Young’s modulus of piezoelectric layer | |||
| Thickness of piezoelectric layer | |||
| Piezoelectric dielectric constant | |||
| Piezoelectric strain constant | |||
| Resistance of the resistor |
| Parameter | ||||||||||
| Value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Chen, H.; Bao, W.; Chen, X.; Gao, T.; Ge, D. Theoretical Modeling of Light-Fueled Self-Harvesting in Piezoelectric Beams Actuated by Liquid Crystal Elastomer Fibers. Mathematics 2025, 13, 3226. https://doi.org/10.3390/math13193226
Zhou L, Chen H, Bao W, Chen X, Gao T, Ge D. Theoretical Modeling of Light-Fueled Self-Harvesting in Piezoelectric Beams Actuated by Liquid Crystal Elastomer Fibers. Mathematics. 2025; 13(19):3226. https://doi.org/10.3390/math13193226
Chicago/Turabian StyleZhou, Lin, Haiming Chen, Wu Bao, Xuehui Chen, Ting Gao, and Dali Ge. 2025. "Theoretical Modeling of Light-Fueled Self-Harvesting in Piezoelectric Beams Actuated by Liquid Crystal Elastomer Fibers" Mathematics 13, no. 19: 3226. https://doi.org/10.3390/math13193226
APA StyleZhou, L., Chen, H., Bao, W., Chen, X., Gao, T., & Ge, D. (2025). Theoretical Modeling of Light-Fueled Self-Harvesting in Piezoelectric Beams Actuated by Liquid Crystal Elastomer Fibers. Mathematics, 13(19), 3226. https://doi.org/10.3390/math13193226





