The Simplest 2D Quantum Walk Detects Chaoticity
Abstract
1. Introduction
2. QW Model
3. Chaotic Signatures: Spectral Behavior and Morphology of the Eigenfunctions
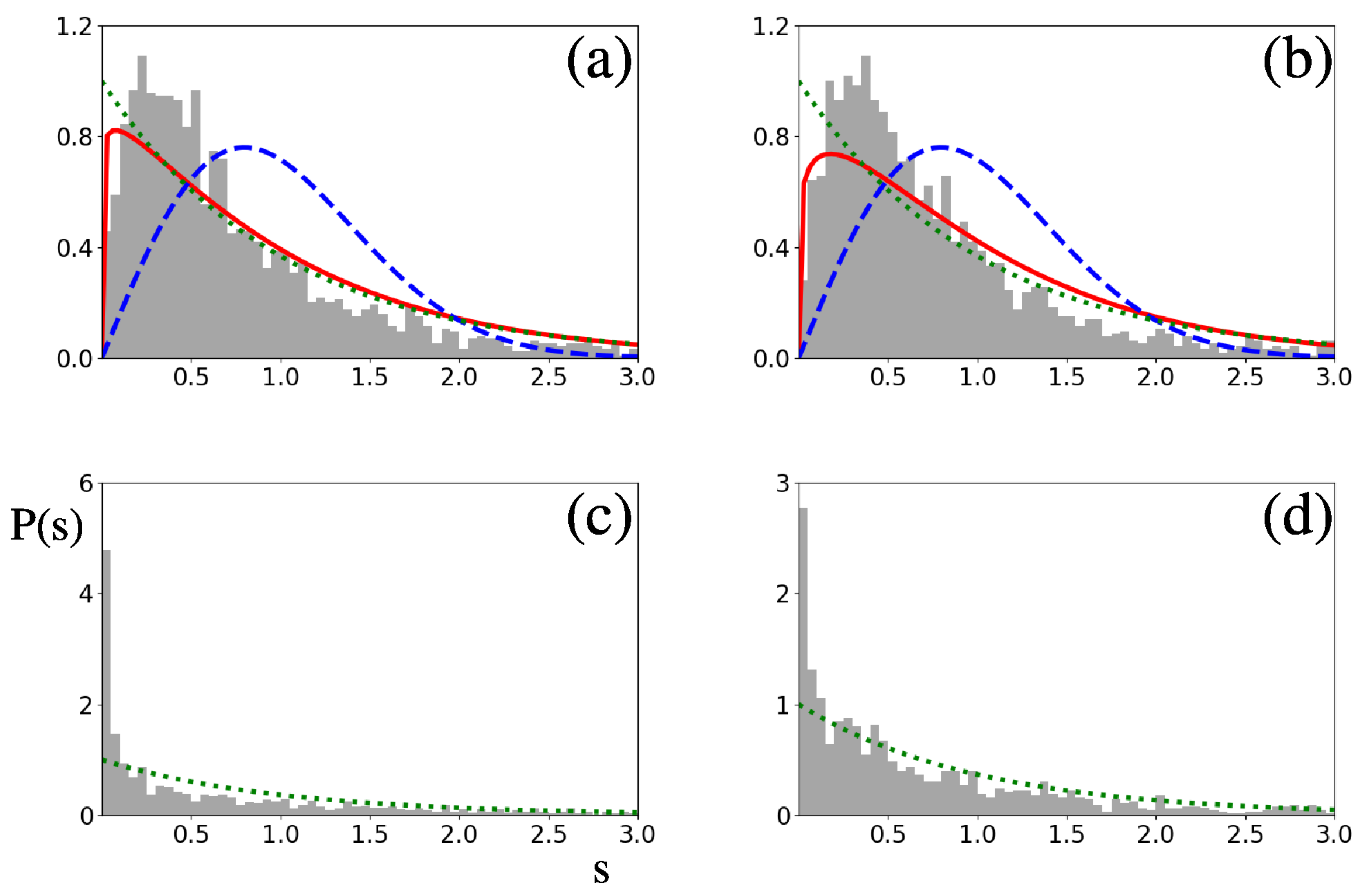
3.1. Spectral Statistics
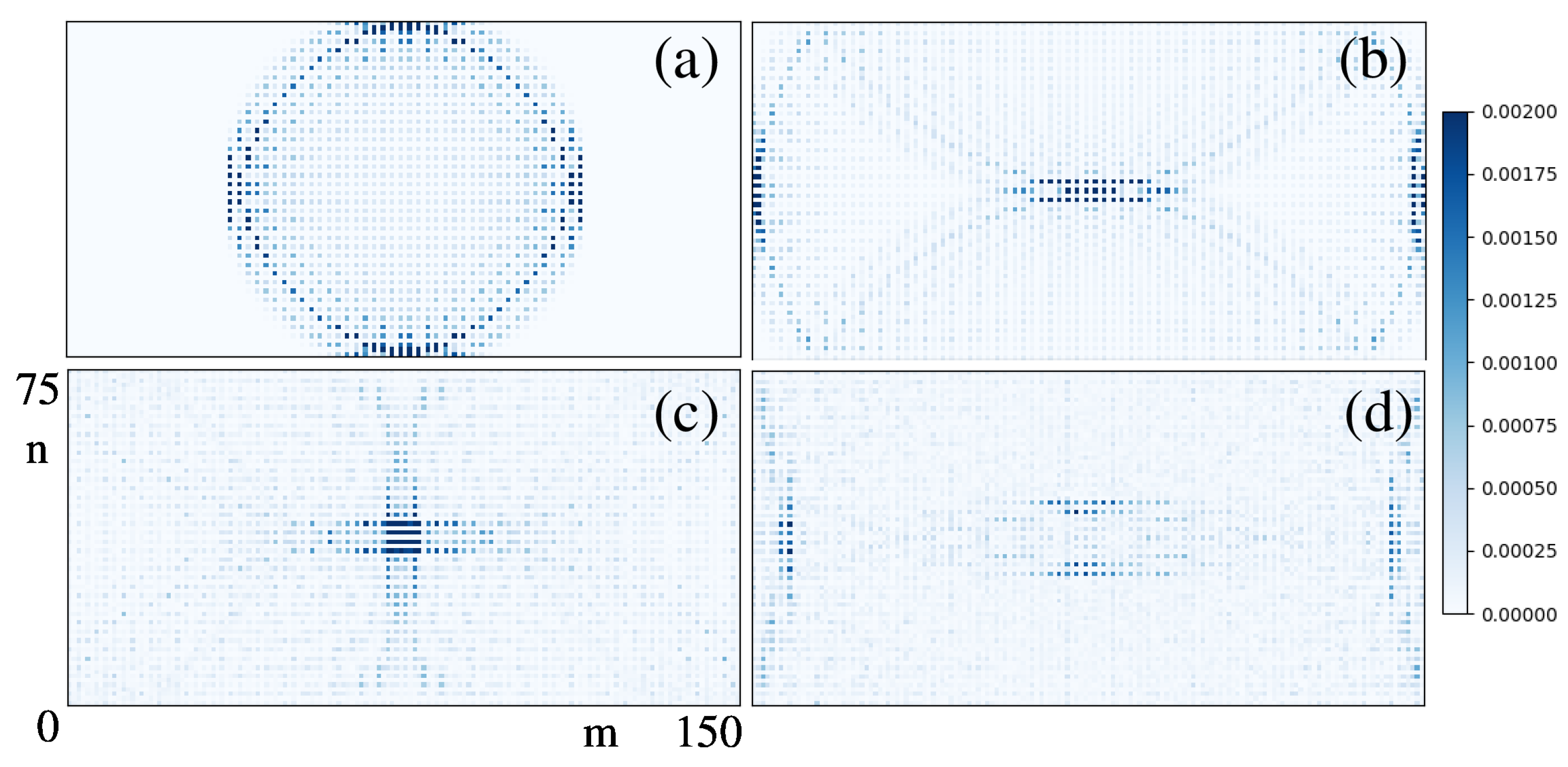
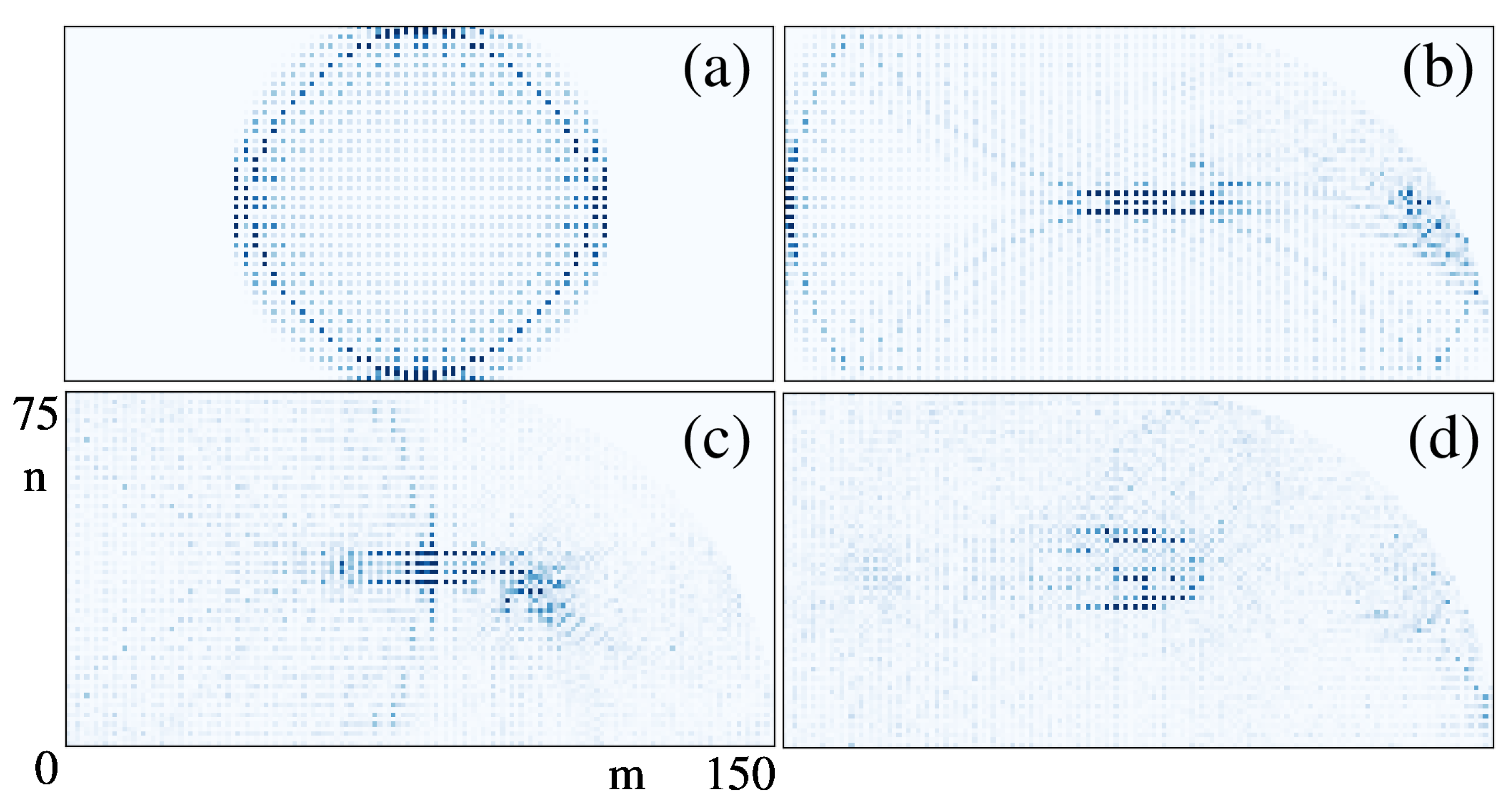
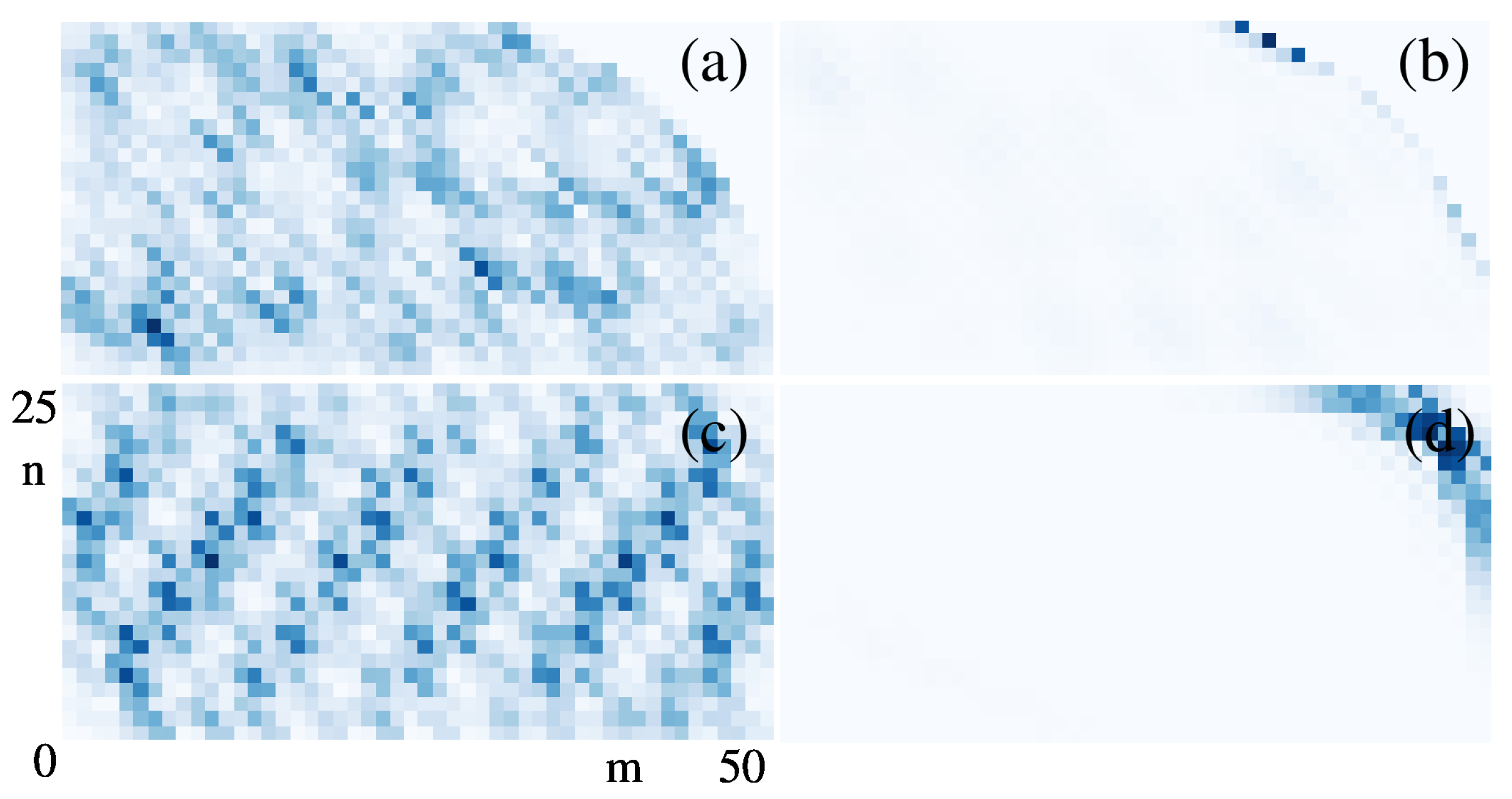
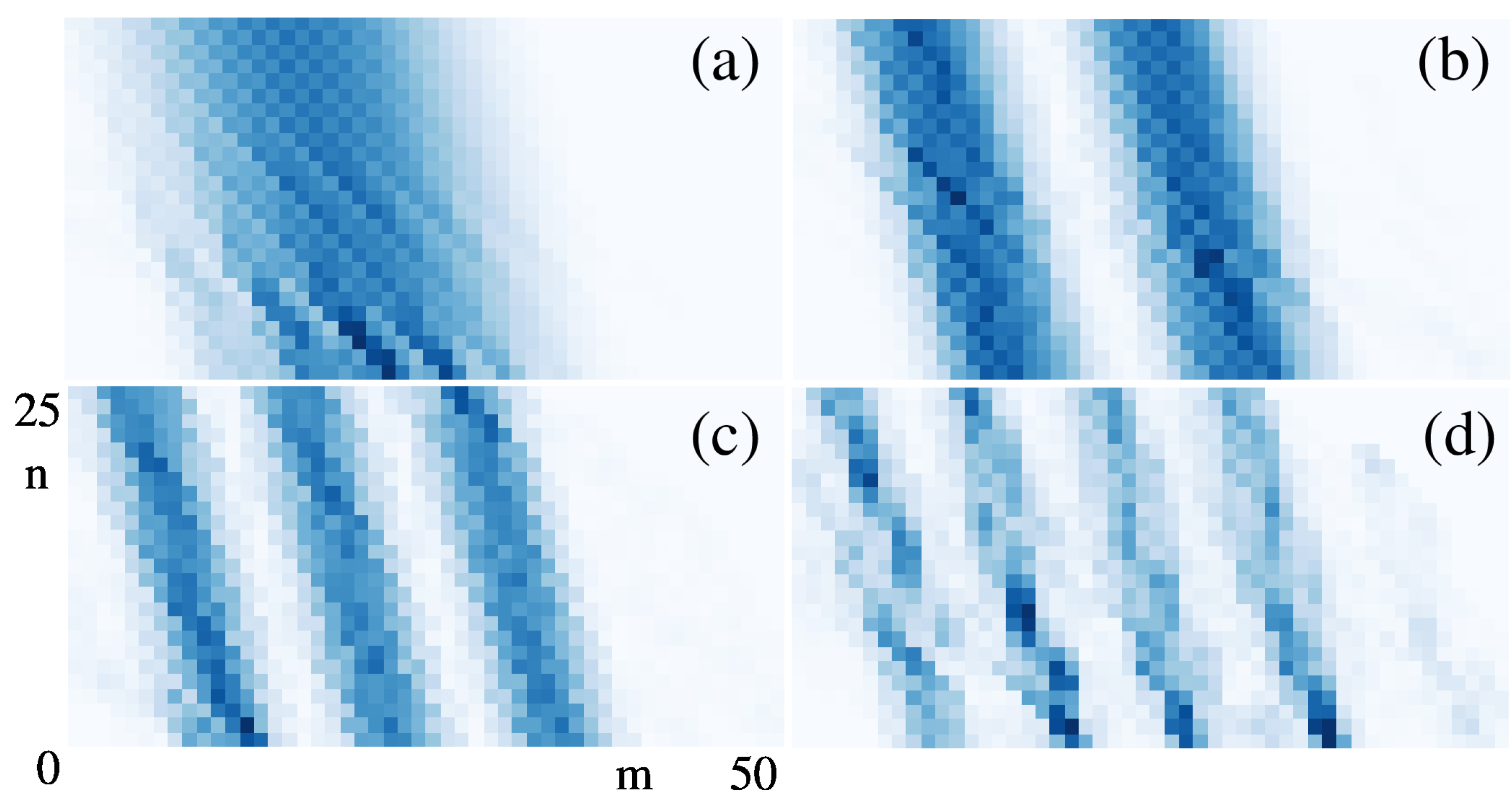
3.2. Eigenfunctions Morphology
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Details of the QW Model
Appendix A.2. Unitarity of the Evolution Operator
References
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687. [Google Scholar] [CrossRef]
- Nosrati, F.; Laneve, A.; Shadfar, M.K.; Geraldi, A.; Mahdavipour, K.; Pegoraro, F.; Mataloni, P.; Franco, R.L. Quantum Information Spreading in a Disordered Quantum Walk. J. Opt. Soc. Am. B 2021, 38, 2570. [Google Scholar] [CrossRef]
- Hines, A.P.; Stamp, P.C.E. Quantum walks, quantum gates, and quantum computers. Phys. Rev. A 2007, 75, 062321. [Google Scholar] [CrossRef]
- Ambianis, A. Quantum search algorithms. ACM SIGACT News 2004, 35, 22. [Google Scholar] [CrossRef]
- Preiss, P.M.; Ma, R.; Tai, M.E.; Lukin, A.; Rispoli, M.; Zupancic, P.; Lahini, Y.; Islam, R.; Greiner, M. Strongly correlated quantum walks in optical lattices. Science 2015, 347, 1229. [Google Scholar] [CrossRef]
- Batalha, G.M.; Volta, A.; Strunz, W.T.; Galiceanu, M. Quantum transport on honeycomb networks. Sci. Rep. 2022, 12, 6896. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Molfetta, G.D.; Herzog, B. Searching via nonlinear quantum walk on the 2D-grid. Algorithms 2020, 13, 305. [Google Scholar] [CrossRef]
- Ladjal, B.; Nadour, M.; Bechouat, M.; Hadroug, N.; Sedraoui, M.; Rabehi, A.; Guermoui, M.; Agajie, T.F. Hybrid deep learning CNN-LSTM model for forecasting direct normal irradiance: A study on solar potential in Ghardaia, Algeria. Sci. Rep. 2025, 15, 15404. [Google Scholar] [CrossRef]
- Tang, H.; Lin, X.; Feng, Z.; Chen, J.; Gao, J.; Sun, K.; Wang, C.; Lai, P.; Xu, X.; Wang, Y.; et al. Experimental twodimensional quantum walk on a photonic chip. Sci. Adv. 2018, 4, 3174. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, Y.; Yu, L.; Zhou, J.; Jin, J.; Xu, X.; Xiong, S.; Xu, Q.; Sun, Z.; Chen, K.; et al. Experimental demonstration of quantum walks with initial superposition states. npj Quantum Inf. 2019, 5, 40. [Google Scholar] [CrossRef]
- Jiao, Z.; Gao, J.; Zhou, W.; Wang, X.; Ren, R.; Xu, X.; Qiao, L.; Wang, Y.; Jin, X. Two-dimensional quantum walks of correlated photons. Optica 2021, 8, 1129. [Google Scholar] [CrossRef]
- Rodrigues, J.; Paunkovic, N.; Mateus, P. A simulator for discrete quantum wals on lattices. Int. J. Mod. Phys. C 2017, 28, 1750055. [Google Scholar] [CrossRef]
- Bach, E.; Coppersmith, S.; Goldschen, M.P.; Joynt, R.; Watrous, J. One dimensional Quantum Walks with absorbing boundaries. J. Comput. Syst. Sci. 2004, 69, 562. [Google Scholar] [CrossRef]
- Panda, A.; Benjamin, C. Order from chaos in quantum walks on cyclic graphs. Phys. Rev. A 2021, 104, 012204. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, X. The defect-induced localization in many positions of the quantum random walk. Sci. Rep. 2016, 6, 25767. [Google Scholar] [CrossRef]
- Zhang, R.; Xue, P.; Twamley, J. One-dimensional quantum walks with single-point phase defects. Phys. Rev. A 2014, 89, 042317. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 1984, 52, 1. [Google Scholar] [CrossRef]
- Grobe, R.; Haake, F. Universality of cubic level repulsion for dissipative quantum chaos. Phys. Rev. Lett. 1989, 62, 2893. [Google Scholar] [CrossRef]
- Villaseñor, D.; Santos, L.F.; Barberis-Blostein, P. Breakdown of the quantum distinction of regular and chaotic classical dynamics in dissipative systems. Phys. Rev. Lett. 2024, 133, 240404. [Google Scholar] [CrossRef]
- Pizzi, A. Quantum Trails and Memory Effects in the Phase Space of Chaotic Quantum Systems. Phys. Rev. Lett. 2025, 134, 140402. [Google Scholar] [CrossRef]
- Franco, C.D.; Gettrick, M.M.; Busch, T. Mimicking the probability distribution of a two-dimensional Grover walk with a single-qubit coin. Phys. Rev. Lett. 2011, 106, 080502. [Google Scholar] [CrossRef]
- Bru, L.A.; Hinarejos, M.; Silva, F.; de Valcárcel, G.J.; Roldán, E. Electric quantum walks in two dimensions. Phys. Rev. A 2016, 93, 032333. [Google Scholar] [CrossRef]
- Roldán, E.; Franco, C.D.; Silva, F.; de Valcárcel, G.J. N-dimensional alternate coined quantum walks from a dispersion-relation perspective. Phys. Rev. A 2013, 87, 022336. [Google Scholar] [CrossRef]
- Bru, L.A.; de Valcárcel, G.J.; Molfetta, G.D.; Pérez, A.; Roldán, E.; Silva, F. Quantum walk on a cylinder. Phys. Rev. A 2016, 94, 032328. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- Prosen, T.; Robnik, M. Energy level statistics in the transition region between integrability and chaos. J. Phys. Math. Gen. 1993, 26, 2371. [Google Scholar] [CrossRef]
- Carlo, G.G.; Vergini, E.G.; Lustemberg, P. Scar functions in the Bunimovich stadium billiard. J. Phys. A Math. Gen. 2002, 35, 7965. [Google Scholar] [CrossRef]
- Vergini, E.G.; Carlo, G.G. Semiclassical quantization with short periodic orbits. J. Phys. A Math. Gen. 2000, 33, 4717. [Google Scholar] [CrossRef]
- Selinummi, S.; Keski-Rahkonen, J.; Chalangari, F.; Räsänen, E. Formation, prevalence, and stability of bouncing-ball quantum scars. Phys. Rev. B 2024, 110, 235420. [Google Scholar] [CrossRef]
- Heller, E.J. Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits. Phys. Rev. Lett. 1984, 53, 1515. [Google Scholar] [CrossRef]
- Revuelta, F.; Vergini, E.G.; Benito, R.M.; Borondo, F. Computationally efficient method to construct scar functions. Phys. Rev. E 2012, 85, 02621. [Google Scholar] [CrossRef]
- Fernández-Hurtado, V.; Mur-Petit, J.; García-Ripoll, J.J.; Molina, R.A. Lattice scars: Surviving in an open discrete billiard. New J. Phys. 2014, 16, 035005. [Google Scholar] [CrossRef]
- Melnikov, A.; Fedichkin, L. Quantum walks of interacting fermions on a cycle graph. Sci. Rep. 2016, 6, 34226. [Google Scholar] [CrossRef]






| Coins | RMS Error | |||
|---|---|---|---|---|
| 0.07 | 0.044 | 0.131 | ||
| 0.15 | 0.069 | 0.154 | ||
| Coins | RMS Error | |
|---|---|---|
| 0.140 | ||
| 0.090 | ||
| Rectangular | Bunimovich | |
|---|---|---|
| Character | regular | chaotic |
| Poisson vs. Brody | RMSE = 0.09 ∼ 0.14 | |
| Average PR | 1500 | 1150 |
| Scarring | no | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso-Lobo, C.; Carlo, G.G.; Borondo, F. The Simplest 2D Quantum Walk Detects Chaoticity. Mathematics 2025, 13, 3223. https://doi.org/10.3390/math13193223
Alonso-Lobo C, Carlo GG, Borondo F. The Simplest 2D Quantum Walk Detects Chaoticity. Mathematics. 2025; 13(19):3223. https://doi.org/10.3390/math13193223
Chicago/Turabian StyleAlonso-Lobo, César, Gabriel G. Carlo, and Florentino Borondo. 2025. "The Simplest 2D Quantum Walk Detects Chaoticity" Mathematics 13, no. 19: 3223. https://doi.org/10.3390/math13193223
APA StyleAlonso-Lobo, C., Carlo, G. G., & Borondo, F. (2025). The Simplest 2D Quantum Walk Detects Chaoticity. Mathematics, 13(19), 3223. https://doi.org/10.3390/math13193223







