Abstract
The transmission lines we consider are constructed from the nonlinear inductors and the nonlinear capacitors. In the first part of the paper we additionally include linear ohmic resistors. Thus, the dissipation being taken into account leads to the existence of shocks—the travelling waves with different asymptotically constant values of the voltage (the capacitor charge) and the current before and after the front of the wave. For the particular values of ohmic resistances (corresponding to strong dissipation) we obtain the analytic solution for the profile of a shock wave. Both the charge on a capacitor and current through the inductor are obtained as the functions of the time and space coordinate. In the case of weak dissipation, we obtain the stationary dispersive shock waves. In the second part of the paper we consider the nonlinear lossless transmission line. We formulate a simple wave approximation for such transmission line, which decouples left/right-going waves. The approximation can also be used for the lossy transmission line, which is considered in the first part of the paper, to describe the formation of the shock wave (but, of course, not the shock wave itself).
MSC:
35L67
1. Introduction
The concept that in a nonlinear wave propagation system the various parts of the wave travel with different velocities, and that wave fronts (or tails) can sharpen into shock waves, is deeply imbedded in the classical theory of fluid dynamics [1]. The nonlinear electrical transmission lines (where the nonlinearity can be either due to nonlinear capacitors or nonlinear inductors forming the line, or both) are of much interest both due to their applications, and as the laboratories to study nonlinear waves [2,3,4,5,6,7,8,9,10,11,12,13]. Nonlinear transmission line technology has historically been used for pulse shaping applications and in digitizing oscilloscopes. Over the years it has proven itself to be a highly credible, robust technology.
A very interesting particular type of signals which can propagate along such lines—the shock waves—has been of interest for many years [14,15]. We published a series of papers on the travelling waves in nonlinear transmission lines: the kinks, the solitons, and the shocks (see the most recent publication of that series and the references therein [16]).
In the present short note, we would like to add to our previous publications on the subject. In the first half of the paper we start from reproducing in a concentrated form the analytic results for the profile of the shock wave in the transmission line with the nonlinear capacitors obtained in Ref. [16]. Those results were obtained by reducing the second order ordinary differential equation describing the travelling waves in the transmission line and factorizing the thus obtained equation for the definite values of the parameters. While in the latter publication only the charge of the capacitors was analyzed as a function of time and the coordinate (which is equivalent to studying the voltage in the line as the function of the time and the coordinate), in the present note, the time and coordinate dependence of the current is also calculated.
The second half of the paper is dedicated to the presentation of the simple wave approximation to the wave equation describing the general lossless transmission line, which allows to decouple the nonlinear wave equation into two separate equations for the right- and left-going waves [17,18,19]. While we used this approximation previously for the Josephson transmission line (JTL) [20], here we formulate the approximation for the case when both the inductors and the capacitors are nonlinear [16].
2. The Circuit Equations
The transmission line constructed from the identical nonlinear inductors and the identical nonlinear capacitors is shown on Figure 1.
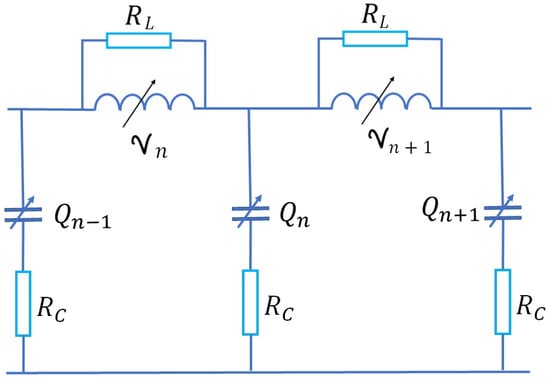
Figure 1.
Lossy nonlinear transmission line.
We take the capacitors charges and the integrated voltages on the inductors
as the dynamical variables. The circuit equations (Kirchhoff laws) are
To close the system (2a,b) we should specify the connection between the voltages on the capacitors and the charges and also between the currents through the inductors and the integrated voltages
In the continuum approximation we treat n as the continuous variable x (we measure distance in the units of the transmission line period) and approximate the finite differences in the r.h.s. of the equations by the first derivatives with respect to x, after which the equations take the form
Further on we will consider the travelling waves, for which all the dependent variables depend upon the single independent variable , where U is the speed of the wave. For such waves, (4a,b) turns into the system of ODE which after integration takes the form
where and are the constants of integration.
Equation (5a,b) contains three arbitrary constants—U, , and . Since we are considering localized travelling waves, it would be convenient to take as the constants , defined by the following equations:
and connected by the following relation:
Thus Equation (5a,b) can be presented as follows:
where and .
The speed of the travelling wave is
Further on we consider the transmission line with linear inductors () and nonlinear capacitors. We can exclude the current from (8a,b) and after incorporating some algebra obtain the closed equation for
and the travelling speed is given by the following equation:
3. Strong Dissipation
3.1. The ODE Which Does Not Contain Explicitly the Independent Variable
Consider the generalized damped Helmholtz-Duffing equation [20]
where n, k, , , are constants, with the boundary conditions
Equation (19) does not contain explicitly the independent variable . This prompts the idea to consider x as the new independent variable and
as the new dependent variable. In the new variables (19) takes the form of Abel equation of the second kind.
The boundary conditions in the new variables are
One can easily check up that for and k connected by the following formula:
the solution of (22) satisfying the boundary conditions (23) is
Hence, we realize that for k and connected by the formula
the solution of (27) satisfying the boundary conditions (23) is
Let us return to (19) and modify it to
Thus, we take into account possible nonlinearity of friction. Thus, instead of (22) we obtain
3.2. Back to the Transmission Line
Now let us return to the transmission line. For Equation (13) with given by (17), using the results of the previous section, we claim that when the parameters of the equation satisfy the relation
the solution of the equation can be expressed in terms of elementary functions:
where
For (13) with given by (15), we claim that when the boundary conditions satisfy the relation
the solution of the equation can be expressed in terms of elementary functions:
where
Previously, we used the linear approximation for in the last term in the l.h.s. of (10). Strictly speaking, since we are considering nonlinear in the r.h.s. of (10) more consistent would be to treat the same way the l.h.s. Equations (33) and (34) allow us to go one step in this direction, that is to consider in the last term in the l.h.s. of (10) in quadratic approximation (for cubic nonlinearity of ). As the result, Equations (35) and (36) slightly change and Equation (36) does not change at all.
The analytic results for the profile of the shock wave were obtained by reducing the second order differential Equation (10) to the first order one
where . However, looking back to Equation (8a,b) we see the opportunity to reduce the system of two first order differential equations to the single first order one
already at this stage. It would be interesting to try to obtain exact analytic solutions of (42) for some values of the parameters.
Postponing such attempt until a later time, shows that Equation (42) allows us to obtain the dependence of the current I, which was absent in our previous publications. To achieve this aim let us rewrite (42) in the following form:
The dependence being found earlier, Equation (43) gives infinite series for , and the first two terms of the series are
4. Weak Dissipation
Let us return to Equation (13) and consider the case of weak dissipation. In this case, it is convenient to rewrite the equation as follows:
where , , and is defined by the following equation:
We will use the method of time averaging [21]. We assume that we know the undamped solution , satisfying the following equation:
and express damped oscillations as follows:
where satisfies the following equation:
the averaging is with respect to the period of the undamped oscillation with the energy , or more explicitly,
the limits of integration in both integrals are found from the equation . Notice that the shock in the considered case can be called the stationary dispersive shock wave [22].
We want to show how the method of time averaging works for given by Equation (15). After the change in variable
Thus the solution of (47) is
() are the roots of cubic equation .
All integrals
where m is an arbitrary natural number and is some polynomial of power p, are expressed through the first integrals and algebraic quantities [24]. and are table integrals [25]:
where K and E are complete elliptic integrals of the first and second kind, respectively, and . To calculate let us integrate the identity
We obtain
Integrating the identity
we obtain
(One should keep in mind that are functions of ). Numerical analysis of the formula obtained in this section one may find in our previous publication [21].
5. The Simple Waves in a Lossless Nonlinear Transmission Line
As it is well known [17], the shock waves exist only in the presence of dissipation. (In the absence of the dissipation, the localized travelling waves in the systems we consider are kinks and solitons [20]). This corresponds to the case of a lossy nonlinear transmission line, considered in the previous part of the paper.
On the other hand, many properties of the shocks in fluids were studied beginning from the XIX century without taking the dissipation explicitly into account, but just postulating the existence of discontinuous solutions and the jump conditions [26]. Similarly to that, the initial phase of the formation of a shock wave can be considered, ignoring the dissipation. The present section is dedicated to a lossless transmission line, constructed from the identical nonlinear inductors and the identical nonlinear capacitors as shown on Figure 2.
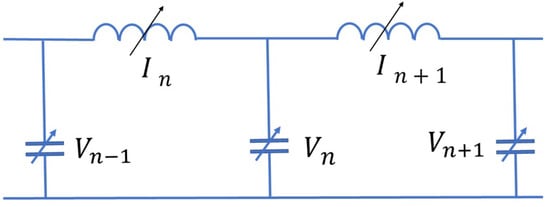
Figure 2.
Lossless nonlinear transmission line.
We take the capacitors voltages and the currents through the inductors as the dynamical variables. The circuit equations (Kirchhoff laws) are
Further on we will consider and as known functions.
In the continuum approximation we treat n as the continuous variable x (we measure distance in the units of the transmission line period) and approximate the finite differences in the r.h.s. of the equations by the first derivatives with respect to x, after which the equations take the form
The simple wave approximation allows to decouple the wave equations into two separate equations for the right- and left-going waves [17,18,19]. In our previous publications, we introduced such an approximation for Equation (69a,b) for the case of half-nonlinear transmission line (more specifically for the case of JTL [20]). In the present section, we formulate the simple wave approximation for the general lossless nonlinear transmission line including both the nonlinear inductors and the nonlinear capacitors.
The simple wave approximation, well known in the theory of nonlinear waves, refers to a wave where the relationship between the wave’s properties (like displacement, pressure, or density) and its spatial and temporal coordinates can be described by a single, independent function. In essence, it is a wave where the relationship between its amplitude and other characteristics is straightforward, and not influenced by other waves or complex interactions. More specifically, it allows to decouple the waves moving in opposite directions (in a 1D case).
To formulate such approximation in our case, let us start from the small amplitude waves on a homogeneous background .
For such waves Equation (69a,b) is simplified to
(for brevity we have discarded lower index 0 in Equation (71a,b)).
The solutions of Equation (71a,b) are right- and left-propagating travelling waves, each depending upon the single variable , propagating with the speed
The voltage and current in the “sound” wave are connected by the equation
where
The simple wave approximation, that is decoupling of (69a,b) into two separate equations for the right- and left-going waves, is achieved by considering V as a function of I (or vice-verse). We emphasize that our approximation (see below) is based on a previously known approach, but the application of the approximation to the fully nonlinear transmission line was (to the best of our knowledge) was never achieved before.
Then from Equation (69a,b) we obtain
or equivalently
Substituting into (69a,b) we obtain a system of two coupled equations for each of the simple waves:
Further on for the sake of definiteness we will talk only about the right-going wave which corresponds to taking the sign minus in the r.h.s. of both equations in (77a,b).
The system (77a,b) simplifies in half-nonlinear cases, that is when either the capacitor or the inductor is linear. In the first case ( const)
and (77a) becomes closed equation for the current
Instead of (77b) we can use equation
In terms of this case, we consider first and foremost the Josephson transmission line. Both Josephson laws can be presented as follows:
thus, we obtain
However, the fully nonlinear case can also be treated easily. If we consider the initial value problem
the solution of Equation (77a,b) can be obtained by inspection [27]
where
The simple wave approximation (77a,b) can be applied also to Equation (4a,b). In fact, the dissipative terms in the equation determine the profile of the shock. On the other hand, if we want to study the formation of the shocks, then assuming these terms to be in some sense small, we can ignore the influence of the dissipation on the process of the formation (until we do not approach to close to the singularity of the dissipationless equation). Thus ignoring the dissipation in (4a,b) we may rewrite the equation in the following form:
which coincides with Equation (69a,b) if we put
After that we can apply the procedure presented above in this section.
Now let us forget about the dissipation and consider the strictly disssipationless case. If we want to study the profile of the travelling waved in such case, additional complication (with respect to the lossy case) arises. In the latter case we started from considering the discrete transmission line, but the presence of the dissipation introduced the space scale into the system, and this scale was implicitly assumed to be much larger than the period of the line. This allowed us to use the continuum approximation, actually ignoring the discrete nature of the system. For the lossless case the scale of the localized travelling wave is determined by the period of the transmission line [20]. This makes the continuum approximation inadequate and we introduced the quasi-continuum approximation [20], which corresponds to approximating the finite differences in the r.h.s. of the Equation (68a,b) by the two first terms in the Taylor expansion [20]. Thus, instead of Equation (69a,b) we obtain
We studied in detail the travelling waves described by these equations for the case of half-nonlinear transmission line (more specifically for the case of JTL [20]). In distinction to the lossy case, where the travelling waves turn out to be the shocks, in the lossless case the travelling waves turn out to be the kinks and the solitons.
We also studied (with much less detail) the formation of the solitons and the kinks via introducing the simple wave approximation for the JTL. Now we want to formulate the simple wave approximation for the general lossless nonlinear transmission line including both the nonlinear inductors and the nonlinear capacitors on top of the quasi-linear approximation.
One must understand that Equation (69a,b) (and hence Equation (77a,b) can describe the formation of the kinks and the solitons (until we do not approach too close to the singularities of the equations). Our present aim is to formulate the approximation which will describe both the formation of the kinks and the solitons and their profiles.
Starting from Equation (88a,b) and repeating the process which led from (69a,b) to (77a,b) we obtain instead of the latter
Let us apply thus improved simple wave approximation to the JTL. In this case, instead of Equation (79) we obtain
If we make an additional assumption , Equation (90) can be written as follows [20]:
where we have ignored the term proportional to . Looking at Equation (91), we recognize the modified Korteweg-de Vries (mKdV) equation [28].
On the other hand, considering small variations in the current on the constant background presented by Equation (70b), from (91) we obtain [20]
where we have ignored the term proportional to . Looking at Equation (92), we recognize the Korteweg-de Vries (KdV) equation [28].
In conclusion, we state that we obtained the exact analytical expressions for the profile of the shock waves (both the current and the voltage) in half-nonlinear transmission lines for the appropriate values of the parameters. We also formulated the simple wave approximation for the lossless discrete nonlinear transmission line.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons Inc.: New York, NY, USA, 1999. [Google Scholar]
- Kengne, E.; Liu, W.M.; English, L.Q.; Malomed, B.A. Ginzburg–Landau models of nonlinear electric transmission networks. Phys. Rep. 2022, 982, 1–124. [Google Scholar] [CrossRef]
- Congy, T.; El, G.A.; Hoefer, M.A. Interaction of linear modulated waves and unsteady dispersive hydrodynamic states with application to shallow water waves. J. Fluid Mech. 2019, 875, 1145–1174. [Google Scholar] [CrossRef]
- French, D.M.; Hoff, B.W. Spatially dispersive ferrite nonlinear transmission line with axial bias. IEEE Trans. Plasma Sci. 2014, 42, 3387–3390. [Google Scholar] [CrossRef]
- Nouri, B.; Nakhla, M.S.; Achar, R. Efficient simulation of nonlinear transmission lines via model-order reduction. IEEE Trans. Microw. Theory Tech. 2017, 65, 673–683. [Google Scholar] [CrossRef]
- Neto, L.P.S.; Rossi, J.O.; Barroso, J.J.; Schamiloglu, E. Hybrid nonlinear transmission lines used for RF soliton generation. IEEE Trans. Plasma Sci. 2018, 46, 3648–3652. [Google Scholar] [CrossRef]
- Nikoo, M.S.; Hashemi, S.M.-A.; Farzaneh, F. Theoretical analysis of RF pulse termination in nonlinear transmission lines. IEEE Trans. Microw. Theory Tech. 2018, 66, 4757–4764. [Google Scholar]
- Silva, L.C.; Rossi, J.O.; Rangel, E.G.L.; Raimundi, L.R.; Schamiloglu, E. Study of pulsed RF signal extraction and irradiation from a capacitive nonlinear transmission line. Int. J. Adv. Eng. Res. Sci. 2018, 5, 121. [Google Scholar] [CrossRef]
- Wang, Y.; Lang, L.-J.; Lee, C.H.; Zhang, B.; Chong, Y.D. Topologically enhanced harmonic generation in a nonlinear transmission line metamaterial. Nat. Comm. 2019, 10, 1102. [Google Scholar] [CrossRef] [PubMed]
- Range, E.G.L.; Rossi, J.O.; Barroso, J.J.; Yamasaki, F.S.; Schamiloglu, E. Practical constraints on nonlinear transmission lines for RF generation. IEEE Trans. Plasma Sci. 2019, 47, 1000–1016. [Google Scholar]
- Kyuregyan, A.S. Large-amplitude shock electromagnetic wave in a nonlinear transmission line based on a distributed semiconductor diode. Semiconductors 2019, 53, 511–518. [Google Scholar] [CrossRef]
- Akem, N.A.; Dikande, A.M.; Essimbi, B.Z. Leapfrogging of electrical solitons in coupled nonlinear transmission lines: Effect of an imperfect varactor. SN Appl. Sci. 2020, 2, 21. [Google Scholar] [CrossRef]
- Fairbanks, A.J.; Darr, A.M.; Garner, A.L. A review of nonlinear transmission line system design. IEEE Access 2020, 8, 148606–148621. [Google Scholar] [CrossRef]
- Landauer, R. Shock waves in nonlinear transmission lines and their effect on parametric amplification. IBM J. Res. Dev. 1960, 4, 391–401. [Google Scholar] [CrossRef]
- Peng, S.T.; Landauer, R. Effects of dispersion on steady state electromagnetic shock profiles. IBM J. Res. Dev. 1973, 17, 299–306. [Google Scholar] [CrossRef]
- Kogan, E. Shock waves in nonlinear transmission lines. Phys. Stat. Sol. (b) 2025, 262, 2400335. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Volume 6; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Rabinovich, M.I.; Trubetskov, D.I. Oscillations and Waves; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1989. [Google Scholar]
- Vinogradova, M.B.; Rudenko, O.V.; Sukhorukov, A.P. The Wave Theory; Nauka Publishers: Moscow, Russia, 1990. [Google Scholar]
- Kogan, E. The Kinks, the Solitons and the Shocks in Series-Connected Discrete Josephson Transmission Lines. Phys. Stat. Sol. (b) 2022, 259, 2200160. [Google Scholar] [CrossRef]
- Kogan, E. Shock wave in series connected Josephson transmission line: Theoretical foundations and effects of resistive elements. J. Appl. Phys. 2021, 130, 013903. [Google Scholar] [CrossRef]
- Kamchatnov, A.M. Theory of Nonlinear Waaves [in Russian]; Printing House of School of Economics: Moscow, Russia, 2024. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards: Washington, DC, USA, 1964.
- Goursat, E. Course d’Analyse Mathematique, Tome I; Gautier-Villars: Paris, France, 1933. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Elsevier Inc.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Krehl, O.K. History of Shock Waves, Explosions and Impact: A chronological and Biographical Reference; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Logan, J.D. An Introduction to Nonlinear Partial Differential Equations, 2nd ed.; John Wiley & Sons, Inc. Publication: Hoboken, NJ, USA, 2008. [Google Scholar]
- Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press: Cambridge, UK, 1989; Volume 2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).