Analysis of a Three-Echelon Supply Chain System with Multiple Retailers, Stochastic Demand and Transportation Times
Abstract
1. Introduction
2. Literature Review
| Paper/Review Policy | Demand | Transportation Time | Shortages at the Retailer | Method |
|---|---|---|---|---|
| [4]/Mixed continuous–periodic review policy | Poisson | Deterministic | Backorders | Approximation method |
| [5]/Single cycle | Constant | Instantaneous | No shortages | Closed form |
| [6]/Stationary nested policies | Deterministic | Negligible | No shortages | Heuristic |
| [7]/Stationary nested policies | Constant | Instantaneous | No shortages | Search algorithm based on the characteristics of the optimal cost curve |
| [8]/Periodic | Random | Constant | Backorders | Closed form |
| [9]/Single cycle | Deterministic | Negligible | No shortages | Order interval division and recursive tightening |
| [10]/Integer-ratio policies | Deterministic | Negligible | No shortages | Iterative procedure based on the balance between the replenishment and the inventory holding costs |
| [11]/Periodic–finite planning horizon | Stochastic (Poisson/normal) | Zero | Lost sales | Approximate dynamic programming/stochastic dynamic programming |
| [12]/Periodic | Correlated/bivariate Poisson | Constant (1 period) | Lost sales | Restricted observation Markov decision process |
| [13]/Periodic | Correlated with inventory and price | Constant | No shortages | Genetic algorithm/fuzzy simulation |
| [14]/Periodic base stock | Deterministic | Constant | Lost sales | Mathematical programming/genetic algorithms |
| [15]/Continuous review (R,Q) policies | Poisson | Constant | Backorders | Approximate optimal solutions |
| [16]/Finite horizon policy | Deterministic dynamic | Negligible | No shortages | Integer programming |
| [17]/Periodic (s,nq) for warehouse/discrete base stock policy for retailers | Stationary i.i.d. random | Deterministic | Backorders | Decomposition |
| [18]/Periodic, integer ratio, echelon stock, order up to policies | Poisson | Constant | Backorders | Exact solution based on the regenerative cycle |
| [19]/Periodic finite horizon policy | Deterministic dynamic | Deterministic | Backorders/lost sales | Decomposition |
| [20]/Cross-docking warehouse/(1,T) policy for retailers | Poisson | Constant | Lost sales | Heuristic |
| [21]/Periodic review base stock, finite horizon | Deterministic dynamic | Constant | Backorders | Mixed-integer linear programming |
| [22]/Continuous review (S−1,S) for the retailers, no replenishment policy for the warehouse | Stochastic | Stochastic | Backorders | Simulation |
| [23]/Continuous review | Deterministic | Normal | Backorders | Numerical iterative algorithm |
| [24]/VMI policy | Deterministic | Deterministic | No shortages | Integer non-linear programming/imperialist competitive algorithm |
| [25]/Periodic review base stock | Deterministic | Constant | Backorders | Mixed-integer linear programming/heuristic |
| [26]/Shipments at regular intervals | Deterministic | Deterministic | No shortages | Iterative procedure based on the concavity property of total profit |
| [27]/Periodic, finite horizon, option for delayed distribution | Stochastic | Negligible | Lost sales | Recursive solution algorithm based on multi-stage stochastic programming |
| [28]/Continuous review | Compound Poisson | Constant | Backorders | Exact analysis of the system based on the probability mass function (pmf) of each retailer’s inventory level |
| [29]/Periodic with an integer-ratio ordering schedule | Poisson | Constant | Backorders | Exact solution based on regenerative cycles |
| [30]/Periodic | Poisson/Gaussian | Constant | Lost sales/partial or complete backordering | Deep reinforcement learning |
| [31]/Periodic | Seasonal/stochastic | No lead time | Backorders | Deep reinforcement learning and multi-stage stochastic programming |
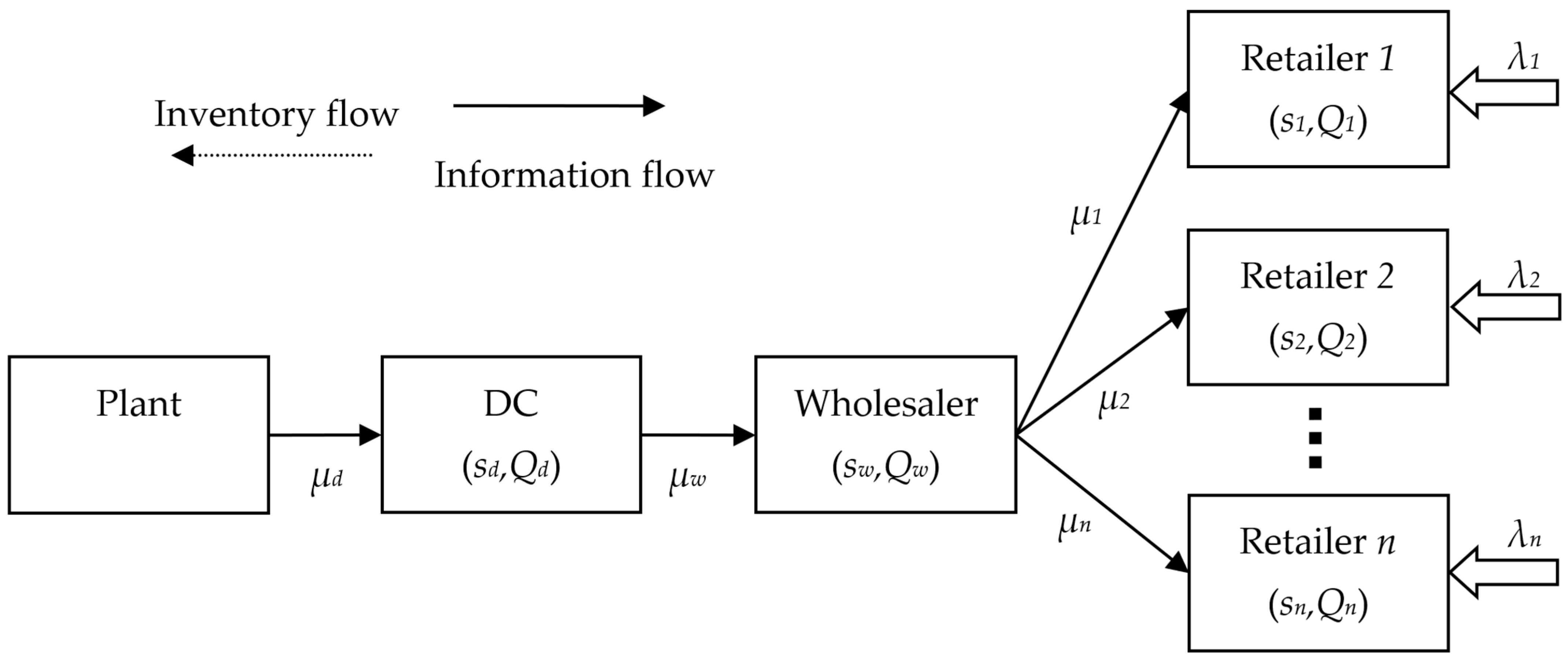
3. System Description
- For our analysis we denote as the decision variables the number of retailers and the parameters of the inventory control policies at each node:
- n: the number of retailers
- sd: the reorder point at the distribution center
- Qd: the replenishment order quantity at the distribution center
- sw: the reorder point at the wholesaler
- Qw: the replenishment order quantity at the wholesaler
- si: the reorder point at retailer i
- Qi: the replenishment order quantity at retailer i
- The other parameters that are necessary to completely define the system are as follows:
- μd: the transportation rate for orders from the plant to the distribution center
- μw: the transportation rate for orders from the distribution center to the wholesaler
- μi: the transportation rate for orders from the wholesaler to retailer i
- λi: the arrival rate of external customers at retailer i
4. Modeling Approach
4.1. States Definition
- : the inventory on hand at the distribution center at time t with 0 ≤ ≤ sd + Qd
- : the inventory in transit to the wholesaler at time t with 0 ≤ ≤ Qw
- : the inventory on hand at the wholesaler at time t with 0 ≤ ≤ sw + Qw
- : the inventory in transit to retailer i at time t with 0 ≤ ≤ Qi
- : the inventory on hand at retailer i at time t with 0 ≤ ≤ si + Qi
- The arrival of an outstanding order from the Plant to the Distribution Centre
- The arrival of an outstanding order from the DC to the wholesaler
- The arrival of an outstanding order at retailer i
- The occurrence of external demand at retailer i
- -
- To state (0,0,0,0,1,2,2) with transition rate μ1—Arrival of a replenishment order at retailer 1 and triggering of a new replenishment order from the wholesaler to retailer 1;
- -
- To state (0,0,1,1,0,1,1) with transition rate λ2—Occurrence of external demand at retailer 2 and triggering of a replenishment order from the wholesaler to retailer 2.
- -
- To state (0,0,2,0,1,1,0) with transition rate λ1—occurrence of external demand at retailer 1.
- -
- To state (2,0,2,0,1,1,1) with transition rate μd—Arrival of a replenishment order at the DC.
4.2. The Infinitesimal Generator Matrix
- : the greatest common divisor of
- : The greatest common divisor of
- : the integer part of
- Step 1: Calculate infinitesimal generator matrix parameters from system parameters (number of basic levels, number of possible inventory levels at each stage, maximum inventory levels where outstanding orders occur)
- Step 2: Create diagonal blocks
- Step 2.1: Create diagonal block B1 for lowest priority retailer 1 and
- Step 2.2: Through an iterative process, create diagonal block Bn for highest priority retailer n and based on block Bn−1
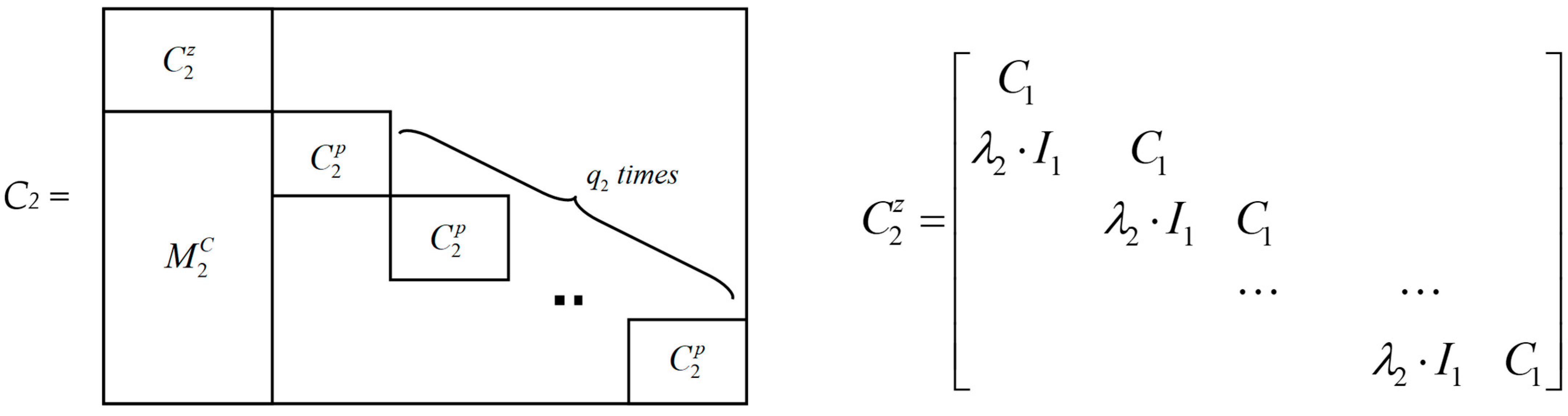
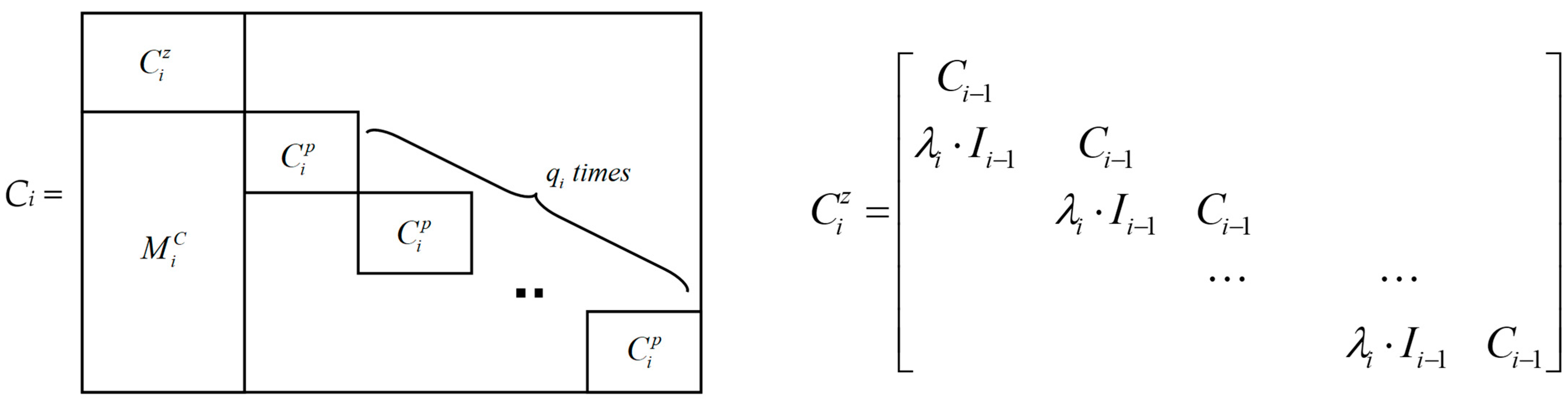
- Step 2.3: Create diagonal block C1 for lowest priority retailer 1 and
- Step 2.4: Through an iterative process, create diagonal block Cn for highest priority retailer n and based on block Cn−1
- Step 2.5: Create the diagonal tier of the infinitesimal generator matrix using blocks Bn and Cn
- Step 3: Insert upper diagonal blocks
- Step 3.1: Insert blocks for the cases when
- Step 3.2: Insert blocks for the cases when (DC stockout)
- Step 4: Insert below the diagonal blocks
- Step 4.1: Add blocks corresponding to the arrival of a replenishment order at the wholesaler
- Step 4.2: Add blocks corresponding to triggering of a replenishment order to a retailer
- Step 5: Calculate numerically the vector of stationary probabilities (steady state solution)using the following algorithm (see Calculation of the steady-state probabilities below)
- Step 6: Calculate performance measures algorithmically from the vector of stationary probabilities
- Calculation of the steady-state probabilities
- Step 1: Calculate matrix A − I (I is the identity matrix)
- Step 2: Calculate (Transposition of A − I)
- Step 3: Take and replace the last row with a new row where all the elements of this new row are equal to 1. Call this new matrix P
- Step 4: Solve the system
4.3. Performance Measures
- Average inventory at the Distribution Centre—WIPd
- Utilization of resource for transportation towards the wholesaler—uw
- Average inventory at the wholesaler—WIPw
- Bn blocks
- Cn blocks
- Average inventory at the retailers—WIPr
- B-type blocks ()
- Retailer 1
- Retailer r, 2 ≤ r ≤ n
- C-type blocks ()
- Retailer 1
- Retailer r, 2 ≤ r ≤ n
- Stock-out probability for Retailer r—SOr
- B-type Blocks ()
- Retailer 1
- Retailer r, 2 ≤ r ≤ n
- C-type blocks ()
- Retailer 1
- Fill Rate of retailer r—FRr
- Throughput of retailer r—Thrr
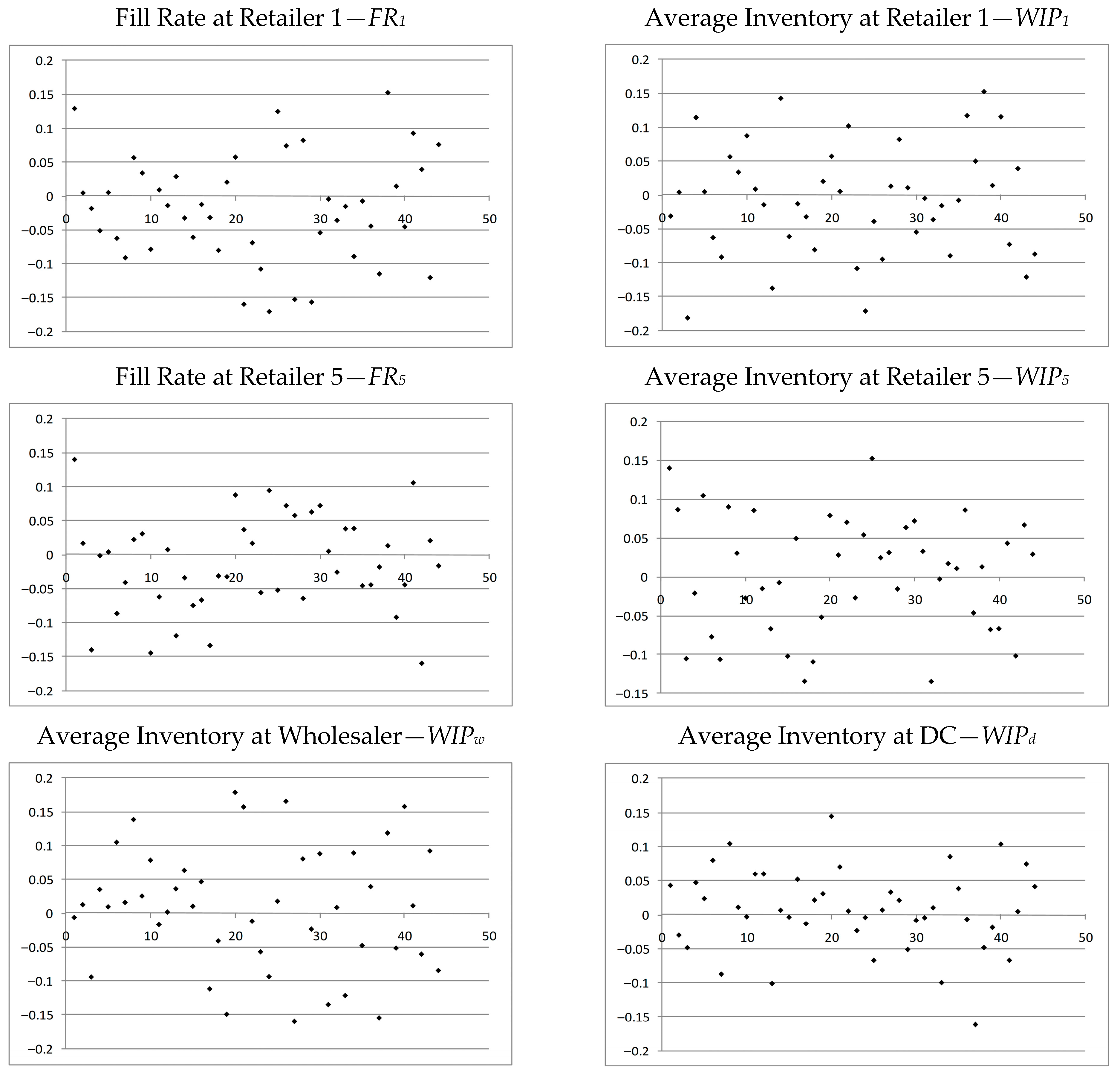
4.4. Validation and Model Performance
- The impact of decision variables (quantity order, reorder point, etc.) on throughput and WIP must be explicitly modeled.
- The system properties, behavior and its sensitivity can be identified because the model is analysed explicitly. This does not hold when approximation methods are used.
- Validation against simulation is required for credibility and decision support.
- System design requires precise performance estimates, validated via both analytical and simulation methods.
- Decision-makers seek to evaluate various maintenance policies under uncertainty.
5. Numerical Results
5.1. The Effect of Policy Parameters—Balanced Systems
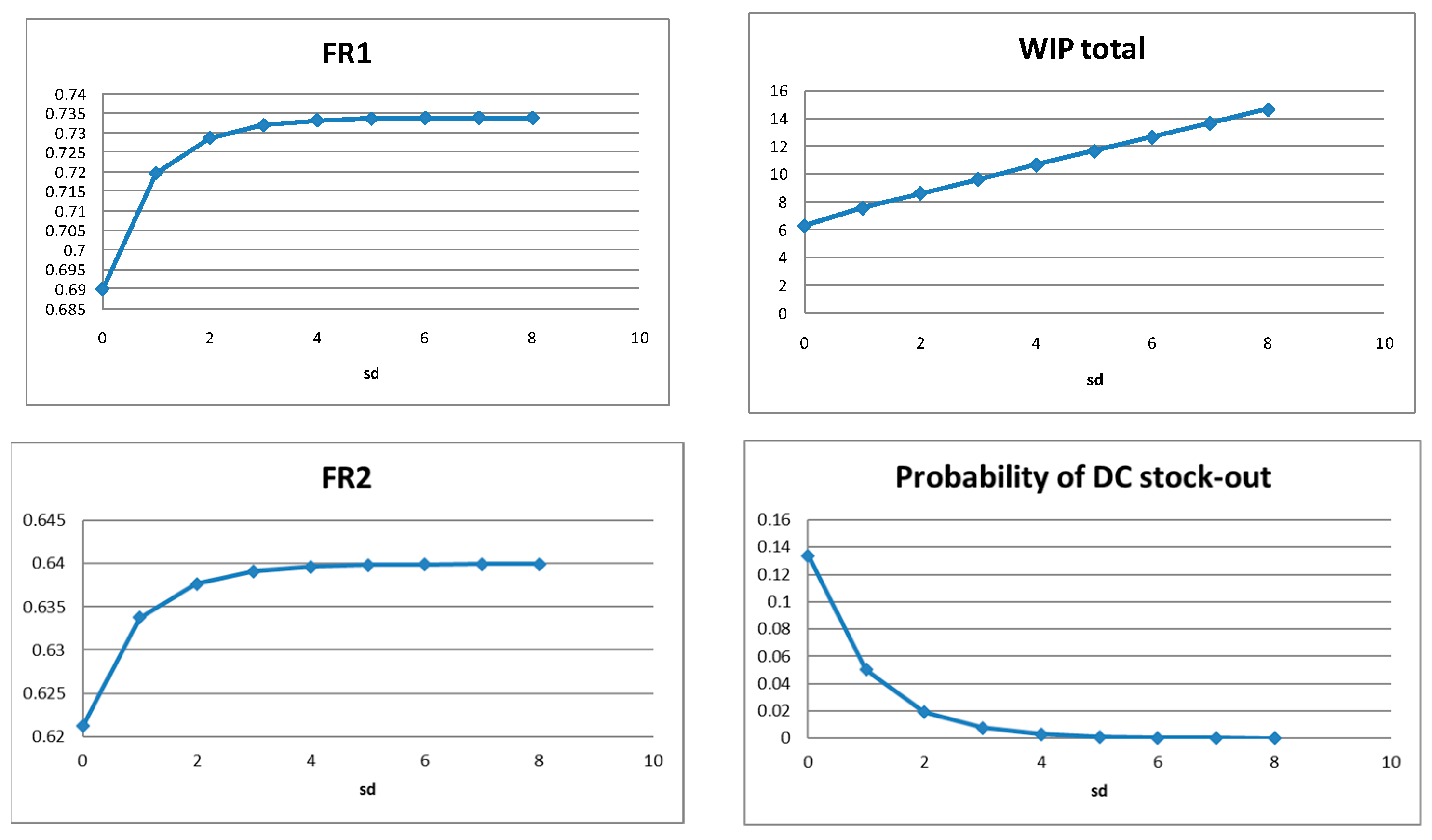
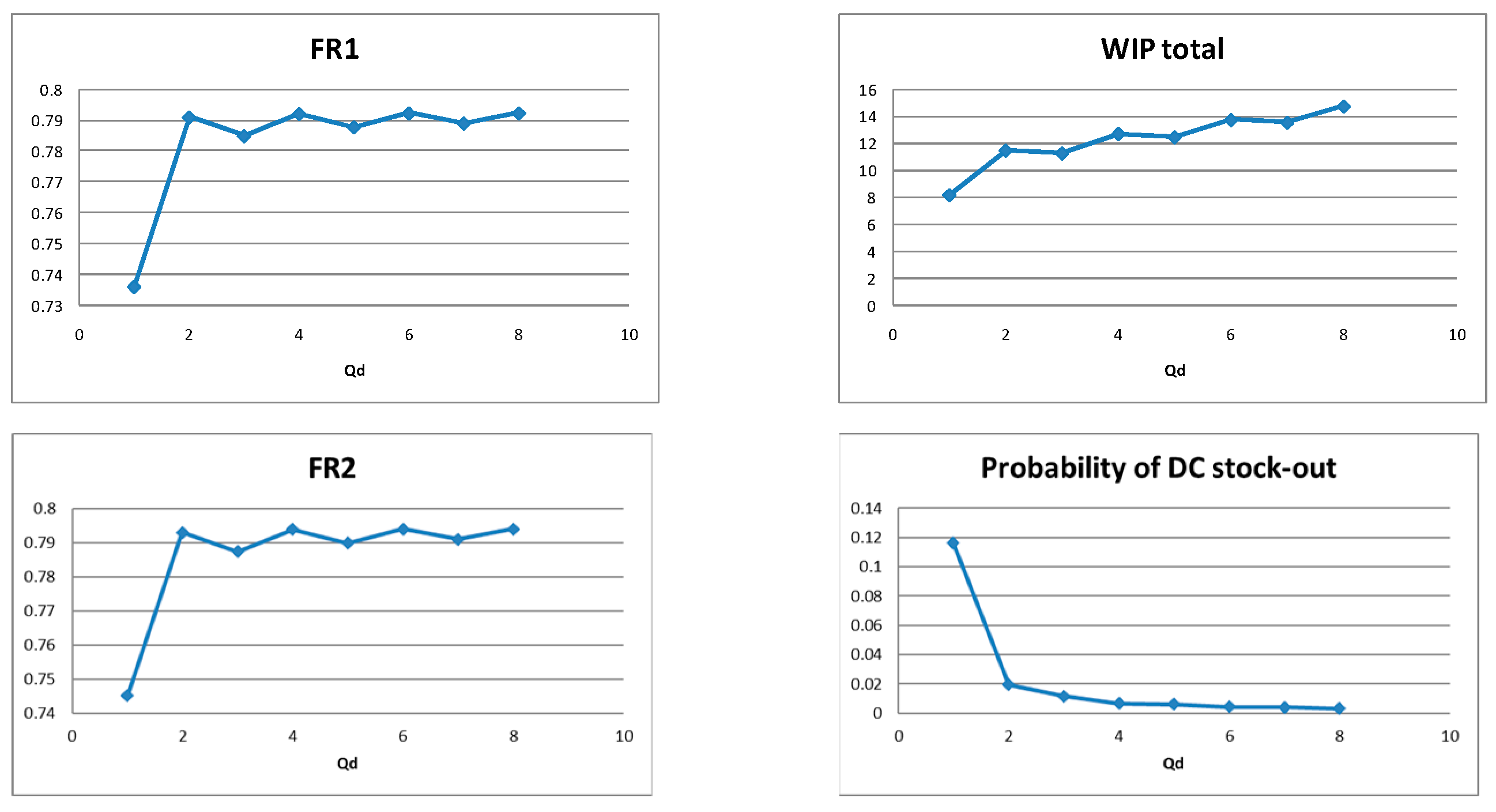
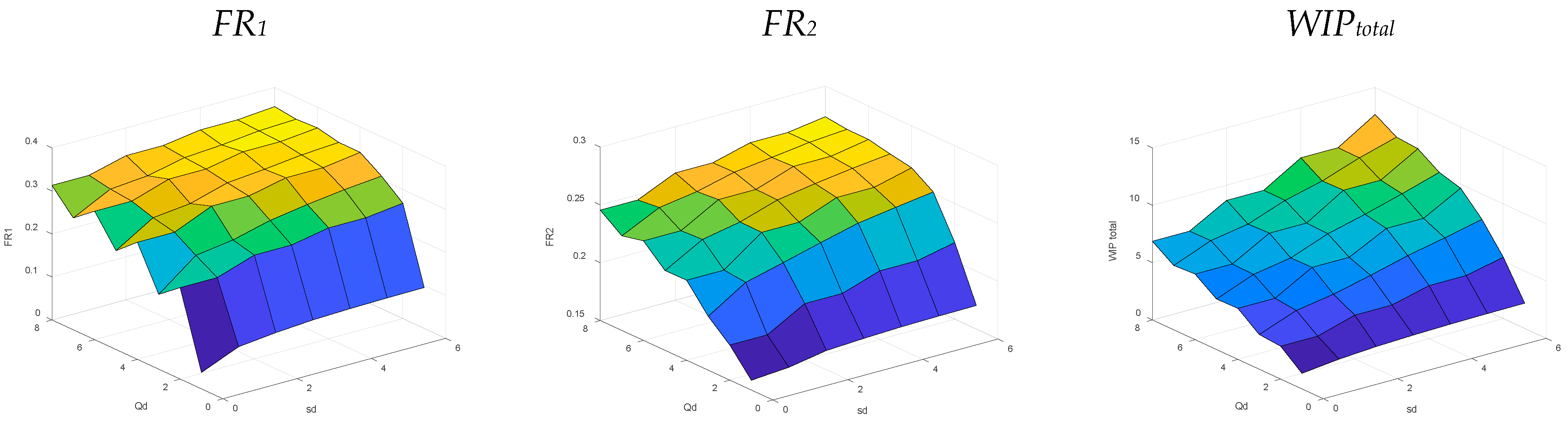
5.1.1. Distribution Center’s Policy (sd, Qd) for Balanced Systems
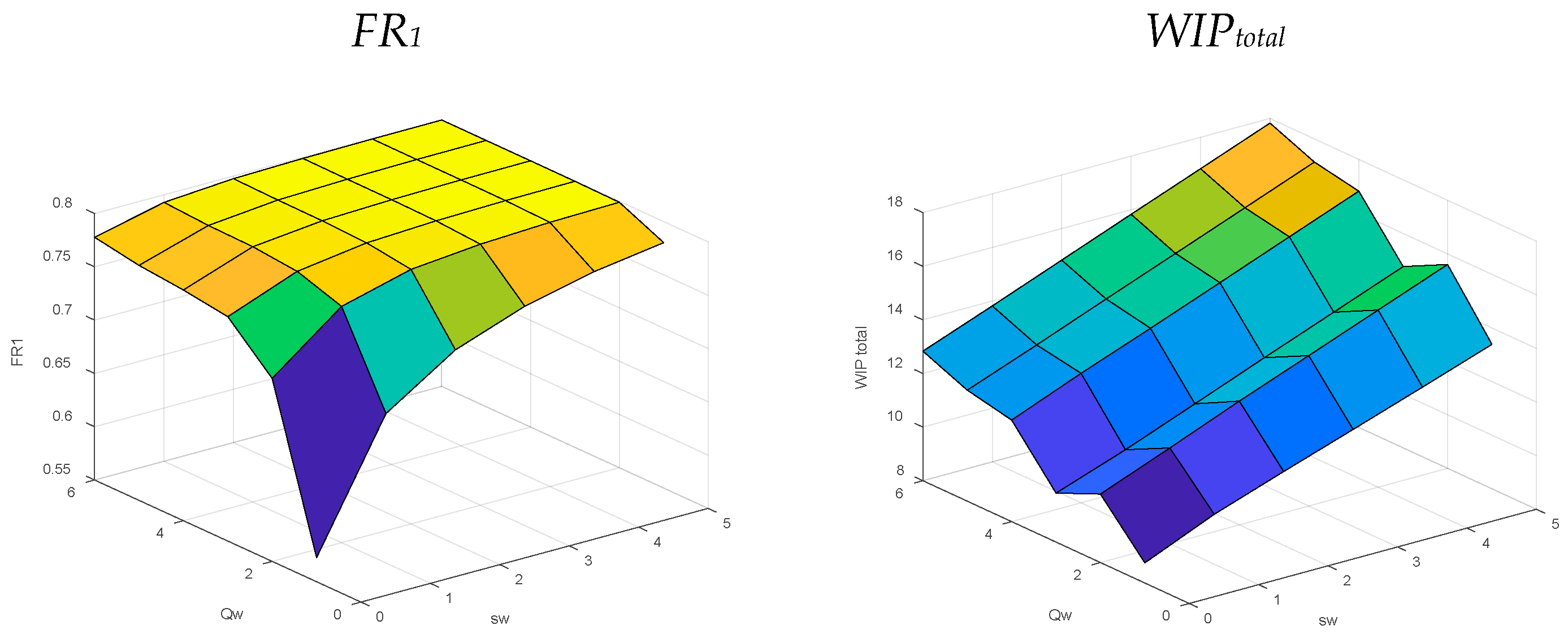
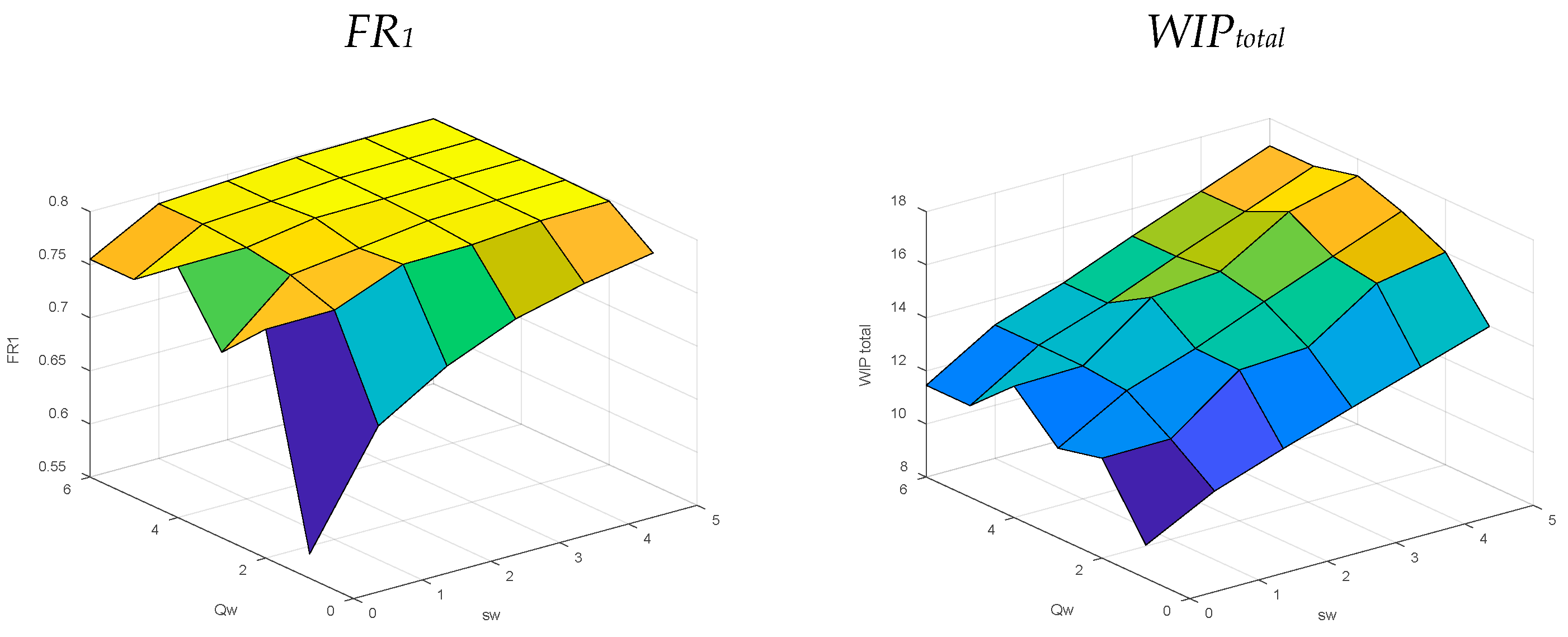
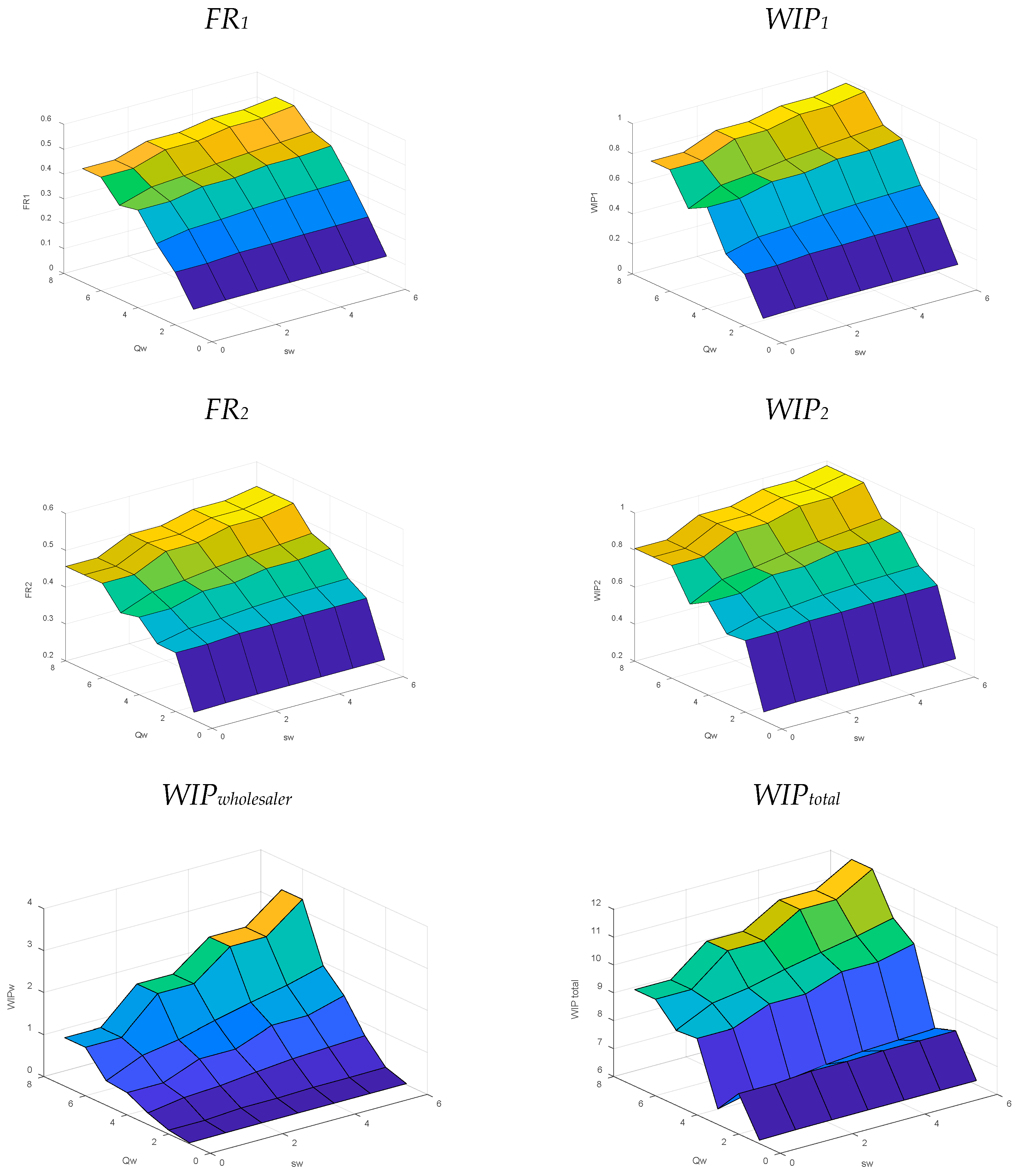
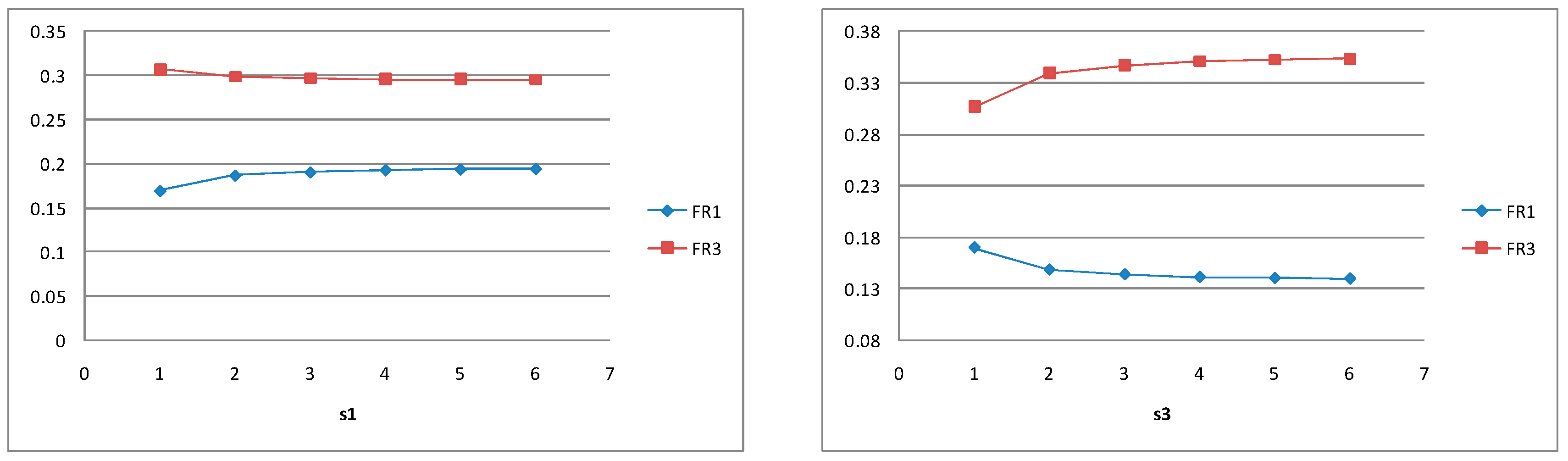
5.1.2. Wholesaler Policy (sw, Qw) for Balanced Systems
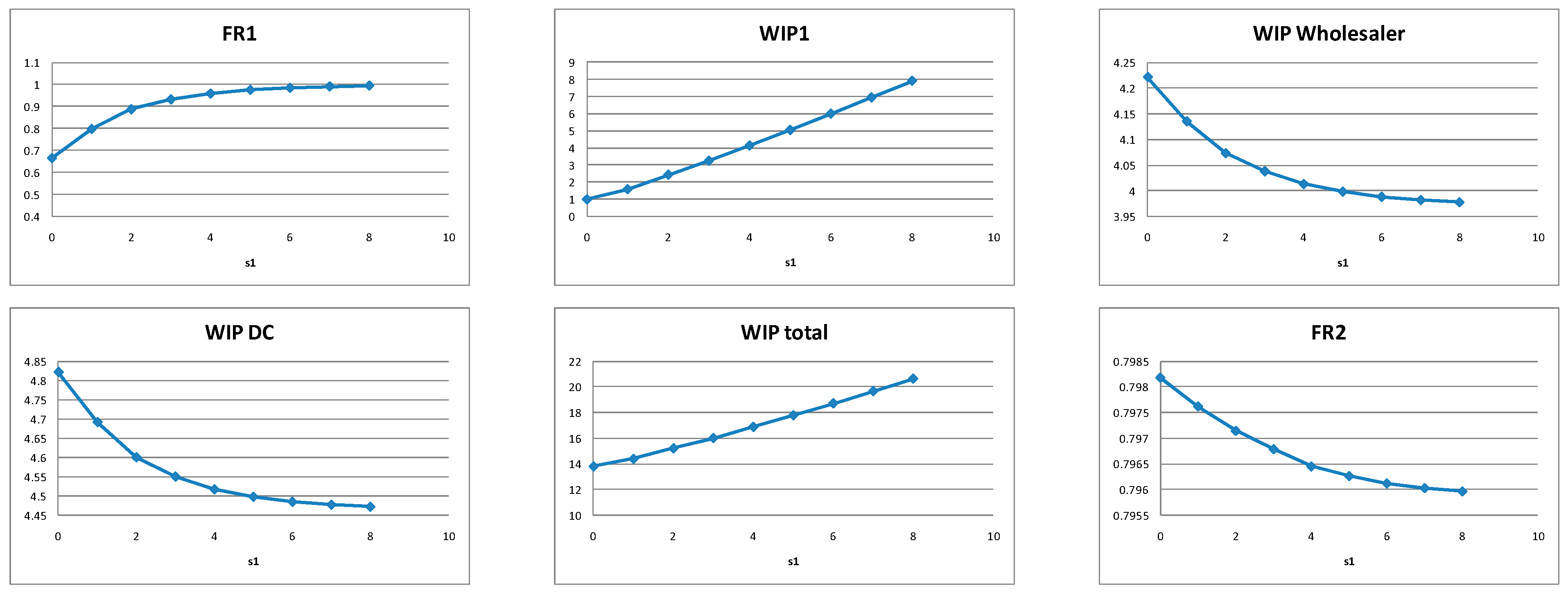
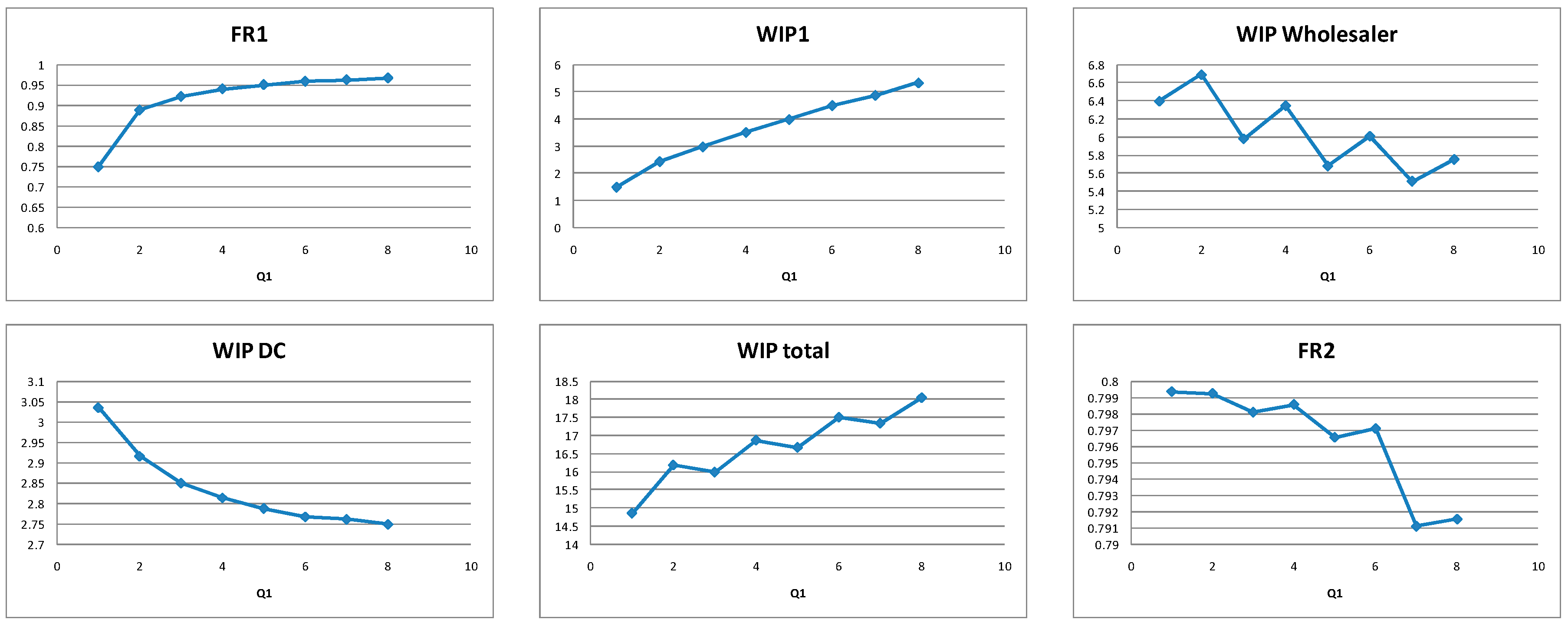
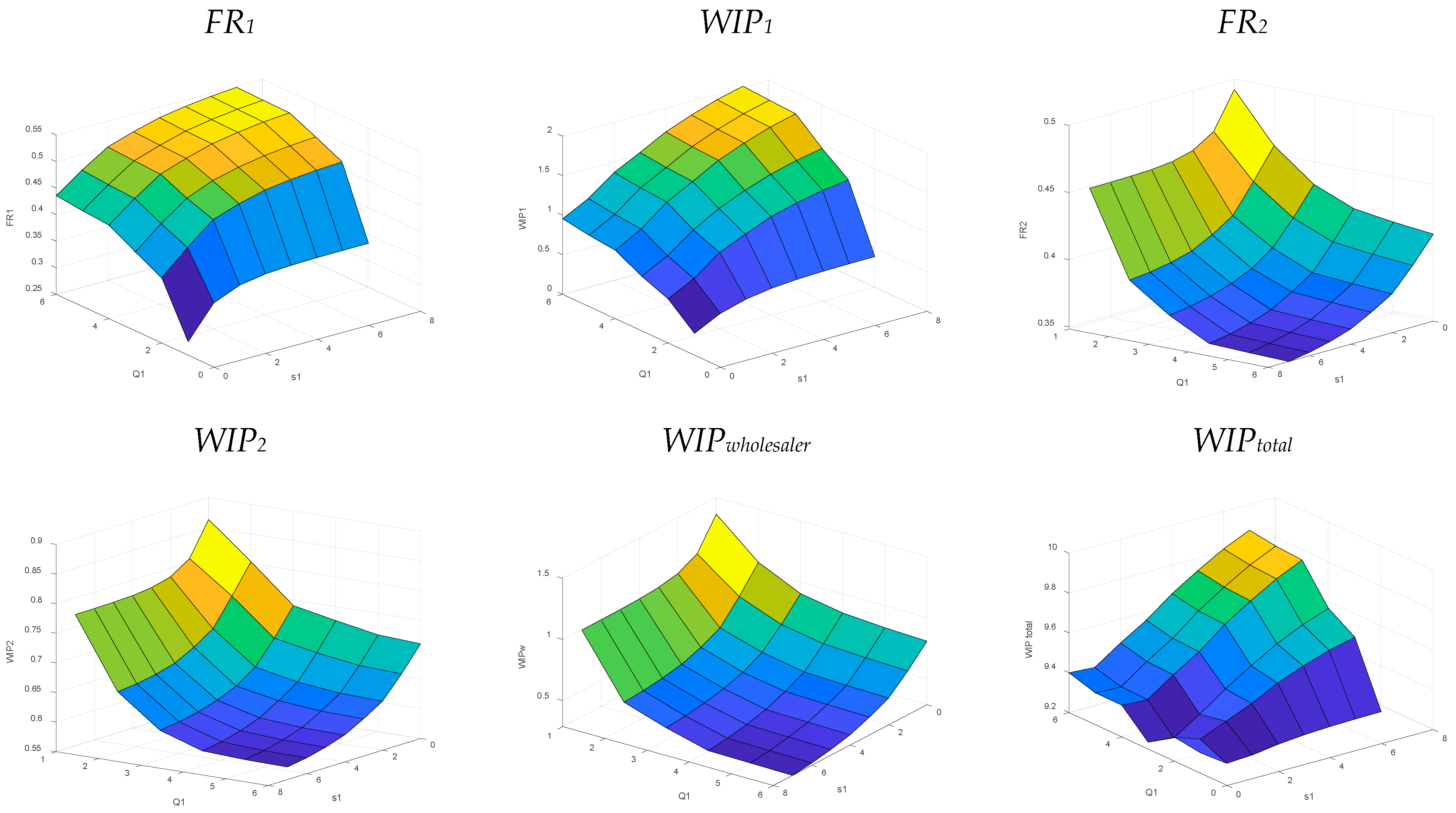
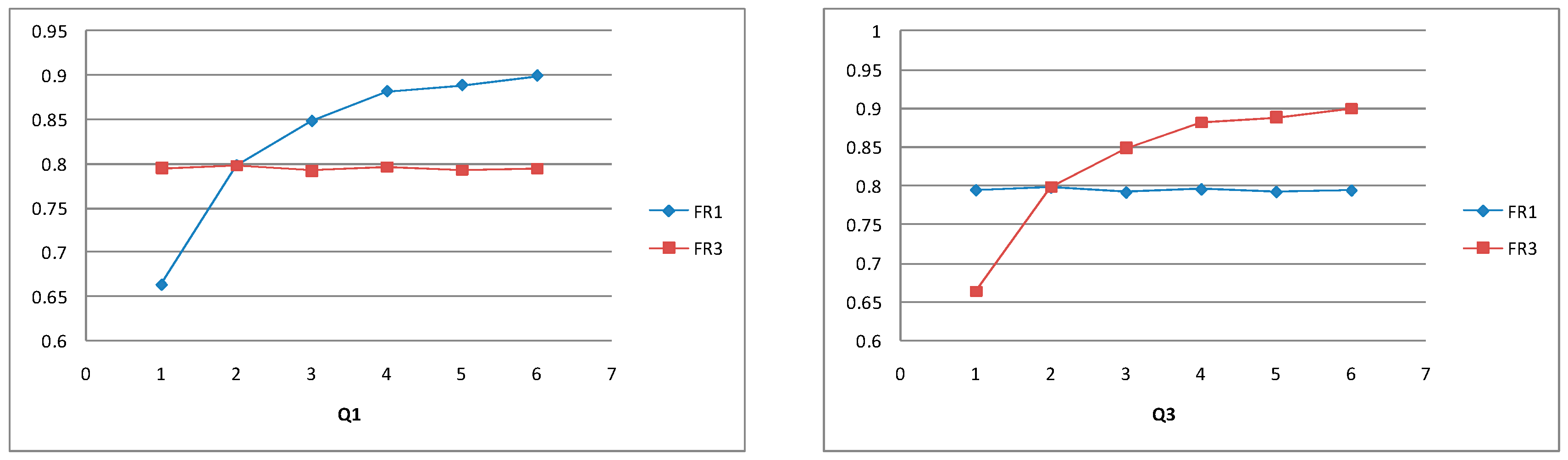
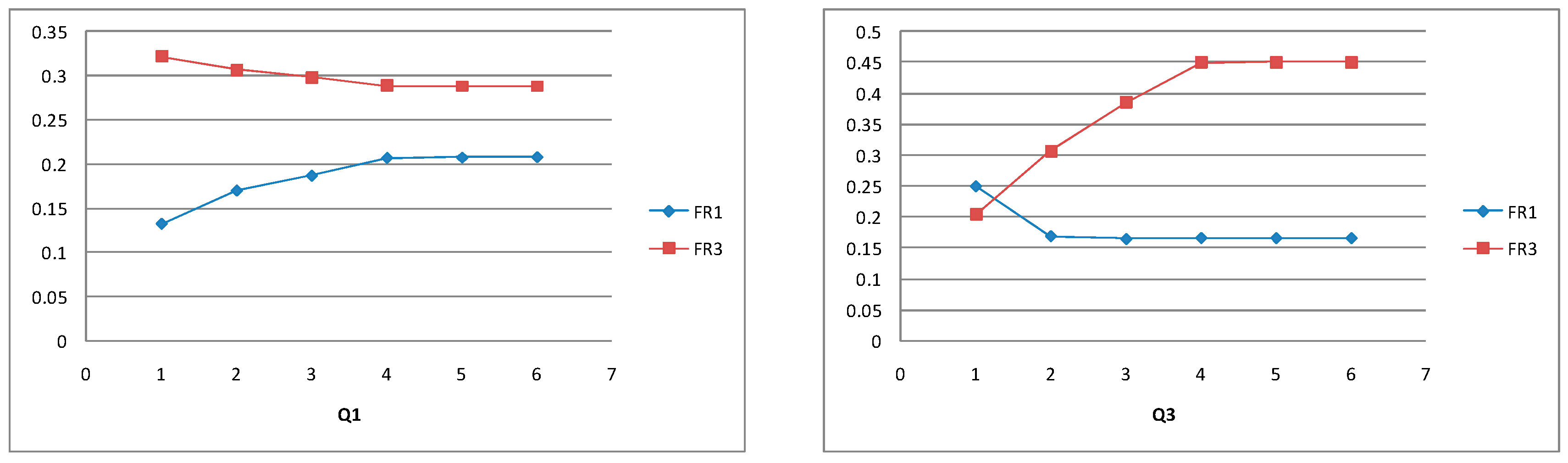
5.1.3. Retailers’ Policy (si, Qi) for Balanced Systems
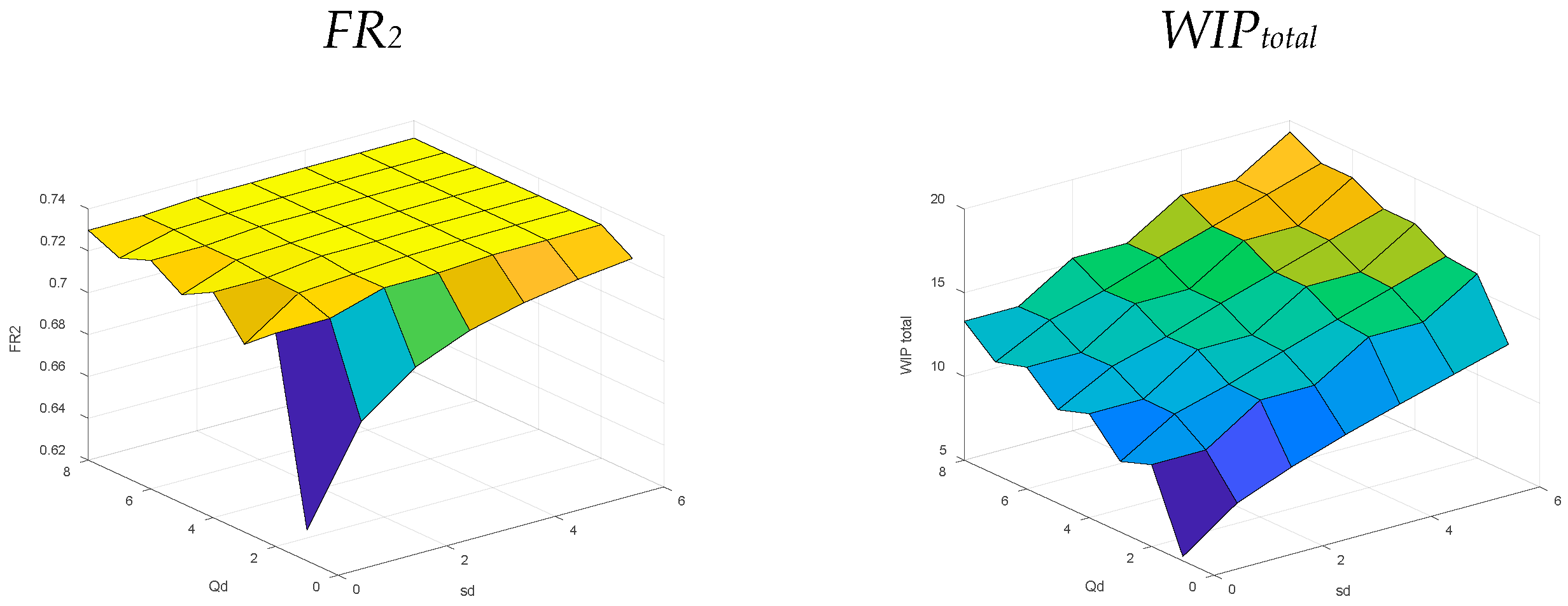
5.2. The Effect of Policy Parameters—Supply-Constrained Systems
5.2.1. Distribution Center’s Policy (sd, Qd) for Supply Constrained Systems
5.2.2. Wholesaler’s Policy (sw, Qw) for Supply Constrained Systems
5.2.3. Retailers’ Policy (si, Qi) for Supply Constrained Systems
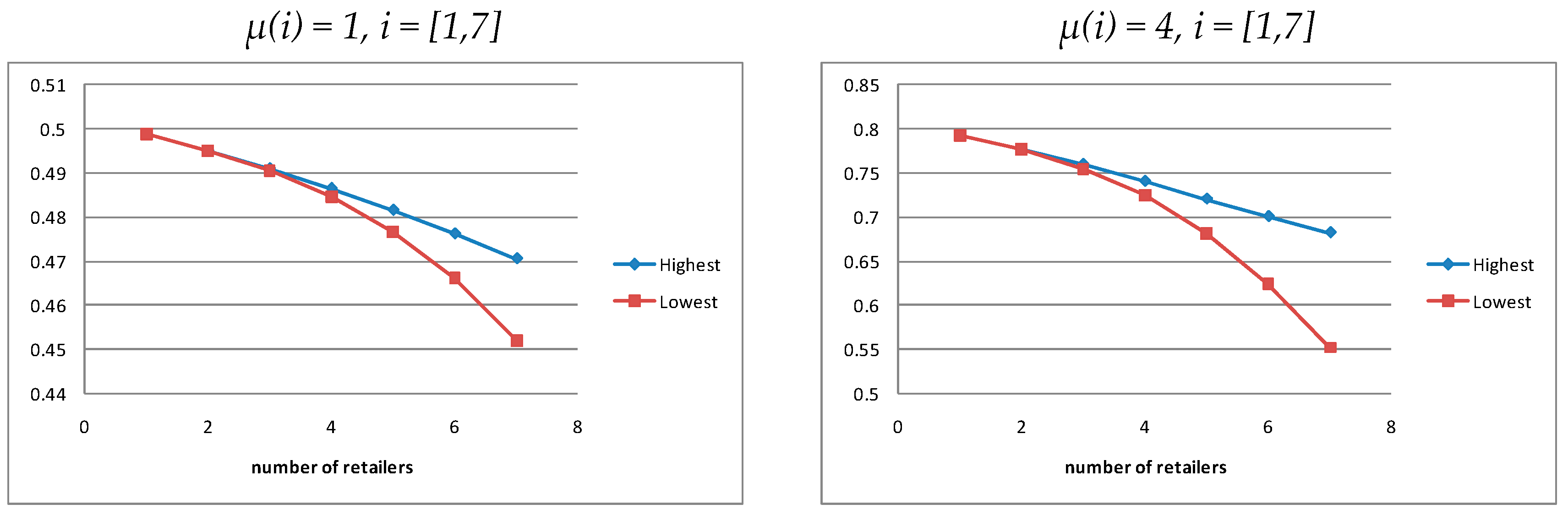
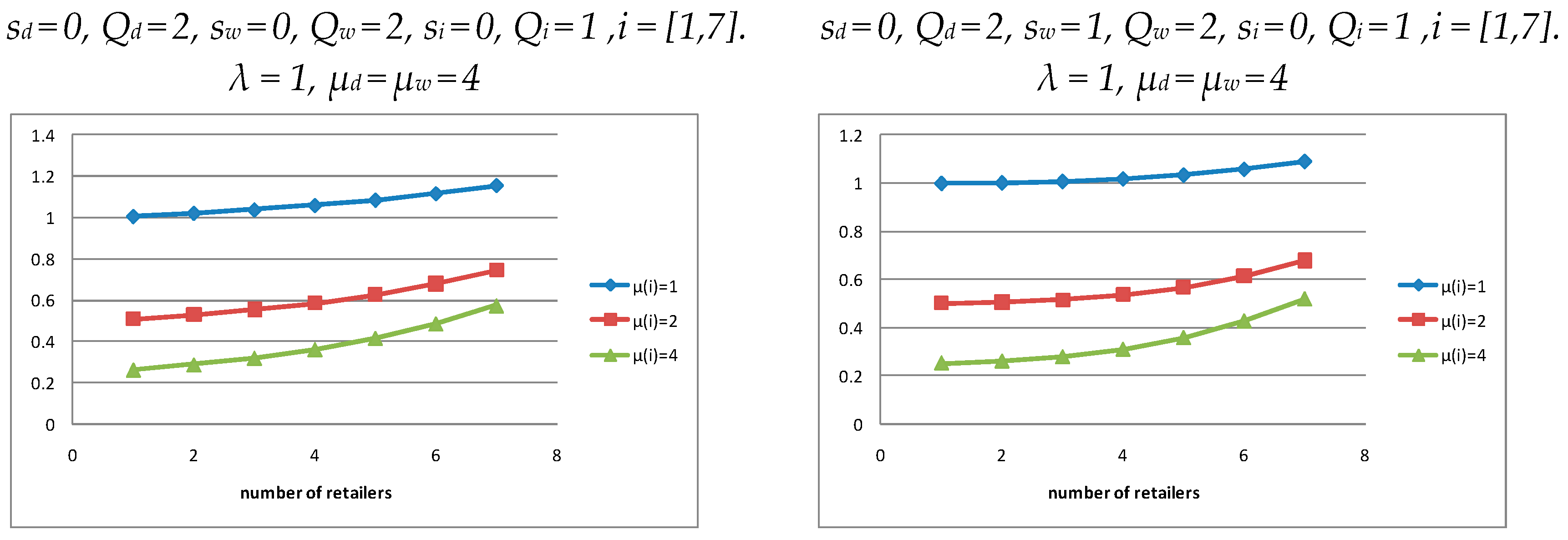
5.3. The Effect of Number of Retailers
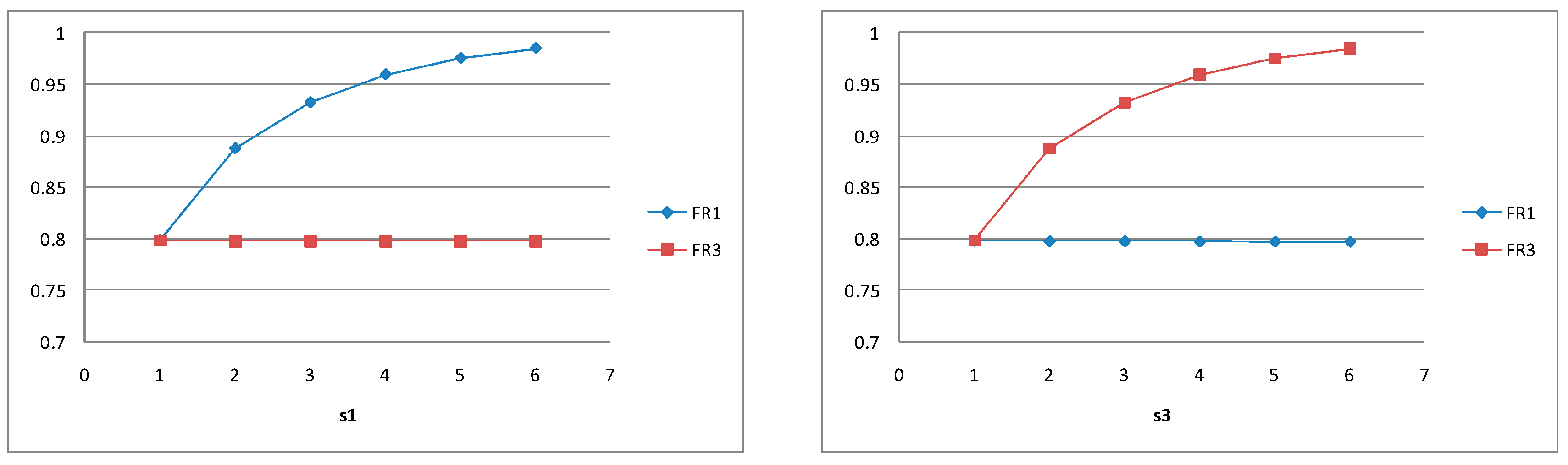
5.3.1. Interactions Between the Retailers
5.3.2. The Effect of Retailer Addition
6. Conclusions
- Our model provides an exact analytical solution for the examined system in contrast with other three-echelon models where approximation methods are used.
- The exact Markov chain solution in this paper can reveal important properties and the general behavior of the system that cannot be identified when approximation techniques are used.
- Beyond its theoretical contribution, the model serves as a benchmarking tool for simulation and heuristic methods, thereby providing both methodological rigor and actionable managerial guidance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Axsäter, S. Inventory Control; International Series in Operations Research & Management Science 225; Springer International Publishing: Cham, Switzerland, 2015; pp. 191–222. [Google Scholar]
- Agrawal, N.; Smith, S.A. Multi-location Inventory Models for Retail Supply Chain Management—A Review of Recent Research. In Retail Supply Chain Management; Agrawal, N., Smith, S.A., Eds.; International Series in Operations Research & Management Science 223; Springer: Berlin/Heidelberg, Germany, 2009; pp. 319–347. Available online: https://link.springer.com/book/10.1007/978-0-387-78902-6 (accessed on 22 September 2025).
- Rofman, E.; González, R.; Sagastizábal, C. Global Optimization of Arborescent Multilevel Inventory Systems. J. Glob. Optim. 1995, 6, 269–292. [Google Scholar] [CrossRef]
- Ahire, S.L.; Schmidt, C.P. A model for a Mixed Continuous-Periodic Review One-Warehouse, N-Retailer inventory system. Eur. J. Oper. Res. 1996, 92, 69–82. [Google Scholar] [CrossRef]
- Yang, P.; Wee, H. An arborescent inventory model in a supply chain system. Prod. Plan. Control 2001, 12, 728–735. [Google Scholar] [CrossRef]
- Abdul-Jalbar, B.; Gutiérrez, J.M.; Sicilia, J. Single cycle policies for the one-warehouse N-retailer inventory/distribution system. Omega 2006, 34, 196–208. [Google Scholar] [CrossRef]
- Yao, M.J.; Wang, Y. A new algorithm for one-warehouse multi-retailer systems under stationary nested policy. Optim. Methods Softw. 2006, 21, 41–56. [Google Scholar]
- Lagodimos, A.; Koukoumialos, S. Service performance of two-echelon supply chains under linear rationing. Int. J. Prod. Econ. 2008, 112, 869–884. [Google Scholar] [CrossRef]
- Hsiao, Y.-C. Optimal single-cycle policies for the one-warehouse multi-retailer inventory/distribution system. Int. J. Prod. Econ. 2008, 114, 219–229. [Google Scholar] [CrossRef]
- Abdul-Jalbar, B.; Segerstedt, A.; Sicilia, J.; Nilsson, A. A new heuristic to solve the one-warehouse N-retailer problem. Comput. Oper. Res. 2010, 37, 265–272. [Google Scholar] [CrossRef]
- Geng, W.; Qiu, M.; Zhao, X. An inventory system with single distributor and multiple retailers: Operating scenarios and performance comparison. Int. J. Prod. Econ. 2010, 128, 434–444. [Google Scholar] [CrossRef]
- Helper, C.M.; Davis, L.B.; Wei, W. Impact of demand correlation and information sharing in a capacity constrained supply chain with multiple-retailers. Comput. Ind. Eng. 2010, 59, 552–560. [Google Scholar] [CrossRef]
- Panda, D.; Maiti, M.K.; Maiti, M. Two warehouse inventory models for single vendor multiple retailers with price and stock dependent demand. Appl. Math. Model. 2010, 34, 3571–3585. [Google Scholar] [CrossRef]
- Paul, B.; Rajendran, C. Rationing mechanisms and inventory control-policy parameters for a divergent supply chain operating with lost sales and costs of review. Comput. Oper. Res. 2011, 38, 1117–1130. [Google Scholar] [CrossRef]
- Guan, R.; Zhao, X. Pricing and inventory management in a system with multiple competing retailers under (r, Q) policies. Comput. Oper. Res. 2011, 38, 1294–1304. [Google Scholar] [CrossRef]
- Solyalı, O.; Süral, H. The one-warehouse multi-retailer problem: Reformulation, classification, and computational results. Ann. Oper. Res. 2012, 196, 517–541. [Google Scholar] [CrossRef]
- Tempelmeier, H. A multi-level inventory system with a make-to-order supplier. Int. J. Prod. Res. 2013, 51, 6880–6890. [Google Scholar] [CrossRef]
- Wang, Q. A periodic-review inventory control policy for a two-level supply chain with multiple retailers and stochastic demand. Eur. J. Oper. Res. 2013, 230, 53–62. [Google Scholar] [CrossRef]
- Gayon, J.-P.; Massonnet, G.; Rapine, C.; Stauffer, G. Constant approximation algorithms for the one warehouse multiple retailers problem with backlog or lost-sales. Eur. J. Oper. Res. 2016, 250, 155–163. [Google Scholar] [CrossRef]
- Tayebi, H.; Haji, R.; Jeddi, B.G. Joint order (1, T) policy for a two-echelon, single-item, multi-retailer inventory system with Poisson demand. Comput. Ind. Eng. 2018, 119, 353–359. [Google Scholar] [CrossRef]
- John, K.; Rajendran, C.; Ziegler, H. A comparative study on allocation/rationing mechanisms operational with/without backorder clearing in divergent supply chains. Sadhana 2019, 44, 231. [Google Scholar] [CrossRef]
- Tsai, S.C.; Ho, I.-Y. Sample average approximation for a two-echelon inventory system with service-level constraints. J. Oper. Res. Soc. 2019, 70, 675–688. [Google Scholar] [CrossRef]
- Hoque, M.A. An optimal solution policy to an integrated manufacturer-retailers problem with normal distribution of lead times of delivering equal and unequal-sized batches. OPSEARCH 2021, 58, 483–512. [Google Scholar] [CrossRef]
- Najafnejhad, E.; Roodsari, M.T.; Sepahrom, S.; Jenabzadeh, M. A mathematical inventory model for a single-vendor multi-retailer supply chain based on the Vendor Management Inventory Policy. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 579–586. [Google Scholar] [CrossRef]
- Kurian, J.; Brijesh, P.; Chandrasekharan, R.; Ziegler, H. Priority fractional rationing (PFR) policy and a hybrid metaheuristic for managing stock in divergent supply chains. Sådhanå 2022, 47, 254. [Google Scholar]
- Lu, C.-J.; Gu, M.; Lee, T.-S.; Yang, C.-T. Integrated multistage supply chain inventory model of multiple retailers with imperfect production and inspection systems. Soft Comput. 2022, 26, 12057–12075. [Google Scholar] [CrossRef]
- Smirnov, D.; Herer, Y.T.; Avrahami, A. The continuous delayed distribution problem. Comput. Oper. Res. 2022, 148, 105976. [Google Scholar] [CrossRef]
- Andersson, J.; Malmberg, F.; Marklund, J. Exact analysis of One-Warehouse-Multiple-Retailer inventory systems with quantity restricted deliveries. Eur. J. Oper. Res. 2023, 309, 1161–1172. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, G. Fixed-interval order-up-to policies and myopic optimal warehouse stock allocation for one-warehouse multiple-retailer systems. Eur. J. Oper. Res. 2023, 309, 1112–1124. [Google Scholar] [CrossRef]
- Kaynov, I.; van Knippenberg, M.; Menkovski, V.; van Breemen, A.; van Jaarsveld, W. Deep Reinforcement Learning for One-Warehouse Multi-Retailer inventory management. Int. J. Prod. Econ. 2024, 267, 109088. [Google Scholar] [CrossRef]
- Stranieri, F.; Fadda, E.; Stella, F. Combining deep reinforcement learning and multi-stage stochastic programming to address the supply chain inventory management problem. Int. J. Prod. Econ. 2024, 268, 109099. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, T.C.E.; Zhang, J. A serial mixed produce-to-order and produce-in-advance inventory model with multiple retailers. Int. J. Prod. Econ. 2012, 136, 378–383. [Google Scholar] [CrossRef]
- Islam, S.S.; Hoque, A.; Hamzah, N. Single-supplier single-manufacturer multi-retailer consignment policy for retailers’ generalized demand distributions. Int. J. Prod. Econ. 2017, 184, 157–167. [Google Scholar] [CrossRef]
- Stauffer, G. Approximation algorithms for k-echelon extensions of the one warehouse multi-retailer problem. Math. Methods Oper. Res. 2018, 88, 445–473. [Google Scholar] [CrossRef]
- Gruson, M.; Bazrafshan, M.; Cordeau, J.-F.; Jans, R. A comparison of formulations for a three-level lot sizing and replenishment problem with a distribution structure. Comput. Oper. Res. 2019, 111, 297–310. [Google Scholar] [CrossRef]
- Gruson, M.; Cordeau, J.-F.; Jans, R. Split demand and deliveries in an integrated three-level lot sizing and replenishment problem. Comput. Oper. Res. 2024, 161, 106434. [Google Scholar] [CrossRef]
- Cunha, J.O.; Melo, R.A. Valid inequalities, preprocessing, and an effective heuristic for the uncapacitated three-level lot-sizing and replenishment problem with a distribution structure. Eur. J. Oper. Res. 2021, 295, 874–892. [Google Scholar] [CrossRef]
- Gharaei, A.; Amjadian, A.; Shavandi, A. An integrated reliable four-level supply chain with multi-stage products under shortage and stochastic constraints. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 1958023. [Google Scholar] [CrossRef]
- Geevers, K.; van Hezewijk, L.; Mes, M.R.K. Multi-echelon inventory optimization using deep reinforcement learning. Central Eur. J. Oper. Res. 2023, 32, 653–683. [Google Scholar] [CrossRef]
- Lin, H.; Lin, J.; Wang, F. An innovative machine learning model for supply chain management. J. Innov. Knowl. 2022, 7, 100276. [Google Scholar] [CrossRef]
- Blancas-Rivera, R.; Cruz-Suárez, H.; Portillo-Ramírez, G.; López-Ríos, R. $(s, S)$ Inventory policies for stochastic controlled system of Lindley-type with lost-sales. AIMS Math. 2023, 8, 19546–19565. [Google Scholar] [CrossRef]
- Akbari, M.; Do, T.N.A. A systematic review of machine learning in logistics and supply chain management: Current trends and future directions. Benchmarking Int. J. 2021, 28, 2977–3005. [Google Scholar] [CrossRef]
- Bijvank, M.; Vis, I.F. Lost-sales inventory theory: A review. Eur. J. Oper. Res. 2011, 215, 1–13. [Google Scholar] [CrossRef]
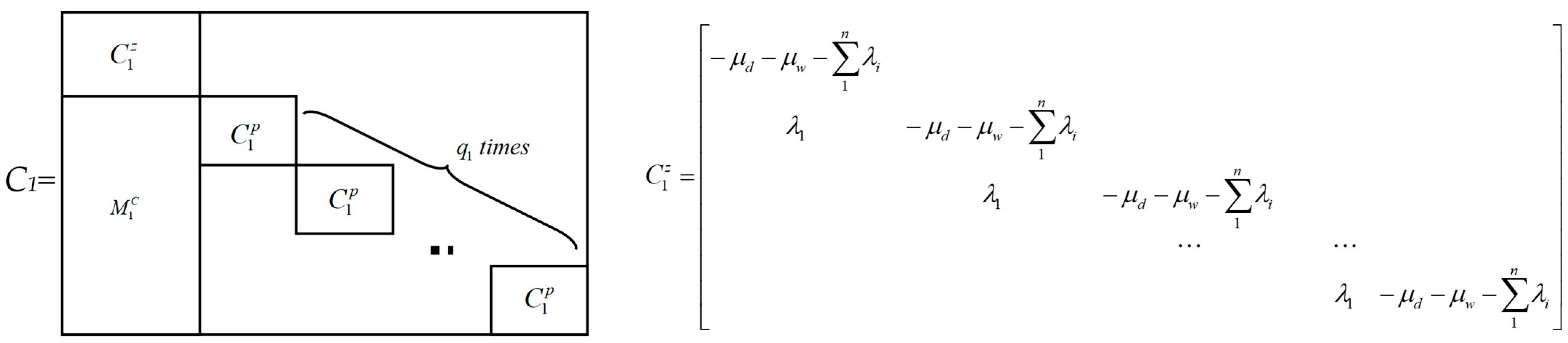


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varlas, G.; Koukoumialos, S.; Diamantidis, A.; Ioannidis, E. Analysis of a Three-Echelon Supply Chain System with Multiple Retailers, Stochastic Demand and Transportation Times. Mathematics 2025, 13, 3199. https://doi.org/10.3390/math13193199
Varlas G, Koukoumialos S, Diamantidis A, Ioannidis E. Analysis of a Three-Echelon Supply Chain System with Multiple Retailers, Stochastic Demand and Transportation Times. Mathematics. 2025; 13(19):3199. https://doi.org/10.3390/math13193199
Chicago/Turabian StyleVarlas, Georgios, Stelios Koukoumialos, Alexandros Diamantidis, and Evangelos Ioannidis. 2025. "Analysis of a Three-Echelon Supply Chain System with Multiple Retailers, Stochastic Demand and Transportation Times" Mathematics 13, no. 19: 3199. https://doi.org/10.3390/math13193199
APA StyleVarlas, G., Koukoumialos, S., Diamantidis, A., & Ioannidis, E. (2025). Analysis of a Three-Echelon Supply Chain System with Multiple Retailers, Stochastic Demand and Transportation Times. Mathematics, 13(19), 3199. https://doi.org/10.3390/math13193199







