On the Recursive Representation of the Permutation Flow and Job Shop Scheduling Problems and Some Extensions

Abstract

In this paper, we propose a formulation of the permutation flow and job shop scheduling problems using special recursive functions and show its equivalence to the existing classical formulation. Equivalence is understood in the sense that both ways of defining the problem describe the same set of feasible schedules for each pair of jobs and machine numbers. In this paper, the apparatus of recursive functions is used to describe and solve three problems: permutation flow shop; permutation flow shop with the addition of the ‘and’ predicate extending the machine chain to an acyclic graph; and permutation job shop. The predicate ‘and’ allows the description of the flow shop with assembly operation tasks. Recursive functions have a common domain and range. To calculate an optimal schedule for each of these three problems, a branch and bound method is considered based on a recursive function that implements a job swapping algorithm. The complexity of the optimization algorithm does not increase compared to the non-recursive description of the PFSP. This article presents some results for the calculation of optimal schedules on several test instances. It is expected that the new method, based on the description of recursive functions and their superposition, will be productive for formulating and solving some extensions of scheduling problems that have practical significance.

1. Introduction

There exist a huge number of publications devoted to the permutation flow shop problem (PFSP) or to the more general case of the flow shop problem (FSP) in the scheduling literature. In both the PFSP and the FSP, all jobs must be processed on a set of m machines according to a fixed technological order. In the PFSP, all jobs are performed by each machine in the same order, while in the FSP, jobs may be performed in different orders on different machines selected to satisfy a specific optimization criterion. Often, the makespan has to be minimized, i.e., the maximum completion time of the complete set of jobs should be minimized. The PFSP is denoted as $F\left|prmu\right|C_{max}$. In [1], an overview of the PFSP with the makespan criterion is presented. Three categories of methods used to solve the PFSP are considered: traditional algorithms, heuristic algorithms, and meta-heuristic algorithms. This study focused on meta-heuristic algorithms due to their effectiveness in solving many application problems. As a result of this study, it was demonstrated that meta-heuristic algorithms play a vital role in solving the PFSP. Most works deal with various heuristics and metaheuristics, see, e.g., [2,3,4,5,6]. Much of the current work in the field of the PFSP is related to Industry 4.0 [7,8]. References [9,10] provide an overview of the FSP with assembly operations (AFSP). The basic assembly process in a workshop is described, consisting of two stages: the manufacturing or machining stage and the assembly stage. The machining and assembly stages use one or more machines operating in parallel. The final products have a hierarchical assembly structure with multiple components and assembly operations. A review of assembly shop models with a methodology for solving the corresponding problems of scheduling theory is presented. No less intensive work has been done for the job shop problem (JSP). We briefly discuss some of the latest publications. A review of more than 120 papers has been presented in [11]. It examines the problem in relation to the new demands of Industry 4.0. This line of research has split into several new independent ones. Another review [12] briefly described the research developments and current state of the art of job shop problems, classifying existing research methods and discussing future directions for the development. Reference [13] described the development of an innovative high-performance genetic algorithm for the JSP. In [14], a genetic algorithm and a simulated annealing one have been proposed for application in the manufacturing industry. Finally, reference [15] provided an overview for a generalization of the classical job shop problem, namely the flexible job shop problem (FJSP).

This paper attempts to use the recursive functions apparatus to initiate systematic formulations of extensions of the problem of scheduling theory. A recursive function, by definition, is calculated using some algorithm. This, in some cases, allows the specifics of the problem extension to be incorporated into the algorithm of the recursive function. It is proposed to formulate and solve the extended problems of scheduling theory using a set of functions and their superposition. At this stage, the paper presents a description of the PFSP using recursive functions, as well as a transition to problems with the ‘and’ predicate and a permutation variant of the job shop problem (PJSP). The PFSP formulation with the ‘and’ predicate allows for solving problems involving assembly operations. All functions have a common domain and range. The authors demonstrate the applicability of the branch and bound method for all three problems. This greatly simplifies their application when using recursive functions. The flexibility requirements of Industry 4.0 manufacturing necessitate the use of PFSP, PFSP with assembly operations, and PJSP models. This can be accomplished by using three models in one solver.

It can be noted that the general PFSP with at least three machines and minimizing the makespan is already NP-hard in the strong sense, so the existence of polynomial solution algorithms is unlikely. Therefore, all exact enumerative algorithms for the PFSP have an exponential complexity. Since the PFSP with assembly operations and also the PJSP contain the PFSP as a special case, these problems are also NP-hard in the strong sense.

This article discusses a new approach through the definition of recursive functions to describe the timing characteristics of the PFSP. The concept of interval calculations is used to describe time domains. The equivalence of the PFSP representation in the existing and the recursive forms is proved. Here, equivalence is understood as the equality of the sets of feasible schedules for each pair of job number and machine number. Then, the transition from interval recursive functions to scalar ones is carried out. It is shown that with a fixed order of operations, scalar functions calculate an optimal schedule on the set of feasible schedules.

Moreover, the recursive representation of the PFSP is extended by including the predicate ‘and’, which allows one to move from chains of machines to trees and acyclic graphs. The branch and bound method (B&B) [16] using the introduced recursive function is considered as an exact optimization method. A description of one of the variants of a lower bound on the makespan and the branching method are given. The branching method is based on an original permutation generator with a given property. The permutation algorithm and the recursive implementation of the B&B method are described. It is shown that the complexity of the algorithm does not increase compared to the known B&B algorithms for the PFSP [16,17].

The rest of this paper is organized as follows. Section 2 reviews some basics of interval calculations relevant for the PFSP. Section 3 proves the equivalence of the existing and the recursive PFSP representations. Section 4 provides a method for implementing the B&B algorithm for the recursive PFSP. Section 5 gives the definition of the ‘and’ function and the extended formulation of the problem. Then, Section 6 discusses the B&B method for the introduced extended formulation of the problem. Section 7 presents some initial results with the suggested algorithm. In Section 8, a recursive function is formulated to describe a variant of the job shop problem.

2. Interval Values and Operations

Interval calculations in mathematics have been known for a long time; see, for example, [18]. In our case, this theory is used at the level of definitions and properties of some interval operations. We will consider the set of values of the time interval as a segment of integers on the number line with starting and end points included.

Definition 1.

Let $N=\{0,1,2,3,\dots ,\widehat{N}\}$ be the finite set of natural numbers from one to $\widehat{N}$ with zero added. Everywhere below, by an interval or domain $[a,b],a\le b$, unless otherwise stated, we denote the closed bounded subset N of the form

$$[a,b]=\left\{x\right|x\in N\wedge a\le x\le b\}.$$

The set of all intervals is denoted by $\mathcal{I}$. We will write the elements of $\mathcal{I}$ in capital letters. If $A\in \mathcal{I}$, then we denote its left and right end points as $\underline{a}$ and $\overline{a}:A=[\underline{a},\overline{a}]$. We will also denote $\underline{A}=\underline{a}$ and $\overline{A}=\overline{a}$. We call the elements of $\mathcal{I}$ interval numbers. Two intervals A and B are equal if and only if $\underline{a}=\underline{b}$ and $\overline{a}=\overline{b}$. According to the total interval approach [18], we can describe operations as follows. Let ∘ be some operation and $A,B\in \mathcal{I}$. In this case, we have

$$A\circ B=\{a\circ b|a\in A,b\in B\}.$$

If $A=[\underline{a},\overline{a}]$ and $B=[\underline{b},\overline{b}]$, then $A\circ B=[\underline{a}\circ \underline{b},\overline{a}\circ \overline{b}].$ We will use only two interval operations: ”+” and ”max”. They are defined as follows:

$$\begin{array}{ccc}\hfill A+B& =& A=[\underline{a}+\underline{b},\overline{a}+\overline{b}];\hfill \\ \hfill \max \{A,B\}& =& [\max \{\underline{a},\underline{b}\},\max \{\overline{a},\overline{b}\}].\hfill \end{array}$$

To illustrate, consider the following example.

Example 1.

Let $A=[12,17]$ and $B=[3,5]$. Then,

$$\begin{array}{ccc}\hfill A+B& =& [12,17]+[3,5]=[12+3,17+5]=[15,22];\hfill \\ \hfill \max \{A,B\}& =& \max \left\{\right[12,17],[3,5\left]\right\}=\left[\max \right\{12,3\},\max \{17,5\left\}\right]\hfill \\ & =& [12,17].\hfill \end{array}$$

If $A=[6,9]$ and $B=[3,12]$, then

$$\max \{A,B\}=\max \left\{\right[6,9],[3,12\left]\right\}=\left[\max \right\{6,3\},\max \{9,12\left\}\right]=[6,12].$$

While in the first case, the interval A is obtained by the operation max, in the second case, a subinterval of B results.

To illustrate, below are some further examples of various options for the max operation:

• $\max \left\{\right[1,4],[2,3\left]\right\}=[2,4];$
• $\max \left\{\right[2,5],[3,6\left]\right\}=[3,6];$
• $\max \left\{\right[5,15],[0,0\left]\right\}=[5,15].$

A confluent interval, i.e., an interval with coinciding end points $a=\underline{a}=\overline{a}$, is identical to the integer a. Thus, $N\subset \mathcal{I}$. If A and B are confluent intervals, then the results of the operations on intervals coincide with ordinary arithmetic operations for non-negative integers. An interval integer is a generalization of an integer, and the interval integer arithmetic is a generalization of the integer arithmetic.

Note also that for $B=[b,b]$, we also write for simplicity $A+B=A+b$. In the theory of intervals, the role of zero is played by the usual 0, which is identified with the confluent interval [0, 0]. In other words,

$$A+0=0+A=A,\max \{A,0\}=\max \{0,A\}=A,\forall A\in \mathcal{I}.$$

The calculations can lead to an interval $\varnothing =[a,b]$ if $a>b$, which, according to Definition 1, represents an empty set.

3. Solving the Permutation Flow Shop Equivalence Problem

Consider the description of the PFSP [19]. Let $\mathcal{J}=\{1,2,\dots ,n\}$ be the set of jobs and $\mathcal{M}=\{1,2,\dots ,m\}$ be the set of machines arranged sequentially. Moreover, let $p_{j,k}$ be the processing time of job j on machine k.

The precedence graph of such a problem (see Figure 1a) is a simple chain in which the vertices are machines, and the edges define precedence relations between the machines. This graph can be “expanded” if we fix some order of the jobs and define precedence relations between the jobs $\mathcal{J}\times \mathcal{J}$ and between the machines $\mathcal{M}\times \mathcal{M}$. Any vertex of such a graph is identified with the pair (job number, machine number). An expanded graph describing precedence relations between the jobs is presented in Figure 1b.

The vertical edges define precedence relations between the jobs for a particular machine. The horizontal edges define precedence relations between the machines for a fixed job. This graph is acyclic and has one start and one end vertex. Consider some schedule and then renumber the jobs in the order in which they are located in the schedule, i.e., for simplicity of the description, consider the schedule $(1,2,...,n)$ with the new numbering. The following assumptions are valid for the PFSP:

• Job assumptions: A job cannot be processed by more than one machine at a time; each job must be processed in accordance with the machine precedence relationship; the job is processed as early as possible, depending on the order of the machines; all jobs are equally important, meaning there are no priorities, deadlines, or urgent orders.
• Machine assumptions: No machine can process more than one job at a time; after starting a job, it must be completed without interruption; there is only one machine of each type; no job is processed more than once by any machine.
• Assumptions about the processing times: The processing time of each job on each machine does not depend on the sequence in which the jobs are processed; the processing time of each job on each machine is specific and integer; the transport time between machines and a setup time, if any, are included in the processing time.

Additional time limits can be set in the scheduling problems. Denote $T(j,k)=[{\underline{t}}_{j,k},{\overline{t}}_{j,k}]$ as the interval completion time of job j on the kth machine. ${\underline{t}}_{j,k}$ is the minimal time for the completion of job j on the kth machine, and ${\overline{t}}_{jk}$ is the corresponding maximal time. The completion time $t_{j,k}$ must satisfy the condition ${\underline{t}}_{j,k}\le t_{j,k}\le {\overline{t}}_{j,k}$; otherwise, the schedule is infeasible. In fact, this is the interval function completion time of job j on machine k. We will assume that in the initial formulation of the problem, a matrix $\parallel T^0(j,k)\parallel =\parallel [{\underline{t}}_{j,k}^0,{\overline{t}}_{j,k}^0]\parallel$ of initial domains of the feasible values for the job completion times has been defined. We will assume, unless otherwise specified, that the initial domains are the interval $[0,T_{max}]$, where $T_{max}$ is a sufficiently large finite value, which will be discussed below. We describe two additional restrictions [19]:

• $r_j$ is the moment when job j arrives for processing, i.e., its release date. This parameter defines the time point from which job j can be scheduled for execution, but its processing does not necessarily begin at this moment. In this case, in the matrix of initial domains, it is necessary to put $T^0(j,k)=[r_j+p_{j,k},T_{max}]$ for $j\in \mathcal{J}$ and $1\le k\le m$.
• $D_j$ is the deadline for processing job j. A deadline cannot be violated, and any schedule that contains a job that finishes after its deadline is infeasible. In this case, in the matrix of initial domains, it is necessary to put $T^0(j,k)=[0,D_j]$ for $j\in \mathcal{J}$ and $1\le k\le m$.

The combination of the constraints $r_j$ and $D_j$ generates initial domains of the form $T^0(j,k)=[r_j+p_{j,k},D_j]$ for $j\in \mathcal{J}$ and $1\le k\le m$. If these restrictions relate to specific operations, they will look like $r_{j,k}$ and $D_{j,k}$. In this case, the following time relations will be satisfied:

$$\begin{array}{c}\hfill p_{1,1}\le t_{1,1},t_{1,1}\le t_{1,2}-p_{1,2},\dots ,t_{1,m-1}\le t_{1,m}-p_{1,m}.\end{array}$$

(1)

$$\begin{array}{c}\hfill t_{1,1}\le t_{2,1}-p_{2,1},\max (t_{1,2},t_{2,1})\le t_{2,2}-p_{2,2},\dots ,\\ \hfill \max (t_{1,m},t_{2,m-1})\le t_{2,m}-p_{2,m}.\\ \hfill ⋮\end{array}$$

(2)

$$\begin{array}{c}\hfill t_{n-2,1}\le t_{n-1,1}-p_{n-1,1},\max (t_{n-2,2},t_{n-1,1})\le t_{n-1,2}-p_{n-1,2},\dots ,\\ \hfill \max (t_{n-2,m},t_{n-1,m-1})\le t_{n-1,m}-p_{n-1,m}.\end{array}$$

(3)

$$\begin{array}{c}\hfill t_{n-1,1}\le t_{n,1}-p_{n,1},\max (t_{n-1,2},t_{n,1})\le t_{n,2}-p_{n,2},\dots ,\\ \hfill \max (t_{n-1,m},t_{n,m-1})\le t_{n,m}-p_{n,m}.\end{array}$$

(4)

Here, we take into account the fact that the interval time $B(j,k)$ for the start of job j on the kth machine is calculated by the following formula:

$$B(j,k)=[{\underline{t}}_{j,k},{\overline{t}}_{j,k}]-p_{j,k}=[{\underline{t}}_{j,k}-p_{j,k},{\overline{t}}_{j,k}-p_{j,k}],1\le j\le n,1\le k\le m.$$

The above inequalities are supplemented by inequalities of the form ${\underline{t}}_{j,k}\le {\overline{t}}_{j,k}$.

The system of inequalities (1)–(4) defines an infinite set of feasible schedules. To reduce this set to a finite one, we will use a positive integer constant $T_{max}$ and supplement the system (1)–(4) with the inequalities

$${\overline{t}}_{j,k}\le T_{max},1\le j\le n,1\le k\le m.$$

(5)

It is possible to assign to $T_{max}$ a value so small that the set of feasible schedules is empty.

Remark 1.

In what follows, we always assume that there is a constant $T_{max}$ such that there is at least one feasible schedule.

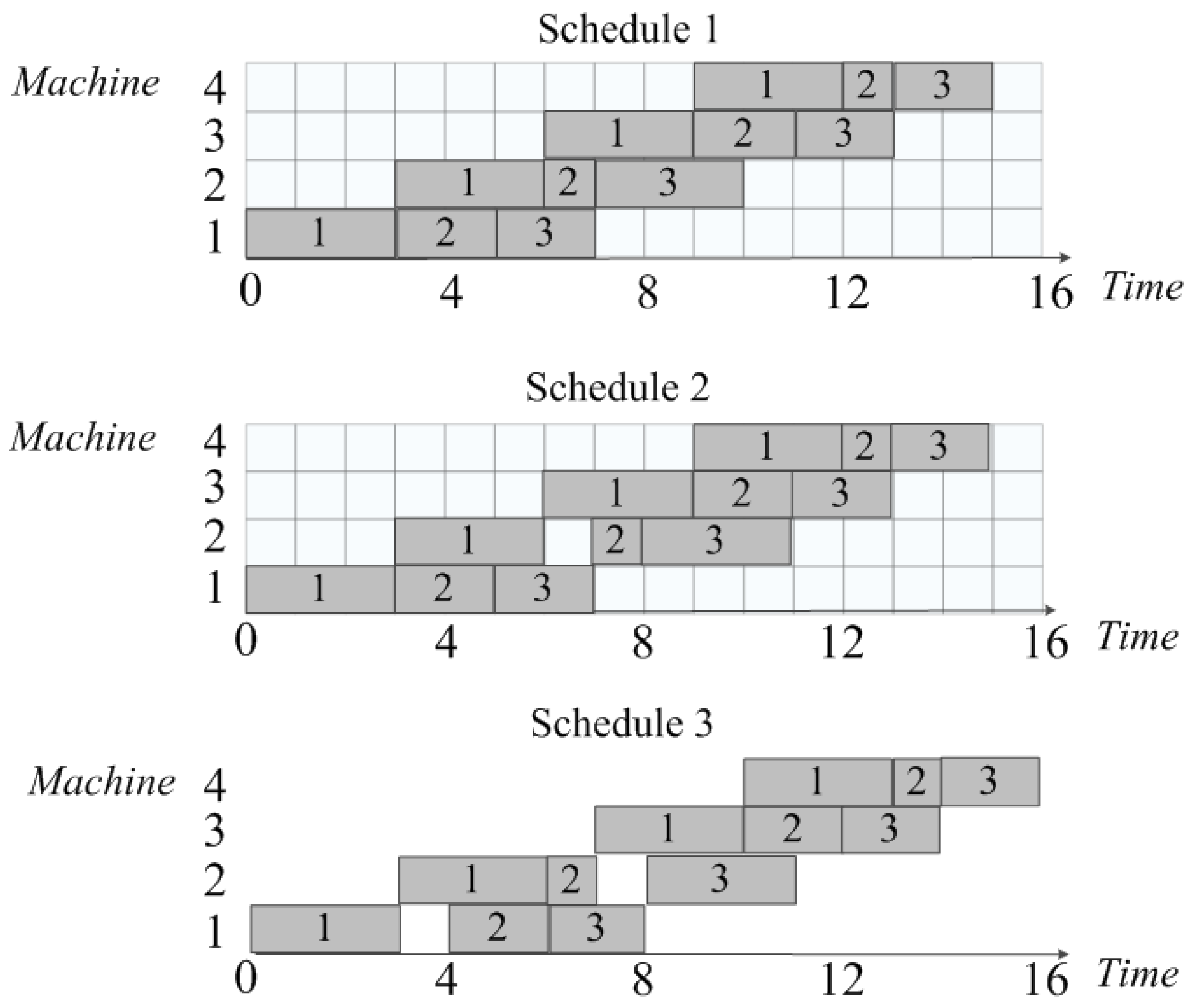
Example 2.

Consider a PFSP with four machines and three jobs.

Table 1. Table of job processing times.

Machine\Job	1	2	3
1	3	2	2
2	3	1	3
3	3	2	2
4	3	1	2

shows the processing times $p_{j,k}$ of the jobs. The rows correspond to the job numbers, and the columns represent the machine numbers.

Let $T_{max}=16$. In this case, the intervals for each pair $(j,k)$ are given in

Table 2. Intervals of job completion times for the machine with feasible schedules.

Machine\Job	1	2	3
1	[3, 4]	[5, 7]	[7, 9]
2	[6, 7]	[7, 9]	[10, 12]
3	[9, 10]	[11, 12]	[13, 14]
4	[12, 13]	[13, 14]	[15, 16]

.

Figure 2 shows the Gantt charts of three variants from the set of feasible schedules. ”Schedule 1” and ”Schedule 2” are optimal schedules (for this sequence), while ”Schedule 2” and ”Schedule 3” have different inserted idle times. It is easy to verify that increasing any interval in Table 2 will lead to the appearance of infeasible schedules, and decreasing any interval will result in the loss of feasible schedules.

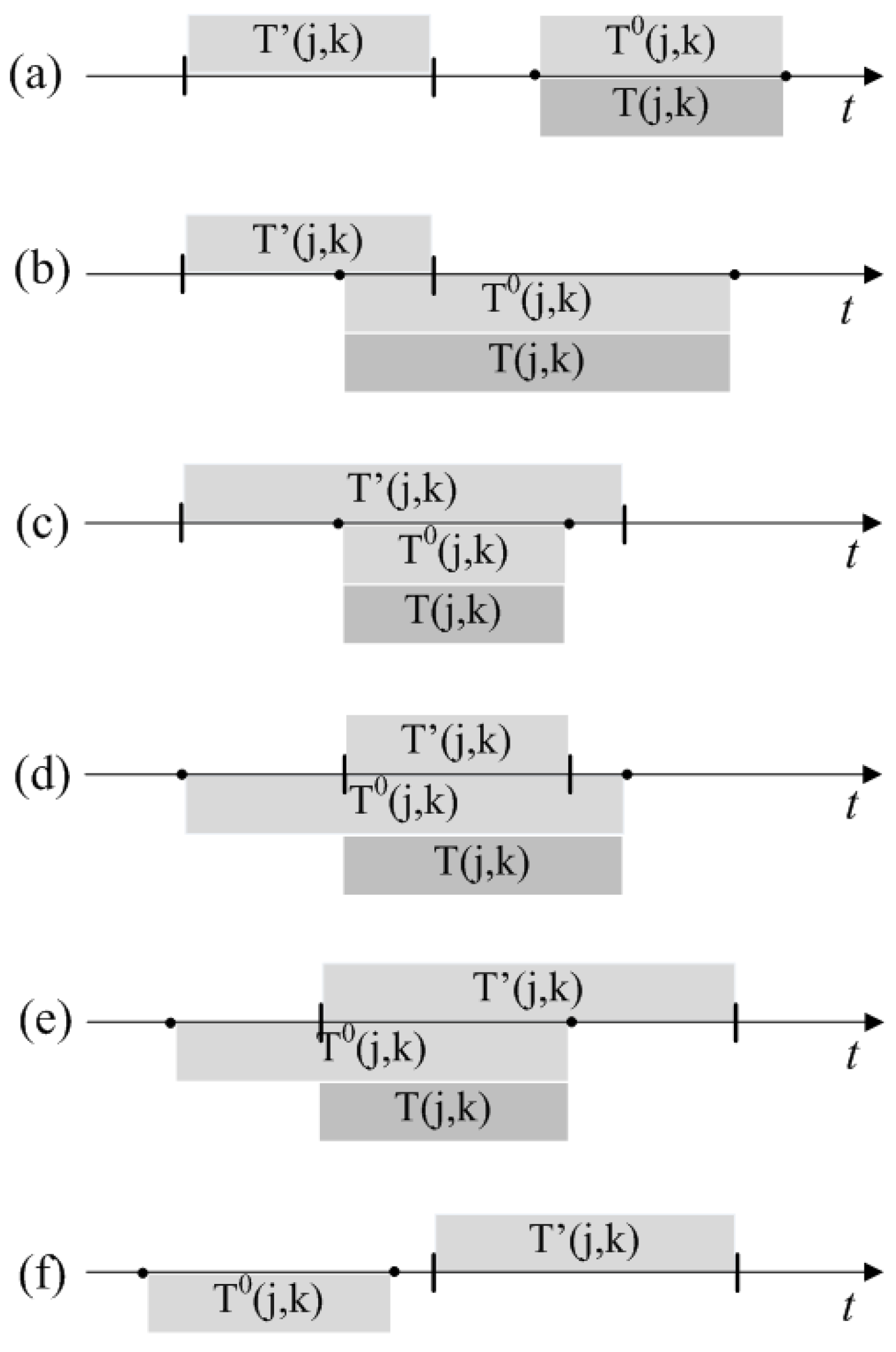
Let $T^{\prime }(j,k)$ be the interval calculated by some algorithm for completing the jth job on the kth machine, and let $T^0(j,k)$ be the corresponding initial domain. According to Figure 3, we define the interval noncommutative operation intersection (∩) as $T(j,k)=T^{\prime }(j,k)\cap T^0(j,k)$. The figure shows all significant cases of interval intersections:

(a)

the interval $T^{\prime }(j,k)$ is to the left of $T^0(j,k)$. The completion time of the jth job on the kth machine should be artificially increased to values from the interval $T^0(j,k)$. Only in this case, the schedule will be feasible;

(b–e)

are clear without additional explanation;

(f)

with this arrangement of intervals, the value of the interval $T(j,k)$ is equal to an empty set, which corresponds to the absence of a feasible schedule.

Thus, we have:

$$T(j,k)=\left\{\begin{array}{cc}\varnothing ,\hfill & {\overline{T}}^0(j,k)<{\underline{T}}^{\prime }(j,k);\hfill \\ \left[\max \{{\underline{T}}^{\prime }(j,k),{\underline{T}}^0(j,k)\},{\overline{T}}^0(j,k)\right],\hfill & otherwise.\hfill \end{array}\right.$$

It can be shown that all feasible sets of time values are uniquely determinable and maximal. Therefore, when searching for an optimal solution, no solution will be lost.

All precedence relations define intervals (including the scalar $c=[c,c]$). Again, for simplicity of the description, consider some schedule and then renumber the jobs in the order in which they are located in the schedule, i.e., consider the schedule $(1,2,...,n)$ with the new numbering. The calculations of these intervals can be divided into four groups. Next, we write them using interval variables, assuming that the initial interval is $T^0(j,k)$ and ${\overline{T}}^0(j,k)\le T_{max}$:

• For the completion of the first job on the first machine $(j=1,k=1)$, we have:

  $$\begin{array}{ccc}\hfill T^{\prime }(1,1)& =& [p_{1,1},p_{1,1}],\hfill \\ \hfill T(1,1)& =& T^{\prime }(1,1)\cap T^0(1,1).\hfill \end{array}$$
• For the completion of the first job on the kth machine $(j=1,1<k\le m)$, we have:

  $$\begin{array}{ccc}\hfill T^{\prime }(1,k)& =& T(1,k-1)+[p_{1,k},p_{1,k}],\hfill \\ \hfill T(1,k)& =& T^{\prime }(1,k)\cap T^0(1,k).\hfill \end{array}$$
• For the completion of job j on the first machine $(1<j\le n,k=1)$, we have:

  $$\begin{array}{ccc}\hfill T^{\prime }(j,1)& =& T(j-1,1)+[p_{j,1},p_{j,1}],\hfill \\ \hfill T(j,1)& =& T^{\prime }(j,1)\cap T^0(j,1).\hfill \end{array}$$
• The interval of the completion time of job j on the kth machine $(1<j\le n,1<k\le m)$ is obtained as follows:

  $$\begin{array}{ccc}\hfill T^{\prime }(j,k)& =& \max \{T(j-1,k),T(j,k-1)\}+[p_{j,k},p_{j,k}],\hfill \\ \hfill T(j,k)& =& T^{\prime }(j,k)\cap T^0(j,k).\hfill \end{array}$$

The PFSP can be formulated using a finite set of special recursive functions. This is due to the existence of precedence relationships between the machines and jobs in the PFSP when the current characteristics of the problem are determined by the preceding ones. Recursive functions have arguments and parameters as data. The arguments of the functions are pairs (job number, machine number). They are passed as function arguments in the normal mathematical sense. Parameters are defined outside the recursive function, and they are essentially global variables in imperative programming terms. Examples of parameters can be $n,m,T_{max},\parallel p_{j,k}\parallel ,\parallel T^0(j,k)\parallel$, and so on. For any recursive function R whose set of arguments is determined by the Cartesian product $A_1\times A_2\times \cdots \times A_l$, the parameters ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots {\mathcal{P}}_h$ and the set of values $\mathcal{I}$ will be written as $R\{{\mathcal{P}}_1,{\mathcal{P}}_2,\dots {\mathcal{P}}_h\}:A_1\times A_2\times \cdots \times A_l\to \mathcal{I}$. If a recursive function has no parameters, they are skipped together with the curly braces in the definition of the recursive function.

We will denote the interval recursive function as

$$\mathcal{T}\{n,m,\parallel p_{j,k}\parallel ,\parallel T^0(j,k)\parallel \}:\mathcal{J}\times \mathcal{M}\to \mathcal{I}.$$

Specific types of recursive functions will be provided subsequently as the PFSP is considered. Let us consider the problem of equivalence of the existing PFSP formulation in the literature and its recursive representation. The equivalence of both formulations is established through the equivalence of the domains of acceptable values of the completion times for each pair (job number, machine number). An optimal solution is within the allowed processing times. This fact allows us to move to the functional representation of the problem and to apply various appropriate methods. We can describe each group by the corresponding recursive functions:

• $\mathcal{T}(1,1)=[p_{1,1},p_{1,1}]\cap T^0(1,1);j=1,k=1.$
• $\mathcal{T}(1,k)=(\mathcal{T}(1,k-1)+[p_{1,k},p_{1,k}])\cap T^0(1,k);j=1,1<k\le m.$
• $\mathcal{T}(j,1)=(\mathcal{T}(j-1,1)+[p_{j,1},p_{j,1}])\cap T^0(j,1);1<j\le n,k=1.$
• $\mathcal{T}(j,k)=(\max \{\mathcal{T}(j-1,k),\mathcal{T}(j,k-1)\}+[p_{j,k},p_{j,k}])\cap T^0(j,k);1<j\le n,1<k\le m.$

This set of functions can be combined into one function:

$$\mathcal{T}(j,k)=\left\{\begin{array}{cc}[p_{1,1},p_{1,1}]\cap T^0(1,1),\hfill & j=1,k=1;\hfill \\ (\mathcal{T}(1,k-1)+[p_{1,k},p_{1,k}])\cap T^0(1,k),\hfill & j=1,1<k\le m;\hfill \\ (\mathcal{T}(j-1,1)+[p_{j,1},p_{j,1}])\cap T^0(j,1),\hfill & 1<j\le n,k=1;\hfill \\ (\max \{\mathcal{T}(j-1,k),\mathcal{T}(j,k-1)\}+[p_{j,k},p_{j,k}])\cap T^0(j,k),\hfill & 1<j\le n,1<k\le m.\hfill \end{array}\right.$$

(6)

The function $\mathcal{T}(j,k)$ is defined for all values of j and k. If $\mathcal{T}(j,k)=\varnothing$, then there is no feasible schedule. It can be seen from the formula that it calculates the only value of the interval. We show that this recursive function defines the same domain for each $(j,k)$ as the set of values defined by the system of inequalities (1)–(5).

Theorem 1.

Let the following conditions be satisfied for both the PFSP given by the system of inequalities (1)–(5) and the recursive PFSP:

• one graph is set for both problems (see Figure 1a);
• consider some schedule and then renumber the jobs in the order in which they are located in the schedule, i.e., consider the schedule $(1,2,...,n)$ with the new numbering;
• the processing time of job j on the kth machine is $p_{j,k}$;
• the same matrix of initial time intervals is specified:

  $$\parallel T^0(j,k)\parallel =\parallel [{\underline{t}}_{j,k}^0,{\overline{t}}_{j,k}^0]\parallel .$$

Taking into account Remark 1, this means that the set of feasible schedules is defined on intervals determined by $\parallel T_0(j,k)\parallel$ from below and $T_{max}$ from above.

Then, the following statement is true: the set of domains $\mathcal{D}(j,k)$ of feasible times for the non-recursive PFSP coincides with the set of domains ${\mathcal{D}}^{\prime }(j,k)$ for the recursive PFSP, i.e., $\mathcal{D}(j,k)={\mathcal{D}}^{\prime }(j,k)$ for $1\le j\le n,1\le k\le m$.

In other words, the sets of feasible schedules for each pair (job number, machine number) are the same, or in both cases, there is no feasible schedule, i.e., there are j and k such that ${\mathcal{D}}_{j,k}={\mathcal{D}}_{j,k}^{\prime }=\varnothing$.

Proof. 

Let the conditions of the theorem be satisfied. The proof is obtained via complete induction. Let us recall the formulation of the principle of complete induction. Let there be a sequence of statements $P_1,P_2,P_3,\dots$. If for any natural i the fact that all $P_1,P_2,P_3,\dots ,P_{i-1}$ are true also implies that $P_i$ is true, then all statements in this sequence are true. Therefore, for $i\in N,i\ge 2$, we have

$$(\forall j\in \{1;\dots ;i-1\}{P}_j\Rightarrow P_i)\Rightarrow (\forall i\in N)P_i.$$

Here, $x\Rightarrow y$ denotes a logical implication. The statement $P_i$ is the equality of the intervals $\mathcal{D}(j,k)={\mathcal{D}}^{\prime }(j,k)$. Let us apply this method to the graph in Figure 1b. From graph theory, it is known that the vertices of an acyclic graph are strictly partially ordered. There exist algorithms for constructing some linear order for a strictly partially ordered graph. Informally, a linear order is when all the vertices of a graph are arranged in a line, and all edges are directed from left to right. Any such algorithm is suitable because:

-

the first vertex is always $(1,1)$ of the original graph,

-

the last vertex is always $(n,m)$,

-

when evaluating the recursive function according to a linear order, its arguments have already been evaluated.

Let us choose a row-by-row traversal. In this case, for a pair $(j,k)$, all pairs $(j^{\prime },k^{\prime })$ with $j^{\prime }<j$ or $k^{\prime }<k$ have already been considered. We will traverse the elements of the matrix of interval variables T in the rows from left to right and from the top row to the bottom one.

• Let us prove the statement $P_1$. From the system of inequalities (1)–(4), it follows that

  $$T(1,1)=[p_{1,1},p_{1,1}]\cap T^0(1,1).$$

  From the definition of the recursive function, it follows that

  $$T^{\prime }(1,1)=\mathcal{T}(1,1)=[p_{1,1},p_{1,1}]\cap T^0(1,1).$$

  Therefore, we have $T(1,1)=T^{\prime }(1,1)$.
• Let us assume that the statements $P_1,\dots ,P_{i-1}$ are true. We now prove that the statement $P_i$ is also true. Among the four groups of relationship types described above, the first type is considered for $j=1,k=1$.
• Let us analyze the remaining three types.

  (a)

  Processing of the first job on the kth machine $(j=1,1<k\le m)$: In this case, the problem satisfies the equality

  $$T(1,k)=(T(1,k-1)+[p_{1,k},p_{1,k}])\cap T^0(1,k).$$

  In turn,

  $$\mathcal{T}(1,k)=(\mathcal{T}(1,k-1)+[p_{1,k},p_{1,k}])\cap T^0(1,k),$$

  and due to the condition $\mathcal{T}(1,k-1)=T(1,k-1)$, we get

  $$\mathcal{T}(1,k)=T(1,k-1)+[p_{1,k},p_{1,k}]=T(1,k).$$

  Therefore, we have $T(1,k)=T^{\prime }(1,k)$.

  (b)

  Processing of job j on the first machine $(1<j\le n,k=1)$: In this case, the problem satisfies the equality

  $$T(j,1)=(T(j-1,1)+[p_{j,1},p_{j,1}])\cap T^0(j,1).$$

  In case of recursion,

  $$\mathcal{T}(j,1)=(\mathcal{T}(j-1,1)+[p_{j,1},p_{j,1}])\cap T^0(j,1).$$

  Due to the condition $\mathcal{T}(j-1,1)=T(j-1,1)$, finally, we get

  $$\mathcal{T}(j-1,1)=T(j-1,1)=T(j,1).$$

  Therefore, we have $T(j,1)=T^{\prime }(j,1)$.

  (c)

  Processing of job j on the kth machine $(1<j\le n,1<k\le m)$ assumes that the problem satisfies the equalities

  $$\mathcal{T}(j-1,k)=T(j-1,k),\mathcal{T}(j,k-1)=T(j,k-1).$$

  In this case,

  $$\begin{array}{ccc}\hfill \mathcal{T}(j,k)& =& (\max \{\mathcal{T}(j-1,k),\mathcal{T}(j,k-1)\}+[p_{j,k},p_{j,k}])\cap T^0(j,k)\hfill \\ & =& (\max \{T(j-1,k),T(j,k-1)\}+[p_{j,k},p_{j,k}])\cap T^0(j,k)=T(j,k).\hfill \end{array}$$

  Therefore, we have $T(j,k)=T^{\prime }(j,k)$.

All possible situations have been analyzed.    □

The main optimization problem in the PFSP is to find the order of job processing so that for some selected criterion, the function value is optimal. The most common criterion is the makespan (i.e., the total time it takes to complete the whole set of jobs). We remember that the vast majority of flow shop problems are treated as a PFSP; see, for example, [17,20,21].

To effectively solve the problem of calculating an optimal schedule, it is necessary to switch from interval recursive functions (6) to scalar recursive functions $C\{n,m,\parallel p_{j,k}\parallel \}:\mathcal{J}\times \mathcal{M}\to N$. Consider the case when all elements of the matrix of initial time intervals are equal to $[0,T_{max}]$. In this case, all the cases of interval intersections shown in Figure 3 will be reduced to case (d) and will look similar to Figure 4. The value of $\overline{T}(j,k)$ will always be equal to $T_{max}$, and the interval value can be replaced by a scalar equal to the lower value of the interval $\underline{T}(j,k)$. Then, the recursive function (6) will look as follows:

$$C(j,k)=\left\{\begin{array}{cc}{p}_{1,1},\hfill & j=1,k=1;\hfill \\ \underline{\mathcal{T}}(1,k-1)+p_{1,k},\hfill & j=1,k>1;\hfill \\ \underline{\mathcal{T}}(j-1,1)+p_{j,1},\hfill & j>1,k=1;\hfill \\ \max (\underline{\mathcal{T}}(j-1,k),\underline{\mathcal{T}}(j,k-1))+p_{j,k},\hfill & j>1,k>1.\hfill \end{array}\right.$$

(7)

or finally

$$C(j,k)=\left\{\begin{array}{cc}{p}_{1,1},\hfill & j=1,k=1;\hfill \\ C(1,k-1)+p_{1,k},\hfill & j=1,1<k\le m;\hfill \\ C(j-1,1)+p_{j,1},\hfill & 1<j\le n,k=1;\hfill \\ \max \{C(j-1,k),C(j,k-1)\}+p_{j,k},\hfill & 1<j\le n,1<k\le m.\hfill \end{array}\right.$$

(8)

The function $C(j,k)$ calculates the completion time of job j on the kth machine. The scalar function (8) is obtained from the interval function (6) by replacing the interval with the lowest value of the interval. These arguments are given for $[0,T_{max}]$, but it can be proven that they are also valid for the intervals $[r_j,T_{max}]$ in accordance with Remark 1.

In Example 2 above, $C(j,k)$ computes only one schedule with minimum completion time, which corresponds to the ”Schedule 1” diagram in Figure 2.

The analysis of Formula (8) shows that when calculating the function $C(n,m)$, the traversal of pairs $(j,k)$ is carried out in the order indicated in Figure 5a.

However, if Function (8) is replaced by an equivalent Function (9) (the difference is in the last expression), then the pairs will be traversed according to the scheme in Figure 5b:

$$C(j,k)=\left\{\begin{array}{cc}{p}_{1,1},\hfill & j=1,k=1;\hfill \\ C(1,k-1)+p_{1,k},\hfill & j=1,1<k\le m;\hfill \\ C(j-1,1)+p_{j,1},\hfill & 1<j\le n,k=1;\hfill \\ \max \{C(j,k-1),C(j-1,k)\}+p_{j,k},\hfill & 1<j\le n,1<k\le m.\hfill \end{array}\right.$$

(9)

Theorem 2.

Let the PFSP include m machines and n jobs. Consider some schedule and then renumber the jobs in the order in which they are located in the schedule, i.e., consider the schedule $(1,2,\dots ,n)$ with the new numbering. In this case, the following equality is true for any $j(1\le j\le n)$ and any $k(1\le k\le m)$:

$$\underline{\mathcal{T}}(j,k)=C(j,k).$$

The point of this theorem is that the scalar function calculates the minimum completion time for any given sequence of jobs. This follows from the principle of the function construction.

Proof. 

If in Formula (7), $C(j,k)$ is replaced by $\underline{\mathcal{T}}(j,k)$, then a formula for calculating $\underline{\mathcal{T}}(j,k)$ is obtained. The direct comparison of the resulting formula with Formula (8) for calculating $C(j,k)$ proves the validity of the theorem.    □

The following important theorem follows from Theorem 2.

Theorem 3.

Let the PFSP be defined for m machines and n jobs. In addition, let Π be the set of all permutations of n jobs and ${\pi }^{*}=({\alpha }_1,{\alpha }_2,...,{\alpha }_n)\in \mathsf{\Pi }$ be the permutation corresponding to the minimum completion time of all jobs, computed as $\underline{\mathcal{T}}({\alpha }_n,m)$ for ${\pi }^{*}$. For the PFSP, such a permutation satisfies the following equality:

$$\underline{\mathcal{T}}({\alpha }_n,m)=C({\alpha }_n,m).$$

The meaning of the theorem is that the minimum completion time of all jobs, computed using interval calculations, is equal to the value of the scalar recursive function for the same permutation.

Proof. 

The set of all permutations $\mathsf{\Pi }$ is finite and has the cardinality $n!$. In this case, as proven by Theorem 2, for any permutation $\pi \in \mathsf{\Pi }$, the equality $\underline{\mathcal{T}}({\alpha }_n,m)=C({\alpha }_n,m)$ holds. Therefore, it also holds for the permutation ${\pi }^{*}$.    □

Let us look at Example 2 again. If, after calculating the intervals in Table 2, we introduce a constraint of the form $r_3=7$ (the moment the job is received for processing), this will lead to a change in the intervals for the third job to $[10,10],[12,12],[14,14]$ and for the fourth job to $[13,13],[14,14],[16,16]$. Among the schedules given in the example in Figure 2, only Schedule 3 will remain feasible. The other schedules will become infeasible. Evaluating the recursive function will not result in a feasible schedule. This example demonstrates the importance of including the constraints in the initial value matrix when evaluating the recursive function.

Theorem 3 states that when computing an optimal schedule for the PFSP, one can move from interval calculations to the scalar recursive function $C(j,k)$ (8), although the cardinality of the set of values of the function $C(j,k)$ is less than or equal to the cardinality of the set of values of the function $\mathcal{T}(j,k)$. If the function $\underline{\mathcal{T}}(n,m)$ has several minima, then the function $C(n,m)$ will have the same number of minima.

The permutation $\pi =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)$ denotes the order of the job numbers, and ${\alpha }_i,i=1,2,\dots ,n$ is the number of the job at position $\alpha$ in the schedule (permutation) $\pi$. The recursive function was defined before to have a fixed order of the processing of the jobs. Let us add the permutation $\pi$ to the definition of the function as a global variable so that we can change the order of the jobs. We define new functions: $\widehat{\mathcal{T}}\{n,m,\parallel p_{j,k}\parallel ,\parallel \pi \parallel \}:\widehat{\mathcal{J}}\times \mathcal{M}\to \mathcal{I}$ and $\widehat{C}\{n,m,\parallel p_{j,k}\parallel ,\parallel \pi \parallel \}:\widehat{\mathcal{J}}\times \mathcal{M}\to N$. $\widehat{\mathcal{J}}$ is the set of job position numbers, and $\alpha \in \widehat{\mathcal{J}}$. We include the permutation $\pi$ in the definitions of the recursive functions (6) and (8) so that we can change the processing order of the jobs:

$$\widehat{\mathcal{T}}(\alpha ,k)=\left\{\begin{array}{cc}[p_{\pi \left(1\right),1},T_{max}],\hfill & \alpha =1,k=1;\hfill \\ \widehat{\mathcal{T}}(1,k-1)+[p_{\pi \left(1\right),k},p_{\pi \left(1\right),k}],\hfill & \alpha =1,1<k\le m;\hfill \\ \widehat{\mathcal{T}}(\alpha -1,1)+[p_{\pi (\alpha ,1},p_{\alpha ,1}],\hfill & 1<\alpha \le n,k=1;\hfill \\ \max \{\widehat{\mathcal{T}}(\alpha -1,k),\widehat{\mathcal{T}}(\alpha ,k-1)\}+[p_{\pi \left(\alpha \right),k},p_{\pi \left(\alpha \right),k}],\hfill & 1<\alpha \le n,1<k\le m.\hfill \end{array}\right.$$

$$\widehat{C}(\alpha ,k)=\left\{\begin{array}{cc}{p}_{\pi \left(1\right),1},\hfill & \alpha =1,k=1;\hfill \\ \widehat{C}(1,k-1)+p_{\pi \left(1\right),k},\hfill & \alpha =1,1<k\le m;\hfill \\ \widehat{C}(\alpha -1,1)+p_{\pi \left(\alpha \right),1},\hfill & 1<\alpha \le n,k=1;\hfill \\ \max \{\widehat{C}(\alpha -1,k),\widehat{C}(\alpha ,k-1)\}+p_{\pi \left(\alpha \right),k},\hfill & 1<\alpha \le n,1<k\le m.\hfill \end{array}\right.$$

In the function $\widehat{C}(\alpha ,k)$, where $\alpha ,\alpha =1,2,\dots ,n,$ is the number of the position in the schedule (permutation) $\pi$ and $k,k\in \mathcal{M},$ is the number of the machine, they are the arguments of the recursive function, and the processing times $p_{j,k}$ and the permutation $\pi$ are the parameters of the function.

Example 3.

Here, we calculate the completion times of jobs 1 and 2 on machines 1 and 2. It should be noted that in this case, the first argument of the function $\widehat{C}$ is the number of the position in the schedule π:

• $\widehat{C}(1,1)=p_{\pi \left(1\right),1};$
• $\widehat{C}(1,2)=\widehat{C}(1,1)+p_{\pi \left(1\right),2}=p_{\pi \left(1\right),1}+p_{\pi \left(1\right),2};$
• $\widehat{C}(2,1)=\widehat{C}(1,1)+p_{\pi \left(2\right),1}=p_{\pi \left(1\right),1}+p_{\pi \left(2\right),1};$
• $\begin{array}{cc}\widehat{C}(2,2)& =\max \{\widehat{C}(1,2),\widehat{C}(2,1)\}+p_{\pi \left(2\right),2}\\ & =\max \{p_{\pi \left(1\right),1}+p_{\pi \left(1\right),2},p_{\pi \left(1\right),1}+p_{\pi \left(2\right),1}\}+p_{\pi \left(2\right),2}.\end{array}$

For simplicity of the description, we have discussed the approach for the PFSP. It can be noted that one can extend this procedure to the FSP with possibly different job sequences on the machines.

4. Implementation of the Branch and Bound Method for the PFSP

It should be noted that the PFSP was one of the first combinatorial optimization problems for which the branch and bound (B&B) method was applied [16] soon after its development [22]. A large number of works were devoted to the application of the B&B method for solving the PFSP. References [17,23] review the most important works on B&B algorithms for the PFSP. Since the B&B method follows very organically from the recursive representation of the PFSP, we consider it subsequently.

Evaluation of the Lower Bound LB1. Taking into account the permutation $\pi$ of jobs, for a certain pair $(\alpha ,k)$, the lower bound LB can be determined as follows:

$$\begin{array}{c}\hfill LB(\alpha ,k)=\widehat{C}(\alpha ,k)+\sum _{i=k+1}^m{p}_{\pi \left(\alpha \right),i}+\sum _{i=\alpha +1}^n{p}_{\pi \left(i\right),m}.\end{array}$$

(10)

Remark 2.

Calculating the value of the function $\widehat{C}(\alpha ,k)$ from the value of the function $\widehat{C}(\alpha -1,k)$ is simpler than calculating $LB(\alpha ,k)$. Therefore, it makes sense to calculate the lower bound only for the pair $(\alpha ,m)$. In [24], the effectiveness of the comparison with the lower bound on the last machine was also justified.

In this case, it is possible to move from formula (10) to the formula for calculating the bound on the last machine:

$$\begin{array}{c}\hfill LB(\alpha ,m)=\widehat{C}(\alpha ,m)+\sum _{i=\alpha +1}^n{p}_{\pi \left(i\right),m}.\end{array}$$

(11)

Next, let us formulate the exact meaning of the bound $LB(\alpha ,k)$. In the described case, this means that for a fixed order of a part of the jobs $1,2,\dots ,\alpha$, the processing times of all jobs cannot be less than $LB(\alpha ,k)$ for any arrival order of the remaining jobs $\alpha +1,\alpha +2,\dots ,n$.

Let $\mathsf{\Pi }$ be the set of permutations of n jobs for which the value $\widehat{C}({\alpha }_n,m)$ has already been calculated. Then, the lower bound $LB1$ for the considered job sequences will be

$$LB1=\underset{\pi \in \mathsf{\Pi }}{min}\widehat{C}({\alpha }_n,m).$$

Thus, if the inequality

$$LB(\alpha ,k)\ge LB1$$

is satisfied for the current pair $(\alpha ,k)$, then this sequence of jobs $1,2,\dots ,\alpha -1,\alpha$ is excluded from consideration as not promising, and the corresponding branch of permutations is cut off. The next one will be one of the sequences $1,2,\dots ,\alpha -1,{\pi }^{\prime }\left(1\right)$ with

$${\pi }^{\prime }\in \mathcal{P}(\alpha ,\alpha +1,\dots ,n)and{\pi }^{\prime }\left(1\right)\ne \pi \left(\alpha \right),$$

where $\mathcal{P}(\alpha ,\alpha +1,\dots ,n)$ is the set of all permutations of the $n-\alpha +1$ remaining jobs.

Branching. First of all, the branching must be consistent with the traversal defined by the recursive function. If

$$LB(\alpha ,k)\ge LB1,$$

it is necessary to change the order of the jobs. However, it is necessary to change the order in such a way as to minimize the loss of information when calculating the functions $\widehat{C}(1,1),\widehat{C}(1,2),\dots ,\widehat{C}(\alpha ,m).$ The literature describes many permutation algorithms with different characteristics. Let $\mathcal{P}(1,\dots ,s)=\{{\pi }_1,{\pi }_2,\dots ,{\pi }_{s!}\}$. $x\mathcal{P}\left(\pi \right)$ assigns an element x to each permutation of the set, i.e., $x\mathcal{P}\left(\pi \right)=\{x{\pi }_1,x{\pi }_2,\dots ,x{\pi }_{s!}\}$. In this case, the algorithm for generating permutations should calculate them in such a sequence that they satisfy the following recursive property:

$$\mathcal{P}(j_1,j_2,\dots ,j_s)=\bigcup _{i=1}^s{j}_i\mathcal{P}(j_1,j_2,\dots ,j_{i-1},j_{i+1},\dots ,j_s).$$

(12)

This property, after calculating the function $C(j,k)$, allows one to study all permutations $\mathcal{P}(j+1,j+2,\dots ,n)$ of the ”tail” of the queue of jobs being scheduled and only then track back.

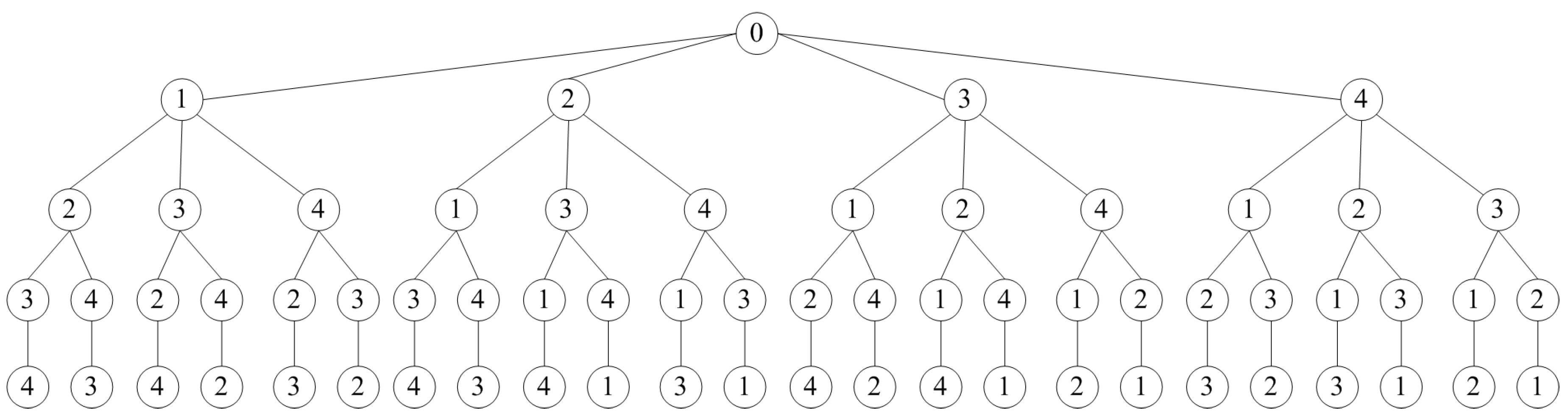
Example 4.

Figure 6 shows an example of a complete permutation tree that satisfies Property (12) for $n=4$. The root of the tree is an auxiliary vertex, and the permutation corresponds to some path from the root. The vertical edge shows the next level of recursion. It connects the initial sequence to its tail. The tree is traversed from top to bottom and from left to right. In this example, the permutations will be generated in the following order: (1,2,3,4), (1,2,4,3), (1,3,2,4), (1,3,4,2), …, (4,3,1,2), (4,3,2,1). There are 24 permutations in total.

This algorithm can be implemented through recursive copying of the tail of permutations. This is a costly operation, but the algorithm can be modified so that the permutation $\pi$ exists in a single instance as a global variable. This is done using forward and reverse permutations of two jobs (when returning along the search tree). The description of the B&B algorithm is given in Appendix A.

5. ‘And’ Function

The flow shop problem discussed above is more a subject of theoretical research and has limited application in practice. In order to bring it closer to practice, various additional elements can be introduced; first of all, various types of constraints. In real production, the main machine chain is served by various preparatory operations, for example, those associated with delivery from the warehouse to the production line; preparatory steps; technological issues; testing, etc.

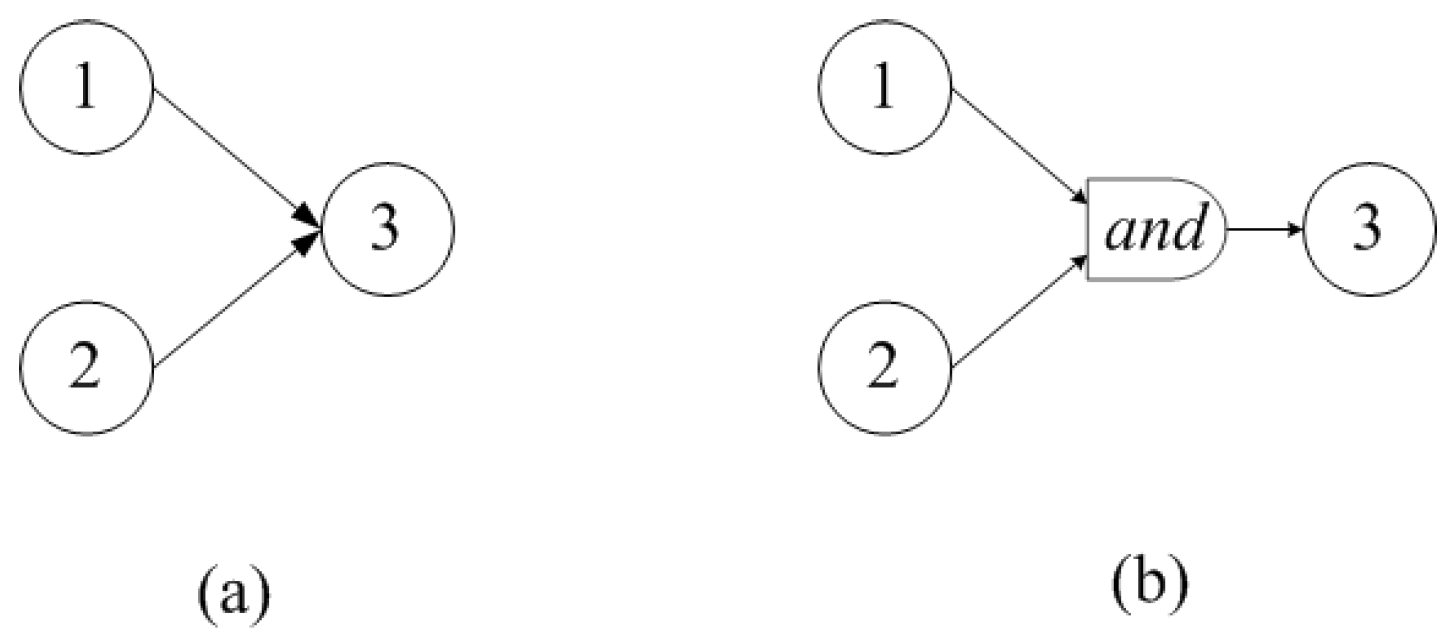
Next, we expand the PFSP by introducing the ‘and’ function. A well-known construction, shown in Figure 7a, denotes a precedence relation in which the execution of a job on machine 3 can only begin after the completion of the jobs on machines 1 and 2. Using the ‘and’ function, it will look similar to Figure 7b. In what follows, we will interpret the ‘and’ function as a machine with zero processing time for any job. Thus, the chained precedence graph for the PFSP is expanded into an acyclic precedence graph when using the ‘and’ function. Therefore, the PFSP is transformed towards an Assembly Line job (AL), but without the presence of a conveyor belt and workstations. This problem can be called the Assembly Permutation Flow Shop Problem (APFSP). The absence of a conveyor belt frees it from the ”cycle time” limitation, and the absence of workstations frees it from solving the balancing problem, i.e., an optimal distribution of the jobs among the stations, taking into account the cycle time.

Despite the absence of assembly line attributes, this model can have wide applications.

The ‘and’ function in the interval representation ${\mathcal{T}}_{and}\{n,m,\parallel p_{j,k}\parallel ,\parallel T^0(j,k)\parallel \}:\mathcal{J}\times \mathcal{M}\to \mathcal{I}$ is as follows:

$${\mathcal{T}}_{and}(j,k)=\max \{\mathcal{T}(j,pre{d}_1\left(k\right)),\mathcal{T}(j,pre{d}_2\left(k\right))\},$$

where $pre{d}_1$ and $pre{d}_2$ are precedence functions that will be defined later. Therefore,

$${\mathcal{T}}_{and}(j,k)=[\max \{\underline{\mathcal{T}}(j,pre{d}_1\left(k\right)),\underline{\mathcal{T}}(j,pre{d}_2\left(k\right))\},\max \{\overline{\mathcal{T}}(j,pre{d}_1\left(k\right)),\overline{\mathcal{T}}(j,pre{d}_2\left(k\right))\}],$$

or in a scalar expression $C_{and}\{n,m,\parallel p_{j,k}\parallel \}:\mathcal{J}\times \mathcal{M}\to N$:

$$C_{and}(j,k)=\max \{C(j,pre{d}_1\left(k\right)),C(j,pre{d}_2\left(k\right))\}.$$

(13)

Accordingly, we get the function ${\widehat{C}}_{and}\{n,m,\parallel p_{j,k}\parallel ,\parallel \pi \parallel \}:\widehat{\mathcal{J}}\times \mathcal{M}\to N$, where $\widehat{\mathcal{J}}$ is the set of job position numbers and $\alpha \in \widehat{\mathcal{J}}$:

$${\widehat{C}}_{and}(\alpha ,k)=\max \{\widehat{C}(\alpha ,pre{d}_1\left(k\right)),\widehat{C}(\alpha ,pre{d}_2\left(k\right))\}.$$

Including the ‘and’ function in the PFSP causes the machines to process the job according to the precedence tree. To set a specific order of the precedence graph traversal, we assume that the function $pre{d}_1$ is always the first one in Formula (13) and determines the upper arc in Figure 7b. Adding the ‘and’ function causes the assumption in Section 3 to be invalid: “a job cannot be processed by more than one machine at a time”, since machines 1 and 2 in Figure 7b can execute the same job simultaneously.

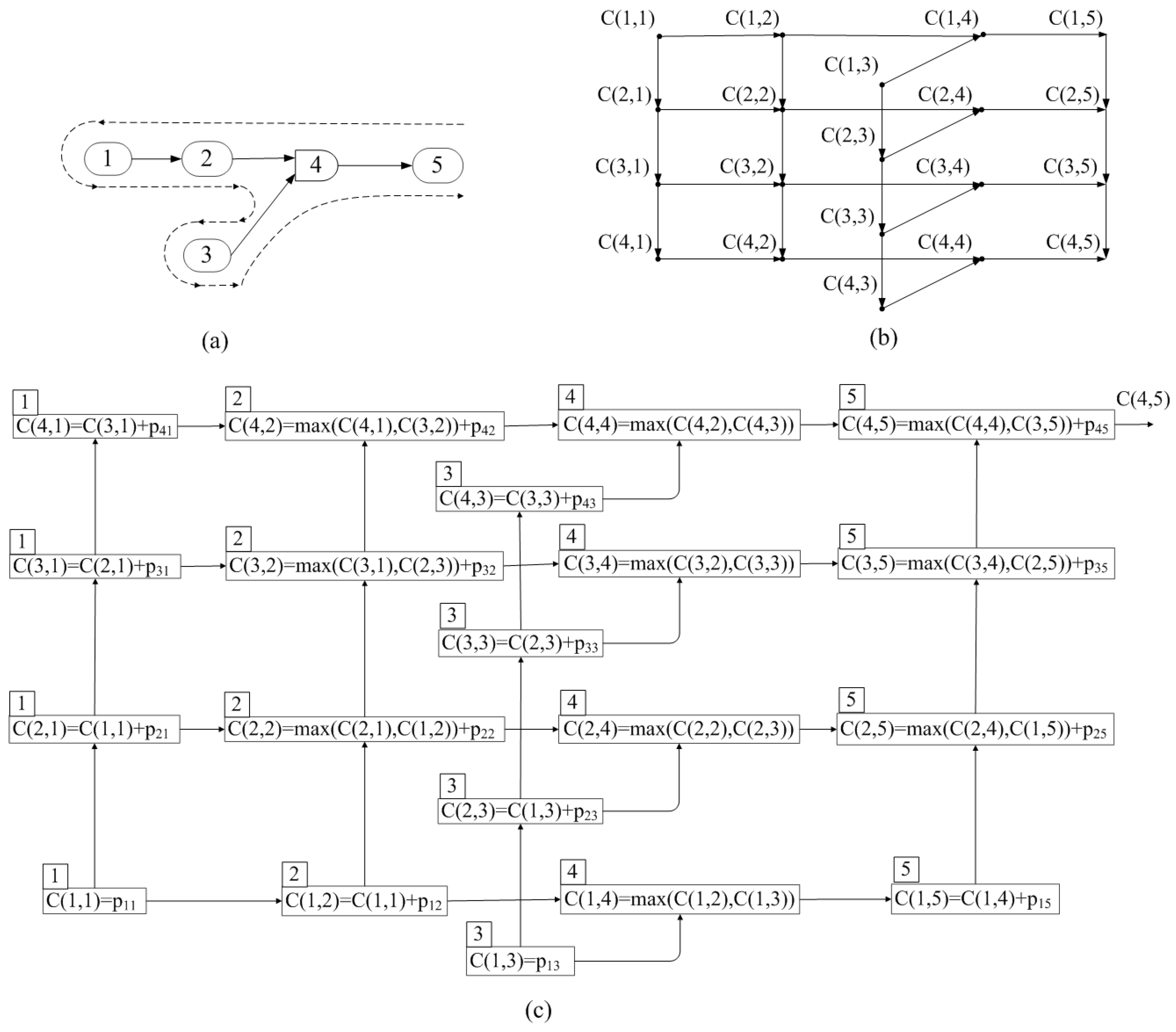
We prove that when adding the ‘and’ function to the PFSP (i.e., $C(j,k)=C_{and}(j,k)$ and $\widehat{C}(\alpha ,k)={\widehat{C}}_{and}(\alpha ,k)$), Theorem 3 remains valid, and the function $C(j,k)$ supplemented by $C_{and}(j,k)$ also implements a greedy algorithm for a fixed sequence of jobs. Figure 8a shows an example of a precedence graph between the machines. Figure 8b shows the precedence graph between the machines and jobs (with a fixed order of jobs). Figure 8c shows the computation (superposition) graph of the recursive function for a certain sequence of four jobs. In the latter case, the arc determines the transfer of the value $C(j,k)$.

Adding the ‘and’ function to the PFSP causes the machines to process a job according to the precedence tree. The graph in Figure 8b is acyclic. In this case, it is convenient to traverse the graph according to the jobs, i.e., the first job tree, the second job tree, etc., in accordance with the job permutation algorithm. The tree of each job is traversed as indicated in the figure by the dotted line.

6. Implementation of the Branch and Bound Method for the APFSP

When implementing any method for the APFSP, it is necessary to switch to a precedence graph representation with typed vertices. Let us define the set $\{sop,op,and\}$ as the following types of vertices:

• $sop$—the starting vertex of the graph (machine);
• $op$—the intermediate or final vertex of a graph (machine);
• and—the vertex corresponding to the ‘and’ function.

Let us define the function $Type:\mathcal{M}\to \{sop,op,and\}$ that gives this type of a vertex. It is necessary to define explicitly the precedence functions for the vertices $pred,pre{d}_1,pre{d}_2:\mathcal{M}\to \mathcal{M}$.

• $pred$ is defined for the vertices of type $op$, $k_1=pred\left(k_2\right)$, meaning that the vertex $k_1$ immediately precedes the vertex $k_2$.
• $pre{d}_1$ and $pre{d}_2$ are defined for the vertices of type ‘and’; $k_1=pre{d}_1\left(k_3\right)$ means that the vertex $k_1$ immediately precedes the vertex $k_3$ along the first incoming edge; $k_2=pre{d}_2\left(k_3\right)$ means that the vertex $k_2$ precedes the vertex $k_3$ along the second incoming edge.

The main issues of the implementation of the method are also the choice of the lower bound (LB) calculating techniques and branching algorithms. Consider the calculation of the lower bound LB1 by traversing the jobs, that is, similar to Figure 5, but with tree traversal. This means that Formulas (8) and (13) are used.

Evaluation of the Lower Bound LB1. Analysis of Formula (8) shows that when calculating the function $C(n,m)$, the operations $(j,k)$ are traversed in the order indicated in Figure 5a. Consider the example in Figure 8a. If the ‘and’ function is present, the job processing tree will be traversed as shown in the figure. Naturally, the value of $LB(\alpha ,k)$ is calculated after calculating $\widehat{C}(\alpha ,k)$. The values of $LB$ for the job $\alpha$$(1<\alpha <n)$ considering that $p_{\alpha ,4}=0$ can be calculated as follows:

• $LB(\alpha ,1)=\widehat{C}(\alpha ,1)+p_{\alpha ,2}+p_{\alpha ,4}+p_{\alpha ,5}+p_{\alpha +1,5}+\dots +p_{4,5};$
• $LB(\alpha ,2)=\widehat{C}(\alpha ,2)+p_{\alpha ,4}+p_{\alpha ,5}+p_{\alpha +1,5}+\dots +p_{4,5};$
• $LB(\alpha ,3)=\widehat{C}(\alpha ,3)+p_{\alpha ,4}+p_{\alpha ,5}+p_{\alpha +1,5}+\dots +p_{4,5};$
• $LB(\alpha ,4)=\widehat{C}(\alpha ,4)+p_{\alpha ,5}+p_{\alpha +1,5}+\dots +p_{4,5};$
• $LB(\alpha ,5)=\widehat{C}(\alpha ,5)+p_{\alpha +1,5}+\dots +p_{4,5}.$

From the example considered, it is clear that the calculation of $LB(\alpha ,k)$ is carried out using the same tree traversal as when calculating $\widehat{C}(\alpha ,k)$. In this case, for $LB(\alpha ,k)$, Equality (10) is transformed into the following equality:

$$\begin{array}{c}\hfill LB(\alpha ,k)=\widehat{C}(\alpha ,k)+\sum _{i\in U_{\alpha ,m}}{p}_{\pi \left(\alpha \right),i}+\sum _{i=\alpha +1}^n{p}_{\pi \left(i\right),m},\end{array}$$

where $U_{\alpha ,m}$ is the set of vertices belonging to the path from $\alpha$ to m in the machine precedence graph. The uniqueness of this path follows from the fact that the machine precedence graph is a tree and m is its root node (see, for example, Figure 8a or Figure 8b). Taking into account Remark 2, Expression (11) can also be used.

Appendix A presents three algorithms used for the solution of the APFSP.

The described algorithms work both for the PFSP and the APFSP. The only difference is in the definitions of the $pred$ function. In the case of the PFSP, $pred\left(k\right)=k-1$. For the APFSP, the precedence functions are determined from the precedence graph or a matrix. In this case, it is obvious that for the APFSP, the complexity of the B&B algorithm does not increase. An important feature should be noted. In the case when the last vertex in the precedence graph is the ‘and’ function, the B&B algorithm executes correctly, but its “predictive power” is reduced to zero.

Recursive functions also allow one to calculate the values of objective functions, different from makespan. This can be done by replacing the function $\widehat{C}(\alpha ,k)$ by

$$C^{*}(\alpha ,k)=\widehat{C}(\alpha ,k);<calculatingthevalueoftheobjectivefunction>.$$

In this case, the calculation of the optimization criterion is concentrated in the body of the function $C^{*}(\alpha ,k)$ and is invariant to the details of the optimization method.

7. Evaluating the Effectivenes of the Algorithm

Existing publications on the B&B method in scheduling theory use tests that are characterized by the computing times using specific hardware. To assess the effectiveness of the B&B method without using pure computing time indicators, it is advisable to determine the reduction in completed elementary calculations due to the fact that some sets of job permutations were deliberately discarded and not checked. There are two possible approaches here:

• consider it elementary to calculate the completion time of the job’s last technological operation (approach L);
• consider it elementary to calculate the completion time of each technological operation of each job (approach A).

In both cases, it is necessary to determine the maximum possible number of such calculations when solving a problem for n jobs and m machines, then to compare it with the number of calculations actually performed.

In the L approach, the maximum number of elementary computations is determined by the permutation generation algorithm (see Appendix A). At each step, this algorithm either adds a new job to the already fixed initial part of the vector $\pi$ or replaces the last job in this fixed part by the next one. In both cases, the completion time of the last technological operation of the last job in the fixed part of $\pi$ is calculated. The completion times of all technological operations of all previous jobs are already known and do not need to be calculated again. Thus, an “elementary computation” is the calculation of m elements of the job completion times matrix ($T_{op}$) row, and the total number of such computations is equal to the number of different variants of the initial part of the vector $\pi$ generated by the algorithm.

Consider, for example, the generation of permutations and the computation of the completion times for three jobs ($n=$3). If the rejection of branches of the search along the lower bound $LB$ is never performed, then the sequence of actions performed by the algorithm is described by

Table 3. Sequence of actions of the algorithm for n = 3 without the rejection of branches.

Recursion Level	Algorithm Argument	$\mathit{\pi }$	$\mathit{\pi }$ Fixed Part	$\mathit{\pi }$ “Tail”	Computed Top Row
0	1	(1,2,3)	()	(1,2,3)	–
1	2	(1,2,3)	(1)	(2,3)	1
2	3	(1,2,3)	(1,2)	(3)	2
3	4	(1,2,3)	(1,2,3)	()	3
2	3	(1,3,2)	(1,3)	(2)	2
3	4	(1,3,2)	(1,3,2)	()	3
1	2	(2,1,3)	(2)	(1,3)	1
2	3	(2,1,3)	(2,1)	(3)	2
3	4	(2,1,3)	(2,1,3)	()	3
2	3	(2,3,1)	(2,3)	(1)	2
3	4	(2,3,1)	(2,3,1)	()	3
1	2	(3,2,1)	(3)	(2,1)	1
2	3	(3,2,1)	(3,2)	(1)	2
3	4	(3,2,1)	(3,2,1)	()	3
2	3	(3,1,2)	(3,1)	(2)	2
3	4	(3,1,2)	(3,1,2)	()	3

.

As a result of the algorithm’s operation, 15 initial parts of the vector $\pi$ were generated (including 6 complete permutations of 3 tasks), and 15 elementary computations of the $T_{op}$ rows were performed. With the size h of the initial part of the vector $\pi (1\le h\le n)$, the total number of such generated initial parts is equal to the number of placements from n to h:

$$A_n^h={\displaystyle \frac{n!}{(n-h)!}}.$$

The total number of initial parts of the vector $\pi$ of all possible sizes from 1 to n is equal to

$$S_{max}\left(n\right)=\sum _{h=1}^n{A}_n^h=\sum _{h=1}^n{\displaystyle \frac{n!}{(n-h)!}}.$$

When using the B&B method, the algorithm will perform all $S_{max}$ elementary calculations extremely rarely. However, this estimate is achievable in practice. Let us consider the degeneration case in which all rows of the matrix $p_{j,\ast }$ are identical. In this case, the $LB$ value calculated using Formulas (10) or (11) will be the same for any values of the arguments, and none of the branches will be discarded. The number of elementary calculations performed by the algorithm will be exactly $S_{max}$. In approach A, the maximum possible number of elementary calculations is m times $S_{max}\left(n\right)$ since every row of the job completion times matrix contains m elements. In the optimized algorithm, the number of real calculations will be less than the given values. The effectiveness of solving a problem can be assessed by the proportion of calculations not performed. If $S_L\left(i\right)$ and $S_A\left(i\right)$ are the numbers of calculations when solving problem number i for n jobs and m machines using approaches L and A, respectively, then the efficiency of the solutions can be estimated using the following formulas:

$$E_L(n,i)={\displaystyle \frac{S_{max}\left(n\right)-S_L\left(i\right)}{S_{max}\left(n\right)}},$$

$$E_A(n,m,i)={\displaystyle \frac{m{S}_{max}\left(n\right)-S_A\left(i\right)}{m{S}_{max}\left(n\right)}}.$$

A zero value of these indicators means that the use of the method did not provide any gain in the number of calculations; a theoretically unattainable value of 1 (or 100%) means that the use of the method completely eliminated the need for calculations.

The authors performed 10,000 tests for problems with 5–11 jobs on random acyclic graphs with random job processing times. The problem generation parameters in these experiments were as follows:

• total number of nodes in the acyclic graph (technological operations): 15;
• number of initial operations: random value in [1,3];
• number of ‘and’ operations: random value in [1,4];
• job processing times ($p_{j,k}$): random value in [1,10].

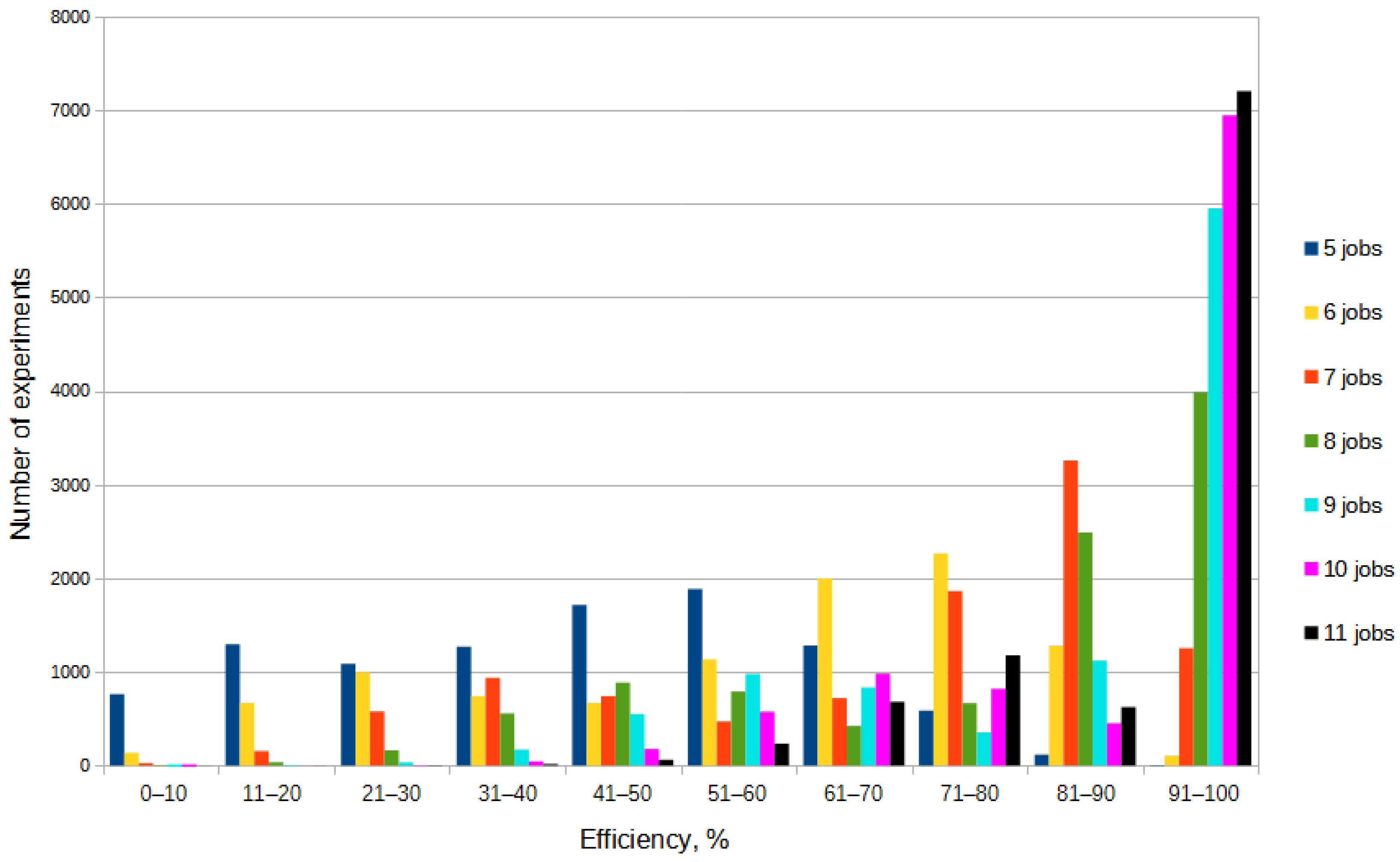
All random values are uniformly distributed integers. For each number of jobs, a histogram of the distribution of the number of experiments in the ranges of the $E_L$ efficiency obtained in the experiment was constructed. Thus, seven histograms were constructed, presented in Figure 9.

The histograms in the figure show how many times a particular $E_L$ efficiency was achieved during the random experiments. The horizontal axis shows the ten-percent efficiency ranges (from “0–10” to “91–100”), and the vertical axis shows the number of experiments out of 10,000 performed in which the corresponding efficiency value was achieved. It can be seen from the figure that as the number of jobs increases, the efficiency of the algorithm also increases. The histogram for five jobs has a maximum around 50%. This means that most of the experiments with five jobs showed a fifty percent efficiency; that is, approximately half of the maximum possible number of elementary calculations for a given task were performed. However, a significant number (about 800) of experiments showed an efficiency of less than 10%. As the number of jobs increases, the histogram maximum moves into the high efficiency region. For 11 jobs, more than 7000 out of 10,000 experiments performed showed an efficiency in the range of 91–100%; i.e., less than 10% of the number of elementary calculations that would be required to solve the problem when analyzing all possible permutations were performed.

8. Job Shop Problem

The job shop problem (JSP) is a generalization of the FSP. For each job, the JSP allows its own set of machines to be used from the set $\mathcal{M}=\{1,2,\dots ,m\}$ and its own order of execution of any job by the machines. The order of execution is determined by the precedence relationships between the machines, and it is possible that a job does not use the entire set of machines. In this section, we consider a special variant of the JSP, namely the permutation job shop problem (PJSP), where the job sequence is identical for all machines. Figure 10a shows an example of a job shop precedence graph for some fixed order of jobs. Just as in Figure 1, each job corresponds to a row of machines. If a job uses a machine, the corresponding graph vertex is shaded. The horizontal arcs represent the precedence relationships between the machines, and the vertical arcs represent the precedence relationships between the jobs for some fixed order of the jobs. We will call the pair (job number, machine number) relevant if machine k is used to perform job j, and we will call machine k relevant for job j and irrelevant otherwise. All machines that are irrelevant for job j are characterized by a zero processing time, i.e., $p_{j,k}=0$. Example Figure 10a shows that for each job, the precedence relationships between the machines are defined only between the machines that are relevant for the given job. Figure 10b shows the graph that results from swapping the third and fifth jobs of the graph in Figure 10a. Obviously, when the jobs are rearranged, the precedence relationships between the machines for each job do not change, but they do change between the jobs. The precedence relations between the machines are defined by the precedence function $predk:\mathcal{J}\times \mathcal{M}\to \mathcal{M}$ as follows:

$$predk(j,k)=\left\{\begin{array}{c}{k}^{\prime },ifinjobjmachine{k}^{\prime }immediatelyprecedesmachinek;\hfill \\ 0,ifthereisnomachineinjobjthatprecedesmachinek.\hfill \end{array}\right.$$

For a fixed sequence of jobs, the function $predk(j,k)$ is implemented by a precedence matrix predefined by the precedence graph. For example, the precedence matrix W for jobs j with respect to machines k and matrix P of the given operation processing times, corresponding to the graph in Figure 10a, will have the following form:   

$$W=\left(\begin{array}{cccc}0& 1& 2& 3\\ 0& 3& 0& 0\\ 0& 4& 0& 3\\ 2& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right),P=\left(\begin{array}{cccc}3& 2& 2& 4\\ 0& 5& 3& 0\\ 0& 3& 1& 1\\ 3& 1& 1& 0\\ 0& 0& 4& 0\end{array}\right).$$

When rearranging the jobs to maintain correspondence, it is enough to carry out the appropriate rearrangement of the precedence matrix rows.

Let us define a recursive function: ${\widehat{C}}_{JS}\{n,m,\pi ,\parallel p_{i,j}\parallel \}:\widehat{\mathcal{J}}\times \mathcal{M}\to N$. Here, $\widehat{\mathcal{J}}$ is the set of job position numbers and $\alpha \in \widehat{\mathcal{J}}$.

$${\widehat{C}}_{JS}(\alpha ,k)=\left\{\begin{array}{cc}{p}_{\pi \left(\alpha \right),k},\hfill & \alpha =1,predk\left(\pi \right(\alpha ),k)=0;\hfill \\ {\widehat{C}}_{JS}(\alpha ,predk(\pi \left(\alpha \right),k))+p_{\pi \left(\alpha \right),k},\hfill & \alpha =1,predk\left(\pi \right(\alpha ),k)\ne 0;\hfill \\ {\widehat{C}}_{JS}(\alpha -1,k)+p_{\pi \left(\alpha \right),k},\hfill & 1<\alpha \le n,predk\left(\pi \right(\alpha ),k)=0;\hfill \\ \max \{{\widehat{C}}_{JS}(\alpha -1,k),\hfill & \\ {\widehat{C}}_{JS}(\alpha ,predk(\pi \left(\alpha \right),k))\}+p_{\pi \left(\alpha \right),k},\hfill & 1<\alpha \le n,predk\left(\pi \right(\alpha ),k)\ne 0.\hfill \end{array}\right.$$

The function is defined for all argument values.

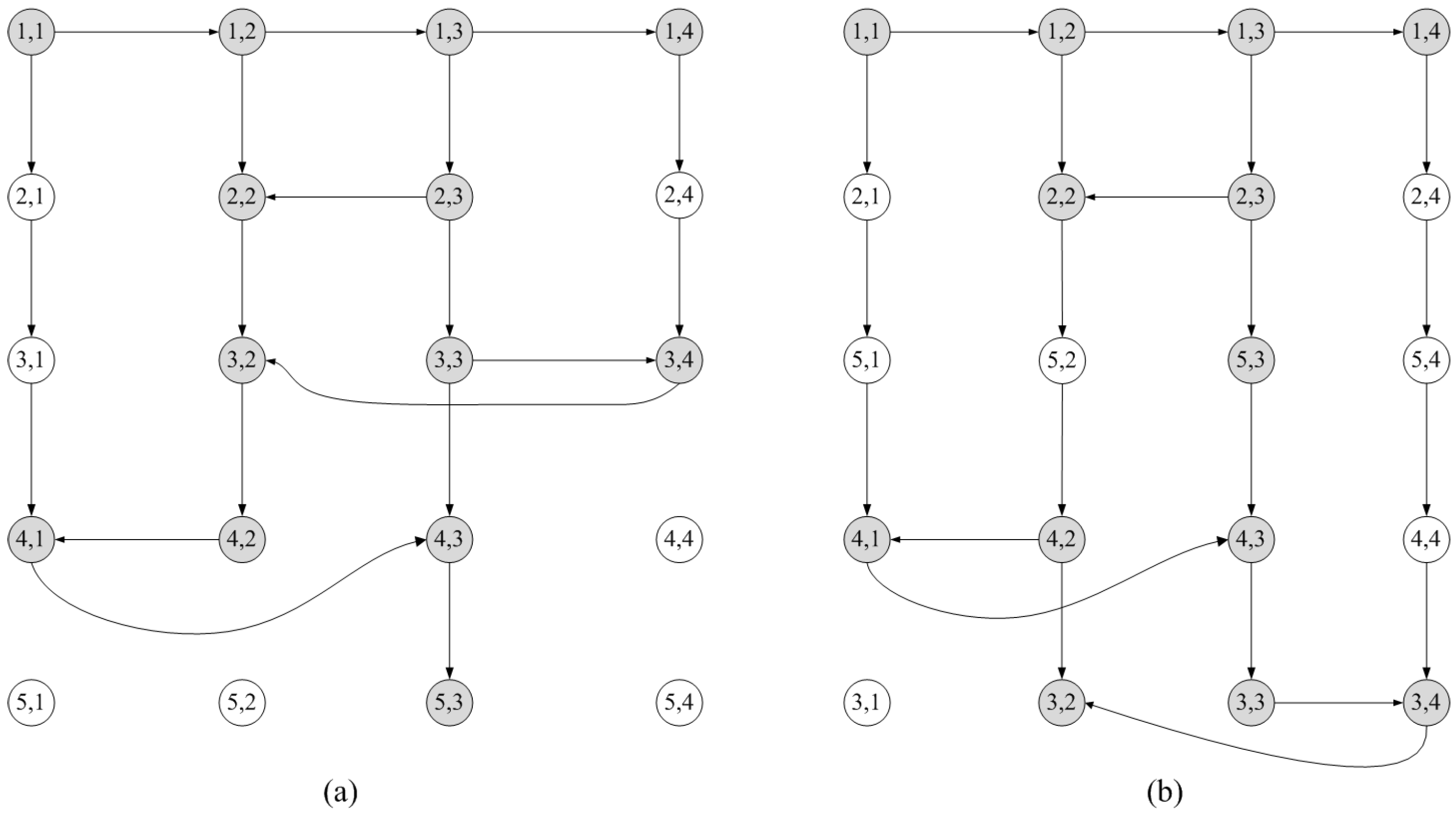
The set of machines relevant to some job, connected by the arcs of the precedence relationships, form one or more simple chains of machines. Thus, in Figure 11a, job 2 includes two simple chains of relevant machines $\left\{\right(2,1),(2,4\left)\right\}$ and $\left\{\right(2,2),(2,3\left)\right\}$. Let us assume that for each job, one of the following two conditions is satisfied:

• a job can contain only one chain of relevant machines;
• if a job contains two or more chains of relevant machines, then these chains cannot have common machines.

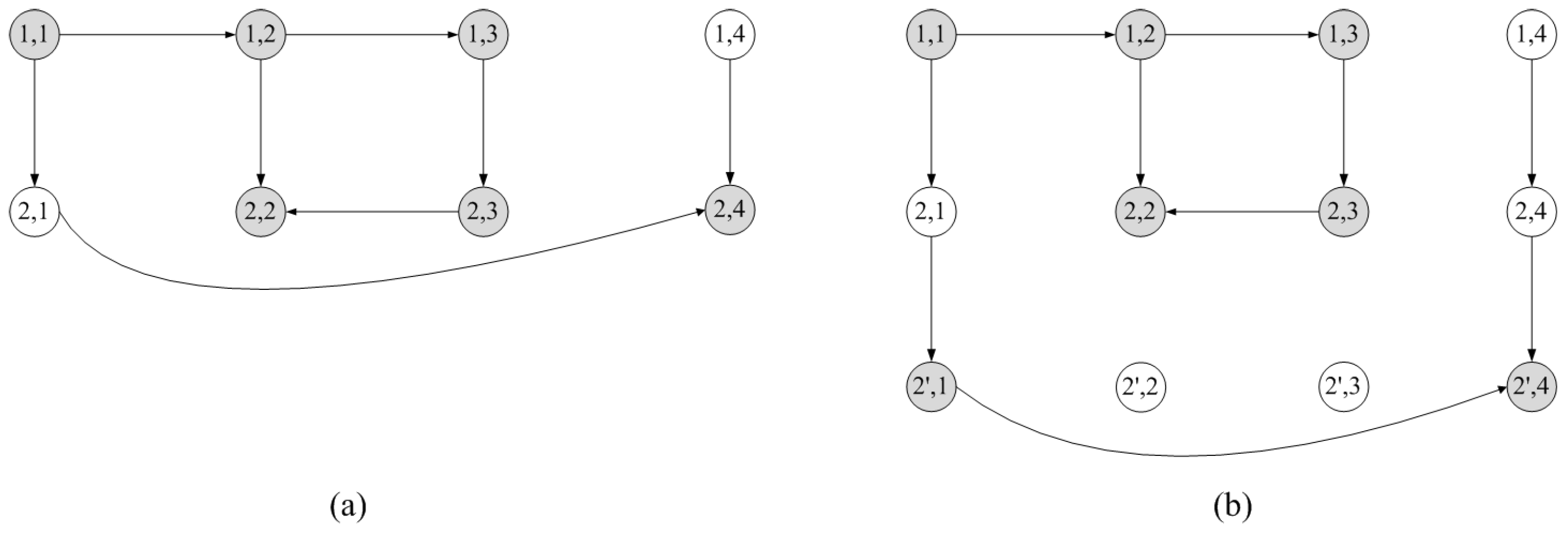
In this case, such a job can be split into two (or more) jobs so that each job contains one chain of machines. An example of such a split is shown in Figure 11. Here, job 2, consisting of two chains (see Figure 11a), is split into two jobs, job 2 and job 2’ (see Figure 11b), such that each of them contains one chain. This division of the job into two or more jobs increases the total number of jobs and the total number of combinatorial options when searching for an optimal job order. It can be proven that with such a split, there exists an optimal schedule with a value of $C_{max}$ for the new set of jobs that will be the same as for the original set of jobs.

Theorem 4.

Let there be a set of n jobs. If some job is a set of w simple chains of machines, then this job can be broken down into w jobs such that each job contains only one chain. If the original set of jobs for some processing order has a completion time of $C_{max}$, then for the new set of $n+w-1$ jobs, there exists an order with a completion time of $C_{max}$.

Proof. 

Let some order of n jobs be fixed, and let the job under consideration have the number $j(1<j\le n)$. Let us make two assumptions. First, suppose that the job contains only two simple chains of machines. Second, for simplicity and clarity, assume that the two chains consist of sequences of adjacent machines, as shown in Figure 12.

Here, the first chain consists of q machines, and the second consists of z machines. The remaining $m-q-z$ machines for job j are irrelevant and are not displayed. These assumptions do not reduce the generality of the problem statement. If the statement can be proved for two chains, then a successive application of the job splitting will allow it to be applied to any other set of chains. The second assumption makes the statement of the theorem more clear, but it does not change the essence of the problem. The completion time of the $k_i$-th machine ($k_1<k_i\le k_q$) $c_{k_i}^x$ depends on the completion time $x_{k_i}$ of job $i(i<j)$ on some $k_i$-th machine and the completion time $c_{k_{i-1}}^x$ of job j on machine $k_{i-1}$. If a machine is the first one in the chain, then its completion time depends only on $x_{k_1}$. The same reasoning applies to the second chain with the times $c_{k_i}^y,y_{k_i}(q+1\le i\le q+z)$. Let us divide job j into two jobs so that each job j and $j^{\prime }$ will contain one chain, as shown in Figure 13. The irrelevant machines of job j will also be irrelevant for the new jobs and are not shown in the figure.

Since the irrelevant machines do not change the completion time when it is transmitted transitively vertically and they have no horizontal connections, then at the output of the two jobs j and $j^{\prime }$, the values of the completion times $c_{k_i}^x$ and $c_{k_i}^y$ do not change. For the machines that are not relevant in both works, the values also do not change. Therefore, if the fixed order corresponded to an optimal schedule, then the new order of the split jobs will have the same completion time value. Moreover, with the new set of jobs, it is possible to have a schedule with a shorter completion time. These arguments apply to job $j>1$. For the first job, similar arguments apply in the absence of the values $x_{k_i}$ and $y_{k_i}$.    □

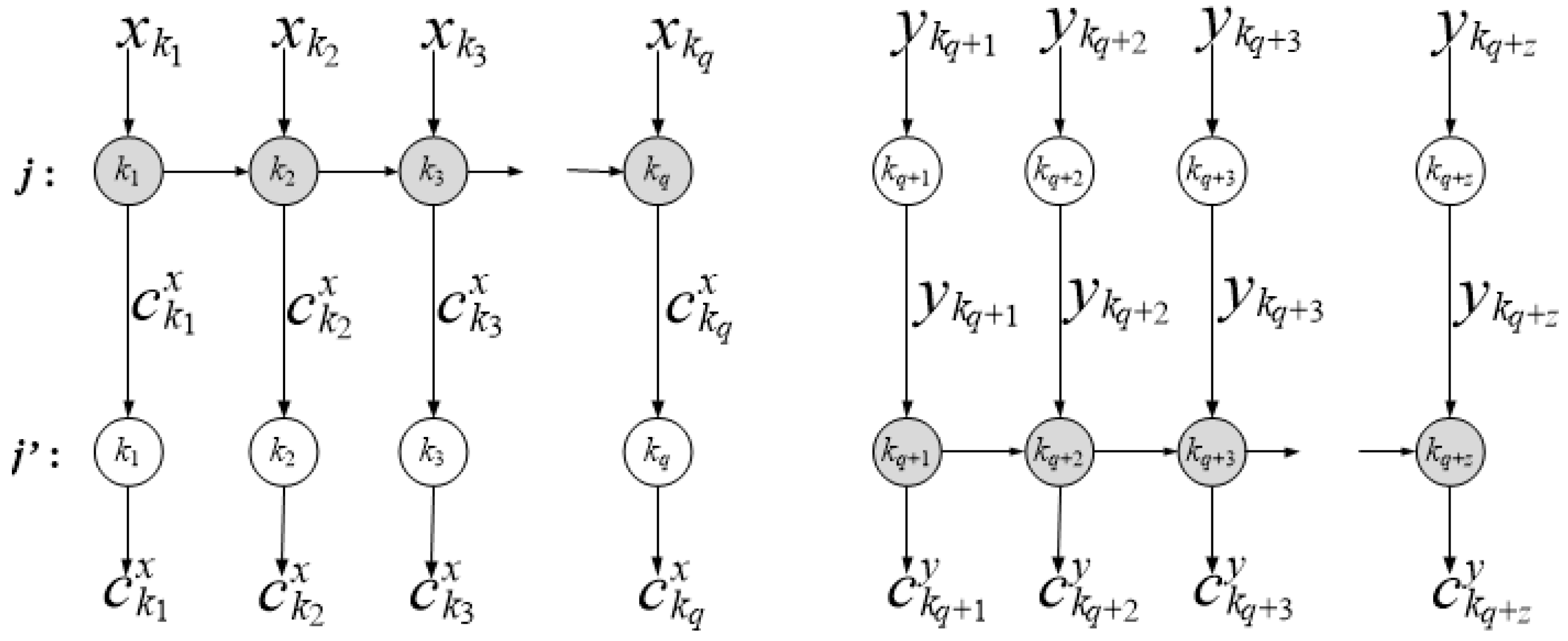
In what follows, we will assume that each job contains one simple chain of relevant machines. To be able to calculate the function ${\widehat{C}}_{JS}(\alpha ,k)$ for all jobs and relevant machines, we will do the following:

• Let us supplement the set $\mathcal{M}$ with the machine $m+1$. This will be a virtual machine, and the time it takes to perform any work will be zero ($p_{j,m+1}=0$ for $1\le j\le n$);
• For each job, we define an additional precedence relation between machine $m+1$ and the last actual machine in the simple chain that performs the given job. The last machine in the chain always precedes machine $m+1$.

The result of the additions for the graph in Figure 10a is shown in Figure 14a. If we call the function ${\widehat{C}}_{JS}(n,m+1)$, then, in the process of calculation, it will go through the machines and jobs in the order shown in Figure 14b using the numbered arrows. If arrows hit vertices where ${\widehat{C}}_{JS}$ has already been evaluated, they are returned (the function is not re-evaluated). This corresponds to a memorized computation, which significantly reduces the overall amount of computation.

It may seem that there is no need to add machine $m+1$, and we can complete the precedence relationships with machine m. However, if machine m for some job j is inside a chain of machines, as in Figure 11a for job 3, then the calculations will be incorrect.

The function ${\widehat{C}}_{JS}(\alpha ,k)$ is completely defined. For the relevant pairs $(\alpha ,k)$, it calculates the time it takes for the k-th machine to complete job $\alpha$. For the irrelevant pairs $(\alpha ,k)$, it computes the completion time of job $\alpha -1$ on machine k. From the example, it is clear that the function ${\widehat{C}}_{JS}(\alpha ,m+1)$ for each job traverses only the relevant machines.

9. Conclusions

This article was devoted to a new methodology of using the apparatus of recursive functions for formulating and solving the PFSP, APFSP, and PJSP classes of scheduling problems. The fact that recursive functions, unlike analytical ones, are calculated by some algorithms significantly expands their capabilities. A recursive function, in addition to its main purpose of calculating the completion time of an operation, can include accompanying algorithms: checking time constraints, calculating objective functions for various purposes, checking the availability of resources, etc. This frees the optimizer from these problems and makes it invariant to different tasks.

When using the B&B method for the PFSP and APFSP, the simplest form of a lower bound has been used. A detailed review of the B&B method and lower bounds for the PFSP are given in [20]. We think that the main result is an organic transition using recursive functions from the PFSP to the more general and relevant APFSP.

For the APFSP, this paper considers tree graphs, but it is obvious that the method is applicable to acyclic graphs. A recursive function, by definition computed using an algorithm, allows one to integrate into this algorithm the features of various problems of scheduling theory. With the domain of the definition of the function and the set of its values unchanged (which was achieved for the three problems under consideration), this will allow one using a common solver for these problems. Approximate scheduling optimization algorithms, such as ant colony (CA) or simulated annealing (SA), only require the function to be computable. Accordingly, specialists who use, e.g., the CA or SA algorithms can use these recursive functions.

This article does not address the issue of computational efficiency. Recursive functions are not efficient when evaluated directly. However, there are transformations of calculations, such as using previously calculated values (memorized computation), switching from recursion to iteration, avoiding the use of a system memory stack, etc., which significantly increase the efficiency.

The following results have been obtained:

• construction of recursive functions with a common domain of definition and a common set of values for calculating the makespan when modeling the PFSP, APFSP, and PJSP;
• development of a B&B algorithm unified for all three problems;
• experimental calculations have been performed with a random generator of test instances; an analytical assessment of the quality of the B&B optimizer has been given as the ratio of the volume of calculations during the elimination of variants to the volume of calculations during the exhaustive search.

The obtained results allow for the following developments in the future:

• development of new recursive functions that allow the PFSP to be extended to solve practical problems;
• improvement of the efficiency of calculating recursive functions and evaluating them on test instances;
• use of heuristic optimization methods such as ant colony, simulated annealing, etc., as a general method for solving a variety of problems described by recursive functions;
• investigation of the applicability of a method based on recursive functions for describing and solving non-permutation flow shop problems.