Abstract
In this article, we present a novel reinforcement learning-based framework in the discrete cosine transform to achieve better image steganography. First, the input image is divided into several blocks to extract semantic and structural features, evaluating their suitability for data embedding. Second, the Proximal Policy Optimization algorithm (PPO) is introduced in the block selection process to learn adaptive embedding policies, which effectively balances image fidelity and steganographic security. Moreover, the Deep Q-network (DQN) is used for adaptively adjusting the weights of the peak signal-to-noise ratio, structural similarity index, and detection accuracy in the reward formulation. Experimental results on the BOSSBase dataset confirm the superiority of our framework, achieving both lower detection rates and higher visual quality across a range of embedding payloads, particularly under low-bpp conditions.
Keywords:
image steganography; deep reinforcement learning; dct block selection; adaptive reward adjustment MSC:
68P30
1. Introduction
Image steganography is a crucial branch of information hiding, playing an irreplaceable role in modern information security and privacy protection. By embedding secret data into digital media such as images in a visually imperceptible manner, steganography enables the transfer of sensitive information without arousing suspicion.
Traditional image steganography methods can be broadly categorized into spatial-domain and transform-domain techniques. Spatial-domain steganographic methods embed secret messages by directly modifying the pixel intensity values of the image, typically operating on raw spatial information without transforming the image into a different domain. The WOW (Wavelet Obtained Weights) [1] algorithm introduces directional filters to estimate embedding distortion based on local predictability, and adaptively embeds data into textured regions to reduce detectability. HILL (High-pass filter, Low-pass filter, Low-pass filter) [2] computes embedding costs based on a combination of high-pass, low-pass, and Laplacian filtering responses, favoring texture-rich regions for message embedding while avoiding smooth areas.
Transform-domain methods hide information by modifying transform coefficients, thereby preserving visual quality. Wang et al. [3] proposed a non-additive distortion model that maintains block boundary consistency in JPEG images, while JoCoP (Joint Cost Learning and Payload Allocation) [4] jointly optimizes embedding cost estimation and payload distribution via attention mechanisms. These approaches typically rely on manually designed distortion functions. However, early algorithms with fixed embedding patterns lack robustness against modern steganalysis, as advanced techniques can easily reveal their traces [5]. Thus, the security of traditional frequency-domain steganography faces increasing challenges.
Deep learning techniques have in recent years brought new opportunities to steganography. Han et al. [6] proposed a deep cross-modal framework utilizing INRs (Implicit Neural Representations) to embed diverse secret data into cover images. StegNet [7] employs a convolutional network to embed an entire image into another of the same size, achieving high-capacity steganography. Shi et al. [8] designed a CEC (Cross-Episodic Curriculum) mechanism to improve Transformer-based embedding efficiency. Chen et al. [9] proposed a high-capacity framework integrating reversible GANs with blockchain transaction fields, while Cs-FNNS [10] employs generative priors for fixed decoding without pixel-level supervision.
Despite their effectiveness, deep learning methods suffer from black-box embedding behavior, unstable GAN training (e.g., mode collapse, gradient vanishing), and vulnerability to CNN-based steganalyzers [11]. For example, StegNet [7] and HiDDeN [12] lack interpretability, while ISGAN [13] often struggles with convergence. These limitations highlight the need for more transparent, robust, and content-aware optimization frameworks.
In addition to these mainstream approaches, researchers have also explored cross-domain and multimodal embedding strategies. For example, color–space-based methods leverage perceptual redundancy across channels (e.g., RGB, YCbCr, HSV) to enhance imperceptibility [14]. Meanwhile, multimodal watermarking frameworks such as RoSMM [15] extend embedding to text–image signals, improving robustness under complex conditions. These directions are complementary but fall outside the focus of our DCT–RL framework.
Reinforcement learning (RL) has recently emerged as a promising direction by framing steganography as a sequential decision-making problem. An RL agent selects embedding actions and updates its policy based on rewards balancing security and imperceptibility. MCTSteg [16] demonstrated adaptability across spatial and JPEG domains, while Tang et al. [17] introduced a reinforcement-driven framework that learns pixel-level embedding costs from data. Yet, RL-based steganography still faces challenges, including large state–action spaces, high training cost, and instability in complex environments.
To overcome these issues, we propose a PPO-based framework that enhances training stability, accelerates convergence, and supports efficient policy learning under visual constraints. Unlike step-wise interaction, our method adopts a global decision-making strategy, where the agent observes the full image and determines an embedding plan in a single episode. This reduces variance, improves adaptivity, and benefits from PPO’s clipped updates for robust convergence.
The main contributions of our work can be summarized as follows:
- (1)
- Image block segmentation and perceptual feature extraction: We first segment the image into spatial blocks and extract semantic and structural features to evaluate their suitability for data embedding. This pre-processing enables a content-aware filtering mechanism that avoids visually sensitive regions, serving as the foundation for reliable and high-quality steganography.
- (2)
- PPO-driven adaptive block selection policy: We formulate block selection as an RL problem and employ the PPO algorithm to learn a global embedding strategy. The agent takes the full feature matrix as input and selects the optimal set of blocks in a single shot, achieving a balance between adaptivity and policy stability.
- (3)
- DQN-based adaptive weight modulation: To further enhance adaptability, we incorporate a secondary DQN module into the PPO framework that dynamically adjusts the reward function’s trade-off weights. This hybrid strategy improves the model’s capacity to balance visual quality and security under varying content conditions.
2. Related Work
In the early development of digital image steganography, many techniques focused on the frequency domain (e.g., JPEG images). A famous example is the F5 algorithm [18], which employs matrix encoding to reduce the number of modifications, achieving high payload capacity while minimizing statistical distortions. However, simple frequency-domain LSB (Least Significant Bit) replacement methods are easily detected, so more robust schemes were introduced [19]. For instance, content-adaptive steganography methods compute image texture complexity to guide embedding locations, concentrating modifications in noisy regions to reduce detectability. This idea was first embodied in the spatial-domain HUGO (Highly Undetectable SteGO) algorithm [20] and later extended to frequency domain steganography. Holub et al. [21] proposed the Spatial Universal Wavelet Relative Distortion (S-UNIWARD) algorithm, which uses a wavelet-domain distortion metric to construct a universal distortion function applicable to embedding in arbitrary domains, including the DCT (Discrete Cosine Transform) [18] coefficient domain. In JPEG steganography, further strategies optimize the distortion function; for example, Guo et al. [22] designed the UED (Uniform Embedding Distortion) method based on a statistical image model. This approach considers the complexity of each DCT coefficient and improves embedding cost assignment to enhance security. Additionally, Sedighi et al. [23] introduced the MiPOD (Minimizing the Power of Optimal Detector) scheme, which assumes a theoretically optimal detector and designs embedding costs to minimize statistical detectability. These frequency-domain steganographic methods, reported in high-tier conferences and journals, have achieved notable progress: they not only improve the stego image quality but also effectively lower the probability of detection by steganalyzers. Nevertheless, traditional distortion-based methods remain limited: their hand-crafted cost functions degrade at high payloads due to an inability to capture complex dependencies, and lack adaptability to advanced CNN-based steganalyzers that exploit image residuals. This drives the need for more flexible, learning-driven solutions.
In recent years, deep learning has been widely applied to image steganography. Compared to hand-crafted features or distortion functions, deep learning enables steganographic strategies to be learned automatically from data. One approach is to use convolutional neural networks to construct end-to-end “encode–decode” steganography models. Hayes et al. [24] were among the first to introduce adversarial training into steganography, training an encoder–decoder network in tandem with a discriminator (steganalyzer) to generate adversarial stego images. Baluja et al. [25] proposed a deep steganographic autoencoder model that hides one image inside another and uses a corresponding decoder network to perfectly recover the secret information. This approach demonstrated that neural networks can learn embedding schemes that are imperceptible to the human eye. Subsequently, Zhu et al. [12] developed the HiDDeN (Hiding Data with Deep Networks) framework, which adds an adversarial discriminator and simulated channel distortion layers between the encoder and decoder, thereby improving the robustness and security of the embedded data. On another front, Tang et al. [26] proposed the ASDL-GAN (Automatic Steganographic Distortion Learning Generative Adversarial Network), which employs a generative adversarial network to automatically learn the distribution of embedding distortions, thereby replacing manually designed cost functions. Lu et al. [27] proposed a large-capacity ISN (Invertible Steganography Network) that efficiently hides and fully reveals secret images through a single invertible architecture, achieving state-of-the-art embedding capacity and quality. Yu et al. [28] introduced CRoSS (Controllable, Robust and Secure Steganography), a diffusion-based steganography framework that offers controllable, robust, and secure embedding without requiring additional training, leveraging the inherent properties of diffusion models. These studies show that deep learning-driven steganography can match or even surpass traditional methods in terms of payload capacity and security. Deep models can learn adversarial embedding patterns tailored to specific detectors, and when the steganalyzer’s parameters are unknown, the artifacts produced by deep steganography are often hard for existing detection methods to recognize, thus enhancing the secrecy of covert communication. However, deep learning-based steganography has shown clear advantages in payload capacity and security, as neural networks are able to learn embedding patterns that adapt to specific steganalyzers and enhance imperceptibility. At the same time, several open challenges remain. Neural architectures generally function as black boxes, which limits interpretability and complicates formal security assessment. GAN-based methods, while effective, can be sensitive to training stability and parameter configurations. In addition, deep models trained on specific detectors may exhibit reduced robustness when facing unseen or adaptively updated steganalyzers. These challenges suggest the need for more adaptive, transparent, and decision-driven frameworks, thereby motivating the adoption of RL to dynamically optimize embedding strategies.
The introduction of RL to optimize steganographic strategies is a novel trend in recent years. An RL agent can iteratively improve its embedding decisions through repeated interactions with the environment to maximize a covert communication utility function. Pan et al. [29] modeled the image steganography process as a “seek-and-hide” game and used deep RL to train a steganographic agent that hides an entire message in images while evading a detector. Their method treats data hiding as a sequential decision process that progressively modifies pixels to embed information, with a reward function encouraging perturbations that remain imperceptible. In addition to per-pixel action sequences, recent works apply RL to higher-level steganographic decisions. Tang et al. [30] proposed a JoPoL (Joint Policy Learning) paradigm that learns non-additive embedding costs within an RL framework. They divide images into small blocks and define the state as features of a pixel block, with actions being a set of joint embedding decisions for that block output by a policy network. By employing a policy network with an attention mechanism and a reward design based on feedback from a deep steganalyzer, the agent learns optimal embedding patterns accounting for interactions between pixels, markedly improving security against detection. Similarly, Mo et al. [31] proposed the ReLOAD (Reinforcement Learning to Optimize Asymmetric Distortion for Additive Steganography) algorithm, which optimizes an asymmetric distortion function via RL. In addition, Long et al. [32] developed the VERY-RL adaptive steganography algorithm, which uses RL to dynamically adjust embedding strategies according to different image contents. In summary, applying RL to steganography enables an automatic exploration of optimal embedding schemes that are difficult to intuitively design by humans. Moreover, while JoPoL [30] introduces joint policy learning at the block level with an attention mechanism, it lacks stable convergence guarantees. ReLOAD [31] focuses on optimizing asymmetric distortion but still depends on manually designed reward weighting. VERY-RL [32] adapts to content but does not utilize modern policy optimization like PPO. In contrast, our PPO-based framework integrates both stability and adaptivity by addressing key limitations of prior RL-based approaches. Specifically, it eliminates the reliance on manually designed reward weights through an adaptive reward formulation embedded in the PPO training loop. At the same time, PPO’s stable update mechanism ensures consistent policy learning across diverse embedding scenarios. Together, these features make our framework a more robust and reliable solution for DCT-based steganography.
In addition to RL- and deep learning-based approaches, researchers have also investigated alternative directions such as cross-domain, multimodal, and robustness-oriented embedding strategies. For example, Khan et al. [14] systematically evaluated the suitability of multiple color spaces and proposed an HSV-based block-wise approach to improve imperceptibility. Meanwhile, Xu et al. [33] introduced the RIIS framework, which achieves robust and reversible steganography even under noise and lossy compression. Beyond unimodal image steganography, recent works have also explored adaptive embedding in generative frameworks. For instance, Zhang et al. [34] investigated Light-Field image multiple reversible robust watermarking against geometric attacks, demonstrating robustness through multidimensional embedding optimization. In addition, Wang et al. [35] proposed Steg-GMAN, a generative multi-adversarial network for steganography that learns adaptive embedding costs, offering complementary insights to reinforcement learning-based block selection. Together, these studies broaden the scope of steganography research and highlight diverse methodological directions for enhancing adaptability and robustness.
3. Methodology
3.1. Image Blocking and Discrete Cosine Transform
Dividing a digital image into fixed-size blocks is a fundamental step for steganographic decision-making. In a typical approach, the image is split into non-overlapping blocks, and a Discrete Cosine Transform is applied to each block. The DCT converts the spatial-domain pixel intensities into frequency-domain coefficients, representing the block’s content as a sum of cosine basis functions at different frequencies. For an block, the DCT is given by:
where , is the pixel value at position in the block. is a normalization factor, for , and for , and similarly for . After the DCT, the top-left coefficient is the DC component representing the average intensity of the block, while the remaining coefficients are AC components corresponding to various frequency details of the block. Low-frequency AC coefficients capture smooth variations in the block, whereas high-frequency coefficients represent fine textures and edges. This block-wise DCT representation enables the extraction of local block features in the frequency domain for guiding data embedding decisions.
3.2. Image Block Feature Extraction Strategy
Once each image block has been transformed, various features can be computed at the block level to assess how suitable the block is for steganographic embedding, as illustrated in Figure 1. Traditional heuristic approaches leverage these features—such as block variance, high-frequency energy, visual saliency, human visual sensitivity, and embedding cost—to score and rank blocks, thereby selecting the optimal regions for data hiding. We define each feature and explain its computation and rationale as follows.

Figure 1.
Illustration of image block partitioning and feature extraction process. The original cover image is first divided into several equally-sized blocks, and then features such as block variance, visual saliency, frequency energy, and visual sensitivity are extracted from each block to evaluate its suitability for steganographic embedding.
3.2.1. Block Variance
This metric measures the dispersion of pixel intensities within a block, serving as a simple indicator of the block’s texture complexity. For example, for an block i, the variance can be defined as
where is the pixel value at position and is the mean pixel value of the block. A higher variance indicates that pixel values vary widely within the block, implying richer texture and more complex content. Blocks with high variance can better mask the slight perturbations caused by embedding, whereas low-variance blocks are more likely to reveal changes.
3.2.2. DCT High-Frequency Energy
This feature captures the strength of the high-frequency content in a block, which correlates with the amount of fine detail and texture. It is computed from the block’s DCT coefficients by measuring the aggregate energy of the higher-frequency AC components, excluding the DC and low-frequency parts. For instance, one can define the high-frequency energy of block i as the sum of squared magnitudes of its high-frequency coefficients:
where denotes the set of index pairs corresponding to high-frequency DCT coefficients. A larger indicates that the block contains abundant rapid intensity variations. Consequently, blocks with high high-frequency energy are deemed good candidates for embedding.
3.2.3. Visual Saliency
This feature reflects how likely a region in an image is to attract human attention. We use a saliency map to represent the importance of each pixel, typically normalized to the range . For each image block i, its saliency score is computed as the average saliency value of all pixels in the block:
A higher indicates that the block is more likely to be noticed by humans, making it less suitable for embedding in steganographic applications. This design is grounded in the Human Visual System (HVS), which tends to focus attention on salient image regions. Perturbations in these areas are more likely to be perceived [36,37], potentially exposing hidden data. Therefore, selecting low-saliency regions for embedding reduces the risk of visual detection. The saliency maps used in this work are generated by biologically inspired models such as the Itti-Koch model [36] or graph-based visual saliency (GBVS) [38], which simulate how the human eye prioritizes regions based on features like color contrast, intensity, and orientation.
3.2.4. Human Visual Sensitivity
This feature quantifies the perceptual sensitivity of the human eye to different frequency components. In the DCT domain, lower frequencies are more noticeable, while high frequencies are less so. We adopt the JPEG quantization table to define the perceptual cost of a block i as:
Here, is the DCT coefficient and is the quantization factor. Higher values of imply greater perceptual risk. Blocks with lower sensitivity scores are preferred for embedding to enhance security.
After extracting features such as texture complexity, frequency energy, visual saliency, and human visual sensitivity from each image block, we can heuristically select suitable regions for data embedding based on these metrics. Typically, blocks with rich textures, strong high-frequency components, and low saliency are considered more secure for steganographic embedding.
Building upon these block-level features, we now introduce an RL-based optimization framework that significantly upgrades the block selection strategy introduced in Section 3, as illustrated in Figure 2. Specifically, the cover image is first divided into blocks with extracted block-wise features. Then, the RL model adaptively selects embedding locations to encode secret data into the stego image. Finally, a steganalyzer evaluates the embedding effect by computing PSNR, SSIM, and detection accuracy, and the resulting score is used as a reward to optimize the agent’s selection policy. By integrating the PPO algorithm, we train an agent to intelligently and adaptively select DCT blocks for steganographic embedding based on learned content-aware policies rather than fixed heuristics. This transforms the traditionally static selection process into a dynamic decision-making task, guided by reward signals directly reflecting steganographic imperceptibility and security. Unlike conventional handcrafted approaches, our method not only achieves more precise control over embedding distortion but also demonstrates strong generalization across image domains and payload conditions. This learning-driven optimization serves as a key enabler for advancing DCT-based steganography towards higher robustness and automation.
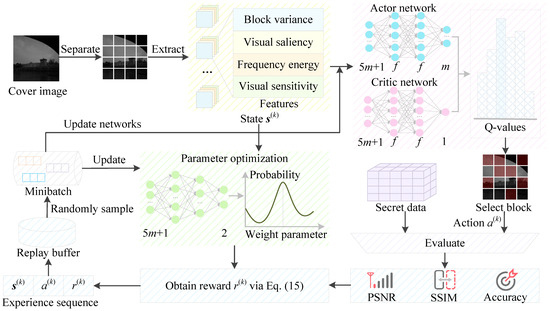
Figure 2.
Framework of the proposed method.
3.3. State
The state vector is composed of multi-dimensional attributes describing the current candidate block and a global progress indicator. The global feature b denotes the proportion of secret bits not yet embedded relative to the total payload:
where is the total number of secret bits and is the number of bits yet to embed. Initially , and once all bits are embedded, . This feature informs the agent of how much of the embedding task remains.
At each embedding step k, the observed state vector consists of the local feature vectors of all image blocks along with a global indicator of remaining bits. Assuming the image is divided into m non-overlapping blocks, the state at time step k is defined as:
where the feature vector for block i is:
The embedding mask indicates whether block i is available for embedding:
In the initial state, for all blocks. After each embedding step, the chosen block’s is set to 0 to mask it from being selected again in subsequent steps.
3.4. Action
An action is defined as the selection of one block from the currently unembedded candidates for data embedding. At each embedding step k, the agent samples an action from a stochastic policy distribution , where denotes the current state, and is the parameter set of the policy network. To ensure the validity of the action, the support of the policy is dynamically constrained by a binary mask , which indicates the availability of each block. Only the blocks satisfying are considered valid for selection:
Only blocks whose current mask is 1 are allowed to be selected as valid actions. To mask out invalid actions, we implement an action mask in the policy, assigning zero selection probability to any action corresponding to a block with . This ensures the agent will only choose legal blocks for embedding the secret data. In this way, the range of action values is automatically constrained by the state, preventing the agent from re-selecting blocks that have already been embedded or are otherwise disallowed. For clarity, consider a simple case where one block contains rich texture with high variance and frequency energy, while another block is smooth and salient. These feature values, computed using the formulas above, are encoded into the state vector. The policy network then assigns higher probability to the textured block, making it more likely to be selected for embedding. After all bits are embedded, the final reward is calculated from PSNR, SSIM, and detection accuracy, guiding the agent toward embedding strategies that balance imperceptibility and security.
3.5. Policy Distribution
At each time step k, the state , consisting of extracted features, is provided to the policy network governed by parameters , which adopts a multilayer perceptron (MLP) architecture with two hidden layers, each consisting of neurons, which we empirically found to provide a good trade-off between model expressiveness and training efficiency. It evaluates all available image blocks and outputs a score for each candidate block , where denotes the set of candidate blocks that have not yet been selected for embedding at time step k.
Based on the scoring results, the network produces a normalized probability distribution over the valid action set , guiding the block selection process. The distribution is defined as:
The value reflects the embedding suitability of block under the current state. The agent samples a block from this distribution to perform the embedding operation.
3.6. Reward
In this framework, the agent only receives a reward signal when an entire embedding episode is completed, which means that all secret bits are embedded. The reward at step k is computed based on the quality and security of the resulting stego image, evaluated using three metrics: peak signal-to-noise ratio (PSNR) , structural similarity index (SSIM) , and detection accuracy .
The PSNR measures the distortion between the stego image and the original cover image. A higher PSNR value indicates better imperceptibility and lower distortion. It is computed as:
where L is the maximum pixel value of the carrier image. is Mean Squared Error (MSE), which is calculated by the following formula:
where and represent the pixel values of the original image and the steganography image at row x and column y, respectively. O represents the total number of rows in the image, and P represents the total number of columns in the image. MSE is a metric used to measure the difference between the original image and the steganography image. A smaller MSE value indicates that there were fewer alterations to the image during the steganography process.
SSIM is a metric used to measure the visual similarity between two images. It derives its final index value by comparing the brightness, contrast, and structure of the two images. The SSIM value ranges from −1 to 1, where a value of 1 indicates that the two images are identical, and smaller values indicate lower similarity between the images. The calculation formula is as follows:
Here, and represent the average brightness of the original image U and the steganography image V. and represent the brightness variances of U and V, and represents the brightness covariance between U and V. and are two stabilization constants used to avoid the problem of the denominator being zero and to improve numerical stability.
The detection accuracy is obtained directly from the output of a pre-trained steganalyzer, which evaluates the likelihood that the stego image contains hidden information. A lower value of implies stronger resistance to detection.
Based on these metrics, the final reward received by the agent at the end of an episode is defined as:
where , are weighting coefficients that balance the contributions of structural quality and security. In the reward function, higher PSNR and SSIM increase the reward, whereas a higher decreases the reward. This design drives the agent, during training, to improve the stego image quality while simultaneously reducing the risk of detection.
To enhance the adaptability of the reward function, we introduce a nested RL module based on the DQN algorithm to dynamically adjust the weight parameters and . This auxiliary agent shares the same state input and receives the exact same reward signal as the main PPO agent, ensuring consistent optimization objectives. The learned weights are then used to balance multiple embedding criteria during reward computation.
At each time step k, the DQN agent receives the current state and outputs a two-dimensional discrete action . Here, adjusts , and adjusts , where , are predefined step sizes.
The policy distribution is implicitly defined by the Q-values predicted by the DQN. An -greedy strategy is adopted for action selection: with probability , the action with the highest estimated Q-value is selected; with probability , a random action is chosen to encourage exploration. The value of decays linearly over training episodes, balancing exploitation and exploration.
For policy update, we adopt the commonly used double-network structure in DQN: a training network and a target network. The target network stabilizes training by decoupling the target value computation from the rapidly changing training network. The target Q-value is computed as:
3.7. Network Update
To ensure stable and effective learning, the agent periodically updates the network parameters using the PPO optimization procedure. At time step k, the agent stores the experience sequence in the memory buffer. When the buffer accumulates T samples, a batch update is triggered.
The state is first fed into the critic network parameterized by . The input layer consists of neurons corresponding to the feature dimensions, followed by two hidden layers with f neurons each. The network outputs the estimated value function .
From the buffer, the agent samples a minibatch of T experience tuples: . For each step z in the sampled batch, the advantage is computed over a temporal window of K steps using discounted rewards:
To prevent excessive policy changes, the actor records the old policy parameters , and clips the probability ratio between the new and old policies. The actor’s objective is defined as:
where the probability ratio is computed as: . The critic network is trained by minimizing the mean squared error between the estimated and empirical advantages:
3.8. Overall Algorithm
The overall workflow of our framework is summarized in Algorithm 1. After extracting block-wise features and constructing the state representation, the PPO agent adaptively selects suitable blocks for embedding at each step. Once a stego image is generated, its quality and security are evaluated using PSNR, SSIM, and detection accuracy. These metrics are combined into a reward function, whose weighting coefficients are dynamically adjusted by an auxiliary DQN module to balance fidelity and security. The adjusted reward is then fed back into the PPO training loop, enabling stable policy optimization with adaptive reward shaping. In this way, PPO and DQN interact throughout the training process: PPO learns the block selection strategy, while DQN continuously refines the reward design to guide policy improvement.
| Algorithm 1: Reinforcement learning-based steganographic framework |
|
4. Experiments
4.1. Settings
4.1.1. Image Set
In our experiments, we employed the BOSSBase v1.01 dataset, which contains 10,000 grayscale images with a resolution of 512 × 512 pixels. Following the common practice in existing steganography studies, all images were uniformly downsampled to 256 × 256 using the “imresize” function in MATLAB 2021a with the default setting. We used this dataset for both training and evaluation. In addition to BOSSBase, we also conducted experiments on the ALASKA dataset, which is widely used in steganography and steganalysis challenges. ALASKA contains approximately 80,000 color images. Following common practice, we converted them into grayscale and resized them to 256 × 256 pixels to match the input format of our framework. Incorporating ALASKA II allows us to further evaluate the generalization ability of the proposed method across different datasets. Unless otherwise specified, the same data preprocessing pipeline was applied to all comparative methods to ensure fairness. Experimental results on the BOSSBase dataset confirm the superiority of our framework, achieving both lower detection rates and higher visual quality across a range of embedding payloads, particularly under low-bpp conditions.
The PPO agent was trained using the Adam optimizer with actor and critic learning rates set to and , respectively. A batch size of 32 was adopted, and the training was conducted for 2000 episodes. The auxiliary DQN module, also optimized with Adam at a learning rate of , updated the reward weights every 10 episodes using a replay buffer of size 1000 and a minibatch size of 32. For detection evaluation, detection accuracy (ACC) was measured using Xu-Net [39], a widely adopted CNN-based steganalyzer.
4.1.2. Steganographic Methods
We compared our proposed method with several classical and learning-based steganographic algorithms. Specifically, the following baselines were selected for comparison:
- (1)
- DCT (Baseline) [18]: A basic JPEG-DCT embedding algorithm without learning. The image is divided into fixed-size 8×8 blocks, and secret bits are embedded into a fixed location. No adaptivity or block ranking is applied, and embedding follows a raster-scan order.
- (2)
- S-UNIWARD [21]: This method divides the image into non-overlapping spatial blocks and extracts a set of perceptually meaningful and structurally indicative features.These features facilitate a content-aware evaluation of block suitability, enabling the selection of visually complex and perceptually secure regions for steganographic embedding.
- (3)
- AdMarks [40]: This method leverages adversarial perturbations generated from object detection models to embed watermarks into images. By encoding detection errors as watermarks, it ensures that the embedded information is imperceptible to human eyes while maintaining high robustness against tampering attacks and preserving image quality.
- (4)
- HiDDeN [12]: An end-to-end deep steganographic framework based on convolutional encoder–decoder networks. HiDDeN integrates adversarial training with a discriminator and introduces simulated channel distortion layers between the encoder and decoder. This design enhances both imperceptibility and robustness, making HiDDeN one of the most representative deep learning-based steganographic methods.
4.2. Evaluation of Visual Quality and Security
To illustrate the perceptual quality of our method, Figure 3 presents a visual comparison between a cover image and its corresponding stego image generated at 0.4 bpp.

Figure 3.
Visual comparison at 0.4 bpp. From left to right: the original cover image, the corresponding stego image generated by our framework, and the amplified difference map (scaled by ×10 for visibility).
In this part, we evaluate and compare the steganographic performance of different methods using three widely adopted metrics: PSNR, SSIM, and ACC measured by a steganalyzer. The results, obtained under a payload of 0.1 bpp, are dynamically illustrated in Figure 4 and summarized below.
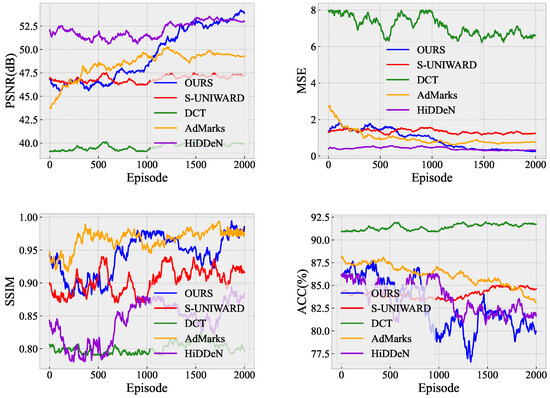
Figure 4.
Comparison of steganographic performance during training on the BOSSBase dataset. Metrics include PSNR (dB), MSE, SSIM, and detection accuracy (ACC, %) across different algorithms.
From the perspective of visual quality, our steganography framework significantly outperforms all other methods. It achieves the highest PSNR of 54.014 dB and SSIM of 0.979, indicating minimal perceptual distortion compared to the cover image. In contrast, the baseline DCT method exhibits the lowest PSNR (39.927 dB) and SSIM (0.801), reflecting noticeable degradation due to naive frequency-domain embedding without adaptivity. S-UNIWARD and AdMarks perform moderately well, with PSNRs of 47.189 dB and 49.260 dB, and SSIMs of 0.917 and 0.976, respectively. In addition to PSNR and SSIM, we also compute the LPIPS (Learned Perceptual Image Patch Similarity) [41] metric to complement our assessment of visual quality. LPIPS leverages deep features extracted from pretrained neural networks to evaluate perceptual similarity from a human vision perspective. As a learning-based metric, LPIPS provides an auxiliary view of image fidelity, particularly useful in capturing subtle distortions that may not be reflected by pixel-wise or structural measures. A lower LPIPS indicates better perceptual fidelity. As shown in Table 1, which reports the converged values under a payload of 0.2 bpp, it achieves competitive performance compared with traditional methods. Our method achieves the lowest LPIPS score of 0.021, significantly outperforming DCT (0.134), S-UNIWARD (0.066), AdMarks (0.037), and HiDDeN (0.053), demonstrating its superiority in preserving imperceptibility. Our framework attains superior fidelity, highlighting the advantage of reinforcement learning in adaptively selecting embedding locations. These results demonstrate that the adaptive block selection mechanism in our framework effectively avoids visually sensitive regions, enabling high-fidelity steganographic embedding.

Table 1.
Performance comparison on the BOSSBase dataset at 0.2 bpp. Metrics include PSNR (dB), MSE, SSIM, LPIPS, and detection accuracy (ACC, %).
Furthermore, when it comes to resistance against steganalysis, our steganography framework also achieves the best performance, with the lowest detection accuracy (ACC = 80.090%) among all methods. This indicates that the stego images produced by our method are the most difficult to distinguish from cover images. In contrast, the baseline DCT method is the most vulnerable to detection, with the highest ACC of 91.727%, followed by S-UNIWARD (84.560%) and AdMarks (83.301%). This result highlights the advantage of RL: by adaptively selecting visually complex and structurally noisy regions for embedding, our method introduces less regular and more secure modification patterns, thereby effectively reducing the detectability of steganographic traces.
It is also worth noting that although DCT and PPO share the same embedding mechanism in the DCT domain, the significant performance gap highlights the importance of intelligent block selection. DCT, which does not consider any feature-driven guidance, often introduces detectable patterns in flat or homogeneous regions, resulting in higher distortion and greater detectability.
In summary, PPO achieves the best overall trade-off between visual quality and security. The results demonstrate the effectiveness of integrating feature-aware evaluation and policy learning in DCT steganography.
4.3. Stability Performance
To further examine the robustness and adaptability of different steganographic methods under varying embedding ratios, we evaluate the stability of each algorithm across five payload levels: 0.1, 0.2, 0.3, 0.4, and 0.5 bpp. These settings span a comprehensive range of embedding intensities, from lightweight to heavy embedding, thereby enabling an assessment of model performance under both typical and generalized scenarios. The converged results for four evaluation metrics—PSNR, MSE, SSIM, and ACC—are reported in Figure 5. PSNR, MSE, and SSIM are widely adopted to measure the visual fidelity of stego images, whereas ACC (classification accuracy of the steganalyzer) evaluates the detectability of hidden data. Together, these metrics provide a comprehensive view of both imperceptibility and security.
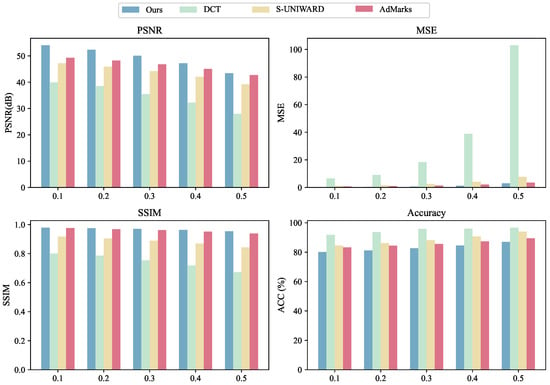
Figure 5.
Comparison of steganographic performance varying with embedding rate (bpp) on the BOSSBase dataset for different algorithms.
Overall, our steganographic framework consistently delivers stable and superior performance across all embedding rates. In terms of visual quality, our method maintains high PSNR values (ranging from 54.014 to 43.409 dB) and low MSE (from 0.258 to 2.966) as the payload increases. Notably, even at high embedding ratios such as 0.4 and 0.5 bpp, our method maintains a PSNR above 43 dB and SSIM above 0.95, significantly outperforming baseline methods. For example, the DCT-based method suffers from dramatic quality degradation, with PSNR dropping to 28.004 dB and MSE exceeding 100 when the embedding rate reaches 0.5 bpp. Similarly, S-UNIWARD and AdMarks show gradual decline in quality as the payload increases, whereas our model exhibits much more graceful degradation.
From the perspective of detectability, our method also demonstrates good stability. While ACC increases as the payload grows (from 80.09% at 0.1 bpp to 86.96% at 0.5 bpp), the rate of increase is relatively mild. This indicates that the PPO-trained policy generalizes well across payload levels without needing curriculum learning or retraining. In contrast, DCT and S-UNIWARD show higher detection rates throughout, with ACC reaching 96.68% and 94.09%, respectively, at 0.5 bpp, reflecting their rigid and less-adaptive embedding strategies.
To further validate the generalization capability of our framework, we also conducted experiments on the ALASKA II dataset at 0.2 bpp. As shown in Table 2, which reports the converged values, our method consistently achieves superior performance in both PSNR and SSIM while maintaining a lower detection accuracy compared to traditional baselines and HiDDeN. These results confirm that the proposed our framework is not only effective on BOSSBase but also transferable to more diverse datasets.

Table 2.
Performance comparison on the ALASKA II dataset at 0.2 bpp. Metrics include PSNR (dB), MSE, SSIM, and detection accuracy (ACC, %).
Although our current framework operates on grayscale inputs, the inclusion of ALASKA II demonstrates our capability to preprocess and adapt color image datasets, paving the way for future extensions to native RGB or multimodal steganography.
These results collectively highlight the robustness of our framework under varying embedding loads. The stability in visual quality and security can be attributed to the RL agent’s ability to adaptively allocate payloads to content-complex regions, avoiding excessive distortion and maintaining resistance to steganalysis. These results collectively highlight the robustness of our framework under varying embedding loads. The stability in visual quality and security can be attributed to the RL agent’s ability to adaptively allocate payloads to content-complex regions, avoiding excessive distortion and maintaining resistance to steganalysis. This performance stability becomes particularly significant at high embedding rates (e.g., 0.4–0.5 bpp), where traditional methods often experience sharp degradation. For instance, DCT-based schemes embed data into fixed frequency components regardless of content, which leads to concentrated distortions in sensitive areas. Similarly, S-UNIWARD uses static distortion models that cannot dynamically respond to increasing payload demands. In contrast, our method benefits from a PPO-driven policy that dynamically selects embedding blocks based on both structural and perceptual features. This enables a more distributed and context-aware embedding strategy, which helps mitigate quality loss and maintain security as embedding rate increases.
5. Conclusions
In this work, we proposed a novel RL-based framework for image steganography in the DCT domain. By introducing a perceptual feature-driven block segmentation scheme, our method identifies suitable embedding regions with high semantic complexity and low visual sensitivity. We further reformulate the block selection process as a sequential decision problem and apply the PPO algorithm to learn adaptive embedding policies that effectively balance image fidelity and steganographic security. To enhance robustness, we integrate content-aware state design and reward modulation strategies that allow the agent to generalize across diverse image distributions. Experimental results on the BOSSBase dataset confirm the superiority of our framework, achieving both lower detection rates and higher visual quality across a range of embedding payloads, particularly under low-bpp conditions.
Although our framework demonstrates clear advantages, two important directions remain open. First, the slight performance degradation at higher payloads suggests that the traditional DCT baseline may face limitations under heavy modification. Replacing it with stronger transform- or hybrid-domain representations could provide a more scalable foundation for reinforcement learning-driven embedding. Second, although our experiments focused on grayscale images, the proposed framework is inherently channel-agnostic and can be naturally extended to color images by jointly modeling multi-channel features. Notably, our experiments on the ALASKA II dataset already involve color image sources, which were converted to grayscale to ensure consistency across baselines and facilitate fair comparison. This preprocessing does not limit the flexibility of our framework but instead showcases its capacity to accommodate diverse image types, paving the way for future extensions to native RGB steganography and cross-modal tasks. Overall, these directions would not only broaden the applicability of our method but also pave the way for its integration with other advanced embedding paradigms in future research.
Author Contributions
Conceptualization, R.Y.; methodology, R.Y.; software, R.Y.; validation R.Y.; formal analysis, R.Y.; investigation, R.Y.; resources, B.H. and F.H.; data curation, R.Y.; writing—original draft preparation, R.Y.; writing—review and editing, R.Y., L.L., and B.H.; visualization R.Y. and L.L.; supervision, B.H.; project administration, B.H.; funding acquisition, B.H. and F.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Science Foundation of China under Grant U22B2062.
Data Availability Statement
The original data presented in this study are openly available in the BOSSBase ver. 1.01 dataset repository at https://dde.binghamton.edu/download/ (accessed on 26 November 2024) (Binghamton University, USA) and in the ALASKA dataset repository at https://www.kaggle.com/competitions/alaska2-image-steganalysis/data (accessed on 4 September 2025) (Kaggle).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the 2012 IEEE International Workshop on iNformation Forensics and Security (WIFS), Costa Adeje, Spain, 2–5 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 234–239. [Google Scholar]
- Li, B.; Wang, M.; Huang, J.; Li, X. A new cost function for spatial image steganography. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4206–4210. [Google Scholar]
- Wang, Y.; Zhang, W.; Li, W.; Yu, N. Non-additive cost functions for JPEG steganography based on block boundary maintenance. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1117–1130. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, Z.; Li, B.; Choo, K.K.R.; Huang, J. Joint cost learning and payload allocation with image-wise attention for batch steganography. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2826–2839. [Google Scholar] [CrossRef]
- Qiao, T.; Xu, S.; Wang, S.; Wu, X.; Liu, B.; Zheng, N.; Xu, M.; Pan, B. Robust steganography in practical communication: A comparative study. EURASIP J. Image Video Process. 2023, 2023, 15. [Google Scholar] [CrossRef]
- Han, G.; Lee, D.J.; Hur, J.; Choi, J.; Kim, J. Deep cross-modal steganography using neural representations. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1205–1209. [Google Scholar]
- Wu, P.; Yang, Y.; Li, X. Stegnet: Mega image steganography capacity with deep convolutional network. Future Internet 2018, 10, 54. [Google Scholar] [CrossRef]
- Shi, L.X.; Jiang, Y.; Grigsby, J.; Fan, L.; Zhu, Y. Cross-episodic curriculum for transformer agents. Adv. Neural Inf. Process. Syst. 2023, 36, 13–34. [Google Scholar]
- Chen, Z.; Zhu, L.; Jiang, P.; He, J.; Zhang, Z. A generic blockchain-based steganography framework with high capacity via reversible gan. In Proceedings of the IEEE INFOCOM 2024—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 241–250. [Google Scholar]
- Li, G.; Li, S.; Qian, Z.; Zhang, X. Cover-separable fixed neural network steganography via deep generative models. In Proceedings of the 32nd ACM International Conference on Multimedia, Melbourne, Australia, 28 October–1 November 2024; pp. 10238–10247. [Google Scholar]
- Yousfi, Y.; Butora, J.; Fridrich, J. CNN Steganalyzers Leverage Local Embedding Artifacts. In Proceedings of the 2021 IEEE International Workshop on Information Forensics and Security (WIFS), Montpellier, France, 7–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. Hidden: Hiding data with deep networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 657–672. [Google Scholar]
- Zhang, R.; Dong, S.; Liu, J. Invisible steganography via generative adversarial networks. Multimed. Tools Appl. 2019, 78, 8559–8575. [Google Scholar] [CrossRef]
- Muhammad, K.; Ahmad, J.; Sajjad, M.; Rho, S.; Baik, S.W. Evaluating the suitability of color spaces for image steganography and its application in wireless capsule endoscopy. In Proceedings of the 2016 International Conference on Platform Technology and Service (PlatCon), Jeju, Republic of Korea, 15–17 February 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–3. [Google Scholar]
- Bui, T.; Agarwal, S.; Yu, N.; Collomosse, J. Rosteals: Robust steganography using autoencoder latent space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 933–942. [Google Scholar]
- Mo, X.; Tan, S.; Li, B.; Huang, J. MCTSteg: A Monte Carlo tree search-based reinforcement learning framework for universal non-additive steganography. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4306–4320. [Google Scholar] [CrossRef]
- Tang, W.; Li, B.; Barni, M.; Li, J.; Huang, J. An automatic cost learning framework for image steganography using deep reinforcement learning. IEEE Trans. Inf. Forensics Secur. 2020, 16, 952–967. [Google Scholar] [CrossRef]
- Westfeld, A. F5—A steganographic algorithm: High capacity despite better steganalysis. In Proceedings of the International Workshop on Information Hiding, Pittsburgh, PA, USA, 25–27 April 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 289–302. [Google Scholar]
- Zhang, T.; Ping, X. A new approach to reliable detection of LSB steganography in natural images. Signal Process. 2003, 83, 2085–2093. [Google Scholar] [CrossRef]
- Pevnỳ, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In Proceedings of the International Workshop on Information Hiding, Calgary, AB, Canada, 28–30 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–177. [Google Scholar]
- Holub, V.; Fridrich, J.; Denemark, T. Universal distortion function for steganography in an arbitrary domain. EURASIP J. Inf. Secur. 2014, 2014, 1. [Google Scholar] [CrossRef]
- Guo, L.; Ni, J.; Shi, Y.Q. Uniform embedding for efficient JPEG steganography. IEEE Trans. Inf. Forensics Secur. 2014, 9, 814–825. [Google Scholar] [CrossRef]
- Sedighi, V.; Cogranne, R.; Fridrich, J. Content-adaptive steganography by minimizing statistical detectability. IEEE Trans. Inf. Forensics Secur. 2015, 11, 221–234. [Google Scholar] [CrossRef]
- Hayes, J.; Danezis, G. Generating steganographic images via adversarial training. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Baluja, S. Hiding images in plain sight: Deep steganography. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Tang, W.; Tan, S.; Li, B.; Huang, J. Automatic steganographic distortion learning using a generative adversarial network. IEEE Signal Process. Lett. 2017, 24, 1547–1551. [Google Scholar] [CrossRef]
- Lu, S.P.; Wang, R.; Zhong, T.; Rosin, P.L. Large-capacity image steganography based on invertible neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10816–10825. [Google Scholar]
- Yu, J.; Zhang, X.; Xu, Y.; Zhang, J. Cross: Diffusion model makes controllable, robust and secure image steganography. Adv. Neural Inf. Process. Syst. 2023, 36, 80730–80743. [Google Scholar]
- Pan, W.; Yin, Y.; Wang, X.; Jing, Y.; Song, M. Seek-and-hide: Adversarial steganography via deep reinforcement learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7871–7884. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Li, B.; Li, W.; Wang, Y.; Huang, J. Reinforcement learning of non-additive joint steganographic embedding costs with attention mechanism. Sci. China Inf. Sci. 2023, 66, 132305. [Google Scholar] [CrossRef]
- Mo, X.; Tan, S.; Tang, W.; Li, B.; Huang, J. ReLOAD: Using reinforcement learning to optimize asymmetric distortion for additive steganography. IEEE Trans. Inf. Forensics Secur. 2023, 18, 1524–1538. [Google Scholar] [CrossRef]
- Long, Y.; Qian, Q.; Cui, Y. VERY-RL: An Adaptive Image Steganography Algorithm Based on Reinforcement Learning. In Proceedings of the 2023 2nd International Symposium on Computing and Artificial Intelligence, Shanghai, China, 13–15 October 2023; pp. 67–71. [Google Scholar]
- Xu, Y.; Mou, C.; Hu, Y.; Xie, J.; Zhang, J. Robust invertible image steganography. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7875–7884. [Google Scholar]
- Wang, C.; Zhang, Q.; Wang, X.; Zhou, L.; Li, Q.; Xia, Z.; Ma, B.; Shi, Y.Q. Light-Field Image Multiple Reversible Robust Watermarking Against Geometric Attacks. IEEE Trans. Dependable Secur. Comput. 2025, 1–15, early access. [Google Scholar] [CrossRef]
- Huang, D.; Luo, W.; Liu, M.; Tang, W.; Huang, J. Steganography Embedding Cost Learning With Generative Multi-Adversarial Network. IEEE Trans. Inf. Forensics Secur. 2024, 19, 15–29. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 20, 1254–1259. [Google Scholar] [CrossRef]
- Bruce, N.; Tsotsos, J. Saliency based on information maximization. In Proceedings of the Advances in Neural Information Processing Systems 18 (NIPS 2005), Vancouver, BC, Canada, 5–8 December 2005; Volume 18. [Google Scholar]
- Harel, J.; Koch, C.; Perona, P. Graph-based visual saliency. In Proceedings of the Advances in Neural Information Processing Systems 19 (NIPS 2006), Vancouver, BC, Canada, 4–7 December 2006; Volume 19. [Google Scholar]
- Xu, G.; Wu, H.Z.; Shi, Y.Q. Structural design of convolutional neural networks for steganalysis. IEEE Signal Process. Lett. 2016, 23, 708–712. [Google Scholar] [CrossRef]
- Ding, Y.; Shao, M.; Wang, J.; Wan, Q. AdMarks: Image Steganography Based on Adversarial Perturbation. In Proceedings of the International Conference on Wireless Artificial Intelligent Computing Systems and Applications, Qindao, China, 21–23 June 2024; Springer: Cham, Switzerland, 2024; pp. 186–198. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).