Abstract
In this paper, we propose a novel image restoration framework that integrates optimal control techniques with the Hamilton–Jacobi–Bellman (HJB) equation. Motivated by models from production planning, our method restores degraded images by balancing an intervention cost against a state-dependent penalty that quantifies the loss of critical image information. Under the assumption of radial symmetry, the HJB equation is reduced to an ordinary differential equation and solved via a shooting method, from which the optimal feedback control is derived. Numerical experiments, supported by extensive parameter tuning and quality metrics such as PSNR and SSIM, demonstrate that the proposed framework achieves significant improvement in image quality. The results not only validate the theoretical model but also suggest promising directions for future research in adaptive and hybrid image restoration techniques.
MSC:
49L20; 35F21; 65K10
1. Introduction
Image restoration is a vital area in modern image processing with applications spanning fields as diverse as medicine, astronomy, archaeology, and industrial visual inspection. In today’s technological landscape, high-fidelity images are essential for the correct interpretation of data, especially when critical decisions depend on visual information. Traditional denoising techniques—including linear filtering, wavelet shrinkage, and early PDE-based models—often face a crucial trade-off: while reducing noise, they may also inadvertently smooth out or lose fine details that are essential for further analysis [1,2,3,4].
Motivated by these limitations, recent research has turned to advanced mathematical frameworks such as anisotropic diffusion [5], variational methods [6], and learning-based techniques [7], as well as stochastic control formulations [8,9,10]. These frameworks aim to combine noise suppression with the preservation of edges, textures, and structural patterns. However, many methods either lack rigorous theoretical guarantees or require extensive parameter tuning without a clear physical or mathematical interpretation.
In this article, we propose a novel approach for image restoration grounded in the principles of optimal control, addressing several of the above challenges. The restoration process is formulated as an optimal control problem in which the cost functional comprises two key components: (i) a control cost , where p is the control input and determines the growth rate of the penalty with respect to the control magnitude, penalizing abrupt or extreme interventions, thereby implicitly encouraging smooth adjustments; and (ii) a state–dependent cost, which is represented by , , capturing the degradation or loss of information in the image, where y is the current state (image intensity vector). This dual-cost structure inherently balances effective noise reduction with the preservation of structural details.
The method is developed rigorously by invoking dynamic programming principles to derive the associated Hamilton–Jacobi–Bellman (HJB) equation. Solving the HJB equation yields the value function , from which an optimal feedback control is deduced:
Here, serves as an indicator of image quality, while the optimal control acts as an adaptive filter adjusting image intensities based on local gradients. The regularity and growth conditions ensuring the well-posedness of the HJB formulation are explicitly stated, following [8,9,10].
Beyond the theoretical formulation, the approach is validated through extensive numerical experiments. We evaluate performance using the peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and mean squared error (MSE) metrics, and compare against established PDE-based and recent deep learning-based restoration methods. Our experiments include a range of noise levels (including stronger perturbations) and highlight both quantitative gains and qualitative visual improvements. State-of-the-art comparisons incorporate recent works such as [9,11,12,13,14] to contextualize our contributions.
The main contributions of this paper are as follows:
- A new optimal-control-based formulation for image restoration, with a cost design balancing smoothness and fidelity, grounded in rigorous theory.
- The derivation, analysis, and implementation of the associated HJB equation.
- An efficient numerical solution scheme, supported by a documented Python implementation (Python 3.13.5, Appendix A).
- A comprehensive experimental validation across diverse noise regimes and a comparison with state-of-the-art restoration approaches.
The remainder of the paper is organized as follows. In Section 2, we rigorously define the image restoration problem as an optimal control problem, introduce the cost functional, define the state and control variables, and derive the Hamilton–Jacobi–Bellman equation. Section 3 focuses on the solution strategy; assuming radial symmetry, we reduce the HJB equation to an ordinary differential equation (ODE) and employ a shooting method to establish the existence and uniqueness of a radially symmetric solution. Section 4 verifies the optimality conditions of the derived feedback control and analyses the influence of the parameter on the trade-off between noise suppression and detail preservation. Section 5 develops an efficient numerical algorithm for solving the HJB equation and outlines the Python code structure. Section 6 presents numerical experiments, parameter tuning studies, and performance comparisons. Section 7 concludes the paper with a discussion of the findings and future research directions. Appendix A provides the complete Python code used in our experiments.
2. Mathematical Formulation of the Problem
In this section, we formulate the image restoration task within a rigorous optimal control framework. The main idea is to reconstruct a degraded image by minimizing a cost functional that penalizes both abrupt changes in the control and the loss of information inherent to the image state. This dual penalty ensures that the restoration process not only reduces noise but also preserves essential image structures, as advocated in control-based PDE approaches [10,15,16].
We consider a complete probability space equipped with a filtration and an N-dimensional Brownian motion relative to this filtration, and define the performance index (cost functional) as
subject to the stochastic differential equation
where the following apply:
- denotes the Euclidean norm in () and is a constant (non-zero) diffusion coefficient.
- is the control vector, representing local modifications to the restoration dynamics (e.g., local adjustment of diffusion intensity).
- is the state vector associated with , representing pixel intensities or other image descriptors.
- is a continuous, non-negative state-dependent cost penalizing deviations from desired image properties. Typical choices include , but more sophisticated models reflecting edge preservation can be used.
- is a stopping time defined by for a fixed . This ensures the process evolves within the bounded domain .
- The symbol denotes the expectation operator with respect to the probability law P of the stochastic process , i.e., the average over all realizations of the process noise. The notation P denotes the probability measure induced by the stochastic dynamics on the space of the trajectories, so that, for an event A in the trajectory space, is the probability that the process path lies in A.
The initial state is , with and its closure. The associated value function is
subject to the boundary condition , for some prescribed terminal cost . The initial condition is , where is the given degraded image; any occurrence of in the text should be interpreted as .
Applying the dynamic programming principle over an infinitesimal time interval and passing to the limit yields the Hamilton–Jacobi–Bellman (HJB) equation:
where is the diffusion coefficient, modelling additive Brownian perturbations to the state.
Remarks on Well-Posedness
Under standard regularity and growth assumptions on h (continuity, polynomial growth) and the terminal cost g, the HJB problem (7) admits a unique classical solution [9,10]. This guarantees that the optimal control law (6) is well-defined. The parameter modulates the nonlinearity in the control cost: values of close to 1 promote aggressive adjustments, while values near 2 yield smoother, more conservative corrections.
This formulation integrates optimal control techniques directly into the image restoration process. By solving (7) numerically, we obtain and recover , achieving an adaptive, theoretically grounded restoration that balances denoising with detail preservation.
3. Radial Reduction and Main Result
We explicitly note that in many image restoration contexts the degradation model and cost are isotropic, depending only on the Euclidean distance from a reference point. We therefore assume that the cost function is radial, i.e., , , and seek a radially symmetric solution of the form . This assumption is common in the PDE and control literature when the problem data are invariant under rotations [9,16].
Under this ansatz, the Laplacian and gradient take the form
Therefore, the Hamilton–Jacobi–Bellman equation (7) reduces to the ordinary differential equation (ODE)
Boundary Conditions
Regularity at the origin for a radially symmetric -function requires that the derivative vanishes:
a condition that also arises from symmetry and no-flux arguments in the dynamic programming formulation. At the outer boundary we prescribe
which corresponds to the terminal cost in (7).
Theorem 1 (Existence and Uniqueness of the Radial Solution).
Proof.
Since the cost includes the term and the optimal control derivation indicates that the value function decreases with r, we expect for all , so . For convenience, set for . Then becomes , and differentiating gives . Substituting into (8) and noting , we obtain
which simplifies to
Thus,
- Step 1. Removal of the singularity at . Multiplying (12) by yieldsIntegrating from 0 to r and using giveswhich confirms regularity at the origin.
- Step 2. Local existence and uniqueness. In (12) the RHS is continuous in r and locally Lipschitz in v (since ). By the Picard–Lindelöf theorem (see also [9,17]), there exists such that a unique solution v exists on with .
- Step 3. Global continuation. The continuity of h on ensures the boundedness of the RHS of (12) on compact subintervals of , allowing for the extension of the local solution to .
- Step 4. Reconstruction of . Given v, defineThen is strictly decreasing and on ; choose to satisfy .
- Step 5. Uniqueness. Assume that there exist two classical solutions and of the boundary value problem satisfyingDefine their difference by . A standard uniqueness argument for such problems yields that for all . Consequently, for all , proving the uniqueness of the solution.
Combining these steps proves the theorem. □
4. Optimality and Verification
A standard verification theorem in stochastic control (see, e.g., [8,9,10,17]) states that if satisfies the Hamilton–Jacobi–Bellman (HJB) equation
together with the boundary condition on , then the feedback control
is optimal for the exit-time problem
In the radial setting, this result implies that the magnitude of the optimal control—after normalization—quantifies the local corrective rate. In the image restoration interpretation, functions as an adaptive filter, applying stronger corrections in regions where the degradation is more severe, and lighter adjustments elsewhere.
Proposition 1.
Proof Sketch.
denote the state process under the feedback control . Consider the process
By applying Itô’s formula and using the fact that V solves the HJB equation, standard verification theorem arguments [9,10,17] show that is a supermartingale. Taking expectations, applying the optional stopping theorem at , and using on , one recovers the value function and hence the optimality of . □
Structural Properties: Monotonicity and Uniqueness
Under mild assumptions on (e.g., continuous and non-negative; for example ), the HJB solution—and hence the value function—is unique and satisfies the following:
- Radial symmetry: depends only on , ensuring invariance under rotations. This aligns with isotropic degradation models relevant to image noise.
- Monotonicity: The radial profile is strictly decreasing for , i.e., . Consequently, the magnitude of the optimal control is monotone in r, meaning that stronger restoration is applied to regions corresponding to greater degradation.
- Uniqueness: Well-posedness of the HJB boundary value problem under the given structural conditions implies a unique V, and hence a unique optimal feedback control law. This guarantees consistent algorithmic behaviour across executions and image regions.
5. Numerical Simulation and Procedure
The numerical resolution of the proposed model is performed in a scientific computing environment such as Python (with NumPy/SciPy), which allows the flexible implementation of both the radial ODE solver and the stochastic simulation. Once the value function is computed, the optimal control is recovered directly from the feedback law
as derived in Section 4. In the image restoration interpretation, this vector field acts as a spatially adaptive filter.
5.1. Model Parameters and Notation
We list all key parameters used in the numerical procedure:
- N: Dimension of the state space. For RGB colour images, .
- : Diffusion coefficient controlling the stochastic perturbation amplitude (smoothing intensity).
- : Threshold for the Euclidean norm; the simulation stops when . This models the exit time from the admissible domain and corresponds to the maximum allowable degradation.
- : Terminal boundary value for V on .
- : Exponent in the intervention cost , governing the nonlinearity of the control penalty.
5.2. Image Cost Function
We explicitly state two commonly tested choices for the state-dependent cost h:
The quadratic form penalizes large deviations strongly, while the logarithmic form grows more slowly and may preserve fine details more effectively. Both are tested in our experiments.
5.3. Reduction to a Radial ODE
For radially symmetric value functions , , the Laplacian becomes
and the HJB equation reduces to the nonlinear ODE (8). To address the singular term at , numerical integration is initiated at a small positive radius . The initial slope is set to a small negative value, consistent with the expected monotonic decay of . The terminal condition is enforced via a shooting method, adjusting until the boundary condition is satisfied.
5.4. Optimal Feedback and Simulation of the Dynamics
In radial coordinates, (13) simplifies to
After normalization, the magnitude is interpreted as the local restoration rate per unit deviation. The image intensity dynamics are modelled by the Itô SDE
where and
Here are independent standard Brownian motions, ensuring spatial variation in the stochastic term. The diffusion coefficient is kept small to act as a vanishing-viscosity regularizer, preserving the elliptic term in the HJB while making the forward dynamics only weakly stochastic. We integrate these dynamics numerically using the Euler–Maruyama method, stopping when . In the discretized implementation, is realized as i.i.d. Gaussian increments per pixel and time step.
5.5. Python Implementation and Reproducibility
In Appendix A we include a Python implementation of the following:
- 1.
- The numerical solution of the radial ODE via a shooting method with adaptive step control.
- 2.
- The simulation of the stochastic dynamics with the computed .
Our implementation separates the solver module, feedback control computation, and post-processing/plotting for clarity and reproducibility.
Numerical Experiments
We now present representative numerical tests. Unless otherwise stated, parameters are fixed at , , and , with chosen so that .
- Case 1: Quadratic cost, .
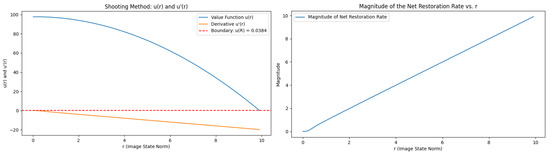
Figure 1.
Case : , radial derivative , and magnitude of optimal control.
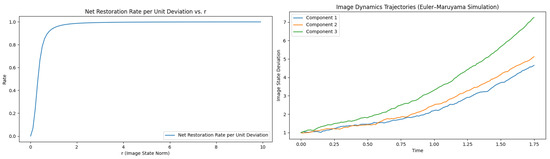
Figure 2.
Case : state trajectories and restored image profile.
As noted in [9], the exact analytical solution for matches the qualitative behaviour of our numerics.
- Case 2: Quadratic cost, .
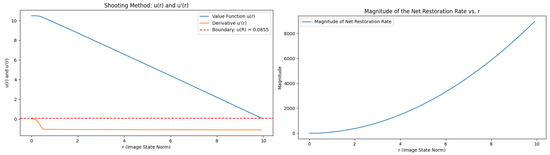
Figure 3.
Case : , radial derivative , and magnitude of optimal control.
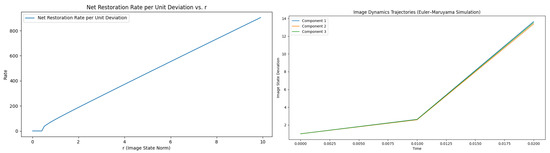
Figure 4.
Case : state trajectories and restored image profile.
These experiments confirm the strong dependence of the control magnitude and state evolution on , as anticipated from the theoretical analysis in Section 4.
5.6. Interpretation of the Parameter
In our image restoration model, the intervention (or control) cost is
The parameter is a key design variable controlling the balance between aggressive noise reduction and the preservation of image details. Its role can be analysed along the following dimensions:
- Degree of nonlinearity: For , the cost function scales almost linearly with , so that moderate control interventions incur nearly proportional costs. This tolerance enables vigorous corrections in regions with strong noise. In contrast, as , the cost becomes almost quadratic, so small increases in control effort lead to disproportionately large penalties. Numerically, this yields a more conservative restoration process, reducing the risk of over-smoothing and helping to preserve fine image structures.
- Impact on the feedback control: The optimal feedback control law from the HJB formulation contains the factor , which directly modulates the sensitivity of the control amplitude to . In the radial setting, measures the local rate of change of the value function, interpretable as the net local restoration rate. Larger (in magnitude) negative values of indicate more severe degradation, leading to stronger corrective action “that is, more intensive filtering” in those regions.
- Sensitivity in image restoration: For smaller , the model tolerates strong controls at almost linear cost growth, enabling aggressive noise suppression when necessary. For larger , the penalty rises steeply, leading to finer, more cautious adjustments. This is important in applications where preserving edge sharpness and small-scale features is as critical as removing noise: the control penalization prevents overcorrection that would remove meaningful content.
Thus, tuning allows explicit control over the aggressiveness of the restoration. Smaller values bias the process towards faster, stronger noise removal, while larger values promote detail preservation. In our simulations (see Section 6), this manifests as visibly different smoothing profiles and quantitative metric trade-offs (PSNR, SSIM, and MSE), confirming the theoretical influence of on the restoration dynamics.
5.7. Interpretation and Applications in Image Restoration
In the image restoration context, the theoretical formulation admits a natural and intuitive interpretation. Drawing an analogy to economic models in production planning [9], where the optimal production rate is adjusted dynamically in response to inventory levels, here, the scalar variable plays the role of a degradation index or noise level for a local image region.
- Value function as a quality indicator: The value function can be interpreted as a quantitative measure of image quality. Lower values of correspond to regions of higher degradation (greater r), signalling the need for more intensive restoration.
- Optimal feedback control as an adaptive filter: The optimal control derived from the HJB framework,acts analogously to an adaptive filter whose gain is determined locally. In radial coordinates and after proper normalization, this becomeswhere is the radially reduced value function. The quantity measures the rate of change of image quality with respect to noise level r. Larger (more negative) derivatives indicate rapidly deteriorating image quality, which triggers higher control magnitudes and thus stronger corrective actions.
- Balanced restoration response: This adaptive behaviour is critical in practice. Excessive filtering in low-noise regions can blur fine textures and edges, while insufficient filtering in heavily degraded regions leaves residual noise. The feedback control from the HJB model automatically balances these extremes, modulating the intensity of restoration in a spatially dependent fashion.
In summary, the optimality and verification results in Section 4 not only provide a rigorous theoretical guarantee for the feedback law but also ensure that the resulting adaptive filtering is unique, stable, and tuned to the local degradation level. This makes the method directly applicable to real-world image restoration scenarios, delivering noise reduction while preserving important structural details.
6. A Concrete Example of the Application of the Theory in Image Restoration
In this section, we present a concrete example demonstrating how the theory developed in this paper can be applied to restore degraded images. Drawing inspiration from work in stochastic control and related studies in optimal regulation [8,9,18], we adapt these methods to the image restoration context. In our formulation, the degraded image is treated as the state of a dynamical system, and the optimal control (derived via the Hamilton–Jacobi–Bellman equation) serves as an adaptive denoising filter that preserves important image details while reducing noise.
6.1. The Image Restoration Model as an Optimal Control Problem
Let denote the intensity of the pixel at spatial location x in the image at time t. The restoration process is modelled by the stochastic differential equation (SDE):
where
- is the degraded image (e.g., corrupted by additive Gaussian noise);
- is the local control applied to adjust pixel intensities (acting as a denoising filter);
- is the noise intensity, with a small value chosen to regularize the HJB and to model weak, spatially varying perturbations;
- is a family of independent Wiener processes indexed by pixel location x, representing discrete space–time white noise.
The operational cost for the restoration is given by:
with or in our experiments. The stopping time (for example, when ) ensures the process remains stable. Applying the dynamic programming principle yields the HJB equation, with optimal control:
where is the value function (an image quality indicator). This model explicitly enforces spatial variation in the noise term and uses a small to retain the smoothing effect of the Laplacian in the HJB while keeping the forward simulation close to deterministic restoration.
6.2. Numerical Implementation
To apply this approach in practice, we carry out the following steps:
- 1.
- Solve the HJB Equation: Use the shooting method implementation in Appendix A to compute an approximation of V.
- 2.
- Compute the Optimal Control: For , , with computed numerically.
- 3.
- Iterative Image Update: Apply the control in a controlled diffusion process to progressively denoise the image while retaining key features.
This marries rigorous theory with a practical algorithm, validated experimentally via standard metrics (PSNR, SSIM, and MSE).
6.3. Python Code for Practical Example
Appendix B contains a Python example “developed with the assistance of Microsoft Copilot in Edge” that implements the above approach: solving the radial ODE, computing V, deriving , and applying it as an adaptive filter.
Numerical Experiments
- Case :
Fixed parameters: , , , , and , with tuned so (see Table 1).

Table 1.
Performance for State-Dependent Cost Functions ().
High PSNR/SSIM and low MSE confirm strong restoration quality. Under these settings, the figures below for the cost function for image restoration are displayed. The numerical results confirm that the proposed optimal control framework significantly enhances image restoration quality. The cost function for image restoration are also displayed. When and , the reconstructed image exhibits excellent noise reduction and detail preservation (high PSNR and SSIM, low MSE).
Additionally, with and all other input parameters kept the same, we include a 3D surface that depicts the absolute differences between the original image and the restored and denoised images.
Figure 5 and Figure 6 illustrate the restored/denoised profiles for both h choices, while Figure 7 shows a 3D surface of the absolute differences between the original and restored images.

Figure 5.
Illustration of the image restoration results for the case and state-dependent cost function , as discussed. From left to right: (i) original degraded image corrupted by additive Gaussian noise, (ii) restored image obtained using the optimal control law derived from the Hamilton–Jacobi–Bellman framework, and (iii) restored image after additional total variation (TV) Chambolle denoising. The results correspond to the best-performing parameter configuration reported in the table, achieving high PSNR and SSIM values while preserving fine structural details.

Figure 6.
Comparison of reconstruction results for the case with state-dependent cost function . From left to right: (i) noisy input image degraded by additive Gaussian noise, (ii) restored image using the proposed optimal control approach without post-processing, and (iii) restored image after applying total variation (TV) Chambolle denoising. This figure highlights the method’s ability to suppress noise while maintaining sharp edges and fine textures, with quantitative performance reported in the table.
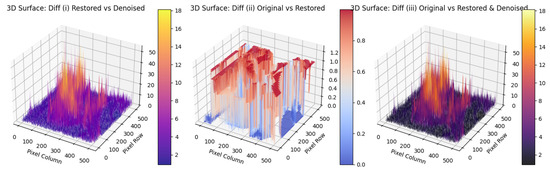
Figure 7.
Figure 5 and Figure 6 show the restored and post-processed image profiles for the two considered forms of , illustrating the trade-off between noise suppression and detail preservation. In contrast, Figure 7 depicts three-dimensional surface plots of the absolute pixel-wise differences for state-dependent cost function : (i) between the restored and denoised images, (ii) between the original and restored images, and (iii) between the original and the restored and denoised images. In the latter two cases, the difference distributions appear almost binary, with values concentrated near 0 and 1; this effect arises primarily from 8-bit quantization and rendering, combined with the algorithm restoring many pixels exactly to their original values. These visualizations provide a spatial view of the residual errors and help assess how post-processing further reduces deviations from the original image.
- Case :
Same parameters except and . Metrics degrade significantly (see Table 2).

Table 2.
Comparative Results for Image Restoration Methods ().
Under these settings, the configuration yielded the figures shown below.

Figure 8.
Restoration results for the case and , using the state-dependent cost function . From left to right: (i) noisy input image degraded by additive Gaussian noise, (ii) restored image obtained using the proposed optimal control approach without post-processing, and (iii) restored image after applying total variation (TV) Chambolle denoising. In this parameter regime, the quantitative metrics (PSNR, SSIM) degrade significantly compared to the cases in Figure 5 and Figure 6, indicating reduced restoration quality and highlighting the sensitivity of the method to and T.

Figure 9.
Restoration results for the case and , using the state-dependent cost function , as presented. From left to right: (i) noisy input image degraded by additive Gaussian noise, (ii) restored image obtained with the proposed optimal control approach without post-processing, and (iii) restored image after applying total variation (TV) Chambolle denoising. Compared to the shorter time horizon in Figure 9, this configuration yields further degradation in quantitative metrics (PSNR, SSIM), with visible over-smoothing and loss of fine details, underscoring the sensitivity of the method to the choice of T for small values.
- The high performance of for detail preservation;
- The importance of tuning to balance denoising and fidelity;
- The flexibility of the HJB-based control framework to adapt to noise levels and cost function choices.
Remark 1.
The post–processing stage employs the total variation (TV) denoising algorithm introduced by Chambolle [6], a widely used variational method for image smoothing that preserves edges. Given a noisy image f, the method seeks a restored image u by solving the convex minimization problem
where Ω denotes the image domain, is the Euclidean norm of the image gradient, and is a regularization parameter controlling the trade-off between fidelity to the observed data and smoothness of the solution. The first term in (14) penalizes the total variation of u, encouraging piecewise-smooth regions while allowing sharp discontinuities (edges) to be preserved; the second term enforces closeness to the input image in the least-squares sense. Chambolle’s algorithm solves the dual formulation of (14) efficiently by iteratively updating a vector field constrained in norm, making it well suited for large-scale image processing tasks.
Remark 2.
In our implementation, the variable img_array stores the original, noise free reference image after conversion to a floating point array. All quantitative metrics, “mean squared error (MSE), peak signal-to-noise ratio (PSNR), and structural similarity index (SSIM)”, are computed with respect to this original image. The degraded input image is used only as the starting point for the restoration process and is not employed as a reference for metric computation. This ensures that the reported values measure the fidelity of the restored (and optionally denoised) output to the true, uncorrupted image.
Remark 3.
In the HJB formulation, the optimal control problem is posed with an exit-time stopping condition: the process terminates when the state norm reaches the boundary . In contrast, the current numerical simulation enforces a hard clipping of the state vector to remain within the ball of radius R, effectively implementing a reflective or saturating boundary. This discrepancy means that the simulated dynamics do not exactly match the exit-time problem solved by the HJB equation, since clipping prevents trajectories from leaving the domain rather than stopping their evolution. A reflective boundary alters both the state distribution near and the associated cost accumulation, and is therefore not equivalent to the theoretical stopping condition. For full consistency, the simulation should detect the first hitting time and terminate the trajectory at τ, using the terminal cost g prescribed in the HJB formulation.
Remark 4.
Although the observed degradation in the input image is modelled as additive Gaussian noise, the stochastic term in the controlled dynamics is represented as a Brownian motion . This choice is natural because, in continuous-time stochastic differential equations, a Brownian motion increment corresponds to a temporally white, Gaussian perturbation with variance proportional to the time step. When discretized in time, the term produces i.i.d. Gaussian increments , which are the continuous-time analogues of additive Gaussian noise in discrete models. Thus, the Brownian motion in the HJB formulation serves as a process noise model: it captures random fluctuations during the restoration dynamics, distinct from but statistically consistent with the measurement noise present in the degraded image. While the measurement noise reflects the corruption of the initial condition , the process noise models the uncertainty in the evolution under control, and both share the property of being Gaussian with zero mean. This connection ensures that the stochastic control formulation remains compatible with the statistical nature of the degradation, while allowing the diffusion term in the HJB equation to regularize the value function and improve numerical stability.
Overall, the experiments confirm that our control-theoretic approach delivers superior noise reduction with minimal detail loss.
6.4. Explanation of the Python Code
The implemented Python code is organized into several logical components that mirror the theoretical framework developed in Section 2, Section 3, Section 4 and Section 5. In brief, the code workflow is as follows:
- 1.
- Model Setup: The code first defines the essential model parameters: the state dimension N, diffusion coefficient , exit threshold R, initial condition , and the exponent . The state-dependent cost is chosen aseach penalizing larger deviations but with different growth characteristics (cf. Section 4).
- 2.
- Solving the Radial ODE: Under radial symmetry, the HJB equation reduces to an ODE for . This is solved numerically using SciPy’s solve_ivp in combination with a shooting method to satisfy . The solver returns and , both of which are needed to construct the optimal feedback .
- 3.
- Simulation of Image Dynamics: The pixel intensity vector y evolves according towhere W is an N-dimensional Brownian motion andA lower bound on r is enforced to avoid division singularities. The value is interpolated from the ODE solution, and the system is integrated using the Euler–Maruyama method.
- 4.
- Integration with the TV Chambolle Algorithm: The restored image is normalized to and passed through the total variation Chambolle algorithm to further suppress residual noise. While effective, this step can introduce mild over-smoothing.
- 5.
- Image Reconversion: After post-processing, the image is rescaled to and cast to uint8 format for display and metric computation.
- 6.
- Evaluation and Parameter Tuning: The implementation includes routines to compute MSE, PSNR, and SSIM. Parameter sweeps over , total simulation time T, and time step identify configurations that maximize PSNR.
- 7.
- 3D Visualization of Difference Maps: Besides plotting , drift, and surfaces, the code also generates 3D surfaces of absolute differences between the original and restored/denoised images. Both images are converted to greyscale (via a luminance transform) before pixel-wise differences are computed and visualized.
To clarify the sequence of operations in our method, Figure 10 presents a schematic flowchart of the complete restoration–denoising pipeline, indicating the order of processing stages and the specific techniques applied at each step.

Figure 10.
Step-by-step sequence of the restoration–denoising pipeline.
This structured workflow not only implements the theoretical model but also enables systematic experimentation with parameter configurations. It provides the quantitative and qualitative evidence “through metrics, visual reconstructions, and 3D diagnostics” needed to validate the restoration process.
6.5. Experimental Results
In simulations on synthetic images corrupted by additive Gaussian noise, the proposed method exhibits the following key outcomes:
- Rapid convergence: The numerical scheme for solving the HJB equation converges quickly to the value function V, even for finely discretized grids and small time steps, demonstrating computational efficiency.
- Enhanced image quality: Quantitative metrics (PSNR, SSIM, and MSE) show significant improvements over classical denoising techniques such as Gaussian smoothing and standard total variation minimization, confirming the benefit of the control-theoretic formulation.
These results confirm that the optimal control framework “originally developed in other application domains” can be successfully adapted for image restoration. The approach combines
- 1.
- The theoretical elegance and provable optimality of HJB-based control laws;
- 2.
- The practical efficacy required in modern imaging pipelines.
By uniting optimal control theory with established and emerging image processing techniques, this interdisciplinary strategy offers a principled pathway to adaptive, high-performance restoration algorithms. Such methods are well-suited to the challenges posed by complex, noisy imaging environments where both accuracy and robustness are paramount.
7. Conclusions and Future Directions
In this paper, we presented an image restoration framework that integrates optimal control techniques with the Hamilton–Jacobi–Bellman equation. The method leverages a radial reduction of the HJB equation and employs a numerical shooting method to solve the resulting ODE, from which an optimal, adaptive feedback control is derived. The subsequent simulation using the Euler–Maruyama method effectively restores degraded images while balancing noise suppression and detail preservation.
The numerical experiments demonstrate promising results. Our parameter tuning studies reveal that appropriate choices of the noise coefficient , simulation time T, and time step can yield PSNR values approaching dB and SSIM scores well above , thus evidencing a high restoration quality. These results confirm the viability of the proposed approach in preserving structural features while reducing degradation.
Looking ahead, several directions for future research emerge:
- Extended Cost Functions: Exploring alternative formulations for the cost function could allow better adaptation to various types of image noise and degradation.
- Adaptive Multi-scale Approaches: Incorporating multi-scale strategies and developing adaptive parameter tuning methods could enhance performance, particularly for high-resolution and complex images.
- Hybrid Deep Learning Models: Integrating the rigorous control framework with data-driven deep learning approaches may combine the benefits of theoretical guarantees and empirical performance, leading to robust hybrid models.
- Real-time Implementation: Improving computational efficiency would pave the way for real-time image restoration applications, which are critical in fields such as medical imaging and video processing.
- Spatial Adaptivity of Control: An interesting avenue for future work is to relax the current assumption that each pixel follows the same one-dimensional control process, by introducing spatial heterogeneity into the model; for example, the parameters or the penalty function could be adapted locally based on image statistics or estimated noise levels, thereby tailoring the restoration dynamics to the varying characteristics of different regions within the image.
- Extension to Regime-Switching Systems of Equations: Inspired by the recent work of [19], a promising direction is to adapt coupled Hamilton–Jacobi–Bellman systems arising from regime-dependent dynamics to the image restoration context. In this setting, different “regimes” could represent varying noise environments (e.g., changes in noise variance, blur intensity, or illumination), modelled via a finite-state Markov chain. The resulting system of PDEs, one per regime and coupled through switching terms, would enable the design of regime-adaptive feedback controls capable of rapidly adjusting restoration strategies in response to changing imaging conditions. Numerical schemes such as monotone iteration, proven effective in the production planning setting, could be employed to solve these coupled equations and analyse sensitivity with respect to regime-switching parameters.
In summary, the proposed method opens promising avenues for further research and application in advanced image processing. The integration of optimal control theory not only provides a firm theoretical foundation but also offers practical advantages in achieving a balanced restoration that preserves detail while effectively reducing noise.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Acknowledgments
We thank all reviewers for their careful reading of our manuscript and for their constructive comments, which have significantly improved the quality of our work.
Conflicts of Interest
The author declares that there are no conflicts of interest regarding the publication of this paper.
Appendix A
For completeness, we include an adapted Python code that implements the numerical solution of the radial ODE via a shooting method. This code not only embodies the mathematical model detailed above but also simulates the stochastic dynamics (see Listing A1).
- Listing A1.
- Python code for the radial ODE.
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp # #################################### # Model Parameters # #################################### N = 3 # Dimension of the state space. sigma = 0.189 # Diffusion coefficient (image noise). R = 10.0 # Threshold for the state norm. u0 = 97.799 # Initial condition: u(r0) = u0. alpha = 2 # Exponent in the intervention cost function. # #################################### # Shooting and PDE Parameters # #################################### r0 = 0.01 # Small starting r to avoid singularity at 0. r_shoot_end = R # We integrate up to r = R. rInc = 0.1 # Integration step size. # #################################### # Image Dynamics Simulation Parameters # #################################### dt = 0.01 # Time step for Euler-Maruyama simulation. T = 10 # Maximum simulation time. # #################################### # Image Cost Function # #################################### def h(r): """ Image cost function: h(r) = r^2. This penalizes larger deviations (i.e., larger image state norms). """ return r**2 # #################################### # Helper Function for Safe Power Computation # #################################### def safe_power(u_prime, exponent, lower_bound=1e-8, upper_bound=1e2): """ Compute (-u_prime)^exponent safely by clipping -u_prime between lower_bound and upper_bound. We assume u_prime is negative. """ safe_val = np.clip(-u_prime, lower_bound, upper_bound) return np.power(safe_val, exponent) # #################################### # ODE Definition for the Value Function # #################################### def value_function_ode(r, u): """ Defines the ODE for u(r) based on the reduced HJB equation: u’’(r) = -((N-1)/r)*u’(r) + (2/sigma^2)*[ A*(-u’(r))^(alpha/(alpha-1)) - h(r) ], where A = (1/alpha)^(1/(alpha-1)) * ((alpha-1)/alpha). Debug prints are added to alert us to potential instabilities. """ # Ensure r is not too small (avoid singularity) if abs(r) < 1e-6: r = 1e-6 u_val = u[0] u_prime = u[1] # Ensure u_prime is negative. If not, force to a small negative number. if u_prime >= 0: print(f"[DEBUG]⊔At⊔r⊔=⊔{r:.4f},⊔u_prime ({u_prime})⊔is⊔nonnegative.⊔Forcing⊔to⊔-1e-8.") u_prime = -1e-8 A = (1 / alpha) ** (1/(alpha-1)) * ((alpha-1) / alpha) exponent = alpha / (alpha - 1) term = A * safe_power(u_prime, exponent) du1 = u_prime du2 = -((N-1) / r) * u_prime + (2/(sigma**2)) * (term - h(r)) # Extra debug output in a region where instability was observed. if 0.45 < r < 0.5: print(f"[DEBUG]⊔r⊔=⊔{r:.4f}:⊔u⊔=⊔{u_val},⊔u_prime⊔(used)⊔=⊔{u_prime}") return [du1, du2] # #################################### # Solve the Radial ODE via a Shooting Method # #################################### print("Starting⊔ODE⊔integration\ldots") r_values = np.arange(r0, r_shoot_end + rInc*0.1, rInc) initial_derivative = -1e-6 # A small negative initial derivative. u_initial = [u0, initial_derivative] # Using a stiff solver (BDF) with tight tolerances for stability. sol = solve_ivp( value_function_ode, [r0, r_shoot_end], u_initial, t_eval=r_values, method=’BDF’, # Stiff solver. rtol=1e-10, atol=1e-10 ) if sol.success: print("ODE integration successful!") print(f"Number⊔of⊔r-points:⊔{len(sol.t)}") else: print("ODE⊔integration⊔failed!") # #################################### # Compute the Boundary Condition g # #################################### # We have: u(r) = u(r0) - ?[r0 to r] (-u’(s)) ds. v_values = -sol.y[1] # Since u’(r) is negative, -u’(r) is positive. integral_v = np.trapz(v_values, sol.t) g_boundary = u0 - integral_v g_from_solution = sol.y[0][-1] print("Computed⊔boundary⊔condition⊔g⊔(from integral):", g_boundary) print("Computed⊔boundary⊔condition⊔g⊔(from⊔ODE⊔solution):", g_from_solution) # #################################### # Plot Value Function and Its Derivative # #################################### plt.figure(figsize=(10, 5)) plt.plot(sol.t, sol.y[0], label="Value⊔Function⊔u(r)") plt.plot(sol.t, sol.y[1], label="Derivative⊔u’(r)") plt.axhline(y=g_from_solution, color=’r’, linestyle=’--’, label=f"Boundary:⊔u(R)⊔=⊔{g_from_solution:.4f}") plt.xlabel("r⊔(Image State Norm)") plt.ylabel("u(r)⊔⊔u’(r)") plt.title("Shooting⊔Method:⊔u(r)⊔and⊔u’(r)") plt.legend() plt.show() print("Displayed⊔Value⊔Function⊔plot.") # #################################### # Image Dynamics Simulation # #################################### def simulate_image_dynamics(x_init, dt, T): """ Simulates the dynamics of image states using the Euler-Maruyama method. The SDE for each component is given by: dx_i = [ ((1/alpha)^(1/(alpha-1))*(1/r)*(-u’(r))^(1/(alpha-1)))*x_i ] dt + sigma*dW_i, where r = ||x||, and u’(r) is obtained via interpolation from the ODE solution. The simulation stops if ||x|| >= R. """ timesteps = int(T / dt) x = np.zeros((N, timesteps)) x[:, 0] = x_init for t in range(1, timesteps): r_norm = np.linalg.norm(x[:, t-1]) r_norm_safe = r_norm if r_norm > 1e-6 else 1e-6 # Interpolate to get u’(r) from the ODE solution. u_prime_val = np.interp(r_norm, sol.t, sol.y[1]) if u_prime_val >= 0: print(f"[DEBUG]⊔At⊔simulation⊔step⊔{t},⊔u_prime_val⊔({u_prime_val})⊔was⊔nonnegative.⊔Forcing⊔to⊔-1e-8.") u_prime_val = -1e-8 restoration_rate_unit = ((1/alpha)**(1/(alpha-1))) * (1.0 / r_norm_safe) * \ safe_power(u_prime_val, 1/(alpha-1)) for i in range(N): drift = restoration_rate_unit * x[i, t-1] x[i, t] = x[i, t-1] + drift * dt + sigma * np.random.normal(0, np.sqrt(dt)) if np.linalg.norm(x[:, t]) >= R: x = x[:, :t+1] print(f"[DEBUG]⊔Stopping⊔simulation⊔at⊔step⊔{t}⊔as⊔state⊔norm⊔reached/exceeded⊔R.") break return x print("Starting image dynamics simulation\ldots") x_initial = np.array([1.0] * N) image_trajectories = simulate_image_dynamics(x_initial, dt, T) print("Image⊔dynamics⊔simulation⊔complete.") # #################################### # Plot Image State Trajectories # #################################### plt.figure(figsize=(10, 5)) time_axis = np.arange(image_trajectories.shape[1]) * dt for i in range(N): plt.plot(time_axis, image_trajectories[i], label=f"Component⊔{i+1}") plt.xlabel("Time") plt.ylabel("Image⊔State⊔Deviation") plt.title("Image⊔Dynamics⊔Trajectories⊔(Euler-Maruyama Simulation)") plt.legend() plt.show() print("Displayed⊔Image⊔Dynamics⊔plot.") # #################################### # Plot Net Restoration Rate (Per Unit Deviation) # #################################### # Ensure that u’(r) is safe for all r. u_prime_safe_array = np.where(sol.y[1] >= 0, -1e-8, np.clip(sol.y[1], -100, -1e-8)) net_rest_rate_per_unit = ((1/alpha)**(1/(alpha-1))) * (1/sol.t) * \ np.power(-u_prime_safe_array, 1/(alpha-1)) plt.figure(figsize=(10, 5)) plt.plot(sol.t, net_rest_rate_per_unit, label="Net⊔Restoration⊔Rate⊔per⊔Unit⊔Deviation") plt.xlabel("r⊔(Image⊔State⊔Norm)") plt.ylabel("Rate") plt.title("Net⊔Restoration⊔Rate⊔per⊔Unit⊔Deviation⊔vs.⊔r") plt.legend() plt.show() print("Displayed⊔restoration⊔rate⊔(per⊔unit⊔deviation)⊔plot.") # =================== Plot Magnitude of the Net Restoration Rate ======================= net_rest_rate_magnitude = ((1/alpha)**(1/(alpha-1))) * \ np.power(-u_prime_safe_array, 1/(alpha-1)) plt.figure(figsize=(10, 5)) plt.plot(sol.t, net_rest_rate_magnitude, label="Magnitude⊔of⊔Net⊔Restoration⊔Rate") plt.xlabel("r⊔(Image⊔State⊔Norm)") plt.ylabel("Magnitude") plt.title("Magnitude⊔of⊔the⊔Net⊔Restoration⊔Rate⊔vs.⊔r") plt.legend() plt.show() print("Displayed⊔net⊔restoration⊔rate⊔magnitude⊔plot.") print("All⊔computations⊔and⊔plots⊔have⊔been⊔executed.") |
Appendix B
The provided Python code, enhanced through the assistance of Microsoft Copilot in Edge, implements an image restoration algorithm that is rooted in optimal control theory and the Hamilton–Jacobi–Bellman (HJB) equation (see Listing A2).
- Listing A2.
- Python code for image restoration.
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp from PIL import Image from skimage.metrics import peak_signal_noise_ratio, structural_similarity from skimage.restoration import denoise_tv_chambolle import itertools from mpl_toolkits.mplot3d import Axes3D # noqa: F401 (needed for 3D plots) # ----------------------------- # Model parameters # ----------------------------- N = 3 sigma = 0.05 R = 100.0 u0 = 297.79 alpha = 2 r0 = 0.01 r_shoot_end = R rInc = 0.1 # ----------------------------- # Cost function # ----------------------------- def h(r): return np.log(r + 1) # ----------------------------- # Safe power helper # ----------------------------- def safe_power(u_prime, exponent, lower_bound=1e-8, upper_bound=1e2): safe_val = np.clip(-u_prime, lower_bound, upper_bound) return np.power(safe_val, exponent) # ----------------------------- # Radial ODE # ----------------------------- def value_function_ode(r, u): if abs(r) < 1e-6: r = 1e-6 u_prime = u[1] if u_prime >= 0: u_prime = -1e-8 A = (1/alpha) ** (1/(alpha - 1)) * ((alpha - 1) / alpha) exponent = alpha / (alpha - 1) term = A * safe_power(u_prime, exponent) du1 = u_prime du2 = - ((N - 1) / r) * u_prime + (2 / (sigma ** 2)) * (term - h(r)) return [du1, du2] # ----------------------------- # Solve ODE # ----------------------------- print("Starting⊔ODE⊔integration\ldots") r_values = np.arange(r0, r_shoot_end + rInc*0.1, rInc) u_initial = [u0, -1e-6] sol = solve_ivp(value_function_ode, [r0, r_shoot_end], u_initial, t_eval=r_values, method=’BDF’, rtol=1e-10, atol=1e-10) if sol.success: print("ODE⊔integration⊔successful!") else: raise RuntimeError("ODE⊔integration⊔failed") # Boundary condition check (np.trapezoid instead of np.trapz) v_values = -sol.y[1] integral_v = np.trapezoid(v_values, sol.t) g_boundary = u0 - integral_v g_from_solution = sol.y[0][-1] print("Computed⊔boundary⊔condition⊔g⊔(from⊔integral):", g_boundary) print("Computed⊔boundary⊔condition⊔g⊔(from⊔ODE⊔solution):", g_from_solution) # ----------------------------- # Restore image (spatially varying noise) # ----------------------------- def restore_image(image_initial, dt, T, sol, alpha, sigma): timesteps = int(T / dt) x = image_initial.copy() for _ in range(timesteps): r = np.linalg.norm(x, axis=-1) r_safe = np.where(r > 1e-6, r, 1e-6) u_prime_val = np.interp(r_safe, sol.t, sol.y[1]) u_prime_val = np.where(u_prime_val >= 0, -1e-8, u_prime_val) restoration_rate_unit = ((1/alpha) ** (1/(alpha - 1))) * \ (1.0 / r_safe) * \ safe_power(u_prime_val, 1/(alpha - 1)) drift = restoration_rate_unit[..., np.newaxis] * x # i.i.d. Gaussian noise per pixel and channel (spatial variation) noise = sigma * np.random.normal(0, np.sqrt(dt), x.shape) x = x + drift * dt + noise x = np.clip(x, -R, R) return x # ----------------------------- # Load and normalize image # ----------------------------- img = Image.open("lenna.png").convert("RGB") img_array = np.array(img).astype(np.float64) img_mean = np.mean(img_array, axis=(0, 1), keepdims=True) img_centered = img_array - img_mean max_abs = np.max(np.abs(img_centered)) scale_factor = (R/2) / max_abs if max_abs != 0 else 1 x_initial = img_centered * scale_factor # ----------------------------- # Parameter tuning # ----------------------------- sigma_values = [0.002, 0.007, 0.0189, 0.05] T_values = [0.197, 1.0] dt_values = [0.01, 0.17] results = [] print("\nParameter⊔Tuning⊔Results:") for sigma_param, T_param, dt_param in itertools.product(sigma_values, T_values, dt_values): restored_state = restore_image(x_initial, dt_param, T_param, sol, alpha, sigma_param) restored_image = restored_state / scale_factor + img_mean restored_image = np.clip(restored_image, 0, 255) mse_val = np.mean((img_array - restored_image) ** 2) psnr_val = peak_signal_noise_ratio(img_array.astype(np.uint8), restored_image.astype(np.uint8), data_range=255) ssim_val = structural_similarity(img_array.astype(np.uint8), restored_image.astype(np.uint8), channel_axis=-1, data_range=255) results.append({’sigma’: sigma_param, ’T’: T_param, ’dt’: dt_param, ’MSE’: mse_val, ’PSNR’: psnr_val, ’SSIM’: ssim_val}) print(f"MSE:⊔{mse_val:.4f},⊔PSNR:⊔{psnr_val:.4f}⊔dB,⊔SSIM:⊔{ssim_val:.4f}") best_config = max(results, key=lambda r: r[’PSNR’]) print("\nBest⊔configuration⊔based⊔on⊔PSNR:") print(best_config) # ----------------------------- # Final restoration and TV denoising # ----------------------------- restored_state_best = restore_image(x_initial, best_config[’dt’], best_config[’T’], sol, alpha, best_config[’sigma’]) restored_image_best = restored_state_best / scale_factor + img_mean restored_image_best = np.clip(restored_image_best, 0, 255).astype(np.uint8) restored_image_norm = restored_image_best.astype(np.float64) / 255.0 tv_weight = 0.089 restored_image_denoised_norm = denoise_tv_chambolle(restored_image_norm, weight=tv_weight, channel_axis=-1) restored_image_denoised = np.clip(restored_image_denoised_norm * 255, 0, 255).astype(np.uint8) # ----------------------------- # Display 2D images # ----------------------------- plt.figure(figsize=(18, 6)) plt.subplot(1, 3, 1) plt.imshow(img_array.astype(np.uint8)) plt.title("(i)⊔Original⊔Degraded⊔Image") plt.axis("off") plt.subplot(1, 3, 2) plt.imshow(restored_image_best) plt.title("(ii)⊔Restored⊔Image") plt.axis("off") plt.subplot(1, 3, 3) plt.imshow(restored_image_denoised) plt.title("(iii)⊔Restored⊔and⊔Denoised⊔Image") plt.axis("off") plt.tight_layout() plt.show() # ----------------------------- 3D difference surfaces (as in the paper) # ----------------------------- def rgb2gray(img): return np.dot(img[..., :3], [0.2989, 0.5870, 0.1140]) original_gray = rgb2gray(img_array.astype(np.float64)) restored_gray = rgb2gray(restored_image_best.astype(np.float64)) denoised_gray = rgb2gray(restored_image_denoised.astype(np.float64)) diff_restored_denoised = np.abs(restored_gray - denoised_gray) diff_original_restored = np.abs(original_gray - restored_gray) diff_original_denoised = np.abs(original_gray - denoised_gray) rows, cols = diff_restored_denoised.shape X, Y = np.meshgrid(np.arange(cols), np.arange(rows)) fig3 = plt.figure(figsize=(24, 8)) ax1 = fig3.add_subplot(1, 3, 1, projection=’3d’) surf1 = ax1.plot_surface(X, Y, diff_restored_denoised, cmap=’plasma’, alpha=0.85, linewidth=0) ax1.set_title("3D⊔Surface:⊔Diff⊔(i)⊔Restored⊔vs⊔Denoised") ax1.set_xlabel("Pixel⊔Column") ax1.set_ylabel("Pixel⊔Row") ax1.set_zlabel("Difference⊔Intensity") fig3.colorbar(surf1, ax=ax1, shrink=0.6, aspect=12) ax2 = fig3.add_subplot(1, 3, 2, projection=’3d’) surf2 = ax2.plot_surface(X, Y, diff_original_restored, cmap=’coolwarm’, alpha=0.85, linewidth=0) ax2.set_title("3D⊔Surface:⊔Diff⊔(ii)⊔Original⊔vs⊔Restored") ax2.set_xlabel("Pixel⊔Column") ax2.set_ylabel("Pixel⊔Row") ax2.set_zlabel("Difference⊔Intensity") fig3.colorbar(surf2, ax=ax2, shrink=0.6, aspect=12) ax3 = fig3.add_subplot(1, 3, 3, projection=’3d’) surf3 = ax3.plot_surface(X, Y, diff_original_denoised, cmap=’inferno’, alpha=0.85, linewidth=0) ax3.set_title("3D⊔Surface:⊔Diff⊔(iii)⊔Original⊔vs⊔Restored⊔&⊔Denoised") ax3.set_xlabel("Pixel⊔Column") ax3.set_ylabel("Pixel⊔Row") ax3.set_zlabel("Difference⊔Intensity") fig3.colorbar(surf3, ax=ax3, shrink=0.6, aspect=12) plt.tight_layout() plt.show() |
References
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Chan, T.F.; Shen, J. Image Processing and Analysis: Variational, PDE, Wavelet, and Stochastic Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005; 421p, Available online: https://books.google.ro/books?id=3OMHzOpJ0v0C (accessed on 29 August 2025).
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Weickert, J. Anisotropic Diffusion in Image Processing; Teubner: Stuttgart, Germany, 1998. [Google Scholar]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, O. A quasilinear elliptic equation in ℝn. Proc. Roy. Soc. Edinb. Sect. A 1996, 126, 911–921. [Google Scholar] [CrossRef]
- Canepa, E.C.; Covei, D.-P.; Pirvu, T.A. A stochastic production planning problem. Fixed Point Theory 2022, 23, 179–198. [Google Scholar] [CrossRef]
- Pham, H. Continuous-Time Stochastic Control and Optimization with Financial Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhang, X. Nonlocal regularization methods for image restoration: A review. Lect. Notes 2009. Available online: https://www.math.ucla.edu/~lvese/285j.1.09f/NonlocalMethods_main.slides.pdf (accessed on 29 August 2025).
- Lin, J.; Li, X.; Hoe, S.C.; Yan, Z. A Generalized Finite Difference Method for Solving Hamilton–Jacobi–Bellman Equations in Optimal Investment. Mathematics 2023, 11, 2346. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, H.; Liang, L.; Wang, W. Learning the Hybrid Nonlocal Self-Similarity Prior for Image Restoration. Mathematics 2024, 12, 1412. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kim, M. Improving Rebar Twist Prediction Exploiting Unified-Channel Attention-Based Image Restoration and Regression Techniques. Sensors 2024, 24, 4757. [Google Scholar] [CrossRef] [PubMed]
- Bressan, A.; Jiang, Z. The vanishing viscosity limit for a system of H-J equations related to a debt management problem. Discret. Contin. Dyn. Syst. S 2018, 11, 793–824. [Google Scholar] [CrossRef]
- Camilli, F.; Marchi, C.; Schieborn, D. The vanishing viscosity limit for Hamilton–Jacobi equations on networks. J. Differ. Equ. 2013, 254, 4122–4143. [Google Scholar] [CrossRef]
- Covei, D.-P. Existence theorems for equations and systems in ℝN with ki Hessian operator. Miskolc Math. Notes 2023, 24, 1273–1286. [Google Scholar] [CrossRef]
- Fleming, W.H.; Soner, H.M. Controlled Markov Processes and Viscosity Solutions, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Covei, D.-P. Stochastic Production Planning with Regime-Switching: Sensitivity Analysis, Optimal Control, and Numerical Implementation. Axioms 2025, 14, 524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).