A Hybrid EGARCH–Informer Model with Consistent Risk Calibration for Volatility and CVaR Forecasting

Abstract

This study proposes a hybrid EGARCH-Informer framework for forecasting volatility and calibrating tail risk in financial time series. The econometric layer (EGARCH) captures asymmetric and persistent volatility dynamics, while the attention layer (Informer) models long-range temporal dependence with sparse attention. The framework produces horizon-specific forecasts (H = 1 and H = 5) that are mapped to VaR and CVaR at α = 0.95 and 0.99. Evaluation covers pointwise accuracy (MAE, RMSE) and risk coverage calibration (CVaR bias and Kupiec’s unconditional coverage), complemented by Conditional Coverage (CC) and Dynamic Quantile (DQ) diagnostics, and distributional robustness via a Student-t mapping of VaR/CVaR. Across four U.S. equity indices (SPX, IXIC, DJI, SOX), the hybrid matches GARCH at the short horizon and yields systematic error gains at the longer horizon while maintaining higher calibration quality than deep learning baselines. MAE and RMSE values remain near 0.0002 at H = 1, with relative improvements of 2–6% at H = 5. CVaR bias stays tightly bounded; DQ rarely rejects, and CC is stricter but consistent with clustered exceedances, and the Student-t results keep the median hit rates near nominal with small, mildly conservative CVaR biases. These findings confirm the hybrid model’s robustness and transferability across market conditions.

1. Introduction

In today’s increasingly complex and interconnected financial markets, managing asset price volatility and mitigating extreme risk events have emerged as central challenges for both institutional investors and regulators. Recent years have witnessed heightened market turbulence driven by geopolitical conflicts, macroeconomic uncertainties, and technological disruptions. For example, the COVID-19 outbreak in early 2020 led to a record 3000-point drop in the Dow Jones Industrial Average in a single day, while the VIX soared to 85.47, indicating severe volatility conditions. Similarly, in 2022, the onset of the Russia-Ukraine war and the U.S. Federal Reserve’s aggressive interest rate hikes resulted in double-digit losses across major indices, with the S&P 500 and the Philadelphia Semiconductor Index (SOX) both declining by more than 18%. Throughout these events, volatility indicators such as the CBOE Volatility Index (VIX), the CBOE NASDAQ-100 Volatility Index (VXN), and the CBOE DJIA Volatility Index (VXD) remained elevated, illustrating the persistent nature of volatility clustering and the systemic impact of tail risk.

Volatility clustering refers to the autocorrelated and time-dependent behavior of financial returns, where periods of high or low volatility occur in concentrated intervals. This implies that latent risks may escalate even during relatively calm periods. In contrast, tail risk encompasses rare but impactful events that fall outside the expectations of standard models, often leading to severe losses. Together, these phenomena underpin the transmission of systemic risk, especially in modern financial systems where market interlinkages amplify contagion. Historical episodes—including the 2008 global financial crisis, the 2015 Chinese equity crash, and the COVID-19 and Russia-Ukraine crises—demonstrate the long-memory effects and asymmetric responses inherent in financial markets. These conditions necessitate modeling frameworks that combine the structural clarity of econometric models with the nonlinear adaptability of deep learning to effectively capture volatility dynamics and extreme risk events.

Volatility clustering has been well documented across global equity markets. Enow [1] applied GARCH models to indices such as JSE, CAC 40, DAX, and NASDAQ, revealing high persistence coefficients—up to 83.1% for NASDAQ. Zhao et al. [2] further examined clustering in intraday and overnight returns across 15 global markets, finding stronger effects in overnight sessions, with a GARCH β of 0.8994 for the S&P 500. These studies also identified directional spillovers from intraday to overnight volatility, highlighting the accumulation of short-term risks.

Amplified volatility often precedes tail risk events. Lin et al. [3] employed the EGB2 option pricing model to detect early warning signals before China’s 2015 stock market crisis, while Chaudhry et al. [4] used extreme value theory to show that technology firms like Facebook and Alibaba have higher tail risk potential than financial institutions, despite lower short-term systemic β values. Extended window analysis, however, revealed growing systemic exposure in the tech sector. Abduraimova [5] identified developed economies as central nodes in global contagion networks, forming a “core-periphery” risk structure. Chatziantoniou et al. [6] observed that tail risk connectedness in the oil market surged to 76.63% during the early stages of the COVID-19 pandemic—levels unseen since the 2008 crisis.

Volatility and tail risk are also prominent in digital asset markets. Peovski et al. [7] found strong GARCH persistence and leverage effects in cryptocurrencies such as ETH and ADA, while DOGE exhibited signs of explosive volatility. To address such risks, Wang et al. [8] proposed ER-based LSTM/GRU models combined with spline quantile approaches, which outperform traditional techniques in estimating VaR and CVaR. Cevik et al. [9] introduced a systemic risk indicator that integrates EGARCH volatility, variance risk premiums, and distance-to-capital metrics, successfully identifying events like the 2023 Silicon Valley Bank collapse.

Recent studies have increasingly focused on modeling systemic risk across asset classes and sectors. Marfè and Pénasse [10] developed a macroeconomic tail risk model using 18 crisis predictors across 42 countries from 1900 to 2020, achieving robust out-of-sample performance. Xie et al. [11] applied the TENET model and LASSO quantile regression to MSCI energy stocks, revealing Europe as a major risk transmitter and CPI as the most influential risk driver. Prüser et al. [12] employed Gaussian Processes with Bayesian quantile regression and shrinkage priors, improving U.S. GDP tail forecasts by up to 25% in CRPS. In the crypto domain, Maghyereh et al. [13] used CAViaR and TVP-VAR to show that Ethereum acts as a primary tail risk transmitter, with indicators like the Fear & Greed Index enhancing forecast accuracy.

Other applications include commodity and textual risk analysis. Feng et al. [14] introduced the Auto-regressive Extreme Value (AEV) model for China’s rebar market, outperforming GARCH benchmarks in tail estimation and margin design. Adämmer et al. [15] leveraged nearly 800,000 news articles through sentiment-adjusted topic models and nonlinear quantile regressions, finding that textual signals significantly enhance tail predictions under high uncertainty.

Cross-sector risk transmission has gained attention in recent work. De et al. [16] proposed a hybrid IMV-LSTM with LassoNet to assess Japanese and U.S. bank interconnectedness, revealing key exporters of systemic risk during crises. Barkai et al. [17] applied the Epsilon Drawdown method to cryptomarkets, showing Litecoin’s high co-movement and drawdown sensitivity. Ali et al. [18] examined tail risk flows between AI and FinTech stocks, identifying VIX and EPU as amplifiers of systemic linkage. Billah et al. [19] investigated Islamic, Sukuk, and green markets, reporting strong short-term dynamics and dominant risk transmission by DJIM. Ouyang and Xiao [20] highlighted sectoral asymmetries in China, with industrials and materials as leading risk exporters during the pandemic. Cont et al. [21] used generative adversarial networks to simulate realistic multiasset price scenarios, accurately capturing tail risks for trading strategies via Value-at-Risk and Expected Shortfall metrics.

Advances in predictive modeling have driven hybrid designs across equities, FX, and portfolios. Srivastava et al. [22] employed multivariate LSTM with association rule mining for NIFTY50 stocks, improving the RMSE and MAPE. Wang and Liu (2025) [23] showed that physical environmental risks and investor attention jointly amplify systemic risk in EU banks. Using mLSTM-CoVaR and QQR models on 26 banks across 12 countries, CoVaR rose during COVID-19 and the Russia-Ukraine conflict. Sheng et al. [24] incorporated CVaR-based portfolio optimization into ML workflows, delivering 17.43% annualized returns. Nsengiyumva et al. [25] developed a GARCH-LSTM hybrid for VaR estimation in Rwanda’s FX market, reducing forecasting errors while preserving model responsiveness. In high-volatility environments, Yao (2025) [26] introduces a time-series nested reinforcement learning (TS-NRL) framework that integrates multi-scale volatility features with a dynamic return-risk optimization engine. The model achieves 91.2% short-term feature accuracy and outperforms traditional baselines with a 24.8% improvement in the return-risk ratio, underscoring the efficacy of reinforcement learning in controlling downside risk under nonlinear financial conditions.

These studies illustrate the increasing demand for hybrid, explainable, and adaptive models that effectively manage tail risk, capture dynamic volatility patterns, and support real-time decision-making under uncertain conditions.

Motivated by these developments, this study proposes a hybrid EGARCH-Informer framework that integrates econometric volatility modeling with attention-based deep learning for analyzing volatility clustering and tail risk across major equity indices. EGARCH captures asymmetric and persistent volatility structures, while Informer efficiently extracts temporal dependencies from long-sequence, multivariate data. The combination enhances both interpretability and predictive power, offering a robust solution for tail event diagnostics under structural market shifts and elevated uncertainty.

The remainder of this paper is organized as follows. Section 2 reviews relevant literature on volatility modeling, deep learning applications, and hybrid risk frameworks. Section 3 presents the EGARCH-Informer architecture and details the data and feature design. Section 4 outlines the experimental design and empirical results. Section 5 concludes with implications and future directions for financial risk management.

2. Literature Review

Financial market behaviors often deviate from linear expectations, exhibiting abrupt shifts and asymmetric responses. These complexities demand forecasting models that adapt to evolving structures while preserving interpretability. As data availability and computational capacity have expanded, risk prediction techniques have transitioned beyond traditional variance-based formulations toward architectures capable of capturing deep patterns and persistent dependencies in market data. From a risk-management standpoint, accuracy and coverage jointly determine capital efficiency; thus, calibration diagnostics and heavy-tailed specifications are integral to model assessment. Simultaneously, modern approaches increasingly incorporate external signals-such as macro-financial uncertainty and market sentiment-to enhance the sensitivity of predictive frameworks. Attention-based sequence models, especially those optimized for long-horizon dependencies and real-time processing, have emerged as viable tools for identifying latent dynamics and amplifying early warning capabilities. Moreover, indicators such as volatility indices and economic uncertainty metrics have demonstrated added value in guiding model responsiveness. This section surveys these methodological developments, covering the evolution of volatility modeling frameworks, the progression of tail risk estimation techniques, the application of Transformer-inspired time series models, and the empirical integration of market-based risk signals.

Understanding and modeling volatility has long been a critical task in financial econometrics. Traditional ARCH and GARCH models remain fundamental tools in this domain, yet the need for more nuanced approaches becomes evident when analyzing markets with asymmetric responses or structural differences. In their examination of Cameroon’s exchange rates, Dinga et al. (2023) [27] employed ARMA-GARCH family models, integrating Skewed Generalized Error Distributions (SGEDs) to account for heavy tails. Their findings revealed that while the USD/XAF rate showed less structural complexity, the CNY/XAF rate displayed pronounced volatility persistence and significant leverage effects, justifying the use of GJR-GARCH specifications for more accurate volatility modeling. The application of volatility models has also gained considerable traction in cryptocurrency research. Yıldırım and Bekun (2023) [28] focused on Bitcoin return dynamics using weekly data, highlighting clear volatility clustering. Their results confirmed GARCH(1,1) as the most suitable model under standard information criteria, while the EGARCH framework captured asymmetric volatility, especially the heightened impact of negative shocks. These results emphasize the limitations of symmetric models in markets dominated by speculative trading and nonlinear investor behavior.

Equity markets in emerging economies present another layer of complexity. Safi et al. (2024) [29] analyzed the BSE-SENSEX index, revealing statistically significant heteroskedasticity and non-normality in return distributions. The GARCH(1,1) model demonstrated strong clustering effects, with a β coefficient of 0.896, while TGARCH captured negative news sensitivity, evidenced by a significant γ value of 0.164. These insights highlight how different GARCH variants provide distinct advantages in forecasting financial risk, especially when market sentiment exhibits asymmetry. Ahmar et al. (2024) [30] extended volatility analysis to currency markets, focusing on the Indonesian Rupiah against the U.S. Dollar. Their study found that GARCH(1,1) models offered substantial improvements over ARCH models in capturing long-run dependencies. They also noted that global macroeconomic forces—such as oil prices and monetary policy shifts—significantly influenced exchange rate behavior. These exogenous shocks further validate the application of models that can incorporate persistence and adaptability in the presence of evolving market regimes.

Political conditions can alter volatility patterns in profound ways. Alim et al. (2024) [31] investigated the influence of political stability on Pakistan’s stock market, revealing how different GARCH-type models interpret such influence. GARCH-M indicated that political stability not only improves returns but also suppresses volatility. In contrast, EGARCH effectively exposed how instability—such as terrorism or coups—magnifies downside risk. These results provide evidence that volatility is shaped not only by market mechanics but also by institutional and geopolitical environments. To address the modeling limitations of standard frameworks, Xu (2025) [32] proposed an extended multivariate EGARCH model capable of handling zero returns and capturing negative spillovers. Applied to DJ30 stock data and multiple asset classes including crude oil and gold, the model revealed significant asymmetric interactions that previous specifications often miss. The flexibility to handle such nuances marks a step forward in building more comprehensive financial risk models.

Estimating tail risk has become a critical task in financial modeling, especially under the growing impact of extreme market events. Lin et al. (2024) [33] designed a CVaR-based optimization model tailored for integrated energy systems, incorporating Gaussian Mixture Models and Frank-Copula functions to model and preserve extreme scenarios. Their work demonstrates that ignoring tail events in scenario generation leads to underestimation of potential losses, reducing planning robustness by approximately 3%. This methodology, though applied to energy markets, offers a transferable risk control structure valuable to financial systems.

Recent advancements have focused on deep learning to enhance traditional risk estimation. Dai and Li (2024) [34] proposed an enhanced index tracking (EIT) framework using a neural architecture comprising four functionally distinct blocks. Their S&P 500 experiment showed that integrating stock and index regime signals led to superior returns (mean excess return = 0.034), Sharpe ratios (0.081), and controlled CVaR (<3%). These findings highlight the importance of integrating nonlinear regime-aware learning mechanisms to respond to tail-heavy events in real time.

The role of generative AI in risk management is also emerging. Yazdi et al. (2024) [35] examined the use of ChatGPT-4 in hazard detection and control planning. While generative models improved risk visualization and speed of response, contextual gaps still exist-suggesting their current value lies more in supplementing human oversight rather than replacing it. Wu (2025) [36] developed a DBN-MDN hybrid model for tail risk prediction in the European carbon market. The model outperformed 8 benchmarks, including ARIMA, CNN, XGBoost, and LSTM, achieving an RMSE of 0.0019 and R² of 0.9332. Importantly, it addressed nonlinear heavy-tailed distributions via a probabilistic density approach, enhancing policy-relevant forecasting under emission trading schemes. Zhu et al. (2025) [37] applied AR-EGARCH and AR-EGARCH-EVT models to quantify tail risks across 14 asset classes. Bitcoin exhibited the highest tail risk (VaR = 6.88%), while gold remained the safest (VaR = 1.43%). During COVID-19, crude oil’s tail risk surged by 38%, demonstrating the necessity of tail-aware models. Their extended EVT framework consistently outperformed in unconditional and conditional coverage tests.

In recent years, Transformer-based models have become the cornerstone of advanced time series forecasting, particularly for financial applications requiring long-term dependencies and multivariate data handling. Casolaro et al. (2023) [38] offered a comprehensive overview of short- and long-term deep learning models, highlighting the evolution from RNNs, CNNs, and GANs to more scalable Transformer variants like Informer, FEDformer, Autoformer, and Crossformer. These architectures consistently outperform traditional models in multivariate tasks. For example, Crossformer achieved an MSE of 0.495 and MAE of 0.515 on the Weather dataset with prediction length P = 336, surpassing Informer and Autoformer in accuracy and stability. Liu and Wang (2024) [39] further extended this landscape by reviewing over 80 models across RNN, CNN, MLP, and Transformer families. They emphasized the dominance of Transformer variants in long sequence forecasting tasks and explored challenges such as distribution shifts, irregular sampling, and the integration of temporal and frequency domains. MLP-based models like DLinear and TiDE are noted for their compactness, while Transformer variants like PatchTST achieved state-of-the-art performance, e.g., MSE = 0.149 on the Weather dataset with P = 96.

Building upon this foundation, Ji et al. (2024) [40] proposed Galformer, which introduces a generative decoder and hybrid loss function to improve inference speed and trend prediction. On the CSI300 index, Galformer achieved an R² of 95.23% with an MAPE of just 0.93%, outperforming traditional Transformer setups by a wide margin. Its hybrid loss effectively improved directional accuracy (ACC = 52.75%), a key factor in financial decision-making.

Transformer variants are not only powerful but also efficient when integrated into hybrid models. Liu et al. (2025) [41] developed a CEEMDAN-GRU-Informer architecture that decomposes financial time series into intrinsic mode functions, using GRU for low-complexity and Informer for high-complexity sequences. On SZ1 and SZ6 datasets, the model reached RMSE values as low as 0.0007 and 0.0009, with statistical superiority confirmed via Model Confidence Set tests.

Chang et al. (2024) [42] empirically validated the superior performance of GRU over LSTM in technology stocks like Apple and Microsoft. Their results also show GRU’s robustness compared to XGBoost and ARIMA, with Apple’s GRU-based RMSE at 3.43 and R² at 0.82.

In 2025, Zeng et al. (2025) [43] designed the WTC-DCA-Informer framework to forecast Australian stock market volatility. This framework integrates wavelet-based feature extraction, dynamic causality analysis, and Informer-based prediction. The model achieved an R² of 0.8633 and MAPE of 13.69%, showing strong robustness across market regimes including pre- and post-COVID periods. Yu et al. (2025) [44] provided one of the most exhaustive reviews to date, analyzing 150+ references across 40 architectures and 30 datasets. They emphasized the role of Informer and its variants in addressing computational bottlenecks via ProbSparse attention, enabling efficient long-sequence modeling. Despite their superior accuracy—often 15–30% better than traditional models—these deep architectures require significant computational resources, highlighting the tradeoff between precision and efficiency. Lastly, Yang et al. (2025) [45] introduced the TFT-ASRO model, which fuses multi-sensor inputs (e.g., price, volume, sentiment) to forecast stock Sharpe ratios. The model achieves a 13.6% reduction in MAE and offers dynamic adaptation to market shifts using uncertainty quantification via Bayesian neural networks and quantile regression. These studies affirm the rise of Transformer-based architectures—especially Informer and its derivatives—as indispensable tools for modeling nonlinear dependencies and volatility in complex financial environments.

Market-based risk indicators, such as implied volatility indices, have become essential tools in financial forecasting, offering real-time insights into investor sentiment and risk expectations. Unlike fundamental or technical metrics, indices like the VIX, VVIX, and SKEW are forward-looking by design, reflecting market anticipations of future volatility. Their integration into predictive models-either as standalone features or within more complex hybrid frameworks-has yielded considerable improvements in both accuracy and economic utility, particularly during periods of market stress. Campisi et al. (2024) [46] examine multiple machine learning methods for forecasting US stock market direction based on volatility indices. Using data from 2011 to 2022 and several CBOE indicators (VIX, VVIX, SKEW, OVX, GVZ), they compare regression and classification settings. Ensemble learning models like Random Forest and Bagging outperform linear baselines in accuracy, AUC, and F-measure, with Lasso regression enhancing feature selection and interpretability. Guidolin and Panzeri (2024) [47] further assess HAR-based models’ predictive performance on the VIX and SKEW indices. While the standard HAR model proves most effective for forecasting VIX, augmented versions like HAR-SK-PUTS and HAR-IV provide better SKEW forecasts, especially on transformed time series. The Model Confidence Set (MCS) approach validates the HAR model’s robustness across numerous forecasting scenarios. Pan et al. (2024) [48] adopt an entropic tilting approach to integrate forward-looking signals from VIX and VVIX into a HARGARCH-NIG model. Their framework significantly improves both point and density forecasts of realized volatility, especially during recessionary periods. Forecast accuracy gains are statistically confirmed through the Diebold-Mariano test, and economic utility is captured via an increase in expected utility per unit of wealth. Bai and Cai (2024) [49] extend VIX prediction using a 278-feature machine learning model powered by Adaptive Boosting. Their method achieves high accuracy (68.2%) and demonstrates strong risk-adjusted performance (Sharpe ratio 1.73). Notably, economic variables and seasonality indicators contribute more predictive value than VIX-based features alone. Gunnarsson et al. (2024) [50] offer a systematic review of AI-based volatility forecasting, analyzing 32 studies filtered from over 380 initial entries. LSTM and Random Forest emerge as dominant algorithms, with macroeconomic and technical indicators shown to enhance forecast quality. However, model explainability remains underexplored, with few studies applying techniques like Shapley values. Lastly, Degiannakis et al. (2025) [51] explore the trading value of multi-day-ahead volatility forecasts. Through simulated trading, they show that longer-horizon forecasts using the HAR-IV-TYVIX model yield superior returns in VIX and S&P500 futures markets, challenging conventional assumptions about forecast horizon alignment with trading frequency.

The reviewed literature demonstrates significant advances in financial volatility and tail risk modeling across various domains. Classical econometric models such as GARCH and its variants continue to provide structural insight, particularly in capturing volatility persistence and asymmetric effects. Deep learning architectures—especially Transformer-based models like Informer [52], FEDformer [53], and TFT [54]—have surpassed traditional benchmarks in long-sequence forecasting, trend inference, and hybrid learning under dynamic regimes. Tail risk estimation has further evolved through CVaR frameworks, EVT extensions, and probabilistic deep models that improve both interpretability and scenario robustness. Meanwhile, the integration of market-based indicators such as VIX, VVIX, and SKEW has enriched the explanatory and predictive power of modern systems, especially under crisis conditions.

Despite these advancements, existing studies often treat econometric and deep learning models in isolation. Few have systematically integrated statistical volatility estimators into Transformer architectures to capture both structural and nonlinear dynamics simultaneously. This gap motivates the present study’s hybrid design, which fuses EGARCH-based volatility signals with the temporal modeling capabilities of Informer to enhance the forecasting of volatility clustering and tail risk transmission across equity markets. In line with current practice, the empirical assessment evaluates not only pointwise accuracy but also risk calibration—combining Kupiec’s unconditional coverage with Conditional Coverage (CC) and Dynamic Quantile (DQ) diagnostics—and further checks distributional robustness by mapping VaR/CVaR under a Student-t specification, so that the credibility of risk thresholds is assessed alongside predictive accuracy.

3. Research Methodology

This section presents the methodological framework adopted to analyze volatility clustering and tail risk in financial time series using a hybrid EGARCH-Informer approach. The methodology is structured into three main components. First, Section 3.1 introduces the dataset, preprocessing procedures, and feature engineering pipeline, including the construction of log returns, EGARCH-based volatility features, and standardized exogenous indicators. Second, Section 3.2 details the modeling architecture, describing the statistical estimation process via EGARCH(1,1), followed by the design of the Informer-based multivariate forecasting module. The integration strategy for estimating tail risk measures such as Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) is also outlined. Finally, Section 3.3 defines the evaluation metrics used to assess both volatility prediction accuracy and tail risk estimation performance, ensuring rigorous and interpretable model validation.

3.1. Data Description and Preprocessing

3.1.1. Data Sources

This study utilizes daily closing price data from four representative U.S. stock indices: the S&P 500 (SPX), NASDAQ Composite (IXIC), Dow Jones Industrial Average (DJI), and the Philadelphia Semiconductor Index (SOX). These indices were selected to capture heterogeneous volatility structures across different market segments, including large-cap equities, technology sectors, industrial components, and semiconductor markets. The data spans from 1 January 2015 to 31 December 2024, providing a sufficiently long time horizon that includes diverse market conditions and volatility regimes. Daily data are retrieved from Yahoo Finance, ensuring accessibility and reproducibility. To enhance the prediction of volatility and tail risk, this research incorporates market-based volatility indices as external explanatory signals. Specifically, the VIX is aligned with SPX, VXN with IXIC, and VXD with DJI. These implied volatility measures reflect market expectations of future price variability and serve as forward-looking risk proxies. Since no dedicated implied volatility index exists for SOX, it is modeled without external volatility inputs. All volatility index data are collected from the official CBOE database.

Two normalization methods are adopted to ensure numerical stability and compatibility with the EGARCH and Informer models. For price series, logarithmic returns are computed as:

$$r_t=\mathrm{l}\mathrm{n}\left({\displaystyle \frac{P_t}{P_{t-1}}}\right)$$

(1)

where $P_t$ is the closing price at time t, and $r_t$ denotes the daily log return. This transformation stabilizes variance, improves stationarity, and emphasizes relative rather than absolute price changes.

For external indicators and EGARCH-generated volatility sequences, Z-score normalization is applied:

$$Z_t={\displaystyle \frac{X_t-{\mu }_X}{{\sigma }_X}}$$

(2)

where $X_t$ is the original value at time t, ${\mu }_X$ is the sample mean, and ${\sigma }_X$ is the sample standard deviation of the series over the training period. This method ensures that input features are centered and scaled, enabling more effective learning and attention-based processing in the Informer model. Logarithmic return transformation is applied to raw index prices to produce stationary input for volatility modeling, while Z-score normalization is applied to bounded but non-stationary features—namely, implied volatility indices and EGARCH outputs—to standardize their magnitude across time. To avoid look-ahead, the mean and standard deviation used in the z-score are estimated on the training partition and kept fixed for validation and test data. Because z-scores are not a robust scaler under stress-period outliers, the empirical assessment also reports calibration diagnostics—Kupiec’s unconditional coverage together with CC and DQ—and examines distributional robustness via a Student-t mapping of VaR/CVaR. All series are synchronized based on trading dates to construct a unified multivariate time-series dataset for downstream modeling.

3.1.2. Feature Engineering

This section outlines the feature engineering process used to construct an informative and temporally aligned multivariate sequence input for the forecasting model. The construction involves three types of features: log returns of stock indices, EGARCH-derived conditional variances, and standardized external volatility indices. Each is designed to encode specific aspects of market behavior-ranging from price momentum and asymmetric risk to investor sentiment embedded in forward-looking risk indicators. The log return series $r_t$ introduced in Section 3.1.1, serves as the base financial signal, reflecting relative day-to-day price changes in a scale-invariant form. While the return series is essential for capturing high-frequency market dynamics, it often exhibits volatility clustering and leverage effects, where large shocks are followed by persistent high variance, and negative returns exert greater influence than positive ones.

To formally model these patterns, this study employs the Exponential Generalized Autoregressive Conditional Heteroskedasticity (EGARCH) model introduced by Nelson (1991) [55]. Unlike traditional GARCH models, EGARCH expresses the conditional variance in logarithmic form, which ensures positivity without parameter constraints and explicitly captures asymmetric responses to past shocks. The EGARCH(1,1) specification is given by:

$$\mathrm{l}\mathrm{n}\left({\sigma }_t^2\right)=\omega +\beta \mathrm{l}\mathrm{n}\left({\sigma }_{t-1}^2\right)+\alpha \left({\displaystyle \frac{\left|{\mathcal{z}}_{t-1}\right|}{\sqrt{\pi }}}\right)+\gamma {\mathcal{z}}_{t-1},{\mathcal{z}}_{t-1}={\displaystyle \frac{r_{t-1}}{{\sigma }_{t-1}}}$$

(3)

where ${\sigma }_t^2$ denotes the conditional variance at time t, ${\mathcal{z}}_{t-1}$ is the standardized residual, and $\omega$, $\beta$, $\alpha$, $\gamma$ are model coefficients. The term $\alpha \left({\displaystyle \frac{\left|{\mathcal{z}}_{t-1}\right|}{\sqrt{\pi }}}\right)$ accounts for volatility magnitude, while $\gamma {\mathcal{z}}_{t-1}$ captures the asymmetric impact of shocks. This property is particularly important in financial markets where negative news tends to increase volatility more than positive news of the same magnitude. The estimated sequence ${\sigma }_t^2$ provides structured volatility features used as exogenous inputs to the Informer model.

In addition to internal volatility, we incorporate exogenous risk perception through implied volatility indices—VIX for S&P 500, VXN for NASDAQ, and VXD for Dow Jones. These indices are forward-looking measures derived from option prices and reflect the market’s expectation of future volatility. However, due to differing scales and market bases, these series must be normalized for effective use in deep learning models. This study applied Z-score standardization for these features. These engineered features form a structured multivariate time series input aligned across dates and dimensions. By combining historical price behavior, model-estimated structural volatility, and real-time market sentiment proxies, the model is equipped to capture both endogenous and exogenous drivers of volatility. All transformations are performed with statistics derived from the training set to preserve out-of-sample integrity during testing.

3.2. Modeling Framework

To address the challenges of modeling volatility clustering and long-range dependencies in financial markets, this study proposes a hybrid forecasting architecture that integrates statistical and deep learning methods. The framework begins with the EGARCH(1,1) model to estimate conditional variance, capturing asymmetric volatility dynamics commonly observed in asset returns. These normalized volatility estimates are then treated as structural risk features and fused with log returns and standardized market-based indicators. The resulting multivariate input is processed by the Informer model, which is designed for efficient long-sequence learning through sparse self-attention and top-k selection. The encoder captures complex temporal patterns, while the decoder outputs a volatility proxy at predefined forecast horizons. The model is optimized via gradient descent using a mean squared error objective, enabling it to jointly learn from statistical patterns and deep sequence representations for improved volatility prediction. The hybrid algorithm is shown in Algorithm 1.

Algorithm 1: Hybrid EGARCH-Informer Forecasting Algorithm

Input: $R_t$: Daily log return of financial index ${\widehat{\sigma }}_t^2$: Estimated conditional variance from EGARCH(1,1) $Z_t\in {\mathbb{R}}^k$: Standardized exogenous risk indicators (e.g., VIX, VXN, VXD) $T$: Length of input sequence $\eta$: Learning rate $h$: Forecast horizon (e.g., 1 and 5 days) Output: ${\widehat{y}}_{t+h}^{\left(n\right)}\in \mathbb{R}$: Forecasted volatility proxy

1. Volatility Estimation via EGARCH Compute the conditional variance sequence ${\widehat{\sigma }}_t^2$ using the EGARCH(1,1) model. Normalize the sequence using z-score and treat it as a structural volatility feature.

2. Input Construction 2.1. Concatenate features into combined vector:     $X_t=\left[R_t,{\widehat{\sigma }}_t^2,Z_t\right]\in {\mathbb{R}}^{1\times d}$ 2.2. Use sliding window to form encoder input:     $X_{t-T+1:t}=\left[X_{t-T+1},\dots ,X_t\right]\in {\mathbb{R}}^{T\times d}$ 3. Informer Encoding 3.1. Feed the encoder input sequence $X_{t-T+1:t}\in {\mathbb{R}}^{T\times d}$ into the Informer model. 3.2. The Informer module processes the sequence using sparse self-attention and top-k selection mechanisms to capture long-range temporal dependencies. 3.3. The encoded representation is denoted as $H_t\in {\mathbb{R}}^{T\times h}$, where each vector embeds the compressed temporal and structural patterns from past observations. 4. Forecasting and Optimization 4.1. Decode representation and generate output:     ${\widehat{y}}_{t+h}=W_0\cdot \mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}\left(H_t\right)+b_0$ 4.2. Compute loss using mean squared error (MSE):     $\mathcal{L}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left({\widehat{y}}_{i,t+h}-y_{i,t+h}\right)}^2$ 4.3. Update model parameters via gradient descent:     $\theta \leftarrow \theta -\eta {\nabla }_{\theta }\mathcal{L}$

The EGARCH-Informer hybrid model offers a complementary fusion of statistical rigor and transformer-based learning capacity. EGARCH(1,1) contributes interpretable volatility estimates grounded in financial theory, highlighting asymmetry and persistence effects in return series. These outputs, once normalized, become part of a broader input context that includes return and risk-based signals. The Informer model then processes this temporal data using its attention-driven architecture to distill key historical insights. Algorithm 1 is model-agnostic with respect to the conditional volatility engine; GJR-GARCH, FIGARCH, or other asymmetric/long-memory specifications can be substituted for EGARCH without altering the training loop. A broader head-to-head comparison is left for future work to maintain focus. By learning from both engineered volatility features and raw market dynamics, the model generates forecasts of future volatility behavior. This dual-path design strengthens forecasting reliability under turbulent market conditions, combining domain-specific volatility modeling with high-dimensional sequence analysis.

3.3. Risk Forecasting with Volatility Proxy

To translate the predicted volatility proxy into meaningful risk measures, this study adopts a distribution-based forecasting strategy for Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR). This approach builds on the theoretical formulation by Rockafellar and Uryasev (2000) [56], which defines CVaR as the expected loss beyond the VaR threshold, and has since been widely applied in financial risk modeling.

Since the Informer model outputs one-day and five-day ahead predictions of squared returns or absolute returns-both commonly used as volatility proxies—these outputs are treated as the basis for estimating risk measures under a parametric assumption. Specifically, it is assumed that the return process follows a zero-mean normal distribution with the predicted volatility serving as the standard deviation. For squared returns, the predicted volatility is taken as the square root of the forecasted value, i.e., ${\widehat{\sigma }}_t=\sqrt{{\widehat{y}}_t}$; for absolute returns, a moment-based adjustment is applied to approximate the standard deviation, following the known relation $\mathbb{E}\left[\left|X\right|\right]=\sqrt{2/\pi }\sigma$ under the Gaussian distribution. The one-step-ahead VaR at confidence level $\alpha$ is then calculated using the inverse cumulative distribution function of the standard normal distribution:

$${\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }={\mathsf{\Phi }}^{-1}\left(\alpha \right)\cdot {\widehat{\sigma }}_t$$

(4)

Here, ${\mathsf{\Phi }}^{-1}\left(\alpha \right)$ denotes the quantile corresponding to confidence level $\alpha$, and ${\widehat{\sigma }}_t$ is the predicted standard deviation based on the model’s output. The corresponding Conditional Value-at-Risk (CVaR) is defined as the expected loss given that the loss exceeds the VaR threshold. Under the same normality assumption, it can be computed as:

$${\mathrm{C}\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }={\displaystyle \frac{1}{1-\alpha }}{\int }_{-\infty }^{{VaR}_t^{\alpha }}x\cdot f\left(x\right)dx={\displaystyle \frac{\varphi \left({\Phi }^{-1}\left(\alpha \right)\right)}{1-\alpha }}\cdot {\widehat{\sigma }}_t$$

(5)

where $f\left(x\right)$ is the probability density function of the standard normal distribution, and $\varphi \left(\cdot \right)$ represents its value at the VaR threshold. This closed-form solution enables a consistent and computationally efficient estimation of tail risk. In subsequent experiments, the predicted VaR and CVaR values will be compared against the realized losses to evaluate model accuracy, robustness, and responsiveness to extreme market conditions. In addition to the normal mapping, this study reports a Student-t mapping of VaR/CVaR, with degrees of freedom estimated from standardized residuals. This provides a direct check on heavy-tail robustness without retraining the models. Calibration is assessed not only with Kupiec’s unconditional coverage but also with CC and DQ tests. DQ targets dynamic misspecification in the violation sequence, while CC jointly evaluates nominal coverage and independence.

4. Experiments and Results Analysis

This section presents the experimental design and results analysis for the proposed volatility forecasting and tail risk estimation framework. The objective is to evaluate the predictive performance of the hybrid EGARCH-Informer architecture against both traditional econometric models and state-of-the-art deep learning approaches. The evaluation covers multiple dimensions, including the accuracy of volatility-proxy forecasts, the estimation of VaR and Conditional CVaR, and performance consistency across different stock indices. To assess risk calibration more comprehensively, the analysis reports Kupiec p-values and complements them with CC and DQ, and also examines distributional robustness by mapping VaR/CVaR under a Student-t specification. All models are trained and tested using identical data partitions, input configurations, and evaluation metrics to ensure comparability. The benchmark models—ranging from statistical baselines to recurrent and transformer-based architectures—enable a comprehensive assessment of strengths and limitations across modeling paradigms. Through this comparative analysis, the study identifies scenarios where each method demonstrates its advantages, while highlighting the robustness and effectiveness of the proposed hybrid framework in volatile financial environments.

4.1. Experimental Setup and Evaluation Metrics

The empirical design of this study reflects both technical precision and a sensitivity to the temporal dynamics of financial markets. Working on a dedicated environment-Windows 11 Pro, NVIDIA GeForce RTX 4090 GPU, Intel^® Core™ i9-12900K CPU, and 32 GB RAM-the analysis draws on daily observations of four major U.S. equity indices: the SPX, IXIC, DJI, and SOX. Each index is paired with its primary volatility benchmark—VIX for SPX, VXN for IXIC, and VXD for DJI—while SOX, lacking a dedicated volatility index, retains a standardized placeholder to maintain consistent feature dimensionality. The data span from 1 January 2015 to 31 December 2024 and are partitioned chronologically into training (2015–2021), validation (2022–2023), and testing (2024) to prevent look-ahead bias. Trading days are aligned across markets using adjusted close prices, ensuring synchronized daily sequences without forward-filled leakage from future values. Daily log returns are calculated and aligned with EGARCH-estimated conditional variances and standardized risk indicators to form the model input vectors $X_t=\left[R_t,{\widehat{\sigma }}_t^2,Z_t\right]$. Normalization is applied using training-set statistics only, preserving the integrity of out-of-sample evaluation. In the tail risk assessment stage, the predicted volatility proxies—either squared returns or absolute returns at one- and five-day horizons—are translated into VaR and CVaR using the parametric Gaussian framework described in Section 3.3. This approach leverages the forecasted volatility as the standard deviation parameter within the distributional assumption, mapping model outputs to economically interpretable risk thresholds. The accuracy of these estimates is evaluated on the 2024 test set by comparing predicted and realized exceedances, quantifying both coverage and magnitude deviation for extreme losses. By integrating volatility forecasting with direct risk measure computation, the framework reflects not only statistical performance but also practical applicability in market risk monitoring.

To evaluate the proposed forecasting framework in both general precision and risk control performance, this study adopts two types of evaluation metrics: accuracy-based metrics, which quantify prediction closeness to actual values, and tail risk-based metrics, which reflect how well the model captures rare but impactful downside events. The accuracy-based metrics include Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE). Both are calculated between the predicted volatility proxy ${\widehat{y}}_t$ and the realized squared return $y_t=R_t^2$, where $R_t$ is the daily log return. The MAE reflects the average magnitude of absolute prediction errors, while the RMSE penalizes larger deviations more strongly due to the square operation, making it more sensitive to outliers. Formally, the MAE and RMSE are defined as:

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left|y_t-{\widehat{y}}_t\right|$$

(6)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{T}}\sum _{t=1}^T{\left(y_t-{\widehat{y}}_t\right)}^2}$$

(7)

where $T$ is the total number of forecast observations.

In parallel, the tail risk-based evaluation focuses on the model’s ability to quantify extreme losses. Three metrics are used: VaR coverage ratio, CVaR bias, and the Kupiec Test. These metrics are based on the distribution-based estimation strategy described in Section 3.3. The VaR coverage ratio is calculated as the proportion of observations where the actual return squared $y_t$ exceeds the predicted ${\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }$. If ${\mathbb{I}}_t=1$ when $y_t$ > ${\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }$, and 0 otherwise, then

$$\mathrm{C}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\mathbb{I}}_t$$

(8)

This value should be close to $\alpha$, the confidence level, under ideal calibration.

CVaR bias is defined as the deviation between the predicted $\mathrm{C}{\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }$ and the empirical average of returns squared $y_t$ that exceed ${\mathrm{V}\mathrm{a}\mathrm{R}}_t^{\alpha }$, revealing whether the model systematically underestimates or overestimates extreme loss magnitude. Lastly, the Kupiec Test [57] is a likelihood ratio-based test that compares the observed exceedance frequency to the expected rate under the null hypothesis. Its test statistic follows a chi-square distribution with one degree of freedom.

These evaluation metrics form a balanced framework that jointly assesses precision and risk estimation capability, ensuring that the model is not only accurate under normal conditions but also reliable when facing market turbulence.

4.2. Comparative Evaluation of Forecasting Models Across Time Horizons

To assess the performance of different forecasting approaches under varying time horizons, this section presents a comparative analysis of five models—ARIMA, GARCH, LSTM, GRU, and the proposed EGARCH-Informer—applied to the SPX index. Two forecasting horizons are considered: H = 1 denotes a one-day ahead prediction, while H = 5 represents a five-day ahead forecast. The evaluation encompasses both accuracy-based metrics (Mean Absolute Error, Root Mean Squared Error) and tail risk metrics (VaR coverage rate, CVaR bias, and Kupiec test statistics). By examining both short- and medium-term forecasting capabilities, this section highlights each model’s strengths and weaknesses in volatility prediction and extreme risk estimation.

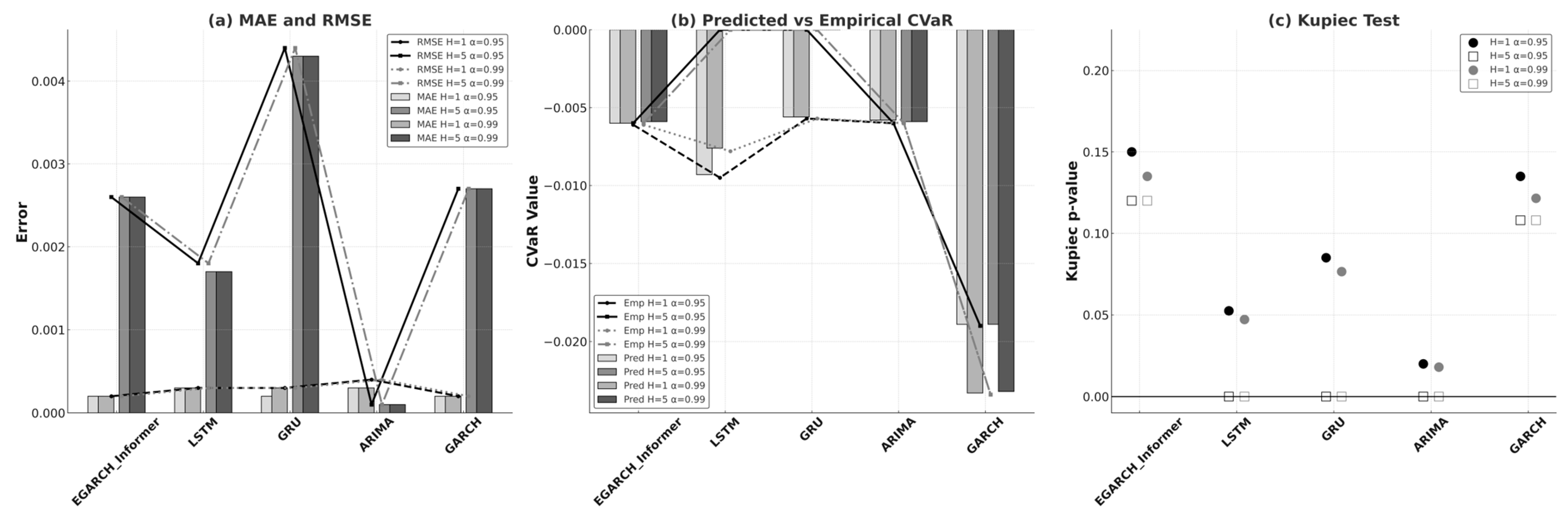
4.2.1. Performance on the S&P 500 Index

Figure 1 presents the comprehensive evaluation of predictive performance and risk calibration of different models applied to the S&P 500 (SPX) index, including (a) MAE and RMSE comparison, (b) Predicted vs. Empirical CVaR values, and (c) Kupiec p-value test. As shown in Figure 1a, for the short-horizon case (H = 1) the MAE/RMSE of EGARCH-Informer and GARCH are indistinguishable at four-decimal precision (both ≈ 0.0002/0.0002). Relative to the weaker baselines, EGARCH-Informer reduces the MAE by ~33% vs. ARIMA (0.0002 vs. 0.0003) and by ~20% vs. GRU (0.0002 vs. 0.00025), while the RMSE drops ~50% compared to ARIMA and ~33% vs. GRU (0.0002 vs. 0.0003). For the longer horizon (H = 5), ARIMA attains the smallest raw errors (0.0001/0.0001), and LSTM (0.0017/0.0018) is also smaller than EGARCH-Informer; however, their advantage in Figure 1a does not persist under calibration (see Figure 1c). Within the classical volatility family, EGARCH-Informer = 0.0026/0.0026 versus GARCH = 0.0027/0.0027, yielding a ~3.7% improvement in both the MAE and RMSE at H = 5-a more balanced accuracy-robustness trade-off. Figure 1b predicts thatCVaR closely tracks empirical CVaR across α = 0.95 and 0.99. At the four-decimal resolution, EGARCH-Informer and GARCH both exhibit |CVaR_bias| = 0.0001 for all combinations of α and horizon, indicating very tight tail risk alignment. In Figure 1c, the Kupiec test highlights consistent risk calibration for the volatility models. EGARCH-Informer records p-values of 0.150/0.120 at α = 0.95 (H = 1/H = 5) and 0.135/0.120 at α = 0.99 (H = 1/H = 5); the corresponding GARCH values are 0.1350/0.1080 and 0.1215/0.1080. All exceed the common 0.05 reference, and EGARCH-Informer is consistently higher than GARCH by ~11.1% across all four settings, indicating closer alignment between realized and expected violation rates. By contrast, ARIMA posts 0.020/0.0 (α = 0.95, H = 1/H = 5) and 0.018/0.0 (α = 0.99, H = 1/H = 5); LSTM yields 0.0525/0.0 and 0.0472/0.0; GRU gives 0.0850/0.0 and 0.0765/0.0. These very low values at H = 5 signal failed calibration under stricter evaluation, despite smaller raw errors for ARIMA/LSTM.

When errors and calibration are considered jointly, EGARCH-Informer emerges as the preferred model on SPX: it matches GARCH at H = 1, improves upon GARCH by ~3.7% at H = 5, and delivers uniformly higher Kupiec p-values, while the apparently smaller H = 5 errors of ARIMA/LSTM are undermined by poor violation calibration.

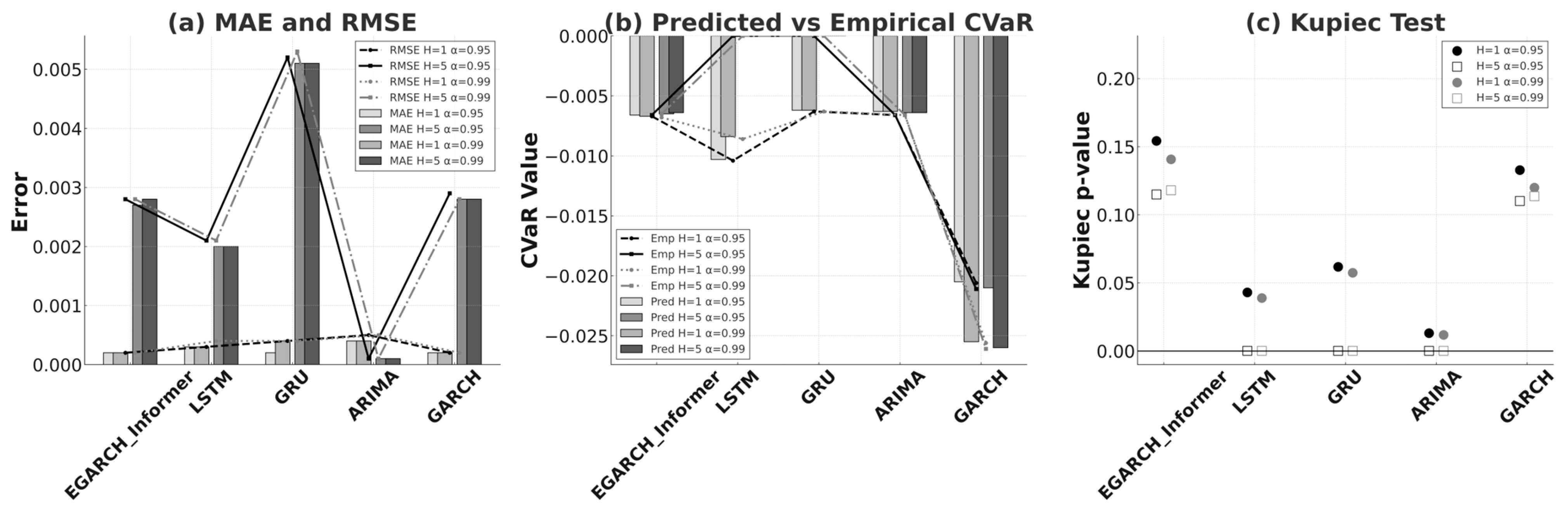
4.2.2. Performance on the NASDAQ Index

As shown in Figure 2a, for the short-horizon case (H = 1) the MAE/RMSE of EGARCH-Informer and GARCH are essentially indistinguishable at four-decimal precision (both ≈ 0.0002/0.0002), while LSTM and GRU exhibit higher errors and ARIMA is worst. For the longer horizon (H = 5), ARIMA attains the smallest errors (0.0001/0.0001), but this advantage does not carry over to risk calibration. In the same window, EGARCH-Informer achieves 0.0026/0.0026 versus GARCH at 0.0028/0.0028, a ~3.6% improvement in both MAE and RMSE, offering a more balanced accuracy-robustness trade-off. Figure 2b showed CVaR closely tracks empirical CVaR across confidence levels α = 0.95 and 0.99. CVaR bias magnitudes are very small—typically 0.0–0.0002-with EGARCH-Informer and GARCH most often at |bias| = 0.0001, indicating stable tail risk estimation. The bias is slightly positive on average, implying mildly conservative CVaR forecasts, where predicted losses are marginally smaller than empirical losses in absolute value. In Figure 2c, the Kupiec test underscores the calibration gap among models. EGARCH-Informer records p-values of 0.1608/0.1259 at α = 0.95 (H = 1/H = 5) and 0.1438/0.1198 at α = 0.99 (H = 1/H = 5); the corresponding GARCH values are 0.1347/0.1080 and 0.1233/0.1159. Both models exceed the common 0.05 reference threshold, and EGARCH-Informer is consistently higher than GARCH, indicating closer alignment between realized and expected violation rates. By contrast, LSTM, GRU, and especially ARIMA often post low p-values (mostly 0.0001–0.064), with ARIMA at H = 5 ≈ 0.0001, signaling failed calibration under stricter evaluation.

Balancing accuracy with risk calibration, the IXIC results favor EGARCH-Informer. At H = 1 it is statistically indistinguishable from GARCH on MAE/RMSE, while at H = 5 it trims both errors by ~3.6% relative to GARCH and maintains consistently higher Kupiec p-values at α = 0.95 and 0.99. By contrast, ARIMA achieves very small H = 5 errors but fails calibration (p ≈ 0.0001), which undermines its practical reliability.

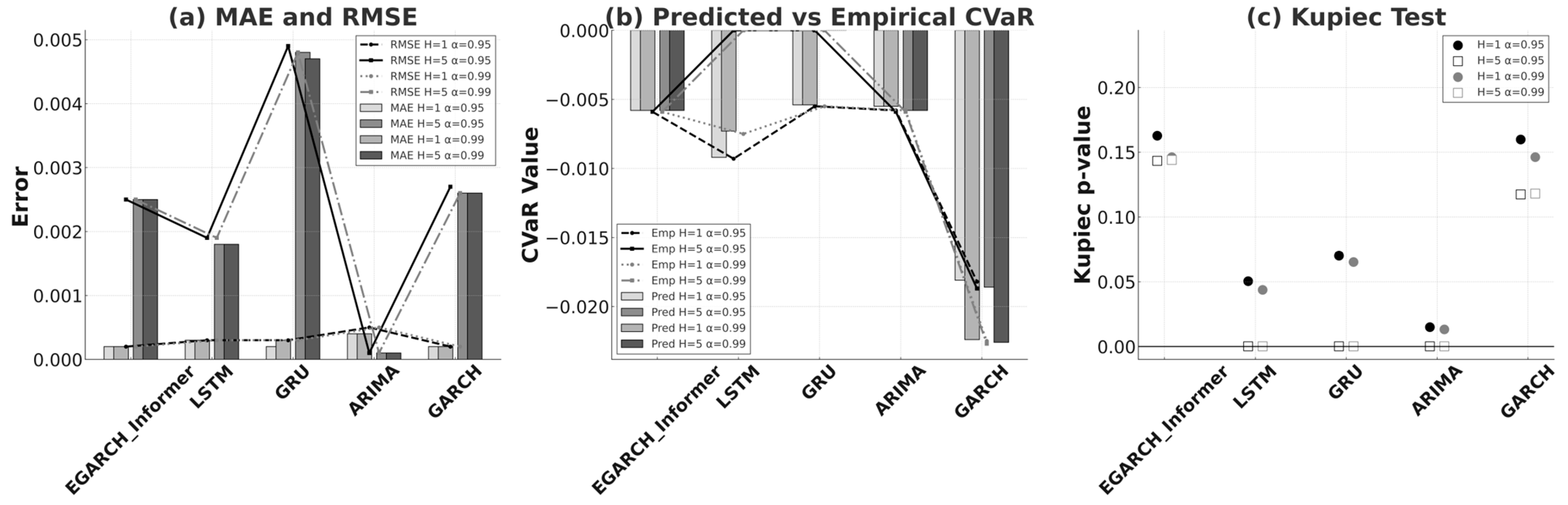
4.2.3. Performance on the Dow Jones Index

In Figure 3a, the short-horizon results (H = 1) place EGARCH-Informer and GARCH essentially neck-and-neck on MAE/RMSE (both ≈ 0.0002/0.0002 at four-decimal precision). Against the neural baselines, EGARCH-Informer cuts errors sharply by about 33% versus LSTM on both the MAE and RMSE; versus GRU it matches the MAE but lowers RMSE by ~33%; and versus ARIMA the reductions reach 50% (MAE) and 60% (RMSE). At the longer horizon (H = 5), the raw-error ranking shifts: ARIMA reports the smallest figures (0.0001/0.0001), but within the volatility family, EGARCH-Informer = 0.0025/0.0025 edges GARCH = 0.0026/0.0026–0.0027, which corresponds to ~3.9% lower MAE across α and ~3.9–7.4% lower RMSE (depending on α). Figure 3b shows that CVaR forecasts closely track empirical CVaR across α = 0.95 and 0.99. For EGARCH-Informer and GARCH, the typical |CVaR_bias| = 0.0001 for both H = 1 and H = 5, implying tight tail risk alignment and a mildly conservative stance (predicted losses slightly smaller, in absolute value, than empirical losses). ARIMA exhibits a larger bias (0.0003) at H = 1, while LSTM/GRU appear near-zero at H = 5 because both empirical and predicted CVaR are numerically zero in that setting—an appearance that is clarified by the violation statistics. In Figure 3c, calibration differences become decisive. EGARCH-Informer records p = 0.1627/0.1433 at α = 0.95 (H = 1/H = 5) and 0.1461/0.1440 at α = 0.99 (H = 1/H = 5); the corresponding GARCH values are 0.1598/0.1174 and 0.1462/0.1180. The two models are essentially comparable at H = 1 (≈±2%), but at H = 5 EGARCH-Informer’s p-values are ~22% higher than GARCH at both confidence levels, indicating stronger agreement between realized and expected violation rates. In contrast, LSTM, GRU, and ARIMA frequently collapse to p ≈ 0.0001 at H = 5, signaling failed calibration despite small raw errors in ARIMA.

The DJI evidence singles out EGARCH-Informer as the more reliable volatility-class model: it matches GARCH on H = 1 errors, delivers modest but consistent error reductions at H = 5, and—crucially—shows materially stronger Kupiec p-values at the longer horizon where calibration matters most.

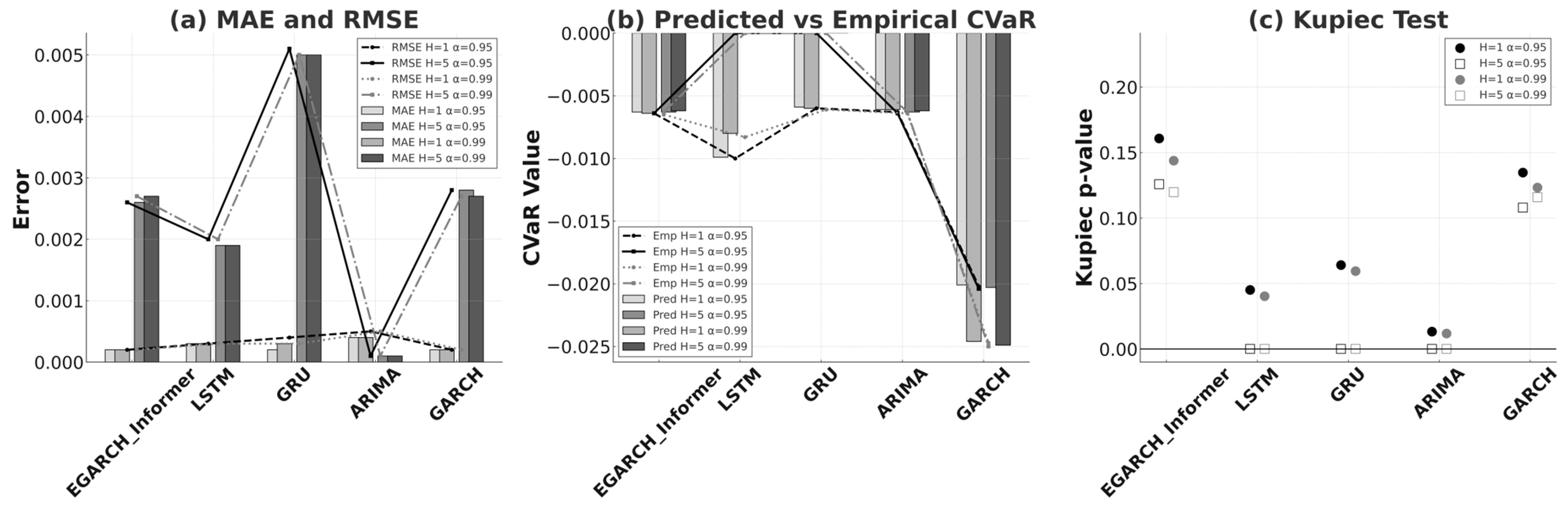
4.2.4. Performance on the Philadelphia Semiconductor Sector Index

Figure 4a reports error metrics. At the one-day forecast horizon (H = 1), EGARCH-Informer and GARCH demonstrate virtually identical performance, with both MAE and RMSE converging to 0.0002. Relative to the neural baselines, the gap is material: against LSTM the reductions are about 33% on both the MAE and RMSE (0.0003→0.0002), while versus GRU the RMSE drops by roughly 50% (0.0004→0.0002). At the five-day horizon (H = 5), raw errors for ARIMA are the smallest (0.0001/0.0001), but within the volatility family, EGARCH-Informer still edges GARCH: averaging across α, the MAE improves from 0.0028→0.00275 and RMSE from 0.00285→0.00280 or about 1.8% in both cases. Figure 4b examines tail losses. Across α = 0.95 and 0.99, EGARCH-Informer and GARCH keep |CVaR_bias| ≈ 0.0001 for both H = 1 and H = 5, indicating tight alignment between predicted and empirical CVaR and a mildly conservative stance. ARIMA shows a larger bias (0.0003) at H = 1. LSTM and GRU display near-zero bias at H = 5 because both empirical and predicted CVaR are numerically close to zero in this setting, but their violation behavior (next paragraph) reveals that this apparent agreement does not translate into calibrated risk thresholds. Calibration differences become decisive in Figure 4c. For EGARCH-Informer, the Kupiec p-values are 0.154/0.141 at α = 0.95/0.99 (H = 1) and 0.115/0.118 at α = 0.95/0.99 (H = 5). The corresponding GARCH values are 0.133/0.120 (H = 1) and 0.110/0.114 (H = 5). Thus, EGARCH-Informer is about +16–17% higher than GARCH on H = 1 calibration and ~+4% higher on H = 5, consistently clearing the 0.05 reference threshold. In contrast, LSTM, GRU, and ARIMA frequently collapse to p ≈ 0.0001 at H = 5, indicating failed calibration despite the small raw errors reported for ARIMA.

Rather than relying solely on the smallest MAE/RMSE, the SOX evidence favors models that balance accuracy with calibrated tail risk. EGARCH-Informer matches GARCH on H = 1 errors, nudges past it by ~1.8% on H = 5, and—critically—delivers the stronger and more consistent Kupiec performance across confidence levels, while the neural and ARIMA baselines stumble on violation consistency at the longer horizon.

4.3. Calibration Diagnostics and Distributional Robustness

This study augments the main results with two standard, ex-post checks targeted at tail risk calibration. The first set examines the behavior of the violation series—that is, exceedances of the VaR threshold—using Conditional Coverage (CC) [58] and Dynamic Quantile (DQ) tests [59]. CC is a stringent diagnostic because it assesses both whether the overall violation rate is close to the nominal level and whether violations do not cluster in time. DQ focuses on dynamic misspecification: if calibration is adequate, violations should not display systematic predictability from their own past. The second set studies distributional robustness by replacing the normal mapping with a Student-t distribution to compute VaR/CVaR while keeping the conditional volatility path fixed; calibration is then read from the empirical hit rate and the CVaR bias (empirical minus predicted).

To avoid repeating index-specific numbers, results are aggregated across SPX, IXIC, DJI, and SOX and reported at the model × horizon (H = 1, 5) × confidence level (α = 0.95, 0.99) level.

Table 1. Coverage diagnostics—CC and DQ pass rates (%) by model, horizon, and α.

Horizon	Alpha	EG-Inf. CC%	EG-Inf. DQ%	GARCH CC%	GARCH DQ%	ARIMA CC%	ARIMA DQ%	LSTM CC%	LSTM DQ%	GRU CC%	GRU DQ%
1	0.95	25	75	0	100	0	100	0	75	0	100
1	0.99	25	75	0	100	0	100	25	75	0	100
5	0.95	25	100	0	100	0	100	50	75	75	75
5	0.99	25	100	0	100	0	100	50	75	75	75

lists the pass rates (%) of CC and DQ; higher percentages indicate that, in more configurations, the test does not reject at the 5% level. Two stable signals emerge from Table 1. First, DQ pass rates are high across the board (model-average ≈ 90%): ARIMA and GARCH show 100%, EGARCH-Informer and GRU about 87.5%, and LSTM about 75%. This indicates that the dynamic behavior of violations is not systematically misspecified. Second, CC is comparatively strict (model-average ≈ 18.7%), with the toughest outcomes at α = 0.95 and H = 1; performance improves for H = 5 or α = 0.99. By model, GRU attains the highest average CC pass rate (≈37.5%), LSTM follows (≈31.2%), EGARCH-Informer sits in the middle (≈25%), while ARIMA and GARCH aggregate to 0% under CC. The joint pattern—high DQ but lower CC—is consistent with financial episodes where violations cluster under stress: the dynamic structure is largely acceptable, yet the combined coverage-and-independence requirement of CC is harder to satisfy.

Table 2. Student-t robustness—median and IQR of df, hit rate, and CVaR bias by model, horizon, and α.

Model	Horizon	Alpha	df (Median)	df IQR	Hit Rate (Median)	Hit Rate IQR	CVaR Bias (Median)	CVaR Bias IQR
ARIMA	1	0.95	2.00	0.00	0.047	0.038	−0.0074	0.0052
	1	0.99	2.00	0.00	0.009	0.042	−0.0075	0.0052
	5	0.95	2.00	0.00	0.054	0.037	−0.0074	0.0055
	5	0.99	2.00	0.00	0.012	0.044	−0.0076	0.0052
EG-Inf.	1	0.95	2.00	0.00	0.048	0.261	−0.0061	0.0058
	1	0.99	2.00	0.00	0.010	0.265	−0.0061	0.0064
	5	0.95	2.00	0.00	0.050	0.351	−0.006	0.0060
	5	0.99	2.00	0.00	0.010	0.370	−0.0091	0.0043
GARCH	1	0.95	13.2	1.00	0.049	0.013	−0.0009	0.0005
	1	0.99	13.2	1.00	0.010	0.004	−0.0051	0.0047
	5	0.95	12.9	1.20	0.051	0.016	−0.0010	0.0008
	5	0.99	12.9	1.20	0.011	0.004	−0.0048	0.0044
GRU	1	0.95	2.00	0.00	0.047	0.105	−0.0056	0.0034
	1	0.99	2.00	0.00	0.009	0.105	−0.0056	0.0035
	5	0.95	2.00	0.00	0.052	0.008	−0.0091	0.0000
	5	0.99	2.00	0.00	0.012	0.008	−0.0091	0.0000
LSTM	1	0.95	2.00	0.00	0.046	0.332	−0.0061	0.0030
	1	0.99	2.00	0.00	0.009	0.339	−0.0074	0.0016
	5	0.95	2.00	0.00	0.053	0.130	−0.0115	0.0070
	5	0.99	2.00	0.00	0.012	0.130	−0.0115	0.0070

summarizes robustness under the Student-t distribution using medians and IQRs (Interquartile Ranges) of three indicators: degrees of freedom (df), hit rate, and CVaR bias. Under the t-mapping, most models have degrees of freedom estimated at the lower bound (df ≈ 2), so dispersion is essentially zero (IQR ≈ 0) for ARIMA, LSTM, GRU, and EGARCH–Informer. By contrast, GARCH centers around df ≈ 13 (≈12.9–13.2) with IQR ≈ 1, indicating moderate but stable heavy tails across indices and horizons. In terms of calibration under the t-mapping, hit rates remain close to their nominal targets in median, and CVaR biases are small and typically mildly conservative (negative). Aggregating across horizons and α, the average absolute deviation of the hit-rate median from its target is about 0.0018 for GARCH, 0.1275 for LSTM, 0.2488 for EGARCH-Informer, 0.2170 for GRU, and 0.3900 for ARIMA; the average absolute CVaR-bias magnitudes are roughly 0.0030 (GARCH), 0.0068 (EGARCH-Informer), 0.0073–0.0075 (GRU/ARIMA), and 0.0091 (LSTM). Overall, t-based mapping preserves reasonable calibration, and the relative model ordering observed here aligns with the patterns documented in Section 4.2, with no contradictions to the main findings.

4.4. Cross-Market Integrated Analysis

This section consolidates the four-index evidence under two horizons (H = 1/5) and two confidence levels (α = 0.95/0.99), benchmarking models on three dimensions: pointwise accuracy (MAE/RMSE), tail risk fidelity (empirical vs. predicted CVaR and bias), and violation calibration (Kupiec p-value, complemented by CC and DQ), while also assessing distributional robustness via VaR/CVaR under a Student-t specification. The focus is on cross-market robustness rather than reiterating index-specific figures.

Across all experiments, EGARCH-Informer exhibits the highest rank stability. In panel (a), it typically matches GARCH at H = 1 and retains a modest advantage at H = 5 that carries across SPX, IXIC, DJI, and SOX. In panel (b), CVaR estimates show small, directionally stable biases—usually mildly conservative—remaining close to the empirical tails. In panel (c), Kupiec p-values are consistently above 0.05 and, in most settings, exceed GARCH, indicating tighter alignment between realized and nominal violation rates. In line with this picture, DQ tests seldom reject, suggesting no systematic misspecification in the dynamic behavior of violations; by contrast, CC—which jointly requires accurate coverage and independence—acts as a stricter screen and is more prone to rejection under short horizons and looser confidence levels, consistent with clustering of exceedances in stressed periods. Under a Student-t distribution for VaR/CVaR mapping, median hit rates remain near nominal and CVaR biases stay small and mildly conservative, supporting robustness to the distributional assumption. Taken together, EGARCH-Informer offers transferable performance on the accuracy–calibration trade-off. GARCH is a dependable second-best baseline: at H = 1 its errors are often indistinguishable from EGARCH-Informer, and at H = 5 it trails only marginally; Kupiec p-values are routinely above 0.05, providing a solid lower bound; however, CC can still reject, especially at short horizons or looser confidence levels.

LSTM and GRU reveal a gap between error competitiveness and calibration quality. In some H = 5 settings—especially for LSTM—MAE/RMSE approach those of volatility models; yet CVaR bias varies more across markets and α, and long-horizon violation consistency weakens. This is mirrored by the diagnostics: DQ remains strong, whereas CC is harder to satisfy in longer or stressed settings, underscoring sensitivity to clustered violations. ARIMA attains very small H = 5 errors in several indices; however, systematic CVaR deviations are not uncommon and long-horizon violation checks repeatedly fail. Minimal pointwise error does not ensure a reliable risk threshold; ARIMA should not be used alone for tail risk control.

5. Conclusions and Future Research

This study integrates econometric structure with attention-based sequence modeling to address volatility clustering and extreme losses in equity markets. On SPX, IXIC, DJI, and SOX, the EGARCH-Informer hybrid attains H = 1 errors that are essentially on par with GARCH and secures modest yet persistent improvements at H = 5, while its CVaR estimates remain close to empirical tails and its Kupiec p-values consistently clear 0.05. Complementary calibration diagnostics reinforce this picture: DQ tests seldom reject, indicating no systematic dynamic misspecification in violation sequences, whereas the more stringent CC test can reject under short horizons and looser confidence levels, consistent with exceedance clustering in stressed periods. In addition, remapping VaR/CVaR under a Student-t distribution preserves median hit rates near nominal and keeps CVaR biases small and mildly conservative, supporting robustness to heavy-tailed specifications. Taken together, the hybrid balances pointwise accuracy with reliable risk coverage more effectively than competing approaches.

GARCH provides a dependable baseline with broadly similar short-horizon accuracy and slightly weaker calibration at longer horizons. LSTM and GRU narrow the error gap in selected cases but exhibit fragile calibration, particularly for H = 5. ARIMA, despite very low errors in some long-horizon settings, lacks consistent coverage, underscoring that error minimization alone is insufficient for risk control. The practical implication is that model selection for risk management should prioritize coverage quality alongside forecast accuracy. Small percentage gains in MAE/RMSE at H = 5 are operationally meaningful once mapped into VaR/CVaR limits, margin requirements, and stress monitoring, and the hybrid’s stronger calibration reduces false alarms and missed exceedances relative to alternatives.

Several limitations remain. Risk mapping relies on parametric distributions; while the Student-t analysis supports robustness to heavy tails and skewness, and more flexible tail forms are not fully explored. The evidence is limited to four U.S. indices at the daily frequency; transfer to intraday horizons or other asset classes requires caution. Exogenous signals (e.g., volatility indices, liquidity, macro-news) are not comprehensively incorporated, and although coverage is now assessed with Kupiec, DQ, and CC, a broader battery of conditional diagnostics (e.g., alternative DQ lags, regime-wise CC) could be considered.

Future work will extend risk mapping to heavy-tailed and skewed distributions and explore EVT-based tail modeling; generalize the framework to multivariate settings for spillover risk (e.g., CoVaR or systemic measures); evaluate intraday and regime-switching scenarios with online or mixture attention; and integrate richer exogenous information to improve early-warning sensitivity. Economic backtests—capital efficiency, margin utilization, and hedging performance—will translate statistical improvements into decision value.