Abstract
The Minimum Spanning Tree (MST) problem addresses the challenge of identifying optimal network pathways for critical infrastructure systems, including transportation grids, communication backbones, power distribution networks, and reliability optimization frameworks. However, inherent uncertainties stemming from disruptive events demand robust analytical models for effective decision-making. This research introduces an uncertainty-theoretic framework to assess MST stability in uncertain network environments through novel constructs: lower set tolerance (LST) and dual lower set tolerance (DLST). Both LST and DLST provide quantifiable measures characterizing the resilience of element sets relative to edge-weighted MST configurations. LST captures the maximum simultaneous risk variation preserving current MST optimality, while DLST identifies the minimal variation required to invalidate it. We evaluate MST robustness by integrating uncertain reliability measures and risk factors, with emphasis on computational methods for set tolerance determination. To overcome computational hurdles in set tolerance derivation, we establish bounds and exact formulations within an uncertainty programming paradigm, offering enhanced efficiency compared with conventional re-optimization techniques.
MSC:
90B15; 90C05; 90C27; 90C70; 90C90
1. Introduction
1.1. Background and Problem Context
The Minimum Spanning Tree (MST) problem is a cornerstone of network optimization, aiming to identify a tree that connects all vertices in a network while minimizing the total weight of edges. This problem is pivotal in fields such as logistics, telecommunications, power grids, computer networks, and transportation infrastructure. However, disruptions like natural disasters introduce uncertainties that compromise network reliability and stability, leading to unpredictable performance and high variability in network parameters. In contexts like communication or power networks, where edges represent failure probabilities (risk factors), the goal shifts to maximizing overall network reliability, often by minimizing cumulative system risk. When precise information about edge functionality is unavailable, relying on probability distributions becomes problematic. Parameters are often expressed as ’belief degrees’ derived from expert judgment, but using probability or fuzzy theory to model these can lead to misleading outcomes due to the occurrence of unlikely events, resulting in greater variance than observed frequencies. Uncertainty theory has emerged as an effective framework to address these challenges [1,2,3].
This study advances the analysis of MST stability in uncertain networks by proposing a novel uncertainty-based model. The model facilitates stability analysis of edge-weighted MSTs under uncertainty by integrating risk factors associated with network edges. Specifically, it addresses the uncertain MST problem by evaluating the robustness of MST solutions against network uncertainties. Central to this approach is the concept of lower set tolerance (LST), defined as the maximum simultaneous risk variation across multiple uncertain elements that preserves the optimality of the current MST. Additionally, we introduce the dual lower set tolerance (DLST), which measures the minimum risk variation across a set of elements that renders the current MST non-optimal. These metrics gauge the sensitivity of an optimal MST to risk changes in multiple edges, with low LST or DLST values indicating that small changes can disrupt optimality. Such insights are critical for decision-makers and network planners to monitor vulnerable edge sets.
This study is the first to focus on the stability of uncertain MSTs without relying on probability distributions or fuzzy membership functions. Although computing set tolerances precisely can be challenging, we demonstrate that they are mathematically well-defined and provide computational formulations using uncertainty programming to efficiently compute or bound them. We derive bounds and exact formulas for LST and DLST, leveraging their relationships with single tolerance counterparts, and compare the results of regular and dual lower set tolerances.
The paper is organized as follows. Section 1.2 reviews relevant literature, highlighting research gaps and the motivation for this study. Section 2 defines the uncertain MST problem and introduces the programming model for -MST. Section 3 presents a tolerance-based stability analysis of the uncertain MST, including bounds and exact formulas for LST and DLST. Section 4 summarizes key findings and proposes directions for future research. Appendix A provides foundational concepts and an overview of uncertainty theory.
1.2. Motivation and Research Contributions
The notions of tolerances and sensitivity play instrumental roles in refining local search heuristics and resolving network-centric difficulties in network architecture and transportation cybernetics. Tolerance-driven methodologies have demonstrated efficacy in enhancing optimization techniques like branch-and-bound for combinatorial challenges, including MST, traveling salesman problem (TSP), shortest path identification, and widest path determination [4,5,6,7,8,9,10].
Building upon recent progress in single tolerances for post-disaster transport networks—which established minimum and maximum cost variations preserving solution optimality for individual elements—we present two novel metrics, lower set tolerance (LST) and dual lower set tolerance (DLST), as network stability gauges. These set-based tolerance measures prove particularly advantageous in scenarios featuring uncertain change distributions but known aggregate estimations, exemplified by transportation networks where traversal times fluctuate unpredictably across connections without certainty regarding affected edges. We mathematically formalize LST and DLST under uncertainty, deduce their properties, and illustrate their utility in uncovering structural characteristics of optimal MST solutions, including identification of elements common to all optima and detection of alternative solution existence. Furthermore, we institute methodologies to compute or bound these set tolerances, frequently leveraging single tolerances, and recognize shared attributes (e.g., independence from selected optimal solution and positive values indicating unique optima) alongside distinctions (e.g., interpretation of infinite values).
This research progresses sensitivity analysis under uncertainty, a critical concentration in operations research, particularly for appraising network functionality during crisis scenarios [11,12,13,14,15,16]. A primary objective has involved evaluating network robustness and pinpointing critical constituents, with diverse frameworks employing metrics to investigate reliability [17]. However, most methodologies depend on probabilistic or fuzzy theoretical foundations [3,18,19], which prove inadequate when network parameters, such as edge functionality, lack sufficient data for reliable probability distribution formation, as witnessed during earthquake emergencies. Various analytical and modeling frameworks have surfaced to explore network reliability utilizing diverse metrics. Within the domain of road network reliability, prevailing studies predominantly concentrate on three fundamental domains: (1) connectivity reliability, (2) travel time reliability, and (3) capacity reliability [20,21,22,23,24,25,26]. Ref. [11] pioneered the modeling of network travel time reliability under stochastic demand, offering one of the earliest methodological foundations for quantifying travel-time variability in congested networks. Ref. [20] introduced a matrix-exponential approach for network reliability analysis, providing an exact probabilistic framework suitable for evaluating large-scale systems with complex failure distributions. Ref. [26] proposed an evaluation framework for carrying capacity reliability in regional rail transit systems, highlighting the importance of reserve capacity and operational resilience in modern rail networks. Ref. [21] analyzed the interaction between travel time reliability and route choice behavior using a generalized Bayesian traffic model, bridging behavioral responses with network reliability outcomes. Ref. [22] presented a comprehensive review of methodological developments in travel time reliability, summarizing advances in measurement, modeling, and integration into traffic assignment. Ref. [25] examined connectivity analysis of transportation networks by incorporating bridges and pavements under uncertainty, offering a practical framework for assessing infrastructure-dependent reliability. Ref. [24] focused on seaborne crude oil networks, proposing a methodology for connectivity reliability evaluation and the selection of most reliable shipping routes, relevant for maritime logistics planning. Ref. [27] applies uncertainty modeling for travel times in distribution logistics, using Monte Carlo and collocation methods to capture variability in travel times and analyze its impact on routing and scheduling decisions. Ref. [23] investigated resilience in flood-disrupted dynamic transportation networks, characterizing link reliability and stability to capture system performance under cascading hazards. Ref. [16] studied max-type reliability in post-disaster networks using sensitivity and stability analysis, extending uncertain network models to capture performance under extreme disruptions. Ref. [12] analyzed connectivity reliability in uncertain networks through stability analysis, providing theoretical foundations closely aligned with uncertainty-driven reliability measures. Ref. [14] developed robustness assessment methods for urban road networks under multiple hazard events, integrating hazard exposure with network structure to evaluate vulnerability. Ref. [15] offered a comprehensive review of transportation system resilience concepts, consolidating definitions, frameworks, and evaluation methods for infrastructure and operational resilience. Ref. [13] investigated the connectivity of intercity passenger transportation in China using a multi-modal network approach, illustrating the significance of integration across transport modes for accessibility and reliability.
However, we note that expert-derived “belief degrees” for edge dependability, when modeled probabilistically, can generate untrustworthy outcomes. To address this limitation, uncertainty theory, pioneered by [1,2], supplies a rigorous framework for managing human-induced uncertainties in network reliability assessment. We propose an innovative approach integrating MST, sensitivity examination, and set tolerances within uncertainty theory. Here, edge reliabilities are represented as uncertain variables—neither fuzzy nor stochastic—enabling precise characterization in data-deficient situations. We investigate how modifications in edge reliabilities influence MST stability, introducing LST and DLST as pivotal metrics in uncertain settings. Employing uncertainty theory, we develop systematic procedures to compute these set tolerances, strengthening network resilience assessment. This investigation contributes to the broader exploration of uncertain network challenges [2,16,28,29,30,31,32,33,34,35,36]. Numerous recent studies have extended uncertainty theory to diverse network design and optimization contexts. Recent works further illustrate how uncertainty can be systematically incorporated into network reliability and optimization models. For instance, Wang and Sheng [37] address both uncertain edge weights and uncertain topology, employing conditional uncertain variables to model networks where edges may or may not exist under uncertainty. Ref. [38] develop an Uncertainty Reliability Indicator (URI) for structural systems under epistemic uncertainty, defining safety-cost trade-offs using uncertain variables. Ref. [10] propose a reliability certification framework for supply chain networks subject to uncertain failures and demand, emphasizing robust design under uncertainty. Hosseini and Wadbro [12] analyzed connectivity reliability in uncertain networks, a direction closely related to our MST stability framework. Ref. [34] incorporated uncertain flows into the p-hub location problem, and Veresnikov et al. [35] applied uncertain programming to technical system design. Ref. [39] modeled environmental supply chain networks under uncertainty, demonstrating applicability in sustainability contexts. In graph optimization, Gao and Jia [40] studied the degree-constrained MST with uncertain edge weights, while [31] extended uncertain multilevel programming to vehicle routing. Ref. [30] provided a bibliometric overview of uncertainty theory applications in supply chains, highlighting future research avenues. More recently, Hosseini [16] explored max-type reliability in post-disaster networks. Guo et al. [28] addressed procurement and routing strategies under uncertain environments, and Wang [29] proposed mixed-uncertainty modeling for coal transportation costs. Together, these contributions illustrate the growing role of uncertainty theory in addressing complex reliability and optimization problems across transportation and supply chain systems. These works collectively demonstrate that uncertainty theory is maturing as a serious alternative to probabilistic/fuzzy methods for modeling human-induced or data-scarce reliability, and they strongly motivate the development of LST and DLST in uncertain network environments.
This work establishes a substantive foundation for analyzing the stability of uncertain minimum spanning trees through LST and DLST applications, effectively merging theoretical progress with practical applicability. As uncertainty increasingly impacts critical infrastructure, demand for such analytical frameworks will escalate, rendering this research a timely and valuable disciplinary contribution. In summary, this investigation delivers three principal contributions: (1) a methodological framework for incorporating “belief degrees” in tolerance-based stability assessment of uncertain MSTs, addressing constraints of probabilistic and fuzzy approaches; (2) verification that LST and DLST are well-defined, solvable, and computable in polynomial time and (3) efficient computational procedures for LST and DLST outperforming iterative re-optimization methods.
2. Modelling and Formulation: Uncertain MST
Consider denoting a network where V represents the node set and the edge set. Let and indicate node and edge (or link) counts, respectively. Unique edges represent connections between node pairs. A spanning tree constitutes a sub-network of N structured as a tree containing edges. Assuming each edge possesses an associated cost, an MST represents a spanning tree minimizing cumulative cost/weight across all spanning trees. We designate as the complete set of spanning trees in N. Specifically, we define subset as spanning trees containing edge , and as those excluding edge .
Each edge features an associated reliability measure quantifying its functional probability. Naturally, we seek a spanning tree maximizing aggregate reliability. Thus, we maximize over the complete spanning tree set . For computational convenience, we transform this maximization into a minimization problem through reliability factor inversion, representing transformed factors as (termed risk factors). Consequently, we approach the reformulated network problem as an MST formulation employing risk factors as edge weights.
The problem now constitutes a standard MST formulation—the minimal risk spanning tree problem. We define the risk of spanning tree as the summation of edge risks within T. Hence, the MST formulation is expressible as follows:
where indicates edge belongs to T and 0 otherwise.
Accordingly, designates the objective function value for the MST problem—the risk value of an MST within the network. In a similar way, we let and denote the risk value of the MST within and , respectively.
MST in Uncertain Settings
Diverging from conventional MST formulations, we examine scenarios featuring an uncertain measure , with uncertain risk variables associated with edges (Appendix A). Specifically, for each edge , there exists an uncertain risk variable . This permits MST analysis under uncertain conditions where edge risks exhibit extreme variability. A spanning tree T with uncertain risk variables constitutes an uncertain family denoted . The uncertain risk variable linked to this tree manifests as the combined edge risks:
Expression (1) specifies the minimization objective (over ) for the uncertain MST problem, targeting identification of minimal-risk spanning trees under uncertain conditions:
The value of remains uncertain; consequently, we must clarify the interpretation of ‘min’ in (2).
Owing to limitations in traditional deterministic or probabilistic approaches for handling uncertain variables, alternative methods must be investigated for addressing the uncertain MST challenge via uncertainty programming techniques. This necessitates the development of comparable models. In contrast to real numbers, the uncertain domain lacks inherent ordering. A fundamental challenge involves establishing a ranking methodology for uncertain variables. To address this, ref. [36] employed the critical value concept (specifically, the pessimistic value) of an uncertain variable. Uncertainty programming incorporating this critical value principle constitutes chance-constrained programming.
Assuming is a network, T a spanning tree, and a predetermined confidence level (user-specified), the -critical value (here, the α-pessimistic value) associated with the uncertain spanning tree is defined as
An uncertain spanning tree qualifies as an -MST if for any alternative tree we have . We observe that for any predetermined confidence level , the -pessimistic value associated with an uncertain spanning tree and the -pessimistic value of any uncertain risk variable constitute increasing, left-continuous functions of . Therefore, the -MST programming model for the uncertain MST formulation is structured as an r-minimization:
To advance, let network signify the transformed version of an uncertain network N, where uncertain risk variables are replaced by their -pessimistic values for specified confidence level . The subsequent theorem establishes that the -MST can be acquired by solving a standard MST problem in this auxiliary network .
Theorem 1
([36]). Assume α constitutes a predetermined confidence level and an uncertain network. Furthermore, assume uncertain risk variables exhibit independence and possess regular distributions . If symbolizes the inverse uncertainty distribution of the uncertain MST, then exists as a continuous, strictly increasing function of α. Additionally, it is established that the α-MST formulation can be equivalently expressed as
where designates the α-pessimistic value of variable and it is defined as
Given that uncertain risk variables are mutually independent with regular distribution functions, we delineate a method for calculating the inverse uncertainty distribution of the uncertain MST in such networks. Specifically, for any , is determinable. Iterating this process enables numerical acquisition of uncertainty distribution to the decision-maker-specified precision. This empowers decision-makers to compute maximally reliable MSTs across risk levels and comprehend network performance under diverse uncertainty scenarios.
Example 1.

The proposed methodology is applied to dual instances corresponding to distinct planning zones within the street network illustrated in Figure 1. Each network edge is associated with an independent uncertain risk variable, reflecting inherent system uncertainty. We let Ψ denote the uncertainty distribution of the uncertain MST, governing MST behavior under uncertainty. By evaluating Ψ, we analyze uncertain MST evolution as a function of network-wide uncertain risk variables.

Figure 1.
Street network configurations based on natural roads in our sample.
Our example employs varied confidence level values. Primarily, we apply Linear and Zigzag uncertainty distributions to links (Appendix A). Constructing these distributions required parameter estimation. Certain parameters (e.g., a, b, c in Definitions A3 and A4) for link distributions were randomly selected from uniform distributions within user-defined bounds. Users also specified uncertainty variable types assigned per link. Once the confidence level is fixed, inverse uncertainty distributions for all are computed. The -MST within is subsequently derived using an MST algorithm (e.g., see [4]).
For a clearer understanding of the network topologies, the risk variables for a bunch of edges, as well as their corresponding -pessimistic values , are displayed in Table 1. This provides insight into the variability and risk associated with specific links within the network, offering a foundation for further analysis of their stability and reliability. We remark that for any link with a constant risk parameter c, we can set for all values of [1,2].

Table 1.
The -pessimistic values for uncertain risk variables across selected edges at characteristic confidence levels .
The corresponding objective function optima for the -MST formulation appear in Figure 2. Note that uncertain MST objective optima originate from the inverse distribution of the uncertain MST; i.e., .
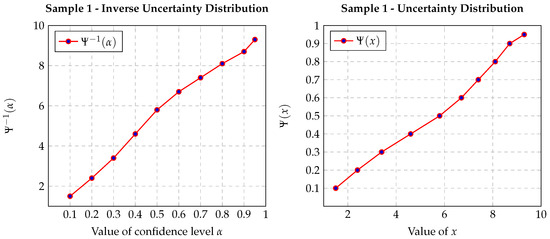
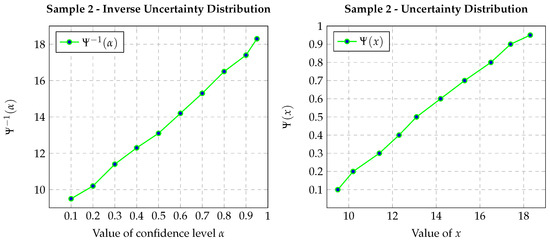
Figure 2.
Inverse uncertainty distribution and uncertainty distribution associated with networks 1-2.
Through incremental adjustment within , we efficiently compute both inverse distribution and overall distribution for the uncertain MST, furnishing a comprehensive behavioral representation under varying confidence levels. This process enables graphical depiction of the relationship between uncertain MST distribution and uncertainty levels, as illustrated in Figure 2.
3. Sensitivity Analysis Based on Lower Set Tolerances
3.1. Single Lower Tolerances
This section introduces and formalizes tolerance-based sensitivity analysis for the uncertain MST. The analysis hinges on the -MST concept, where tolerances are computed as confidence level functions. As the confidence level varies, both MST and tolerances dynamically adapt. Tolerance formulas are presented, demonstrating their variation relative to confidence level. For general uncertain MST formulations, lower tolerances illuminate how optimal spanning trees are affected by edge risk factor modifications. Specifically, lower tolerance quantifies risk factor reduction impacts. Computing these tolerances constitutes a combinatorial challenge, further complicated in uncertain networks where analysis involves uncertain variables rather than deterministic factors.
Remark 1.
Our exposition demonstrated that any uncertain MST formulation on N is convertible to an α-MST formulation on modified network for given α. In this auxiliary network , risk variables cease to be ‘uncertain’; they are replaced by definite α-pessimistic values. Consequently, we simply implement variable transformations then apply MST algorithms (e.g., Kruskal) to identify an MST in . Assuming represents α-pessimistic values for variables in network N, we substitute all in the uncertain network with . Edge transformation initialization consumes time; thus, algorithm complexity is typically where m is the edge count. Utilizing efficient disjoint-set data structures (e.g., Union-Find) reduces time complexity to , where n is node count [4].
Definition 1
(-Network). Denote by the network for , where edge value (denoted ) is replaced by , with other values unchanged:
Assuming is a specified confidence level and is an -MST (i.e., MST in ), lower tolerance is defined as the supremum permitting link weight reduction—typically within the -MST—while maintaining spanning tree -MST status, with other factors invariant. Thus, we formalize the single lower tolerance for a link relative to as
For technical analysis, the function proves particularly useful. It signifies the minimal objective function value for the MST formulation in without perturbations. Specifically, it provides the uncertain MST value in N for preset :
where is the spanning tree set in . We also note that set in is identical to set in N.
It is established [36] that for given confidence level and , and for any edge :
- (a1) if then : ,
- (a2) if then : .
Consequently, we deduce that when lower tolerances exist, full edge set examination is unnecessary. Instead, we only consider edges in E excluded from ; i.e., . Thus, lower tolerance existence for edge implies for some -MST . Namely, for every -MST pair and in , for any edge we have
This implies that for any fixed , lower tolerances are independent of any specific -MST. Therefore, we now reference tolerances without explicit -MST specification. This generalization facilitates broader comprehension of edge tolerances in uncertain networks, enabling more flexible and comprehensive tolerance-based analysis.
Lemma 1
([36]). Let α be a predetermined confidence level for an uncertain network . If some α-MST excludes , then lower tolerance is obtainable via the following:
where signifies the α-MST value in containing edge , calculable as
3.2. Set-Based Lower Tolerances
The single lower tolerance concept extends to scenarios where risk factors for edge sets are perturbed by constants, yielding lower set tolerances. Thus, as a tolerance extension, we introduce a generalized tolerance analysis problem, set tolerance analysis, where multiple elements vary concurrently and independently over predefined sets to evaluate how such variations impact current MST optimality. To this end, we posit that is the edge set (collection) undergoing modification, and is a collection of non-negative real-valued perturbation variables for . Henceforth, given network , we denote by the network where edge factor is perturbed by , and .
Assuming is a specified confidence level and is an -MST, we define the lower set tolerance of relative to as the supremum such that risks for all edges remain non-increasing with total reduction and retains optimality, provided risks for all other edges are unaltered.
For a lower set tolerance, the corresponding infimum definition is non-equivalent to the supremum definition. Therefore, we define the dual lower set tolerance as follows:
identifies a pathway—potentially an -MST post-perturbation—achievable with minimal effort/reduction.
Remark 2.
Consider as the transformed version of for a preset confidence level α, an α-MST, and the edge set undergoing modification. If lower and dual lower set tolerances exist, the complete set need not be considered. For (dual) lower set tolerance computation, we only examine elements of excluded from , i.e., . Consequently, whenever discussing (dual) lower set tolerance for set , it implies the existence of α-MST such that .
Remark 3.
Assuming and represent risk values of and in the perturbed network , then for any edge set :
- (a) if then ∀ vector : ,
- (b) if then ∀ vector : .
Lemma 2.
For any uncertain network and confidence level α, lower set tolerances are independent of α-MST—for every α-MST pair and and any edge set :
Proof.
Per Lemma 2 results, (dual) lower set tolerances for any set are independent of -MST. Consequently, we henceforth denote set tolerances without specific -MST indication. Additionally, examining LST and DLST definitions (14) and (15) reveals that for any -MST :
where lower tolerance is obtainable via Lemma 1.
Lemma 3.
Consider an uncertain network and a predetermined confidence level α. Let be the edge set undergoing changes. Then the following statements are equivalent.
- (a)
- (b)
- ,
- (c)
- .
Proof.
Note that the spanning tree set in is identical to in N for any .
(a) ⇒ (b): Since is a subset of no spanning tree, reducing the risk of edge leaves spanning tree risks unchanged. Thus, optimal solutions (-MSTs) in remain optimal for . Consequently, .
(a) ⇐ (b): Assume and is -MST in with . Suppose a spanning tree exists with . Thus, at least one edge belongs to T. Define perturbation vector with components:
where and . Then,
where and denote T’s risk values in the perturbed network and , respectively. Here, cannot be -MST for . Therefore, , contradicting . Thus, holds.
(a) ⇔ (c): Since is a subset of no spanning tree , . Thus, any edge is excluded from every spanning tree, and reducing ’s risk leaves spanning tree risk values unchanged. Hence, -MSTs persist as optimal, justifying , establishing the result. Finally, (a) ⇐ (c) follows from the equivalence of expressions. □
Lemma 4.
Consider uncertain network , predetermined confidence level α, and (with defined lower set tolerance) as the edge set subject to changes. Let vector (components ) with be a perturbation vector satisfying . Then, set intersects every α-MST in .
Proof.
First, since has defined a lower set tolerance, some -MST in satisfies . Proof by contradiction: suppose not, i.e., some -MST T exists in with . Since spanning tree set in matches that of for any , T is a feasible spanning tree in , so . As , Remark 3 implies
By lower set tolerance definition and , cannot be -MST for . Alternatively, T also cannot be -MST for . This contradicts T’s optimality, hence intersects every -MST in . □
Theorem 2.
Consider uncertain network , predetermined confidence level α, and as the modifying edge set. The following bounds for lower and dual lower set tolerances hold.
- (a)
- ,
- (b)
- ,
- (c)
- .
Proof.
(b): Assume is -MST in with . For the first inequality, assume the contrary: . Thus, for at least one edge , . Define satisfying . Define specific perturbation vector with components:
By lower set tolerance definition, for all with , is not MST for . Since , this contradicts the lower tolerance definition (14).
For the second inequality, assume the contrary: . Define satisfying and with . Define perturbation vector (components ) with such that is -MST of . Therefore, some spanning tree T and edge satisfy
implying
contradicting ’s optimality in .
(c): First show . Assume the contrary: . Some edge satisfies . Define satisfying . Define perturbation vector with components:
By dual lower set tolerance definition (15), for all with , is not -MST for . This yields a contradiction since .
Now prove . Assume the contrary: . Considethe r perturbation vector (components ) with
such that is not -MST in . Thus, some spanning tree T satisfies
Case 1: If , Remark 3 implies
contradicting the inequality.
Case 2: If , then at least one edge satisfies . Select the edge with . We immediately derive
contradicting Lemma 1. □
Corollary 1.
Consider an uncertain network and a predetermined confidence level α. Let be the modifying edge set. Then the following statements are equivalent.
- (a)
- (b)
- ,
- (c)
- .
Corollary 2.
Uncertain network instances exist where for certain MSTs and a given confidence level α, the following cases occur:
- (a)
- ,
- (b)
- ,
- (c)
- .
Lemma 5.
Consider uncertain network , predetermined confidence level α, the complete set of α-MSTs in N, and the modifying edge set. Then
- (a)
- ,
- (b)
- .
Proof.
(a): Since , for any edge , . Thus, by single lower tolerance definition and Lemma 1 computation, . Consequently,
Finally, Theorem 2(b,c) establishes and . The reverse direction in (a) follows from expression equivalence. Note that (b)’s reverse direction generally fails. □
Corollary 3.
Consider an uncertain network , a predetermined confidence level α. Then the following statements are equivalent.
- (a)
- Exactly one α-MST exists in .
- (b)
- .
- (c)
- .
In this section, we have developed a practical toolkit to assess how much risk can shift in a network before its Minimum Spanning Tree (MST) loses optimality. The foundation is Lemma 1, which provides a formula for the single lower tolerance , quantifying how much risk an edge can lose before the -MST changes. This gives network managers a quick metric to gauge individual edge stability. Building on this, Lemma 2 proves that these tolerances are independent of the specific -MST chosen, ensuring reliable results across different network configurations.
Scaling up, Theorem 2 delivers two critical tools: lower set tolerance (LST) and dual lower set tolerance (DLST). LST, as shown in Theorem 2(b), measures the maximum total risk reduction a set of edges can sustain while keeping the -MST intact, with bounds . These bounds allow quick assessment of network resilience without intensive computations. Meanwhile, Theorem 2(c) defines DLST as , pinpointing the smallest risk drop—computed via Lemma 1—that disrupts the MST. Network managers can use DLST to identify and reinforce critical edges, such as vulnerable power lines or shipping routes, to prevent failures during disruptions.
The uniqueness of the -MST is addressed in Corollary 3, which states that if only one -MST exists, then for any set . This signals that the network can tolerate some risk reductions without shifting the MST. If multiple MSTs exist, low tolerances from Lemma 1 on non-MST edges warn of potential instability, prompting preemptive action. Managers can test this by computing for non-MST edges to spot weak points.
Computationally, these tools are efficient. Single tolerances from Lemma 1 are calculated in polynomial time, and Theorem 2’s bounds avoid costly re-optimization. For large networks, like logistics systems with thousands of routes, LST and DLST can be mapped in real time. Use Theorem 2(b) for a fast resilience check, then apply Theorem 2(c) to prioritize critical edge reinforcements before disruptions, such as storms, hit. This approach ensures networks stay operational with minimal overhead.
3.3. Analysis of Tolerances for Network Planning
The single-edge tolerances () and set tolerances (LST, DLST) provide a quantitative basis for a multi-scale assessment of network robustness. They precisely measure the susceptibility of the current optimal solution () to improvements in alternative connections.
3.3.1. Interpreting Single-Edge Tolerances
Consider a non-tree edge from Example 1 with a relatively low single-edge tolerance () of , for, e.g., This indicates that the weight (or risk) needs to be reduced by only units before the edge becomes cost-effective enough to enter a new optimal MST, displacing an existing tree edge. In practical terms, this alternative edge is a highly competitive threat; the current network configuration is highly vulnerable to even minor improvements along this route. A network planner might see this as an opportunity for a low-cost intervention or as a risk if a competitor were to upgrade this link.
Conversely, consider another non-tree edge from Example 1 (for, e.g., ) with a high single-edge tolerance () of signifies that the weight must be reduced significantly (by units) before it becomes a viable alternative. The current tree is highly robust to improvements on this specific link. A planner might deprioritize investment here, as a large effort is required to make this alternative competitive.
3.3.2. Interpreting Set Tolerances for Coordinated Planning
The true power of the framework is revealed when analyzing sets of edges. Consider a set representing edges in a zone slated for development. The LST of , bounded by and , quantifies the collective investment required to make the set disruptive.
- A narrow gap between these bounds implies the set’s impact is capped by its single most competitive member; coordinated investment offers little synergistic advantage.
- A wide gap, as in this example, suggests strong potential synergy. A coordinated upgrade across the entire set could be far more effective at shifting the optimal network solution than improving edges individually, providing a compelling rationale for area-wide projects.
3.3.3. Computational Feasibility and Practical Implementation
A key advantage of this framework is its computational tractability. The methods developed herein calculate these tolerance metrics—either exactly or within tight bounds—in polynomial time, making them applicable to realistic network problems. This efficiency is further scalable through parallel computing architectures. These tools enable a shift from deterministic planning to risk-aware design. Planners can now make decisions explicitly aligned with their risk tolerance, leading to the design of more robust infrastructure and more precise risk assessments. This is particularly critical in disaster management, where the reliability of an evacuation route hinges on the dependability of its links. A path from an uncertain MST, though potentially longer, offers a higher guarantee of functionality under duress. Prioritizing high-tolerance routes ensures that rescue operations prioritize probability of arrival over nominal distance.
To fully realize this potential in large-scale applications, integration with Geographic Information Systems (GIS) is a critical next step. Embedding our computational framework within a GIS would allow the direct incorporation of spatial data—elevation, hazard maps, land use—into the uncertainty model. This would enable not only the calculation of tolerances but also the spatial visualization of critical corridors and the optimal siting of emergency facilities, thereby bridging the gap between theoretical network robustness and actionable spatial planning.
4. Discussion and Conclusions
This paper has tackled the challenge of evaluating stability in Minimum Spanning Trees (MSTs) within uncertain networks, a problem critical to applications such as transportation, communication, power networks, and reliability optimization. We introduced two novel concepts—lower set tolerance (LST) and dual lower set tolerance (DLST)—to assess how simultaneous changes in risk factors across multiple network elements impact the optimality of MST solutions. LST represents the supremum decrease in risk that preserves the current MST’s optimality, while DLST measures the infimum decrease required to render it non-optimal. By embedding these measures within an uncertainty programming framework, we have developed an efficient alternative to traditional re-optimization approaches, providing exact formulas and bounds to compute set tolerances and enhance decision-making under uncertainty. While our methods provide efficient computational solutions for LST and DLST, their complexity warrants deeper investigation, presenting an opportunity to optimize performance in large-scale applications.
The significance of this research lies in its demonstration that uncertainty programming can effectively address combinatorial optimization problems like the MST. By incorporating uncertain reliability and risk factors, our framework advances theoretical insights into network stability while offering practical tools for fields such as transportation, logistics, network design, and cybernetics. The ability to analyze multiple cost changes simultaneously through LST and DLST not only strengthens sensitivity analysis but also supports optimization algorithms by evaluating the consequences of including or excluding network elements, making it highly relevant to real-world scenarios where disruptions are common.
Integrating Travel Time and Capacity. One promising direction for future research is exploring uncertain travel time reliability in post-crisis transportation networks, where obtaining reliable travel time distribution data poses a significant challenge. Further enhancements could involve integrating edge reliability and capacity into our models to address more complex network dynamics.
Dynamic and Sequential Frameworks. A fundamental assumption of our model is the static nature of the network and its uncertainties. A highly impactful direction for future research involves extending the LST and DLST concepts to dynamic settings. Real-world networks evolve over time, and disruptions often trigger sequential recovery decisions. A dynamic version of this framework could model time-dependent uncertain weights and analyze how tolerances evolve throughout a disruption event or recovery process. Integrating our robustness measures with multi-stage stochastic programming or Markov Decision Processes could provide powerful tools for designing optimal adaptive policies for network monitoring, hardening, and recovery. This would transform the static robustness measures presented here into dynamic indicators for sequential decision-making under deep uncertainty.
Computation of Exact Set Tolerances. We also note that while the bounds and provide polynomial-time computable estimates for the LST of set A, the problem of computing the exact value is a non-linear optimization problem over the space of perturbation vectors . The gap between the upper and lower bounds can be significant, particularly in dense graphs where multiple edges in can tolerate non-zero perturbations concurrently without violating the optimality conditions of . Closing this computational gap presents an interesting problem for future work. Potential approaches include the development of approximation algorithms or heuristic methods. One promising heuristic might involve an iterative greedy procedure: initialize based on the single-edge tolerances and then sequentially attempt to redistribute perturbation within while continuously verifying the optimality of through efficient MST verification routines. A more rigorous approach could involve formulating the problem as a bilinear program or leveraging column generation techniques. The exploration of these methods will be essential for applying set tolerance concepts to very large-scale networks.
Dependent Uncertainties. A key limitation of our current framework is the assumption that uncertain variables are independent. This is often unrealistic in practice, as the failure risk or cost of one network element can be highly correlated with others (e.g., edges sharing a common physical resource or geographical location). Extending the LST and DLST concepts to model such dependencies presents a substantial but valuable challenge. The primary difficulty lies in redefining the perturbation mechanism. Under independence, the perturbation applies only to edge . Under dependence, perturbing one edge’s uncertainty distribution may inherently alter the distributions of others. This means the feasible set of perturbations is no longer a simple Cartesian product of intervals but a complex, constrained space defined by a joint uncertainty distribution (e.g., via a copula) or a correlated uncertainty set. We leave the formalization and computational exploration of these ideas for future research. Future work could explore two potential paradigms:
- A distributional approach using vine copulas or other flexible dependence models to define the joint law of , though computing tolerances would likely require sophisticated Monte Carlo methods; or
- A set-based approach within robust optimization, where uncertainties reside in a correlated set (e.g., ), and the tolerance becomes the maximum scaling factor such that the MST remains optimal for all .
In summary, this work establishes a robust foundation for stability analysis in uncertain MSTs using LST and DLST, blending theoretical innovation with practical utility. As uncertainties increasingly influence critical infrastructure, the need for such frameworks will continue to grow, positioning this research as a timely and impactful contribution to the field.
Funding
This research was carried out with the support of ARIS: Slovenian Research And Innovation Agency (Javna agencija za znanstvenoraziskovalno in inovacijsko dejavnost Republike Slovenije) through the research core funding for the program Knowledge Technologies (No. P2-0103).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We are profoundly grateful to the Editor and the anonymous Reviewers for their invaluable time and expertise. Their insightful comments and constructive criticisms were instrumental in significantly improving the quality, clarity, and impact of this manuscript. The thoughtful engagement with our work challenged us to refine our theoretical contributions and, crucially, to better articulate the implications of our framework for network planning under uncertainty.
Conflicts of Interest
There are no conflicts of interest or competing interests.
Appendix A. An Overview on Key Concepts of Uncertainty Theory
This section presents the essential concepts and foundational principles of uncertainty theory. For a comprehensive introduction, we recommend the seminal works by Liu [1,2]. A common challenge arises when reliable data are insufficient, rendering accurate estimation of probability distributions unfeasible. In such cases, uncertainty must be characterized through uncertain variables. The available data often reflect belief degrees provided by domain experts. However, addressing belief degrees using fuzzy or probability theory can lead to inconsistencies, as these degrees may exhibit greater variability than actual frequencies. Unlike belief degrees, which evolve with knowledge, frequency—a cornerstone of probability theory—remains a stable, observable property. This distinction underscores the need for a distinct approach to managing belief degrees. Liu [2] introduced uncertainty theory, establishing a formal system to model human decision-making under uncertainty, complete with key concepts and operational rules. Both theoretical and practical studies have validated the effectiveness of uncertainty theory in handling non-deterministic data, particularly in subjective estimations.
To manage belief degrees systematically, let be a non-empty universal set and a -algebra over . The pair forms a measurable space, while the triplet constitutes an uncertainty space. Each is a measurable set, termed an event. To axiomatically define an uncertain measure, we assign a value to any , representing the degree to which E is expected to occur. This assignment, , is a set function. If it satisfies the following axioms, it qualifies as an uncertain measure.
The probability measure, while satisfying the first four axioms, cannot be considered a subset of uncertainty theory, as the product probability measure fails to meet the fifth axiom’s requirements. Based on the principles of normality and self-duality, the uncertain measure of the empty set is zero. Thus, for any event , the uncertain measure ranges from . Unlike frequency-based probability, the uncertain measure reflects a subjective belief about an event’s likelihood, shaped by an individual’s knowledge and understanding.
Definition A1.
An uncertain variable ξ is termed a non-negative variable if , and a positive variable if . More information can be found in Liu [1,2].
Definition A2.
The uncertainty distribution of ξ is defined as a function for any real number x. It is considered regular if it is a continuous and strictly increasing function of x, satisfying the following:
- if ,
- if .
Observation A1
(Liu [1,2]). For any uncertain variable with a regular uncertainty distribution , there exists a well-defined, continuous, and strictly increasing inverse uncertainty distribution over the open interval such that .
Theorem A1
(Liu [1,2]). Let be a function. It is an uncertainty distribution if and only if it is monotonically increasing, excluding cases where is constantly 0 or 1. Additionally, a function is an inverse uncertainty distribution if and only if it is continuous and strictly increasing.
Theorem A2
(Liu [1,2]). Let be independent uncertain variables with regular uncertainty distributions . If the new variable is strictly increasing with respect to and strictly decreasing with respect to , then ξ is also an uncertain variable with an inverse uncertainty distribution given by
Furthermore, the (chance) constraint is equivalent to
Definition A3
(Zigzag Uncertainty Distribution). We denote as Zigzag (with parameters a, b, c where ) if it has the following uncertainty distribution . The Zigzag distribution is regular, with an inverse distribution as follows:
Definition A4
(Linear Uncertainty Distribution). We denote as Linear (with parameters a and b) if it has the following uncertainty distribution . The Linear distribution is regular, with an inverse distribution as follows:
References
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin, Germany, 2010. [Google Scholar]
- Liu, B. Uncertainty Theory, 5th ed.; Uncertainty Theory Laboratory: Beijing, China, 2015. [Google Scholar]
- Wang, J.; Zhu, J.; Yang, H. Reliable path selection problem in uncertain traffic network after natural disaster. Math. Probl. Eng. 2013, 2013, 413034. [Google Scholar] [CrossRef]
- Ahuja, R.; Magnanti, T.; Orlin, J. Network flows: Theory, Algorithms, and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Gal, T. Sensitivity Analysis, Parametric Programming, and Related Topics: Degeneracy, Multicriteria Decision Making Redundancy; Walter de Gruyter: Berlin, Germany, 1995. [Google Scholar]
- Punnen, A. Postoptimal Analysis, Parametric Programming, and Related Topics: Degeneracy, Multicriteria Decision Making, Redundancy; De Gruyter: Berlin, Germany, 1997. [Google Scholar]
- Mathwieser, C.; Çela, E. Special Cases of the Minimum Spanning Tree Problem under Explorable Edge and Vertex Uncertainty. Networks 2024, 83, 587–604. [Google Scholar] [CrossRef]
- Ramaswamy, R.; Orlin, J.; Chakravarti, N. Sensitivity analysis for shortest path problems and maximum capacity path problems in undirected graphs. Math. Program. 2005, 102, 355–369. [Google Scholar] [CrossRef]
- Pettie, S. Sensitivity analysis of minimum spanning trees in sub-inverse-Ackermann time. In Proceedings of the International Symposium on Algorithms and Computation, Sanya, China, 19—21 December 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 964–973. [Google Scholar]
- Chandra, A.; Kim, J. Reliability Certification of Supply Chain Networks under Uncertain Failures and Demand. Ann. Oper. Res. 2025. [Google Scholar] [CrossRef]
- Clark, S.; Watling, D. Modelling network travel time reliability under stochastic demand. Transp. Res. Part B Methodol. 2005, 39, 119–140. [Google Scholar] [CrossRef]
- Hosseini, A.; Wadbro, E. Connectivity reliability in uncertain networks with stability analysis. Expert Syst. Appl. 2016, 57, 337–344. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, A.; Zhang, Y. Connectivity of intercity passenger transportation in china: A multi-modal and network approach. J. Transp. Geogr. 2018, 71, 263–276. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheu, J.; Wang, J. Robustness assessment of urban road network with consideration of multiple hazard events. Risk Anal. 2017, 37, 1477–1494. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Yang, H. Resilience of transportation systems: Concepts and comprehensive review. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4262–4276. [Google Scholar] [CrossRef]
- Hosseini, A. Max-type reliability in uncertain post-disaster networks through the lens of sensitivity and stability analysis. Expert Syst. Appl. 2024, 241, 122486. [Google Scholar] [CrossRef]
- Xing, T.; Zhou, X. Finding the most reliable path with and without edge travel time correlation: A lagrangian substitution based approach. Transp. Res. Part B Methodol. 2011, 45, 1660–1689. [Google Scholar] [CrossRef]
- Ma, W.; Tang, S.; Ke, W. Competitive analysis for the most reliable path problem with on-line and fuzzy uncertainties. Int. J. Pattern Recognit. Artif. Intell. 2008, 11, 195–206. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D.; Jung, J. An algorithm for acquiring reliable path in abnormal traffic condition. In Proceedings of the 2008 International Conference on Convergence and Hybrid Information Technology, Daejeon, Republic of Korea, 28–29 August 2008; pp. 682–686. [Google Scholar]
- Alkaff, A.; Qomarudin, M.N.; Bilfaqih, Y. Network reliability analysis: Matrix-exponential approach. Reliab. Eng. Syst. Saf. 2020, 204, 107192. [Google Scholar] [CrossRef]
- Zhu, Z.; Mardan, A.; Zhu, S.; Yang, H. Capturing the interaction between travel time reliability and route choice behavior based on the generalized Bayesian traffic model. Transp. Res. Part B Methodol. 2021, 143, 48–64. [Google Scholar] [CrossRef]
- Zang, Z.; Xu, X.; Qu, K.; Chen, R.; Chen, A. Travel time reliability in transportation networks: A review of methodological developments. Transp. Res. Part C Emerg. Technol. 2022, 143, 103866. [Google Scholar] [CrossRef]
- Dong, S.; Gao, X.; Mostafavi, A.; Gao, J.; Gangwal, U. Characterizing resilience of flood-disrupted dynamic transportation network through the lens of link reliability and stability. Reliab. Eng. Syst. Saf. 2023, 232, 109071. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Lai, C. Connectivity reliability evaluation and most reliable shipping route choice in a seaborne crude oil network. Heliyon 2024, 10, e36295. [Google Scholar] [CrossRef]
- Xin, J.; Frangopol, D.M.; Akiyama, M.; Han, X. Connectivity analysis of transportation networks incorporating bridges and pavements under uncertainty. In Bridge Maintenance, Safety, Management, Digitalization and Sustainability; CRC Press: Boca Raton, FL, USA, 2024; pp. 1916–1921. [Google Scholar]
- Chen, Y.; Ju, Y.; Yin, J.; Jiang, D. Evaluation of Carrying Capacity Reliability for Regional Rail Transit System. Transp. Res. Rec. 2025, 2679, 03611981251337463. [Google Scholar] [CrossRef]
- Ait Mamoun, K.; Hammadi, L.; El Ballouti, A.; Novaes, A.; Souza de Cursi, E. Modeling Uncertain Travel Times in Distribution Logistics. Appl. Sci. 2023, 13, 11242. [Google Scholar] [CrossRef]
- Guo, F.; Liang, J.; Niu, R.; Huang, Z.; Liu, Q. Robust optimization of a procurement and routing strategy for multiperiod multimodal transport in an uncertain environment. Eur. J. Oper. Res. 2025, 327, 115–135. [Google Scholar] [CrossRef]
- Wang, X. Coal Transportation Cost Prediction under Mixed Uncertainty Based on Graph Attention Networks. Int. J. High Speed Electron. Syst. 2025, 34, 2540348. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Peng, J.; Xiao, Q. Supply chain management based on uncertainty theory: A bibliometric analysis and future prospects. Fuzzy Optim. Decis. Mak. 2024, 23, 599–636. [Google Scholar] [CrossRef]
- Gao, R.; Ma, Y.; Ralescu, D. Uncertain multilevel programming with application to omni-channel vehicle routing problem. J. Ambient Intell. Humaniz. Comput. 2023, 14, 9159–9171. [Google Scholar] [CrossRef]
- Hosseini, A. Time-dependent optimization of a multi-item uncertain supply chain network: A hybrid approximation algorithm. Discret. Optim. 2015, 18, 150–167. [Google Scholar] [CrossRef]
- Guo, H.; Wang, X.; Zhou, S. A transportation problem with uncertain costs and random supplies. Int. J. E-Navig. Marit. Econ. 2015, 2, 1–11. [Google Scholar] [CrossRef]
- Qin, Z.; Gao, Y. Uncapacitated p-hub location problem with fixed costs and uncertain flows. J. Intell. Manuf. 2017, 28, 705–716. [Google Scholar] [CrossRef]
- Veresnikov, G.; Pankova, L.; Pronina, V. Uncertain programming in preliminary design of technical systems with uncertain parameters. Procedia Comput. Sci. 2017, 103, 36–43. [Google Scholar] [CrossRef]
- Hosseini, A. Uncertainty modeling and stability assessment of minimum spanning trees in network design. Mathematics 2024, 12, 3812. [Google Scholar] [CrossRef]
- Wang, J.; Sheng, Y. The MST Problem in Network with Uncertain Edge Weights and Uncertain Topology. Soft Comput. 2023, 27, 13825–13834. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, J.; Zhang, Q.; Huang, Y.; Wen, M. Uncertainty Theory-Based Structural Reliability Analysis and Design Optimization under Epistemic Uncertainty. Appl. Sci. 2022, 12, 2846. [Google Scholar] [CrossRef]
- Shen, J. An environmental supply chain network under uncertainty. Phys. A Stat. Mech. Its Appl. 2019, 542, 123478. [Google Scholar] [CrossRef]
- Gao, X.; Jia, L. Degree-constrained minimum spanning tree problem with uncertain edge weights. Appl. Soft Comput. 2017, 56, 580–588. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).