1. Introduction
In group decision-making, diverging opinions among decision-makers often lead to disagreements or conflicts. Designing an effective consensus-reached process (CRP) is critical for ensuring robust outcomes [
1,
2]. Non-cooperative behaviors during the CRP constitutes a major impediment, potentially causing deviations in group decisions or hindering the decision-making process altogether. This issue has garnered significant scholarly attention. Yang et al. [
3] classified non-cooperative behaviors based on confidence levels and trust relationships, emphasizing that minority opinions should not be prematurely labeled as non-cooperative. Zhou et al. [
4] developed a dynamic consensus model using probabilistic linguistic term sets and Tanimoto coefficients to reconcile minority opinions and non-cooperative behaviors in large-scale group decision-making. Xu et al. [
5] examined management strategies for addressing minority opinions and non-cooperative behaviors in large-scale groups. Regarding the management and detection of non-cooperative behaviors, scholars have proposed various methods, such as innovative behavior monitoring [
6], multi-attribute evaluation matrices [
7], and cooperation intention indices [
8], to minimize the impact of non-cooperative behaviors on group consensus formation. Additionally, Yuan et al. [
9] proposed a budget-constrained consensus framework designed to minimize group conflicts and address non-cooperative behaviors. Existing research on non-cooperative behaviors has broadly addressed elements such as trust relationships [
1,
10,
11,
12] and conflict dynamics. However, studies focusing on decision-makers’ willingness to adjust their own behavior remain insufficiently explored.
In the process of multi-stage negotiation for group decisions, cost-effectiveness is a key consideration in the CRP. Ben-Arieh et al. [
13] first introduced the concept of minimum-cost consensus (MCC) and developed solution frameworks for achieving MCC under both linear and quadratic cost functions. Wang et al. [
14] leveraged cooperative game theory to construct a holistic consensus optimization model that incorporates individual adjustment preferences. Subsequently, to strike a balance between cost minimization and benefit maximization, Ma et al. [
15] integrated a dual social network framework into a consensus optimization model. Subsequent research has witnessed continuous innovation in consensus-related methodologies, with scholars actively integrating cross-disciplinary theories to advance the field [
16,
17,
18,
19,
20,
21]. In order to address the impact of unit cost changes, researchers have incorporated robust optimization techniques into consensus model construction, enhancing the resilience of decision frameworks [
22]. Traditional robust optimization methodologies encompass box, ellipsoidal, and polyhedral uncertainty sets. By incorporating diverse uncertainty sets, researchers can construct distinct consensus models that account for data uncertainty [
23,
24,
25]. Advancing this line of research, Li et al. [
26] integrated stochastic programming with robust optimization techniques to develop a robust two-stage optimization consensus model. While also adopting a two-stage framework, Ma et al. [
27] proposed a two-stage distributed robust maximum expert consensus model, and Zhu et al. [
28] introduced a novel distributed robust opportunity-constrained maximum expert consensus model, further addressing cost asymmetry and distributed fuzziness in group decision-making to enhance decision efficiency under uncertainty. Furthermore, Han et al. [
29] incorporated confidence levels to formulate a chance-constrained robust minimum-cost consensus model (MCCM). Li et al. [
30] proposed a CRP framework for uncertain large-scale group decision-making based on robust discrete optimization, controlling the conservatism of optimal consensus opinions, and computing optimal corrective opinions for decision-makers. Through a comparative analysis with conventional robust optimization techniques, their approach demonstrated significant reductions in solution conservatism.
Complementing such chance-constrained frameworks, data-driven robust optimization methodologies offer an alternative approach to mitigate the inherent over-conservatism of traditional models [
31]. Han et al. [
32] specifically addressed weight uncertainty in group decision aggregation by devising a data-driven robust MCCM framework, establishing a critical linkage between distributional robustness and consensus efficiency. Wei et al. [
33] pioneered a quadratic cost function to quantify complex resistance dynamics in expert opinion adjustment, subsequently developing a data-driven robust maximum expert consensus model. Their empirical analysis substantiates that such data-driven robust methodologies simultaneously elevate consensus achievement levels and mitigate solution conservatism. Robust optimization has been substantially applied to group decision-making, with significant advances. However, research on leveraging data-driven uncertainty sets for consensus model optimization remains relatively underexplored. This research gap presents a key point for future methodological innovation.
In light of the information above, this study develops a data-driven robust MCCM that incorporates non-cooperative behaviors characterized by individual adjustment willingness. The model is validated through a real-world case of house demolition compensation negotiations in a community in Guiyang, thus demonstrating its feasibility and effectiveness in practice. The main contributions of this paper are as follows: (1) An individual adjustment willingness function is proposed. It explicitly identifies and quantifies non-cooperative behaviors within the group decision-making process and captures the influence of participants’ adjustment willingness on both individual behavior and consensus dynamics. This function overcomes the limitation of traditional methods that lack a mechanistic representation of non-cooperation. (2) Data-driven uncertainty sets are constructed using Principal Component Analysis (PCA) and Kernel Density Estimation (KDE). They not only address uncertainty in unit consensus costs but also reduce the conservatism inherent in traditional robust optimization approaches. (3) A robust MCCM is developed that explicitly considers non-cooperative behaviors and the unit cost uncertainty. This model provides a quantitative framework for behavioral deviations and enhances decision robustness under uncertainty. It addresses a critical gap in existing research where the coupling effect of behavior and uncertainty is often neglected.
The remainder of this paper is organized as follows.
Section 2 provides the basic knowledge of MCCM and non-cooperative behaviors.
Section 3 describes the construction process of the data-driven robust MCCM.
Section 4 offers a case study to prove the applicability of the proposed model. Conclusions are presented in
Section 5.
4. Case Study
4.1. Case Background
With the rapid acceleration of global urbanization, urban renewal has emerged as a vital strategy for optimizing city structures and stimulating economic growth. As an essential component of this transformation, demolition and relocation of aging residential districts have become socioeconomically inevitable. Homeowners affected by such initiatives, however, exhibit complex and diversified attitudes toward demolition. Certain groups actively endorse governmental policies and willingly cooperate. Others strategically view demolition as an economic opportunity to secure financial compensation. A distinct segment, meanwhile, staunchly resists displacement from their established communities due to deep-rooted place attachment. Hence, to ensure the smooth implementation of urban renewal projects, governments must establish a harmonious negotiation mechanism with homeowners to minimize aggregate social costs and maintain socio-spatial justice.
In this context, a residential community named “Harmony Home” in Guiyang was designated for demolition and relocation according to urban planning requirements. The local government intended to construct a new commercial center in this area to further promote Guiyang’s economic development. Regarding compensation, ten homeowner representatives were selected to engage in negotiations with the local government. The compensation package covered several components, including land compensation, property compensation, decoration reimbursement, resettlement allowances, and relocation fees. Each representative proposed an initial expected total compensation amount, represented by the vector o = (251, 220, 322, 305, 272, 283, 332, 292, 288, 208) (in CNY 10,000). Considering various factors such as individual influence and the size and number of properties owned by individuals, corresponding weights for each homeowner were assigned as ω = (0.10, 0.08, 0.05, 0.16, 0.12, 0.06, 0.13, 0.07, 0.14, 0.09). To ensure fairness and limit individual deviations from the group consensus, a consensus threshold was introduced, denoted as ε = (0.85, 0.70, 0.80, 0.85, 0.76, 0.88, 0.79, 0.85, 0.76, 0.86). This threshold defines the maximum acceptable difference between each individual opinion and the group consensus. Furthermore, to quantify non-cooperative negotiation behaviors, this study introduces an individual adjustment willingness parameter δ. A homeowner is considered non-cooperative if their δ value is below 0.5. Reckoned with factors such as acceptance of the new environment and personal financial capability, the adjustment willingness values were determined as δ = (0.1, 0.8, 0.2, 0.3, 0.5, 0.5, 0.6, 0.2, 0.4, 0.8).
4.2. Numerical Results
As the total compensation amount consists of multiple payment categories, 100 sample data points regarding the compensation amount were collected by visiting homeowners, assessing the current condition of their houses, and understanding their family situations, as shown in
Table 1.
The average vector
μ0 corresponding to the sample data in
Table 1 can be obtained by Equation (7), and the covariance matrix
S can be obtained by preliminary normalization of the sample data by Equations (8) and (9), as shown below.
By eigenvalue decomposition of the covariance matrix
S, the matrix
p can be obtained, consisting of 10 eigenvectors. According to Equation (10),
v is a diagonal matrix of all eigenvalues in descending order:
v = diag{10,965.93, 7816.47, 6382.80, 4610.96, 3165.41, 1311.51, 592.33, 138.02, 39.95, −0.01}. The matrix
p is as follows:
According to Equations (11)–(15), the lower bound vector = (0.00, −0.10, −0.29, −0.56, −0.12, −0.22, −0.01, −0.04, −0.02, −0.87) of the principal component and the upper bound vector = (0.00, 0.20, 0.07, 0.04, 0.13, 0.10, 0.15, 1.21, 0.32, 0.01) are obtained by projecting uncertainty data onto principal components. Then, the above data were used as inputs to the model (M8) and calculated using the LINGO software, and finally, the adjustment opinions of each homeowner were obtained as = 276.10, = 276.25, = 277.75, = 276.63, = 276.19, = 277.83, = 277.74, = 277.80, = 277.71, and = 276.09, the consensus opinion = 276.95, and the total consensus cost was CNY 929,656,200. That is, the local government ultimately requires a total of CNY 929,656,200 to reach consensus with homeowners. Beyond direct compensation payments, this total consensus cost also encompasses ancillary expenditures, including construction delays caused by prolonged negotiations, additional property appraisal fees, and stakeholder engagement costs such as public relations and media communications. As a result, government authorities involved in demolition negotiations must proactively incorporate these hidden cost contingencies into their decision-making frameworks. To minimize overall costs, targeted strategies must be implemented, such as enhancing policy transparency by improving the dissemination of demolition regulations to raise homeowner awareness and introducing calibrated compensation adjustments to raise relocation standards and better safeguard residents’ interests. These measures can significantly lower conflict-related costs. Ultimately, promoting smooth and effective negotiations with homeowners, mitigating or preventing demolition disputes, and reducing the incidence of non-cooperative behaviors during the demolition process are crucial to advancing government-led demolition and resettlement initiatives at minimal cost.
4.3. Sensitivity Analysis
4.3.1. Consensus Threshold Analysis
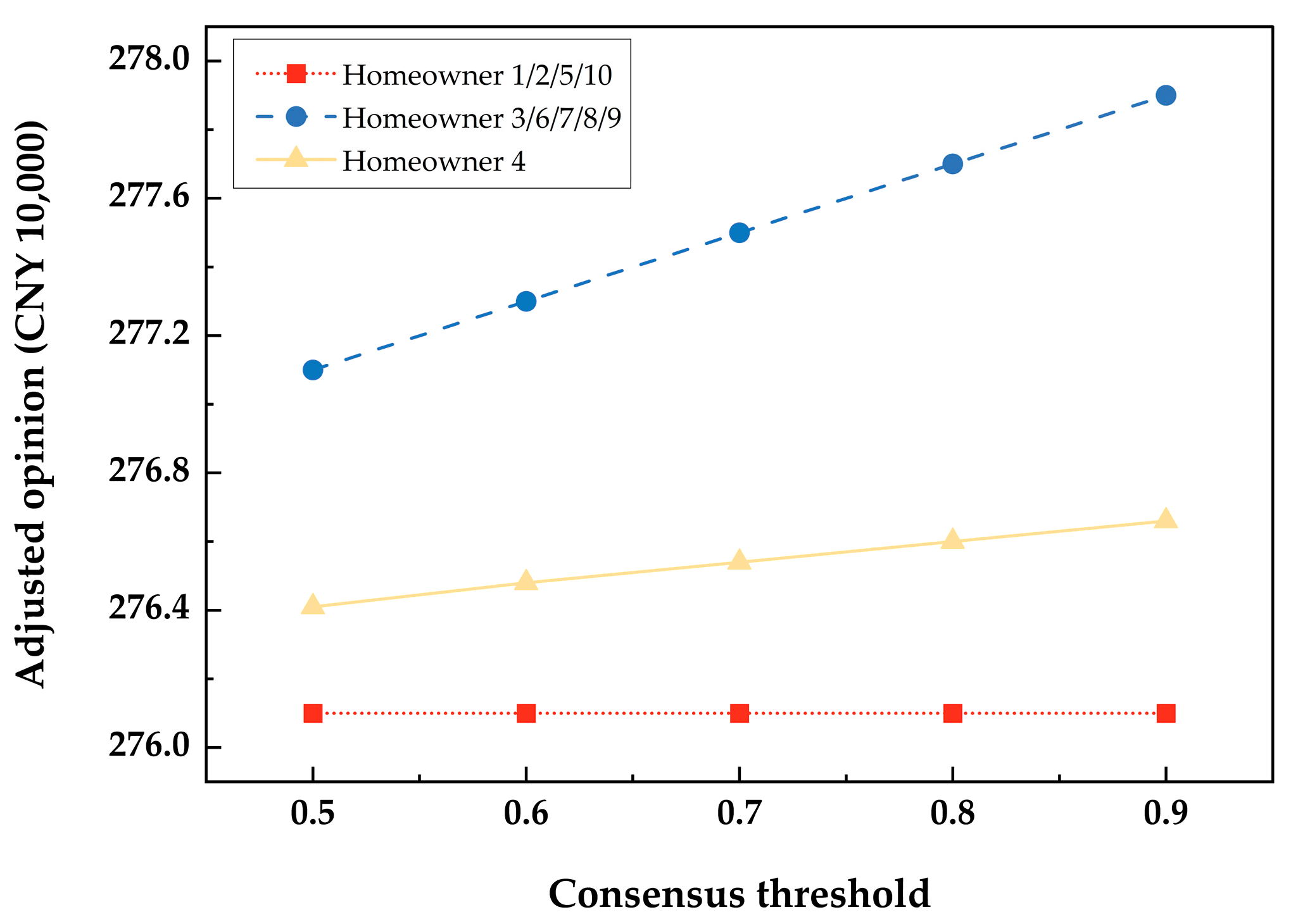
Based on empirical case study data and calculated results, we examine the influence of consensus thresholds in the decision model and reveal changes in the adjustment opinions of individual decision-makers under different consensus thresholds. As shown in
Figure 1, we analyzed opinion adjustments of ten homeowners involved in decision-making under different consensus thresholds. We summarized their behavior patterns into three categories.
Category 1: Homeowners 1, 2, 5, and 10. Their adjusted opinions remained unchanged (consistently at CNY 2.761 million) as the consensus threshold changed. This suggests these homeowners may have a high-risk appetite, making them susceptible to external influences during decision-making.
Category 2: Homeowner 4. While adjustments were insignificant, Homeowner 4 showed a willingness to adjust opinions to a certain extent based on changes in consensus. Such decision-makers exhibit flexibility in decision-making: their risk appetite drives them to accept changes within a limited range. With proper guidance from coordinators, they may adjust further to benefit the group.
Category 3: Homeowners 3, 6, 7, 8, and 9. Their adjusted opinion values had a significant positive correlation with the consensus threshold. These decision-makers demonstrate high cooperation in the group: they willingly adjust opinions based on changes in collective views to enhance group decision consistency and effectiveness. However, they may be more vulnerable to social influence and group pressure.
4.3.2. Individual Adjustment Willingness and Robustness Analysis
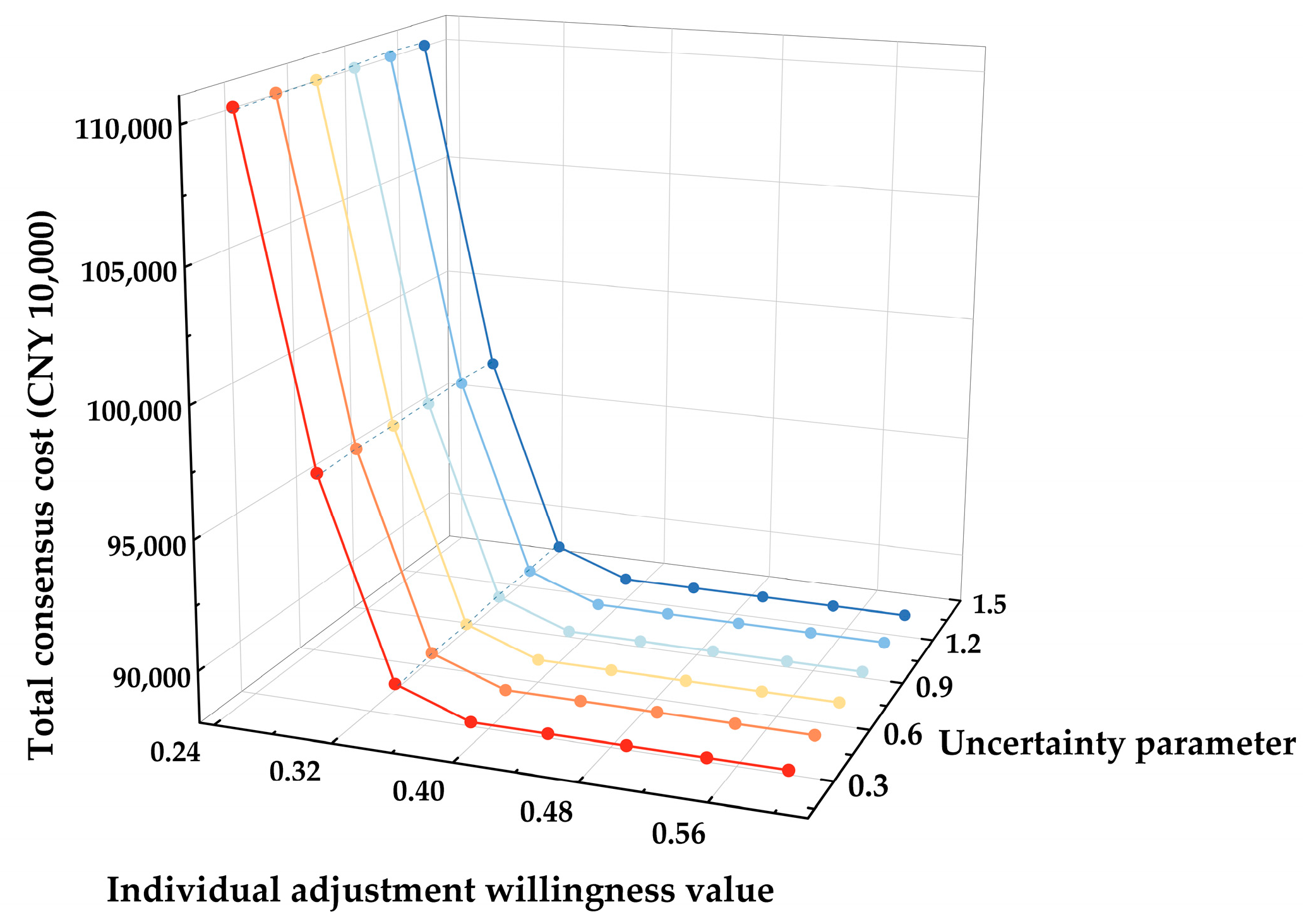
For the convenience of analysis, assuming that all individuals have the same adjustment willingness value, we explore the impact of individual adjustment willingness value
δ on the consensus cost. The relationship between the individual adjustment willingness value and the total consensus cost is shown in
Figure 2. When the individual adjustment willingness value is 0.25, it can be regarded as a situation where all decision-makers are non-cooperators, and the consensus cost reaches more than CNY 110 million. This phenomenon highlights the negative influence of non-cooperative behaviors on the cost of the consensus in group decision-making. As the value of individual adjustment willingness increases, the consensus cost shows a decreasing trend, indicating that cooperative behaviors help to reduce the cost of reaching consensus. When the willingness value exceeds 0.45, the consensus cost is no longer affected and remains constant. This suggests that in group decision-making, once decision-makers hold a neutral attitude toward adjustment willingness or are willing to cooperate, further increasing their adjustment willingness will no longer significantly reduce the consensus cost. In addition, it is evident in
Figure 2 that when individual adjustment willingness is greater than 0.45, the consensus cost is much lower than the cost when individual adjustment willingness is 0.25, further confirming the importance of cooperative behaviors in reducing the consensus cost. Therefore, the influence of non-cooperative behaviors in group decision-making cannot be ignored.
In the model proposed in this paper, the uncertainty parameter
φ is introduced to control and represent the robustness of the method. The adjustment of this parameter directly affects the robustness of the model and thus impacts the final value of the objective function. By setting different values of
φ, its effect on the total consensus cost is analyzed, and the results are shown in
Figure 2. With the increase in
φ, the consensus cost shows a steady upward trend. Specifically, when the
φ increases from 0 to 1.4, the consensus cost increases by only CNY 7000. This small increase highlights the model’s ability to adapt to uncertain changes, thus demonstrating the robustness of the model. In order to strike a balance between robustness and cost-effectiveness, this paper chooses
φ = 0.8 as the optimal parameter value, considering the adaptability of the model to uncertainty and the need for cost control.
4.3.3. Individual Adjustment Willingness and Model Analysis
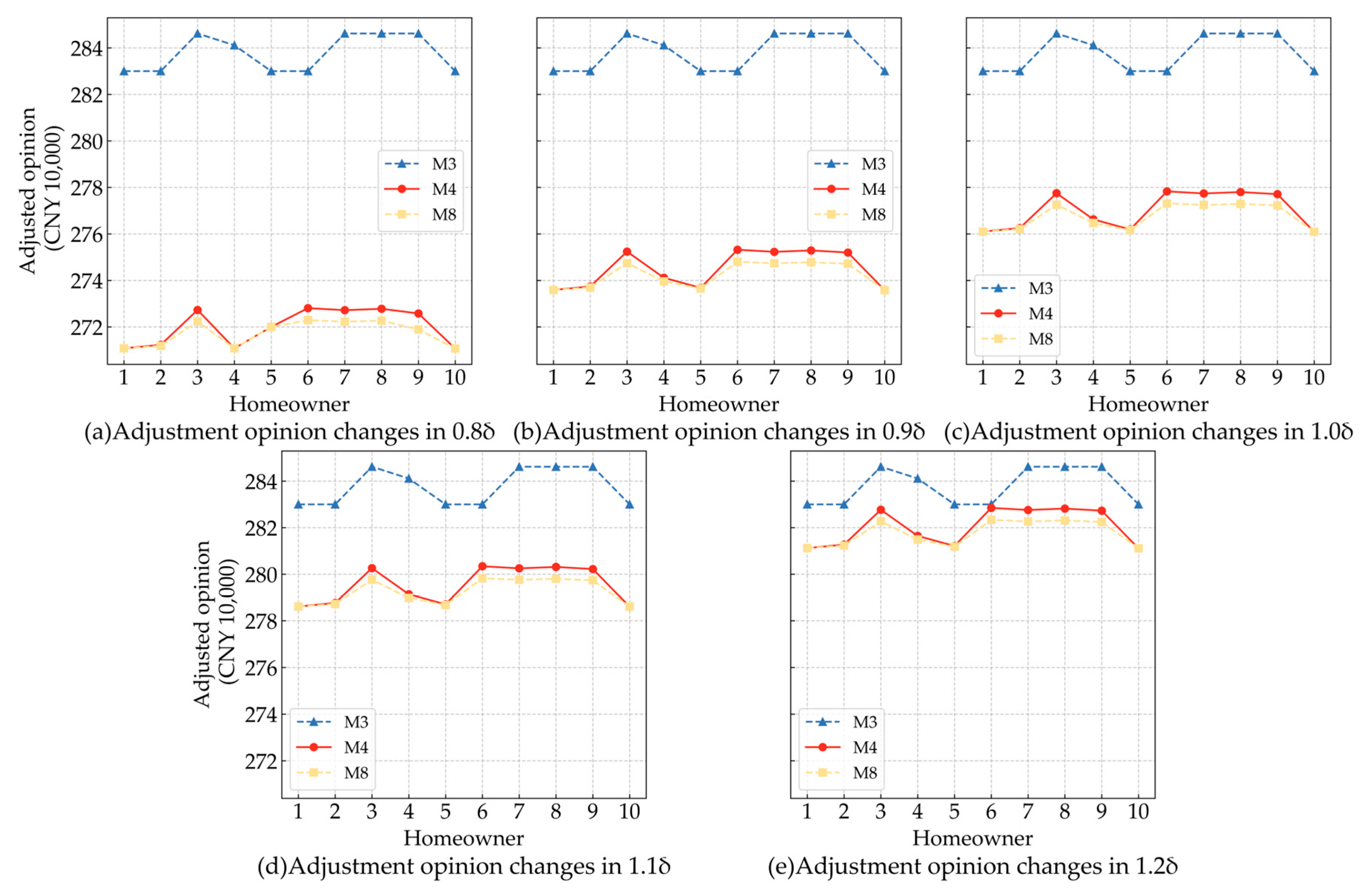
To explore how individual adjustment willingness
δ influences decision-makers’ opinion adjustments across different consensus models, this study systematically scaled
δ to 0.8–1.2 times its original value.
Figure 3 illustrates the resulting opinion changes in models (M3), (M4), and (M8). It can be seen from
Figure 3 that with the increase in
δ, both the consensus model (M4), considering only individual willingness, and the data-driven robust model (M8), considering non-cooperative behaviors proposed in this paper, show a significant positive correlation growth trend. In contrast, the traditional consensus model (M3), without considering individual willingness, remains unchanged and is unaffected by
δ variations. In addition, under the five zoom levels of
δ, the fluctuation amplitude of the adjusted opinion value in model (M8) is always lower than that of model (M3). This phenomenon indicates that model (M8) is more robust to the fluctuation of individual adjustment willingness
δ because it is integrated with a data-driven uncertainty set, and its adjustment results are more stable. In summary, the analysis results effectively verify the superiority of the proposed data-driven robust consensus model (M8). Unlike the traditional models (M3 and M4), (M8) accounts for non-cooperative behaviors. Notably, it balances responsiveness to individual willingness and maintenance of system stability.
4.4. Comparative Analysis
4.4.1. Comparison of Methods
The model proposed in this paper is compared and analyzed with existing studies, as shown in
Table 2. It can be seen that only this paper has considered all four aspects: non-cooperative behaviors, individual willingness, and data-driven and robust optimization. Xu et al. [
5], Yuan et al. [
9], and Shang et al. [
37] have considered non-cooperative behaviors in group decision-making, but have not explored the causes of non-cooperative behaviors in depth from the perspective of the decision-maker’s individual willingness, and have not assessed the problem of uncertainty that exists in group decision-making in general. Zhang et al. [
36] and Zhong et al. [
38] both consider the individual willingness of the decision-maker, and Zhang et al. [
36] only adopt the data-driven robust optimization method for the uncertainty of unit adjustment cost in the decision-making process, but do not involve the non-cooperative behaviors that may arise in the decision-making process. Zhong et al. [
38] consider non-cooperative behaviors and individual willingness, but do not incorporate data-driven robust optimization, and thus fail to fully consider the uncertainty in the decision-making process.
Robust optimization has significant advantages in dealing with parameter uncertainty in the decision-making process, and data-driven uncertainty sets can effectively alleviate the problem of over-conservative classical robust optimization. While considering the behavior of decision-makers, Zhang et al. [
39] constructed a consensus model based on three classical robust optimization uncertainties. However, among the reviewed literature, only this paper, Zhang et al. [
36], and Wei et al. [
40] considered the data-driven robust optimization method. In contrast, the data-driven robust MCCM, considering non-cooperative behaviors proposed in this paper, not only analyzes the non-cooperative behaviors of decision-makers from the perspective of individual willingness but also uses the data-driven robust optimization method to deal with the uncertainty of unit adjustment cost in the process of consensus-reaching. In addition, the proposed model also solves the problem of over-conservatism of the solution that may be caused by traditional robust optimization.
4.4.2. Model Comparison
The data-driven robust MCCM (M8) proposed in this paper, which considers non-cooperative behaviors, is compared with the classical MCCM (M3) and the MCCM (M4) that considers only non-cooperative behaviors. The case data were substituted into models (M3), (M4), and (M8) for calculation, and the corresponding consensus opinion
and the total consensus cost c were obtained, as shown in
Table 3. It can be seen that the model (M3), as the MCCM in the ideal state, achieves consensus at the highest opinion value and incurs the lowest total consensus cost. However, this model assumes all decision-makers are fully cooperative, a scenario that does not align well with most real-world group decision-making contexts. Compared with model (M3), model (M4) accounts for the non-cooperative behaviors of decision-makers. Although this results in a lower consensus opinion and an increased total consensus cost, it is more representative of actual decision-making scenarios. Furthermore, the comparison demonstrates that non-cooperative behaviors significantly impact both consensus-reaching and cost. Building upon model (M4), model (M8) further incorporates the uncertainty of the decision-making environment. It employs a data-driven robust optimization method to address uncertainty while mitigating the excessive conservatism associated with traditional robust optimization. Compared to model (M4), model (M8) achieves the same consensus opinion, but incurs a higher total consensus cost. This increase stems from the data-driven robust optimization approach, which focuses not only on the cost of current decisions but also accounts for potential future uncertainties and their implications. The comparison of these models highlights that we should not rely solely on decisions derived from an ideal state in increasingly complex decision-making contexts. Instead, it is crucial to consider realistic decision-maker behaviors, various uncertainties, and minimize their impacts.
5. Conclusions
This paper proposes a data-driven robust MCCM that accounts for non-cooperative behaviors. This is achieved by introducing an individual adjustment willingness function and constructing data-driven uncertainty sets. Compared with traditional MCCMs, the proposed approach not only captures the influence of non-cooperative behaviors but also incorporates robust optimization techniques to address uncertainty in unit adjustment costs. This dual approach effectively mitigates the over-conservatism which is typical of traditional robust models, and improves practical applicability in uncertain environments.
The results of the case analysis reveal the following key findings: (1) The effect of consensus threshold variation on opinion adjustment is individual-specific. By guiding different types of decision-makers with tailored interventions, the decision-making process can be made more efficient. (2) Higher adjustment willingness leads to improved cooperation and reduced consensus cost. However, when the willingness reaches a certain level, its marginal effect on cost reduction diminishes. (3) The model exhibits strong robustness, maintaining performance in the presence of uncertainty and variability, confirming its suitability for real-world decision scenarios. These findings directly address the core research problem of achieving a cost-efficient consensus amid behavioral uncertainty and cost fluctuations. They provide a theoretical and practical foundation for designing more adaptive and behavior-aware consensus mechanisms, with implications for policy-making and facilitation practices in participatory decision environments such as medical care, supply chain management, multi-stakeholder management, and collaborative governance. For example, in multidisciplinary consultations within healthcare, quantitative expert adjustment willingness can be used to identify and mitigate non-cooperative behaviors, thereby promoting more efficient multidisciplinary consensus.
Despite these demonstrated strengths, the model is not without limitations. Specifically, this study identifies non-cooperative behaviors solely through the adjustment willingness function. However, analyzing such behaviors from the perspective of observable decision-maker behavior patterns may offer additional insights. Future research could therefore expand the behavioral analysis framework by incorporating measurable decision actions and dynamic behavioral cues—such as communication frequency, or inconsistency in preference elicitation. In addition, developing dynamic consensus mechanisms that account for evolving environmental contexts and the temporal shifts in decision-makers’ preferences enhances the model’s practical relevance and robustness in real-time applications.