Enhancing Instance Segmentation in High-Resolution Images Using Slicing-Aided Hyper Inference and Spatial Mask Merging Optimized via R-Tree Indexing

Abstract

Instance segmentation in high-resolution images is essential for applications such as remote sensing, medical imaging, and precision agriculture, yet remains challenging due to factors such as small object sizes, irregular shapes, and occlusions. Tiling-based approaches, such as Slicing-Aided Hyper Inference (SAHI), alleviate some of these challenges by processing smaller patches but introduce border artifacts and increased computational cost. Overlapping tiles can mitigate certain boundary effects but often result in duplicate detections and boundary inconsistencies, particularly along patch edges. Conventional deduplication techniques, including Non-Maximum Suppression (NMS) and Non-Mask Merging (NMM), rely on Intersection over Union (IoU) thresholds and frequently fail to merge fragmented or adjacent masks with low mutual IoU that nonetheless correspond to the same object. To address deduplication and mask fragmentation, Spatial Mask Merging (SMM) is proposed as a graph clustering approach that integrates pixel-level overlap and boundary distance metrics while using R-tree indexing for efficient candidate retrieval. SMM was evaluated on the iSAID benchmark using standard segmentation metrics, with tile overlap configurations systematically examined to determine the optimal setting for segmentation accuracy. The method achieved a nearly 7% increase in precision, with consistent gains in F1 score and Panoptic Quality over existing approaches. The integration of R-tree indexing facilitated faster candidate retrieval, enabling computational performance improvements over standard merging algorithms alongside the observed accuracy gains.

1. Introduction

In computer vision, interpreting and analyzing high-resolution images is critical for applications such as remote sensing, medical diagnostics, autonomous driving, and industrial inspection. These images often span gigapixel scales, where even large objects occupy only a small fraction of the overall scene. This scale disparity, combined with dense object distributions, complex shapes, and background clutter, makes precise instance segmentation particularly challenging [1]. Additionally, direct full-resolution processing imposes prohibitive memory and computational requirements, necessitating strategies that divide the image into more manageable regions [2].

Instance segmentation extends object detection by producing pixel-level masks for each object, enabling accurate delineation of object boundaries [3]. While this capability is essential for analyzing large-scale imagery, the size and complexity of such data often require tiled inference. Tiling allows segmentation models to operate on smaller image patches without aggressive downsampling, preserving fine details while reducing computational load. Among tiling strategies, SAHI [4] is widely adopted, supporting both non-overlapping and overlapping configurations. Overlapping tiles improve boundary preservation and object completeness but introduce duplicate or fragmented detections, especially along tile edges. Post-processing is essential to reconcile these duplicates into coherent object instances. Standard approaches such as NMS [5] and NMM [6] rely primarily on Intersection over Union (IoU) thresholds to eliminate or merge detections. However, in tiled high-resolution inference, adjacent fragments may have minimal overlap despite representing the same object, leading to missed merges and inconsistent boundaries.

Recent frameworks have explored various strategies to improve detection performance in large-scale images. Telcceken et al. [7] proposed a multi-stage object detection pipeline combining an Image Slicing Algorithm (ISA), the Segment Anything Model (SAM), and super-resolution (SRGAN) to enhance small object detection in satellite and aerial imagery [8,9]. SegTrackDetect [10] introduced a region-of-interest-driven, window-based approach for tiny object detection, combining semantic segmentation and tracking to limit inference to relevant sub-windows and aggregating results with overlapping box suppression. Yang et al. [11] proposed RS-YOLOX, an improved YOLOX-based detector for remote sensing images that integrates Efficient Channel Attention (ECA), Adaptively Spatial Feature Fusion (ASFF), and the varifocal loss function, with inference adapted to the SAHI tiling framework. While these methods achieve strong performance in detection tasks, they primarily operate at the bounding-box level and focus on architectural or pre-processing improvements, without directly addressing the merging of fragmented masks during post-processing.

Merging fragmented or spatially disjoint instance masks remains a persistent challenge in tiled high-resolution inference. Furthermore, scalable, deduplication methods that explicitly account for spatial proximity and boundary alignment remain underexplored. This gap motivates the development of a post-processing algorithm specifically optimized for workflows in high-resolution imagery, capable of efficiently merging fragmented or misaligned masks beyond the limitations of IoU-based heuristics.

The main contributions of this work are as follows:

• Evaluation of a tiling-based training strategy in which large high-resolution aerial images are cropped into 512 × 512 tiles for model training. Our approach, evaluated with YOLOv11, aims to improve large-scale detection by consolidating overlaps while reducing computation. The resulting training dataset is published as iSAID-512Tiles [12] to support reproducibility and further research.
• Systematic evaluation of the SAHI method under varying tile overlap configurations to determine the optimal balance between segmentation accuracy and computational efficiency.
• Introduction of a novel deduplication algorithm, Spatial Mask Merging (SMM), which merges overlapping or fragmented masks based on pixel-level inclusion and boundary distance metrics and is optimized using R-tree spatial indexing to enable efficient and scalable post-processing.
• Comparative evaluation of SMM against established methods, including NMS and NMM, on the iSAID [13] benchmark using standard segmentation performance metrics.

The remainder of this paper is organized as follows: Section 2 reviews related work on instance segmentation in large-scale images, tile-based inference strategies, and deduplication algorithms. Section 3 describes the experimental setup, including the proposed SMM algorithm, the tiling strategy for large-image segmentation, and the datasets used. Section 4 presents the experimental results, including the impact of tile overlap on performance and a comparative analysis of SMM against traditional deduplication methods. Section 5 discusses the advantages, limitations, and broader applicability of the proposed SMM algorithm. Finally, Section 6 concludes the paper and outlines directions for future research.

2. Related Work

Instance segmentation of small, irregular objects in high-resolution images remains challenging due to complex shapes, dense object distributions, and extreme scale variations, particularly in domains such as remote sensing and medical imaging [14,15]. Processing such data imposes significant memory and computational demands. To address these challenges, several strategies have been explored, including training on image crops rather than downscaling [16], applying multi-scale fusion and transformer-based models [14], and designing specialized architectures such as EU-Net for water body extraction [17]. Other promising directions include GAN-assisted training and synthetic data generation to reduce reliance on large annotated datasets [18]. However, relatively few studies investigate the benefits of training on tiled inputs instead of full-resolution images, despite their potential for substantial computational savings.

Slicing-Aided Hyper Inference (SAHI) [4] is a model-agnostic tiling strategy designed to efficiently process high-resolution images by dividing them into smaller tiles. This approach alleviates memory and computational constraints and has been widely adopted in medical imaging, remote sensing, and aerial surveillance. SAHI supports both non-overlapping and overlapping tile configurations: non-overlapping tiles improve efficiency but often miss or fragment objects at tile boundaries, whereas overlapping tiles capture boundary objects more completely, improving accuracy for small or partially visible instances [19].

NMS [5] is a standard post-processing method in object detection that removes redundant detections by retaining the highest-confidence candidate among overlapping boxes, based on an Intersection over Union (IoU) threshold. While computationally efficient, NMS struggles with fragmented or adjacent objects exhibiting low overlap, a frequent occurrence in instance segmentation. Syncretic-NMS, or Non-Maximum Merge (NMM) [6], addresses this limitation by merging highly correlated neighboring boxes after suppression, preserving more complete object representations in dense scenes. These shortcomings are particularly evident in crowded scenes or tiled inference workflows, where improper suppression may lead to false positives or missed detections [20].

Despite advances in object detection and segmentation post-processing, there remains limited focus on deduplication strategies tailored to tiled inference with overlapping tiles. In high-resolution domains such as satellite and medical imaging, tiling is essential for managing memory and computation, yet it often fragments large objects across tile boundaries. Recent frameworks have advanced tiling-based detection pipelines through enhanced pre-processing, model improvements, and bounding-box-level merging strategies. However, standard NMS and NMM still struggle in these settings, failing to associate detections that exhibit minimal overlap or lie outside predefined spatial search radii [21]. This lack of robust deduplication methods represents a clear gap in the literature. Furthermore, although spatial indexing techniques such as R-trees are widely used in geographic information systems, map services, and spatial databases, they remain underexplored in instance segmentation workflows, where they could accelerate candidate mask retrieval for merging across tile boundaries. A detailed overview of R-tree structure, operations, and applications is provided in Appendix B.

In summary, while prior work has advanced large-scale image analysis through improved detection models and tiling strategies, the integration of spatially efficient post-processing for overlapping-tile instance segmentation, particularly through the use of R-tree indexing for scalable candidate retrieval, remains insufficiently addressed.

3. Materials and Methods

This section explains the proposed SMM deduplication algorithm as a post-processing method, along with the dataset, segmentation backbone, and training strategy used for its evaluation.

3.1. Dataset

iSAID [13] is a benchmark dataset designed explicitly for instance segmentation in aerial imagery. It contains 655,451 object instances across 2806 high-resolution images, covering 15 commonly occurring object categories such as vehicles, ships, buildings, and sports fields.

iSAID is characterized by several distinctive properties: (a) a large number of high-resolution images, (b) dense instance-level annotations, (c) high object density and class imbalance, (d) significant variation in object scale and orientation, and (e) small, ambiguous instances requiring contextual reasoning. Annotations follow the COCO format and were created and validated by professional annotators. The imagery used in iSAID originates from the DOTA-v1.0 dataset [22], which comprises very large aerial images (ranging from $800\times 800$ to $20,000\times 20,000$ pixels) acquired from various sensors, including Google Earth and JL-1 and GF-2 satellites. All usage of imagery from Google Earth must comply with its terms of use. Both the iSAID and DOTA datasets are available strictly for academic purposes; any commercial use is prohibited.

To facilitate the training of deep segmentation models on standard hardware, a derived dataset, iSAID-512Tiles, has been prepared and publicly released [12]. It consists of approximately 10,000 tiles of size $512\times 512$ pixels, extracted from the iSAID training and validation splits. Each tile includes YOLO-format annotations with normalized bounding boxes and class IDs, aligned with iSAID categories. The tiles are partitioned into training (70%), validation (20%), and test (10%) subsets using a random split, ensuring that all tiles from the same original image remain in the same subset to prevent data leakage [23]. This tiling strategy preserves spatial diversity while substantially reducing the memory and computational resources required to process full-size aerial images.

3.2. Segmentation Backbone and Training Protocol

The baseline segmentation model for evaluating the proposed post-processing pipeline is the YOLOv11s-seg architecture [24], a lightweight instance segmentation network optimized for real-time applications. It comprises 203 layers and approximately 10.1 million parameters, with a computational cost of 35.6 GFLOPs. The architecture integrates convolutional backbones with C2PSA attention modules to enhance spatial awareness with minimal overhead, C3k2 blocks for cross-stage feature reuse, and multi-scale heads for refining mask predictions across network depths.

Training and evaluation were conducted using the Ultralytics YOLOv11 framework in PyTorch [25] (version 8.3.159), on an NVIDIA A100-SXM4 GPU (40 GB VRAM) with Automatic Mixed Precision (AMP) enabled to accelerate computation and reduce memory usage. The model was trained for 100 epochs using a batch size of 16, a learning rate of 0.01, and the SGD optimizer with momentum 0.9, as automatically selected by the framework. Inference benchmarks achieved an average processing speed of 0.9 ms per image (excluding I/O). Evaluation followed standard metrics: precision, recall, mean Average Precision at IoU 0.50 (${\mathrm{mAP}}_{50}$), and mean Average Precision across IoU thresholds 0.50–0.95 (${\mathrm{mAP}}_{50:95}$), reported for both bounding boxes and segmentation masks.

Initialization used pretrained weights from a prior YOLOv11s-seg model trained on the same dataset split but a reduced subset of ∼6000 images. This earlier model, trained for 100 epochs using the AdamW optimizer (lr = 0.000526, momentum = 0.9), achieved 77.6% precision, 61.2% recall, 67.7% ${\mathrm{mAP}}_{50}$, and 41.5% ${\mathrm{mAP}}_{50:95}$ for mask segmentation. These weights provided a better initialization, facilitating faster convergence in the final training run. The resulting model served solely as the baseline segmentation backbone in the subsequent evaluation of the proposed post-processing method.

3.3. Spatial Mask Merging Algorithm (SMM)

The proposed algorithm resolves duplicate, adjacent, or fragmented instance masks by casting merging as a global graph clustering problem [26]. Unlike IoU-only post-processing, decisions are taken at the mask level and integrate spatial geometry and semantic consistency. Candidate relations are restricted using an R-tree spatial index that retrieves neighbors within a fixed search radius $\rho$, after which a weighted compatibility graph is clustered to yield globally consistent groups.

Let $\mathcal{O}=\{o_1,\dots ,o_n\}$ denote predictions with $o_i=(M_i,b_i,s_i,{\ell }_i)$, where $M_i\subset {\mathbb{Z}}^2$ is a binary mask with boundary $\partial M_i$, $b_i$ is an axis-aligned box, $s_i\in [0,1]$ is a confidence, and ${\ell }_i\in \mathcal{Y}$ is a class label. Define the boundary distance and mask IoU, as follows:

$$D(M_i,M_j)=\underset{p\in \partial M_i,q\in \partial M_j}{min}{\parallel p-q\parallel }_2,I(M_i,M_j)={\displaystyle \frac{|M_i\cap M_j|}{|M_i\cup M_j|}}.$$

(1)

Neighborhoods are pruned by the R-tree as

$$N\left(i\right)=\left\{j\ne i:\mathrm{dist}(b_i,b_j)\le \rho \right\},$$

(2)

where $\mathrm{dist}$ is the minimum $L_2$ box distance and $N\left(i\right)$ is retrieved in $O(logn+|N\left(i\right)\left|\right)$ time using an R-tree built over ${\left\{b_i\right\}}_{i=1}^n$. For each candidate pair $(i,j)\in N\left(i\right)$, an edge weight combines geometric overlap, proximity, and confidence, as follows:

$$w_{ij}={\beta }_1·{\left(1-\frac{D(M_i,M_j)}{{\tau }_d}\right)}_{+}+{\beta }_2·I(M_i,M_j)+{\beta }_3·min(s_i,s_j),w_{ij}\leftarrow 0\mathrm{if}{\ell }_i\ne {\ell }_j,$$

(3)

with ${\left(x\right)}_{+}=max(x,0)$ and coefficients ${\beta }_1,{\beta }_2,{\beta }_3\ge 0$. The weighted graph is $G=(V,E,W)$ with vertices $V=\{1,\dots ,n\}$, edges $E=\left\{\right(i,j):j\in N(i\left)\right\}$, and weights $W=\left\{w_{ij}\right\}$.

Global grouping is obtained via correlation clustering by minimizing

$$\underset{\{A_1,\dots ,A_r\}}{min}\sum _{(i,j)\in E}\left[\mathbf{1}\{i,j\mathrm{separated}\}{w}_{ij}+\lambda \mathbf{1}\{i,j\mathrm{merged}\}(1-w_{ij})\right],$$

(4)

where $\lambda >0$ controls the trade-off between over-merging and under-merging.

A common issue in mask merging is chained merging, where objects are grouped indirectly (e.g., A overlaps with B, B overlaps with C, but A and C are dissimilar). To avoid this, a pairwise validity constraint is enforced, as follows:

$$\forall k,\forall a,b\in A_k:{\mathcal{C}}_{\gamma }(o_a,o_b)=1,$$

(5)

with

$${\mathcal{C}}_{\gamma }(o_i,o_j)=\mathbf{1}\{{\ell }_i={\ell }_j\}\mathbf{1}\left\{\left(D(M_i,M_j)\le {\tau }_d\vee I(M_i,M_j)\ge {\tau }_i\right)\wedge w_{ij}\ge \gamma \right\},$$

(6)

where $\gamma$ is a threshold ensuring that all members of a cluster are mutually compatible. This constraint prevents weakly related instances from being linked through intermediates. Algorithm 1 outlines the proposed SMM, where the same class masks within radius $\rho$ are linked, and each edge weight blends spatial distance, overlap (IoU), and detection score.

Algorithm 1 Proposed Spatial Mask Merging

Require: Predictions ${\left\{o_i\right\}}_{i=1}^n$ with $(M_i,b_i,s_i,{\ell }_i)$; search radius $\rho$; thresholds ${\tau }_d,{\tau }_i,\gamma$; weights ${\beta }_1,{\beta }_2,{\beta }_3$; clustering penalty $\lambda$ Ensure: Merged instances $G_{\mathrm{out}}$ 1: $V\leftarrow \{1,\dots ,n\}$; build R -tree index R over $\left\{b_i\right\}$ 2: Initialize $E\leftarrow \varnothing$, weight map W                ▹${(·)}_{+}=max(·,0)$ 3: for $i=1$ to n do 4:     $N\leftarrow R.\mathtt{query}(b_i,\rho )$ 5:     for each $j\in N,j>i$ do 6:         if ${\ell }_i\ne {\ell }_j$ then 7:            $w_{ij}\leftarrow 0$; continue 8:         end if 9:         Compute $D_{ij},I_{ij}$ via (1) 10:         $w_{ij}\leftarrow {\beta }_1{\left(1-\frac{D_{ij}}{{\tau }_d}\right)}_{+}+{\beta }_2{I}_{ij}+{\beta }_{3}min(s_i,s_j)$ 11:         if $w_{ij}>0$ then 12:            $E\leftarrow E\cup \left\{\right(i,j\left)\right\}$; $W\left[(i,j)\right]\leftarrow w_{ij}$         ▹ undirected: $W\left[(j,i)\right]\leftarrow w_{ij}$ 13:         end if 14:     end for 15: end for 16: $G\leftarrow (V,E,W)$ 17: Cluster G via (4) under constraint (5), yielding partition $\mathcal{P}=\left\{A_k\right\}$ 18: For each $A\in \mathcal{P}$, compute $o_{\mathrm{new}}=\Phi \left(A\right)$ by mask fusion, box update, and score aggregation 19: return $G_{\mathrm{out}}=\{o_{\mathrm{new}}:A\in \mathcal{P}\}$

This method formulates mask deduplication as a global graph clustering problem, modeling all predicted instances as vertices in a weighted graph, which are then partitioned into clusters by optimizing a unified objective function. Unlike greedy heuristics that make local, stepwise decisions, the clustering approach evaluates the whole graph structure, ensuring globally consistent groupings and preventing indirect or chained merges. The detailed mathematical formulation of the merging function $\Phi \left(A\right)$ is provided in Appendix A.

3.3.1. Algorithm Parameters

Spatial thresholds, edge weighting factors, and clustering penalties govern the SMM algorithm. Their roles and typical ranges are summarized in

Table 1. Tunable hyperparameters for SMM.

Parameter	Description	Suggested Range
${\tau }_d$	Distance scale (in pixels) serving as a normalizing factor for spatial proximity in $w_{ij}$.	5–30
${\tau }_i$	IoU threshold serving as a normalizing factor for overlap contribution.	0.1–0.9
$\rho$	R-tree search radius (in pixels) for candidate edge generation.	10–50
${\beta }_1$	Weight of the distance contribution in $w_{ij}$.	0.2–0.4
${\beta }_2$	Weight of the IoU contribution in $w_{ij}$.	0.4–0.6
${\beta }_3$	Weight of the confidence contribution in $w_{ij}$.	0.1–0.3
$\lambda$	Correlation clustering penalty balancing over-merging vs. under-merging.	0.1–2.0
$\gamma$	Pairwise threshold enforcing the anti-chaining constraint in (5).	0.3–0.7

.

While ${\tau }_d,{\tau }_i,\rho$ primarily control candidate generation, the edge-weight coefficients ${\beta }_1,{\beta }_2,{\beta }_3$, penalty $\lambda$, and anti-chaining threshold $\gamma$ regulate the partitioning resolution. Optimal values are application-dependent and vary with object density, morphology, and whether inference is tiled or global.

3.3.2. Time and Space Complexity Analysis

The performance of the SMM algorithm is analyzed in terms of time and space complexity and compared against conventional deduplication methods. Let n denote the number of predicted objects before merging, m the average number of spatial neighbors retrieved per R-tree query, and k the average number of elements in a merge cluster, where typically $m,k\ll n$. Let $T_{\mathrm{comp}}$ denote the cost of computing edge weights $w_{ij}$ (distance, IoU, and score similarity) and $T_{\mathrm{merge}}$ the cost of applying the merging function $\Phi$ to k objects.

The algorithm begins with R-tree construction over n bounding boxes, requiring $\mathcal{O}(nlogn)$ time and $\mathcal{O}\left(n\right)$ space. Graph construction requires examining m neighbors per object, yielding

$$T_{\mathrm{graph}}=\mathcal{O}(n·m·T_{\mathrm{comp}}).$$

(7)

The correlation clustering step is NP-hard in the worst case; however, approximate solvers (LP relaxation with rounding or local heuristics) achieve near-linear complexity in the number of edges, i.e.,

$$T_{\mathrm{cluster}}\approx \tilde{\mathcal{O}}\left(\right|E\left|\right)=\tilde{\mathcal{O}}(n·m),$$

(8)

where $\tilde{\mathcal{O}}(·)$ hides logarithmic factors. The merging of final clusters adds $\mathcal{O}(n·T_{\mathrm{merge}})$. Thus, the overall expected runtime is

$$T_{\mathrm{SMM}}=\mathcal{O}(nlogn+n·m·T_{\mathrm{comp}}+n·T_{\mathrm{merge}}+T_{\mathrm{cluster}}).$$

(9)

Since m is bounded by local density and k is small, the runtime scales close to $\mathcal{O}(nlogn)$ in practice.

The space complexity is linear in the number of vertices and edges, as follows:

$$S_{\mathrm{SMM}}=\mathcal{O}(n+m),$$

(10)

dominated by the storage of masks and the R-tree index.

In contrast, NMS sorts predictions by confidence and performs pairwise IoU comparisons, requiring $\mathcal{O}(n^2·T_{\mathrm{IoU}})$ time in the worst case. NMM includes additional mask merges, yielding $\mathcal{O}(n^2·(T_{\mathrm{IoU}}+T_{\mathrm{merge}}))$. Both methods require $\mathcal{O}\left(n\right)$ space.

Table 2. Time and space complexity comparison for SMM, NMS, and NMM.

Algorithm	Time Complexity	Approx. Time	Space Complexity
SMM (graph)	$\mathcal{O}(nlogn+n·m·T_{\mathrm{comp}}+T_{\mathrm{cluster}})$	$\mathcal{O}(nlogn)$	$\mathcal{O}(n+m)$
NMS	$\mathcal{O}(n^2·T_{\mathrm{IoU}})$	$\mathcal{O}\left(n^2\right)$	$\mathcal{O}\left(n\right)$
NMM	$\mathcal{O}(n^2·(T_{\mathrm{IoU}}+T_{\mathrm{merge}}))$	$\mathcal{O}\left(n^2\right)$	$\mathcal{O}\left(n\right)$

summarizes the asymptotic complexity of each method.

The efficiency of SMM stems from avoiding exhaustive pairwise comparisons by restricting edges via R-tree queries, while the clustering formulation ensures global consistency and prevents chained merging. This enables scalability to dense detection scenarios where NMS and NMM suffer quadratic degradation. Performance of the proposed SMM-based instance segmentation pipeline was evaluated using standard detection and segmentation metrics, including accuracy, precision, recall, F1 score, and Panoptic Quality (PQ). These measures were selected to capture both recognition and mask-level agreement, and their formal definitions are provided in Appendix C.

4. Results

This section presents the results of our experiments, focusing on the evaluation of tile-based training, optimal overlap configurations in SAHI, and the performance of the SMM algorithm compared with traditional deduplication methods.

4.1. Segmentation Accuracy on the iSAID Dataset

To evaluate the segmentation accuracy of the YOLOv11s-seg model, validation on the iSAID dataset across 15 aerial object classes was performed, including both large and small targets. Key metrics include precision, recall, mean Average Precision at an IoU threshold of 0.50 (mAP50), the stricter mAP averaged from 0.50 to 0.95 (mAP50–95), and the F1 score. Detailed per-class and overall results are presented in

Table 3. Segmentation performance metrics per object class on the iSAID dataset.

Class ID	Precision	Recall	mAP50	mAP50–95	F1 Score
Small Vehicle (0)	0.694	0.385	0.468	0.186	0.495
Large Vehicle (1)	0.781	0.614	0.686	0.400	0.688
Ship (2)	0.942	0.856	0.912	0.584	0.897
Plane (3)	0.870	0.695	0.769	0.479	0.773
Helicopter (4)	0.920	0.841	0.897	0.531	0.879
Swimming Pool (5)	0.831	0.638	0.702	0.319	0.723
Roundabout (6)	0.825	0.707	0.757	0.362	0.762
Soccer Ball Field (7)	0.812	0.560	0.631	0.458	0.664
Harbor (8)	0.929	0.842	0.898	0.727	0.883
Basketball Court (9)	0.735	0.619	0.666	0.381	0.672
Ground Track Field (10)	0.759	0.671	0.724	0.559	0.712
Bridge (11)	0.538	0.224	0.234	0.115	0.316
Baseball Diamond (12)	0.775	0.408	0.496	0.325	0.532
Storage Tank (13)	0.721	0.583	0.642	0.430	0.645
Tennis Court (14)	0.793	0.716	0.712	0.336	0.752
Overall	0.795	0.624	0.680	0.413	0.699

.

The model performs exceptionally well on structured and well-defined objects such as tennis courts (mAP50–95 = 72.7%) and planes (mAP50–95 = 58.4%). For densely clustered or irregular objects like small vehicles, the model’s performance drops (mAP50–95 = 18.6%), which is consistent with known challenges in segmenting small and overlapping objects in aerial scenes. The bridge class, with few annotated instances and complex geometries, exhibits the lowest performance (mAP50–95 = 11.5%). Despite these outliers, the model achieves an overall segmentation performance of 68.0% mAP50 and 41.3% mAP50–95, along with an F1 score of 0.699, indicating strong generalization across diverse object scales and types.

Efficiency metrics are summarized in

Table 4. Computational efficiency metrics.

Metric	Value	Unit
Time per Epoch (avg.)	1.69	min
Epochs per Minute	0.59	epochs/min
Average Inference Time per Tile	0.9	ms
Pre-processing Time per Image	0.1	ms
Post-processing Time per Image	1.9	ms
GPU Memory Utilization (peak)	40.5	GB
Total Training Time (100 epochs)	2:48:39	h:m:s
Model Checkpoint Size	20.5	MB

. Inference is highly efficient, with an average per-tile time of 0.9 milliseconds. Pre-processing and post-processing contribute minimally to latency, at 0.1 ms and 1.9 ms, respectively. Peak GPU memory usage reached 40.5 GB on an NVIDIA A100-40GB, validating that tile-based training is feasible even on memory-constrained systems.

4.2. Impact of Overlap Ratio on Segmentation Accuracy and Efficiency

To evaluate the trade-off between segmentation quality and computational cost in tile-based inference, an analysis of the effect of varying tile overlap ratios using the SAHI framework was performed. The goal was to identify an overlap range that offers strong segmentation performance without incurring prohibitive inference time.

Figure 1 compares segmentation performance and computational cost across different overlap ratios. The left plot illustrates several segmentation metrics and provides a comprehensive view of both overall consistency and performance variation across the dataset. The right plot shows the average inference time per image, measured over 30 randomly selected samples.

The results show that segmentation performance improves as the overlap ratio increases from 0% to around 6%, where metrics such as F1 score and recall peak. Between 6% and 9%, these metrics plateau, indicating diminishing returns. Beyond 9%, segmentation performance begins to decline or stagnate, suggesting that additional overlap does not provide meaningful benefit. Average precision remains relatively stable across all overlaps, ranging between 0.53 and 0.59, while accuracy stays consistently high, reflecting robust background classification even in worst-case scenarios.

In contrast, inference time increases sharply with higher overlap ratios. For low overlap values (3–9%), average inference time remains under 5 s per image. However, as overlap exceeds 12%, redundancy from overlapping tiles significantly increases processing time, with inference exceeding 6.5 s per image at 18% and above. This highlights the trade-off between segmentation accuracy and computational efficiency, reinforcing the value of identifying an optimal overlap range.

Figure 2 presents a qualitative comparison for the image P0864. The left panel shows the ground truth (GT) instance annotations, while the right panel depicts the prediction results using a 9% tile overlap during inference. For this particular image, the average F1 score improved by approximately 10.4% when increasing the overlap ratio from 0% to 9%. This reflects a more accurate alignment between predicted and ground truth masks, in terms of both object coverage and classification.

Figure 3 shows segmentation results using 0% (blue) and 6% (red) tile overlap. The comparison highlights how even a small overlap improves object coverage, especially near tile boundaries, by recovering instances missed at 0%. Although higher overlaps offer marginal gains in some metrics, the increased computational cost does not justify their use in most scenarios. Therefore, an overlap ratio in the range of 6% to 9% as the optimal configuration is recommended, as this range achieves strong segmentation performance while maintaining reasonable inference times.

4.3. Evaluation of Proposed SMM on the iSAID Dataset

This section evaluates the performance of the proposed SMM algorithm on the challenging iSAID dataset and compares it against NMS, NMM, and Greedy NMM (GNMM) baselines. The iSAID dataset, being a large-scale instance segmentation benchmark with a significant proportion of small objects, presents unique challenges. Alongside segmentation quality, runtime performance was treated as a key evaluation metric, enabling a direct comparison of the computational efficiency of SMM with NMS, NMM, and GNMM. Our evaluation highlights both runtime and accuracy trade-offs across the methods.

The most pronounced gains with the SMM algorithm were observed in Panoptic Quality (PQ) and Precision, where SMM outperformed the next-best method, NMM, by 3.1% and 6.9%, respectively. The F1 score also increased by 3.2%, reflecting a better balance between false positives and false negatives. Accuracy improved by 2.6%, while recall exhibited a marginal gain of 0.06% compared with the runner-up algorithm. These consistent improvements highlight the effectiveness of the mask merging strategy in SMM, particularly in densely packed scenes with many small and overlapping objects, as characteristic of the iSAID dataset. While SMM exhibits higher execution time and memory usage compared with NMS, which is highly efficient but does not perform any merging, it demonstrates clear advantages over NMM and GNMM, offering the best trade-off between computational overhead and segmentation quality. In this context, SMM’s ability to consolidate overlapping masks leads to measurable accuracy gains, underscoring the value of mask merging for large-scale instance segmentation.

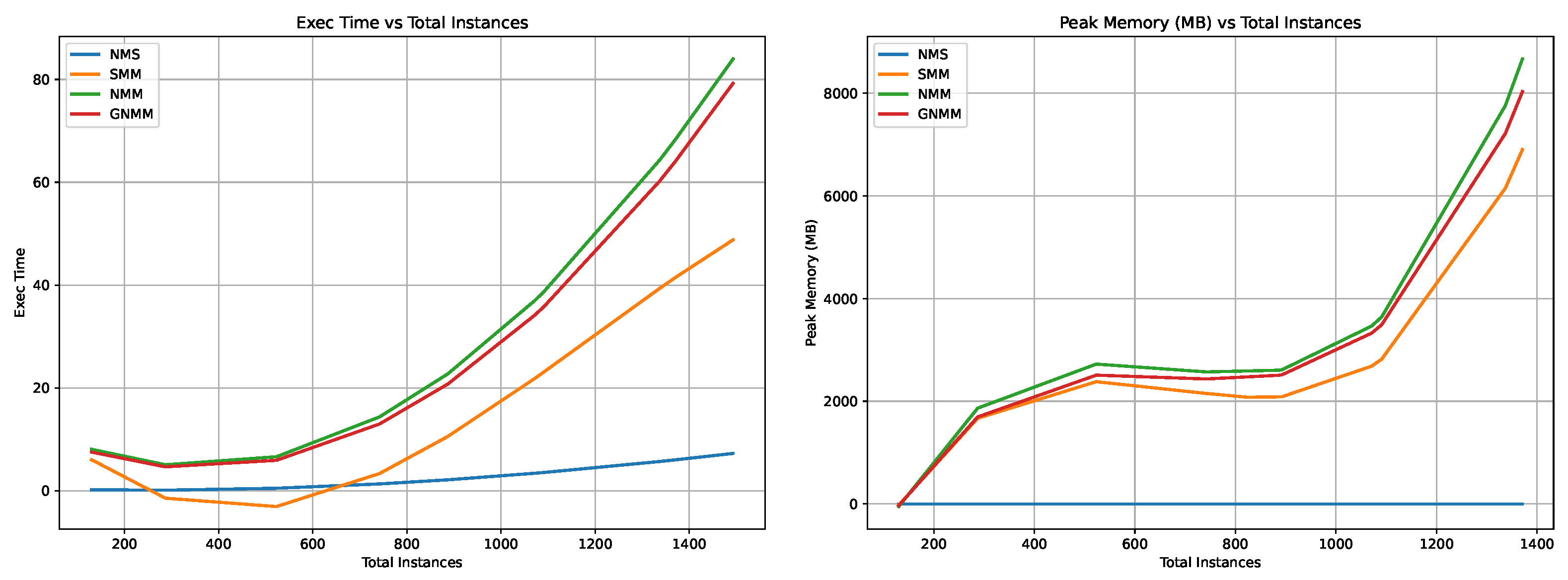
Figure 4 illustrates the computational efficiency of the evaluated methods across varying instance densities. NMS clearly dominates in both speed and memory, maintaining nearly flat trends regardless of instance count. SMM demonstrates favorable scalability, with execution time and memory growing moderately with the number of instances, peaking well below GNMM and NMM. GNMM incurs higher overhead than SMM but remains consistently lighter than NMM, which exhibits the steepest rise in both runtime and memory. These results validate SMM as a strong compromise between efficiency and segmentation refinement, particularly in dense scenes where NMS underperforms due to the absence of merging.

A Tree-structured Parzen Estimator (TPE), a Bayesian optimization algorithm over the predefined ranges in Table 1, was run on the iSAID validation split to maximize the mean F1 across prediction–GT pairs. Each trial evaluated the complete file set using GPU-accelerated, batched mask IoUs, while a median-based pruner stopped underperforming trials early. The best configuration achieved a mean F1 of 0.7585.

Table 5. SMM optimization on iSAID: best hyperparameters and their importance.

Parameter	Best Value	Importance
${\tau }_d$ (dist. scale)	6	0.001
${\tau }_i$ (IoU norm.)	0.859	0.064
$\rho$ (R-tree radius)	39	0.228
${\beta }_1$ (dist. wt.)	0.362	0.245
${\beta }_2$ (IoU wt.)	0.461	0.150
${\beta }_3$ (score wt.)	0.120	0.040
$\lambda$ (clustering penalty)	0.777	0.109
$\gamma$ (edge-accept. thr.)	0.476	0.162

reports the selected hyperparameters together with their post hoc relative importances from the hyperparameter tuning study.

The most influential factors are ${\beta }_1$, $\rho$, and $\gamma$, with ${\beta }_1$ highlighted as the most dominant parameter. This aligns with iSAID’s crowded, small-object scenes, where careful spatial gating and conservative clique formation reduce over-merging of adjacent instances. The high value for ${\tau }_i$ (0.859) favors merges only when overlap is substantial, again appropriate for densely packed vehicles and ships. $\lambda$ shows moderate impact, while ${\beta }_3$ (confidence weight) and ${\tau }_d$ have low importances. ${\tau }_d$ is largely subsumed by the neighborhood defined via $\rho$. All best values lie comfortably inside the suggested ranges, indicating that those ranges are well chosen. Subsequent tuning could focus on $\rho \in [30,40]$, ${\beta }_1\in [0.30$$0.37$], and ${\tau }_i\in [0.8,0.9]$ for iSAID-like distributions.

In summary, the overall improvements introduced by SMM are consistent and well targeted. The most significant gain is in PQ, where SMM outperforms the next-best method by 3.1% and exceeds NMS by more than 40%. Precision also improves by nearly 7% compared with the next-best baseline, highlighting SMM’s enhanced ability to suppress false positives. Alongside modest but steady gains in Accuracy, Recall, and F1 score, these results establish SMM as a robust and flexible merging strategy, balancing computational cost with notable gains in segmentation quality on the challenging iSAID benchmark.

5. Discussion

SMM models the entire set of predictions as a weighted graph, where edges encode similarity through a combination of boundary distance, IoU, and confidence. This global formulation allows clustering under a single optimization objective rather than local, stepwise merging. The inclusion of an anti-chaining constraint further ensures that all members of a cluster are mutually compatible, avoiding indirect merges where objects are linked only through intermediate connections. The favorable runtime scaling of SMM relative to NMM (Figure 4) is directly attributable to the use of R-tree spatial indexing, which reduces neighbor retrieval from quadratic to near-linear complexity. Graph clustering adds an optimization step, but approximate solvers operate in polynomial time and remain efficient in practice, validating the feasibility of this global approach without the need for an explicit ablation.

While SMM delivers measurable gains in segmentation quality, these improvements come with computational overheads. As shown in

Table 6. Quantitative comparison of SMM and baseline methods on iSAID dataset.

Metric (Unit)	NMS [5]	SMM	NMM [6]	GNMM [4]
Execution Time (s)	3.001	18.987	19.318	34.906
Peak Memory Usage (MB)	0.022	2265	3650	3425
Accuracy	0.5793	0.6123	0.5966	0.5954
Mean Error	195.35	187.49	195.28	195.18
Precision	0.7724	0.8548	0.7997	0.7983
Recall	0.6794	0.6811	0.6807	0.6797
F1 Score	0.7232	0.7585	0.7350	0.7340
PQ	0.4281	0.6044	0.5863	0.5459

, SMM incurs a longer execution time and higher peak memory usage than NMS, which remains the most efficient baseline. Overhead arises primarily from computing edge weights (distance and IoU) and performing clustering. Although R-tree indexing mitigates this by restricting unnecessary comparisons, memory usage increases with the number of candidate edges stored in dense scenes. Bold values in Table 6 indicate the best results across algorithms.

Another limitation is the sensitivity of SMM to its hyperparameters. While the Bayesian-guided search produced robust configurations on iSAID, transferring the same values to datasets with different object scales, densities, or score calibration may degrade performance. Moreover, the current formulation is frame-wise and does not enforce temporal consistency. Extending SMM with sequence-level constraints (e.g., track-aware clustering or temporal smoothness on edges) is a promising direction for future work.

The main advantages of SMM are as follows:

• Improved precision and Panoptic Quality, achieved by integrating multiple cues into a global clustering objective that reduces false positives and merges fragmented detections.
• Globally consistent merging through full-graph evaluation and anti-chaining constraints that prevent inconsistent groupings often introduced by greedy heuristics.
• Scalable candidate retrieval enabled by R-tree indexing, which ensures sub-quadratic edge construction and supports large-scale datasets.
• Robust tile-aware consolidation that resolves both redundant overlaps and fragmented boundaries, producing coherent outputs across tiled image regions.
• Compatibility with diverse pipelines, as SMM is model-agnostic and functions purely as a post-processing step for both tiled and non-tiled inference workflows.

Consequently, SMM can be applied to other domains where fragmented or duplicated detections occur. Applications include medical imaging (merging fragmented organ or lesion segmentations across overlapping fields of view), industrial inspection (consolidating detections of small defects on high-resolution product scans), and autonomous driving (resolving duplicated detections of pedestrians or vehicles across overlapping sensor fields).

This work builds on general principles of correlation clustering. Still, it adapts them uniquely to mask merging by defining task-specific edge weights, introducing an anti-chaining constraint and integrating R-tree acceleration and a dedicated merging function. These adaptations address a persistent gap in existing deduplication methods. By combining global optimization with efficient spatial indexing, SMM achieves consistent gains in precision, F1 score, and PQ, without prohibitive cost, and represents a practical and generalizable post-processing strategy.

6. Conclusions

This paper examines post-processing challenges in instance segmentation for high-resolution imagery, with a focus on handling objects across overlapping tiles. In this work, low-resolution tiling was deliberately adopted to reduce computational demands and enable training on memory-constrained hardware. We evaluated the feasibility of training instance segmentation models on such tiles and demonstrated that tile-based approaches not only reduce computational demands but also enhance local precision. Furthermore, an optimal overlap ratio in the range of 6% to 9% was identified when using slicing-aided hyper inference, balancing improved segmentation performance with computational efficiency. Notably, an overlap of just 6% yielded a 10.4% improvement in F1 score when compared with the non-overlapping baseline.

To reduce the adverse effects of tiling on detection redundancy, the SMM algorithm is introduced as an R-tree-accelerated graph clustering method that integrates pixel-level overlap, boundary proximity, and detection confidence, rather than relying solely on box IoU, and that is well suited for scenarios involving a high number of predicted instances. Comparative analysis against baseline algorithms demonstrated that SMM more effectively handles fragmented and adjacent instance detections, leading to consistent improvements in segmentation performance. Specifically, SMM achieved a 3.2% increase in F1 score, a nearly 7% gain in precision, and a 3.1% improvement in Panoptic Quality (PQ) over the next-best method.

Future research will be directed toward adaptive parameter tuning for the SMM algorithm, which will also be explored further to optimize deduplication behavior across additional datasets and segmentation models. Incorporating temporal consistency will be another direction, particularly for video or time-series segmentation. Additionally, integration with real-time inference pipelines should be investigated to facilitate faster and more scalable deployment in practical applications.