Finding the Number of Spanning Trees in Specific Graph Sequences Generated by a Johnson Skeleton Graph

Abstract

Using equivalent transformations, complicated circuits in physics that need numerous mathematical operations to analyze can be broken down into simpler equivalent circuits. It is also possible to determine the number of spanning trees—graph families in particular—using these adjustments and utilizing our knowledge of difference equations, electrically equivalent transformations, and weighted generating function rules. In this paper, we derive the exact formulas for the number of spanning trees of sequences of new graph families created by a Johnson skeleton graph 63 and a few of its related graphs. Lastly, a comparison is made between our graphs’ entropy and other graphs of average degree four.

1. Introduction

A spanning tree is a subgraph of an undirected, connected graph that has every vertex in the main graph $G$ but only employs the fewest required edges to construct a tree structure (i.e., no cycles). It essentially connects every node in a network without generating unnecessary loops.

These days, physics has a function τ where the number of spanning trees $\tau (G)$ is employed as an invariant to calculate the entropy of certain networks associated with physical processes [1,2,3]. In the discipline of network analysis [4,5,6], $\tau$ is also used in relation to other metrics that show how reliable a network is when represented by graph $G$. Furthermore, there are numerous mathematical uses for the number of spanning trees τ(G). The current fastest approach, for instance, employs the scaling factor of the coordinate system to embed a three-connected planar graph as a $3D$ polytope. There are many subgraphs within a fixed graph $G$. A graph with $\left|E(G)\right|$ edges can actually have $2^{\left|E(G)\right|}$ different subgraphs. Some of these subgraphs are obviously trees. We are especially interested in a subset of these trees known as spanning trees. The practice of counting the number of spanning trees $\tau (G)$ of a graph $G$ dates to 1842, when German mathematician Gustav Kirchhoff [7] established a connection between the number of spanning trees of a graph $G$ and the determinant of a particular submatrix that is connected to it as follows:

For a connected graph $G=(V,E)$ with $n$ vertices, the Kirchhoff matrix $L$ is an $n\times n$ characteristic matrix $L=D-A$, where $A$ is the adjacency matrix of $G$, and $D$ is the diagonal matrix of the degrees of $G$, such that $L=[a_{ij}]$ is defined as follows:

$$L=[a_{ij}]=\left\{\begin{array}{c}\mathit{deg}(v_i)ifi=j\\ -1if(v_i,v_j)\in E(G)\\ 0if(v_i,v_j)\notin E(G)\end{array}\right.$$

The number of spanning trees in a graph $G$ is equal to each co-factor of $L$.

For big graphs, this approach is not practical. Because of this, people have devised ways to overcome challenges and have focused more on obtaining clear and straightforward formulas for certain classes of graphs. See [8,9,10]. Daoud [11] developed this technique and derived the explicit formula for counting the number of spanning trees of cartesian and composition products of complete and complete bipartite and tripartite graphs as well as the explicit formula for counting the number of spanning trees of classes of pyramid graphs generated by wheel and gear graphs [12].

Feussner’s recursive formula [13,14], the fundamental combinatorial concept for counting $\tau (G)$ in a graph $G$, is very simple to understand. Let $e$ be any edge of an undirected simple graph $G$. Each spanning tree in $G$ can be divided into two sections: all spanning trees without $e$ as a tree edge are included in one section, and all spanning trees with $e$ as a tree edge are included in the other.

The subgraph $G-e$ that results from taking a graph $G$ and removing an edge $e$ while leaving all other edges and vertices intact is represented by the first section, which has the same number of spanning trees as the graph. In the second section, the graph $G.e$ (not a subgraph) is created by compressing the edge $e=\{u,v\}$ until the two vertices $u$ and $v$ meet, and it has the same number of spanning trees as the graph. This new vertex is identified by $uv.$

Compared to $G$, both $G-e$ and $G.e$ have fewer edges. Thus, it is possible to count the number of spanning trees in $G$ in a recursive manner. Assume now that $\mathcal{T}(G)$ represents the collection of all spanning trees of $G$; thus $\tau (G)=\left|\mathcal{T}(G)\right|.$ This set consequently broke down into two disjoint sets ${\mathcal{T}}_1 \mathrm{and} {\mathcal{T}}_2$, one of which ${\mathcal{T}}_1$ consists of trees containing selected edge $e\in E(G)$, while the other ${\mathcal{T}}_2$ consists of trees that do not contain $e$. It is evident that $\left|{\mathcal{T}}_1\right|=\left|\mathcal{T}(G.e)\right|$ since every edge of them matches a spanning tree of $G.e$ and $\left|{\mathcal{T}}_2\right|=\left|\mathcal{T}(G-e)\right|$, because every one of its edges is a spanning tree of $G-e$ and inversely, $\tau (G)=\tau (G-e)+\tau (G.e)$. In 1889, British mathematician A. Cayley [15] determined how many spanning trees there are in a full graph: $\tau (K_n)=n^{n-2}$. It was demonstrated using a variety of methods, including some combinatorial techniques [16]. The explicit formula for calculating the number of spanning trees of chain graphs and wheel-related graphs was derived by Daoud [17,18] using this technique.

2. Electrically Equivalent Transformations

Kirchhoff was inspired to study electrical networks through the idea that an edge-weighted graph, with weights representing the conductance of the corresponding edges, may be considered an electrical network. The effect conductance between two vertices $u,v$ can be expressed as the quotient of the (weighted) number of spanning trees and the (weighted) number of so-called thickets, spanning forests with exactly two components and the property that each component contains precisely one of the vertices $u,v$ [19,20]. Using this technique, Daoud [21] has determined the number of spanning trees for certain pyramid graphs based on Fritsch graphs.

A few simple changes and their effects on the number of spanning trees are listed below. Here, $\tau \left(G\right)$ indicates the weighted number of spanning trees $G$. Let $G$ be an edge-weighted graph and $\Gamma$ the electrically equivalent graph that goes with it.

• Parallel edges: The number of spanning trees in $\Gamma$, $\tau (\Gamma )$, stays the same when two parallel edges in $G$ with conductances $u$ and $v$ are combined into a single edge in $\Gamma$ with a conductance of $u+v$.
• Serial edges: The number of spanning trees in $\Gamma$, $\tau (\Gamma )$, can be computed as $(1/(u+v)$ multiplied by $\tau (G)$ if two serial edges in $G$ with conductances $u$ and $v$ are joined to form a single edge in $\Gamma$ with a conductance of $uv/(u+v)$.
• Δ-Y Transformation: The number of spanning trees in $\Gamma$, $\tau (\Gamma )$, can be calculated as $(\mathit{uv}+\mathit{vw}+\mathit{wu}{)}^2/uvw$ multiplied by $\tau (G)$, when a triangle in $G$ with conductances $u,v$ and $w$ is converted into an electrically equivalent star graph in $\Gamma$ with conductances $x=(\mathit{uv}+\mathit{vw}+wu)/u,y=(\mathit{uv}+\mathit{vw}+wu)/v$, and $z=(\mathit{uv}+\mathit{vw}+\mathit{wu})/w$.
• Y-Δ Transformation: The number of spanning trees in $\Gamma$, $\tau (\Gamma )$, can be calculated as $1/(u+v+w)$ multiplied by $\tau (G)$. when a star graph in $G$, with conductances $u,v$ and $w$, is converted into an electrically equivalent triangle in $\Gamma$ with conductances $x=vw/(u+v+w),y=uw/(u+v+w)$, and $z=uv/(u+v+w)$.

3. Main Results

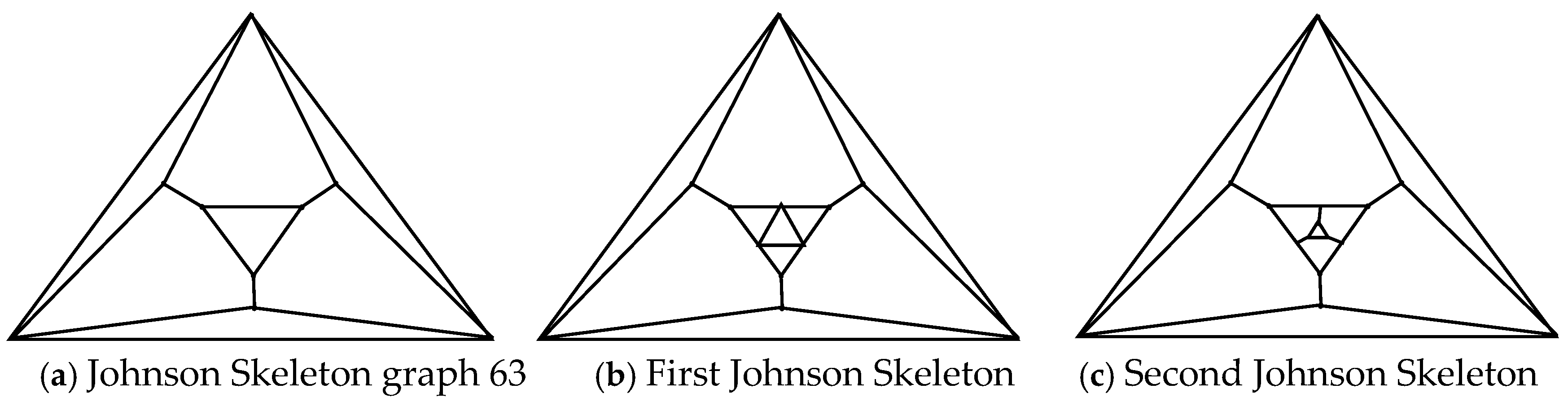
A Johnson graph is a specific kind of undirected graph that is defined using systems of sets. Two vertices (subsets) are close when they meet and contain $(k-1)$-elements. The $k -$ element subsets of an $n -$ element collection are the vertices of the Johnson graph $J(n,k)$. In other words, the Johnson graph $J(n,k)$ has vertices given by the k-subsets of $\{\mathrm{1,2},\dots ,n\}$, with two vertices connected if and only if their intersection has size $k-1$. The Johnson skeleton graph $63$ is a minimal unit-distance forbidden graph.

This study will identify the number of spanning trees in the graph sequences, $J{S}_n$, generated by the Johnson skeleton graph 63 and two related graph sequences, $R_{1}J{S}_n$ and $R_{2}J{S}_n$, generated by two graphs associated with Johnson skeleton graph 63; these are defined as follows:

The first Johnson-skeleton-related graph is a graph that is produced by replacing the internal triangle of Johnson skeleton graph 63 with a star (3,3)-gon graph. See Figure 1b.

The second Johnson-skeleton-related graph is a graph that is produced by replacing the internal triangle of Johnson skeleton graph 63 with another Johnson skeleton graph 63. See Figure 1c.

3.1. The Number of Spanning Trees in the Graph Sequence $J{S}_n$

The graph sequence $J{S}_1,J{S}_2,\dots ,J{S}_n$ is a recursive definition using the graphs $J{S}_2$ and $J{S}_1$ (triangle or $K_3$): A replica of $J{S}_2$ is used in place of the middle triangle of $J{S}_2$ to create the graph $J{S}_3$. The central triangle in the graph $J{S}_{n-1}$ is typically swapped out for $J{S}_2$ to make $J{S}_n$ as shown in Figure 2. $\left|V(J{S}_n)\right|=27n-24$ and $\left|E(J{S}_n)\right|=54n-51,n=\mathrm{1,2},\dots$ are the total vertices and edges of $J{S}_n$, respectively. According to this architecture in the large $n$ limit, the average degree of $J{S}_n$ is 4.

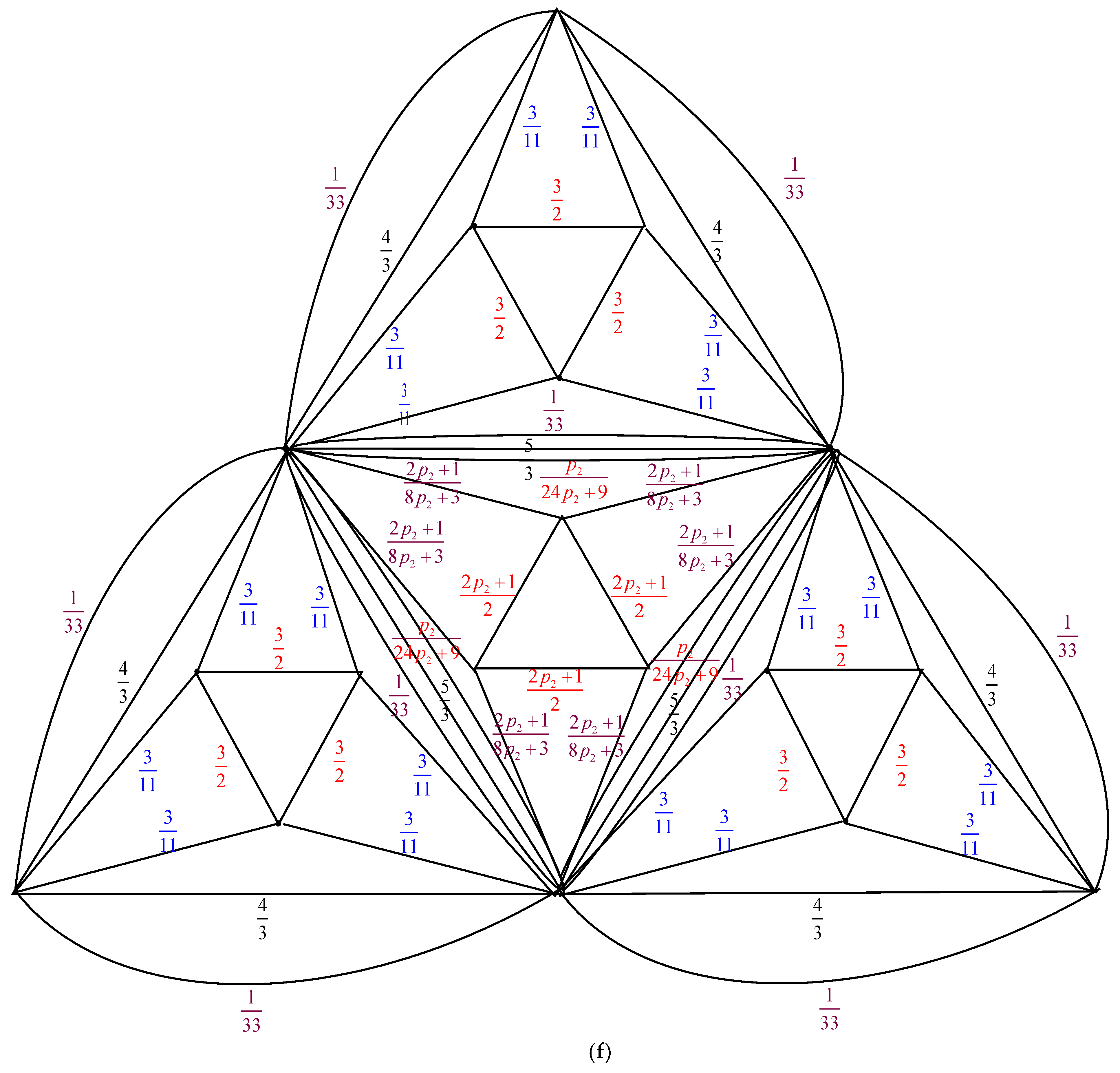
Theorem 1.

For $n\ge 1$, the number of spanning trees in the graph sequence $J{S}_n$ is determined by

$$3\times {\left(5984\right)}^{n-1}{\left({\displaystyle \frac{{\left(\frac{70841449+738172\sqrt{9210}}{34969}\right)}^{n-1}\left(19080+199\sqrt{9210}\right)-11\left(60-\sqrt{9210}\right)}{15{\left(\frac{70841449+738172\sqrt{9210}}{34969}\right)}^{n-1}\left(1349+14\sqrt{9210}\right)-1815}}\right)}^2$$

$${\left(\left({\displaystyle \frac{12463}{2}}+{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953+62\sqrt{9210}\right)}^{n-2}+\left({\displaystyle \frac{12463}{2}}-{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953-62\sqrt{9210}\right)}^{n-2}\right)}^2$$

Proof. 

We convert $J{S}_i$ to $J{S}_{i-1}$ using the electrically equivalent transformation. The process of change from $J{S}_2$ to $J{S}_1$ is depicted in Figure 3.

When the ten adjustments listed above are combined, we obtain

$$\tau (J{S}_2)={\displaystyle \frac{1}{9^{4}a}}\times 4^9\times {(3a+1)}^3\times {({\displaystyle \frac{11}{4}})}^9\times {({\displaystyle \frac{(9a+2)}{(3a+1)}})}^3\times {({\displaystyle \frac{18}{11}})}^3\times {\displaystyle \frac{18a}{(9a+2)}}\times {\displaystyle \frac{(99a+22)}{9(208a+45)}}\times {({\displaystyle \frac{930a+203}{99a+22}})}^3\times {\displaystyle \frac{306(208a+45)}{11(930a+203)}}\tau (J{S}_1)$$

Thus

$$\tau (J{S}_2)=5984(10230P_2+2233{)}^2 \tau (J{S}_1).$$

(1)

Further

$$\begin{gathered} \tau \left(J{S}_n\right)=\prod _{i=2}^{n}5984(10230P_i+2233{)}^2\tau (J{S}_1), \\ =3\times 5984^{n-1}{P}_1^2[ \prod _{i=2}^n(10230P_i+2233){]}^2 \end{gathered}$$

(2)

where $p_{i-1}={\displaystyle \frac{9673p_i+2108}{10230p_i+2233}},i=\mathrm{2,3},\dots ,n.$ The characteristic equation for this is like $10230r^2-7440r-2108=0$ with roots $r_1={\displaystyle \frac{60-\sqrt{9210}}{165}}$ and $r_2={\displaystyle \frac{60+\sqrt{9210}}{165}}$. When two roots are subtracted from both sides of $p_{i-1}={\displaystyle \frac{9673p_i+2108}{10230p_i+2233}}$, we get

$$p_{i-1}-{\displaystyle \frac{60-\sqrt{9210}}{165}}={\displaystyle \frac{9673p_i+2108}{10230p_i+2233}}-{\displaystyle \frac{60-\sqrt{9210}}{165}}=(5953+62\sqrt{9210}).{\displaystyle \frac{p_i-(\frac{60-\sqrt{9210}}{165})}{10230p_i+2233}}$$

(3)

$$p_{i-1}\hspace{0.17em}-{\displaystyle \frac{60+\sqrt{9210}}{165}}={\displaystyle \frac{9673\hspace{0.17em}{p}_i+2108}{10230\hspace{0.17em}{p}_i+2233}}-{\displaystyle \frac{60+\sqrt{9210}}{165}}=\hspace{0.17em}(5953-62\sqrt{9210})\hspace{0.17em}\hspace{0.17em}.\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{p_i\hspace{0.17em}-(\frac{60+\sqrt{9210}}{165})}{10230\hspace{0.17em}{p}_i\hspace{0.17em}+2233}}$$

(4)

Let $q_i={\displaystyle \frac{p_i-\frac{60-\sqrt{9210}}{165}}{p_i-\frac{60+\sqrt{9210}}{165}}}$. Then, by Equations (3) and (4), we get $q_{i-1}=({\displaystyle \frac{70841449+738172\sqrt{9210}}{34969}})q_i$ and $q_{i-1}=({\displaystyle \frac{70841449+738172\sqrt{9210}}{34969}}{)}^{n-i}{q}_n$. Therefore, $p_i={\displaystyle \frac{(\frac{70841449+73817\sqrt{9210}}{34969}{)}^{n-i}(\frac{60+\sqrt{9210}}{165})q_n-\frac{60-\sqrt{9210}}{165}}{(\frac{70841449+73817\sqrt{9210}}{34969}{)}^{n-i}{q}_n-1}}.$ Thus

$$p_1={\displaystyle \frac{(\frac{70841449+73817\sqrt{9210}}{34969}{)}^{n-1}(\frac{60+\sqrt{9210}}{165})q_n-\frac{60-\sqrt{9210}}{165}}{(\frac{70841449+73817\sqrt{9210}}{34969}{)}^{n-1}{q}_n-1}}.$$

(5)

Using the formula $p_{n-1}={\displaystyle \frac{9673p_n+2108}{10230x_n+2233}}$ and denoting the coefficients of $9673p_n+2108$ and $10230p_n+2233$ as ${\delta }_n$ and ${\sigma }_n$, we have

$$\begin{gathered} 10230p_n+2233={\delta }_0(9673p_n+2108)+{\sigma }_0(10230p_n+2233),10230p_{n-1}+2233 \\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{{\delta }_1(9673p_n+2108)+{\sigma }_1(10230p_n+2233)}{{\delta }_0(9673p_n+2108)+{\sigma }_0(10230p_n+2233)}},10230p_{n-2}+2233 \\ ={\displaystyle \frac{{\delta }_2(9673p_n+2108)+{\sigma }_2(10230p_n+2233)}{{\delta }_1(9673p_n+2108)+{\sigma }_1(10230p_n+2233)}}, \\ ⋮ \\ 10230p_{n-i}+2233={\displaystyle \frac{{\delta }_i(9673p_n+2108)+{\sigma }_i(10230p_n+2233)}{{\delta }_{i-1}(9673p_n+2108)+{\sigma }_{i-1}(10230p_n+2233)}}, \end{gathered}$$

(6)

$$\begin{gathered} 10230p_{n-(i+1)}+2233={\displaystyle \frac{{\delta }_{i+1}(9673p_n+2108)+{\sigma }_{i+1}(10230p_n+2233)}{{\delta }_i(9673p_n+2108)+{\sigma }_i(10230p_n+2233)}}, \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⋮ \\ 10230p_2+2233={\displaystyle \frac{{\delta }_{n-2}(9673p_n+2108)+{\sigma }_{n-2}(10230p_n+2233)}{{\delta }_{n-3}(9673p_n+2108)+{\sigma }_{n-3}(10230p_n+2233)}}, \end{gathered}$$

(7)

Thus, we get

$$\tau (J{S}_n)=3\times 5984^{n-1}{p}_1^2[{\delta }_{n-2}(9673p_n+2108)+{\sigma }_{n-2}(10230p_n+2233){]}^2$$

(8)

where ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=10230,{\sigma }_1=2233$. By the expression $p_{n-1}={\displaystyle \frac{9673p_n+2108}{10230p_n+2233}}$ and using Equations (6) and (7), we have

$${\delta }_{i+1}=26{\delta }_i-{\delta }_{i-1}; {\sigma }_{i+1}=26{\sigma }_i-{\sigma }_{i-1}$$

(9)

Equation (9) has a characteristic equation of $t^2-11906t+34969=0$ with roots $t_1=5953+62\sqrt{9210}$ and $t_2=5953-62\sqrt{9210}$. The general solutions of Equation (9) are ${\delta }_i=a_1{t}_1^i+a_2{t}_2^i; {\sigma }_i=b_1{t}_1^i+b_2{t}_2^i$. Using the initial conditions ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=10230,{\sigma }_1=2233$, yields

$$\begin{gathered} {\mathsf{\delta }}_{\mathrm{i}}={\displaystyle \frac{11\sqrt{9210}}{1228}}(5953+62\sqrt{9210}{)}^{\mathrm{i}}-{\displaystyle \frac{11\sqrt{9210}}{1228}}(5953-62\sqrt{9210}{)}^{\mathrm{i}}; \\ {\mathsf{\sigma }}_{\mathrm{i}}=({\displaystyle \frac{307-2\sqrt{9210}}{614}})(5953+62\sqrt{9210}{)}^{\mathrm{i}}+({\displaystyle \frac{307+2\sqrt{9210}}{614}})(5953-62\sqrt{9210}{)}^{\mathrm{i}} \end{gathered}$$

(10)

Should $p_n=1, J{S}_n$ is devoid of any electrically equivalent transformation. Entering (10) into Equation (8), we get

$$\tau \left(J{S}_n\right)=3\times {\left(5984\right)}^{n-1}{ p}_1^2{\left(\begin{array}{c}\left({\displaystyle \frac{12463}{2}}+{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953+62\sqrt{9210}\right)}^{n-2}+\\ \left({\displaystyle \frac{12463}{2}}-{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953-62\sqrt{9210}\right)}^{n-2}\end{array}\right)}^2,n\ge 2$$

(11)

When $n=1$, $\tau (J{S}_1)=3$, which satisfies Equation (11). Therefore, the number of spanning trees in the sequence of the graph $J{S}_n$ is given by

$$\tau \left(J{S}_n\right)=3\times {\left(5984\right)}^{n-1}{ p}_1^2{\left(\begin{array}{c}\left({\displaystyle \frac{12463}{2}}+{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953+62\sqrt{9210}\right)}^{n-2}+\\ \left({\displaystyle \frac{12463}{2}}-{\displaystyle \frac{79739\sqrt{\frac{15}{614}}}{2}}\right){\left(5953-62\sqrt{9210}\right)}^{n-2}\end{array}\right)}^2,n\ge 1$$

(12)

where

$$p_1={\displaystyle \frac{{(\frac{70841449+738172\sqrt{9210}}{34969})}^{n-1}(19080+199\sqrt{9210})-11(60-\sqrt{9210})}{15{(\frac{70841449+738172\sqrt{9210}}{34969})}^{n-1}(1349+14\sqrt{9210})-1815}},n\ge 1$$

(13)

Equation (13) is inserted into Equation (12), yielding the desired result. □

3.2. The Number of Spanning Trees in the Graph Sequence $R_{1}J{S}_n$

The graph sequence $R_{1}J{S}_1,R_{1}J{S}_2,\dots ,R_{1}J{S}_n$ is a recursive definition using the graphs $R_{1}J{S}_2$ and $R_{1}J{S}_1$ (triangle or $K_3$): A replica of $R_{1}J{S}_2$ is used in place of the middle triangle of $R_{1}J{S}_2$ to create the graph $R_{1}J{S}_3$. The central triangle in the graph $R_{1}J{S}_{n-1}$ is typically swapped out for $R_{1}J{S}_2$ to make $R_{1}J{S}_n$, as shown in Figure 4. $\left|V(R_{1}J{S}_n)\right|=39n-36$ and $\left|E(R_{1}J{S}_n)\right|=78n-75,n=\mathrm{1,2},\dots$ are the total vertices and edges of $R_{1}J{S}_n$, respectively. According to this architecture in the large $n$ limit, the average degree of $R_{1}J{S}_n$ is $4$.

Theorem 2.

For $n\ge 1$, the number of spanning trees in the sequence of the graph $R_{1}J{S}_n$ is given by $3\times {\left(9718272\right)}^{n-1}$

$${\left({\displaystyle \frac{{\left(\frac{11480479303+151532\sqrt{5739992547}}{494209}\right)}^{n-1}\left(1944411145+25706\sqrt{5739992547}\right)-1517\left(20488-\sqrt{5739992547}\right)}{{\left(\frac{11480479303+151532\sqrt{5739992547}}{494209}\right)}^{n-1}\left(2068303018+27223\sqrt{5739992547}\right)-154972169}}\right)}^2$$

$${\left(\begin{array}{c}\left({\displaystyle \frac{157435}{2}}+{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}\right){\left(75766+\sqrt{5739992547}\right)}^{n-2}+\\ \left({\displaystyle \frac{157435}{2}}-{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}\right){\left(75766-\sqrt{5739992547}\right)}^{n-2}\end{array}\right)}^2$$

Proof. 

We convert $R_{1}J{S}_i$ to $R_{1}J{S}_{i-1}$ using the electrically equivalent transformation. The process of change from $R_{1}J{S}_2$ to $R_{1}J{S}_1$ is depicted in Figure 5.

When the sixteen modifications mentioned above are combined, the result is:

$$\begin{array}{c}\tau \left(R_{1}J{S}_2\right)=3^{12}\times {\displaystyle \frac{a^3}{9^9{\left(2a+1\right)}^6}}\times 6^9\times {\left(4a+2\right)}^3\times {\left({\displaystyle \frac{11}{3}}\right)}^9\times {\left({\displaystyle \frac{8a+3}{3a}}\right)}^3\times \left({\displaystyle \frac{2^3}{3^{11}}}\right)\times {\displaystyle \frac{2}{\left(2a+1\right)}}\times {\left({\displaystyle \frac{111}{22}}\right)}^9\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\left({\displaystyle \frac{\left(2a+1\right)\left(24a+13\right)}{\left(16a+6\right)}}\right)}^3\times {\left({\displaystyle \frac{54}{37}}\right)}^3\times {\displaystyle \frac{\left(36a+18\right)}{\left(24a+13\right)}}\times {\displaystyle \frac{\left(888a+481\right)}{9\left(1849a+1000\right)}}\times {\left({\displaystyle \frac{8283a+4482}{\left(888a+481\right)}}\right)}^3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\displaystyle \frac{342\left(1849a+1000\right)}{37\left(2761a+1494\right)}}\tau (R_{1}J{S}_1)\hfill \end{array}$$

Thus, we have

$$\tau (R_{1}J{S}_2)=9718272(102157P_2+55278{)}^2\tau (R_{1}J{S}_1).$$

(14)

Further

$$\tau (R_{1}J{S}_n)=\prod _{i=2}^{n}9718272(102157P_i+55278{)}^2\tau (R_{1}J{S}_n)=3\times 718272^{n-1}{P}_1^2[ \prod _{i=2}^n(102157P_i+55278){]}^2$$

(15)

where $p_{i-1}={\displaystyle \frac{96254p_i+52079}{102127p_i+55278}},i=\mathrm{2,3},\dots ,n.$ Its characteristic equation is $102157{ r}^2-40976 r-52079=0$ with roots $r_1={\displaystyle \frac{20488-\sqrt{5739992547}}{102157}}$ and $r_2={\displaystyle \frac{20488-\sqrt{5739992547}}{102157}}$. Subtracting these two roots into both sides of $p_{i-1}={\displaystyle \frac{96254p_i+52079}{102127p_i+55278}}$, we get

$$\begin{gathered} p_{i-1}-{\displaystyle \frac{20488-\sqrt{5739992547}}{102157}}={\displaystyle \frac{96254p_i+52079}{102127p_i+55278}}-{\displaystyle \frac{20488-\sqrt{5739992547}}{102157}} \\ =(75766+\sqrt{5739992547}).{\displaystyle \frac{p_i-\frac{20488-\sqrt{5739992547}}{102157}}{102157(10257p_i+55278)}} \end{gathered}$$

(16)

$$\begin{gathered} p_{i-1}-{\displaystyle \frac{20488+\sqrt{5739992547}}{102157}}={\displaystyle \frac{96254p_i+52079}{102127p_i+55278}}-{\displaystyle \frac{20488+\sqrt{5739992547}}{102157}} \\ =(75766-\sqrt{5739992547}).{\displaystyle \frac{p_{i }-\frac{20488+\sqrt{5739992547}}{102157}}{102157(10257p_i+55278)}} \end{gathered}$$

(17)

Let $q_i={\displaystyle \frac{p_i-\frac{20488-\sqrt{5739992547}}{102157}}{p_i-\frac{20488+\sqrt{5739992547}}{102157}}}$. Then by Equations (16) and (17), we get $q_{i-1}=({\displaystyle \frac{11480479303+151532\sqrt{5739992547}}{494209}})q_i$ and $q_{i-1}=({\displaystyle \frac{11480479303+151532\sqrt{5739992547}}{494209}}{)}^{n-i}{q}_n$.

Therefore

$$p_i={\displaystyle \frac{(\frac{11480479303+151532\sqrt{5739992547}}{494209}{)}^{n-i}(\frac{20488+\sqrt{5739992547}}{102157})q_n-\frac{20488-\sqrt{5739992547}}{102157}}{(\frac{11480479303+151532\sqrt{5739992547}}{494209}{)}^{n-i}{q}_n-1}}$$

Thus

$$p_1={\displaystyle \frac{(\frac{11480479303+151532\sqrt{5739992547}}{494209}{)}^{n-1}(\frac{20488+\sqrt{5739992547}}{102157})q_n-\frac{20488-\sqrt{5739992547}}{102157}}{(\frac{11480479303+151532\sqrt{5739992547}}{494209}{)}^{n-1}{q}_n-1}}$$

(18)

Using the expression $p_{n-1}={\displaystyle \frac{96254p_n+52079}{102157x_n+55278}}$ and denoting the coefficients of $96254p_n+52079$ and $102157p_n+55278$ as ${\delta }_n$ and ${\sigma }_n$, we have

$$\begin{array}{l}102157p_n+55278={\delta }_0\hspace{0.17em}(96254p_n+52079)+{\sigma }_0\hspace{0.17em}(102157p_n+55278),\\ 102157p_{n-1}+55278={\displaystyle \frac{{\delta }_1(96254p_n+52079)+{\sigma }_1(102157p_n+55278)}{{\delta }_0\hspace{0.17em}(96254p_n+52079)+{\sigma }_0\hspace{0.17em}(102157p_n+55278)}},\\ 102157p_{n-2}+55278={\displaystyle \frac{{\delta }_2(96254p_n+52079)+{\sigma }_2(102157p_n+55278)}{{\delta }_1\hspace{0.17em}(96254p_n+52079)+{\sigma }_1\hspace{0.17em}(102157p_n+55278)}},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⋮\end{array}$$

$$102157p_{n-i}+55278={\displaystyle \frac{{\delta }_i(96254p_n+52079)+{\sigma }_i(102157p_n+55278)}{{\delta }_{i-1}(96254p_n+52079)+{\sigma }_{i-1}(102157p_n+55278)}},$$

(19)

$$\begin{gathered} 102157p_{n-(i+1)}+55278={\displaystyle \frac{{\delta }_{i+1}(96254p_n+52079)+{\sigma }_{i+1}(102157p_n+55278)}{{\delta }_i(96254p_n+52079)+{\sigma }_i(102157p_n+55278)}}, \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⋮ \\ 102157p_2+55278={\displaystyle \frac{{\delta }_{n-2}(96254p_n+52079)+{\sigma }_{n-2}(102157p_n+55278)}{{\delta }_{n-3}(96254p_n+52079)+{\sigma }_{n-3}(102157p_n+55278)}}, \end{gathered}$$

(20)

Thus, we obtain

$$\tau (R_{1}J{S}_n)=3\times 9718272^{n-1}{p}_1^2[{\delta }_{n-2}(96254p_n+52079)+{\sigma }_{n-2}(102157p_n+55278){]}^2$$

(21)

where ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=102157,{\sigma }_1=55278$. By the expression $p_{n-1}={\displaystyle \frac{96254p_n+52079}{102157p_n+55278}}$ and using Equations (19) and (20), we have

$${\delta }_{i+1}=151532{\delta }_i-494209{\delta }_{i-1};{\sigma }_{i+1}=151532{\sigma }_i-494209{\sigma }_{i-1}$$

(22)

The characteristic equation of Equation (22) is $t^2-151532t+494209=0$ with roots $t_1=75766+\sqrt{5739992547}$ and $t_2=75766-\sqrt{5739992547}$. The general solutions of Equation (22) are ${\delta }_i=a_1{t}_1^i+a_2{t}_2^i; {\sigma }_i=b_1{t}_1^i+b_2{t}_2^i$. Using the initial conditions ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=102157,{\sigma }_1=55278$, yields

$$\begin{gathered} {\delta }_i={\displaystyle \frac{102157\sqrt{5739992547}}{11479985094}}(75766+\sqrt{5739992547}{)}^i-{\displaystyle \frac{102157\sqrt{5739992547}}{11479985094}}(75766-\sqrt{5739992547}{)}^i; \\ {\sigma }_i=({\displaystyle \frac{5739992547-20488\sqrt{5739992547}}{11479985094}})(75766+\sqrt{5739992547}{)}^i+({\displaystyle \frac{5739992547+20488\sqrt{5739992547}}{11479985094}})(75766- \\ \sqrt{5739992547}{)}^i \end{gathered}$$

(23)

If $p_n=1$, it means that $R_{1}J{S}_n$ is without any electrically equivalent transformation. Plugging Equation (23) into Equation (21), we have

$$\tau \left(R_{1}J{S}_n\right)=3\times {(9718272)}^{n-1}{ p}_1^2{\left(\begin{array}{c}({\displaystyle \frac{157435}{2}}+{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}){(75766+\sqrt{5739992547})}^{n-2}+\\ ({\displaystyle \frac{157435}{2}}-{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}){(75766-\sqrt{5739992547})}^{n-2}\end{array}\right)}^2,n\ge 2$$

(24)

When $n=1$, $\tau (R_{1}J{S}_1)=3$, which satisfies Equation (24). Therefore, the number of spanning trees in the sequence of the graph $R_{1}J{S}_n$ is given by

$$\left(R_{1}J{S}_n\right)=3\times {(9718272)}^{n-1}{ p}_1^2{\left(\begin{array}{c}({\displaystyle \frac{157435}{2}}+{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}){(75766+\sqrt{5739992547})}^{n-2}+\\ ({\displaystyle \frac{157435}{2}}-{\displaystyle \frac{3975908667\sqrt{\frac{3}{1913330849}}}{2}}){(75766-\sqrt{5739992547})}^{n-2}\end{array}\right)}^2,n\ge 1$$

(25)

where

$$p_1={\displaystyle \frac{{(\frac{11480479303+151532\sqrt{5739992547}}{494209})}^{n-1}(1944411145+25706\sqrt{5739992547})-1517(20488-\sqrt{5739992547})}{{(\frac{11480479303+151532\sqrt{5739992547}}{494209})}^{n-1}(2068303018+27223\sqrt{5739992547})-154972169}}, n\ge 1$$

(26)

Equation (26) is inserted into Equation (25), yielding the desired outcome. □

3.3. The Number of Spanning Trees in the Graph Sequence $R_{2}J{S}_n$

The graph sequence $R_{2}J{S}_1,R_{2}J{S}_2,\dots ,R_{2}J{S}_n$ is a recursive definition using the graphs $R_{2}J{S}_2$ and $R_{2}J{S}_1$ (triangle or $K_3$): A replica of $R_{2}J{S}_2$ is used in place of the middle triangle of $R_{2}J{S}_2$ to create the graph $R_{2}J{S}_3$. The central triangle in the graph $R_{2}J{S}_{n-1}$ is typically swapped out for $R_{2}J{S}_2$ to make $R_{2}J{S}_n$, as shown in Figure 6. $\left|V( R_{2}J{S}_n)\right|=51n-48$ and $\left|E( R_{2}J{S}_n)\right|=90n-87,n=\mathrm{1,2},\dots$ are the total vertices and edges of $R_{2}J{S}_n$, respectively. According to this architecture in the large $n$ limit, the average degree of $R_{2}J{S}_n$ is $3.53$.

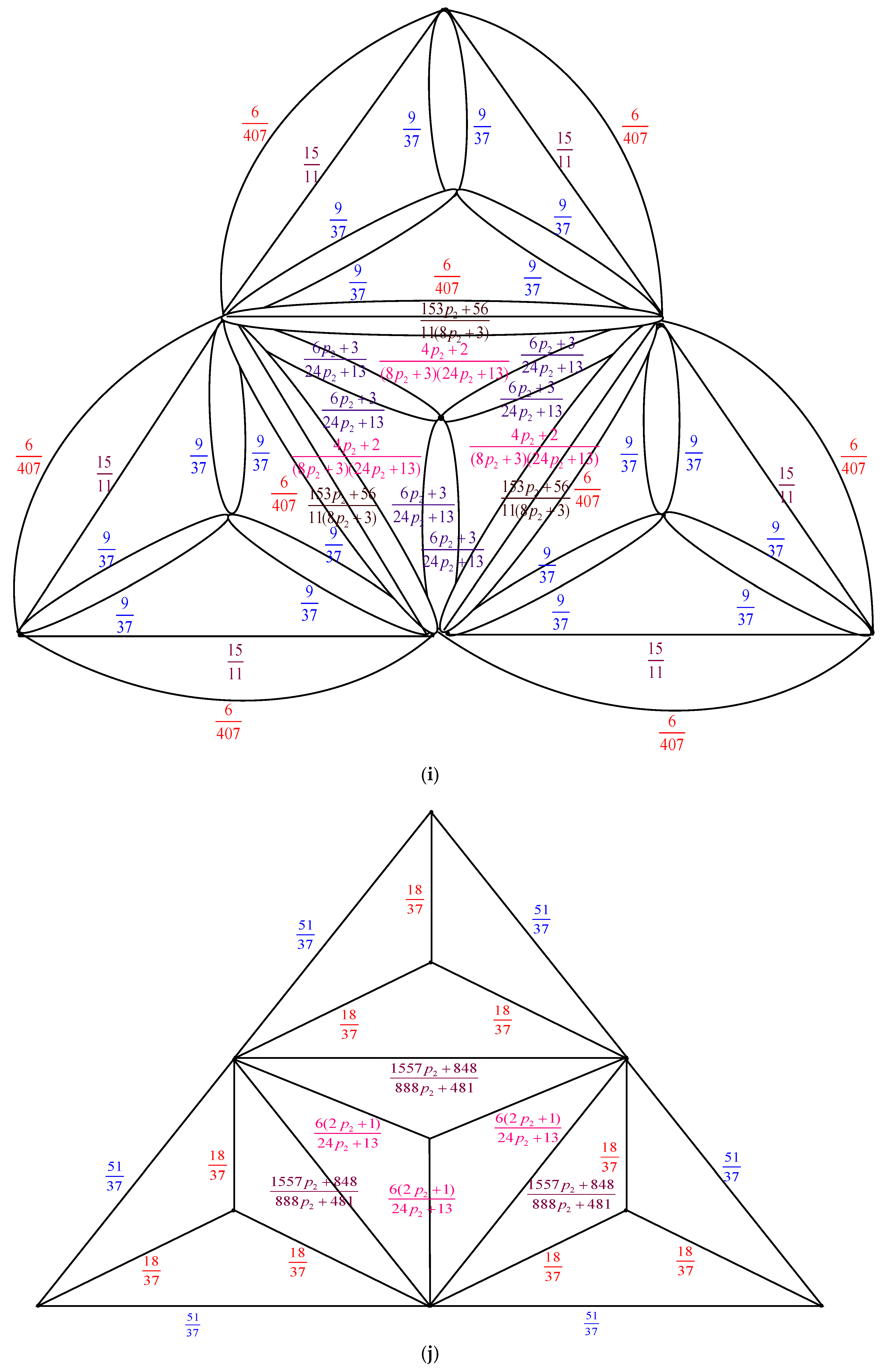
Theorem 3.

For $n\ge 1$, the number of spanning trees in the graph sequence $R_{2}J{S}_n$ is given by

$$3\times {\left(40974336\right)}^{n-1}\times {\left({\displaystyle \frac{{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592})}^{n-1}\times \frac{1748546196125+120105233\sqrt{212385577}}{180183255712}-\frac{830867-89\sqrt{212385577}}{2260088}}{{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592})}^{n-1}(\frac{1862489411129+127200669\sqrt{212385577}}{180183255712})-1}}\right)}^2$$

$${\left(\begin{array}{c}(681568+{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051+89\sqrt{212385577}}{2}})}^{n-2}+\\ (681568-{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051-89\sqrt{212385577}}{2}})}^{n-2}\end{array}\right)}^2$$

Proof. 

We convert $R_{2}J{S}_i$ to $R_{2}J{S}_{i-1}$ using the electrically equivalent transformation. The process of change from $R_{2}J{S}_2$ to $R_{2}J{S}_1$ is depicted in Figure 7.

When the seventeen modifications mentioned above are combined, the result is:

$$\begin{array}{c}\tau (R_{2}J{S}_2)=[{\displaystyle \frac{1}{9^{4}a}}\times {(4)}^9\times {(3a+1)}^3\times {({\displaystyle \frac{11}{4}})}^9\times {({\displaystyle \frac{9a+2}{3a+1}})}^3\times {({\displaystyle \frac{18}{11}})}^3\times ({\displaystyle \frac{18a}{9a+2}})\times {\displaystyle \frac{{11}^3}{9^4\times 6^3}}\times ({\displaystyle \frac{9a+2}{5a+1}})\times {({\displaystyle \frac{29}{11}})}^9\\ \times {({\displaystyle \frac{24a+5}{9a+2}})}^3\times {({\displaystyle \frac{76}{29}})}^9\times {({\displaystyle \frac{13+63a}{24a+5}})}^3\times {({\displaystyle \frac{27}{19}})}^3\times ({\displaystyle \frac{6(15a+3)}{63a+13}})\times {\displaystyle \frac{1}{9}}({\displaystyle \frac{4788a+988}{9955a+2053}})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \times {({\displaystyle \frac{44607a+9201}{76(63a+13)}})}^3\times ({\displaystyle \frac{351(9955a+2053)}{38(14869a+3067)}})]\tau (R_{2}J{S}_1)\hfill \end{array}$$

Thus, we have

$$\tau (R_{2}J{S}_2)=40974336(1130044P_2+233092{)}^2\tau (R_{2}J{S}_1).$$

(27)

Further

$$\tau (R_{2}J{S}_n)=\prod _{i=2}^{n}40974336(1130044P_i+233092{)}^2\tau (R_{2}J{S}_1)=3\times 40974336^{n-1}{P}_1^2[\prod _{i=2}^n(1130044P_i+233092){]}^2,$$

(28)

where $p_{i-1}={\displaystyle \frac{1063959p_i+219453}{1130044p_i+233092}},i=\mathrm{2,3},\dots ,n.$ Its characteristic equation is $1130044r^2-830867r-219453=0$ with roots are $r_1={\displaystyle \frac{830867-89\sqrt{212385577}}{22690088}}$ and $r_2={\displaystyle \frac{830867+89\sqrt{212385577}}{2260088}}$. Subtracting these two roots into both sides of $p_{i-1}={\displaystyle \frac{1063959p_i+219453}{1130044p_i+233092}}$, we get

$$\begin{gathered} p_{i-1}-{\displaystyle \frac{830867-89\sqrt{212385577}}{2260088}}={\displaystyle \frac{1063959p_i+219453}{1130044p_i+233092}}-{\displaystyle \frac{830867-89\sqrt{212385577}}{2260088}} \\ =(1297051+89\sqrt{212385577}).{\displaystyle \frac{p_i-\frac{830867-89\sqrt{212385577}}{2260088}}{2(1130044p_i+233092)}} \end{gathered}$$

(29)

$$\begin{gathered} p_{i-1}-{\displaystyle \frac{830867+89\sqrt{212385577}}{2260088}}={\displaystyle \frac{1063959p_i+219453}{1130044p_i+233092}}-{\displaystyle \frac{830867+89\sqrt{212385577}}{2260088}} \\ =(1297051-89\sqrt{212385577}).{\displaystyle \frac{p_i-\frac{830867+89\sqrt{212385577}}{2260088}}{2(1130044p_i+233092)}} \end{gathered}$$

(30)

Let $q_i={\displaystyle \frac{p_i-\frac{830867-89\sqrt{212385577}}{2260088}}{p_i-\frac{830867+89\sqrt{212385577}}{2260088}}}$. Then, by Equations (29) and (30), we get

$$q_{i-1}=({\displaystyle \frac{1682323726009+115437539\sqrt{212385577}}{17570592}})q_i$$

And

$$q_{i-1}=({\displaystyle \frac{1682323726009+115437539\sqrt{212385577}}{17570592}}{)}^{n-i}{q}_n$$

Therefore

$$p_i={\displaystyle \frac{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592}{)}^{n-i}(\frac{830867+89\sqrt{212385577}}{2260088})q_n-\frac{830867-89\sqrt{212385577}}{2260088}}{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592}{)}^{n-i} q_n-1}}.$$

Thus

$$p_1={\displaystyle \frac{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592}{)}^{n-1}(\frac{830867+89\sqrt{212385577}}{2260088}){ q}_n-\frac{830867-89\sqrt{212385577}}{2260088}}{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592}{)}^{n-1} q_n-1}}$$

(31)

Using the expression $p_{i-1}={\displaystyle \frac{1063959p_i+219453}{1130044p_i+233092}}$ and denoting the coefficients of $1063959p_n+219453$ and $1130044p_n+233092$ as ${\delta }_n$ and ${\sigma }_n$, we have

$$\begin{array}{c}1130044p_n+233092={\delta }_0\left(1063959p_n+219453\right)+{\sigma }_0\left(1130044p_n+233092\right),1130044p_{n-1}+233092\\ ={\displaystyle \frac{{\delta }_1\left(1063959p_n+219453\right)+{\sigma }_1\left(1130044p_n+233092\right)}{{\delta }_0\left(1063959p_n+219453\right)+{\sigma }_0\left(1130044p_n+233092\right)}},1130044p_{n-2}+233092\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{{\delta }_2\left(1063959p_n+219453\right)+{\sigma }_2\left(1130044p_n+233092\right)}{{\delta }_1\left(1063959p_n+219453\right)+{\sigma }_1\left(1130044p_n+233092\right)}},\hfill \\ ⋮\\ 1130044p_{n-i}+233092={\displaystyle \frac{{\delta }_i(1063959p_n+219453)+{\sigma }_i(1130044p_n+233092)}{{\delta }_{i-1}(1063959p_n+219453)+{\sigma }_{i-1}(1130044p_n+233092)}},\end{array}$$

(32)

$$\begin{gathered} 1130044p_{n-(i+1)}+233092={\displaystyle \frac{{\delta }_{i+1}(1063959p_n+219453)+{\sigma }_{i+1}(1130044p_n+233092)}{{\delta }_i(1063959p_n+219453)+{\sigma }_i(1130044p_n+233092)}}, \\ ⋮ \\ 1130044p_2+233092={\displaystyle \frac{{\delta }_{n-2}(1063959p_n+219453)+{\sigma }_{n-2}(1130044p_n+233092)}{{\delta }_{n-3}(1063959p_n+219453)+{\sigma }_{n-3}(1130044p_n+233092)}}, \end{gathered}$$

(33)

Thus, we obtain

$$\tau \left(R_{2}J{S}_n\right)=3\times 40974336^{n-1}{p}_1^2\times [{\delta }_{n-2}(1063959p_n+219453)+{\sigma }_{n-2}(1130044p_n+233092){]}^2$$

(34)

where ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=1130044,{\sigma }_1=233092$. By the expression $p_{n-1}={\displaystyle \frac{1063959p_n+219453}{1130044p_n+233092}}$ and using Equations (32) and (33), we have

$${\delta }_{i+1}=1297051{\delta }_i-8785296{\delta }_{i-1};{\sigma }_{i+1}=1297051{\sigma }_i-8785296{\sigma }_{i-1}$$

(35)

The characteristic equation of Equation (35) is $t^2-1297051t+8785296=0$ with roots $t_1={\displaystyle \frac{1297051+89\sqrt{212385577}}{2}}$ and $t_2={\displaystyle \frac{1297051-89\sqrt{212385577}}{2}}$. The general solutions of Equation (35) are ${\delta }_i=a_1{t}_1^i+a_2{t}_2^i;{\sigma }_i=b_1{t}_1^i+b_2{t}_2^i$. Using the initial conditions ${\delta }_0=0,{\sigma }_0=1$ and ${\delta }_1=1130044,{\sigma }_1=233092$, yields

$$\begin{array}{c}{\delta }_i\hfill \\ ={\displaystyle \frac{1130044\sqrt{212385577}}{18902316353}}({\displaystyle \frac{1297051+89\sqrt{212385577}}{2}}{)}^i\hfill \\ -{\displaystyle \frac{1130044\sqrt{212385577}}{18902316353}}({\displaystyle \frac{1297051-89\sqrt{212385577}}{2}}{)}^i;{\sigma }_i\hfill \\ =({\displaystyle \frac{18902316353-830867\sqrt{212385577}}{37804632706}})({\displaystyle \frac{1297051+89\sqrt{212385577}}{2}}{)}^i\hfill \\ +({\displaystyle \frac{18902316353+830867\sqrt{212385577}}{37804632706}})({\displaystyle \frac{1297051-89\sqrt{212385577}}{2}}{)}^i\hfill \end{array}$$

(36)

If $p_n=1$, it means that $R_{2}J{S}_n$ is without any electrically equivalent transformation. Plugging Equation (36) into Equation (34), we have

$$\begin{array}{c}\tau \left(R_{2}J{S}_n\right)\hfill \\ =3\times {\left(40974336\right)}^{n-1}{ p}_1^2\hfill \\ \times {\left(\begin{array}{c}(681568+{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051+89\sqrt{212385577}}{2}})}^{n-2}+\\ (681568-{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051-89\sqrt{212385577}}{2}})}^{n-2}\end{array}\right)}^2,n\ge 2\hfill \end{array}$$

(37)

When $n=1$, $\tau (R_{2}J{S}_1)=3$, which satisfies Equation (37). Therefore, the number of spanning trees in the sequence of the graph $R_{2}J{S}_n$ is given by

$$\mathsf{\tau }\left({\mathrm{R}}_2\mathrm{J}{\mathrm{S}}_{\mathrm{n}}\right)=3\times {\left(40974336\right)}^{\mathrm{n}-1}{\mathrm{p}}_1^2\times {\left(\begin{array}{c}(681568+{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051+89\sqrt{212385577}}{2}})}^{\mathrm{n}-2}+\\ (681568-{\displaystyle \frac{884019670672}{89\sqrt{212385577}}}){({\displaystyle \frac{1297051-89\sqrt{212385577}}{2}})}^{\mathrm{n}-2}\end{array}\right)}^2,\mathrm{n}\ge 1$$

(38)

where

$$p_1={\displaystyle \frac{{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592})}^{n-1}\times \frac{1748546196125+120105233\sqrt{212385577}}{180183255712}-\frac{830867-89\sqrt{212385577}}{2260088}}{{(\frac{1682323726009+115437539\sqrt{212385577}}{17570592})}^{n-1}(\frac{1862489411129+127200669\sqrt{212385577}}{180183255712})-1}}n\ge 1$$

(39)

Equation (39) can be inserted into Equation (38), yielding the desired result. □

4. Numerical Results

The values of the number of spanning trees in the sequence graphs $J{S}_n$, $R_{1}J{S}_n$, and $R_{2}J{S}_n$ are shown in the following

Table 1. Some values of the sequence graph $J{S}_n$.

$\mathit{n}$	$\mathit{\tau }(\mathit{J}{\mathit{S}}_{\mathit{n}})$
$1$	$3$
$2$	$2491593283872$
$3$	$2112437751486969285553152$
$4$	$1790988962651356816536555493874761728$
$5$	$1518454906483793748865840366762786491366191923200$

,

Table 2. Some values of the sequence graph $R_{1}J{S}_n$.

$\mathit{n}$	$\mathit{\tau }({\mathit{R}}_1\mathit{J}{\mathit{S}}_{\mathit{n}})$
$1$	$3$
$2$	$641484054515879424$
$3$	$143141158665083478581380003174023168$
$4$	$31940638527102636925754646727860195059034384242835456$
$5$	$7127260943349184929722120116724599408515777828964115381942103696211968$

and

Table 3. Some values of the sequence graph $R_{2}J{S}_n$.

$\mathit{n}$	$\mathit{\tau }({\mathit{R}}_2\mathit{J}{\mathit{S}}_{\mathit{n}})$
$1$	$3$
$2$	$202472185401828605952$
$3$	$13956830898768814530639892676989396451328$
$4$	$962073629817096776737016091553641615759689294887929803440128$
$5$	$66317753357005266372021022857195352821313530548303482328825760901236213921349632$

:

5. Spanning Tree Entropy

Once we have exact formulas for the number of spanning trees of the three sequence graphs $J{S}_n$, $R_{1}J{S}_n$, and $R_{2}J{S}_n$, we can compute the spanning tree entropy Z, a finite number, and an interesting metric defining the network topology. In [10,22], this is explained as follows: Regarding graph $G$,

$$Z(G)=\underset{n\to \infty }{lim}{\displaystyle \frac{\mathit{ln}\tau (G)}{\left|V(G)\right|}}.$$

(40)

$$\begin{gathered} Z\left(J{S}_n\right)={\displaystyle \frac{1}{27}}\left( \mathrm{l}\mathrm{n}\left[5984\right]+2\mathrm{l}\mathrm{n}\left[5953+62\sqrt{9210}\right] \right)=1.01726, \\ Z\left(R_{1}J{S}_n\right)={\displaystyle \frac{1}{39}}\left( \mathrm{l}\mathrm{n}\left[9718272\right]+2\mathrm{l}\mathrm{n}\left[75766+\sqrt{5739992547}\right] \right)=1.02427, \\ Z\left(R_{2}J{S}_n\right)={\displaystyle \frac{1}{51}}( \mathrm{l}\mathrm{n}[54618462093312]+2\mathrm{l}\mathrm{n}\left[1297051+89\sqrt{212385577}\right] )=1.19949. \end{gathered}$$

We now compare our sequence graphs’ entropy values to those of other graphs. It is evident that the $R_{2}J{S}_n$ graph has a higher entropy than the other two graphs, whereas the $J{S}_n$ graph has a lower entropy. Furthermore, the entropy of the two-dimensional Sierpinski gasket [23] and the fractal scale free lattice [20] both have entropies of 1.166 and 1.040 and are of the same average degree 4, respectively, while the entropy of the $R_{2}J{S}_n$ graph is greater than that of the fractal scale free lattice and lower than that of the two dimensional Sierpinski gasket.

6. Conclusions

In this study, we used electrically equivalent transformations to determine the number of spanning trees of sequence graphs produced from the Johnson skeleton graph and other related graphs. This technique’s strength is its ability to avoid the laborious computation of Laplacian spectra, which is a requirement for a general approach to spanning tree determination. Furthermore, our findings indicate a relationship between the entropy and the graph’s average degree.