Probing Chirality of the Quantum Hall Effect via the Landauer–Büttiker Formalism with Two Current Sources
Abstract
1. Introduction
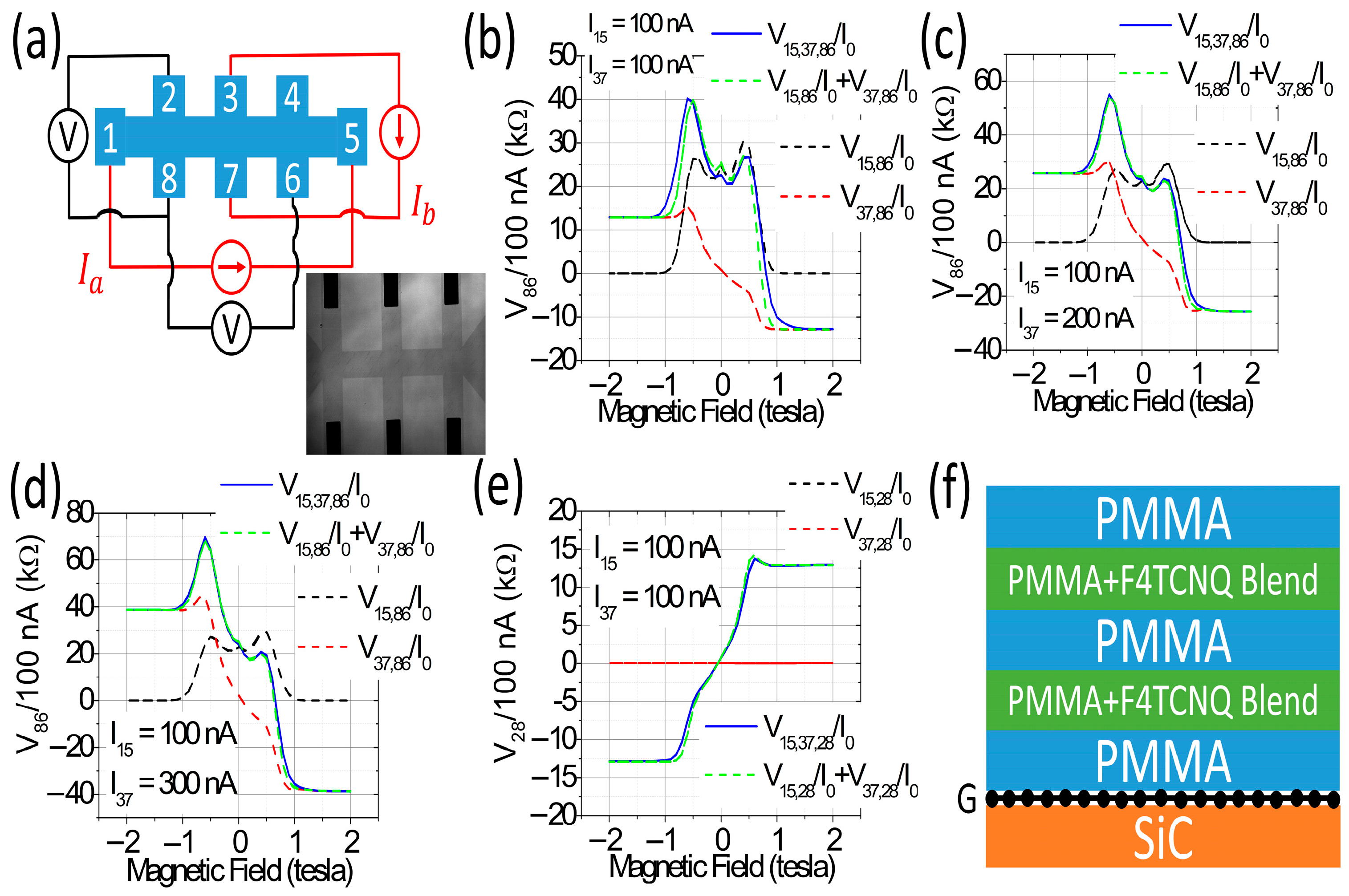
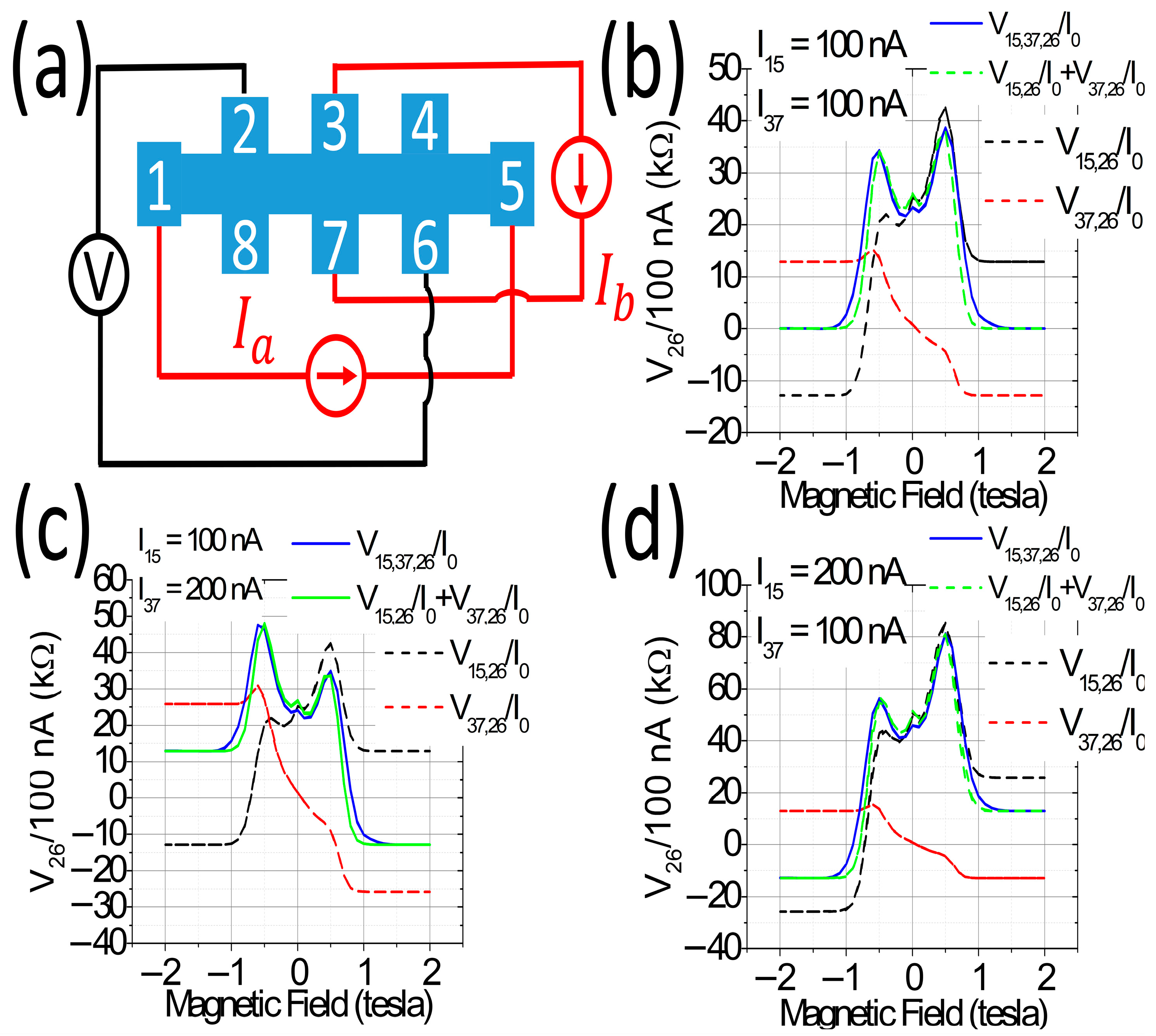
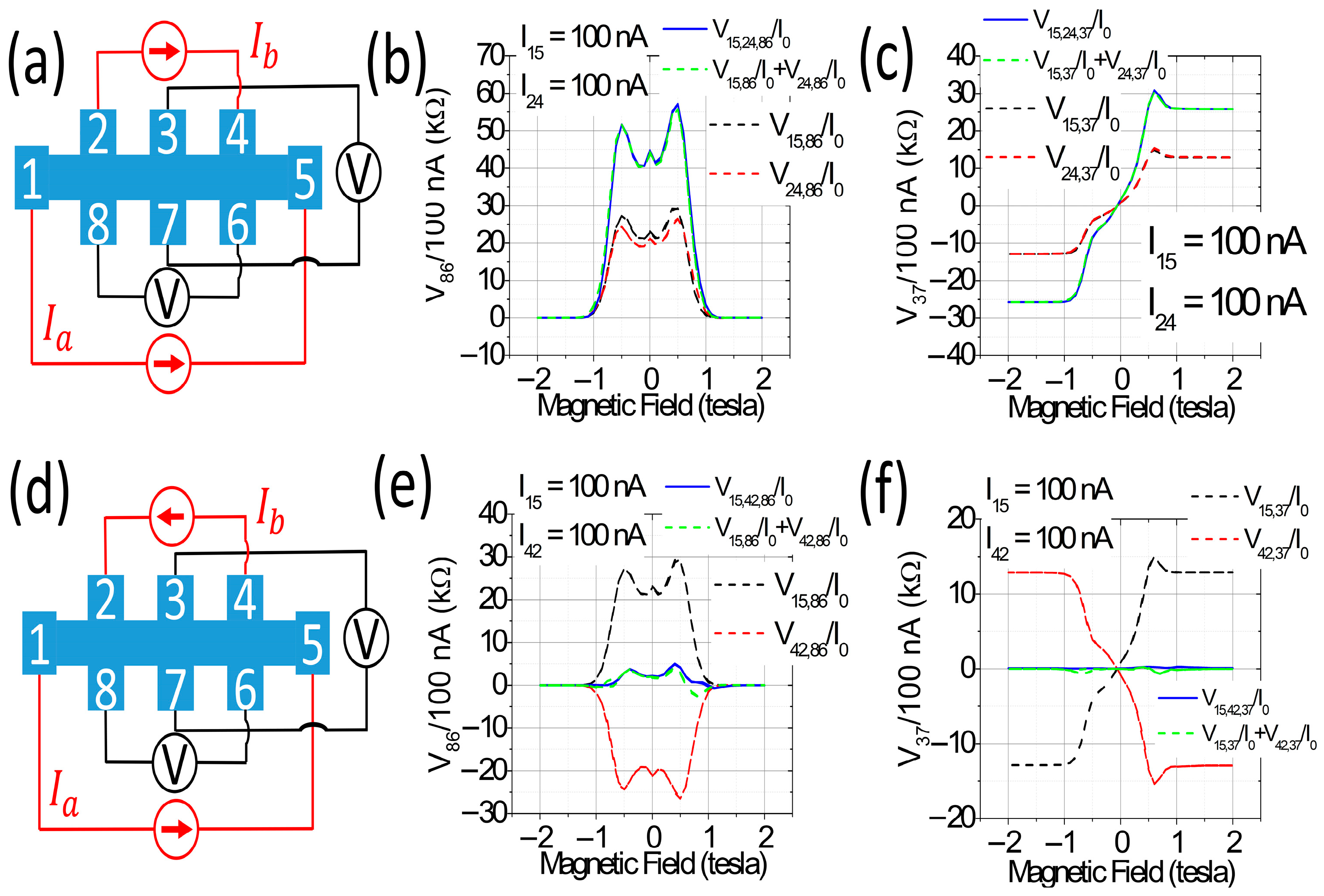
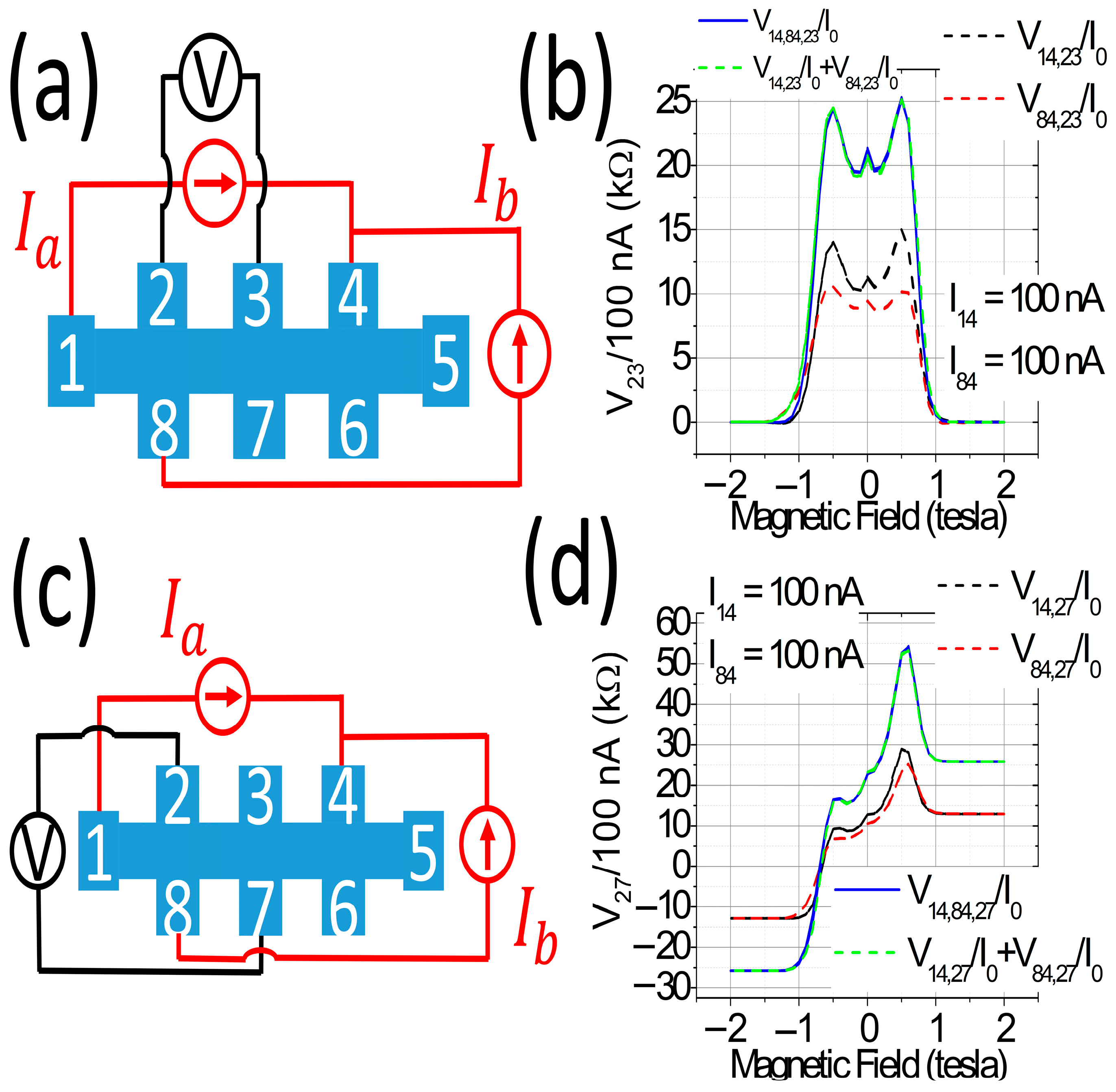
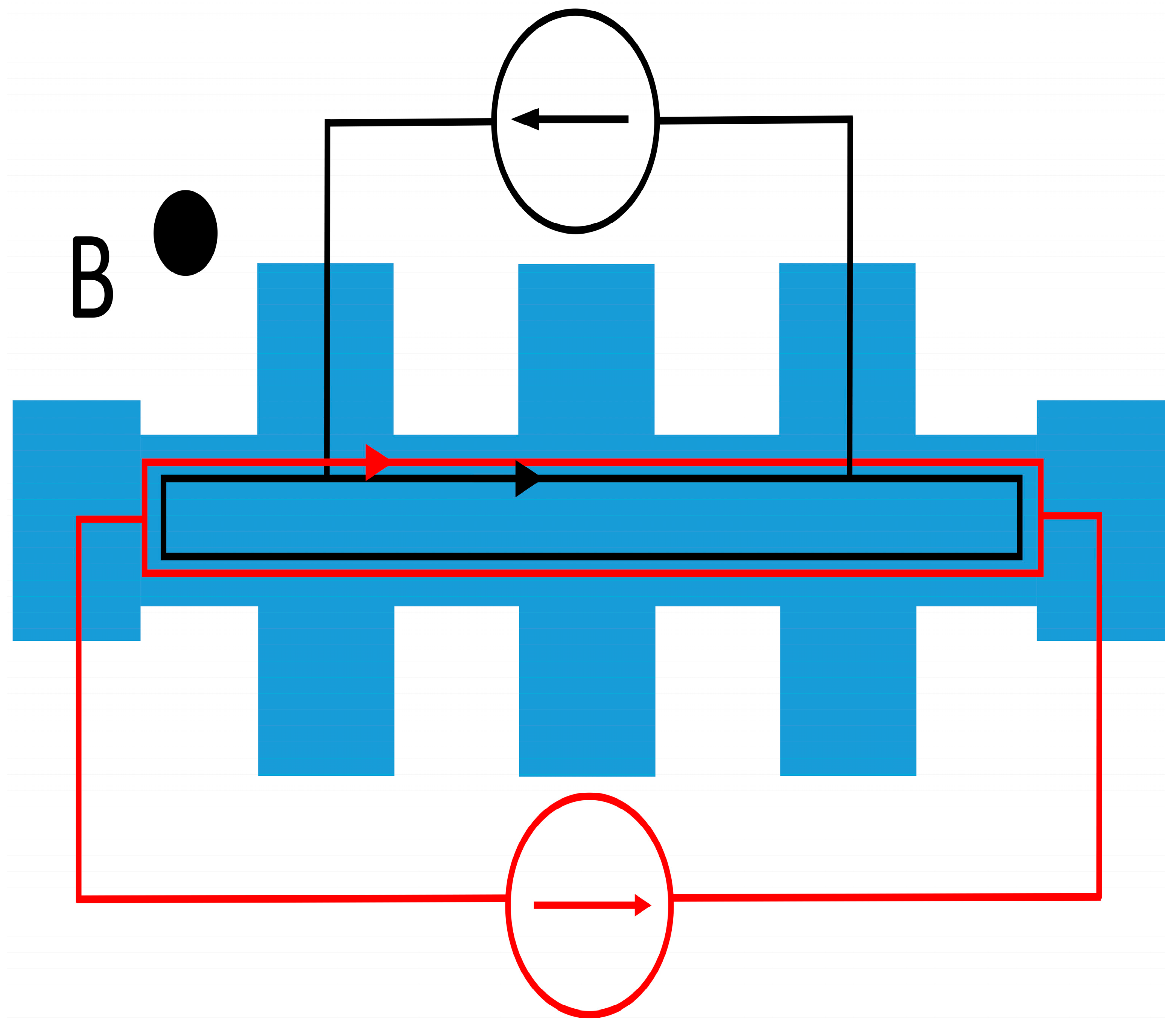
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QHE | Quantum Hall Effect |
| TCS | Two Current Sources |
| LBF | Landauer–Büttiker formalism |
| QH | Quantum Hall |
References
- Tong, D. Lectures on the Quantum Hall Effect. arXiv 2016, arXiv:1606.06687. [Google Scholar] [CrossRef]
- von Klitzing, K.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Stormer, H.L.; Tsui, D.C.; Gossard, A.C. The fractional quantum Hall effect. Rev. Mod. Phys. 1999, 71, S298–S305. [Google Scholar] [CrossRef]
- von Klitzing, K. The quantum Hall effect—An edge phenomenon? Physical B 1993, 184, 1–6. [Google Scholar] [CrossRef]
- Avron, J.E.; Osadchy, D.; Seiler, R. A topological look at the quantum Hall effect. Phys. Today 2003, 56, 38–43. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697–3700. [Google Scholar] [CrossRef]
- Tzalenchuk, A.; Lara-Avila, S.; Kalaboukhov, A.; Paolillo, S.; Syväjärvi, M.; Yakimova, R.; Kazakova, O.; Janssen, T.J.B.M.; Fal’ko, V.; Kubatkin, S. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 2010, 5, 186–189. [Google Scholar] [CrossRef]
- He, H.; Cedergren, K.; Shetty, N.; Lara-Avila, S.; Kubatkin, S.; Bergsten, T.; Eklund, G. Accurate graphene quantum Hall arrays for the new International System of Units. Nat. Commun. 2022, 13, 6933. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Liu, C.-X.; MacDonald, A.H. Colloquium: Quantum anomalous Hall effect. Rev. Mod. Phys. 2023, 95, 011002. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Zhang, S.-C. Quantum Spin Hall Effect. Phys. Rev. Lett. 2006, 96, 106802. [Google Scholar] [CrossRef] [PubMed]
- Kendirlik, E.M.; Sirt, S.; Kalkan, S.B.; Ofek, N.; Umansky, V.; Siddiki, A. The local nature of incompressibility of quantum Hall effect. Nat. Commun. 2017, 8, 14082. [Google Scholar] [CrossRef] [PubMed]
- Komiyama, S.; Sakuma, H.; Ikushima, K.; Hirakawa, K. Electron temperature of hot spots in quantum Hall conductors. Phys. Rev. B 2006, 73, 045333. [Google Scholar] [CrossRef]
- Rickhaus, P.; Makk, P.; Liu, M.-H.; Tóvári, E.; Weiss, M.; Maurand, R.; Richter, K.; Schönenberger, C. Snake trajectories in ultraclean graphene p–n junctions. Nat. Commun. 2015, 6, 6470. [Google Scholar] [CrossRef]
- Haug, R.J. Edge-state transport and its experimental consequences in high magnetic fields. Semicond. Sci. Technol. 1993, 8, 131–153. [Google Scholar] [CrossRef]
- Tang, F.; Ren, Y.; Wang, P.; Zhong, R.; Schneeloch, J.; Yang, S.A.; Yang, K.; Lee, P.A.; Gu, G.; Qiao, Z.; et al. Three-dimensional quantum Hall effect and metal–insulator transition in ZrTe5. Nature 2019, 569, 537–541. [Google Scholar] [CrossRef]
- Delahaye, F. Series and parallel connection of multiterminal quantum Hall-effect devices. J. Appl. Phys. 1993, 73, 7914–7920. [Google Scholar] [CrossRef]
- Mani, R.G.; von Klitzing, K. Hall effect under null current conditions. Appl. Phys. Lett. 1994, 64, 1262–1264. [Google Scholar] [CrossRef]
- Mani, R.G. Transport study of GaAs/AlGaAs heterostructure- and n-type GaAs-devices in the anti Hall bar within a Hall bar configuration. J. Phys. Soc. Jpn. 1996, 65, 1751–1759. [Google Scholar] [CrossRef]
- Mani, R.G. Experimental technique for realizing dual and multiple Hall effects in a single specimen. Europhys. Lett. 1996, 34, 139–144. [Google Scholar] [CrossRef]
- Mani, R.G. Steady-state bulk current at high magnetic fields in Corbino-type GaAs/AlGaAs heterostructure devices. Europhys. Lett. 1996, 36, 203–208. [Google Scholar] [CrossRef]
- Oswald, M.; Oswald, J.; Mani, R.G. Voltage and current distribution in a doubly connected two-dimensional quantum Hall system. Phys. Rev. B 2005, 72, 035334. [Google Scholar] [CrossRef]
- Oswald, J.; Oswald, M. Magnetotransport in a doubly connected two-dimensional quantum Hall system in the low magnetic field regime. Phys. Rev. B 2006, 74, 153315. [Google Scholar] [CrossRef]
- Uiberacker, C.; Stecher, C.; Oswald, J. Microscopic details of the integer quantum Hall effect in an anti-Hall bar. Phys. Rev. B 2012, 86, 045304. [Google Scholar] [CrossRef][Green Version]
- Ji, Z.; Park, H.; Barber, M.E.; Hu, C.; Watanabe, K.; Taniguchi, T.; Chu, J.-H.; Xu, X.; Shen, Z.-X. Local probe of bulk and edge states in a fractional Chern insulator. Nature 2024, 635, 578–583. [Google Scholar] [CrossRef]
- Ilani, S.; Martin, J.; Teitelbaum, E.; Smet, J.H.; Mahalu, D.; Umansky, V.; Yacoby, A. The microscopic nature of localization in the quantum Hall effect. Nature 2004, 427, 328–332. [Google Scholar] [CrossRef]
- de Picciotto, R.; Reznikov, M.; Heiblum, M.; Umansky, V.; Bunin, G.; Mahalu, D. Direct observation of a fractional charge. Nature 1997, 389, 162–164. [Google Scholar] [CrossRef]
- Garg, M.; Maillet, O.; Samuelson, N.L.; Wang, T.; Feng, J.; Cohen, L.A.; Watanabe, K.; Taniguchi, T.; Roulleau, P.; Sassetti, M.; et al. Enhanced shot noise in graphene quantum point contacts with electrostatic reconstruction. arXiv 2025, arXiv:2503.17209. [Google Scholar] [CrossRef]
- Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 1988, 38, 9375–9389. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Marks, S.; Pinard, P.; Burgess, S.; Bithell, J.; Beanland, R. Measuring the Thickness of 2D Materials Using EDS. Microsc. Microanal. 2020, 26 (Suppl. S2), 1212. [Google Scholar] [CrossRef]
- He, H.; Kim, K.H.; Danilov, A.; Montemurro, D.; Yu, L.; Park, Y.W.; Lombardi, F.; Bauch, T.; Moth-Poulsen, K.; Iakimov, T.; et al. Uniform doping of graphene close to the Dirac point by polymer-assisted assembly of molecular dopants. Nat. Commun. 2018, 9, 3956. [Google Scholar] [CrossRef]
- Yager, T.; Lartsev, A.; Cedergren, K.; Yakimova, R.; Panchal, V.; Kazakova, O.; Tzalenchuk, A.; Kim, K.-H.; Park, Y.-W.; Lara-Avila, S.; et al. Low contact resistance in epitaxial graphene devices for quantum metrology. AIP Adv. 2015, 5, 087134. [Google Scholar] [CrossRef]
- Janssen, T.J.B.M.; Rozhko, S.; Tzalenchuk, A.; Alexander-Webber, J.A.; Nichoas, R.J. Breakdown of the quantum Hall effect in epitaxial graphene. In Proceedings of the 29th Conference on Precision Electromagnetic Measurement (CPEM 2014), Rio de Janeiro, Brazil, 24–29 August 2014; IEEE: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Haremski, P.; Mausser, M.; Gauß, A.; von Klitzing, K.; Weis, J. Electrically induced breakdown of the quantum Hall effect at different Hall bar widths: Visualizing the edge- and bulk-dominated regimes within a quantum Hall plateau. Phys. Rev. B 2020, 102, 205306. [Google Scholar] [CrossRef]
- Nachtwei, G. Breakdown of the quantum Hall effect. Physical E 1999, 4, 79–101. [Google Scholar] [CrossRef]
- Chida, K.; Hata, T.; Arakawa, T.; Matsuo, S.; Nishihara, Y.; Tanaka, T.; Ono, T.; Kobayashi, K. Avalanche electron bunching in a Corbino disk in the quantum Hall effect breakdown regime. Phys. Rev. B 2014, 89, 235318. [Google Scholar] [CrossRef]
- Eaves, L.; Sheard, F.W. Size-dependent quantized breakdown of the dissipationless quantum Hall effect in narrow channels. Semicond. Sci. Technol. 1986, 1, 346. [Google Scholar] [CrossRef]
- Streda, P.; von Klitzing, K. Critical non-dissipative current of the quantum Hall regime. J. Phys. C Solid State Phys. 1984, 17, L483. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.H. Probing Chirality of the Quantum Hall Effect via the Landauer–Büttiker Formalism with Two Current Sources. Mathematics 2025, 13, 2981. https://doi.org/10.3390/math13182981
Kim KH. Probing Chirality of the Quantum Hall Effect via the Landauer–Büttiker Formalism with Two Current Sources. Mathematics. 2025; 13(18):2981. https://doi.org/10.3390/math13182981
Chicago/Turabian StyleKim, Kyung Ho. 2025. "Probing Chirality of the Quantum Hall Effect via the Landauer–Büttiker Formalism with Two Current Sources" Mathematics 13, no. 18: 2981. https://doi.org/10.3390/math13182981
APA StyleKim, K. H. (2025). Probing Chirality of the Quantum Hall Effect via the Landauer–Büttiker Formalism with Two Current Sources. Mathematics, 13(18), 2981. https://doi.org/10.3390/math13182981




