Performance Analysis and Cost Optimization of the M/M/1/N Queueing System with Working Vacation and Working Breakdown
Abstract
1. Introduction
- The two-dimensional continuous-time Markov chain for the M/M/1/N queueing system, which incorporates setup time, working vacation, and working breakdown strategies, is developed. Additionally, a finite quasi birth-and-death (QBD) representation is established. The stationary probability vector and various performance measures are calculated using the matrix geometric method.
- The total cost optimization function for unit time is constructed. Under the cost minimization scenario, the sparrow search algorithm (SSA) optimizes the machine’s service rates during regular busy periods, working vacation, and working breakdown.
- To further demonstrate the search capabilities and effectiveness of the SSA, its optimization results are compared with those of the cuckoo search (CS) and particle swarm optimization (PSO).
2. Problem Description and Assumptions
3. Finite QBD Process and Solution
3.1. Steady-State Equations and Infinitesimal Generator
3.2. Stationary Probability Vector
4. Performance Measures
- System availability and output varianceLet denote the covariance between the number of visits to state i and state j over n service cycles starting from an initial state. These covariances () are critical for analyzing system availability and output variance in finite-capacity queueing networks. The stationary probability vector was derived in Section 3.2. Let P be the system’s probability transition matrix. According to [53,54], the fundamental matrix of this QBD process is expressed aswhere I is the identity matrix and e is the ()-dimensional column vector with all elements equal to 1. For , then , whereThe covariance matrix of the system is determined by the following equation.Let U denote the set of effective of the server states, comprising the working vacation, working breakdown, and normal busy states, i.e., ; the availability of the system and output variance are then given by
- System throughput rate
- The expected number of customers in the system
- Probability that the system is in the idle period
- Probability that the server is in the regular busy states
- Probability that the server is in the setup states
- Probability that the system is in working vacation states
- Probability that the system is in the working breakdown states
5. Cost Optimization Model
6. Numerical Analysis
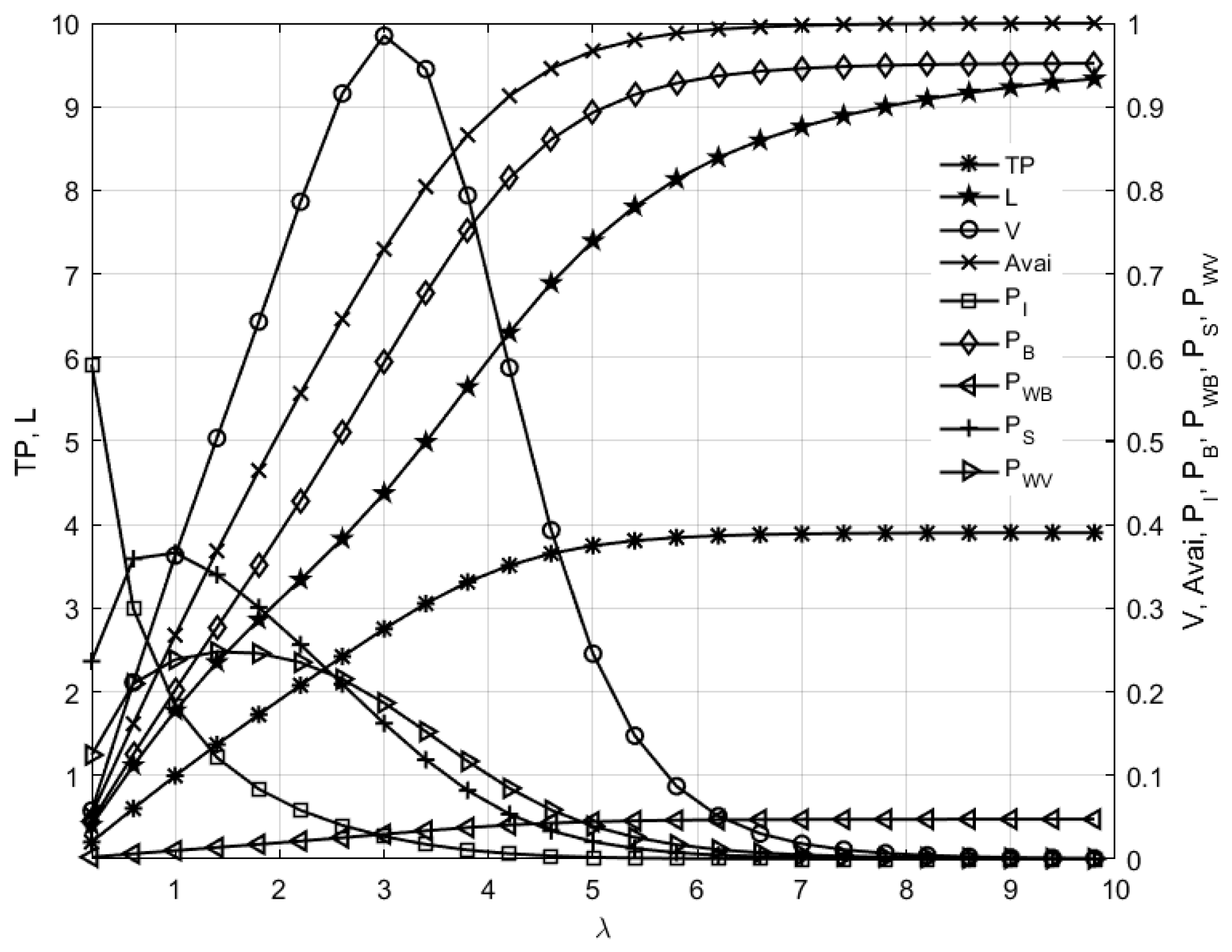
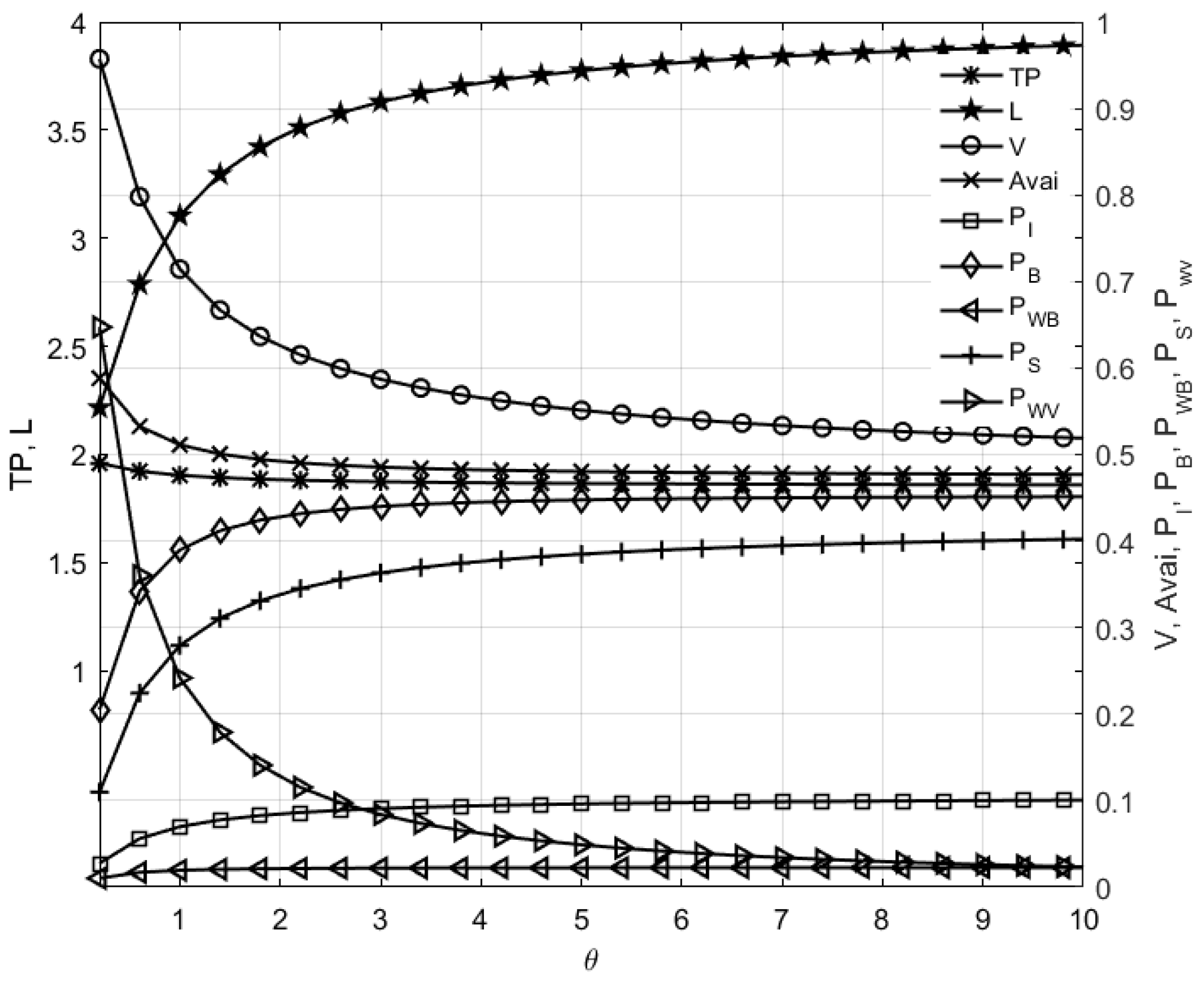
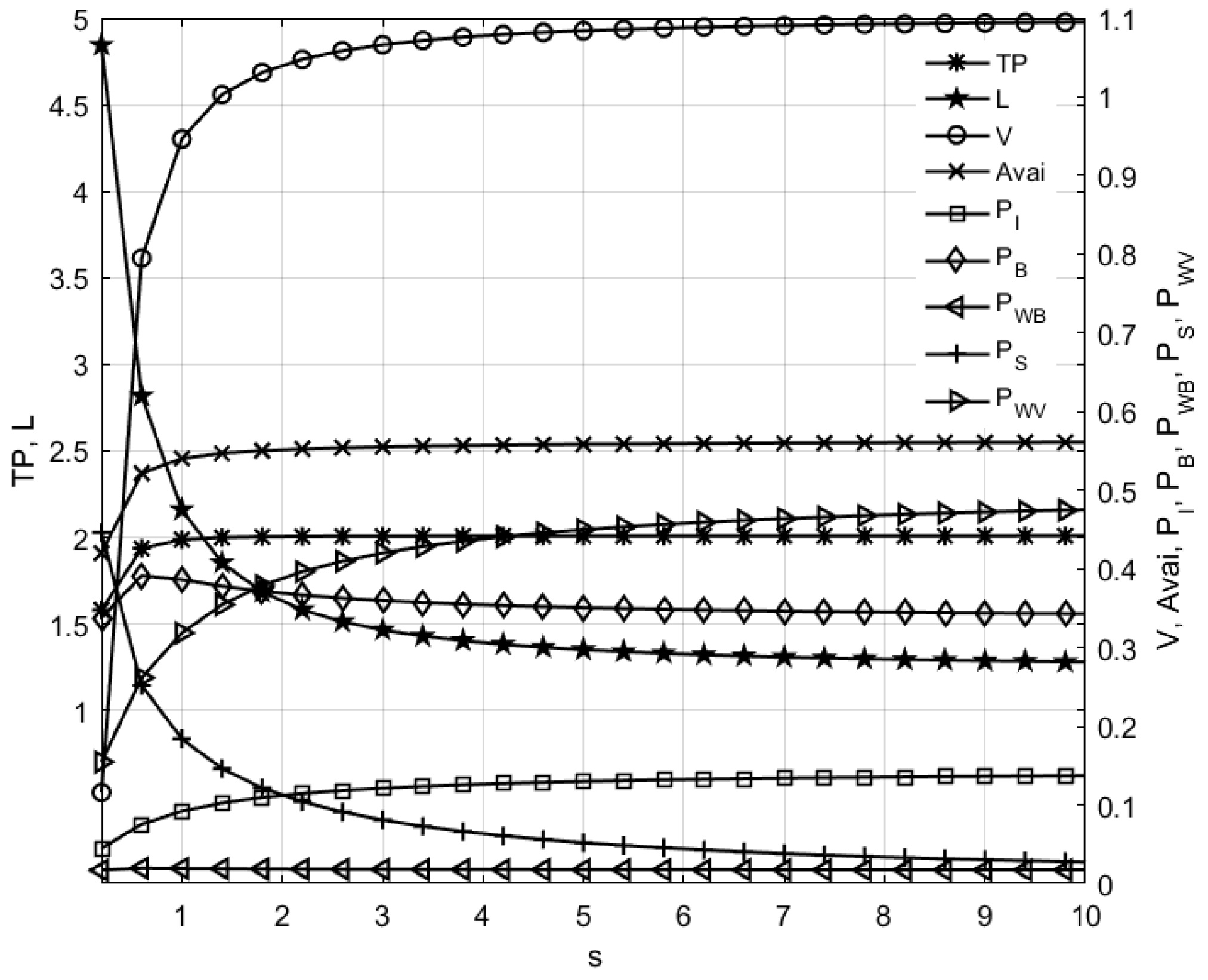
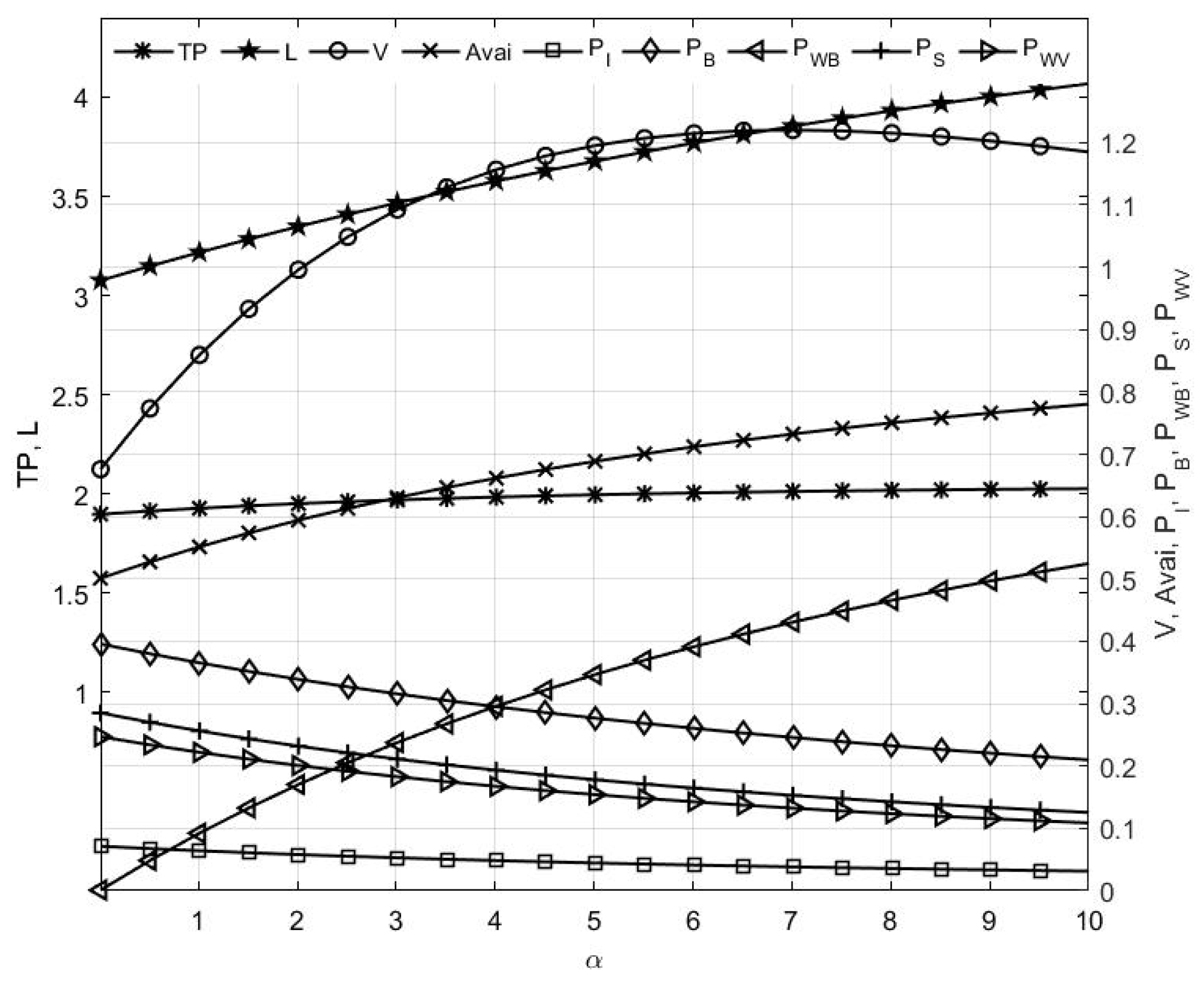
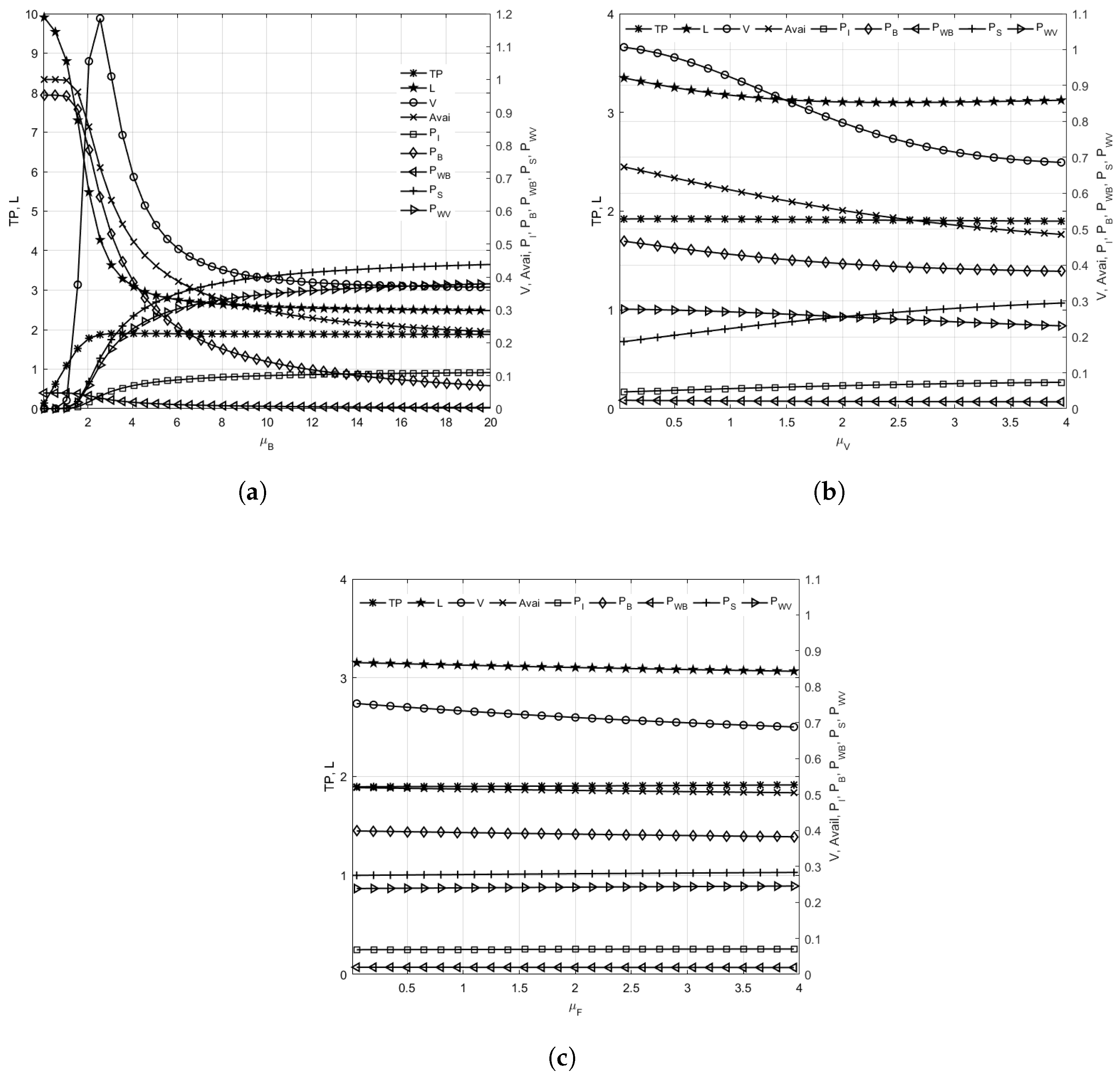
6.1. Sensitivity Analysis of System Performance Measures
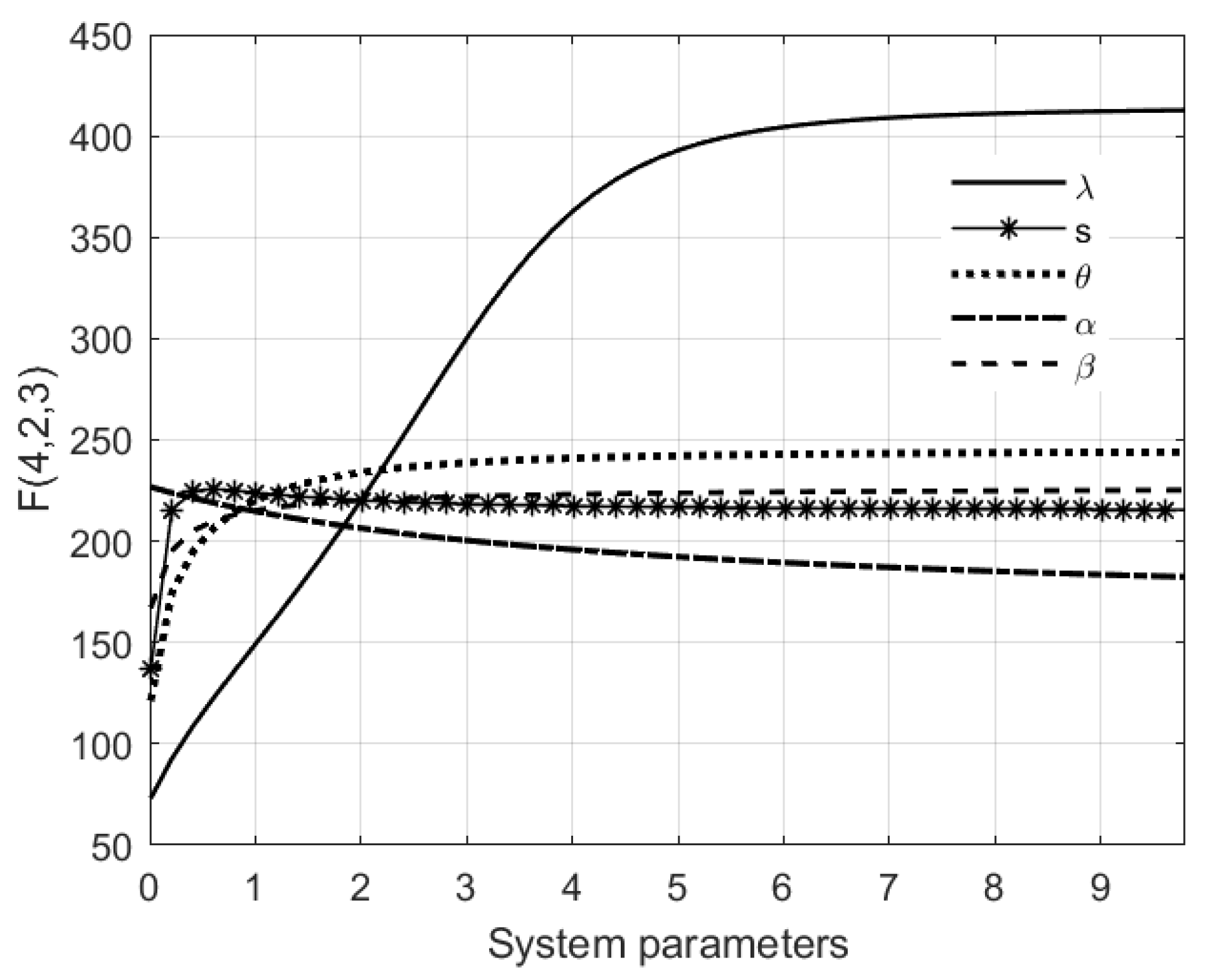
6.2. Sensitivity Analysis of the Cost Optimization Function
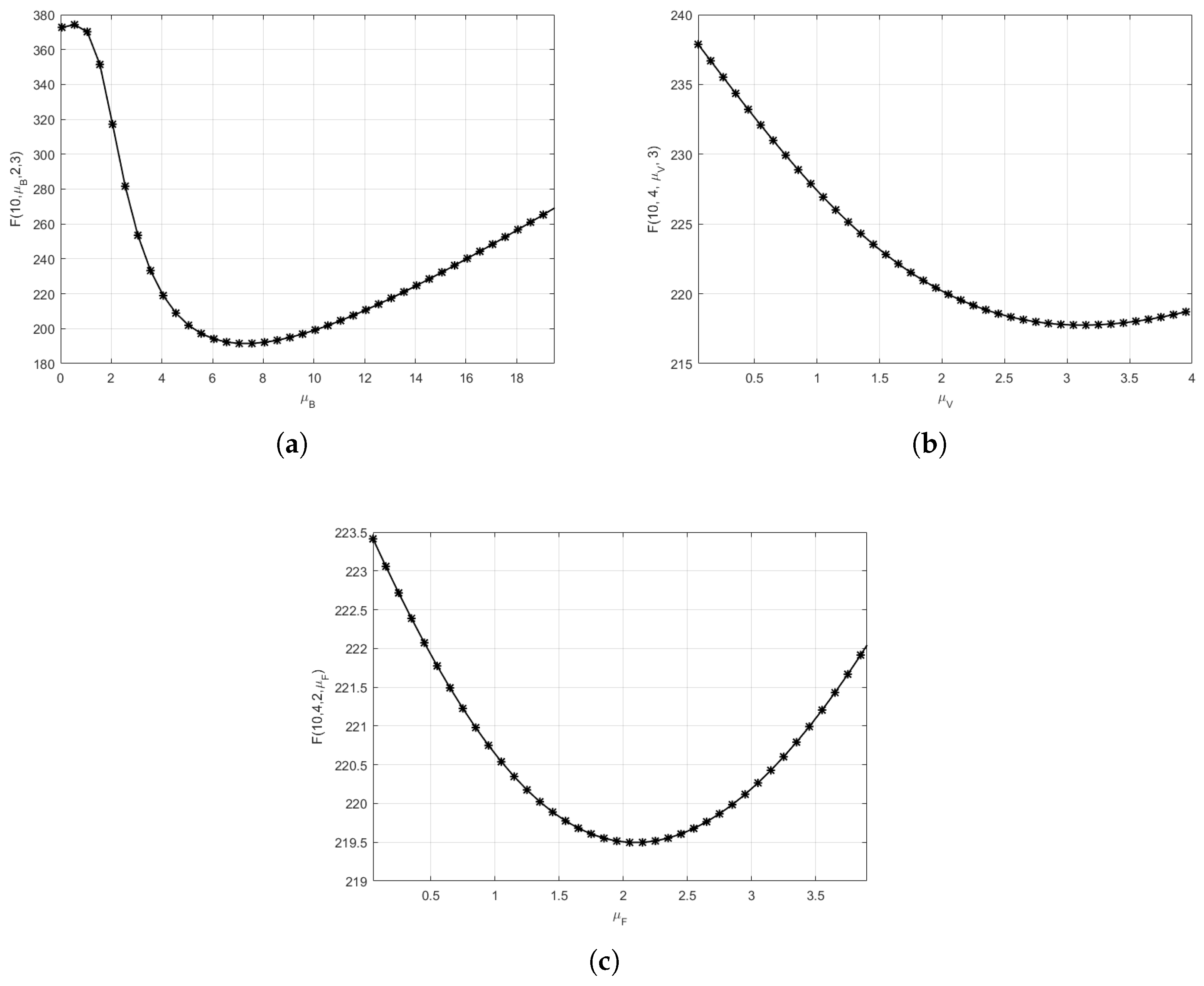
6.3. Optimization Analysis of Cost Optimization Function
- The average and maximum values of / computed by the SSA are close to 1.00000, which implies that the SSA exhibits strong robustness and effective optimization capabilities throughout all test cases.
- The average and maximum values of / calculated by the CS are also close to 1.00000; however, the SSA converges at a notably faster pace and is less likely to fall into local optima. The CPU calculation time for the SSA varies from 587.5432 s to 660.4522 s. In contrast, for the CS, it ranges from 834.2787 to 3012.6651 s. Not only is the CPU time of the SSA less variable, but it is also significantly shorter than that of the CS.
- The CPU calculation time for the PSO spans from 373.6041 to 406.3137 s, demonstrating a higher calculation speed compared to the SSA. However, the mean and maximum values of / obtained by the PSO range from 1.10572 to 1.31742 and from 1.13416 to 1.38687, respectively, which indicates poor robustness. Moreover, the convergence speed of the PSO is significantly slower than that of the SSA.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, X.; Niu, Z.; Zhou, S.; Kumar, P. Delay-constrained energy-optimal base station sleeping control. IEEE J. Sel. Areas Commun. 2016, 34, 1073–1085. [Google Scholar] [CrossRef]
- Xu, J.; Wu, X.; Huang, Q.; Sun, P. How Should the Server Sleep?—Age-Energy Tradeoff in Sleep-Wake Server Systems. IEEE Trans. Green Commun. Netw. 2023, 7, 1620–1634. [Google Scholar] [CrossRef]
- Servi, L.D.; Finn, S.G. M/M/1 queues with working vacations (M/M/1/WV). Perform. Eval. 2002, 50, 41–52. [Google Scholar] [CrossRef]
- Kalidass, K.; Kasturi, R. A queue with working breakdowns. Comput. Ind. Eng. 2012, 63, 779–783. [Google Scholar] [CrossRef]
- Jain, M.; Sharma, G.C.; Sharma, R. Working vacation queue with service interruption and multi optional repair. Int. J. Inf. Manag. Sci. 2011, 22, 157–175. [Google Scholar]
- Li, T.; Wang, Z.; Liu, Z. Geo/Geo/1 retrial queue with working vacations and vacation interruption. J. Appl. Math. Comput. 2012, 39, 131–143. [Google Scholar] [CrossRef]
- Hu, C.; Zhu, Y. Equilibrium distributions of the queue length in Geo/Geo/1 queue system with negative customer, feedback and multiple working vacations. Syst. Eng.-Theory Pract. 2012, 2, 1494–1500. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Y. Geo/Geo/1 retrial queue with non-persistent customers and working vacations. J. Appl. Math. Comput. 2013, 42, 103–115. [Google Scholar] [CrossRef]
- Yu, M.; Alfa, A. Strategic queueing behavior for individual and social optimization in managing discrete time working vacation queue with Bernoulli interruption schedule. Comput. Oper. Res. 2016, 73, 43–55. [Google Scholar] [CrossRef]
- Yang, B.; Hou, Z.; Wu, J. Analysis of the equilibrium strategies in the Geo/Geo/1 queue with multiple working vacations. Qual. Technol. Quant. Manag. 2017, 15, 663–685. [Google Scholar] [CrossRef]
- Barbhuiya, F.; Gupta, U. A Discrete-Time GIX/Geo/1 Queue with Multiple Working Vacations Under Late and Early Arrival System. Methodol. Comput. Appl. Probab. 2020, 22, 599–624. [Google Scholar] [CrossRef]
- Wu, S.; Lan, S. Analysis of repairable discrete-time queueing systems with negative customers, disasters, balking customers and interruptible working vacations under Bernoulli schedule. Math. Comput. Simul. 2025, 232, 102–122. [Google Scholar] [CrossRef]
- Artalejo, J.; Gómez-Corral, A. Retrial Queueing Systems: A Computational Approach; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Atencia-Mckillop, I.; Sánchez-Merino, S.; Fortes-Ruiz, I.; Galán-García, J.L. Discrete-Time Retrial Queuing Systems with Last Come-First-Served (LCFS) and First-Come-First-Served (FCFS) Disciplines: Negative Customer Impact and Stochastic Analysis. Mathematics 2025, 13, 107. [Google Scholar] [CrossRef]
- Rajadurai, P.; Saravanarajan, M.C.; Chandrasekaran, V.M. A study on M/G/1 feedback retrial queue with subject to server breakdown and repair under multiple working vacation policy. Alex. Eng. J. 2018, 57, 947–962. [Google Scholar] [CrossRef]
- Sun, W.; Li, S.; Wang, Y.; Tian, N. Comparisons of exhaustive and non-exhaustive M/M/l/N queues with working vacation and threshold policy. J. Syst. Sci. Syst. Eng. 2019, 28, 154–167. [Google Scholar] [CrossRef]
- Li, S.; Yang, X.; Peng, D.; Chen, J. Analysis of M/M/1/N working vacation queueing system with setup times and repairable service station. Control Decis. 2020, 35, 319–328. [Google Scholar]
- Jain, M.; Dhibar, S.; Sanga, S.S. Markovian working vacation queue with imperfect service, balking and retrial. J. Ambient Intell. Humaniz. Comput. 2022, 13, 1907–1923. [Google Scholar] [CrossRef]
- Majid, S. Analysis of customer’s impatience in queues with Bernoulli schedule server working vacations and vacation interruption. Afr. Mat. 2022, 33, 1–13. [Google Scholar] [CrossRef]
- Ammar, S.; Alharbi, Y.; Zhao, Y. Analysis of Vacation Fluid M/M/1 Queue in Multi-Phase Random Environment. Mathematics 2023, 11, 4444. [Google Scholar] [CrossRef]
- Sindhu, S.; Krishnamoorthy, A.; Kozyrev, D. On Queues with Working Vacation and Interdependence in Arrival and Service Processes. Mathematics 2023, 11, 2280. [Google Scholar] [CrossRef]
- Lai, C.; Kasim, E.; Muhammadhaji, A. Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations. Mathematics 2024, 12, 3999. [Google Scholar] [CrossRef]
- Vijaya Laxmi, P.; Girija Bhavani, E.; George, A.A. Retention of impatient customers in a multi-server Markovian queueing system with optional service and working vacations. Commun. Stat.-Theory Methods 2023, 52, 5195–5212. [Google Scholar] [CrossRef]
- Liu, T.H.; Chiou, K.C.; Chen, C.M.; Chang, F.M. Multiserver Retrial Queue with Two-Way Communication and Synchronous Working Vacation. Mathematics 2024, 12, 1163. [Google Scholar] [CrossRef]
- Sundarapandiyan, S.; Nandhini, S. Sensitivity analysis of a non-Markovian feedback retrial queue, reneging, delayed repair with working vacation subject to server breakdown. Int. J. Math. Eng. Manag. Sci. 2024, 9, 21025–21052. [Google Scholar] [CrossRef]
- Lv, S.; Yin, S.; Zan, Y. The queueing inventory system with working vacations and breakdowns. IAENG Int. J. Appl. Math. 2024, 54, 2198–2208. [Google Scholar]
- Fiems, D. Queues with Working Vacations: A Survey. Mathematics 2025, 13, 1894. [Google Scholar] [CrossRef]
- Ma, Z.; Cui, G.; Wang, P. M/M/1 vacation queueing system with working breakdowns and variable arrival rate. J. Comput. Inf. Syst. 2015, 11, 1–8. [Google Scholar]
- Chen, J.; Yen, T.; Wang, K. Cost optimization of a single-server queue with working breakdowns under the N policy. J. Test. Eval. 2016, 44, 2059–2067. [Google Scholar] [CrossRef]
- Jiang, T.; Xin, B. Computational analysis of the queue with working breakdowns and delaying repair under a Bernoulli-schedule-controlled policy. Commun. Stat.-Theory Methods 2019, 48, 926–941. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.; Li, S.; Wu, F. Performance analysis of M/M/1/N queue with setup time and working breakdown. Control Theory Appl. 2019, 36, 561–569. [Google Scholar]
- Li, J.; Li, T. An MX/G/1 G-queue with single vacation, setup time and working breakdown. Eng. Lett. 2020, 28, 1100–1107. [Google Scholar]
- Zhang, M.; Gao, S. The disasters queue with working breakdowns and impatient customers. RAIRO-Oper. Res. 2020, 54, 815–825. [Google Scholar] [CrossRef]
- Yen, T.C.; Wang, K.; Chen, J. Optimization analysis of the N policy M/G/1 queue with working breakdowns. Symmetry 2020, 12, 583. [Google Scholar] [CrossRef]
- Yang, D.; Chen, Y.; Wu, C. Modelling and optimisation of a two-server queue with multiple vacations and working breakdownsn. Int. J. Prod. Res. 2020, 58, 3036–3048. [Google Scholar] [CrossRef]
- Yang, D.; Wu, C. Evaluation of the availability and reliability of a standby repairable system incorporating imperfect switchovers and working breakdowns. Reliab. Eng. Syst. Saf. 2021, 207, 1–16. [Google Scholar] [CrossRef]
- Li, T.; Zhang, L. Discrete-time Geo/Geo/1 queue with negative customers and working breakdowns. IAENG Int. J. Appl. Math. 2017, 47, 442–448. [Google Scholar]
- Lan, S.; Tang, Y. Performance analysis of a discrete-time queue with working breakdowns and searching for the optimum service rate in working breakdown period. J. Syst. Sci. Inf. 2017, 5, 176–192. [Google Scholar] [CrossRef]
- Lv, S.; Li, F.; Li, J. The M/M/c retrial queueing system with impatient customers and server working breakdown. IAENG Int. J. Appl. Math. 2024, 54, 1499–1506. [Google Scholar]
- Wu, C.; Yang, D.; He, T. Matrix-augmentation approach for machine repair problem with generally distributed repair times during working breakdown periods. Math. Comput. Simul. 2024, 225, 1019–1038. [Google Scholar] [CrossRef]
- Jain, M.; Sharma, R.; Meena, R.K. Performance modeling of fault-tolerant machining system with working vacation and working breakdown. Arab. J. Sci. Eng. 2018, 44, 2825–2836. [Google Scholar] [CrossRef]
- Rajadurai, P. Sensitivity analysis of an M/G/1 retrial queueing system with disaster under working vacations and working breakdowns. RAIRO-Oper. Res. 2018, 35, 913–930. [Google Scholar] [CrossRef]
- Yang, D.; Chung, C.; Wu, C. Sojourn times in a Markovian queue with working breakdowns and delayed working vacations. Comput. Ind. Eng. 2021, 156, 1–13. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.; Wang, H.; Wu, F. Performance analysis of M/M/1/N queueing system with working vacation and working breakdown. Control Theory Appl. 2021, 38, 2031–2044. [Google Scholar]
- Jain, A.; Raychaudhuri, C. Cost optimization using Genetic Algorithm in customers intolerance Markovian model with working vacation and multiple working breakdowns. Int. J. Math. Eng. Manag. Sci. 2022, 7, 656–669. [Google Scholar] [CrossRef]
- Manoharan, P.; Subathra, S. Non Markovian retrial queue, balking, disaster under working breakdown and working vacation. J. Comput. Anal. Appl. 2023, 31, 244–255. [Google Scholar]
- Thakur, S.; Jain, A.; Ahuja, A. Analysis of MAP/PH/1 model with working vacation, working breakdown and two-phase repair. Arab. J. Sci. Eng. 2024, 49, 7431–7451. [Google Scholar] [CrossRef]
- Nisha; Upadhyaya, S.; Shekhar, C. Maximum entropy solution for MX/G/1 priority reiterate G-queue under working breakdown and working vacation. Int. J. Math. Eng. Manag. Sci. 2024, 9, 163–187. [Google Scholar] [CrossRef]
- Liu, T.H.; Hsu, H.Y.; Chang, F.M. Multi-server two-way communication retrial queue subject to disaster and synchronous working vacation. Algorithms 2025, 18, 24. [Google Scholar] [CrossRef]
- Neuts, M. Matrix-Geometric Solution in Stochastic Models; The Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Tian, N.; Yue, D. Quasi Birth and Death Process and Matrix Geometric Solution; Science Press: Beijing, China, 2002. [Google Scholar]
- Elhafs, E.H.; Molle, M. On the solution to QBD processes with finite state space. Stoch. Anal. Appl. 2007, 25, 763–779. [Google Scholar] [CrossRef]
- Kemeny, J.G.; Snell, J.L. Finite MARKOV Chains; Springer: New York, NY, USA, 1976. [Google Scholar]
- Kemeny, J.G. Generalization of a fundamental matrix. Linear Algebra Its Appl. 1981, 38, 193–206. [Google Scholar] [CrossRef][Green Version]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xue, J. Research and Application of a Novel Swarm Intelligence Optimization Technique: Sparrow Search Algorithm. Ph.D. Thesis, Donghua University, Shanghai, China, 2020. [Google Scholar]
- Fu, H.; Liu, H. Improved sparrow search algorithm with multi-strategy integration and its application. Control Decis. 2022, 37, 87–96. [Google Scholar]






| Symbol | Description |
|---|---|
| cost per unit time for each customer in the system | |
| cost per unit time for the server being idle | |
| cost per unit time for the server being busy | |
| setup cost per unit time for a customer entering the system | |
| cost per unit time for the server in working vacation states | |
| cost per unit time for the server in working breakdown states | |
| cost per customer served during regular busy period | |
| cost per customer served during working vacation period | |
| cost per customer served during working breakdown period |
| PSO | ||||||
| Mean | Max | |||||
| (0.8, 0.2, 0.5, 2, 1) | 71.0713 | 3.3910 | 1.3008 | 0.8448 | 1.10572 | 1.13416 |
| (1.8, 0.5, 0.5, 2, 1) | 96.6617 | 4.9554 | 1.2769 | 2.2022 | 1.26818 | 1.32063 |
| (3, 0.5, 0.5, 2, 1) | 114.2587 | 4.4687 | 2.4216 | 4.2888 | 1.18776 | 1.21466 |
| (1.8, 0.1, 0.5, 2, 1) | 91.1652 | 7.2137 | 2.8388 | 0.7249 | 1.30232 | 1.35421 |
| (1.8, 0.5, 0.9, 2, 1) | 95.3813 | 4.1226 | 1.3073 | 3.892 | 1.24235 | 1.26960 |
| (1.8, 0.5, 0.9, 1, 1) | 92.2048 | 3.3515 | 1.9473 | 2.5267 | 1.26412 | 1.28532 |
| (1.8, 0.5, 0.9, 2, 0.5) | 90.2650 | 2.8999 | 1.5020 | 2.8998 | 1.31724 | 1.38687 |
| CS | ||||||
| Mean | Max | |||||
| (0.8, 0.2, 0.5, 2, 1) | 70.4989 | 2.3775 | 1.2884 | 1.2686 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.5, 2, 1) | 94.3731 | 2.9357 | 1.3609 | 2.9356 | 1.00000 | 1.00000 |
| (3, 0.5, 0.5, 2, 1) | 114.0640 | 4.2372 | 2.3050 | 4.2311 | 1.00000 | 1.00000 |
| (1.8, 0.1, 0.5, 2, 1) | 86.0849 | 2.9485 | 2.7834 | 2.7295 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 2, 1) | 91.6702 | 3.0552 | 1.8765 | 2.9599 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 1, 1) | 89.9696 | 5.5602 | 2.2362 | 0.9533 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 2, 0.5) | 90.2644 | 2.8927 | 1.4788 | 2.8926 | 1.00000 | 1.00000 |
| SSA | ||||||
| Mean | Max | |||||
| (0.8, 0.2, 0.5, 2, 1) | 70.4989 | 2.3759 | 1.2853 | 1.2718 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.5, 2, 1) | 94.3731 | 2.9345 | 1.3570 | 2.9344 | 1.00000 | 1.00000 |
| (3, 0.5, 0.5, 2, 1) | 114.064 | 4.2388 | 2.3039 | 4.2387 | 1.00000 | 1.00000 |
| (1.8, 0.1, 0.5, 2, 1) | 86.0849 | 2.9432 | 2.7778 | 2.7357 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 2, 1) | 91.6702 | 3.0584 | 1.8768 | 2.9591 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 1, 1) | 89.9696 | 5.5779 | 2.2318 | 0.9390 | 1.00000 | 1.00000 |
| (1.8, 0.5, 0.9, 2, 0.5) | 90.2644 | 2.8983 | 1.4757 | 2.8982 | 1.00000 | 1.00000 |
| PSO | CS | SSA | |
|---|---|---|---|
| (0.8, 0.2, 0.5, 2, 1) | 373.6041 | 877.4292 | 592.4291 |
| (1.8, 0.5, 0.5, 2, 1) | 380.1668 | 1113.5692 | 613.4993 |
| (3, 0.5, 0.5, 2, 1) | 397.8724 | 3012.6651 | 587.5432 |
| (1.8, 0.1, 0.5, 2, 1) | 393.5976 | 877.0753 | 606.6444 |
| (1.8, 0.5, 0.9, 2, 1) | 395.3651 | 834.2787 | 656.0716 |
| (1.8, 0.5, 0.9, 1, 1) | 406.7137 | 945.1267 | 660.4522 |
| (1.8, 0.5, 0.9, 2, 0.5) | 402.1338 | 1553.0157 | 651.2009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, Y.; Wang, B.; Li, X.J. Performance Analysis and Cost Optimization of the M/M/1/N Queueing System with Working Vacation and Working Breakdown. Mathematics 2025, 13, 2980. https://doi.org/10.3390/math13182980
Yang X, Zhang Y, Wang B, Li XJ. Performance Analysis and Cost Optimization of the M/M/1/N Queueing System with Working Vacation and Working Breakdown. Mathematics. 2025; 13(18):2980. https://doi.org/10.3390/math13182980
Chicago/Turabian StyleYang, Xijuan, Yaqing Zhang, Bo Wang, and Xue Jun Li. 2025. "Performance Analysis and Cost Optimization of the M/M/1/N Queueing System with Working Vacation and Working Breakdown" Mathematics 13, no. 18: 2980. https://doi.org/10.3390/math13182980
APA StyleYang, X., Zhang, Y., Wang, B., & Li, X. J. (2025). Performance Analysis and Cost Optimization of the M/M/1/N Queueing System with Working Vacation and Working Breakdown. Mathematics, 13(18), 2980. https://doi.org/10.3390/math13182980







