A Symmetric Quantum Perspective of Analytical Inequalities and Their Applications
Abstract
1. Introduction
- What are the estimates of the symmetric quantum average integral for convex mappings?
- What is the weighted form of symmetric quantum HH inequality via symmetric mappings?
- Development of unified error approximations of quadrature procedures pertaining to Breckner’s convexity.
2. Main Results
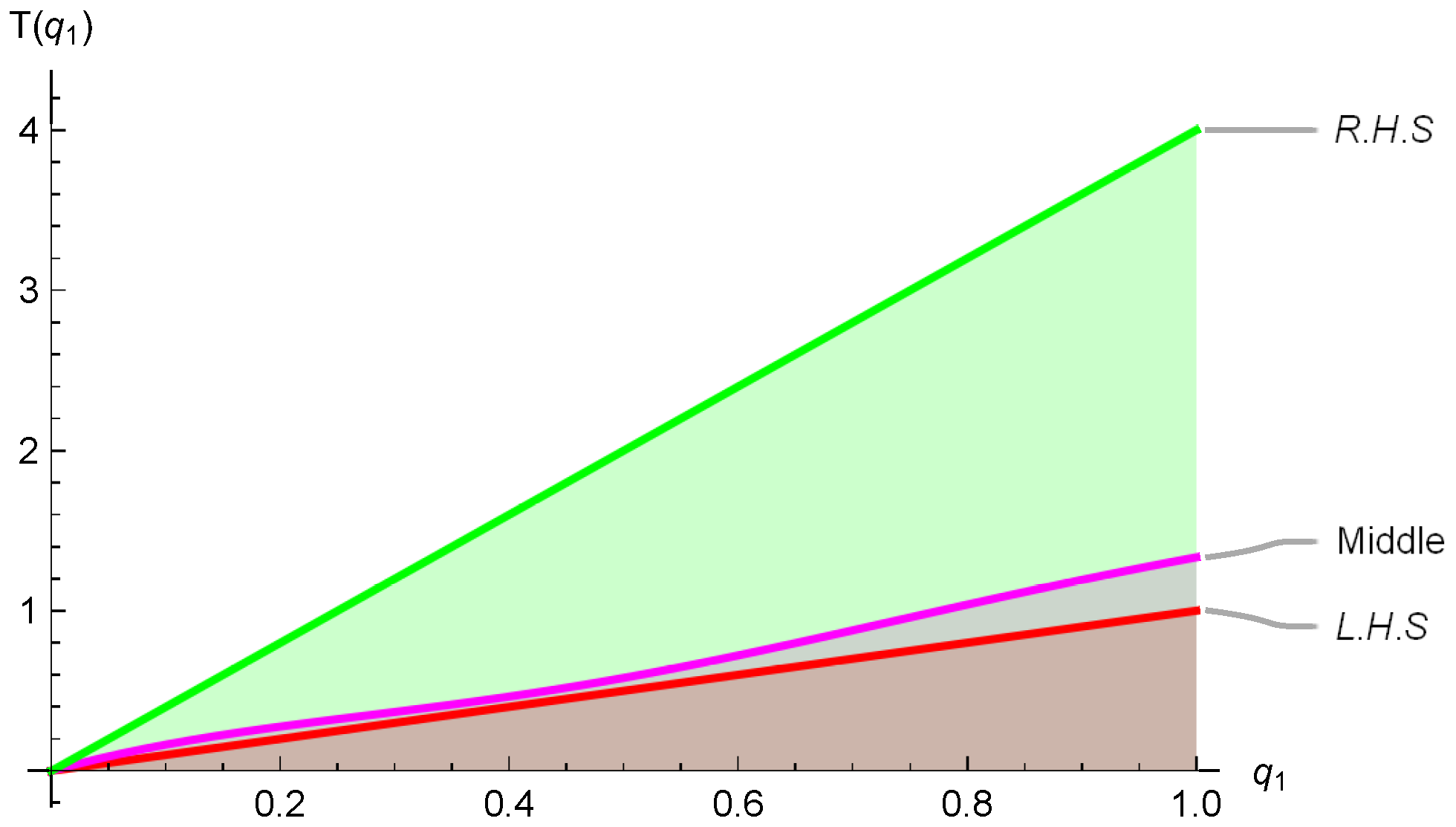
2.1. Symmetric Quantum Hermite–Hadamard’s Inequality
2.2. Hermite–Hadamard–Fejér Inequality
2.3. Symmetric Quantum Differentiable Generic Identity
- Putting in Lemma 1, we get the following general identity to derive the midpoint inequalities:
- By taking in (5), we get the following identity:
- By taking and in Lemma 1, we get the following equation to generate the bounds for general Simpson’s inequality:
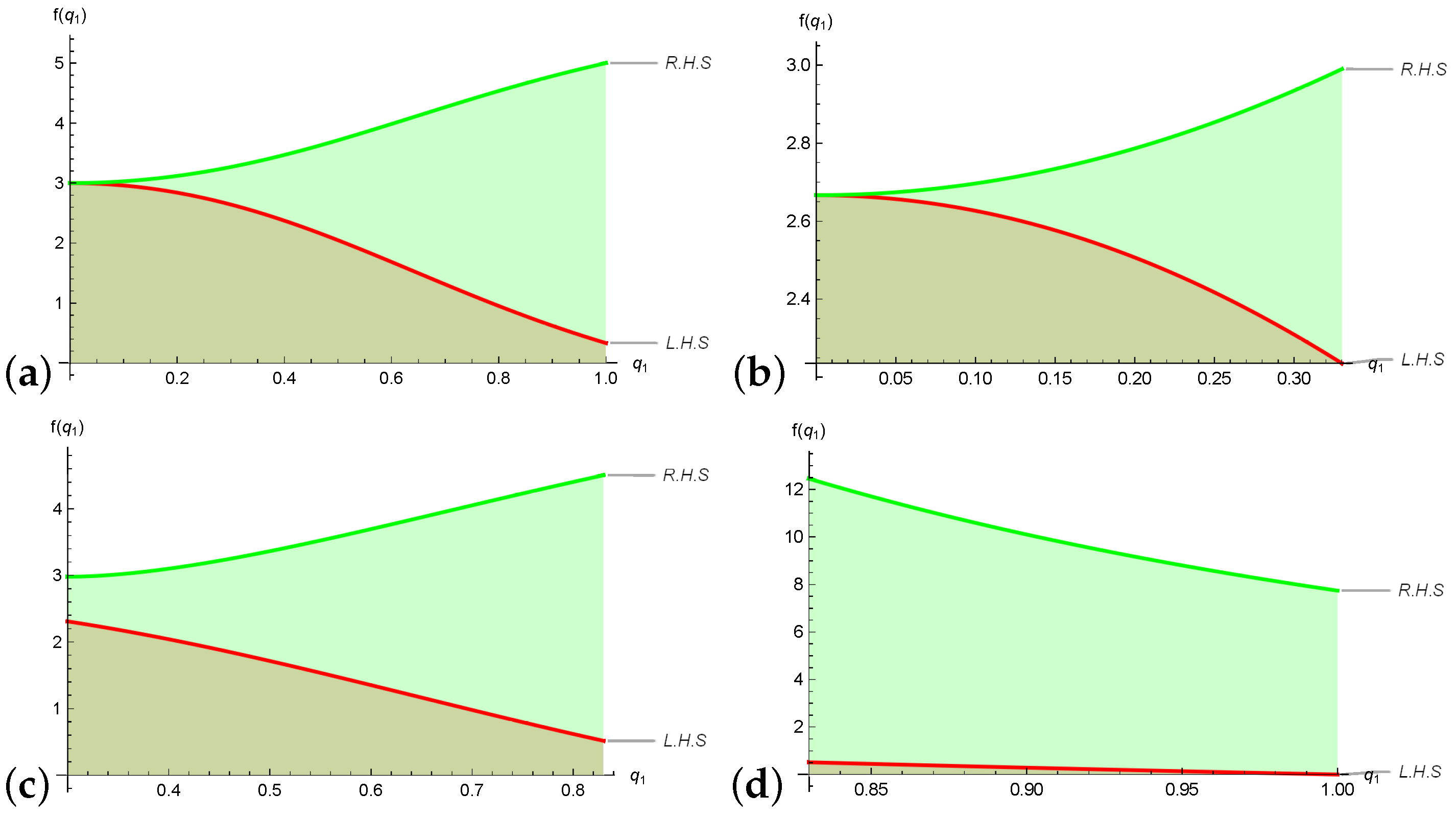
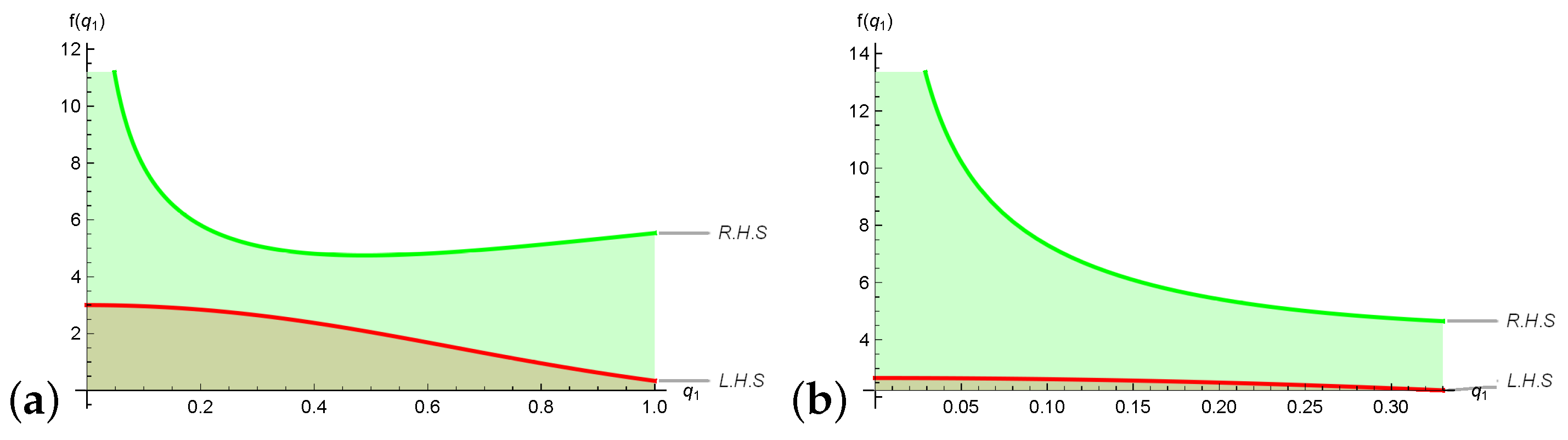
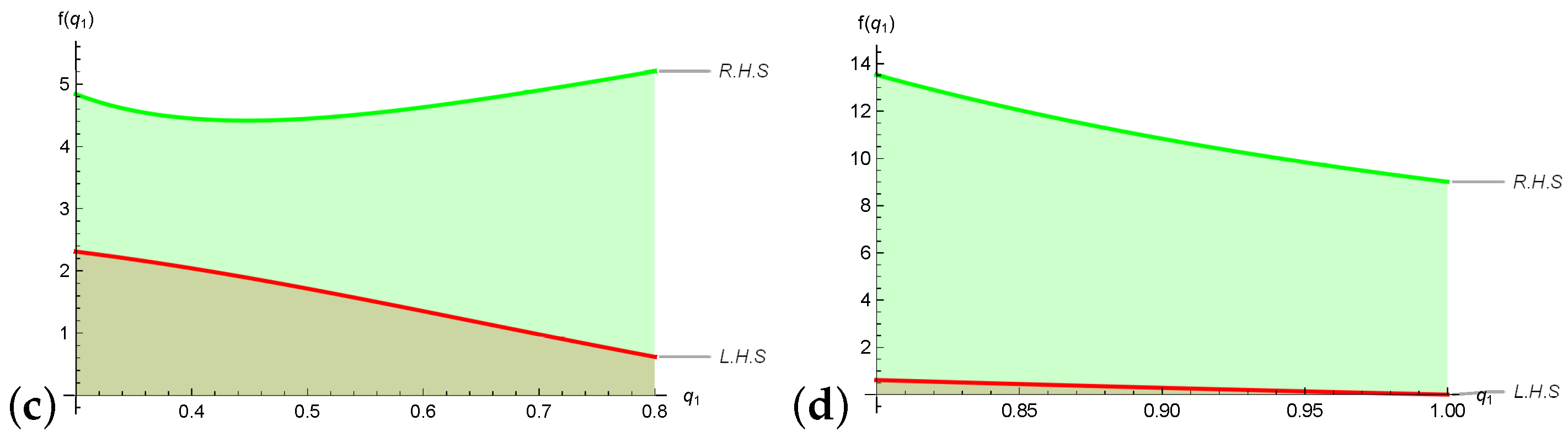
2.4. Parametric Symmetric Quantum Estimates of Error Inequalities via Breckner’s Convexity
3. Applications
- The weighted arithmetic mean is as follows:
- The generalized r-log-mean is as follows:
3.1. Application to Means
3.2. Unified Symmetric Quantum Error Boundaries of Composite-Type Scheme
4. Concluding Remarks and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roberts, A.W.; Varberg, D.E. Convex Functions, 1st ed.; Academic Press: New York, NY, USA, 1974; Volume 57. [Google Scholar]
- Dragomir, S.S.; Fitzpatrick, S. The Jensen inequality for s-Breckner convex functions in linear spaces. Demonstr. Math. 2000, 33, 43–50. [Google Scholar] [CrossRef]
- Beckenbach, E.F. Convex functions. Bull. Am. Math. Soc. 1948, 54, 439–460. [Google Scholar] [CrossRef]
- Niculescu, C.; Persson, L.E. Convex Functions and Their Applications; Springer: New York, NY, USA, 2006; Volume 23. [Google Scholar]
- Dragomir, S.S.; Fitzpatrick, S. The Hadamard inequalities for s-convex functions in the second sense. Demonstr. Math. 1999, 32, 687–696. [Google Scholar] [CrossRef]
- Tseng, K.L.; Hwang, S.R.; Dragomir, S.S. On some new inequalities of Hermite-Hadamard Fejér type involving convex functions. Demonstr. Math. 2007, 40, 51–64. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Pearce, C. Selected topics on Hermite–Hadamard inequalities and applications. Sci. Direct Work. Pap. 2003, S1574-0358-04. Available online: https://ssrn.com/abstract=3158351 (accessed on 12 April 2018).
- Butt, S.I.; Pecaric, J. Generalized Hermite–Hadamard’s inequality. Proc. A Razmadze Math. Inst. 2013, 163, 9. [Google Scholar]
- Srivastava, H.M.; Mehrez, S.; Sitnik, S.M. Hermite–Hadamard-type integral inequalities for convex functions and their applications. Mathematics 2022, 10, 3127. [Google Scholar] [CrossRef]
- Alomari, M. Several Inequalities of Hermite–Hadamard, Ostrowski and Simpson Type for s-Convex, Quasi-Convex and r-Convex Mappings and Applications. Ph.D. Thesis, Universiti Kebangsaan Malaysia, Bangi, Malaysia, 2008. [Google Scholar]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Alomari, M.; Darus, M.; Dragomir, S.S. New inequalities of Simpson’s type for s-convex functions with applications. Res. Rep. Coll. 2009, 12, 4. [Google Scholar]
- Tariboon, J.; Ntouyas, S.K. Quantum calculus on finite intervals and applications to impulsive difference equations. Adv. Differ. Equ. 2013, 2013, 282. [Google Scholar] [CrossRef]
- Alp, N.; Sarıkaya, M.Z.; Kunt, M.; İşcan, İ. q-Hermite–Hadamard inequalities and quantum estimates for midpoint type inequalities via convex and quasi-convex functions. J. King Saud Univ. Sci. 2018, 30, 193–203. [Google Scholar] [CrossRef]
- Kunt, M.; Baidar, A.W.; Sanli, Z. Some quantum integral inequalities based on left-right quantum integrals. Turk. J. Sci. Technol. 2022, 17, 343–356. [Google Scholar] [CrossRef]
- Da Cruz, A.M.C.B. Symmetric Quantum Calculus. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2012. [Google Scholar]
- Bilal, M.; Iqbal, A.; Rastogi, S. Quantum symmetric analogues of various integral inequalities over finite intervals. J. Math. Inequal. 2023, 17, 615–627. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Javed, M.Z.; Awan, M.U.; Dragomir, S.S.; Zidan, A.M. Properties and applications of symmetric quantum calculus. Fractal Fract. 2024, 8, 107. [Google Scholar] [CrossRef]
- Sudsutad, W.; Ntouyas, S.K.; Tariboon, J. Quantum integral inequalities for convex functions. J. Math. Inequal. 2015, 9, 781–793. [Google Scholar] [CrossRef]
- Jhanthanam, S.; Tariboon, J.; Ntouyas, S.K.; Nonlaopon, K. On q-Hermite–Hadamard inequalities for differentiable convex functions. Mathematics 2019, 7, 632. [Google Scholar] [CrossRef]
- Kunt, M.; Kashuri, A.; Du, T.S.; Baidar, A.W. Quantum Montgomery identity and quantum estimates of Ostrowski type inequalities. AIMS Math. 2020, 5, 5439–5457. [Google Scholar] [CrossRef]
- Bin-Mohsin, B.; Javed, M.Z.; Awan, M.U.; Khan, A.G.; Cesarano, C.; Noor, M.A. Exploration of quantum Milne–Mercer-type inequalities with applications. Symmetry 2023, 15, 1096. [Google Scholar] [CrossRef]
- Ali, M.A.; Budak, H.; Fečkan, M.; Khan, S. A new version of q-Hermite–Hadamard’s midpoint and trapezoid type inequalities for convex functions. Math. Slovaca 2023, 73, 369–386. [Google Scholar] [CrossRef]
- Khan, M.A.; Mohammad, N.; Nwaeze, E.R.; Chu, Y.M. Quantum Hermite–Hadamard inequality by means of a Green function. Adv. Differ. Equ. 2020, 2020, 99. [Google Scholar] [CrossRef]
- Saleh, W.; Meftah, B.; Lakhdari, A. Quantum dual Simpson type inequalities for q-differentiable convex functions. Int. J. Nonlinear Anal. Appl. 2023, 14, 63–76. [Google Scholar]
- Du, T.S.; Luo, C.Y.; Yu, B. Certain quantum estimates on the parameterized integral inequalities and their applications. J. Math. Inequal. 2021, 15, 201–228. [Google Scholar] [CrossRef]
- Bin-Mohsin, B.; Javed, M.Z.; Awan, M.U.; Budak, H.; Kara, H.; Noor, M.A. Quantum integral inequalities in the setting of majorization theory and applications. Symmetry 2022, 14, 1925. [Google Scholar] [CrossRef]
- Budak, H.; Ali, M.A.; Tarhanaci, M. Some new quantum Hermite–Hadamard-like inequalities for coordinated convex functions. J. Optim. Theory Appl. 2020, 186, 899–910. [Google Scholar] [CrossRef]
- Nosheen, A.; Ijaz, S.; Khan, K.A.; Awan, K.M.; Albahar, M.A.; Thanoon, M. Some q-symmetric integral inequalities involving s-convex functions. Symmetry 2023, 15, 1169. [Google Scholar] [CrossRef]
- Butt, S.I.; Aftab, M.N.; Seol, Y. Symmetric quantum inequalities on finite rectangular plane. Mathematics 2024, 12, 1517. [Google Scholar] [CrossRef]
- Liu, Q.; Javed, M.Z.; Awan, M.U.; Ciurdariu, L.; Alkahtani, B.S. Hermite–Hadamard’s like inequalities via symmetric quantum calculus. Ain Shams Eng. J. 2025, 16, 103372. [Google Scholar] [CrossRef]
- Nosheen, A.; Ijaz, S.; Khan, K.A.; Awan, K.M.; Budak, H. Quantum symmetric integral inequalities for convex functions. Math. Methods Appl. Sci. 2024, 47, 14878–14895. [Google Scholar] [CrossRef]
- Wang, Y.; Javed, M.Z.; Awan, M.U.; Bin-Mohsin, B.; Meftah, B.; Treanta, S. Symmetric quantum calculus in interval valued framework: Operators and applications. AIMS Math. 2024, 9, 27664–27686. [Google Scholar] [CrossRef]
- İşcan, İ. A new generalization of some integral inequalities and their applications. Int. J. Eng. 2013, 3, 8269. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, M.Z.; Naeem, N.; Awan, M.U.; Wang, Y.; Alsalami, O.M. A Symmetric Quantum Perspective of Analytical Inequalities and Their Applications. Mathematics 2025, 13, 2910. https://doi.org/10.3390/math13182910
Javed MZ, Naeem N, Awan MU, Wang Y, Alsalami OM. A Symmetric Quantum Perspective of Analytical Inequalities and Their Applications. Mathematics. 2025; 13(18):2910. https://doi.org/10.3390/math13182910
Chicago/Turabian StyleJaved, Muhammad Zakria, Nimra Naeem, Muhammad Uzair Awan, Yuanheng Wang, and Omar Mutab Alsalami. 2025. "A Symmetric Quantum Perspective of Analytical Inequalities and Their Applications" Mathematics 13, no. 18: 2910. https://doi.org/10.3390/math13182910
APA StyleJaved, M. Z., Naeem, N., Awan, M. U., Wang, Y., & Alsalami, O. M. (2025). A Symmetric Quantum Perspective of Analytical Inequalities and Their Applications. Mathematics, 13(18), 2910. https://doi.org/10.3390/math13182910






