On the Autocorrelation and Stationarity of Multi-Scale Returns

Abstract

In this article, we conduct a statistical analysis of the autocorrelation functions (ACF) of multi-scale logarithmic returns computed over maximal monotonic uninterrupted trends (runs) in financial indices’ daily data. We analyze the Dow Jones Industrial Average (DJIA) and the Mexican IPC (Índice de Precios y Cotizaciones) over a period from 30 October 1978 to 19 May 2025. We examine how deterministic alternation of signs shapes the ACF of multi-scale returns, and we evaluate covariance stationarity via formal tests (e.g., Augmented Dickey–Fuller and Phillips–Perron). We conclude that, despite the persistent long-memory oscillations in the ACF, multi-scale return series pass the stationarity tests, an outcome with interesting implications for econometric modeling of financial time series.

1. Introduction to Multi-Scale (Trend) Returns in Financial Markets

Financial markets are complex economic systems that exhibit dynamic behavior across multiple time scales. Analyzing these behaviors requires a framework that captures both short-term fluctuations and long-term trends.

In this context, we introduced the concept of multi-scale returns or Trend Returns, as we termed them in [1,2], as a robust observable for the analysis of market dynamics, constructed over non-arbitrary time scales, specifically, the durations of uninterrupted elementary trends or price runs in financial indices or individual stocks. For the classical mathematical introduction to runs, see [3]. For additional references to classical papers and applications of runs, including those in finance, see [4].

This approach is based on the principles of econophysics and econometrics, two complementary disciplines in our view, that have significantly advanced the study of financial systems. By combining these insights, the concept of multi-scale returns can be employed to detect underlying trends that traditional single-scale approaches may overlook.

Multi-scale returns are the aggregate of daily same-sign, consecutive returns, or equivalently, the returns calculated from uninterrupted alternated uptrends and downtrends over different time intervals given by the durations of these daily uninterrupted trends. This naturally accounts for different non-arbitrary time scales, allowing for the identification of short-lived market same-direction variations. In addition, due to their construction, multi-scale returns balance the proportion of positive and negative values in their dataset, which is important for studying market symmetry and asymmetry. These properties make multi-scale returns particularly useful for identifying periods of market inefficiency, understanding risk dynamics, and detecting potential arbitrage opportunities [5,6,7,8,9].

As described in Section 2, and based on their construction, given that multi-scale returns are derived from price runs in financial indices, the terms of their corresponding time series clearly alternate in sign. This introduces long-range correlations, making the variable not strictly stationary. In this paper, we study the structure of the autocorrelation function (ACF) of this observable in Section 4, where we show that it exhibits damped oscillations with envelopes characterized by exponential and power-law decays. Furthermore, in Section 5, we examine the stationarity of the multi-scale returns time series using standard statistical tests, which they pass, perhaps unexpectedly, highlighting the nature of this variable. We conclude the article with a discussion and summary of our findings in Section 6.

In our opinion, multi-scale returns offer a robust tool for analyzing financial data across different time scales. As an approach of potential interest to both the physical modeling of econophysics and the statistical rigor of econometrics, it enhances our understanding of financial markets by offering insights into their complex behavior and a broader perspective on market trends and risks.

2. Data Sample

The dataset analyzed in this article consists of daily closing values for the Dow Jones Industrial Average (DJIA) and the Mexican Índice de Precios y Cotizaciones (IPC), obtained from Yahoo Finance (www.yahoo.com/finance, accessed on 19 May 2025) and Investing.com (https://www.investing.com, accessed on 19 May 2025). It covers the period from 30 October 1978 to 19 May 2025. The DJIA sample consists of 11,773 records, while the IPC sample comprises 11,634 records.

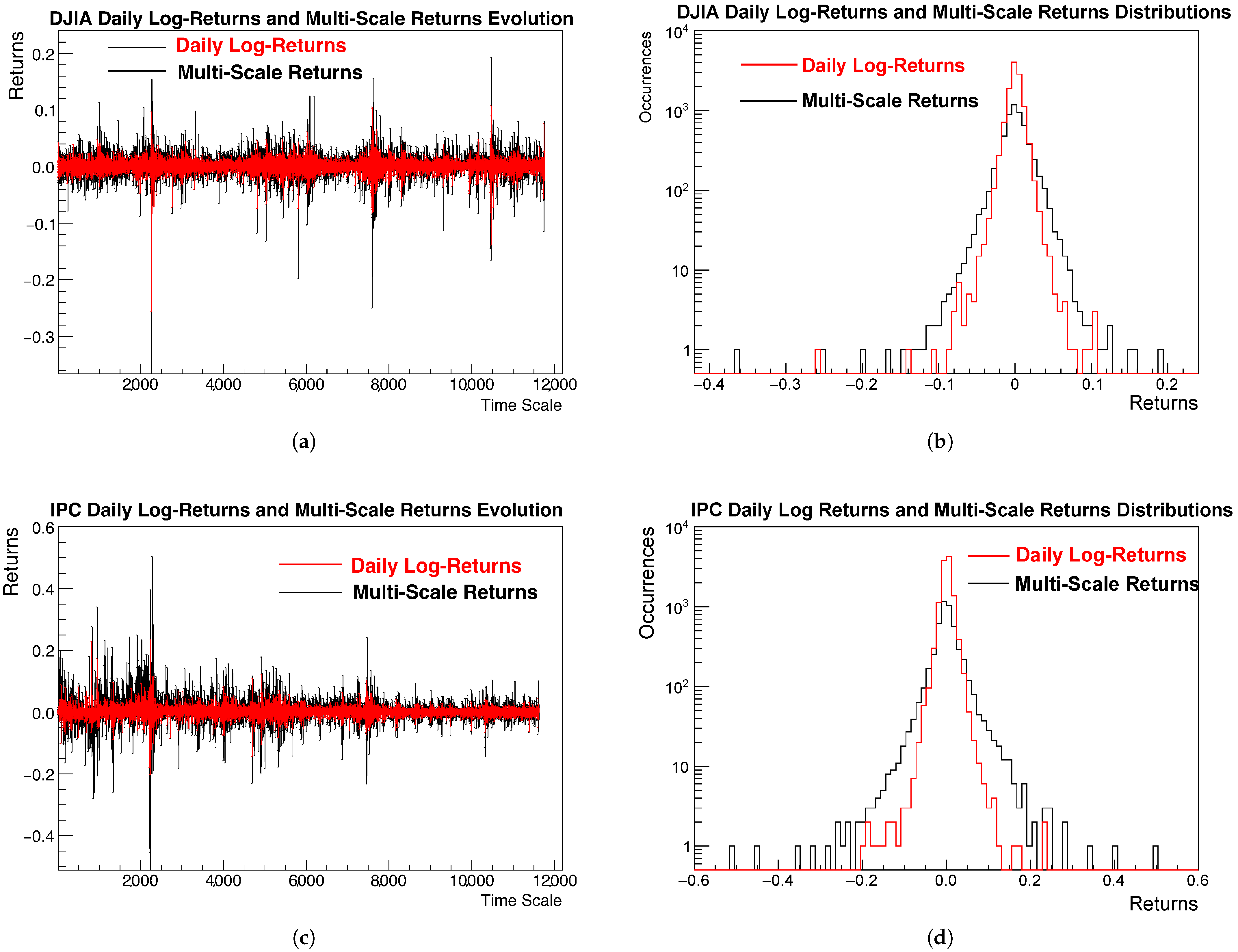
Figure 1 shows and compares the time evolution of standard daily returns (in red) and the multi-scale returns (in black) for the DJIA (panel (a)) and IPC (panel (c)). Panels (b) and (d) show their corresponding return distributions.

To overlay and compare the evolution of the two return types, multi-scale returns are accumulated and plotted over time by aggregating daily returns with the same sign.

Regarding the distributions of both return types, it remains unclear whether multi-scale returns are strictly or weakly stationary. However, their time series do not exhibit trends, and the means of both return types are close to zero.

At this initial stage, it is sufficient to compare multi-scale returns with conventional daily logarithmic returns, keeping in mind that the former are computed as the logarithmic difference between the extreme prices of each uninterrupted trend identified in the daily data of the financial indices under study. A more detailed discussion of the construction of multi-scale returns is provided in Section 3, and their stationarity is addressed in Section 5.

The four panels of Figure 1 show that multi-scale returns exhibit larger variations than the standard daily returns, as expected, since the former accumulate same-sign daily variations. We also observe that the variance of multi-scale returns exceeds that of the daily returns. Additionally, the means of both return series are effectively zero.

All these properties are confirmed by the descriptive statistics of both types of returns for the two studied financial markets displayed in

Table 1. Descriptive statistics of the multi-scale and daily returns for the DJIA and IPC indices. For each time series, the table reports the number of entries, the mean, the root mean square (RMS), the skewness, and the kurtosis. The multi-scale returns exhibit larger variability and higher absolute skewness and kurtosis values compared with the daily returns, reflecting their aggregated nature.

Index	Returns Type	Entries	Mean	RMS	Skewness	Kurtosis
DJIA	Multi-Scale	5994	$6.67\times {10}^{-4}$	$0.022$	$-1.19$	$22.37$
DJIA	Daily	11,773	$3.37\times {10}^{-4}$	$0.011$	$-1.38$	$36.11$
IPC	Multi-scale	5014	$2.24\times {10}^{-3}$	$0.042$	$0.046$	$20.05$
IPC	Daily	11,634	$9.65\times {10}^{-4}$	$0.017$	$0.004$	$20.38$

.

The following section explains how our analyzed observables are constructed from the DJIA and IPC data samples.

3. Methodology and Construction of Our Observables

The construction of multi-scale returns, or Trend Returns, consists in aggregating consecutive daily logarithmic returns with the same sign, either positive for upward movements or negative for downward movements, until a change in sign occurs in the next return. This is equivalent to computing the multi-scale return as the logarithmic difference between the initial and final prices of a price run, that is, an uninterrupted sequence of increasing or decreasing prices. Each multi-scale return is thus obtained by subtracting the logarithm of the initial price of the run from the logarithm of its final price.

More formally, we begin by identifying all uninterrupted monotonic trends within a financial time series ${\left\{P_t\right\}}_{t=1}^N$, where N denotes the total number of observations, and $P_t$ denotes the price of an asset or an index value at discrete time t. The i-th uninterrupted monotonic trend of duration k (measured in days, in our case), starting at time $t=l$ and ending at $t=l+k$, is defined as a sequence of $k+1$ consecutive prices moving consistently in the same direction, either upward or downward, without reversals:

$$\mathrm{Upward}\mathrm{Trend}:P_{l_0}^i<P_{l_1}^i<\dots <P_{l_k}^i,$$

(1)

$$\mathrm{Downward}\mathrm{Trend}:P_{l_0}^i>P_{l_1}^i>\dots >P_{l_k}^i,$$

(2)

where $l=l_0$ and $l+k=l_k$ explicitly denote the initial and final time steps of the i-th uninterrupted trend, respectively.

It is known that the distribution of the duration of uninterrupted trends exhibits exponential decay in the continuous [10] case and geometric decay in the discrete setting [4].

In what follows, we shall refer to an uninterrupted monotonic trend simply as a trend.

Calculating Multi-Scale Returns

For each one of the uninterrupted trends, we compute the associated multi-scale return by using the logarithmic difference between the final and initial prices of the trend i-th:

$$R_{l_k}^i=log\left({\displaystyle \frac{P_{l_k}^i}{P_{l_0}^i}}\right)=log{P}_{l_k}^i-log{P}_{l_0}^i,$$

(3)

where $i=1,2,\dots m$, $m<N$ is the number of trends or multi-scale returns, and $R_{l_k}^i$ denotes the multi-scale return associated with the i-th trend, which begins at time $l_0$ and ends at time $l_k$. The sequence of trends is constructed such that the ending price of one trend becomes the initial price of the next, i.e.,

$$P_{l_k}^{\left(i\right)}=P_{{(l+k)}_0}^{(i+1)}.$$

(4)

This procedure yields a sequence of m multi-scale returns:

$$R_{l_1}^1,R_{l_2}^2,\dots ,R_{l_m}^m,$$

where each return corresponds to a distinct trend. It is important to note that the total number of multi-scale returns, m, is equal to the number of identified trends, and the sum of the durations of all trends satisfies

$$\sum _{i=1}^m\left(t_k^i-t_0^i\right)=N,$$

where N, as previously stated, denotes the total number of time steps covered by the full price series, and our notation specifies that the sum is performed on the extremes of trends.

Multi-scale returns capture the cumulative price change over the duration of the trend, whether it is upward or downward. Importantly, the duration of each trend, defined as $t_k-t_0$ varies depending on the persistence of the monotonic movement in prices. This natural variability in trend lengths enables the construction of a return series over multiple, data-driven time scales rather than over arbitrarily fixed intervals, providing a more adaptive perspective on market dynamics.

4. Methodology ACF Analysis

It is well known that the autocorrelation function (ACF) of standard daily returns decays rapidly to zero, whereas the ACF of absolute or squared returns exhibits long-term memory, decaying slowly as a power law [11]. For the type of multi-scale returns analyzed in this work, we expect the ACF to display long-memory behavior. This expectation stems from the construction of the multi-scale returns, where a positive multi-scale return is necessarily followed by a negative one, and vice versa. As a consequence, an oscillatory ACF centered around zero naturally emerges.

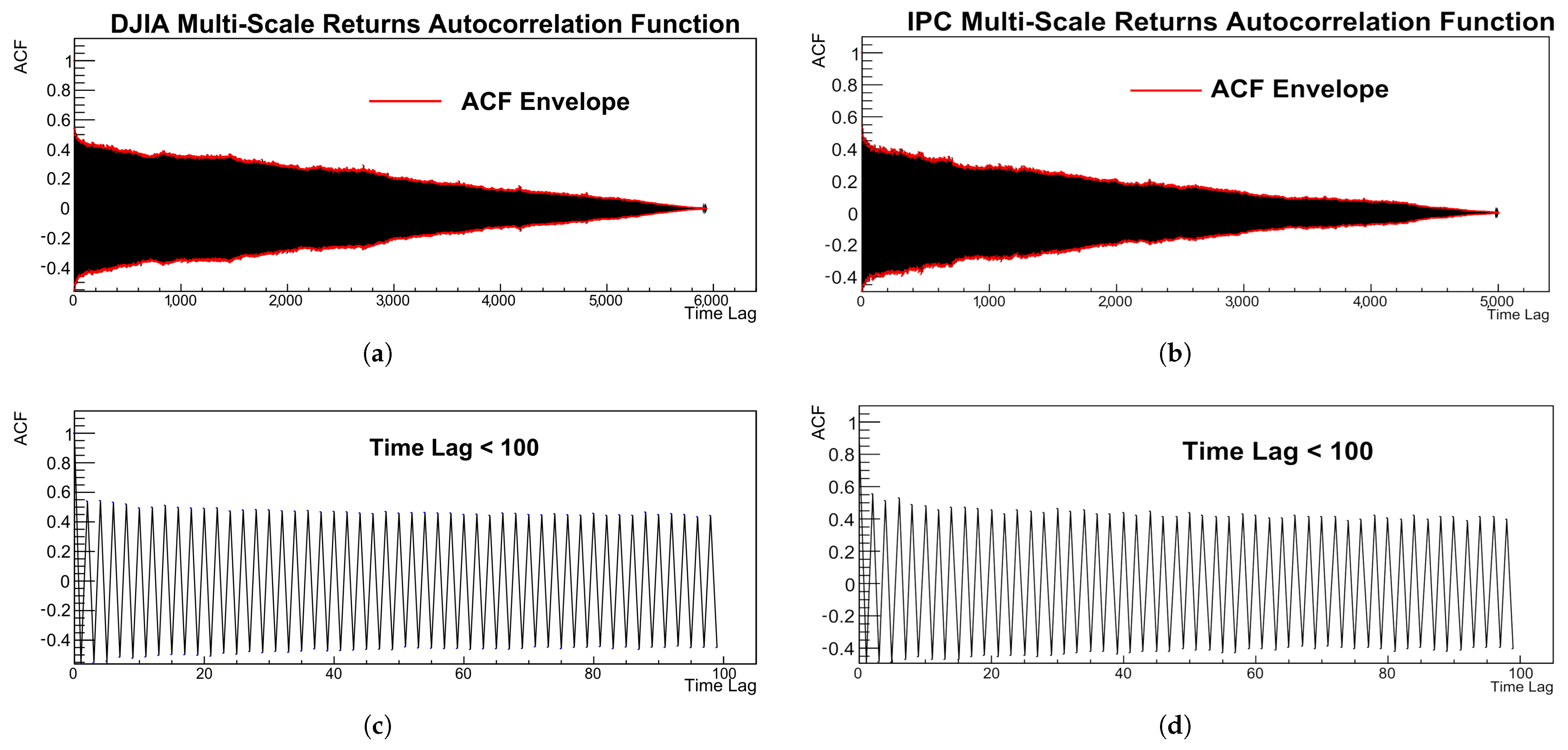
As expected, the ACF of the multi-scale returns, shown in Figure 2, reveals a distinctive, slowly decaying oscillatory pattern for both the DJIA and IPC indices. This pattern is characterized by alternating positive and negative correlations whose amplitudes gradually diminish with increasing lag, resembling damped oscillations. The oscillatory behavior is particularly evident in the zoomed-in views of the short-lag domain (panels (c) and (d)), while the upper panels (a) and (b) display the full ACF along with its asymmetric positive and negative envelopes (red lines).

To better understand and model the structure of these autocorrelations, we analyze the functional form of the ACF envelopes. In particular, we fit exponential decays in the short-lag regime and power-law decays in the intermediate-lag regime. The methodology and results of these envelope fits are presented below, for both the DJIA and the IPC indices.

ACF Envelope Fitting

To fit the envelopes of the autocorrelation function (ACF), we use ROOT version 6.36.00 [12], a data analysis software developed at CERN (European Organization for Nuclear Research), widely used in high-energy physics and well suited for statistical modeling and visualization. In our case, the positive and negative envelopes of the ACF of multi-scale returns are fitted using two different functional forms, depending on the time-lag regime: exponential decay for short lags and power-law decay for intermediate lags.

For the short-lag regime, we apply an exponential fit of the form:

$$f\left(x\right)=e^{(p_0+p_{1}x)},$$

(5)

where $p_0$ and $p_1$ are free parameters optimized during the fit. This expression is equivalent to

$$f\left(x\right)=A·e^{Bx}\mathrm{with}A=e^{p_0},\mathrm{and}B=p_1.$$

(6)

ROOT reports $p_0$ as the “Constant” and $p_1$ as the “Slope” in the fit output. Since the ACF values are typically small for financial time series, $p_0$ is often negative, resulting in an amplitude $A<1$. The fits are performed in linear coordinates, while the results are displayed on a logarithmic vertical scale to visually linearize the exponential decay.

For the intermediate-lag regime, we assume a power-law decay of the form:

$$f\left(x\right)=C·x^{-\alpha },$$

(7)

where C is a constant and $\alpha$ is the decay exponent. Instead of fitting this function directly, we apply a logarithmic transformation to both the time lag and the ACF values, obtaining a linear relation:

$$logf\left(x\right)=logC-\alpha logx.$$

(8)

This allows us to fit a straight line to the transformed data using ROOT’s linear fitting tools. Specifically, we plot $log\left(\mathrm{ACF}\right)$ vs. $log\left(\mathrm{time}\mathrm{lag}\right)$ for the positive envelope, and $log(-\mathrm{ACF})$ vs. $log\left(\mathrm{time}\mathrm{lag}\right)$ for the negative envelope, and fit the linear model:

$$y=p_0+p_{1}x,$$

(9)

where $p_1=-\alpha$, $p_0=logC$, $y=logf\left(x\right)$, $x=log\left(\mathrm{Time}\mathrm{Lag}\right)$. The slope $p_1$ thus directly yields the power-law exponent. This transformation enables robust estimation of the long-memory decay observed in the intermediate-lag region.

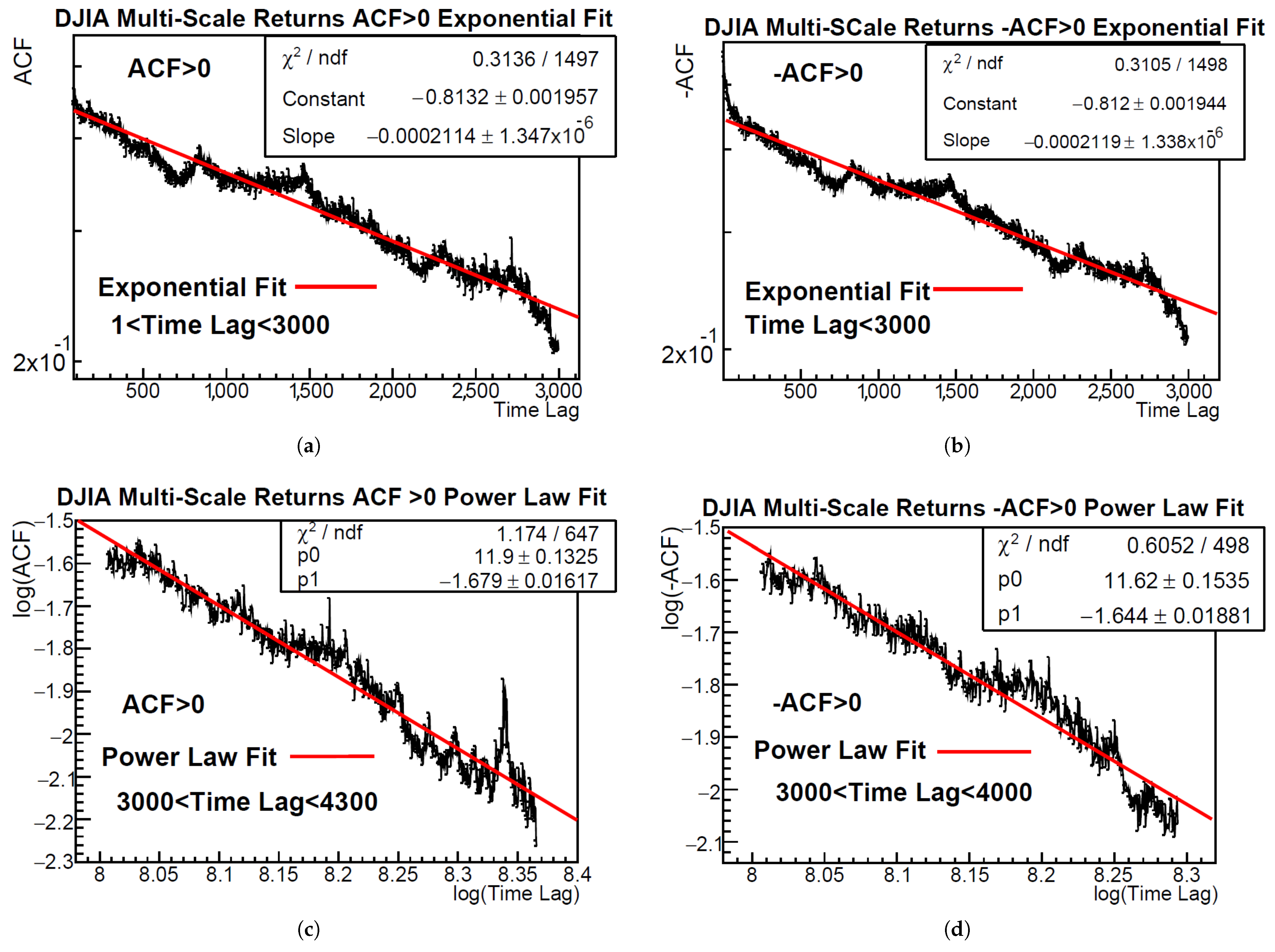
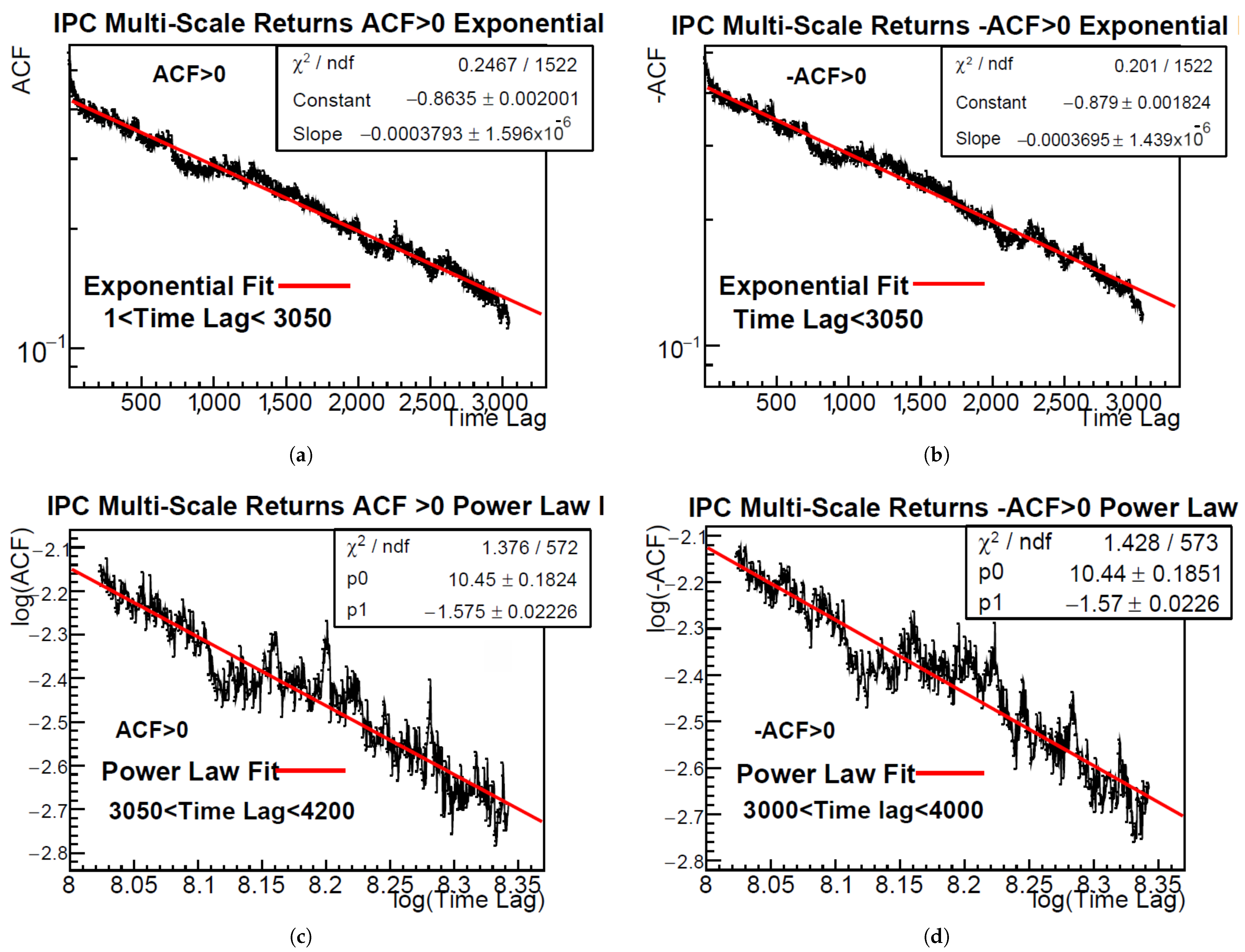
The results of these fits are illustrated in Figure 3 and Figure 4, which display the exponential and power-law fits to the positive and negative envelopes of the ACF for both the DJIA and IPC multi-scale returns. The exponential fits, shown for short time lags, exhibit excellent agreement with the data in linear-log scale, while the power-law fits applied to intermediate lags display a clear linear trend in log–log coordinates. These figures confirm the presence of distinct scaling behaviors across different lag regimes and highlight the suitability of the proposed functional forms.

The following tables summarize the results of the ROOT fits applied to the positive and negative envelopes of the ACF for both the DJIA and IPC indices. All fits were performed in lag intervals where the empirical behavior suggests approximate power-law decay.

Although from Figure 3 and Figure 4 and

Table 2. Root exponential fits of the autocorrelation function (ACF) envelopes for DJIA and IPC multi-scale returns in the short-lag regime. The table shows the slope and constant of the exponential fit for both positive and negative envelopes. A logarithmic vertical scale was used for visualization. The ${\chi }^2/\mathrm{ndf}$ and the pass/fail result of the fit are also reported.

Market	Envelope	Lag	Slope ${\mathit{p}}_1$	Constant ${\mathit{p}}_0$	${\mathit{\chi }}^2/\mathbf{ndf}$	Result
DJIA	Positive	$(1,3000)$	$(-211.4\pm 1.3)\times {10}^{-6}$	$-0.813\pm 0.002$	0.3136/1497	Pass
DJIA	Negative	$(0,3000)$	$(-211.9\pm 1.3)\times {10}^{-6}$	$-0.812\pm 0.002$	0.3105/1498	Pass
IPC	Positive	$(1,3050)$	$(-379.3\pm 1.6)\times {10}^{-6}$	$-0.864\pm 0.002$	0.2467/1522	Pass
IPC	Negative	$(0,3050)$	$(-369.5\pm 1.4)\times {10}^{-6}$	$-0.889\pm 0.002$	0.201/1522	Pass

and

Table 3. Root power-law fits of the autocorrelation function (ACF) envelopes for DJIA and IPC multi-scale returns. For each envelope (positive and negative), a linear fit was applied to the logarithms of ACF and time lag. The table reports the intercept, exponent, and goodness-of-fit statistic ${\chi }^2/\mathrm{ndf}$. The result column indicates whether the fit passes the standard goodness-of-fit criterion ${\chi }^2/\mathrm{ndf}<2$.

Market	Envelope	Lag	Intercept ${\mathit{p}}_0$	Exponent ${\mathit{p}}_1$	${\mathit{\chi }}^2/\mathbf{ndf}$	Result
DJIA	Positive	$(3000,4300)$	$11.90\pm 0.13$	$-1.679\pm 0.016$	1.174/647	Pass
DJIA	Negative	$(3000,4000)$	$11.62\pm 0.15$	$-1.644\pm 0.189$	0.605/498	Pass
IPC	Positive	$(3050,4200)$	$10.45\pm 0.18$	$-1.575\pm 0.022$	1.376/572	Pass
IPC	Negative	$(3000,4000)$	$10.44\pm 0.19$	$-1.570\pm 0.023$	1.428/573	Pass

the fits appear to be good, and although a low ${\chi }^2/\mathrm{ndf}$ value is generally interpreted as a good fit, values significantly smaller than 1 may indicate that the uncertainties assigned to the data points may be overestimated or that the model is overfitting the data [13]. To provide a more robust assessment of the fits, we now present the results of three complementary goodness-of-fit tests: the coefficient of determination ($R^2$), the bootstrap-based 95% confidence interval for $R^2$, and the Anderson–Darling (AD) goodness-of-fit test. The coefficient of Determination $R^2$ measures the proportion of variance in the empirical ACF explained by the fitted power-law model. A value close to 1 indicates excellent fit quality. The Bootstrap Confidence Interval for $R^2$ assesses the stability of the $R^2$ estimate, and we used bootstrap resampling with 1000 iterations. This yields a confidence interval for the expected $R^2$, helping to verify the robustness of the fit against sample variability and the Anderson–Darling (AD) test applied to the residuals, which verifies whether the residuals follow a normal distribution.

Results of these complementary fits are displayed in

Table 4. Goodness-of-fit statistics for the exponential and power-law models fitted to the ACF envelopes of multi-scale returns. The table reports the coefficient of determination ($R^2$), bootstrap confidence intervals for $R^2$ (95% CL), the Anderson–Darling (AD) test statistic, and the test result at the 10% significance level. All fits were performed over the relevant lag intervals for each model.

Market	Envelope	Model	${\mathit{R}}^2$	Bootstrap CI for ${\mathit{R}}^2$	AD Statistic	AD Test @10%
DJIA	Positive	Exponential	0.950	[0.945, 0.954]	3.53	Pass
DJIA	Negative	Exponential	0.953	[0.949, 0.957]	3.54	Pass
IPC	Positive	Exponential	0.981	[0.978, 0.983]	0.77	Pass
IPC	Negative	Exponential	0.981	[0.980, 0.983]	0.31	Pass
DJIA	Positive	Power Law	0.943	[0.932, 0.953]	2.25	Pass
DJIA	Negative	Power Law	0.939	[0.929, 0.948]	0.19	Pass
IPC	Positive	Power Law	0.918	[0.906, 0.930]	1.23	Pass
IPC	Negative	Power Law	0.864	[0.840, 0.886]	0.16	Pass

below.

Regarding the Anderson–Darling (AD) test, all models pass at the 10% significance level. While a few cases show elevated AD statistics (marked with an asterisk), these values remain within acceptable bounds at this relaxed threshold. This suggests that although minor deviations from ideal residual behavior exist, likely due to heavy tails or non-Gaussian fluctuations, these do not invalidate the underlying fitted models. In summary, the complementary goodness-of-fit tests show that both exponential and power-law models accurately describe the decay behavior of the ACF envelopes across different lag regimes. All fits exhibit high $R^2$ values and narrow bootstrap confidence intervals, confirming the consistency and reliability of the models. As commented previously, all fitted models pass the Anderson–Darling test at the 10% significance level. This result, together with high $R^2$ values and narrow bootstrap confidence intervals, supports the reliability of the exponential and power-law fits to the ACF envelopes. In contrast, the asymptotic behavior of the ACF envelopes, although suggestive of power-law decay, did not pass our goodness-of-fit criteria. Further investigation is needed to clarify the nature of these asymptotic decays in the context of multi-scale returns.

5. Testing the Stationarity of Returns Multi-Scale

The stationarity analysis was performed using Mathematica version 14.2 [14]. Before presenting the formal results, it is worth noting from Figure 1b,d that the empirical distribution of multi-scale returns suggests that the underlying process may be stationary. In particular, the histogram exhibits a stable and well-defined shape over the entire time span, with no visible spreading or distortion that would indicate a time-evolving distribution. Moreover, the evolution over time of multi-scale returns shown in Figure 1a,c does not display persistent trends or shifts in the mean, which are common indicators of non-stationarity. These qualitative observations support the hypothesis that the statistical properties of the series are stable over time, thus motivating a more rigorous stationarity assessment.

To assess the stationarity of the log multi-scale returns derived from the DJIA and the Mexican IPC financial indices, we applied four standard unit root tests: the Dickey–Fuller F-test, Dickey–Fuller t-test, Phillips–Perron F-test, and Phillips–Perron t-test [15]. All tests were conducted under the null hypothesis that the time series contains a unit root, using an autoregressive model of order 1 without a constant offset and without a deterministic trend. The results are shown in

Table 5. Stationarity test results for DJIA and IPC multi-scale returns. “t” denotes the t-statistic for the unit root coefficient; “F” denotes the corresponding F-statistic for the joint hypothesis tests.

Index	Test	Test Statistic	p-Value
DJIA	Dickey–Fuller (ADF) F	$-9268.75$	$4.85\times {10}^{-25}$
DJIA	Dickey–Fuller (ADF) t	$-145.07$	$3.64\times {10}^{-30}$
DJIA	Phillips–Perron (PP) F	−10,105.20	$2.40\times {10}^{-25}$
DJIA	Phillips–Perron (PP) t	$-133.16$	$1.43\times {10}^{-29}$
IPC	Dickey–Fuller (ADF) F	$-7466.73$	$2.82\times {10}^{-24}$
IPC	Dickey–Fuller (ADF) t	$-120.91$	$6.66\times {10}^{-29}$
IPC	Phillips–Perron (PP) F	$-9237.39$	$4.99\times {10}^{-25}$
IPC	Phillips–Perron (PP) t	$-107.58$	$4.30\times {10}^{-28}$

:

From results shown in Table 5, we observe that all statistics are highly negative with p-values extremely small, thereby confirming that the DJIA and IPC multi-scale return series pass the stationarity tests of Dickey–Fuller F-test, Dickey–Fuller t-test, Phillips–Perron F-test, and Phillips–Perron t-test [16]. These extremely small p-values arise due to the large (negative) values of the test statistics, which lie far into the left tail of the asymptotic distributions under the null hypothesis. In long time series with high signal-to-noise ratios and strong mean reversion, such outcomes are not uncommon. They indicate statistical evidence against the unit root hypothesis.

So far, we have shown that multi-scale returns fail the ACF-based stationarity test, since the autocorrelation function does not decay rapidly toward zero, suggesting that this observable is not stationary, yet they do pass other stationarity tests, such as those used here. We will discuss this further in Section 6.

6. Conclusions

Although this paper focuses on two stock indices (DJIA and IPC), the general aggregation mechanism underlying multi-scale returns can be applied to any asset price series, suggesting that the observed features may be universal. Further studies are needed to test this across markets and conditions.

Multi-scale returns exhibit a distinctive structure characterized by alternating signs and longer durations between changes in direction. This construction induces a slowly decaying autocorrelation function (ACF), which would traditionally suggest the presence of long memory and, hence, non-stationarity. In fact, when evaluated using ACF-based criteria, the time series does not pass the stationarity test.

However, other standard tests for weak stationarity, such as the Augmented Dickey–Fuller (ADF) test, yield strong evidence in favor of stationarity for both the DJIA and IPC multi-scale return series. These tests indicate that the mean and variance of the series remain stable over time and that no unit roots are present.

There is no real contradiction between observing that multi-scale returns fail the ACF-based criterion for stationarity and that they pass the formal stationarity tests presented in this article. What we observe is simply a weaker form of stationarity than conventional weak stationarity, one that even standard daily returns fail to satisfy. The slow decay of the ACF arises from the sign-alternating nature of multi-scale returns, which is deterministic in structure and not a result of evolving statistical properties or stochastic non-stationarity.

In this context, the Augmented Dickey–Fuller and Phillips–Perron tests, designed to detect unit roots and assess constancy of the mean, do not reject the null hypothesis of stationarity for the multi-scale return series. These tests are not sensitive to time-varying volatility or heteroskedasticity, which are well-known features of financial returns. As with conventional returns, multi-scale returns are better described as stationary in mean but conditionally heteroskedastic. Thus, while they exhibit an even weaker form of stationarity than fixed-scale returns, they can still be treated as stationary for analytical and econometric purposes, which may be the most significant implication of our study. Accordingly, our future work will focus on studying and characterizing the statistical distribution and properties of multi-scale returns.

By construction, multi-scale returns are well suited to study, among other topics, the symmetry properties of financial time series, to detect extreme events such as dragon kings, and remain open to further identification of the stylized facts they may exhibit [11,17,18].

Hence, a natural direction for future work is to investigate the underlying mechanisms responsible for the heavy tails and non-Gaussian features observed in multi-scale return distributions. Such an analysis would require exploring how known stylized facts manifest in this new framework, which lies beyond the scope of the present study but builds directly on the stationarity results established here.

Finally, the reported empirical features, such as the characterization of the slowly decaying ACF, provide new benchmarks that any realistic financial market simulation or agent-based model should aim to reproduce. In this sense, our results may serve as nontrivial validation criteria for synthetic models. Nevertheless, further theoretical and numerical investigations are required to determine the conditions under which this behavior emerges and to gain a deeper understanding of its implications for market modeling.