Abstract
This study investigates the dynamic behavior of a discrete epidemic model as affected by media coverage through integrated analytical and numerical methods. The main objective is to quantitatively assess the impact of media coverage on disease outbreak models through mathematical modeling. We use the central manifold theorem and bifurcation theory to perform a rigorous analysis of the periodic solutions, focusing on the coefficients and conditions governing the flip bifurcation. On this basis, state feedback and hybrid control are utilized to control the system chaotically. Under certain conditions, the chaos and bifurcation of the system can be stabilized by the control strategy. Numerical simulations further reveal the bifurcation dynamics, chaotic behavior, and control techniques. Our results show that media coverage is a key factor in regulating the intensity and chaos of disease transmission. Control techniques can effectively prevent large-scale outbreaks of epidemics. Notably, enhanced media coverage can effectively increase public awareness and defensive behaviors, thus contributing to mitigating disease spread.
MSC:
39A28; 39A30
1. Introduction
Infectious disease modeling links mathematical theory with public health practice, and has always played a key role in the long history of human fight against infectious diseases. The outbreak of major infectious diseases not only threatens human health but also poses a serious challenge to economic development and social security. In order to cope with this threat, it is of great theoretical and practical significance to explore the complex dynamic behavior of the mathematical model of infectious diseases. Through the classical models such as SIR and SIS constructed by scholars and their extended research, human beings can quantitatively analyze the law of virus transmission, and predict the development trend of the epidemic [1,2,3,4]. The classical SIR model is suitable for diseases that acquire lifelong immunity after cure, while some diseases that do not acquire immunity after cure can be modeled with the SIS model [5,6,7,8].
On this basis, prevention and control strategies such as isolation and vaccination have been adopted to prevent the spread of diseases. Nowadays, media coverage plays an equally important role in the spread and control of infectious diseases [9,10,11]. During the COVID-19 pandemic, timely and transparent outbreak notification increased public protective behavior compliance by 37%, and information pushed through social media platforms more accurately blocked the potential for a super spread event [12]. However, discrete models may better reflect the periodic nature of reporting and individual interactions. This is because infectious disease statistics are for a given time interval, and the mode of transmission is also individual to individual rather than continuous [13,14,15,16]. It is suitable for describing nonlinear dynamics and their chaotic behavior.
Several scholars have developed discrete mathematical models to explore different types of bifurcations, yielding interesting system dynamics [17,18,19,20]. Hu et al. [21] discuss discrete-time SIR epidemic models, proving flip bifurcation and Hopf bifurcation using the central manifold theorem and bifurcation theory. Li et al. [22] applied Euler’s method to convert the continuous epidemic model into a discrete model and verified the existence of transcritical bifurcation, flip bifurcation, Hopf bifurcation types, and chaotic phenomena. The creation of chaos can mean the outbreak of infectious diseases that threaten social and economic development. Therefore, it is necessary to control chaos so that it can be delayed or even disappear. Chaos control can be divided into feedback control [23,24] and non-feedback control. Luo et al. [25] propose a hybrid control strategy to control the system from a high stable -period orbit to a low stable -period orbit . The paper focuses on analyzing state feedback control and hybrid control, which effectively slow or even eliminate chaos in the provided system.
In this paper, we consider a classical SI classical infectious disease model [26]:
where and denote the number of susceptible and infected individuals at time t, respectively. denotes the constant input rate to the population, denotes the transmission rate, denotes the natural mortality rate, and denotes the recovery rate of the disease. All parameters are assumed to be positive constants.
Within the Euler discrete framework, this paper establishes a novel quantitative relationship between media reporting parameters and bifurcation types. The paper is organized as follows. Section 2 introduces the discrete models and the equilibrium points. Then, in Section 3, we quantitatively analyze the stability conditions of the equilibrium points, and discuss the bifurcation and chaos of the equilibrium points. In Section 4, we use state feedback control technique and hybrid control technique to control the models, respectively. Chaos is delayed or even eliminated by control. In Section 5, we demonstrate the accuracy and validity of the theory through numerical simulations. Finally, Section 6 concludes the paper.
2. Establishment of the System and the Point of Equilibrium
In this section, we discretize the continuous model using Euler’s method and analyze the conditions for the existence of stable equilibrium points.
This is based on an epidemic model and incorporates the effect of media coverage on the rate of disease transmission [27], where m denotes the coefficient of influence of media communication on the rate of transmission of infectious diseases. When , the rate of transmission of the infectious disease remains constant; when , the rate of transmission of the infectious disease decreases. Influence factors in the form of indices are suitable for short-term prediction without intervention at the beginning of an epidemic. System (1) after discretization using Euler’s method can be written as follows:
It is crucial to note that the model presented in system (2) is a standalone discrete-time system, directly derived to capture the state transitions over fixed time intervals of length h. It is obvious that system (2) has a boundary equilibrium point
and a positive equilibrium point
where
and W is the Lambertian W function. The Jacobi matrix of system (2) at any equilibrium point can be described as follows:
Similarly, system (1) can incorporate a media coverage function as a contact spread rate [28], where m denotes the coefficient of influence of media communication on the rate of transmission of infectious diseases. The nonlinear form of the impact factor is more relevant and dynamically reflects the impact of the intervention on media coverage.
The Jacobi matrix of system (6) at any equilibrium point can be described as follows:
The Jacobi matrix of the equilibrium point is, where ,
then the characteristic polynomial can be further expressed as follows:
where, when ,
when ,
and .
Zhao et al. [29] used the relationship between roots and coefficients to prove the stability of the equilibrium point and obtained the following lemma:
Lemma 1.
Suppose and , where P, Q are real numbers and , are two roots of . The following conclusions are given:
- (1)
- and if and only if , , then the immobile point E is called a sink when the immobile point E is asymptotically stable;
- (2)
- and , or and if and only if , then the immobile point E is called the saddle point;
- (3)
- and if and only if , , then the immobile point E is called the source, and at this time the immobile point E is unstable.
Obviously, the conclusions can be reached from Lemma 1.
Theorem 1.
The characteristic equation of the systems (2) and (6) at the boundary equilibrium point has two eigenvalues, , the following conclusion is true
- (1)
- If , then and , is a sink;
- (2)
- If , or , then and , or and , is a saddle point;
- (3)
- If , then and , is a source.
Theorem 2.
For the equilibrium points , the following conclusion is true
- (1)
- If , then and , is a sink;
- (2)
- If , then and , or and , is a saddle point;
- (3)
- If , then and , is a source.
In order to verify the correctness of the theory, the following numerical simulations are carried out. The equilibrium point of systems (2) and (6) satisfies Theorem 1 of (1), see Figure 1. Numerical simulations of the stability of the equilibrium points are shown in Figure 2 and Figure 3.
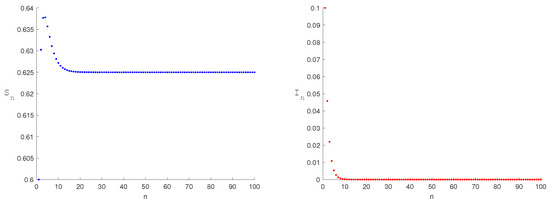
Figure 1.
The equilibrium points are stable when the parameter , and the initial value is (0.6, 0.1).
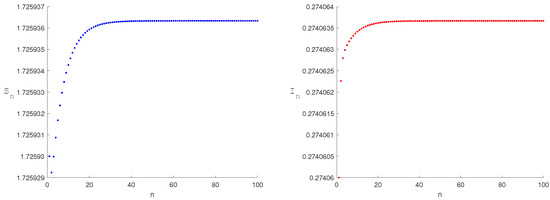
Figure 2.
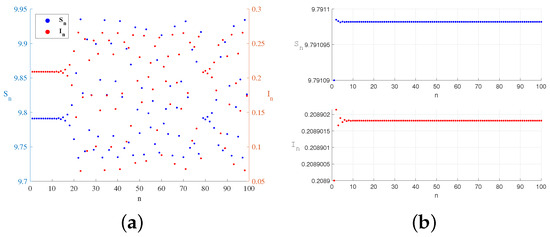
The equilibrium point is stable when the parameter , and the initial value is (1.72593, 0.27406).
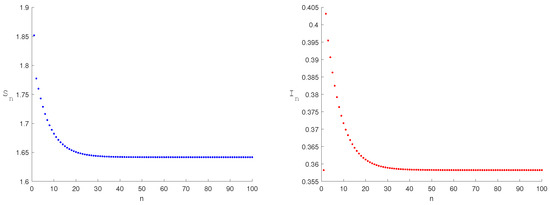
Figure 3.
The equilibrium point is stable when the parameter , and the initial value is (1.85179, 0.35825).
3. Bifurcation Analysis of Equilibrium Points
In this section, flip bifurcations of systems (2) and (6) are explored using the central manifold theorem and bifurcation theory.
3.1. Flip Bifurcation at Using Central Manifold Theory
In order to prove that system (2) undergoes a flip bifurcation at the equilibrium point and h as a bifurcating parameter, a transformation , can be used.
When , where
one eigenvalue of system (14) is , and it satisfies . Suppose the other eigenvalue has a mode less than 1, we get . Give a small perturbation of the parameter h around , i.e., , with . Then system (14) is
The characteristic polynomial at this time can be given as follows:
The corresponding eigenvalue is
The transversal condition is
If , flip bifurcation occurs at the positive equilibrium point . Define
Assuming that one eigenvalue of the matrix is , i.e., , the eigenvector is . Similarly, the other eigenvalue is then the eigenvector is . Let , i.e.,
The corresponding inverse matrix is given by
where , . Using the transformation = , system (14) can be transformed into
the coefficient is derived from system (14) based on the transformation, where
Using the transformation =T , system (20) can be transformed into
the coefficient is derived from system (20) based on the transformation, where
Theorem 3.
Let satisfy ; a flip bifurcation occurs at when the parameter h varies in a small domain of and neither is zero, where and are given by Equation (28).
Proof.
In a sufficiently small neighborhood with parameter , there exists a central manifold located at (0, 0) as follows:
If system (13) undergoes a flip bifurcation, then it must satisfy the following conditions:
With parameters , flip bifurcation occurs at the equilibrium point , and the proof is complete. □
3.2. Flip Bifurcation at Using Central Manifold Theory
In order to verify the correctness of the theory, numerical simulations are carried out, see Figure 4 and Figure 5. Similarly, system (6) undergoes a flip bifurcation, which can be demonstrated using the central manifold theorem and the bifurcation theory described above, see Figure 6 and Figure 7.
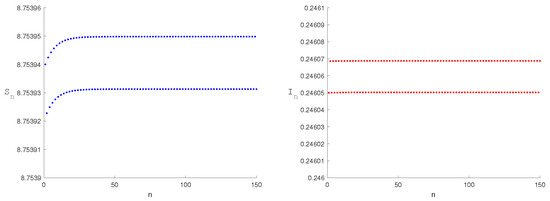
Figure 4.
Periodic solution near the flip bifurcation point at .
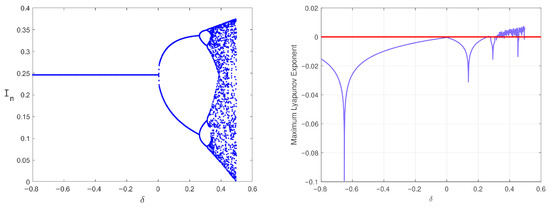
Figure 5.
Bifurcation of system (2) in the plane and Maximal Lyapunov Exponent at .
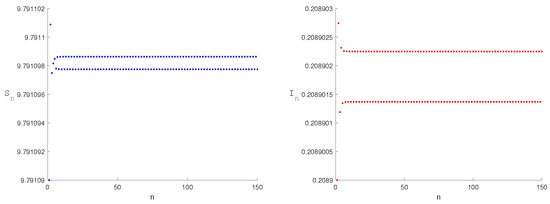
Figure 6.
Periodic solution near the flip bifurcation point at .
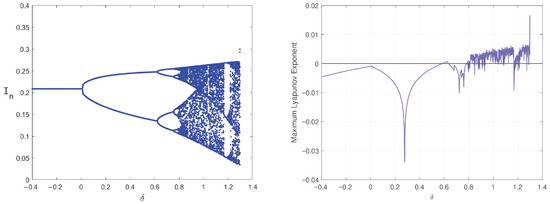
Figure 7.
Bifurcation of system (6) in the plane and Maximal Lyapunov Exponent at .
4. Chaos Control
Chaos control represents a method for the stabilization of unstable periodic orbits (UPO). It achieves this by introducing small perturbations to the system. These methods aim to transform the irregular dynamics unique to chaotic systems into canonical and predictable patterns. In a discrete-time model, multiple control strategies have been developed [30]. This section is focused on a state feedback control technique at equilibrium point and hybrid control technique at equilibrium point .
4.1. State Feedback Control
This method adopts an efficient control strategy to stabilize the chaotic state by converting the system into a piecewise linear system. The method includes designing a controller to reduce the maximum threshold of the system parameters while addressing an optimization problem within specified constraint conditions. This method is utilized to stabilize chaotic orbits at an unstable equilibrium point of system (2). The specific controlled systems are as follows:
Here, is feedback control force at equilibrium point and are feedback gains. The Jacobian matrix at is
The corresponding characteristic equation is
For eigenvalues and associated with the characteristic Equation (31), the trace (sum) and determinant (product) of the dynamical system’s Jacobian matrix satisfy the following relationships:
Theorem 4.
Proof.
The marginal stability lines can be obtained from the conditions
For the conditions , Equation (33) gives the following:
Similarly for , it is obtained
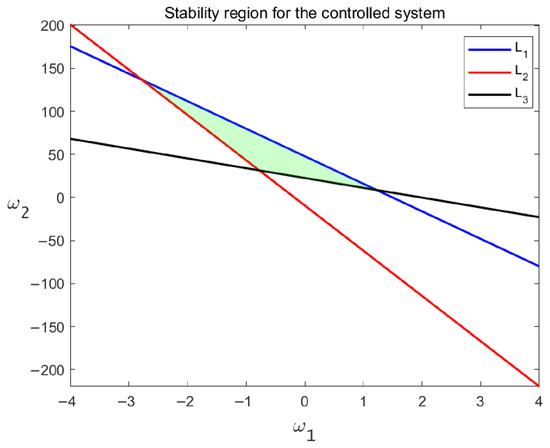
The lines give the conditions for the eigenvalues that have an absolute value less than 1. The triangular region surrounded by these line segments gives stable eigenvalues. Numerical simulations are shown in Figure 8, Figure 9, Figure 10 and Figure 11. □

Figure 8.
Stability region for the controlled system (29) when flip bifurcation occurs.

Figure 9.
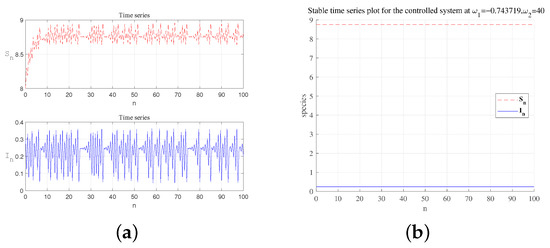
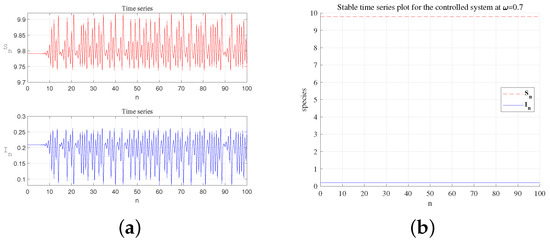
A time series is drawn at . Taking feedback gains , the system changes from unstable (a) to stable (b).

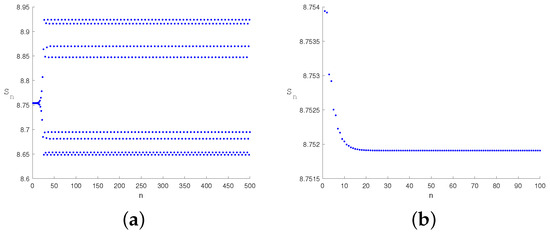
Figure 10.
Changes in over time at when values of perturbation are taken and the system changes from unstable (a) to stable (b).

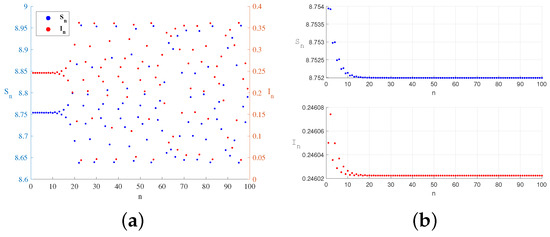
Figure 11.
Changes in over time at when values of perturbation are taken and the system changes from unstable (a) to stable (b).
4.2. Hybrid Control Method
The hybrid control method is a strategy for chaos control that combines state feedback and parameter perturbation to stabilize UPO embedded within the chaotic attractor of the system [31]. The collaborative method can ensure that the parameters in the controlled framework can remain stable when the parameters change greatly. By deploying a hybrid control technique, the specific controlled systems are as follows:
Within this dynamic framework, the parameter controls chaotic transitions. When an appropriate value of the control parameter is chosen, chaos can be delayed or completely eradicated. The Jacobian matrix of system (37) corresponding to is
Let
Theorem 5.
Proof.
The characteristic equation of (39) gives the following:
System (37) achieves stability if the zeros of Equation (43) lie in a unit disc. In other words, and . Here,
Therefore, system (37) is asymptotically stable under conditions (40)–(42). Numerical simulations are shown in Figure 12, Figure 13 and Figure 14. □

Figure 12.
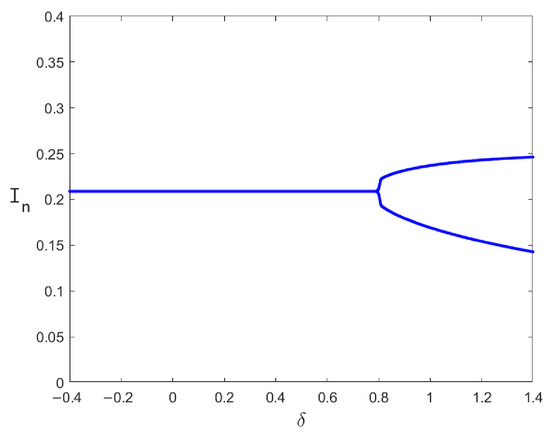
Flip bifurcation diagram with respect to for system (37) with .

Figure 13.
A time series is drawn at . Taking control parameter , the system changes from unstable (a) to stable (b).

Figure 14.
Changes in over time at when values of perturbation are taken and the system changes from unstable (a) to stable (b).
5. Numerical Simulation
To further validate the obtained results and investigate the intricate dynamics within the system, a series of numerical simulations were conducted, systematically varying different parameters.
For the complex dynamical behavior of system (2) occurring at the equilibrium point , consider the following set of parameters: , . For the complex dynamical behavior of the system (6) occurring at the equilibrium point , consider the following set of parameters: , . Parameter groups not explicitly identified in the figure are taken using the above parameters.
The equilibrium point of systems (2) and (6) satisfy Theorem 1 of (1), see Figure 1. Numerical simulations of the stability of the equilibrium points are shown in Figure 2 and Figure 3. From a biological perspective, a stable curve emerges at the disease-free equilibrium , where media coverage disrupts the disease transmission chain, ultimately achieving disease elimination. Similarly, a stable curve manifests at the endemic equilibrium . Media influence suppresses the infection rate to minimally acceptable levels, preventing periodic outbreaks and chaotic fluctuations.
Figure 4 and Figure 6 demonstrate the periodic solution induced by a flip bifurcation in the systems (2) and (6) under a critical parameter value. Figure 5 and Figure 7 present the bifurcation diagram accompanied by the Maximum Lyapunov Exponent (MLE) to characterize the system’s transition to chaos. The positive MLE values confirm the chaotic dynamics. Positive MLE values confirm chaotic dynamics. As perturbation varies within or , the susceptible population transitions from period-2 to period-4 oscillations and ultimately to chaotic regimes. Under different media influence factors, the system flip bifurcation occurs. The bifurcation diagram shows that the system dynamics undergo sudden and discontinuous changes, resulting in a sharp outbreak of the epidemic. This inherent unpredictability constitutes a core feature of chaotic dynamics. Disease propagation shows unpredictable fluctuations due to small perturbations, emphasizing the need for the precise regulation of parameters to avoid uncontrolled or repeated outbreaks.
Figure 8, Figure 9, Figure 10 and Figure 11 show that the system suppresses flip bifurcation-induced chaos under different parameter conditions. Figure 8 depicts that the controlled system (29) is stable in the green triangle region under certain parameters and reveals the critical condition of bifurcation. The time series in Figure 9, Figure 10 and Figure 11 show that the application of specific feedback gains (e.g., ) can effectively regulate the system from a destabilized state (e.g., chaos) to a stable equilibrium. Specifically, bifurcation diagrams in Figure 9 and Figure 10 show period-8 oscillations and chaotic attractors converging to stability. Strategic adjustment of media coverage intensity and feedback gains suppresses epidemic outbreaks and recurrences. Sustained, moderate media publicity (maintaining a certain level of m) to raise public awareness and reduce exposure rates, striving to keep the system operating within the stable zone (the green area in Figure 9) to prevent large-scale outbreaks. The theoretical results can provide useful prevention and treatment methods for preventing the outbreak of epidemic diseases.
For the hybrid control method, Figure 12, Figure 13 and Figure 14 further demonstrate that the variation of the control parameter in system induces the dynamic evolution of the system state variables and , verifying the robustness of the control strategy. Adjusting this parameter is equivalent to strengthening public health measures such as media reports, which can suppress bifurcation and restore the system (infectious disease) from unstable (outbreak) to stable (controlled), providing a theoretical basis for formulating dynamic adaptive prevention and control strategies. Implementation involves intensifying media coverage through major platforms by disseminating infection sources, transmission routes, case counts, and patient trajectories (as demonstrated during COVID-19). These interventions effectively combat epidemics.
Figure 15 represents the Maximum Lyapunov Exponential plot of the flip bifurcation at points for system (2) and system (6) taking the same parameter values, respectively. The set of parameters taken is: . When taking the same media coverage impact factor m, system (6) is earlier than system (2) in terms of the emergence of chaos and higher than system (2) in terms of the complexity of chaos. The data presented in the numerical model suggests that media coverage is more effective in preventing and controlling disease outbreaks when the impact factor is exponential.
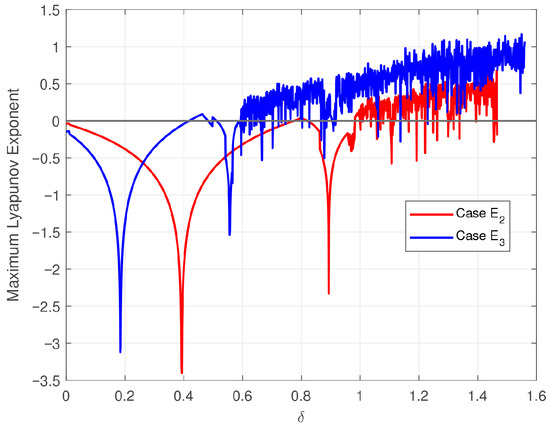
Figure 15.
Maximal Lyapunov Exponent at .
Figure 16 represents the Maximum Lyapunov exponent when system (2) changes only the value of the media coverage impact factor take and flip bifurcation occurs at equilibrium . The set of parameters taken is: . In particular, b is a localized zoomed-in view of a. When the media report different impact factors m, it is earlier at than at as far as the emergence of chaos is concerned. The data in the numerical model suggest that judicious use of media coverage factors can be effective in mitigating and controlling infectious disease outbreaks.
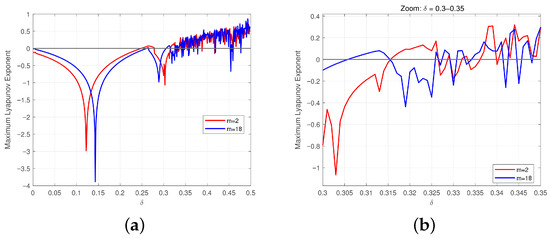
Figure 16.
Maximal Lyapunov Exponent at : (a) the complete curve; (b) a magnified view within the interval [0.3, 0.35].
6. Conclusions
This paper explores a discrete epidemic model influenced by media coverage. We develop a discrete epidemic model and then incorporate different forms of media coverage influence. Local stability and instability conditions associated with equilibrium points within the system are analyzed. We describe the flip bifurcation of two positive equilibrium points and identify critical thresholds through coefficient analysis. We derive and control the chaotic dynamics through state feedback control and hybrid control methods to stabilize the bifurcation-induced instability. The above numerical simulations verify the occurrence of bifurcation and chaos in the system. The different effects of the two forms of media coverage influence factors are comparatively analyzed.
The results show that media coverage can modulate the intensity of an epidemic and amplify the chaos mechanism, and that outbreaks of large-scale infectious diseases can be effectively prevented by controlling the chaos mechanism. The exponential form was found to be suitable for short-term prediction without intervention at the beginning of an epidemic, which is efficient and fast, and has a high intensity in a short period of time. The nonlinear form is closer to reality, can dynamically reflect the impact of media coverage interventions, and is suitable for long-term prediction. The intensity of media coverage can be used appropriately to combat epidemics efficiently.
Current research lacks a comprehensive interdisciplinary investigation bridging media coverage, discrete modeling, and bifurcation theory. This article addresses this gap by constructing a more realistic discrete model of media influence and establishing a corresponding bifurcation analysis framework tailored to this model. The Euler discrete method proposed in this paper shows higher computational efficiency. When the same solution accuracy is achieved, the calculation time and strength are greatly reduced. At the same time, it also has rich dynamic properties, which reduces the threshold of practical application. Therefore, it provides an efficient, stable, and practical tool for solving discrete and bifurcation problems. These results have demonstrated that the dynamic behavior of the discrete model is more complex. Consequently, discrete epidemic modeling has emerged as a significant direction for future research.
Author Contributions
Writing—original draft, Y.L.; Conceptualization, Y.L. and W.W.; Visualization, Y.L. and W.W.; Writing—review and editing, Y.L. and W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities (Grant No. 2572022DJ04).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hui, J.; Zhu, D. Global stability and periodicity on SIS epidemic models with backward bifurcation. Comput. Math. Appl. 2005, 50, 1271–1290. [Google Scholar] [CrossRef]
- Li, X.Z.; Wang, J.; Ghosh, M. Stability and bifurcation of an SIVS epidemic model with treatment and age of vaccination. Appl. Math. Model. 2010, 34, 437–450. [Google Scholar] [CrossRef]
- Alexander, M.E.; Moghadas, S.M. Periodicity in an epidemic model with a generalized non-linear incidence. Math. Biosci. 2004, 189, 75–96. [Google Scholar] [CrossRef]
- Vargas-De-León, C. On the global stability of SIS, SIR and SIRS epidemic models with standard incidence. Chaos Solitons Fractals 2011, 44, 1106–1110. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361–367. [Google Scholar] [CrossRef] [PubMed]
- Korobeinikov, A.; Wake, G.C. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef]
- Li, J.; Ma, Z. Stability analysis for SIS epidemic models with vaccination and constant population size. Discret. Contin. Dyn. Syst. B 2004, 4, 635–642. [Google Scholar] [CrossRef]
- Zhang, J.; Chu, Y.; Du, W.; Chang, Y.; An, X. Stability and Hopf Bifurcation in a Delayed SIS Epidemic Model with Double Epidemic Hypothesis. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 561–571. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.A. The impact of media coverage on the dynamics of infectious disease. Int. J. Biomath. 2008, 1, 65–74. [Google Scholar] [CrossRef]
- Al Basir, F.; Ray, S.; Venturino, E. Role of media coverage and delay in controlling infectious diseases: A mathematical model. Appl. Math. Comput. 2018, 337, 372–385. [Google Scholar] [CrossRef]
- Qin, W.; Zhang, J.; Dong, Z. Media impact research: A discrete SIR epidemic model with threshold switching and nonlinear infection forces. Math. Biosci. Eng. 2023, 20, 17783–17802. [Google Scholar] [CrossRef] [PubMed]
- Mohsen, A.A.; AL-Husseiny, H.F.; Zhou, X.; Hattaf, K. Global stability of COVID-19 model involving the quarantine strategy and media coverage effects. AIMS Public Health 2020, 7, 587–605. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Yakubu, A.A. Dispersal, disease and life-history evolution. Math. Biosci. 2001, 173, 35–53. [Google Scholar] [CrossRef]
- Satsuma, J.; Willox, R.; Ramani, A.; Grammaticos, B.; Carstea, A.S. Extending the SIR epidemic model. Phys. A Stat. Mech. Its Appl. 2004, 336, 369–375. [Google Scholar] [CrossRef]
- Chen, L.; Yu, X.; Sun, C. Characteristic Modeling Approach for High-Order Linear Dynamical Systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5405–5413. [Google Scholar] [CrossRef]
- Santra, P.K.; Mahapatra, G.S. Dynamical study of discrete-time prey-predator model with constant prey refuge under imprecise biological parameters. J. Biol. Syst. 2020, 28, 681–699. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Ruan, S.; Xiao, D. Bifurcations in a discrete predator–prey model with nonmonotonic functional response. J. Math. Anal. Appl. 2018, 464, 201–230. [Google Scholar] [CrossRef]
- Cao, H.; Zhou, Y.; Ma, Z. Bifurcation analysis of a discrete SIS model with bilinear incidence depending on new infection. Math. Biosci. Eng. 2013, 10, 1399–1417. [Google Scholar] [CrossRef]
- Yu, X.; Liu, M.; Zheng, Z.; Hu, D. Complex dynamics of a discrete-time SIR model with nonlinear incidence and recovery rates. Int. J. Biomath. 2023, 16, 2250131. [Google Scholar] [CrossRef]
- Yi, N.; Liu, P.; Zhang, Q. Bifurcations analysis and tracking control of an epidemic model with nonlinear incidence rate. Appl. Math. Model. 2012, 36, 1678–1693. [Google Scholar] [CrossRef]
- Hu, Z.; Teng, Z.; Zhang, L. Stability and bifurcation analysis in a discrete SIR epidemic model. Math. Comput. Simul. 2014, 97, 80–93. [Google Scholar] [CrossRef]
- Li, L.; Sun, G.Q.; Jin, Z. Bifurcation and chaos in an epidemic model with nonlinear incidence rates. Appl. Math. Comput. 2010, 216, 1226–1234. [Google Scholar] [CrossRef]
- Chakraborty, K. Ecological complexity and feedback control in a prey–predator system with Holling type III functional response. Complexity 2016, 21, 346–360. [Google Scholar] [CrossRef]
- Auerbach, D.; Grebogi, C.; Ott, E.; Yorke, J.A. Controlling chaos in high dimensional systems. Phys. Rev. Lett. 1992, 69, 3479–3482. [Google Scholar] [CrossRef]
- Luo, X.S.; Chen, G.; Wang, B.H.; Fang, J.Q. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems. Chaos Solitons Fractals 2003, 18, 775–783. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical models in population biology and epidemiology. Appl. Math. Mech. 2012, 40, 267–291. [Google Scholar]
- Cui, J.; Sun, Y.; Zhu, H. The Impact of Media on the Control of Infectious Diseases. J. Dyn. Differ. Equ. 2008, 20, 31–53. [Google Scholar] [CrossRef]
- Xiao, D.; Ruan, S. Global analysis of an epidemic model with nonmonotone incidence rate. Math. Biosci. 2007, 208, 419–429. [Google Scholar] [CrossRef]
- Zhao, M.; Li, C.; Wang, J. Complex dynamic behaviors of a discrete-time predator-prey system. J. Appl. Anal. Comput. 2017, 7, 478–500. [Google Scholar]
- Din, Q. Complexity and chaos control in a discrete-time prey-predator model. Commun. Nonlinear Sci. Numer. Simul. 2017, 49, 113–134. [Google Scholar] [CrossRef]
- Yuan, L.G.; Yang, Q.G. Complexity and chaos control in a discrete-time prey-predator model. Appl. Math. Model. 2015, 39, 2345–2362. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).