Stabilized Nitsche-Type CIP/GP CutFEM for Two-Phase Flow Applications

Abstract

This work presents a stabilized Nitsche-type Cut Finite Element Method (CutFEM) for simulating two-phase flows with complex interfaces. The method addresses the challenges of capturing discontinuities in material properties and governing equations that arise from implicitly defined interfaces. By employing a Continuous Interior Penalty (CIP) method, Nitsche’s method for weak interface coupling, and Ghost Penalty (GP) terms for stability, the formulation enables an accurate representation of abrupt changes in physical properties across cut elements. A stability analysis and a priori error estimation, utilizing Oseen’s formulation, demonstrate the method’s robustness. At the same time, a numerical convergence study incorporating adaptivity and a best-fit quadratic level-set interpolation validates its accuracy. Finally, the method’s efficacy in mitigating spurious currents is confirmed through the Spurious Current Test, demonstrating its potential for reliable simulation of multi-phase flow phenomena.

1. Introduction

Two-phase flow, central to many engineering applications, involves the interaction of immiscible fluids (e.g., liquid and gas) separated by an interface. Across this interface, physical properties like density and viscosity may vary abruptly, introducing challenges such as discontinuities in velocity and pressure fields, surface tension effects, and spurious currents. Accurately modeling these phenomena is crucial for simulating processes such as droplet coalescence and capillary flows realistically. Accurate simulation of these phenomena requires solving complex Partial Differential Equations (PDEs), often in intricate geometries. While standard FEM performs well in single-phase problems, it struggles with two-phase flows due to its reliance on body-fitted meshes, which require remeshing as interfaces move. It also lacks built-in mechanisms to accurately handle discontinuities across interfaces, limiting stability and accuracy without additional modifications.

Two-phase flow simulations require accurate and effective interface tracking between the phases. Interface-capturing methods, such as the level-set method, excel at this by implicitly representing the interface, making them effective tools for simulating complex two-phase flow phenomena. See, for example [1,2]. The level-set method handles two-phase flow by implicitly representing the interface as the zero level set of an auxiliary function, typically a signed distance function, defined on a fixed grid. This implicit representation facilitates the simulation of complex interfacial phenomena, including merging and breakup, without requiring frequent mesh updates. However, this implicit representation can lead to significant discontinuities in material properties within elements intersected by the interface, potentially affecting the accuracy of the simulation.

On the other hand, standard FEM, relying on smooth polynomial shape functions, struggles to accurately represent the sharp gradients in material properties across the interface. This limitation often leads to inaccurate stress or strain predictions near the interface, necessitating specialized techniques for improved fidelity. To overcome this challenge, common approaches include smoothing material properties across the interface within the cut elements and approximating the surface tension force as a body force distributed over a narrow band around the interface. This approach, known as the Continuum Surface Force (CSF) method [3], is inspired by techniques used in finite difference and finite volume methods. Similar approaches for handling surface tension are employed in finite difference and finite volume methods; see, for example [4].

The extended finite element method (XFEM), initially proposed for crack propagation problems, offers an alternative approach. XFEM enriches the standard finite element shape functions to represent arbitrary discontinuities within elements explicitly. This versatile method has been successfully applied to various problems, including fluid–structure interaction, premixed combustion, and two-phase flow (see, e.g., [5,6,7]). In two-phase flow, the velocity field typically exhibits kinks across the interface due to the differing fluid properties. However, the pressure field can exhibit more complex behavior. Pressure jumps and discontinuities in the pressure gradient may occur at the interface, significantly influencing the fluid flow dynamics. To improve accuracy, XFEM enhances standard FEM by using special enrichment functions (kink enrichments for velocity and jump enrichments for pressure) to better capture the expected discontinuities in two-phase flow (e.g., [8]). In contrast, some studies (e.g., [9,10]) applied enrichment only to the pressure field, without incorporating kink enrichments for velocity.

Building on XFEM, the Cut Finite Element Method (CutFEM) further refines this approach by directly addressing the challenges posed by the cut elements. Unlike standard FEM approaches that rely on body-fitted meshes aligned with the interface, CutFEM does not require the finite element mesh to align with the interface, providing greater flexibility in mesh generation; see [11]. By incorporating stabilization techniques, such as Nitsche’s method and Ghost Penalty (GP) methods, CutFEM provides a robust framework for handling the complexities arising from the interface intersections.

This study employs a Nitsche-type extended variational multiscale method for two-phase flow. The effectiveness of the Nitsche method has been extensively studied and validated across various fields of computational mechanics and applied mathematics. Fundamental theoretical insights into penalty methods and their application to boundary value problems were provided in [12,13]. Subsequent research has extended the method to handle more complex boundary conditions and non-matching grids, enhancing its versatility and applicability. For further details, refer to [14].

Building upon the Nitsche method, the Ghost Penalty (GP) method was developed to address challenges associated with cut or embedded finite element meshes. This technique enhances stability by introducing additional penalty terms that improve the conditioning of the solution, particularly for small or irregularly shaped elements. The concept of face-oriented ghost penalty terms was first introduced in [15] and later adapted for the Stokes problem in [16]. These terms play a crucial role in regulating the enriched solution values, thereby ensuring stability of the numerical scheme and achieving optimal error convergence. An example of employing a GP-stabilized Nitsche method for two-phase flow governed by the stationary Stokes equations can be found in [17].

The main focus of this article revolves around developing a formulation for two-phase flow, where we operate under the assumption of continuous velocity distribution throughout the domain, while acknowledging a discontinuous pressure distribution across interfaces. This formulation draws inspiration from the research conducted by Schott and Wall [18,19,20], which pioneered the development of a stable extended finite-element-based computational approach. Initially designed for simulating single-phase flows governed by the nonlinear incompressible Navier–Stokes equations, their approach was later extended to multiphase flow. It incorporates a Nitsche-type method to weakly enforce boundary conditions and employs CIP stabilizations to tackle instabilities within the fluid domain, as outlined by Burman et al. [21]. To address issues caused by poorly intersected finite elements and to stabilize fluid velocity and pressure near boundaries, GP stabilization, introduced by Burman and Hansbo [16], has been extended to the incompressible Navier–Stokes equations.

Research conducted by Massing et al. [22] has demonstrated that the formulation maintains inf-sup stability. This stability has allowed for the establishment of optimal a priori error estimates in an energy norm for a linearized auxiliary problem governed by the Oseen equations, as detailed in the same work by Massing et al. Building on this foundation, Schott [20] extended the method to address multiphase flow scenarios. We aim to further develop this approach for cases where the velocity field remains continuous, but the pressure exhibits discontinuities across interfaces. In such problems, the interface between the two fluids acts as a discontinuity surface for the pressure field due to the presence of capillary forces, while the velocity remains continuous to satisfy the incompressibility condition and the no-slip interfacial coupling. This modeling assumption is commonly used in incompressible multiphase flow and is further justified in Section 3, where we discuss its physical motivation and numerical advantages.

In the numerical solution of the nonlinear, implicit, time-dependent Navier–Stokes equations, each time step involves solving a linear system corresponding to the Oseen problem studied in this paper. Depending on the chosen linearization strategy, the convective velocity is either evaluated using the solution from the previous time step (semi-implicit scheme) or updated iteratively using the current approximation in a fully nonlinear approach. To stabilize the resulting saddle-point problem, we introduce CIP/GP terms, as will be detailed in Theorem 1. While these stabilization terms are effective, they can potentially affect the accuracy of the solution. However, Theorem 2 will establish that the method remains consistent and that the convergence rates of the finite element method are preserved.

In addition to the theoretical advancements outlined above, we aim to validate this formulation through numerical experimentation and investigate its convergence behavior. To achieve this, we implement all the presented methods using the Finite-Element Multi-Grid library FEMuS, developed at the Department of Mathematics and Statistics of Texas Tech University.

The novelty of this work lies in applying a unified CIP/GP stabilization within a CutFEM framework, tailored for multiphase problems with pressure discontinuities, and implemented without enrichment functions. Unlike prior XFEM-based or linear-only formulations [20,22], our method supports nonlinear multiphase flows with higher physical fidelity and is validated through convergence studies and standard multiphase benchmarks.

2. Two-Phase Flow

We consider two-phase flow within the domain $\Omega \subset {\mathbb{R}}^d$, where d denotes the spatial dimension of the problem. The time-dependent moving phase interface $\Gamma$ divides the domain $\Omega$ into two disjoint subdomains ${\Omega }^1\left(t\right)$ and ${\Omega }^2\left(t\right)$, that is $\Omega ={\Omega }^1\cup {\Omega }^2$, representing the two phases. For the boundary of the subdomain ${\Omega }^i$, we define the Dirichlet and Neumann boundary parts of the fluid domain as ${\Gamma }_D^i$ and ${\Gamma }_N^i$, respectively. We assume that ${\Gamma }^i={\Gamma }_D^i\cup {\Gamma }_N^i\cup \Gamma$ (see Figure 1). The unit normal vector n on the interface $\Gamma$ is defined as pointing toward the subdomain ${\Omega }^1$. For each subdomain ${\Omega }^i$, where $i\in \{1,2\}$, we denote by $n^i$ the unit normal vector pointing outward from ${\Omega }^i$. On the interface $\Gamma$, this implies that $n=n^2=-n^1$. Assuming the phases are immiscible, the flow in both subdomains ${\Omega }^1$ and ${\Omega }^2$ is governed by the Navier–Stokes equations

$$\begin{array}{ccc}\hfill {\rho }^i{\displaystyle \frac{\partial u_i}{\partial t}}+{\rho }^i(u^i·\nabla )u^i+\nabla p^i-2{\mu }^i\nabla ·ϵ\left(u^i\right)& =f^i\hfill & \hfill \hspace{1em}\hspace{1em}\forall x\in {\Omega }^i\left(t\right),\end{array}$$

(1)

$$\begin{array}{ccc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \nabla ·u^i& =0\hfill & \hfill \hspace{1em}\hspace{1em}\forall x\in {\Omega }^i\left(t\right),\end{array}$$

(2)

where ${\rho }^i$ and ${\mu }^i$ are the density and dynamic viscosity of the corresponding fluid, and are considered constant within each phase. Furthermore, $u_i$ is the velocity and $p_i$ the pressure in the domain ${\Omega }^i$, $ϵ\left(u^i\right)=1/2\left(\nabla u^i+{(\nabla u^i)}^T\right)$ is the rate of deformation tensor, and $f^i={\rho }^{i}g$ is the body force, where g is the gravity acceleration vector.

Appropriate initial conditions are prescribed in ${\Omega }^i$, along with boundary conditions on the external portion of ${\Gamma }^i$, which lies on the boundary of the overall domain $\Omega$, following standard practice. At time $t=0$, a divergence free velocity field $u_0^i$ is prescribed:

$$u^i(x,t=0)=u_0^i\left(x\right)\mathrm{in}{\Omega }^i.$$

(3)

Dirichlet and Neumann boundary conditions on ${\Gamma }_D^i$ and ${\Gamma }_N^i$, respectively, are given as

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em} u^i& =u_D^i\mathrm{on}{\Gamma }_D^i,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \overline{\sigma }(u^i,p^i)·n^i& =h_N^i\mathrm{on}{\Gamma }_N^i,\hfill \end{array}$$

(5)

where $\overline{\sigma }(u^i,p^i)=-p^i\mathit{I}+2{\mu }^iϵ\left(u^i\right)$ denotes the Cauchy-stress tensor, where $\mathit{I}$ denotes the $d\times d$ identity matrix.

In our study, we consider a scenario where the velocity field is continuous across the interface, while the pressure field is allowed to be discontinuous. Specifically, we enforce the condition that the jump in velocity across the interface is zero, denoted as

$$⟦u⟧=0\mathrm{on}\Gamma ,$$

(6)

where $⟦·⟧={\left(·\right)}^1-{\left(·\right)}^2$ denotes the jump operator across the interface $\Gamma$. This ensures that the fluid flow does not exhibit any discontinuities at the interface.

Furthermore, we consider the jump in the stress tensor across the interface. The stress tensor $\overline{\sigma }(u,p)$, which depends on the velocity u and pressure p, experiences a discontinuity that is balanced by the surface tension effects. Mathematically, this is represented by

$$⟦\overline{\sigma }(u,p)⟧·n=-{\iota }_{st}\kappa n\mathrm{on}\Gamma ,$$

(7)

where ${\iota }_{st}$ is the surface-tension coefficient, and $\kappa$ is the curvature of the interface. This condition ensures that the difference in the normal stress across the interface is balanced by the surface tension force, which is proportional to the curvature of the interface.

3. Variational Multiscale Formulation for One Phase

The functional space for admissible fluid velocities is ${\mathcal{V}}_{u_D^i}^i\stackrel{\mathrm{def}}{=}{\left[H_{{\Gamma }_D^i,u_D^i}^1\left({\Omega }^i\left(t\right)\right)\right]}^d\subset {\left[H^1\left({\Omega }^i\left(t\right)\right)\right]}^d$. The corresponding space of admissible test functions, ${\mathcal{V}}_0^i$, is defined to have a vanishing trace on ${\Gamma }_D^i$. For the pressure field, the trial and test function space is set as ${\mathcal{P}}^i=L^2\left({\Omega }^i\left(t\right)\right)$ when ${\Gamma }_N^i\ne \varnothing$, and as ${\mathcal{P}}^i=L_0^2\left({\Omega }^i\left(t\right)\right)$ when ${\Gamma }_N^i=\varnothing$. The resulting variational formulation for the incompressible flow problem is given below.

For all $t\in (0,T]$, find fluid velocity and pressure $U^i\left(t\right)=(u^i\left(t\right),p^i\left(t\right))\in {\mathcal{V}}_{u_D^i}^i\times {\mathcal{P}}^i$, such that for all $V^i=(v^i,q^i)\in {\mathcal{V}}_0^i\times {\mathcal{P}}^i$

$$\begin{array}{cc}\hfill & {\left({\rho }^i{\displaystyle \frac{\partial u^i}{\partial t}},v^i\right)}_{{\Omega }^i}+{\left({\rho }^i{u}^i·\nabla u^i,v^i\right)}_{{\Omega }^i}-{\left(p^i,\nabla ·v^i\right)}_{{\Omega }^i}+{\left(2{\mu }^iϵ\left(u^i\right),ϵ\left(v^i\right)\right)}_{{\Omega }^i}\hfill \\ \hfill & +{\left(\nabla ·u^i,q^i\right)}_{{\Omega }^i}-{\left(\overline{\sigma }(u^i,p^i)·n^i,v^i\right)}_{\Gamma }={\left(f^i,v^i\right)}_{{\Omega }^i}+{(h_N^i,v^i)}_{{\Gamma }_N^i}.\hfill \end{array}$$

(8)

Here, ${(·,·)}_{{\Omega }^i}$, ${(·,·)}_{{\Gamma }_N^i}$, and ${(·,·)}_{\Gamma }$ denote the usual $L_2$ inner products in ${\Omega }^i$, ${\Gamma }_N^i,$ and $\Gamma$, respectively.

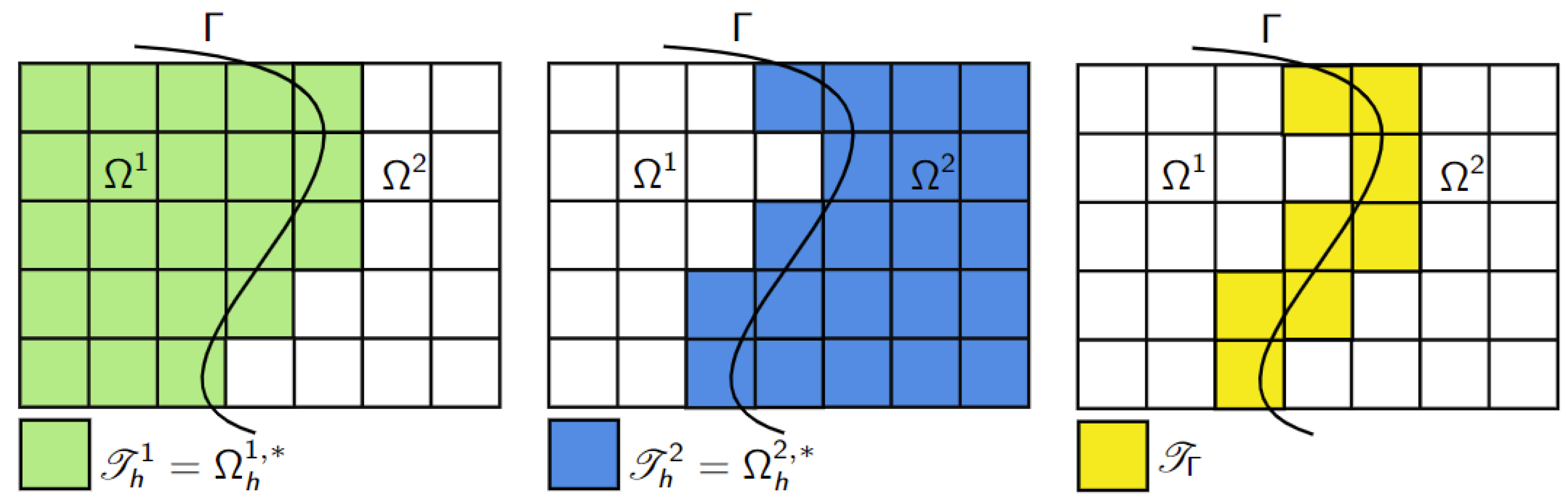
3.1. Computational Domains and Meshes

The finite-dimensional space is constructed by defining the computational domain and generating a mesh as follows. Let ${\widehat{\mathcal{T}}}_h$ be a background mesh with mesh size defined by a positive, piecewise constant function h over each element, covering an open and bounded physical domain $\Omega$. The faces intersected by the interface $\Gamma$ are integrated across their entire surface area. We refer to ${\mathcal{T}}_{\Gamma }$ as the set of elements that contain a part of the interface $\Gamma$.

$${\mathcal{T}}_{\Gamma }=\{T\in {\widehat{\mathcal{T}}}_h:T\cap \Gamma \ne \varnothing \}.$$

We also define the set ${\mathcal{T}}_h^i$ within subdomain ${\Omega }^i$, that consists of all mesh elements T from the background mesh ${\widehat{\mathcal{T}}}_h$ such that the intersection of the element T with the subdomain ${\Omega }^i$ is non-empty. This active portion of the mesh includes all faces F in the interface zone, where at least one adjacent element intersects the interface.

$${\mathcal{T}}_h^i=\{T\in {\widehat{\mathcal{T}}}_h:T\cap {\Omega }^i\ne \varnothing \}={\Omega }_h^{i,*}$$

See Figure 2 for a graphical representation of ${\mathcal{T}}_h^i$ and ${\mathcal{T}}_{\Gamma }$. For notational convenience, we denote the union of all active elements ${\mathcal{T}}_h^i$ by ${\Omega }_h^{i,*}$, representing the active part of the computational domain as a continuous region.

3.2. Continuous Interior Penalty (CIP) Stabilization Method

The core concept of the CIP method involves enhancing the discrete variational form by incorporating a stabilization term (see [23]). In the context of the Navier–Stokes equation, CIP introduces specific terms to address instabilities and enhance numerical stability. These additional terms are crucial in mitigating errors and ensuring accurate simulations of fluid flow phenomena. Distinct sets of CIP terms are applied to the Navier–Stokes equation for the domains ${\Omega }^1$ and ${\Omega }^2$. The CIP terms for the Navier–Stokes equation are as follows:

$${\mathcal{L}}_h^{i,CIP}(U_h^i,V_h^i)\stackrel{\mathrm{def}}{=}{s}_{\beta }^i(u_h^i,v_h^i)+s_u^i(u_h^i,v_h^i)+s_p^i(p_h^i,q_h^i).$$

(9)

Let $u_{n,\infty ,F}^i\stackrel{\mathrm{def}}{=}{∥u_h^i·n^i∥}_{0,\infty ,F}$ and let $\beta$ be the advective velocity field. Then, the (weakly) consistent symmetric jump-penalty stabilization operators in (9) are defined as

$$\begin{array}{cc}\hfill s_{\beta }^i(u_h^i,v_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_{\beta }\sum _{F\in {\mathcal{F}}^i}{\varphi }_{\beta ,F}^i{\left({\rho }^i{u}_{n,\infty ,F}^i\right)}^{2}h{\left(⟦\nabla u_h^i⟧,⟦\nabla v_h^i⟧\right)}_F,\hfill \\ \hfill s_u^i(u_h^i,v_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_u\sum _{F\in {\mathcal{F}}^i}{\varphi }_{u,F}^{i}h{\left(⟦\nabla ·u_h^i⟧,⟦\nabla ·v_h^i⟧\right)}_F,\hfill \\ \hfill s_p^i(p_h^i,q_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_p\sum _{F\in {\mathcal{F}}^i}{\varphi }_{p,F}^{i}h{\left(⟦\nabla p_h^i⟧,⟦\nabla q_h^i⟧\right)}_F,\hfill \end{array}$$

with non-dimensional stabilization parameters ${\gamma }_{\beta },{\gamma }_u,{\gamma }_p>0,$ and element-wise scaling functions

$${\varphi }_T^i={\mu }^i+c_u^i{\rho }^i\left({∥\beta ∥}_{0,\infty ,T}{h}_T\right)+c_{\sigma }^i{\rho }^i\left(\sigma h_T^2\right),{\varphi }_{\beta ,T}^i={\varphi }_{p,T}^i=h_T^2{\left({\varphi }_T^i\right)}^{-1},{\varphi }_{u,T}^i={\varphi }_T^i,$$

and according to face averages ${\varphi }_{\beta ,F}^i,{\varphi }_{u,F}^i,{\varphi }_{p,F}^i$ at the interior faces $F\in {\mathcal{F}}^i$, where ${\mathcal{F}}^i$ is the set of interior faces shared by exactly two elements, denoted as $T_F^{+}$ and $T_F^{-}$, in the mesh ${\mathcal{T}}_h^i$.

The penalty parameters used in the Nitsche, CIP, and ghost penalty stabilization terms play a crucial role in ensuring the consistency, coercivity, and numerical stability of the formulation. Following guidelines from prior work (e.g., [24,25,26,27]), we adopt the following scaling strategy. For the CIP stabilization, we set ${\gamma }_{\beta }={\gamma }_p=0.05$ for hexahedral and wedge elements, and ${\gamma }_{\beta }={\gamma }_p=0.01$ for tetrahedral elements, as suggested in [28]. The velocity stabilization parameter is set as ${\gamma }_u=0.05{\gamma }_{\beta }$, consistent with the recommendations in [21]. Convective and reactive stabilization scaling factors are chosen as $c_u=1/6$ and $c_{\epsilon }=1/12$, respectively, based on the analysis in [28,29].

Note that we denote the mesh size function by h, defined over the entire computational domain. The function h is piecewise constant, and it takes a constant value on each mesh element T. This value, denoted by ${h|}_T=h_T$, represents a characteristic length of the element.

CIP-based discrete variational multiscale formulation for each subdomain is thus obtained by introducing CIP terms (9) in the projected variational form (8), where we seek the velocity and pressure pair $(u_h^i,p_h^i)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$ such that for all $(v_h^i,q_h^i)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$,

$$\begin{array}{cc}\hfill & {\left({\rho }^i{\displaystyle \frac{\partial u_h^i}{\partial t}},v_h^i\right)}_{{\Omega }^i}+{\left({\rho }^i{u}_h^i·\nabla u_h^i,v_h^i\right)}_{{\Omega }^i}-{\left(p_h^i,\nabla ·v_h^i\right)}_{{\Omega }^i}+{\left(2{\mu }^iϵ\left(u_h^i\right),ϵ\left(v_h^i\right)\right)}_{{\Omega }^i}\hfill \\ \hfill & +{\left(\nabla ·u_h^i,q_h^i\right)}_{{\Omega }^i}+s_{\beta }^i(u_h^i,v_h^i)+s_u^i(u_h^i,v_h^i)+s_p^i(p_h^i,q_h^i)\hfill \\ \hfill & -{\left(\overline{\sigma }(u_h^i,p_h^i)·n^i,v_h^i\right)}_{\Gamma }={\left(f^i,v_h^i\right)}_{{\Omega }^i}+{(h_N^i,v_h^i)}_{{\Gamma }_N^i}.\hfill \end{array}$$

(10)

3.3. Coupled Variational Multiscale Formulation

Beginning with Equation (10), the first step towards a coupled variational formulation for two-phase flow is achieved by summing the individual phase formulations. Using the jump operator and the unit normal vector, the interface terms on the left-hand side can be expressed as follows:

$$\begin{array}{cc}\hfill {\int }_{\Gamma }⟦v_h·\overline{\sigma }(u_h,p_h)·n^{\Gamma }⟧ds=& -{\left(\overline{\sigma }(u_h^1,p_h^1)·n^1,v_h^1\right)}_{\Gamma }-{\left(\overline{\sigma }(u_h^2,p_h^2)·n^2,v_h^2\right)}_{\Gamma }\hfill \\ \hfill =& -{\left(⟦v_h⟧·n^{\Gamma },\left\{p_h\right\}\right)}_{\Gamma }+{\left(⟦v_h⟧,\left\{2\mu ϵ\left(u_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma }-{\left(\langle v_h\rangle ,{\gamma }_{st}\kappa n^{\Gamma }\right)}_{\Gamma },\hfill \end{array}$$

where we used the following weighted average operators

$$\left\{x\right\}=w^2{x}^2+w^1{x}^1\mathrm{and}\langle x\rangle =w^1{x}^2+w^2{x}^1,$$

(11)

with positive weights $w^1$ and $w^2$, such that $w^1+w^2=1$. In this work, we utilize the coupling condition for fluxes, $⟦\overline{\sigma }(u,p)·n^{\Gamma }⟧=-{\gamma }_{st}\kappa n^{\Gamma }$ on $\Gamma$.

Nitsche’s method is employed to weakly enforce interface coupling constraints. For a comprehensive understanding of this method, readers are referred to [12,13,14,30]. The core principle of Nitsche’s method for viscous-dominated problems involves the addition of terms related to viscous and pressure adjoint consistency, analogous to the existing viscous and pressure consistency terms

$${\left(⟦u_h⟧,\left\{2\mu \epsilon \left(v_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma },{\left(⟦u_h⟧·n^{\Gamma },\left\{q_h\right\}\right)}_{\Gamma }.$$

(12)

The corresponding penalty Nitsche-type terms are

$${\left(\gamma \left(\right\{\phi \}/2)⟦u_h⟧,⟦v_h⟧\right)}_{\Gamma },{\left(\gamma \left(\right\{\rho \varphi /h\}/2)⟦u_h⟧·n^{\Gamma },⟦v_h⟧·n^{\Gamma }\right)}_{\Gamma },$$

where $\gamma$ and ${\varphi }^i$ denote the penalty parameter and stabilization scaling for different flow regimes, respectively. Note, the weights in (11) for $\left\{·\right\}$, $\langle ·\rangle$ are defined as $w^1\stackrel{\mathrm{def}}{=}{\phi }^2/({\phi }^1+{\phi }^2)$ and $w^2\stackrel{\mathrm{def}}{=}{\phi }^1/({\phi }^1+{\phi }^2)$, where ${\phi }^i\stackrel{\mathrm{def}}{=}{\mu }^i{\left(f^i\right)}^2$, and $f^i$ is a scaling factor derived from a weakened trace inequality. In the simplest case, this scaling satisfies ${\left(f^i\right)}^2\approx 1/h_N^i$.

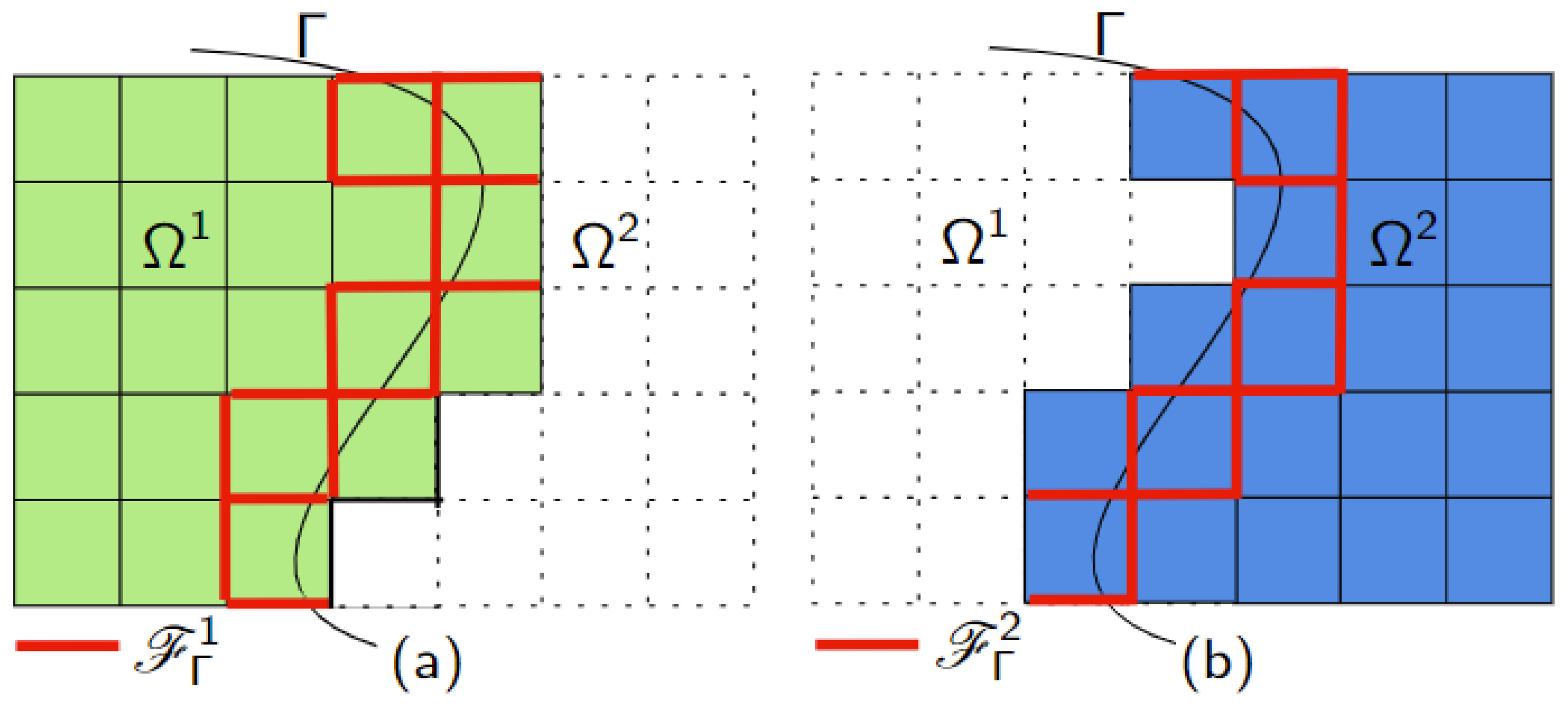
3.4. Face-Oriented Interface Zone Fluid Stabilizations

To ensure proper stabilization of the two-phase flow formulation and achieve optimal error convergence, face-oriented ghost penalty stabilization terms are applied specifically in the interface zone. These terms are strategically integrated in regions where significant interfacial interactions occur, as shown in Figure 3. Additionally, distinct ghost penalty terms are employed for the two separate domains, tailored to effectively address the unique characteristics and challenges encountered within each domain. By incorporating these carefully designed stabilization techniques, the computational model achieves enhanced accuracy and stability, which is crucial for the reliable simulation of complex fluid dynamics phenomena in two-phase flows. By defining $u_{\infty ,F}^i\stackrel{\mathrm{def}}{=}{∥u_h^i∥}_{0,\infty ,F}$, the interface zone face-jump ghost penalty terms for the Navier–Stokes equations are given by the following:

$${\mathcal{G}}_h^{i,GP}(U_h^i,V_h^i)=(g_{\beta }^i+g_u^i+g_p^i+g_{\mu }^i+g_{\sigma }^i)(U_h^i,V_h^i),$$

(13)

with

$$\begin{array}{cc}\hfill g_{\beta }^i(u_h,v_h)=& {\gamma }_{\beta }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k{\varphi }_{\beta ,F}^i{h}^{2j-1}{\left({\rho }^i{u}_{\infty ,F}^i\right)}^2{\left(⟦{\partial }_n^j{u}_h^i⟧,⟦{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \\ \hfill g_u^i(u_h,v_h)=& {\gamma }_u\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^{k-1}{\varphi }_{u,F}^i{h}^{2j+1}{\left(⟦\nabla ·{\partial }_n^j{u}_h^i⟧,⟦\nabla ·{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \\ \hfill g_p^i(p_h,q_h)=& {\gamma }_p\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k{\varphi }_{p,F}^i{h}^{2j-1}{\left(⟦{\partial }_n^j{p}_h^i⟧,⟦{\partial }_n^j{q}_h^i⟧\right)}_F,\hfill \\ \hfill g_{\mu }^i(u_h,v_h)=& {\gamma }_{\mu }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k{\mu }^i{h}^{2j-1}{\left(⟦{\partial }_n^j{u}_h^i⟧,⟦{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \\ \hfill g_{\sigma }^i(u_h,v_h)=& {\gamma }_{\sigma }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k\sigma {\rho }^i{h}^{2j+1}{\left(⟦{\partial }_n^j{u}_h^i⟧,⟦{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \end{array}$$

with non-dimensional stabilization parameters ${\gamma }_{\beta },{\gamma }_u,{\gamma }_p,{\gamma }_{\mu },{\gamma }_{\sigma }>0$, element-wise scaling functions

$${\varphi }_T^i={\mu }^i+c_u^i{\rho }^i\left({∥\beta ∥}_{0,\infty ,T}{h}_T\right)+c_{\sigma }^i{\rho }^i\left(\sigma h_T^2\right),{\varphi }_{\beta ,T}^i={\varphi }_{p,T}^i=h_T^2{\left({\varphi }_T^i\right)}^{-1},{\varphi }_{u,T}^i={\varphi }_T^i,$$

and according to face averages ${\varphi }_{\beta ,T}^i,{\varphi }_{u,T}^i,{\varphi }_{p,T}^i$ at interior faces $F\in {\mathcal{F}}_{\Gamma }^i$.

Combining all constituents of the proposed approach, the final coupled variational multiscale formulation for incompressible two-phase flow in the entire domain $\Omega$ reads as follows: Find $(u_h^i,p_h^i)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$, such that for all $(v_h^i,q_h^i)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$,

$$\begin{array}{cc}\hfill \sum _{i\in \{1,2\}}& \left\{{\left({\rho }^i{\displaystyle \frac{\partial u_h^i}{\partial t}},v_h^i\right)}_{{\Omega }^i}+{\left({\rho }^i{u}_h^i·\nabla u_h^i,v_h^i\right)}_{{\Omega }^i}-{\left(p_h^i,\nabla ·v_h^i\right)}_{{\Omega }^i}\right.\hfill \\ \hfill & +{\left(2{\mu }^iϵ\left(u_h^i\right),ϵ\left(v_h^i\right)\right)}_{{\Omega }^i}+{\left(\nabla ·u_h^i,q_h^i\right)}_{{\Omega }^i}+s_{\beta }^i(u_h^i,v_h^i)+s_u^i(u_h^i,v_h^i)+s_p^i(p_h^i,q_h^i)\hfill \\ \hfill & \left.+g_{\beta }^i(u_h^i,v_h^i)+g_u^i(u_h^i,v_h^i)+g_p^i(p_h^i,q_h^i)+g_{\mu }^i(u_h^i,v_h^i)+g_{\overline{\sigma }}^i(u_h^i,v_h^i)\right\}\hfill \\ \hfill & -{\left(⟦v_h⟧·n^{\Gamma },\left\{p_h\right\}\right)}_{\Gamma }+{\left(⟦v_h⟧,\left\{2\mu ϵ\left(u_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma }\hfill \\ \hfill & +{\left(⟦u_h⟧·n^{\Gamma },\left\{q_h\right\}\right)}_{\Gamma }+{\left(⟦u_h⟧,\left\{2\mu \epsilon \left(v_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma }\hfill \\ \hfill & +{\left(\gamma \left(\right\{\phi \}/2)⟦u_h⟧,⟦v_h⟧\right)}_{\Gamma }+{\left(\gamma \left(\right\{\rho \varphi /h\}/2)⟦u_h⟧·n^{\Gamma },⟦v_h⟧·n^{\Gamma }\right)}_{\Gamma }\hfill \\ \hfill & =\sum _{i\in \{1,2\}}\left\{{\left(f^i,v_h^i\right)}_{{\Omega }^i}+{(h_N^i,v_h^i)}_{{\Gamma }_N^i}\right\}+{\left(\langle v_h\rangle ,\gamma \kappa n^{\Gamma }\right)}_{\Gamma }.\hfill \end{array}$$

(14)

The definitions of CIP and GP terms are given by Equations (9) and (13), respectively.

In this flow scenario, we assume that the velocity field is continuous across the interface, denoted as $⟦u⟧=⟦v⟧=0$, meaning there is no jump in the velocity components. However, we allow the pressure field to be discontinuous at the interface $\Gamma$. This setup reflects the physical situation where the fluid’s speed does not change abruptly as it crosses the interface, but the pressure may differ on either side of the interface. This modeling choice is physically motivated: in incompressible multiphase flows, continuity of velocity is essential to satisfy conservation of mass and to prevent unphysical fluid separation at the interface. At the same time, a discontinuity in pressure is expected due to interfacial forces such as surface tension or abrupt changes in material properties. From a numerical perspective, assuming velocity continuity simplifies the weak formulation and stabilization design. If both velocity and pressure were allowed to be discontinuous, the formulation would require interface enrichment or additional stabilization terms to maintain consistency and stability, significantly increasing computational complexity. Our assumption enables a stable, efficient formulation that still captures key multiphase interface phenomena.

Given these conditions, we simplify the Nitsche-type CutFEM (14) for the coupled flow scenario by appropriately handling the dissipative terms. The Nitsche method is adapted to manage the interface conditions efficiently, ensuring numerical stability and accuracy despite the discontinuity in pressure. Under these assumptions, the following terms in (14) vanish:

$$\begin{array}{cc}& {\left(⟦v_h⟧·n^{\Gamma },\left\{p_h\right\}\right)}_{\Gamma },{\left(⟦v_h⟧,\left\{2\mu ϵ\left(u_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma },{\left(⟦u_h⟧·n^{\Gamma },\left\{q_h\right\}\right)}_{\Gamma },\hfill \\ & {\left(⟦u_h⟧,\left\{2\mu \epsilon \left(v_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma },{\left(\gamma \left(\right\{\phi \}/2)⟦u_h⟧,⟦v_h⟧\right)}_{\Gamma },{\left(\gamma \left(\right\{\rho \varphi /h\}/2)⟦u_h⟧·n^{\Gamma },⟦v_h⟧·n^{\Gamma }\right)}_{\Gamma }.\hfill \end{array}$$

This assumption allows us to simplify the coupled variational multiscale formulation into the following expression:

$$\begin{array}{cc}\hfill \sum _{i\in \{1,2\}}& \left\{{\left({\rho }^i{\displaystyle \frac{\partial u_h^i}{\partial t}},v_h^i\right)}_{{\Omega }^i}+{\left({\rho }^i{u}_h^i·\nabla u_h^i,v_h^i\right)}_{{\Omega }^i}-{\left(p_h^i,\nabla ·v_h^i\right)}_{{\Omega }^i}\right.\hfill \\ \hfill & +{\left(2{\mu }^iϵ\left(u_h^i\right),ϵ\left(v_h^i\right)\right)}_{{\Omega }^i}+{\left(\nabla ·u_h^i,q_h^i\right)}_{{\Omega }^i}+s_{\beta }^i(u_h^i,v_h^i)+s_u^i(u_h^i,v_h^i)+s_p^i(p_h^i,q_h^i)\hfill \\ \hfill & \left.+g_{\beta }^i(u_h^i,v_h^i)+g_u^i(u_h^i,v_h^i)+g_p^i(p_h^i,q_h^i)+g_{\mu }^i(u_h^i,v_h^i)+g_{\sigma }^i(u_h^i,v_h^i)\right\}\hfill \\ \hfill & =\sum _{i\in \{1,2\}}\left\{{\left(f^i,v_h^i\right)}_{{\Omega }^i}+{(h_N^i,v_h^i)}_{{\Gamma }_N^i}\right\}+{\left(\langle v_h\rangle ,\gamma \kappa n^{\Gamma }\right)}_{\Gamma }.\hfill \end{array}$$

(15)

Next, we will prove the global inf-sup condition and establish a priori error estimates for the formulation in (15). To simplify this analysis, we consider Oseen’s equations as an approximation to the Navier–Stokes equations.

Oseen’s equations provide a linearized model for fluid flow by approximating the convective terms in the Navier–Stokes equations. This linearization introduces an advective velocity field, $\beta$, and neglects certain nonlinear terms, making the analysis more manageable while still capturing the key flow dynamics.

4. A CutFEM for Oseen’s Problem in Two-Phase Flow

The Oseen equations are a simplified version of the Navier–Stokes equations, which describe the motion of viscous fluid substances. While the Navier–Stokes equations are highly nonlinear due to the convective acceleration term $(u·\nabla )u$, the Oseen equations linearize this term to make the analysis and computation more tractable.

The Oseen equations are derived by assuming that the flow has a predominant steady advective velocity field, denoted as $\beta$. This advective velocity represents the primary direction and speed of the flow. By linearizing the convective term around this advective velocity, the Oseen equations can be written as follows:

$$\begin{array}{ccc}\hfill \sigma \rho u+\rho (\beta ·\nabla u)+\nabla p-\nabla ·\left(2\mu ϵ\left(u\right)\right)& =f\hfill & \hfill \mathrm{in}\Omega ,\\ \hfill \nabla ·u& =0\hfill & \hfill \mathrm{in}\Omega .\end{array}$$

The Oseen-type momentum equation consists of a (pseudo-)reactive term with a reaction coefficient $\sigma >0$, typically introduced through temporal discretization of the time-derivative ${\partial }_{t}u$ using a finite difference scheme, an elliptic term $\nabla ·\left(2\mu ϵ\right(u\left)\right)$ involving the viscosity $\mu >0$, and a volumetric force term $f\in {\left[L^2(\Omega )\right]}^d$. The nonlinear convective term in the Navier–Stokes equations is linearized into an advective term $(\beta ·\nabla )u$, where the advective velocity field $\beta$ is assumed to be divergence-free (i.e., $\nabla ·\beta =0$) and independent of the flow variable u. Moreover, we assumed $\beta =0$ at the interface.

The presentation of the discrete stabilized formulation with cut finite element meshes relies on generalized notation on CutFEMs. In particular, we define

$${\mathcal{X}}_h^k\stackrel{\mathrm{def}}{=}\{v_h\in C^0\left({\Omega }_h^{*}\right):v_h{|}_T\in {\mathbb{P}}^k\left(T\right)\forall T\in {\mathcal{T}}_h\}.$$

These spaces and their vector-valued counterparts form the basis of the discrete approximation spaces for velocity and pressure, which are assumed to be interpolated using the same polynomial order, i.e.,

$${\mathcal{V}}_h\stackrel{\mathrm{def}}{=}{\left[{\mathcal{X}}_h^k\right]}^d,{\mathcal{Q}}_h\stackrel{\mathrm{def}}{=}{\mathcal{X}}_h^k,{\mathcal{W}}_h\stackrel{\mathrm{def}}{=}{\mathcal{V}}_h\times {\mathcal{Q}}_h.$$

4.1. Nitche-Type CIP/GP-CutFEM for Oseen’s Two-Phase Flow

Let ${\mathcal{W}}_h={\mathcal{W}}_h^1\oplus {\mathcal{W}}_h^2=({\mathcal{V}}_h^1\times {\mathcal{Q}}_h^1)\oplus ({\mathcal{V}}_h^2\times {\mathcal{Q}}_h^2)$, then a Nitsche-type stabilized formulation for coupling incompressible flows read as follows.

Find the fluid velocity and pressure $U_h^i\left(t\right)=(u_h^i\left(t\right),p_h^i\left(t\right))\in {\mathcal{W}}_h^i$, such that for all $V_h^i\left(t\right)=(v_h^i\left(t\right),q_h^i\left(t\right))\in {\mathcal{W}}_h^i$

$$A_h(U_h,V_h)=\sum _{i\in \{1,2\}}{\left(f^i,v_h^i\right)}_{{\Omega }^i}+{\left(\gamma \kappa n^{\Gamma },\langle v_h\rangle \right)}_{\Gamma }$$

(16)

with $U_h\in {\mathcal{W}}_h$, $V_h\in {\mathcal{W}}_h$, and where

$$A_h(U_h,V_h)=\sum _{i\in \{1,2\}}({\mathcal{B}}_h^i+{\mathcal{L}}_h^{i,CIP}+{\mathcal{G}}_h^{i,GP})((u_h^i,p_h^i),(v_h^i,q_h^i))$$

(17)

with

$$\begin{array}{cc}\hfill {\mathcal{B}}_h^i(U_h^i,V_h^i)& =a_h^i(u_h^i,v_h^i)+b_h^i(p_h^i,v_h^i)-b_h^i(q_h^i,u_h^i)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathcal{L}}_h^{i,CIP}(U_h^i,V_h^i)& =(s_{\beta }^i+s_u^i+s_p^i)(U_h^i,V_h^i),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathcal{G}}_h^{i,GP}(U_h^i,V_h^i)& =(g_{\beta }^i+g_u^i+g_p^i+g_{\mu }^i+g_{\sigma }^i)(U_h^i,V_h^i), \hfill \end{array}$$

(20)

where

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{a}_h^i(u_h^i,v_h^i)& ={\left(\sigma {\rho }^i{u}_h^i,v_h^i\right)}_{{\Omega }^i}+{\left({\rho }^i(\beta ·\nabla )u_h^i,v_h^i\right)}_{{\Omega }^i}+{\left(ϵ\left(u_h^i\right),2{\mu }^iϵ\left(v_h^i\right)\right)}_{{\Omega }^i}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill b_h^i(p_h^i,v_h^i)& =-{\left(p_h^i,\nabla ·v_h^i\right)}_{{\Omega }^i}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill b_h^i(q_h^i,u_h^i)& =-{\left(q_h^i,\nabla ·u_h^i\right)}_{{\Omega }^i}.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(23)

CIP stabilization terms are defined as Equation (9).

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{s}_{\beta }^i(u_h^i,v_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_{\beta }\sum _{F\in {\mathcal{F}}^i}{\varphi }_{\beta ,F}^{i}h{\left(⟦{\rho }^i({\beta }_h·\nabla )u_h^i⟧,⟦{\rho }^i({\beta }_h·\nabla )v_h^i⟧\right)}_F,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \hspace{1em}{s}_u^i(u_h^i,v_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_u\sum _{F\in {\mathcal{F}}^i}{\varphi }_{u,F}^{i}h{\left(⟦\nabla ·u_h^i⟧,⟦\nabla ·v_h^i⟧\right)}_F,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill s_p^i(p_h^i,q_h^i)\stackrel{\mathrm{def}}{=}& {\gamma }_p\sum _{F\in {\mathcal{F}}^i}{\varphi }_{p,F}^{i}h{\left(⟦\nabla p_h^i⟧,⟦\nabla q_h^i⟧\right)}_F.\hfill \end{array}$$

(26)

As a final component in formulating a CIP-based CutFEM for the Oseen problem on unfitted meshes, different GPs for velocity and pressure are required

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{g}_{\beta }^i(u_h^i,v_h^i)=& {\gamma }_{\beta }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^{k-1}{\varphi }_{\beta ,F}^i{h}^{2j+1}{\left(⟦{\rho }^i({\beta }_h·\nabla ){\partial }_n^j{u}_h^i⟧,⟦{\rho }^i({\beta }_h·\nabla ){\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}{g}_u^i(u_h^i,v_h^i)=& {\gamma }_u\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^{k-1}{\varphi }_{u,F}^i{h}^{2j+1}{\left(⟦\nabla ·{\partial }_n^j{u}_h^i⟧,⟦\nabla ·{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill g_p^i(p_h^i,q_h^i)=& {\gamma }_p\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k{\varphi }_{p,F}^i{h}^{2j-1}{\left(⟦{\partial }_n^j{p}_h^i⟧,⟦{\partial }_n^j{q}_h^i⟧\right)}_F,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill g_{\mu }^i(u_h^i,v_h^i)=& {\gamma }_{\mu }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k{\mu }^i{h}^{2j-1}{\left(⟦{\partial }_n^j{u}_h^i⟧,⟦{\partial }_n^j{v}_h^i⟧\right)}_F,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill g_{\sigma }^i(u_h^i,v_h^i)=& {\gamma }_{\sigma }\sum _{F\in {\mathcal{F}}_{\Gamma }^i}\sum _{j=0}^k\sigma {\rho }^i{h}^{2j+1}{\left(⟦{\partial }_n^j{u}_h^i⟧,⟦{\partial }_n^j{v}_h^i⟧\right)}_F.\hfill \end{array}$$

(31)

The piecewise constant scaling functions ${\varphi }_{\beta },{\varphi }_u,{\varphi }_p$ are

$${\varphi }_T^i={\mu }^i+c_u^i{\rho }^i\left({∥{\beta }^{*}∥}_{0,\infty ,T}{h}_T\right)+c_{\sigma }^i{\rho }^i\left(\sigma h_T^2\right),{\varphi }_{\beta ,T}^i={\varphi }_{p,T}^i=h_T^2{\varphi }_T^{-i},{\varphi }_{u,T}^i={\varphi }_T^i,$$

(32)

where the respective face averages are written as ${\varphi }_{\beta ,T}^i,{\varphi }_{u,T}^i,{\varphi }_{p,T}^i$, where $T\in {\mathcal{F}}^i$. Here, ${\beta }_h$ refers to the discrete (finite element) interpolated counterpart of $\beta$, while ${\beta }^{*}$ denotes an extension of the advective velocity field, typically defined in a larger domain or used for numerical stabilization purposes. For assumptions on the functions ${\beta }^{*}$ and ${\beta }_h$ in the boundary zone, please refer to [20].

Remark 1.

As introduced above, in this model we assume a continuous velocity field ($⟦u⟧=⟦v⟧=0$) and a discontinuous pressure field across the interface Γ. This assumption is motivated by the physical behavior of incompressible multiphase flows, where the velocity typically remains continuous across fluid–fluid interfaces, while the pressure may exhibit jumps due to surface tension or material property contrasts. Mathematically, this choice also simplifies the weak formulation by removing the need for interface enrichment and reducing numerical complexity. As a result of these interface conditions, several terms in the weak formulation vanish identically:

$${\left(⟦v_h⟧·n^{\Gamma },\left\{p_h\right\}\right)}_{\Gamma },{\left(⟦v_h⟧,\left\{2\mu ϵ\left(u_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma },{\left(⟦u_h⟧·n^{\Gamma },\left\{q_h\right\}\right)}_{\Gamma },{\left(⟦u_h⟧,\left\{2\mu \epsilon \left(v_h\right)·n^{\Gamma }\right\}\right)}_{\Gamma },$$

$${\left(\gamma \left(\right\{\phi \}/2)⟦u_h⟧,⟦v_h⟧\right)}_{\Gamma },{\left(\gamma \left(\right\{\rho \varphi /h\}/2)⟦u_h⟧·n^{\Gamma },⟦v_h⟧·n^{\Gamma }\right)}_{\Gamma }$$

These cancellations are consistent with the interface assumptions and help streamline the formulation.

4.2. Stability and Error Analysis for Nitsche-Type CIP/GP-CutFEM for Oseen’s Two-Phase Flow

We begin by establishing norms and semi-norms tailored for boundary-fitted meshes. These norms are essential for accurately characterizing the behavior of discretized solutions near geometric boundaries.

4.2.1. Norms for Boundary-Fitted Meshes

For the velocity $u_h^i\in {\mathcal{V}}_h^i$ and the pressure $p_h^i\in {\mathcal{Q}}_h^i$, appropriate norms and semi-norms are defined based on terms from the discrete variational formulation, as follows:

$$\begin{array}{c}\hfill {\left|\left|\left|u_h\right|\right|\right|}^2\stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}{\left|\left|\left|u_h^i\right|\right|\right|}^2,{\left|\left|\left|p_h\right|\right|\right|}^2\stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}{\left|\left|\left|p_h^i\right|\right|\right|}^2\end{array}$$

(33)

where ${\left|\left|\left|u_h^i\right|\right|\right|}^2,{\left|\left|\left|p_h^i\right|\right|\right|}^2$, and the pressure semi-norm are defined as

$$\begin{array}{cc}\hfill {\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left|\left|\left|u_h^i\right|\right|\right|}^2& \stackrel{\mathrm{def}}{=}{\parallel {\left(\sigma {\rho }^i\right)}^{{\displaystyle \frac{1}{2}}}{u}_h^i\parallel }_{{\Omega }^i}^2+{\parallel {\left({\mu }^i\right)}^{{\displaystyle \frac{1}{2}}}\nabla u_h^i\parallel }_{{\Omega }^i}^2+s_u^i(u_h,u_h)+s_{\beta }^i(u_h,u_h),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\left|\left|\left|p_h^i\right|\right|\right|}^2& \stackrel{\mathrm{def}}{=}{\Phi }_p^i\parallel p_h^i{\parallel }_{{\Omega }^i}^2+{\left|p_h^i\right|}_{{\Omega }^i}^2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill |p_h^i{|}_{{\Omega }^i}^2& \stackrel{\mathrm{def}}{=}{s}_p^i(p_h,p_h),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(36)

and the $L^2$-norm scaling in (35) is defined as,

$${\Phi }_p^i\stackrel{\mathrm{def}}{=}{\mu }^i+{∥\beta ∥}_{0,\infty ,{\Omega }_i}{\rho }^i{C}_P+\sigma {\rho }^i{C}_P^2+{\rho }^i{\left({\displaystyle \frac{{∥\beta ∥}_{0,\infty ,{\Omega }_i}{C}_P}{\sqrt{{\mu }^i+\sigma C_P^2}}}\right)}^2,$$

(37)

where $C_P$ is the so-called Poincaré constant, and scales as the diameter of the domain. The norm for the product space ${\mathcal{W}}_h^i={\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$ is given as

$${\left|\left|\left|V_h\right|\right|\right|}^2\stackrel{\mathrm{def}}{=}{\left|\left|\left|u_h\right|\right|\right|}^2+{\left|\left|\left|p_h\right|\right|\right|}^2,\forall V_h\stackrel{\mathrm{def}}{=}(u_h,p_h)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i.$$

(38)

Burman et al. [21] established inf-sup stability and energy-type error estimates for fitted meshes using similar norms.

4.2.2. Norms Related to the CIP/GP CutFEM

The extended versions of semi-norms and energy-norms provided in (33)–(38) according to the Nitsche-type CutFEM (18) for velocity $u_h^i\in {\mathcal{V}}_h^i$ and the pressure $p_h^i\in {\mathcal{Q}}_h^i$ are defined by

$$\begin{array}{c}\hfill {\left|\left|\left|u_h\right|\right|\right|}_{*}^2\stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}{\left|\left|\left|u_h^i\right|\right|\right|}_{*}^2,{\left|\left|\left|p_h\right|\right|\right|}_{*}^2\stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}{\left|\left|\left|p_h^i\right|\right|\right|}_{*}^2,\end{array}$$

(39)

where

$$\begin{array}{cc}\hfill {\left|\left|\left|u_h^i\right|\right|\right|}_{*}^2& \stackrel{\mathrm{def}}{=}{\left|\left|\left|u_h^i\right|\right|\right|}^2+g_{\sigma }^i(u_h,u_h)+g_{\mu }^i(u_h,u_h)+g_{\beta }^i(u_h,u_h)+g_u^i(u_h,u_h),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\left|\left|\left|p_h^i\right|\right|\right|}_{*}^2& \stackrel{\mathrm{def}}{=}{\left|\left|\left|p_h^i\right|\right|\right|}^2+g_p^i(p_h,p_h).\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(41)

With an extended pressure semi-norm with respect to ${\Omega }_h^{i,*}$

$$|p_h^i{|}_{*}^2\stackrel{\mathrm{def}}{=}{s}_p^i(p_h,p_h)+g_p^i(p_h,p_h).$$

(42)

We now define a semi-norm on the product space ${\mathcal{W}}_h$. Given $U_h\in {\mathcal{W}}_h$, $U_h^i\in {\mathcal{W}}_h^i$, we define

$$|U_h{|}_{*}^2\stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}|U_h^i{|}_{*}^2\mathrm{where}{|U_h^i|}_{*}^2\stackrel{def}{=}{|(u_h^i,p_h^i)|}_{*}^2={\left|\left|\left|u_h^i\right|\right|\right|}_{*}^2+{\left|p_h^i\right|}_{*}^2.$$

(43)

Finally, we define a full energy-type norm:

$$\begin{array}{cc}\hfill {\left|\left|\left|U_h\right|\right|\right|}_{*}^2& \stackrel{\mathrm{def}}{=}\sum _{i\in \{1,2\}}{\left|\left|\left|U_h^i\right|\right|\right|}_{*}^2\hfill \\ \hfill {\left|\left|\left|U_h^i\right|\right|\right|}_{*}^2& \stackrel{\mathrm{def}}{=}|U_h^i{|}_{*}^2+\parallel {\left({\varphi }_u^i\right)}^{{\displaystyle \frac{1}{2}}}\nabla ·u_h^i{\parallel }_{{\Omega }^i}^2+{\displaystyle \frac{1}{1+{\omega }_h^i}}\parallel {\left({\varphi }_{\beta }^i\right)}^{{\displaystyle \frac{1}{2}}}({\rho }^i(\beta ·\nabla )u_h^i+\nabla p_h^i){\parallel }_{{\Omega }^i}^2+{\Phi }_p^i{\parallel p_h^i\parallel }_{{\Omega }^i}^2,\hfill \end{array}$$

(44)

with the norm-dimensional scaling function

$${\omega }_h^i=h^2{\left({\rho }^i\right)}^2{\left|\beta \right|}_{1,\infty ,{\Omega }_h}{({\mu }^i+\sigma {\rho }^i{h}^2)}^{-1}.$$

(45)

4.2.3. Global Inf-Sup Stability $A_h(U_h,V_h)$, with Respect to the Energy Norm

The bilinear form $A_h(U_h,U_h)$ defined in (16) satisfies an inf-sup condition with respect to the energy-type norm (44), which is constructed from the semi-norm $|U_h{|}_{*}^2$ (43). This finally ensures the existence and uniqueness of the discrete velocity and pressure solution for the cut finite element formulation (16). The corresponding global inf-sup stability estimate is given below.

Theorem 1

(Global Inf-Sup Stability). Let $U_h^i=(u_h^i,p_h^i)\in {\mathcal{W}}_h^i$ be a pair of discrete velocity and pressure functions. The cut finite element formulation is inf-sup stable

$${\left|\left|\left|U_h\right|\right|\right|}_{*}\lesssim \underset{V_h^i\in {\mathcal{W}}_h^i\setminus \left\{0\right\}}{sup}{\displaystyle \frac{A_h(U_h,V_h)}{{\left|\left|\left|V_h\right|\right|\right|}_{*}}},$$

(46)

where the hidden stability constant is independent of the mesh size h and the position of the boundary relative to the background mesh.

Proof. 

A full, detailed version of the proof is available in the unpublished Ph.D. thesis of one of the co-authors. Due to space constraints, we provide here only the key ideas and structure of the argument. Interested readers are welcome to contact us directly to receive the complete proof.

The proof strategy follows the general framework introduced in [20] for single-phase flows. However, our setting differs substantially, as we consider a two-phase flow problem with a continuous velocity field and a discontinuous pressure field across the interface. Under these assumptions, several interface terms in the weak formulation vanish, and the analysis must be adapted accordingly. We extend the methodology in [20] by incorporating these interface conditions and proving stability for the two-phase system.    □

Remark 2.

Under the assumptions of Theorem 1, the stabilized Nitsche-type CIP/GP-CutFEM formulation for the two-phase Oseen problem admits a unique discrete solution $U_h^i=(u_h^i,p_h^i)\in {\mathcal{W}}_h^i$. This follows from the coercivity and boundedness of the bilinear form in the discrete setting, as is standard in finite element theory.

Remark 3.

The discrete formulation is inf-sup stable with respect to the energy norm ${\left|\left|\left|U_h\right|\right|\right|}_{*}$ defined on the background mesh ${\mathcal{T}}_h^i$, as shown in Theorem 1. The ghost penalty operators $g_{\mu }^i,g_{\sigma }^i,g_{\beta }^i,g_u^i,g_p^i$ provide additional control over discrete functions on cut elements, which is known to improve the conditioning of the resulting linear system. Similar benefits of ghost penalty stabilization for CutFEM have been studied in [16,22].

4.2.4. Energy-Type a Priori Error Estimates

Using (46), we now introduce an a priori error estimate. The theorem below establishes the main a priori error estimate for the velocity in a natural energy norm and for the pressure in the $L^2$ norm.

Theorem 2.

Suppose that the solution $U^i\stackrel{\mathrm{def}}{=}(u^i,p^i)\in {\left[H^r(\Omega )\right]}^d\times H^s(\Omega )$ is the weak solution of the Oseen problem and let $U_h^i\stackrel{\mathrm{def}}{=}(u_h^i,p_h^i)\in {\mathcal{V}}_h^i\times {\mathcal{Q}}_h^i$ denote the discrete solution of the Nitsche-type cut finite element formulation (16). Then,

$$\begin{array}{cc}\hfill \left|\left|\left|u^{i,*}-u_h^i\right|\right|\right|& \lesssim {(1+{\omega }_h^i)}^{{\displaystyle \frac{1}{2}}}{({\mu }^i+{∥\beta ∥}_{0,\infty ,{\Omega }^i}{\rho }^{i}h+\sigma {\rho }^i{h}^2)}^{{\displaystyle \frac{1}{2}}}{h}^{r_u-1}{∥u^i∥}_{r_u,{\Omega }^i}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\underset{T\in {\mathcal{T}}_h^i}{max}\{{\displaystyle \frac{1}{{\mu }^i+{∥\beta ∥}_{0,\infty ,{\Omega }^i}{\rho }^{i}h+\sigma {\rho }^i{h}^2}}{\}}^{{\displaystyle \frac{1}{2}}}{h}^{s_p}{∥p^i∥}_{s_p,{\Omega }^i},\hfill \\ \hfill {∥p^{i,*}-p_h^i∥}_{{\Omega }^i}& \lesssim {\left({\Phi }_p^i\right)}^{-{\displaystyle \frac{1}{2}}}{(1+{\omega }_h^i)}^{{\displaystyle \frac{1}{2}}}{({\mu }^i+{∥\beta ∥}_{0,\infty ,{\Omega }^i}{\rho }^{i}h+\sigma {\rho }^i{h}^2)}^{{\displaystyle \frac{1}{2}}}{h}^{r_u-1}{∥u^i∥}_{r_u,{\Omega }^i}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & +\left(1+{\left({\Phi }_p^i\right)}^{-{\displaystyle \frac{1}{2}}}\underset{T\in {\mathcal{T}}_h^i}{max}\{{\displaystyle \frac{1}{{\mu }^i+{∥\beta ∥}_{0,\infty ,{\Omega }^i}{\rho }^{i}h+\sigma {\rho }^i{h}^2}}{\}}^{{\displaystyle \frac{1}{2}}}\right)h^{s_p}{∥p^i∥}_{s_p,{\Omega }^i},\hfill \end{array}$$

(48)

where $r_u\stackrel{\mathrm{def}}{=}min\{r,k+1\}$ and $s_p\stackrel{\mathrm{def}}{=}min\{s,k+1\}$. The constants ${\Phi }_p^i$ and the bounded scaling function ${\omega }_h^i$ are defined in (37) and (45), respectively. It is important to note that the hidden constants are independent of the mesh size h, and in particular, do not depend on how the boundary intersects the mesh $\mathcal{T}{h}^i$.

Proof. 

The proof of Theorem 1 follows an approach analogous to that used in [20]. It begins by showing that the discrete formulation satisfies a weakened form of Galerkin orthogonality. Next, it is demonstrated that the remainder term arising from this weakened orthogonality does not compromise the convergence rate of the proposed scheme, thereby ensuring weak consistency. Finally, an a priori error estimate is derived for both the velocity and pressure.    □

Remark 4.

Depending on the dominant term in the Oseen equations, the velocity component of the energy norm error scales as expected: with ${\mu }^i$ for viscous-dominated flows, with ${∥\beta ∥}_{0,\infty ,{\Omega }^i}{\rho }^{i}h$ for advection-dominated flows, and with $\sigma {\rho }^i{h}^2$ when the reaction term dominates. The pressure error, in contrast, exhibits the inverse scaling behavior.

Remark 5.

A priori error estimates would yield just ${\left|\left|\left|u^i-u_h^i\right|\right|\right|}_{{\Omega }^i}={∥u^i-u_h^i∥}_{{\Omega }^i}={∥p^i-p_h^i∥}_{{\Omega }^i}=\mathcal{O}\left(h^k\right)$, where k is the polynomial degree of the approximation spaces for velocity and pressure. However, as shown in the work by Burman et al. [21], optimal error convergence in the velocity $L^2$-norm, ${∥u^i-u_h^i∥}_{{\Omega }^i}=\mathcal{O}\left(h^{k+1}\right)$, can be obtained using the adjoint-consistent Nitsche formulation. This result follows from the standard Aubin–Nitsche duality argument combined with the energy-norm estimate. A detailed proof, however, lies beyond the scope of this paper.

5. Numerical Convergence Study

5.1. Bivariate Quadratic Level-Set Approach for Two-Phase Interfaces

To model the interface between the two phases $\Gamma$, we employ a level-set method. Specifically, we begin our analysis with a bivariate quadratic level-set function.

$$f(x,y)=A{x}^2+Bxy+C{y}^2+Dx+Ey+F.$$

(49)

The coefficients $A,B,C,D,E,$ and F are chosen to shape the interface. By solving the level-set equation, we can evolve this function over time to simulate the dynamics of the two-phase flow. Bivariate quadratic level-set functions can represent a variety of geometric shapes, including ellipses, parabolas, hyperbolas, circles, saddle-shaped surfaces, and parabolic curves.

In this study, we employ quadrilateral elements shaped as parallelograms (see Figure 4) for the numerical discretization. Let $L_x=x_2-x_1$ and $L_y=y_3-y_2$ denote the side lengths in the x and y directions, respectively. The nodes of the parallelogram satisfy the following relations:

$$\begin{array}{cc}\hfill x_2& =x_1+L_x,x_3=x_4+L_x,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill y_3& =y_2+L_y,y_4=y_1+L_y.\hfill \end{array}$$

(51)

5.1.1. The Bivariate Quadratic Equation in Terms of Reference Coordinates

Let $(x_i,y_i)$ be the coordinates of the nodes of an element in the physical space. The coordinates $(x,y)$ of any point within the element can be interpolated using the shape functions $N_i(\xi ,\eta )$ as

$$x(\xi ,\eta )=\sum _{i=1}^4{N}_i(\xi ,\eta )x_i\mathrm{and}y(\xi ,\eta )=\sum _{i=1}^4{N}_i(\xi ,\eta )y_i,$$

(52)

where $\xi$ and $\eta$ are the reference coordinates. We can rewrite the bivariate quadratic Equation (49) in terms of the reference coordinates $(\xi ,\eta )$ using (50)–(52) as follows:

$$f(\xi ,\eta )=A^{\prime }{\xi }^2+B^{\prime }\xi \eta +C^{\prime }{\eta }^2+D^{\prime }\xi +E^{\prime }\eta +F^{\prime }.$$

(53)

With coefficients

$$\begin{array}{cc}\hfill A^{\prime }& ={\displaystyle \frac{1}{4}}\left(A{L}_x^2+(-B{L}_x-C{y}_2)y_{12}\right),\hfill \\ \hfill B^{\prime }& ={\displaystyle \frac{1}{4}}\left(B{L}_x{L}_y-2A{L}_x{x}_{14}+B{x}_{14}{y}_{12}-2C{L}_y{y}_{12}\right),\hfill \\ \hfill C^{\prime }& ={\displaystyle \frac{1}{4}}\left(C{L}_y^2+(-B{L}_y+A{x}_{14})x_{14}\right),\hfill \\ \hfill D^{\prime }& ={\displaystyle \frac{1}{4}}\left(2D{L}_x+B{L}_x{L}_y+2A{L}_x{L}_{x14}-2E{y}_1-2C{L}_y{y}_1-B{x}_1{y}_1-B{x}_4{y}_1-2C{y}_1^2\right.\hfill \\ \hfill & \left.+(2E+2C{L}_y+B(2L_x+x_1+x_4))y_2+2C{y}_2^2)\right),\hfill \\ \hfill E^{\prime }& ={\displaystyle \frac{1}{4}}\left(2E{L}_y-2x_{14}(D+A{L}_{x14})+2C{L}_y{L}_{y12}+B(L_x{L}_y-x_1(y_1+y_2)+x_4(2L_y+y_1+y_2))\right),\hfill \\ \hfill F^{\prime }& ={\displaystyle \frac{1}{4}}\left(4F+2D{L}_{x14}+A{L}_{x14}^2+L_{y12}(2E+B{L}_{x14}+C{L}_{y12})\right),\hfill \end{array}$$

where $L_{x14}=L_x+x_1+x_4,L_{y12}=L_y+y_1+y_2,x_{14}=x_1-x_4$ and $y_{12}=y_1-y_2$.

5.1.2. Normal and Curvature Calculation

The normal vector at any point ${\mathbf{x}}_p=(x_p,y_p)$ on the level-set $f(x,y)=c$ (where c is a constant) is derived from the gradient of the function $f(x,y)$. The gradient vector $\nabla f=\left(f_x,f_y\right)$ points in the direction of the steepest ascent of the level-set function. The normal vector $\widehat{\mathbf{n}},$ at any point ${\mathbf{x}}_p$, is then given by the normalized gradient:

$$\widehat{\mathbf{n}}={\displaystyle \frac{\nabla f}{∥\nabla f∥}}=〈{\displaystyle \frac{f_x}{\sqrt{f_x^2+f_y^2}}},{\displaystyle \frac{f_y}{\sqrt{f_x^2+f_y^2}}}〉,$$

(54)

where

$$f_x=2A{x}_p+B{y}_p+D,f_y=2C{y}_p+B{x}_p+E,$$

(55)

The unit normal vector is perpendicular to the interface and is crucial for determining the direction of movement or flux across the interface.

For a level-set function, the curvature can be computed using the divergence of the normalized gradient, which represents the variation in the normal vector across the level set:

$$\kappa =\nabla ·\left({\displaystyle \frac{\nabla f}{∥\nabla f∥}}\right)={\displaystyle \frac{\mathcal{A}-\mathcal{B}}{{\mathcal{C}}^{3/2}}},$$

(56)

where

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathcal{A}& =8A{C}^2{y}_p^2+2C\left[{(D+2A{x}_p)}^2+4A(E+B{x}_p)y_p-B^2{y}_p^2\right],\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill \mathcal{B}& =-2(E+B{x}_p)\left[-AE+B(D+A{x}_p+B{y}_p)\right], \hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \mathcal{C}& =\left[{(D+2A{x}_p+B{y}_p)}^2+{(E+B{x}_p+2C{y}_p)}^2\right].\hfill \end{array}$$

(59)

This formula for curvature incorporates second derivatives of the level-set function, reflecting the local geometric properties of the interface.

5.2. Line Integrals in Adaptive Refinement for Cut Elements

In the numerical simulations of multi-phase flows, it is common to encounter scenarios in which the interface does not align precisely with the mesh elements. This misalignment gives rise to so-called cut elements, wherein only portions of the elements intersect with the interface. To address this challenge and maintain the accuracy of the numerical simulations, we employ an adaptivity technique.

In our case, we focus on an adaptive mesh refinement aimed at improving the integration accuracy near the interface. This refinement process selectively increases the mesh resolution in regions where the interface intersects with elements, ensuring more precise numerical integration along the interface.

The adaptive refinement process begins by identifying the cut elements, defined as those intersected by the interface (see Figure 5). The maximum number of refinement levels, $L_{\max }$, is set based on the desired accuracy and available computational resources. In Figure 5, we choose $L_{\max }=2$ for simplicity of illustration. Initially, the cut element is mapped to the parent element, denoted as Level 0 ($L_0$). At $L_0$, the element is refined into four sub-elements: $L_{1,0}$, $L_{1,1}$, $L_{1,2}$, and $L_{1,3}$. These sub-elements are then mapped to Level 1 ($L_1$), where each is checked to determine whether it contains the interface. For instance, in the figure, only $L_{1,3}$ contains the interface, while $L_{1,0}$, $L_{1,1}$, and $L_{1,2}$ do not. Consequently, no further refinement is performed on these three sub-elements, and standard integration is applied to them.

The sub-element $L_{1,3}$ is further refined and mapped to Level 2 ($L_2$), subdividing it into four new sub-elements: $L_{2,0}$, $L_{2,1}$, $L_{2,2}$, and $L_{2,3}$. At $L_2$, it is identified that $L_{2,0}$, $L_{2,2}$, and $L_{2,3}$ contain the interface, while $L_{2,1}$ does not. Since the maximum refinement level is set to two, the refinement process terminates at this stage. Elements not intersected by the interface are integrated conventionally. For elements containing the interface, a custom quadrature rule developed by Aulisa and Jonathon [31] is applied. Since this rule is designed for elements intersected by a straight line, the interface is approximated by a straight segment within each cut element.

This approach ensures accurate integration near the interface by dynamically refining the mesh where needed. The general structure of the adaptive refinement is described in Algorithm 1.

Algorithm 1 Adaptive Refinement for Cut Elements

1: Identification of Cut Elements: Identify elements intersected by interfaces. 2: Maximum Refinement Levels: Determine the maximum number of refinement levels $L_{\max }$ based on the desired accuracy and available resources. 3: Initial Level Mapping: Map each cut element to a parent element at the base level. 4: First Level Refinement: Refine the base-level elements, creating sub-elements according to the refinement strategy. 5: Level Mapping: Map each sub-element to the next refinement level and check if it intersects the interface. 6: Subsequent Level Refinement: Further refine intersecting sub-elements, repeating until $L_{\max }$ is reached or convergence criteria are satisfied. 7: Integration and Quadrature: Integrate full elements normally. For elements containing interfaces, apply specialized quadrature techniques.

5.3. Linear Approximation of Bivariate Quadratic Functions

As outlined in Section 5.2, we employ an adaptive mesh refinement strategy to improve resolution near the interface. Upon reaching the maximum refinement level ($L_{\max }$), we encounter challenges in performing line integration for elements with interfaces represented by bivariate quadratic functions (53).

To address these challenges and ensure accurate representation and integration, we employ a best-fit quadratic level-set interpolation method. This involves approximating the complex interface with a linear function using a least squares approach to define the cost function (see Figure 6). By minimizing the discrepancy between the linear representation and the actual interface, we achieve precise numerical integration without the need for further refinement or remapping of the bivariate quadratic functions.

Within each parent element, we use a linear approximation of the bivariate quadratic functions. For simplicity, we consider coordinates x and y in this context. This linear approximation takes the following form:

$$A^{*}x+B^{*}y+C^{*}=0.$$

(60)

To determine the optimal coefficients $A^{*}$, $B^{*}$, and $C^{*}$ for the linear approximation of the bivariate quadratic functions within each parent element, we solve the following best-fit problem. We consider n data points within the element. In this new reference system, the objective is to minimize the cost function $\mathcal{C}$, given by

$$\mathcal{C}=\sum _{i=1}^n{\displaystyle \frac{1}{2}}{w}_i{\left(A^{*}{x}_i+B^{*}{y}_i+C^{*}-Z(x_i,y_i)\right)}^2,$$

(61)

where $w_i=exp\left(-{\displaystyle \frac{100Z^2(x_i,y_i)}{s^2}}\right)$ and $s^2={\sum }_{i=1}^n{\displaystyle \frac{Z^2(x_i,y_i)}{n}}$. Also, $x_i$ and $y_i$ denote the coordinates of the i-th data point, and $Z(x_i,y_i)$ represents the actual value of the level-set function $Z(x,y)$ at the point $(x_i,y_i)$. In our numerical study, we typically consider around 25 data points uniformly distributed (e.g., a $5\times 5$ grid) in the vicinity of the interface to ensure adequate representation.

In the cost function (61), we incorporate weights $w_i$ to account for the varying importance of data points based on their distance from the interface. Here, $s^2$ represents the standard deviation, with the average $\mu$ being zero. Also, $w_i$ represents the weight assigned to the i-th data point, which depends on its distance from the interface. The distance is calculated using the absolute value of the level set, with $Z(x_i,y_i)$ representing the bivariate quadratic functions evaluated at the nodal values.

To determine the optimal coefficients $A^{*}$, $B^{*}$, and $C^{*}$ that minimize the cost function (61), we compute the partial derivatives of the cost function with respect to each coefficient and set them equal to zero. This process ensures that we find the minimum of the cost function.

$${\displaystyle \frac{\partial \mathcal{C}}{\partial A^{*}}}=\sum _{i=1}^n{w}_i{x}_i\left(A^{*}{x}_i+B^{*}{y}_i+C^{*}-Z(x_i,y_i)\right)=0,$$

$${\displaystyle \frac{\partial \mathcal{C}}{\partial B^{*}}}=\sum _{i=1}^n{w}_i{y}_i\left(A^{*}{x}_i+B^{*}{y}_i+C^{*}-Z(x_i,y_i)\right)=0,$$

$${\displaystyle \frac{\partial \mathcal{C}}{\partial C^{*}}}=\sum _{i=1}^n{w}_i\left(A^{*}{x}_i+B^{*}{y}_i+C^{*}-Z(x_i,y_i)\right)=0.$$

By solving these equations simultaneously, we obtain the optimal values of $A^{*}$, $B^{*}$, and $C^{*}$ that minimize the cost function. Once these coefficients are determined, we apply the previously developed custom formula to perform exact Gaussian quadrature over the cut element presented in [31].

5.4. Numerical Implementation of Ghost Penalty

The implementation of GP terms in our finite element method (FEM) framework involves several non-standard procedures. Unlike standard FEM, this method requires a more intricate approach due to the need to handle boundary integrals across interfaces within the elements.

To ensure effective stabilization of the two-phase flow formulation and achieve optimal error convergence, we employ face-oriented ghost penalty (GP) stabilization terms within the interface zone, denoted as ${\mathcal{T}}_{\Gamma }$. These terms are applied exclusively in this region (see Figure 3), targeting areas with significant interfacial interaction. Moreover, separate GP terms are tailored for each domain to address the specific numerical challenges encountered within them, thereby enhancing the overall stability and accuracy of the formulation. Faces integrated for ${\Omega }_1$ and ${\Omega }_2$ are denoted as ${\mathcal{F}}_{\Gamma }^1$ and ${\mathcal{F}}_{\Gamma }^2$, respectively (refer to Figure 3). Thus, in the numerical simulation, the first step is to identify interface elements. Essentially, we take an element and examine its neighborhood to identify the interface.

The identification process involves locating the Gauss points on the interface. Subsequently, the velocity, pressure, and advective velocity field are evaluated on both sides of the interface; these are the relevant quantities whose discontinuities are captured through boundary integrals. This procedure requires the computation of boundary integrals that capture the discontinuities (jumps) across the interface. The GP method is not a typical Lagrangian FEM; it requires additional steps:

• Identify the surrounding elements for each element in the mesh.
• Determine the interface shared between two elements.
• Perform boundary integrals along this interface.
• Apply the exact Gaussian quadrature rule along the line representing the interface, evaluating the relevant quantities within the element on both sides of the interface.

This implementation is particularly complex in a parallel computing setting. In a parallel environment, each processor may not have information about elements handled by other processors. Therefore, information must be exchanged between processors to ensure consistency and accuracy in the implementation of GP terms.

The overall process involves substantial work beyond the standard assembly of FEM. It requires identifying neighboring elements, determining interfaces, and performing boundary integrals, all while managing data exchange across processors. This complexity underscores the significant effort involved in implementing GP terms in a parallel computing environment.

Remark 6.

CIP terms are computed over all faces within each subdomain, while GP terms focus exclusively on interface faces. This separation allows for efficient parallel computation, as CIP terms remain localized, and GP terms are limited to interfacial regions.

6. Benchmarking Results

Following the implementation of our method, a critical evaluation is conducted to assess its performance and effectiveness. We focus our experiments on the Oseen problem rather than the full Navier–Stokes equations. This choice allows us to isolate key aspects of stabilization and interface treatment without the added complexities of nonlinear solver convergence. Additionally, the Global Inf-Sup Stability theorem presented earlier is established only for the Oseen setting. Extending both the theoretical and numerical analysis to the full Navier–Stokes system is part of our planned future work.

6.1. Spurious Current Test: Circular Interface Benchmark

As the initial step in our evaluation process, we conducted the Spurious Current Test using a circular interface. This involved transforming the previously utilized bivariate quadratic function (49) into a circular shape. The choice of a circular interface allows for a controlled and well-defined test scenario, enabling us to assess the method’s performance under idealized conditions. By simulating flow dynamics around a circular interface, we aimed to analyze the method’s ability to accurately capture and resolve fluid behavior, while also evaluating its effectiveness in suppressing spurious currents.

6.1.1. Methodology

The methodology for the Circular Interface Benchmark involved several key steps. Firstly, we defined a unit circular interface within our computational domain as $\Gamma \stackrel{\mathrm{def}}{=}\{x=(x_1,x_2)\in {\mathbb{R}}^2|x_1^2+x_2^2=1\}$. In this setup, the analytic velocity field is zero and remains continuous throughout the domain, while the pressure is discontinuous. When we impose a surface tension $\overline{\sigma }=1$, we expect to observe a velocity profile of zero and a resulting pressure jump of 1. Specifically, $P_1=0$ and $P_2=1$ represent the pressure in each phase.

The Circular Interface Benchmark was conducted using a comprehensive set of parameters to ensure the accuracy and reliability of the numerical simulation. The key parameters utilized in the benchmark can be divided into two sets and are outlined in

Table 1. Summary of physical parameters for the two test cases.

Set	${\mathit{\rho }}_1$	${\mathit{\rho }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	$\overline{\mathit{\sigma }}$
Set 1	1.0	1.0	1.0	1.0	1.0
Set 2	1.0	100.0	1.0	0.1	1.0

.

Note that we conducted our tests considering different values of the density and viscosity of phase 2, ${\rho }_2$ and ${\mu }_2$, respectively.

Table 2. Summary of Nitsche, GP, CIP, and refinement parameters used in all the numerical simulations.

Parameter	Description	Value
$\gamma$	Nitsche penalty parameter	35
${\gamma }_{\mu },{\gamma }_{\beta },{\gamma }_p,{\gamma }_u,{\gamma }_{\sigma }$	Ghost penalty parameters	0.01, 0.01, 0.01, 0.01, 0.0005
$c_u$, $c_{\epsilon }$	CIP scaling constants	1/6, 1/12
$L_{max}$	Refinement Criterion	5

summarizes the parameter values adopted for the Nitsche, Ghost Penalty, and CIP stabilization techniques, which are used consistently across all simulations in this section. Note that ${\gamma }_{\mu }={\gamma }_{\beta }={\gamma }_p={\gamma }_u=0.01$ for the viscous ghost penalty term (31). The (pseudo-)reactive ghost-penalty term (30), however, is scaled using a significantly smaller coefficient, specifically ${\gamma }_{\sigma }=0.05{\gamma }_{\mu }$.

The computational analysis was performed using the FEMuS library developed by Texas Tech University. The simulation domain was discretized into various grid resolutions, ranging from $n=8\times 8$ to $n=128\times 128$. Adaptive refinement was applied up to a maximum level of $L_{max}=5$, providing enhanced resolution where necessary. This was determined to be the optimal level, as increasing it further did not result in noticeable differences. For the velocity and pressure fields, quadrilateral elements with 4, 8, and 9 nodes were used. Homogeneous Dirichlet boundary conditions were applied throughout the analysis.

In the next sections, we present the results of the Error and Convergence simulations conducted with various element types for velocity and pressure, as well as different density and viscosity parameters. The objective is to analyze how the choice of element type and parameter values influences the numerical accuracy and convergence behavior of the simulation.

The error analysis was conducted by comparing the numerical solutions with exact solutions. For the velocity, we computed errors using the $L^2$ norm, semi-norm, and energy norm, denoted as $∥·∥$, $\left|·\right|$, and $\left|\left|\left|·\right|\right|\right|$, respectively. For the pressure, we considered discontinuous pressure using the Heaviside function and computed the $L^2$ norm.

6.1.2. Results with Quadrilateral Elements with 4 Nodes (Quad4)

We used quadrilateral elements with 4 nodes (Quad4) for these simulations, which are known for their simplicity and computational efficiency. These elements are shaped like a quadrilateral and have nodes at each of the four corners. Each node represents a point where the field variables, such as velocity and pressure in our case, are computed.

Table 3. Error and convergence order with analytic solution for spurious current test (Quad4), with Set 1 of parameters.

Quad4/Quad4	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathit{u}-{\mathit{u}}_{\mathit{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	8.396 × ${10}^{-4}$	4.098 × ${10}^{-3}$	5.916 × ${10}^{-3}$	2.737 × ${10}^{-2}$	2.564 × ${10}^{-3}$
conv order	1.260	1.144	1.148	3.027	0.349
n = 16 × 16	3.505 × ${10}^{-4}$	1.855 × ${10}^{-3}$	2.669 × ${10}^{-3}$	3.359 × ${10}^{-3}$	2.013 × ${10}^{-3}$
conv order	2.064	2.132	2.129	2.530	1.523
n = 32 × 32	8.380 × ${10}^{-5}$	4.231 × ${10}^{-4}$	6.100 × ${10}^{-4}$	5.817 × ${10}^{-4}$	7.003 × ${10}^{-4}$
conv order	1.958	1.938	1.939	2.426	1.810
n = 64 × 64	2.157 × ${10}^{-5}$	1.104 × ${10}^{-4}$	1.591 × ${10}^{-4}$	1.083 × ${10}^{-4}$	1.997 × ${10}^{-4}$
conv order	1.994	1.930	1.932	2.164	1.950
n = 128 × 128	5.415 × ${10}^{-6}$	2.898 × ${10}^{-5}$	4.170 × ${10}^{-5}$	2.416 × ${10}^{-5}$	5.168 × ${10}^{-5}$

presents the Error and Convergence order using the exact solution, with parameters ${\rho }_1=1.0$, ${\rho }_2=1.0$, ${\mu }_1=1.0$, ${\mu }_2=1.0$, and $\overline{\sigma }=1.0$ (Set 1).

We then considered different parameters: ${\rho }_1=1.0$, ${\rho }_2=100.0$, ${\mu }_1=1.0$, ${\mu }_2=0.1$, $\overline{\sigma }=1.0$ (Set 2). This set of parameters presents greater challenges for the numerical simulations due to the higher density and viscosity ratios between the two phases. The numerical errors and corresponding convergence orders are reported in

Table 4. Error and convergence order with analytic solution for spurious current test (Quad4), with Set 2 of parameters.

Quad4/Quad4	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	7.997 × 10 −4	3.010 × 10 −3	3.994 × 10 −3	3.043 × 10 −2	4.746 × 10 −3
conv order	2.765	2.078	2.126	3.136	0.278
n = 16 × 16	1.176 × 10 −4	7.128 × 10 −4	9.151 × 10 −4	3.461 × 10 −3	3.915 × 10 −3
conv order	3.460	2.644	2.666	2.328	2.002
n = 32 × 32	1.069 × 10 −5	1.140 × 10 −4	1.442 × 10 −4	6.894 × 10 −4	9.772 × 10 −4
conv order	1.913	1.713	1.716	2.346	2.076
n = 64 × 64	2.838 × 10 −6	3.477 × 10 −5	4.389 × 10 −5	1.356 × 10 −4	2.318 × 10 −4
conv order	1.763	1.488	1.491	2.126	2.079
n = 128 × 128	8.365 × 10 −7	1.240 × 10 −5	1.562 × 10 −5	3.106 × 10 −5	5.488 × 10 −5

.

By analyzing Table 3 and Table 4, we can conclude that for $\parallel \mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\parallel =\mathcal{O}\left(h^2\right)$ and $|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|=|\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||=\mathcal{O}\left(h\right)$, the errors decrease consistently regardless of varying parameter densities and viscosities. Comparing these results with Theorem 2, we note that using Quad4 elements corresponds to a polynomial degree $k=1$ for the velocity and pressure approximation spaces. Therefore, the results obtained are consistent with theoretical predictions, achieving the optimal convergence rate for $\parallel \mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\parallel$, as established by Burman et al.

This behavior is also observed in Figure 7, which displays the error values alongside the theoretical convergence rates (dashed lines). The results show good agreement with the expected theoretical behavior.

Similarly, for pressure, we observe analogous results. In this case, we considered discontinuous pressure, and for both pressure components, the $L^2$ norm error decreases with increasing grid resolution. For $\parallel P_1-P_{1_{ex}}\parallel =\parallel P_2-P_{2_{ex}}\parallel =\mathcal{O}\left(h^2\right)$, we initially expected a convergence order of 1, in line with the theoretical prediction of Theorem 2. However, the numerical results exhibit a higher convergence rate, suggesting an additional convergence effect. This behavior remains consistent across different parameter settings.

6.1.3. Results with Quadrilateral Elements with 8 Nodes (Quad8)

Quadrilateral elements with 8 nodes, commonly referred to as Quad8 elements, are a higher-order finite element used in numerical simulations. These elements have a quadrilateral shape and feature nodes at each of the four corners, as well as at the midpoints of each side, resulting in a total of eight nodes per element. Each node corresponds to a point where field variables (such as velocity and pressure in fluid dynamics) are evaluated, allowing for improved accuracy over lower-order elements.

Table 5. Error and convergence order with analytic solution for spurious current test (Quad8), with Set 1 of parameters.

Quad8/Quad8	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	2.539 × 10 −4	2.116 × 10 −3	3.014 × 10 −3	1.423 × 10 −3	4.147 × 10 −4
conv order	6.387	6.219	6.221	6.697	5.316
n = 16 × 16	3.034 × 10 −6	2.841 × 10 −5	4.040 × 10 −5	1.371 × 10 −5	1.041 × 10 −5
conv order	3.780	3.450	3.453	3.146	3.867
n = 32 × 32	2.209 × 10 −7	2.599 × 10 −6	3.689 × 10 −6	1.549 × 10 −6	7.130 × 10 −7
conv order	3.829	3.551	3.552	2.197	3.557
n = 64 × 64	1.554 × 10 −8	2.218 × 10 −7	3.144 × 10 −7	3.379 × 10 −7	6.056 × 10 −8
conv order	3.188	3.311	3.310	2.055	2.665
n = 128 × 128	1.705 × 10 −9	2.235 × 10 −8	3.170 × 10 −8	8.124 × 10 −8	9.502 × 10 −9

presents the Error and Convergence order with the exact solution, considering Set 1 of parameters (see Table 1). Considering the parameter Set 2, we achieved consistent results that are reported in

Table 6. Error and convergence order with analytic solution for spurious current test (Quad8), with Set 2 of parameters.

Quad8/Quad8	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	1.887 × 10 −4	1.333 × 10 −3	1.701 × 10 −3	3.107 × 10 −3	5.142 × 10 −3
conv order	6.815	6.126	6.141	7.499	7.450
n = 16 × 16	1.676 × 10 −6	1.908 × 10 −5	2.410 × 10 −5	1.718 × 10 −5	2.941 × 10 −5
conv order	4.215	3.216	3.223	3.263	3.809
n = 32 × 32	9.024 × 10 −8	2.053 × 10 −6	2.581 × 10 −6	1.789 × 10 −6	2.098 × 10 −6
conv order	3.820	2.860	2.862	2.337	3.852
n = 64 × 64	6.391 × 10 −9	2.828 × 10 −7	3.551 × 10 −7	3.541 × 10 −7	1.453 × 10 −7
conv order	3.140	2.707	2.708	2.107	2.912
n = 128 × 128	7.249× 10 −10	4.330 × 10 −8	5.435 × 10 −8	8.227 × 10 −8	1.933 × 10 −8

.

Based on the results in Table 5 and Table 6, and on Figure 7, we observe a consistent decrease in the errors of both the velocity and pressure fields as the grid resolution increases, regardless of variations in parameters such as density and viscosity.

In the case of the velocity field, we observe a substantial reduction in error from coarse to fine grids. The convergence rates reported in the tables indicate that the error $\parallel \mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\parallel$ scales as $\mathcal{O}\left(h^3\right)$, while the semi-norm error $|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$ and the energy norm $\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$ scale as $\mathcal{O}\left(h^2\right)$. These results confirm that the numerical method achieves optimal convergence rates, which are consistent with, and in most cases exceed, the theoretical predictions of Theorem 2, where $1\le k\le 2$ for Quad8 elements.

This behavior is also evident in Figure 8, which presents the error values alongside the theoretical convergence rates. As in the Quad4 case, the results align well with the expected theoretical behavior.

The pressure field analysis also demonstrates substantial error reduction as the grid is refined. As shown in Table 5 and Table 6, and in Figure 8, the $L^2$-norm errors for pressure decrease systematically, exhibiting convergence rates consistent with $\parallel P_1-P_{1_{ex}}\parallel =\parallel P_2-P_{2_{ex}}\parallel =\mathcal{O}\left(h^2\right)$. These results are consistent across the two parameter settings.

6.1.4. Results with Quadrilateral Elements with 9 Nodes (Quad9)

Quad9 elements are quadrilateral-shaped and contain nine nodes: one at each corner, one at the midpoint of each side, and one at the center of the element.

Table 7. Error and convergence order with analytic solution for spurious current test (Quad9), with Set 1 of parameters.

Quad9/Quad9	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	2.548 × 10 −4	2.183 × 10 −3	3.108 × 10 −3	1.615 × 10 −3	5.871 × 10 −4
conv order	6.388	6.163	6.165	6.554	5.625
n = 16 × 16	3.042 × 10 −6	3.047 × 10 −5	4.330 × 10 −5	1.718 × 10 −5	1.190 × 10 −5
conv order	3.783	3.492	3.494	3.342	3.824
n = 32 × 32	2.210 × 10 −7	2.708 × 10 −6	3.843 × 10 −6	1.694 × 10 −6	8.402 × 10 −7
conv order	3.830	3.580	3.581	2.312	3.555
n = 64 × 64	1.554 × 10 −8	2.265 × 10 −7	3.211 × 10 −7	3.411 × 10 −7	7.146 × 10 −8
conv order	3.188	3.306	3.306	2.073	2.815

presents the Error and Convergence order obtained using the exact solution with parameter Set 1 (see Table 1). Consistent results were achieved with parameter Set 2, as reported in

Table 8. Error and convergence order with analytic solution for spurious current test (Quad9), with Set 2 of parameters.

Quad9/Quad9	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	1.864 × 10 −4	1.396 × 10 −3	1.779 × 10 −3	2.693 × 10 −3	1.600 × 10 −3
conv order	6.809	6.082	6.096	6.921	5.878
n = 16 × 16	1.663 × 10 −6	2.061 × 10 −5	2.601 × 10 −5	2.222 × 10 −5	2.720 × 10 −5
conv order	4.177	3.228	3.234	3.530	3.707
n = 32 × 32	9.190 × 10 −8	2.200 × 10 −6	2.765 × 10 −6	1.924 × 10 −6	2.082 × 10 −6
conv order	3.860	2.882	2.884	2.419	3.752
n = 64 × 64	6.327 × 10 −9	2.984 × 10 −7	3.746 × 10 −7	3.597 × 10 −7	1.545 × 10 −7
conv order	3.147	2.707	2.707	2.121	2.950
n = 128 × 128	7.144× 10 −10	4.570 × 10 −8	5.737 × 10 −8	8.267 × 10 −8	1.999 × 10 −8

.

Table 7 and Table 8 display the error reduction across various grid resolutions, emphasizing their impact on the velocity and pressure fields.

For the velocity field, errors decrease significantly as the grid resolution increases, regardless of parameter variations (see Table 7 and Table 8). Table 7 shows that $\parallel \mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\parallel =|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|=|\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||=\mathcal{O}\left(h^3\right)$. While we theoretically expect $|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|=|\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||=\mathcal{O}\left(h^2\right)$, the results indicate an additional convergence effect. For Table 8, the observed results are in line with theoretical expectations.

A similar trend is observed in Figure 9, which shows the error values together with the theoretical convergence rates for the velocity and the pressures. As in the earlier cases, the results closely follow the expected theoretical behavior.

For the pressure field, the analysis reveals a significant reduction in errors with increasing grid resolution, achieving a convergence order of $\parallel P_1-P_{1_{ex}}\parallel =\parallel P_2-P_{2_{ex}}\parallel =\mathcal{O}\left(h^2\right)$, which aligns with the theoretical results of $k=2$. These consistent results across different parameters underscore the effectiveness of Quad9 elements in handling pressure distributions and mitigating spurious currents.

For Quad9 elements, we also computed the pressure profiles at various grid resolutions. A color map was generated to visualize the interpolated pressure between $P_1$ and $P_2$. These profiles help assess how the numerical method captures the pressure distribution and reveal the influence of spurious currents at different resolutions.

Figure 10 illustrates the pressure profile with a color map of horizontal velocity for different grid sizes. As the grid resolution becomes finer, the spurious velocities decrease, approaching zero. The velocity remains continuous across the entire domain, maintaining the same value both inside and outside the interface. Moreover, the expected pressure difference $\Delta P=P_2-P_1=1$ (since we consider $\overline{\sigma }=1.0$ and unit radius) is accurately captured in the simulations across all grid resolutions. In particular, the pressure outside the interface $P_1$ remains close to zero, while the pressure inside $P_2$ approaches 1.

Concluding, the convergence analysis confirms the accuracy, stability, and generalizability of the numerical method across varying parameters and approximation spaces. The observed convergence orders align with theoretical predictions, validating the effectiveness of the stabilization techniques. Consistent pressure distributions and minimal spurious currents further highlight the method’s robustness, providing a strong foundation for more complex simulations and future refinements.

6.2. Elliptical Interface Benchmark

In addition to the Spurious Current Test with Circular Interface, we conducted a similar study for an elliptical interface to further validate the effectiveness and accuracy of our numerical method. The elliptical interface presents a different set of challenges due to its varying curvature, which tests the method’s ability to accurately capture and resolve the interface dynamics under different geometrical configurations. The following sections present the results and analysis of this test.

6.2.1. Methodology

Here, we considered an elliptical interface defined as $\Gamma \stackrel{\mathrm{def}}{=}\{x=(x_1,x_2)\in {\mathbb{R}}^2|1.2x_1^2+0.8x_2^2=1\}$, characterized by a continuous velocity field and a discontinuous pressure field. In this numerical test, we varied the density ${\rho }_2$ values as 10.0 and 100.0. For all the simulations, we considered ${\rho }_1=$ 1.0, ${\mu }_1=$ 1.0, ${\mu }_2=$ 1.0, $\overline{\sigma }=$ 1.0.

The discretization and boundary conditions follow the same approach used for the circular interface (see Section 6.1.1). To assess accuracy and convergence for the elliptical interface, we analyzed errors by comparing successive numerical solutions. Although the lack of an analytical solution presents limitations, this iterative analysis offers meaningful insights into the method’s performance around elliptical interfaces. The error metrics used are the same as those described for the circular case in Section 6.1.

6.2.2. Results with Quad4 Elements

Table 9. Error and convergence order with two consecutive solutions for elliptical interface (Quad4) with ${\rho }_1=1.0$, ${\rho }_2=10.0$.

Quad4/Quad4	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	3.537 × 10 −3	2.182 × 10 −2	3.116 × 10 −2	3.956 × 10 −2	9.052 × 10 −2
conv order	1.176	0.618	0.623	1.001	0.892
n = 16 × 16	1.566 × 10 −3	1.422 × 10 −2	2.023 × 10 −2	1.977 × 10 −2	4.877 × 10 −2
conv order	1.889	1.229	1.237	2.606	1.694
n = 32 × 32	4.228 × 10 −4	6.068 × 10 −3	8.580 × 10 −3	3.247 × 10 −3	1.507 × 10 −2
conv order	2.596	1.250	1.249	2.268	2.408
n = 64 × 64	6.991 × 10 −5	2.552 × 10 −3	3.610 × 10 −3	6.740 × 10 −4	2.839 × 10 −3

illustrates the Error and Convergence order between two consecutive solutions, considering ${\rho }_1=1.0$ and ${\rho }_2=10.0$. Analyzing the results, we observe that for both velocity and pressure, the error defined by all types of norms decreases as the grid resolution increases. For example, in Table 9, the $L^2$ norm error for velocity is $3.537\times {10}^{-3}$ at a grid resolution of $n=8\times 8$, which decreases to $6.991\times {10}^{-5}$ at a grid resolution of $n=128\times 128$, indicating a significant improvement. The same pattern is observed for the pressure field.

The convergence order for velocity is $\left|\right|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}\left|\right|=\mathcal{O}\left(h^2\right)$, which aligns with the theoretical results discussed in Theorem 2. In fact, for Quad4 elements, where $k=1$, the expected optimal convergence order for $\left|\right|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}\left|\right|$ is $\mathcal{O}\left(h^{k+1}\right)=\mathcal{O}\left(h^2\right)$. For the semi-norm and triple norm of velocity, we observe a convergence order of $\mathcal{O}\left(h\right)$, as theoretically $|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}|=|\left|\right|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}\left|\right||=\mathcal{O}\left(h\right)$. For pressure, we observe a convergence order of $\mathcal{O}\left(h^2\right)$, which is higher than expected, as the theoretical convergence order for pressure is $\mathcal{O}\left(h\right)$. In all cases, the numerical results are consistent with the theoretical expectations.

6.2.3. Results with Quad8 Elements

By analyzing

Table 10. Error and convergence order with two consecutive solutions for elliptical interface (Quad8) with ${\rho }_1=1.0$, ${\rho }_2=10.0$.

Quad8/Quad8	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	4.581 × 10 −3	2.515 × 10 −2	3.600 × 10 −2	4.710 × 10 −2	1.344 × 10 −1
conv order	1.608	1.169	1.187	3.873	1.731
n = 16 × 16	1.503 × 10 −3	1.118 × 10 −2	1.581 × 10 −2	3.215 × 10 −3	4.051 × 10 −2
conv order	2.705	1.755	1.767	1.632	2.341
n = 32 × 32	2.304 × 10 −4	3.313 × 10 −3	4.645 × 10 −3	1.037 × 10 −3	7.996 × 10 −3
conv order	3.493	2.201	2.191	2.036	2.706
n = 64 × 64	2.046 × 10 −5	7.204 × 10 −4	1.017 × 10 −3	2.529 × 10 −4	1.225 × 10 −3

, similar results can be observed with Quad8 elements. For both velocity and pressure, the error decreases with increasing grid resolution, despite varying density values. We obtained an optimal convergence rate for the $L^2$ norm of velocity, which is 3, and the convergence orders for all the other norms are $\mathcal{O}\left(h^2\right)$, aligning perfectly with theoretical results.

6.2.4. Results with Quad9 Elements

With Quad9 elements, we achieved similar (and thus consistent) results even considering ${\rho }_2=100.0$ (refer to

Table 11. Error and convergence order with two consecutive solutions for elliptical interface (Quad9) with ${\rho }_1=1.0$, ${\rho }_2=100.0$.

Quad9/Quad9	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	1.194 × 10 −3	1.022 × 10 −2	1.350 × 10 −2	1.120 × 10 −2	9.466 × 10 −2
conv order	2.776	2.009	1.957	2.766	2.015
n = 16 × 16	1.743 × 10 −4	2.539 × 10 −3	3.477 × 10 −3	1.647 × 10 −3	2.342 × 10 −2
conv order	2.435	1.447	1.420	1.616	2.738
n = 32 × 32	3.223 × 10 −5	9.309 × 10 −4	1.300 × 10 −3	5.375 × 10 −4	3.511 × 10 −3
conv order	3.133	1.838	1.825	2.852	3.359
n = 64 × 64	3.672 × 10 −6	2.604 × 10 −4	3.667 × 10 −4	7.443 × 10 −5	3.422 × 10 −4

). By analyzing

Table 12. Error and convergence order with two consecutive solutions for elliptical interface (Quad9) with ${\rho }_1=1.0$, ${\rho }_2=10.0$.

Quad9/Quad9	$\left|\right|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right|$	$|\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}|$	$\left|\right||\mathbf{u}-{\mathbf{u}}_{\mathbf{ex}}\left|\right||$	$\left|\right|{\mathit{P}}_1-{{\mathit{P}}_1}_{\mathit{ex}}\left|\right|$	$\left|\right|{\mathit{P}}_2-{{\mathit{P}}_2}_{\mathit{ex}}\left|\right|$
n = 8 × 8	2.717 × 10 −3	1.905 × 10 −2	2.673 × 10 −2	6.949 × 10 −3	6.901 × 10 −2
conv order	2.295	1.515	1.525	1.607	1.870
n = 16 × 16	5.536 × 10 −4	6.667 × 10 −3	9.284 × 10 −3	2.282 × 10 −3	1.888 × 10 −2
conv order	2.912	1.790	1.775	1.454	2.303
n = 32 × 32	7.354 × 10 −5	1.928 × 10 −3	2.712 × 10 −3	8.328 × 10 −4	3.826 × 10 −3
conv order	3.464	1.922	1.918	2.724	3.000
n = 64 × 64	6.664 × 10 −6	5.088 × 10 −4	7.178 × 10 −4	1.260 × 10 −4	4.784 × 10 −4

(with ${\rho }_2=10.0$) and Table 11 (with ${\rho }_2=100.0$), we observe that the error decreases with increasing grid resolution. The convergence order for $\left|\right|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}\left|\right|=\mathcal{O}\left(h^3\right)$ aligns with the theoretical results for $k=2$. For $|{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}|$ and $\left|\right||{\mathbf{u}}_{\mathbf{n}}-{\mathbf{u}}_{\mathbf{n}+\mathbf{1}}\left|\right||$, we obtained a convergence order of $\mathcal{O}\left(h^2\right)$, and for the pressure terms, we also observed a convergence order of $\mathcal{O}\left(h^2\right)$, occasionally observing an extra convergence rate.

7. Conclusions

In this work, we developed a stabilized Nitsche-type Cut Finite Element Method (CutFEM) incorporating Continuous Interior Penalty (CIP) and Ghost Penalty (GP) techniques for multi-phase flow applications governed by the Navier–Stokes equations. We also applied the same formulation to the Oseen equations, performing a comprehensive stability analysis and deriving a priori error estimators to demonstrate the stability and precision of the proposed method. A key novelty of this work is the extension of this approach to cases in which the velocity field is continuous, while the pressure exhibits discontinuities across interfaces.

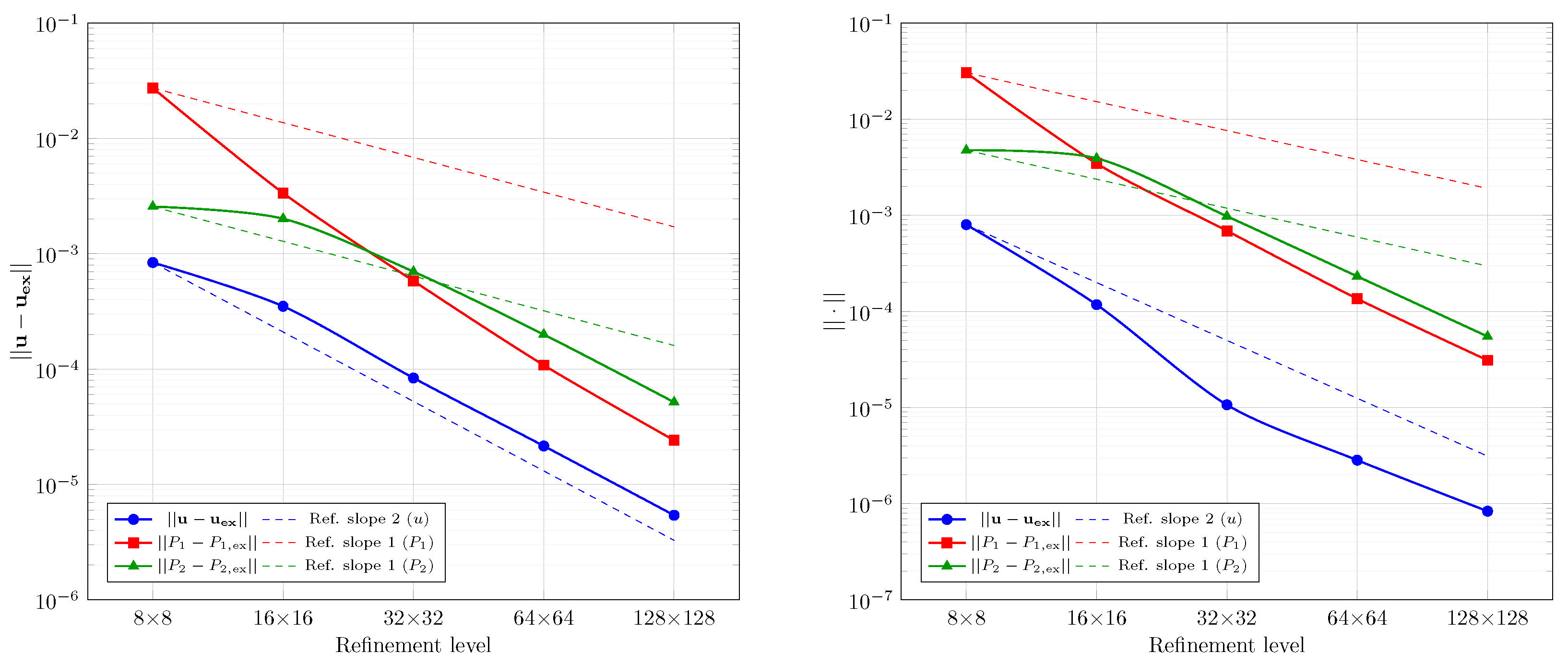
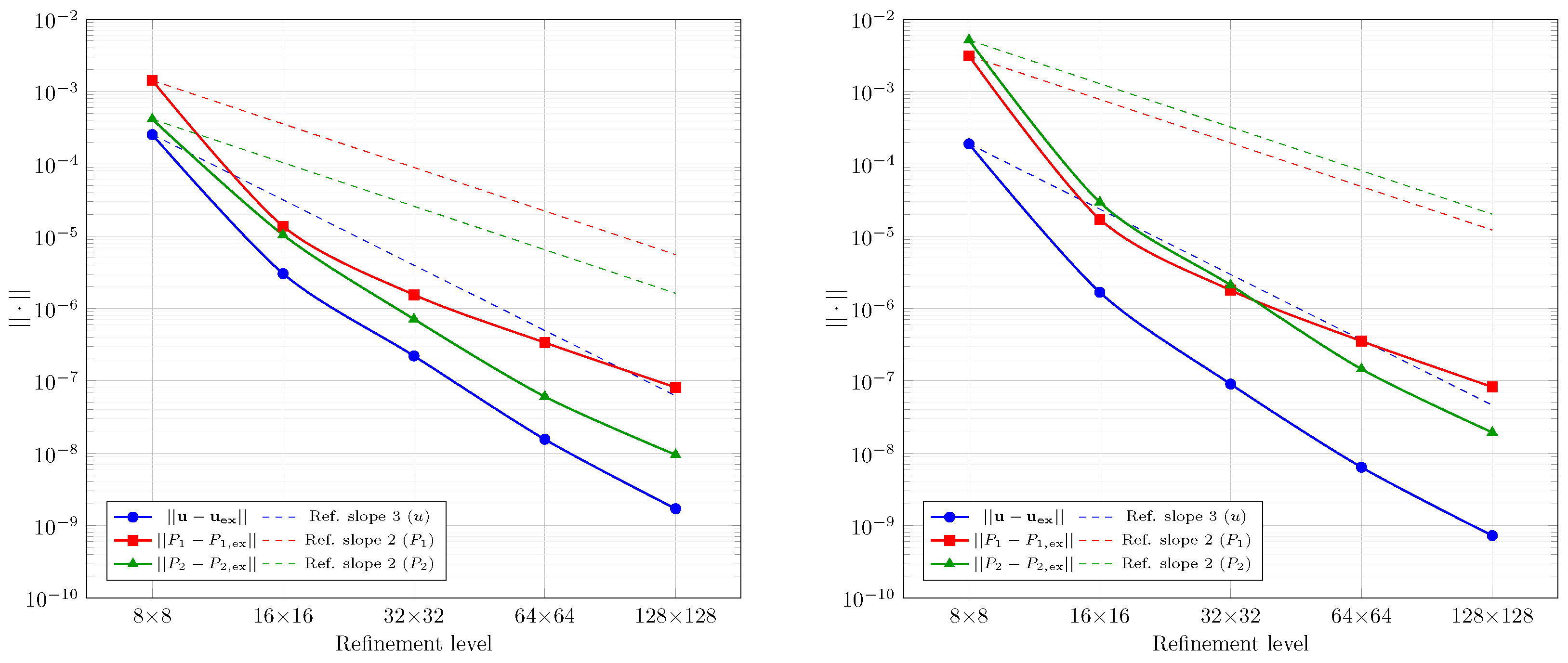
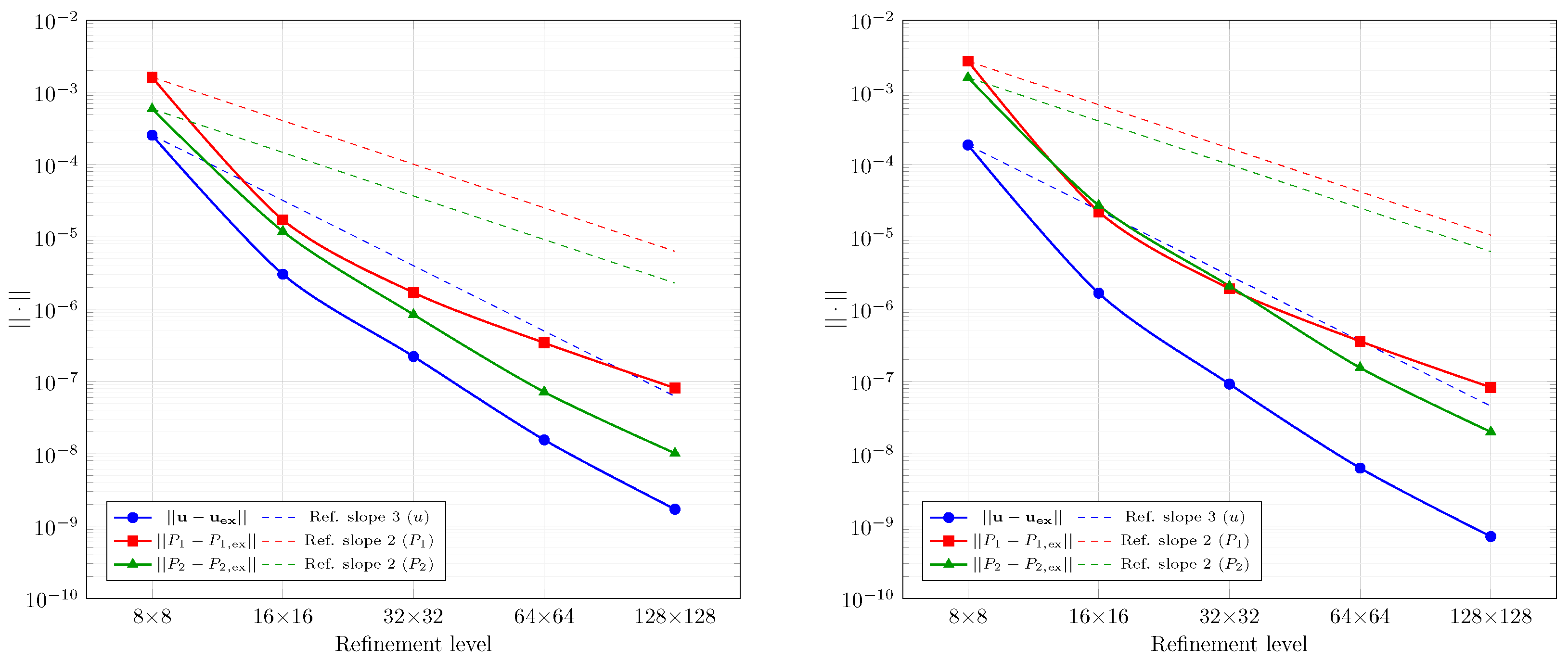
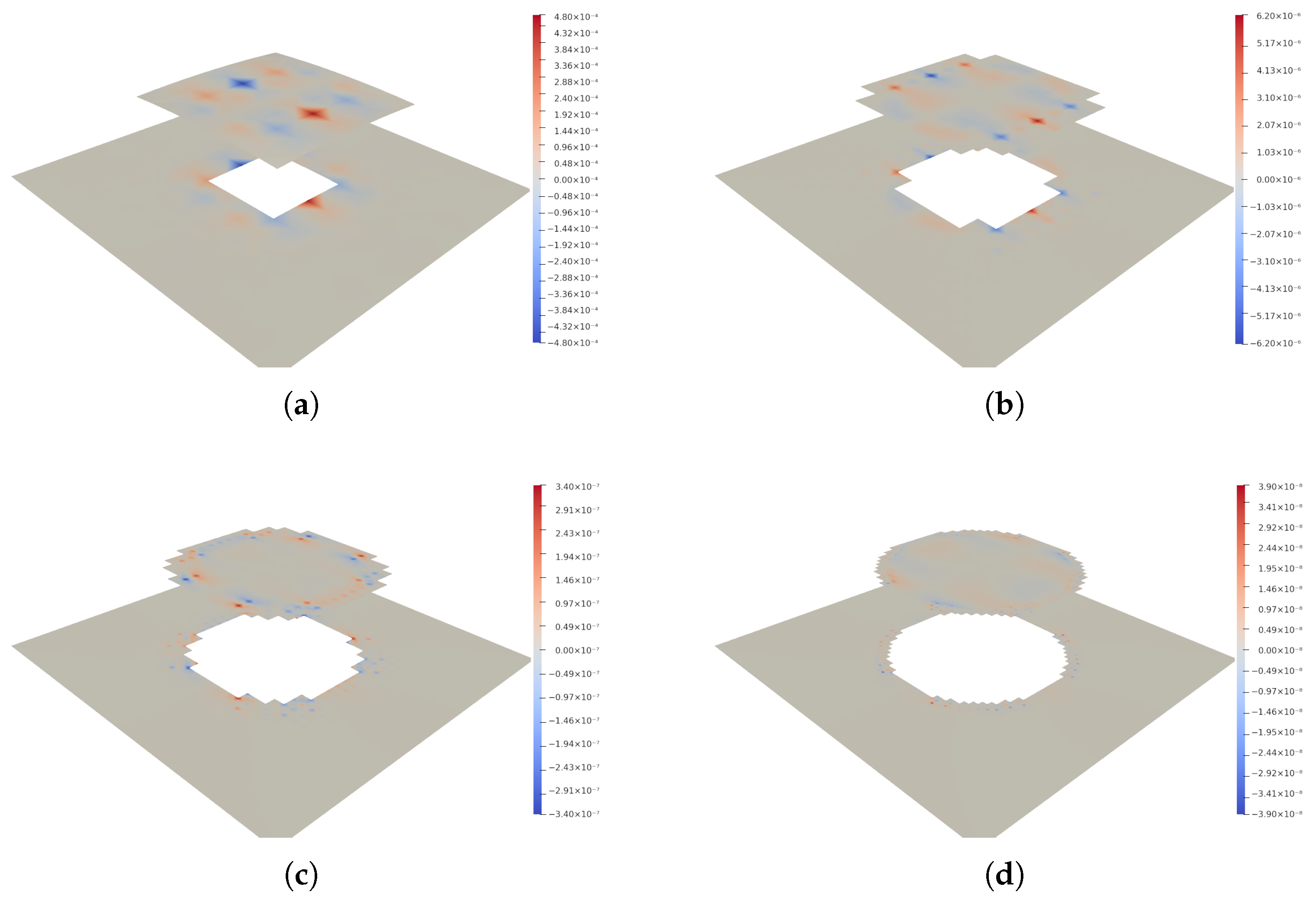
In Section 5 and Section 6, we evaluated the proposed method for two-phase flows with complex interfaces using benchmark tests with circular and elliptical geometries. Simulations across multiple element types, mesh resolutions, and physical parameters consistently showed optimal convergence rates for velocity and pressure, matching theoretical predictions. The method effectively captured pressure jumps and suppressed spurious currents, with accuracy improving under mesh refinement. For the circular case, convergence was verified against known solutions, while for the elliptical interface, error trends were assessed through successive numerical approximations. Despite geometric complexity, the method demonstrated stable and reliable behavior, confirming its suitability for two-phase flow problems with evolving interfaces.

This work provides a useful starting point for future studies on more complex interface dynamics, varying viscosity ratios, and possible three-dimensional extensions. Such investigations will further clarify the method’s capabilities and extend its applicability to a broader class of multiphase flow problems. While the proposed method has been developed and tested in the context of two-phase flow with a single interface, extending it to general multiphase flow scenarios, particularly those involving intersecting interfaces or triple junctions, would require additional considerations. These include enhanced interface tracking methods and modified stabilization strategies near junctions. Exploring such extensions is a promising direction for future work.

Another promising direction is the extension of the method to dynamic interface benchmarks, such as capillary wave propagation and droplet coalescence, to further assess its performance in evolving interface scenarios. A meaningful next step will also be to conduct quantitative comparisons with other interface-capturing methods such as XFEM, level-set, and phase field approaches, particularly in terms of mass conservation and spurious currents.