Abstract
Grid structured visual data such as forms, tables, and game boards require models that pair pixel level perception with symbolic consistency under global constraints. Recent Pixel Language Models (PLMs) map images to token sequences with promising flexibility, yet we find they generalize poorly when observable evidence becomes sparse or corrupted. We present GridMNIST-Sudoku, a benchmark that renders large numbers of Sudoku instances with style diverse handwritten digits and provides parameterized stress tracks for two tasks: Completion (predict missing cells) and Correction (detect and repair incorrect cells) across difficulty levels ranging from 1 to 90 altered positions in a 9 × 9 grid. Attention diagnostics on PLMs trained with conventional one dimensional positional encodings reveal weak structure awareness outside the natural Sudoku sparsity band. Motivated by these findings, we propose a lightweight Row-Column-Box (RCB) positional prior that injects grid aligned coordinates and combine it with simple sparsity and corruption augmentations. Trained only on the natural distribution, the resulting model substantially improves out of distribution accuracy across wide sparsity and corruption ranges while maintaining strong in distribution performance.
Keywords:
Pixel Language Models; visual symbolic reasoning; GridMNIST-Sudoku benchmark; structured spatial prior; Explainable AI MSC:
68T37
1. Introduction
Grid–structured visual data are pervasive across modalities in signal processing and artificial intelligence: digitized forms, tables, spreadsheets, answer sheets, score cards, and game boards all present 2D arrays of localized symbol evidence that must be mapped to consistent, globally constrained symbolic outputs. Robustly inferring missing or corrupted entries in such grids requires models that couple pixel-level perception with structured reasoning under domain constraints (e.g., mutual exclusion, row/column rules, region consistency). Despite rapid advances in vision–language modeling, there is a lack of standardized benchmarks that expose these challenges under controlled levels of occlusion, corruption, and handwriting variability.
Pixel Language Models (PLMs) [1] offer an attractive framework: by converting pixel patches into token-like embeddings and applying sequence modeling, PLMs unify visual perception and language generation in a single pipeline. Prior work has explored pixel/visual tokenization for language understanding, multimodal transfer, and vocabulary bottleneck reduction [1,2,3,4,5,6]. Cross-lingual and semantic extensions further illustrate the flexibility of pixel-centric representations [7,8], while autoregressive pixel modeling continues to mature [9]. Nevertheless, real-world deployment of such models remains hindered by robustness gaps: performance often degrades under distribution shift, structured sparsity (missing data), or systematic input corruption [7,10].
Explainable Artificial Intelligence (XAI) techniques [11] can help diagnose where such robustness gaps arise by surfacing attention, relevance, or attribution patterns within deep models [12,13,14,15]. While XAI signals do not, by themselves, improve accuracy, they can guide targeted model design, data augmentation strategies, and curriculum construction. In this work we use interpretability analyses to probe how pixel-to-sequence transformers attend across grid locations when asked to complete or repair structured symbol arrays; these diagnostics informed a lightweight spatial prior that materially improves performance in low-data and high-corruption regimes.
We adopt Sudoku as a canonical, rule-driven testbed for grid reasoning [16,17,18]. Although Sudoku itself is a puzzle domain, its mutually constrained grid conveniently instantiates the broader class of row/column/region consistency problems encountered in document understanding and quality assurance pipelines. Building on insights from rule-aware relational modeling (e.g., REM over RRN [18]), we construct a synthetic yet challenging handwritten benchmark by rendering large corpora of Sudoku instances with MNIST digits [19] under controlled patterns of erasure (missing cells) and corruption (incorrect cells). This enables systematic stress-testing of visual perception, symbolic constraint satisfaction, and model calibration across difficulty settings that extend well beyond the narrow blank-cell ranges of existing Sudoku corpora.
In this paper we introduce GridMNIST-Sudoku, a benchmark for visual symbolic grid completion and correction, and we provide strong neural and rule-based baselines. Our primary modeling baseline is a PLM built on a T5-style transformer encoder with pixel embeddings; motivated by XAI diagnostics, we augment it with a Row–Column–Box (RCB) positional prior that injects Sudoku’s structural constraints directly into the positional encoding space. Unlike generic sinusoidal 1D encodings, the RCB prior supplies disentangled row, column, and region coordinates, akin in spirit to learned 2D local attention maps [20] yet parameter-free and domain-aware. We also explore data perturbation strategies related to masked modeling [21] to improve robustness under sparsity.
We evaluate models on two tasks supported by the benchmark: (i) Completion: predicting missing entries from partially observed grids, and (ii) Correction: detecting and repairing erroneous entries. Difficulty is swept from 1 to 90 altered cells, enabling controlled analysis of failure modes and generalization. Attention-based diagnostics reveal how the RCB prior helps the transformer allocate context along Sudoku-relevant structural axes, and quantitative results show consistent gains across wide sparsity ranges.
Our main contributions are:
- GridMNIST-Sudoku Benchmark: A large-scale, parameterized dataset of 1M handwritten grid puzzles with controllable levels of erasure and corruption, supporting puzzle-completion and error-correction tasks for visual–symbolic reasoning research.
- Domain-Guided Positional Prior: A lightweight Row–Column–Box positional encoding that injects structured grid constraints into pixel-to-sequence transformers, improving robustness under severe sparsity.
- XAI-Guided Model Diagnostics: We use attention analyses to expose failure modes and motivate the proposed positional prior and augmentation regime, illustrating a practical design loop between interpretability and model improvement.
2. Data and Benchmark Construction
Our objective is to construct a controlled yet challenging benchmark that exercises visual perception, symbolic consistency, and robustness to missing or corrupted evidence in grid-structured data. Many practical documents and artifacts (forms, tables, score sheets, game boards) consist of two-dimensional arrays of localized symbol evidence that must satisfy global constraints. Sudoku provides a convenient, well-defined instance of such a constraint system. By rendering large numbers of Sudoku puzzles with varied handwritten digit styles and by systematically varying the amount and type of missing or incorrect evidence, we obtain a testbed that stresses pixel-to-sequence models well beyond the narrow difficulty band found in standard Sudoku corpora.
We refer to the resulting resource as GridMNIST-Sudoku. It is derived by combining a large text-based Sudoku repository with handwritten digit imagery from MNIST and packaging the result into three benchmark tracks: a Core track, a Completion-Stress track with controlled sparsity, and a Correction-Stress track with controlled corruption. Details follow.
While Sudoku provides a clean instantiation of grid-structured reasoning with its strict row-column-box constraints, it represents an idealized case compared to real-world grid data like tables and forms. Unlike Sudoku’s uniform single-digit cells and absolute constraints (each digit 1–9 must appear exactly once per row-column-box), practical document grids often contain heterogeneous content types (text, numbers, symbols), variable cell spans, and softer constraints (e.g., “total must equal sum of items” rather than strict uniqueness). Additionally, real-world grids frequently exhibit irregular structures with merged cells and hierarchical relationships not present in Sudoku’s perfectly partitioned 9 × 9 layout. Nevertheless, the core challenges of coupling pixel-level perception with symbolic reasoning under structural constraints remain fundamentally similar. Our benchmark specifically targets the foundational capability of maintaining consistency across row/column relationships under varying evidence conditions—a capability directly transferable to table parsing, form completion, and spreadsheet validation where local symbol recognition must respect global structural rules. The controlled nature of Sudoku allows us to isolate and systematically stress these reasoning capabilities without the confounding complexity of variable layouts, making it an appropriate first step toward more generalized grid reasoning systems.
2.1. Source Sudoku Corpus
We start from the One-Million Sudoku dataset [22], which contains 1,000,000 puzzle and solution pairs. Each sample provides an 81-character quiz string in row-major order, where the character ‘0’ marks an empty cell, and a corresponding 81-character fully solved solution string. We partition the text corpus at random into training (80 percent) and held-out evaluation (20 percent) splits. Random seeds for reproducibility are provided with the code release.
2.2. Handwritten Rendering Pipeline
To introduce realistic symbol variability, we render every nonempty Sudoku cell using a randomly sampled handwritten digit image from the MNIST dataset [19] that matches the required numeral. We enforce writer disjointness by drawing from the MNIST training split when rendering training puzzles and from the MNIST test split when rendering all evaluation puzzles. This encourages cross-writer generalization.
All digit crops are resized to 32 × 32 grayscale patches and normalized to the range [0,1]. Empty cells are rendered as uniform blank patches (all zeros). Sampling is done with replacement, so a single grid typically contains a mixture of handwriting styles across its 81 cells, increasing intra-grid diversity.
For convenience, each rendered puzzle is stored in two formats: (i) an 81 × 1 tensor of 32 × 32 patches (suitable for direct model ingestion), and (ii) a composite 288 × 288 tiled image for visualization. Metadata files record the ground-truth digit sequence, observed mask, and (when applicable) corruption mask.
2.3. Benchmark Tracks
We construct three complementary evaluation tracks. All inherit the same underlying text split described above but are rendered independently.
2.3.1. Core Track
The Core track renders the original quiz strings exactly as provided in the source corpus. These puzzles exhibit a narrow band of difficulty: the number of blanks per grid lies almost entirely between 44 and 52 cells (see Section 2.4). This track serves as the nominal training distribution for our models unless otherwise stated.
2.3.2. Completion-Stress Track
To measure robustness to sparsity, we start from fully solved grids (solution strings) and randomly remove k digits, replacing them with blank cells. We sweep k from 1 to 90. For each k, we generate 2500 evaluation puzzles, yielding 200,000 total instances. The task is to infer the complete grid from the partially observed handwritten input.
2.3.3. Correction-Stress Track
To measure robustness to symbol corruption, we again start from solved grids and randomly select k cell positions. Each selected cell is overwritten with an incorrect digit drawn uniformly from the remaining eight classes, and then rendered with a corresponding MNIST image. We sweep k from 1 to 80 and generate 2500 puzzles per setting, for another 200,000 evaluation instances. The task is to detect and repair all incorrect entries and output the corrected grid.
2.4. Dataset Bias in the Core Track
Because Sudoku puzzle design typically targets human-solvable difficulty, the natural distribution of blank cells in the source corpus is sharply skewed. In both the training and held-out splits, more than 92 percent of puzzles contain exactly 46, 47, or 48 blanks (Table 1). Models trained only on this distribution often learn heuristics tied to the observed sparsity range and degrade when presented with grids that are substantially more or less complete. This observation motivated two design decisions: (i) creation of the Completion-Stress and Correction-Stress tracks that span extreme sparsity and corruption regimes, and (ii) incorporation of a structured Row/Column/Subgrid positional prior (introduced in Section 3.5) after attention diagnostics revealed that standard one-dimensional positional encodings failed to generalize across sparsity shifts.

Table 1.
Percentage distributions of items to be filled in training and test sets, highlighting the imbalance; values are shown as percentage (%).
3. Method
We model grid structured visual symbolic reasoning as a pixel to sequence prediction problem. Each Sudoku puzzle in GridMNIST-Sudoku (Section 2) is rendered as 81 handwritten digit patches arranged in a 9 × 9 grid; blank cells and corrupted cells are explicitly marked in the input image tensor. Our baseline system adapts a T5 style transformer encoder to operate over a linearized sequence of image embeddings and to predict the complete 81 digit solution in row major order. Because vanilla one dimensional positional encodings discard the two dimensional structure that governs Sudoku constraints, we further introduce a lightweight Row Column Box (RCB) positional prior that injects structural coordinates aligned with Sudoku rules. Data augmentation policies derived from the benchmark tracks (Section 2.3) expose the model to a broad range of sparsity and corruption regimes.
3.1. Problem Formulation
Let a rendered puzzle be represented by an ordered sequence
where each is a 32 × 32 grayscale image patch corresponding to grid location i. We index cells in row major order so that
and we define the 3 × 3 box index
with . For blank cells, is a uniform blank patch; for corrupted cells, shows an incorrect handwritten digit (see Section 2.3). The prediction target is the length 81 sequence
where is the correct digit at location i.
We consider two supervised tasks: (1) Completion: Some are blank; others show the correct digit. Predict all . (2) Correction: All show a digit but an unknown subset are incorrect. Predict all , overriding visible errors.
Both tasks reduce to multi class classification at each position. Global Sudoku consistency is evaluated downstream (Section 4).
3.2. Pixel Embedding Front End
Each image patch is passed through a small convolutional feature extractor that outputs a fixed dimensional vector . In our implementation and . The extractor is trained end to end with the transformer. Alternatives such as frozen CNN backbones or ViT style patch linears are supported but not used in the main results.
3.3. Baseline Pixel to Grid Transformer
Given the embedded sequence , we append standard sinusoidal one dimensional positional encodings and form token representations
These are fed to a transformer encoder stack (we use a T5 style architecture with multi-head self-attention, layer normalization, and feed-forward blocks). The encoder contextualizes each token against the entire grid sequence and produces hidden states . A classification head projects each to logits over the 9 digit classes:
Because Sudoku grids have fixed length, we adopt this encoder plus per position classifier design rather than an autoregressive decoder. This simplifies training and improves stability in sparse input regimes.
An overview of the architecture is shown in the upper (gray) portion of Figure 1.
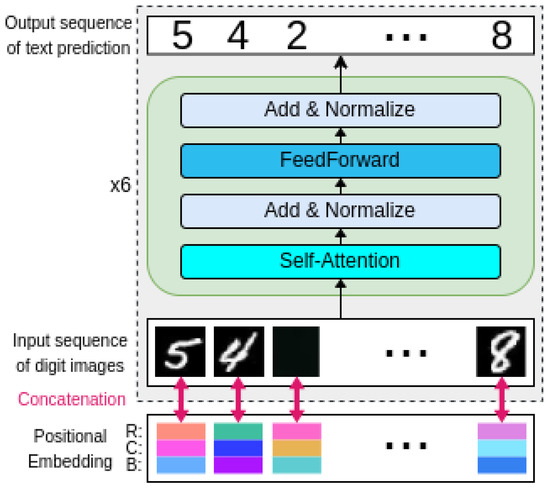
Figure 1.
Architecture of the proposed Pixel Language Model (PLM) for solving Sudoku puzzles. The upper part (in gray) represents the baseline model configuration, while the lower part introduces the newly proposed positional embeddings, where R, C, and B denote Row, Column, and Box, respectively.
3.4. Data Aware Training Augmentations
The Core track (Section 2.4) supplies puzzles with 44 to 52 blanks in most cases. Models trained naively on this narrow sparsity band perform poorly when blank counts are much lower or higher. We therefore apply stochastic augmentations during training that resample visibility patterns and inject controlled corruptions. Let denote a subset of blank cells to be populated with their correct digits, a subset of visible correct digits to be hidden (blanked), and a subset of visible correct digits to be replaced by incorrect digits. For each training puzzle we independently sample these operations with the probabilities in Table 2. When both and are active, operations are applied in random order and constrained so that cells are not modified twice. Training labels always remain the ground truth Y even when visible evidence is misleading.

Table 2.
Stochastic augmentation operations applied during training. Probabilities are per puzzle.
These augmentations simulate the Completion and Correction stress conditions defined in the benchmark. They substantially expand the effective training distribution and encourage the transformer to rely on longer range structural cues.
3.5. Row Column Box Positional Prior
Linearizing the Sudoku grid into a 1D sequence misrepresents structural proximity in positional encoding: cells sharing a column (or row/box) exhibit large index distances despite strict Sudoku constraints. Consequently, transformers trained with standard positional encodings exhibit overly local attention patterns and fail under sparsity distributional shifts (Section 2.4).
To address the core challenge of generalizing from the narrow natural Sudoku distribution (44–52 blanks) to extreme sparsity/corruption without distributional expansion, we introduce the Row-Column-Box (RCB) positional prior. Critically, RCB leverages structural constraints within the original training distribution—unlike data augmentation, which artificially broadens it. This distinction is pivotal: our evaluation isolates whether structural priors alone can bridge the distribution gap to extreme test regimes, a necessity in real-world settings where augmentation is infeasible (e.g., due to data scarcity or privacy constraints).
Attention analysis directly motivated RCB’s design. Baseline models exhibited two critical failures: (1) Structural incoherence: Attention weights for cells in shared rows/columns/boxes were diffuse rather than concentrated along constraint axes; (2) Distributional fragility: These patterns collapsed under sparsity shifts (e.g., near-complete grids with 2 blanks), where models neglected structurally relevant peers. These observations confirm that linearized positions obscure the disentangled row, column, and box constraints—prompting RCB’s explicit three-component encoding to supply structure-aligned positional cues.
For each location i we compute integer indices , , and as defined in Section 3.1. Each index is mapped to a sinusoidal embedding using the formulation of Vaswani et al. [23]. Let denote the sinusoidal mapping from to . We obtain
We concatenate these vectors and project them to the model dimension with a learned linear layer :
where denotes concatenation. The final token representation becomes
Intuitively, allows self attention heads to more easily learn rule relevant patterns such as uniqueness within a row, column consistency, and subgrid constraints, without requiring the network to infer two dimensional relationships from index distance alone. The lower portion of Figure 1 illustrates the RCB augmentation; Figure 2 depicts the three coordinate channels.
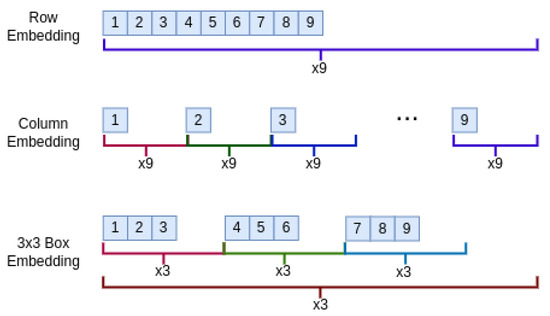
Figure 2.
Multi-level positional embedding: Row, Column, and 3x3 Box (RCB) embeddings, presented from top to bottom, respectively. The color of the lines indicates how many times each embedding ID is repeated.
3.6. Training Objective
Models are trained to minimize cross entropy loss over the 9 digit classes at each location. Let be the predicted probability that cell i takes digit d. The loss is
We do not explicitly enforce Sudoku constraints during training; all structural knowledge must be inferred from data and positional priors. At inference time the model outputs the argmax class per cell. Constraint satisfaction metrics are computed post hoc.
4. Experiments
We evaluate the proposed models on the benchmark tracks introduced in Section 2. An important distinction must be made regarding comparative approaches. While traditional rule-based Sudoku solvers represent an upper bound for symbolic reasoning given perfect digit recognition, they operate on already-digitized grids rather than raw pixel inputs and therefore cannot address our benchmark’s core challenge of integrating visual perception with symbolic reasoning. Similarly, neuro-symbolic models like Recurrent Relational Networks typically assume clean, pre-recognized digit inputs rather than processing raw pixel sequences. The true innovation of our Pixel Language Model approach lies precisely in its ability to unify these traditionally separate stages of visual perception and symbolic reasoning into a single end-to-end framework. Unless stated otherwise, all models are trained exclusively on the Core track training split (natural Sudoku sparsity, MNIST training writers) and evaluated without additional fine tuning on the held out Core split and on the two stress tracks that vary sparsity (Completion) and corruption (Correction). This protocol measures out of distribution robustness.
4.1. Implementation Details
Our implementation is built upon the T5-small encoder architecture with 6 layers, 512 hidden dimensions, and 8 attention heads. All models were trained on a single NVIDIA RTX 4090 GPU with CUDA 12.2. We employed the Adam optimizer with a learning rate of and a batch size of 1280. For the Row-Column-Box (RCB) positional prior, we used a dimension of 256 for each coordinate embedding (row, column, and box), which were then concatenated and projected to match the model dimension. Training proceeded for a maximum of 100 epochs with early stopping based on validation performance.
4.2. Experimental Setup and Metrics
4.2.1. Training Data
Core track training split (Section 2.3), rendered with MNIST training digits. Augmentations described in Section 3.4 are optionally applied.
4.2.2. Evaluation Data
- Core test split: natural blank distribution, MNIST test digits.
- Completion-Stress: for each k in blanks per grid, 2500 puzzles rendered with MNIST test digits; reported in five aggregated ranges.
- Correction-Stress: for each k in corrupted cells, 2500 puzzles; reported in five aggregated ranges.
4.2.3. Metrics
- Cell Accuracy = fraction of 81 cells predicted correctly (macro averaged over puzzles in a group).
4.2.4. Model Variants
- Baseline: pixel embedding plus one dimensional positional encoding (Section 3.3).
- Baseline + Aug: Baseline trained with stochastic sparsity and corruption augmentations (Section 3.4).
- Baseline + RCB: Baseline augmented with the Row Column Box positional prior (Section 3.5); no data augmentation unless stated.
4.3. Core Track Results
The Core track reflects the same sparsity distribution seen in training (44 to 52 blanks; Section 2.4). As expected, all models achieve high Cell Accuracy, with the RCB prior providing a small gain (Table 3). Strong results here confirm that the pixel embedding front end and transformer capacity are sufficient to fit the in distribution task, but this setting does not diagnose robustness.

Table 3.
Core track performance (natural Sudoku sparsity). Reported metric is Cell Accuracy on the held out Core split. Best results are indicated in bold.
4.4. Completion-Stress: Varying Blank Cells
We next evaluate generalization when the number of observed digits departs sharply from the Core distribution. Completion-Stress puzzles are generated by blanking k random cells in solved grids; results are grouped by percentage range of blanks. The unaugmented Baseline degrades substantially outside the 21 to 60 range and is especially brittle when only a few blanks remain, which is counterintuitive but consistent with training bias. Data augmentation partially mitigates this effect. Adding the RCB prior yields large gains in the low blank regime (1 to 20) and modest improvements elsewhere (Table 4). Performance drops for extreme sparsity (81 to 100) in all models, although RCB remains best.

Table 4.
Completion-Stress track. Cell Accuracy (%) for predicting missing digits at different blank ratios (percent of cells blank). Acc. Imp. row reports absolute improvement of the best RCB setting over the best non RCB setting in each range. Best results are indicated in bold.
This improved performance in low-blank settings indicates that the RCB prior enhances the model’s ability to exploit global Sudoku constraints, allowing it to make accurate predictions even when minimal evidence is available. By encoding row, column, and 3 × 3 box relationships directly into the positional representation, the model gains a stronger inductive bias toward grid-level consistency, enabling more effective integration of contextual cues across the entire puzzle. This structural awareness supports robust reasoning in sparse regimes, not through sequential focus, but through a globally informed, parallel interpretation of the grid.
4.5. Attention Diagnostics for Completion
To understand why the RCB prior helps, we inspect multi head self attention maps from representative puzzles with 2, 40, and 80 blanks in Figure 3, which shows multi-head self-attention maps for three model variants: Baseline, Baseline + Aug., and Baseline + RCB, on Sudoku puzzles with 2, 40, and 80 blank cells. Each panel visualizes the attention distribution from a selected query cell, marked in red, to illustrate how the model attends across the grid. In the Baseline model, attention is scattered and primarily local, but failing to consistently capture column or 3 × 3 box relationships despite their importance for constraint satisfaction. This reflects the limitation of standard 1D positional encodings, which encode order rather than 2D structure. When data augmentation is added, attention becomes somewhat more global with better alignment along rows and columns, suggesting improved sensitivity to structural cues through exposure to diverse sparsity patterns. However, attention to 3 × 3 box neighbors remains weak, showing that data diversity alone cannot fully induce grid-level reasoning. In contrast, the RCB-enhanced model exhibits sharp, consistent attention along all three Sudoku constraint axes: row, column, and box, across all sparsity levels. By injecting explicit coordinate information through the RCB prior, the model learns to aggregate context in a way that aligns with the game’s rules, enabling more reliable and interpretable reasoning. This structural awareness explains the RCB model’s superior performance, particularly in low-clue settings, and demonstrates how architectural design can guide attention toward meaningful symbolic relationships.
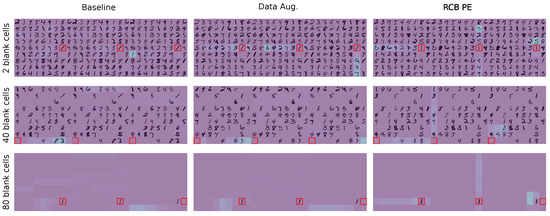
Figure 3.
Attention diagnostics on Completion-Stress puzzles with 2, 40, and 80 blanks. Columns: Baseline, Baseline + Aug, Baseline + RCB. Each panel shows three concatenated attention heads. Red outline marks the query cell. RCB induces row, column, and subgrid focus across sparsity levels.
Example qualitative predictions are shown in Figure 4. The model with RCB solves nearly complete and moderately sparse grids reliably but fails when information content becomes too low (80 blanks). Figure 4 illustrates qualitative results for three increasingly sparse scenarios: 2, 40, and 80 blank cells (from top to bottom). In the first two cases, the proposed RCB model successfully recover the correct solution, demonstrating their ability to complete grids when sufficient contextual clues are present. However, when 80 cells are blank, the model fails to produce a valid solution, with multiple constraint violations across rows, columns, and 3 × 3 boxes. This highlights a key limitation: unlike humans, who can start from minimal clues and build solutions incrementally by enforcing Sudoku rules, the model does not inherently learn the underlying constraints from data. Despite strong performance in low-to-moderate sparsity regimes, its behavior depends heavily on learned appearance and context patterns from the training distribution (44–52 blanks), rather than abstract rule understanding. The failure under extreme sparsity reveals that high accuracy on standard puzzles does not imply genuine symbolic reasoning or rule internalization.
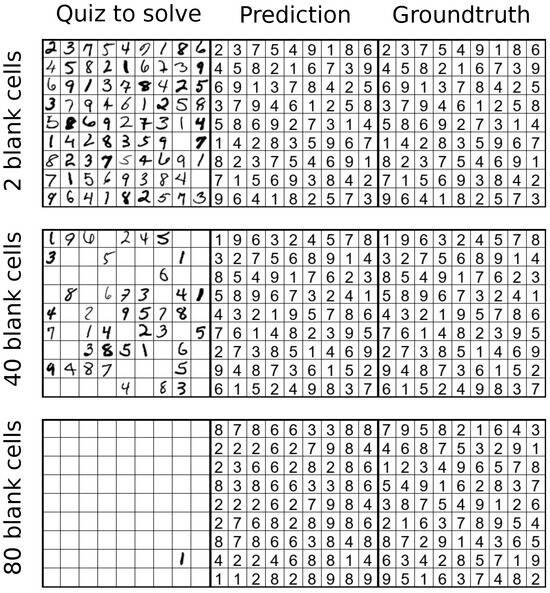
Figure 4.
Qualitative Completion-Stress examples with 2, 40, and 80 blanks. Columns: input, prediction, ground truth. Baseline + RCB succeeds when moderate context remains and degrades at extreme sparsity.
4.6. Correction-Stress: Varying Corrupted Cells
We now test the ability to detect and repair incorrect digits. Correction-Stress puzzles contain k corrupted cells replaced by random wrong digits. Table 5 reports Cell Accuracy grouped by corruption ratio. Patterns mirror the Completion results: augmentation helps substantially, and the RCB prior delivers consistent gains at low to moderate corruption levels. At very high corruption (61 to 80), performance collapses for all models and the Baseline slightly edges out RCB, suggesting that the structured prior may amplify misleading context when errors dominate.

Table 5.
Correction-Stress track. Cell Accuracy (%) for detecting and repairing corrupted digits at different corruption ratios (percent of cells incorrect). Acc. Imp. row reports absolute improvement of the best RCB setting over the best non RCB setting in each range. Best results are indicated in bold.
4.7. Discussion
Three trends emerge. First, fitting the in distribution Core track is easy for all variants and therefore not diagnostic of robustness. Second, exposure to synthetic sparsity and corruption through augmentation improves out of distribution generalization but does not close the gap. Third, the RCB positional prior provides large benefits when evidence is scarce or partially misleading, validating the idea of supplying structure aligned spatial cues to pixel to sequence transformers. Failure at extreme corruption suggests future work combining learned priors with constraint aware decoding or confidence calibrated detection modules.
Our analysis of extreme scenarios (81–100% corruption rates) reveals that performance degradation stems primarily from logical conflicts rather than visual ambiguity. This indicates that structural awareness degrades unevenly under severe corruption, with box constraints becoming particularly vulnerable while row relationships remain relatively resilient. Notably, in these high-stress conditions, the RCB model’s structural awareness, which provides significant benefits in moderate corruption regimes, can become counterproductive as the model over-relies on corrupted structural patterns rather than recognizing input inconsistency. These observations highlight a fundamental challenge in visual-symbolic reasoning: when local evidence conflicts with global constraints, models need explicit mechanisms to resolve these tensions, pointing to promising future directions in constraint-aware decoding that could dynamically weigh structural priors against evidence reliability.
5. Conclusions
We introduced GridMNIST-Sudoku, a benchmark for visual symbolic grid reasoning that couples large scale Sudoku corpora with style diverse handwritten digit renderings and controlled sparsity and corruption stress tracks. Using this resource, we studied pixel-to-sequence transformers for grid completion and correction, revealing a critical tension in visual-symbolic reasoning: while domain-guided structural priors substantially improve robustness under moderate sparsity and corruption, they can become counterproductive when evidence is severely misleading, as models over-rely on corrupted structural patterns rather than recognizing input inconsistency. Attention-based diagnostics on models trained with conventional one-dimensional positional encodings revealed poor structure awareness and brittle generalization outside the natural Sudoku sparsity band. Guided by these observations, we proposed a lightweight Row-Column-Box positional prior that injects grid-aligned coordinates derived from Sudoku rules. Combined with sparsity and corruption augmentations, the prior substantially improves accuracy when visible evidence is scarce or partially misleading, while maintaining strong in-distribution performance. Our stress-testing framework identifies promising directions for future work, particularly in high-corruption scenarios where integrating structural priors with constraint-aware decoding mechanisms could further enhance robustness. This work highlights both the value of domain-guided spatial cues in visual language models and how interpretability can productively feed back into model design, while establishing GridMNIST-Sudoku as a valuable testbed for developing more robust visual-symbolic reasoning systems.
Author Contributions
Conceptualization, L.K. and X.F.; methodology, L.K., X.F., M.A.S., A.B. and L.G.; validation, J.V.-C., A.F. and E.V.; investigation, L.K., X.F. and D.K.; data curation, L.K. and X.F.; writing—original draft, L.K. and X.F.; writing—review and editing, L.K., X.F., A.F., E.V. and D.K.; supervision, D.K.; funding acquisition, L.K., X.F., L.G., J.V.-C., A.F., E.V. and D.K.. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially supported by the Beatriu de Pinós del Departament de Recerca i Universitats de la Generalitat de Catalunya (2022 BP 00256), the predoctoral program AGAUR-FI ajuts (2025 FI-2 00470) Joan Oró, which is backed by the Secretariat of Universities and Research of the Department of Research and Universities of the Generalitat of Catalonia, as well as the European Social Plus Fund, European Lighthouse on Safe and Secure AI (ELSA) from the European Union’s Horizon Europe programme under grant agreement No 101070617, Ramon y Cajal research fellowship RYC2020-030777-I/AEI/10.13039/501100011033, grants PID2021-128178OB-I00, PID2024-162555OB-I00 funded by MCIN/AEI/10.13039/501100011033 and by ERDF/EU, Riksbankens Jubileumsfond, grant M24-0028: Echoes of History: Analysis and Decipherment of Historical Writings (DESCRYPT), the Spanish projects CNS2022-135947 (DOLORES, 2023-2025) and PID2021-126808OB-I00 (GRAIL, 2022-2024), the Consolidated Research Group 2021 SGR 01559 from the Research and University Department of the Catalan Government, and PID2023-146426NB-100 funded by MCIU/AEI/10.13039/501100011033 and FSE+.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rust, P.; Lotz, J.F.; Bugliarello, E.; Salesky, E.; de Lhoneux, M.; Elliott, D. Language modelling with pixels. arXiv 2022, arXiv:2207.06991. [Google Scholar]
- Gao, T.; Wang, Z.; Bhaskar, A.; Chen, D. Improving Language Understanding from Screenshots. arXiv 2024, arXiv:2402.14073. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; PMLR 139; pp. 8748–8763. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. Llama: Open and efficient foundation language models. arXiv 2023, arXiv:2302.13971. [Google Scholar] [CrossRef]
- Davis, B.; Morse, B.; Price, B.; Tensmeyer, C.; Wigington, C.; Morariu, V. End-to-end document recognition and understanding with dessurt. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 280–296. [Google Scholar]
- Xiao, C.; Huang, Z.; Chen, D.; Hudson, G.T.; Li, Y.; Duan, H.; Lin, C.; Fu, J.; Han, J.; Moubayed, N.A. Pixel Sentence Representation Learning. arXiv 2024, arXiv:2402.08183. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Changpinyo, S.; Piergiovanni, A.; Padlewski, P.; Salz, D.; Goodman, S.; Grycner, A.; Mustafa, B.; Beyer, L.; et al. Pali: A jointly-scaled multilingual language-image model. arXiv 2022, arXiv:2209.06794. [Google Scholar]
- Tai, Y.; Liao, X.; Suglia, A.; Vergari, A. PIXAR: Auto-Regressive Language Modeling in Pixel Space. arXiv 2024, arXiv:2401.03321. [Google Scholar] [CrossRef]
- Lee, K.; Joshi, M.; Turc, I.R.; Hu, H.; Liu, F.; Eisenschlos, J.M.; Khandelwal, U.; Shaw, P.; Chang, M.W.; Toutanova, K. Pix2struct: Screenshot parsing as pretraining for visual language understanding. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; PMLR 202. pp. 18893–18912. [Google Scholar]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Comput. Surv. 2023, 55, 194. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Zhu, S.C. Visual interpretability for deep learning: A survey. Front. Inf. Technol. Electron. Eng. 2018, 19, 27–39. [Google Scholar] [CrossRef]
- Puiutta, E.; Veith, E.M. Explainable reinforcement learning: A survey. In Proceedings of the International Cross-Domain Conference for Machine Learning and Knowledge Extraction, Dublin, Ireland, 25–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 77–95. [Google Scholar]
- Yu, L.; Xiang, W.; Fang, J.; Chen, Y.P.P.; Chi, L. ex-vit: A novel explainable vision transformer for weakly supervised semantic segmentation. Pattern Recognit. 2023, 142, 109666. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Felgenhauer, B.; Jarvis, F. Mathematics of sudoku I. Math. Spectr. 2006, 39, 15–22. [Google Scholar]
- Tsai, P.S.; Wu, T.F.; Chen, J.Y.; Huang, J.F. Integrating of Image Processing and Number Recognition in Sudoku Puzzle Cards Digitation. J. Internet Technol. 2022, 23, 1573–1584. [Google Scholar] [CrossRef]
- Cheewaprakobkit, P.; Shih, T.K.; Lau, T.; Lin, Y.C.; Lin, C.Y. Rule-based explaining module: Enhancing the interpretability of recurrent relational network in Sudoku solving. Mach. Graph. Vis. 2023, 32, 125–145. [Google Scholar] [CrossRef]
- LeCun, Y. The MNIST Database of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 1 January 2025).
- Parmar, N.; Vaswani, A.; Uszkoreit, J.; Kaiser, L.; Shazeer, N.; Ku, A.; Tran, D. Image transformer. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR 80. pp. 4055–4064. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Park, B. 1 Million Sudoku Games. 2017. Available online: https://www.kaggle.com/datasets/bryanpark/sudoku (accessed on 1 January 2025). Kaggle dataset.
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 6000–6010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).