Abstract
Power batteries are one of the important components of electric vehicles, but the manufacturing process of vehicle power batteries is complex and diverse. Traditional scheduling methods face challenges such as low production efficiency and inadequate quality control in complex production environments. To address these issues, a multi-objective optimization model with makespan, total machine load, and processing quality as the established objectives, and a Multi-objective Particle Swarm Energy Valley Optimization (MPSEVO) is proposed to solve the problem. MPSEVO integrates the advantages of Multi-objective Particle Swarm Optimization (MOPSO) and Energy Valley Optimization (EVO). In this algorithm, the particle stability level is combined in MOPSO, and different update strategies are used for particles of different stability to enhance both the convergence and diversity of the solutions. Furthermore, a local search strategy is designed to further enhance the algorithm to avoid the local optimal solutions. The Hypervolume () and Inverted Generational Distance () indicators are often used to evaluate the convergence and diversity of multi-objective algorithms. The experimental results show that MPSEVO’s and indicators are better than other algorithms in 10 computational experiments, which verifies the effectiveness of the proposed strategy and algorithm. The proposed method is also applied to solve the actual battery workshop scheduling problem. Compared with MOPSO, MPSEVO reduces the total machine load by 7 units and the defect rate by 0.05%. In addition, the effectiveness of each part of the improved algorithm was analyzed by ablation experiments. This paper provides some ideas for improving the solution performance of MOPSO, and also provides a theoretical reference for enhancing the production efficiency of the vehicle power battery manufacturing workshop.
Keywords:
workshop scheduling; multi-objective optimization; vehicle power battery; particle swarm optimization; flexible job shop scheduling MSC:
90B35
1. Introduction
1.1. Research Background
The growing severity of global environmental issues and the energy crisis has led to widespread attention and rapid development of electric vehicles. Electric vehicles not only help reduce greenhouse gas emissions, but also reduce the dependence on fossil fuels and promote the transformation of the energy structure [1,2]. As a key component of electric vehicles, the demand for vehicle power batteries is steadily increasing. The quality and cost of vehicle power batteries directly affect the market competitiveness and user experience of electric vehicles, and their production lines have unique production characteristics and process requirements [3,4]. In the management and operation mode of traditional vehicle power batteries, manufacturing enterprises have long focused on maintaining the basic operation of the workshop. Therefore, there is insufficient emphasis on the iterative upgrading of production scheduling methods. Under this management model, traditional production scheduling methods gradually exhibit limitations in dynamic market demand and complex production environments [5,6].
As the core optimization problem of the modern manufacturing industry, the Flexible Job Shop Scheduling Problem (FJSP) provides a key idea to deal with the above challenges [7]. There is a deep coupling relationship between the FJSP and the power battery manufacturing process: the power battery manufacturing process covers multiple key processes, such as raw material processing, cell assembly, and module integration, and each process usually involves the selection of multiple devices. The process is highly consistent with the many-to-many mapping feature of the “operation–machine” system in the FJSP [8,9]. Therefore, how to improve production efficiency, reduce production costs, and ensure product quality based on the FJSP is an important issue faced by automotive power battery manufacturers. The intelligent scheduling of the production process based on the FJSP can not only save management costs but also improve the production efficiency of vehicle power batteries. This is of great significance for enterprises to achieve lean management of production activities.
1.2. Literature Review
The FJSP is a typical mathematical optimization problem, which has gained substantial research attention from scholars around the world [10]. At present, academic research on workshop scheduling problems can be summarized in three dimensions: research objectives, research methods, and research applications.
- (1)
- Research objectives
In the actual work at the workshop, many factors such as makespan, machine energy consumption, quality, workers, and machine breakdown will all affect job shop scheduling.
For example, Zhang et al. established a mixed integer programming model to minimize the makespan and total energy consumption for the green scheduling problem of a flexible job shop, while considering constraints including transportation time, machine pre-maintenance, and energy consumption [11]. Wei et al. considered the transfer time of both workers and workpieces during processing and employed a multi-objective calculation method to solve the optimization model, which aims to minimize the maximum accomplishment time, resource consumption, worker cost, and maximum worker workload [12]. Aqil et al. established two minimization objectives for the flow shop scheduling problem, namely the makespan and the total delay time [13]. Sun et al. established an optimization model to minimize the makespan and machine load balance for the flexible scheduling of the processing system [14]. Wu et al. developed a flexible job shop scheduling model that incorporates both energy-saving measures. They proposed a green scheduling heuristic algorithm aimed at optimizing the makespan, energy consumption, and the number of machine start-ups and shut-downs [15]. Inspired by real-life scenarios, Zhang et al. studied a multi-objective hybrid flow shop scheduling problem with consistent sub-batches, aiming to simultaneously optimize two conflicting objectives: the maximum production cycle and the total number of sub-batches [16]. Hou et al. aimed to solve the Multi-objective Distributed Flexible Job Shop Scheduling Problem (MO-DFJSP) and established an optimization model to minimize the makespan, total delay rate, and carbon emissions [17].
- (2)
- Solving methods
The research methods for the workshop scheduling problem can mainly be divided into exact and approximate methods [18]. Exact methods include mathematical programming methods, tree search, and branch-and-bound methods, and approximate methods include dispatching rules, local search methods, and meta-heuristic algorithms.
For exact methods, Ham et al., in view of the uncertainties existing in the workshop scheduling, put forward the idea of taking the shutdown strategy into account within the problem. Meanwhile, they utilized a mixed integer linear programming model to access the established mathematical optimization model [19]. Soto et al. introduced an innovative parallel branch-and-bound algorithm that leverages the renowned Non-dominated Sorting Genetic Algorithm II (NSGA-II) to set its upper bound, marking the first effective resolution of optimal solutions for a set of multi-objective flexible job shop scheduling problems [20]. Liu et al. developed a refined serial schedule generation methodology, introduced a novel lower bound calculation framework, and presented a tree-based heuristic search algorithm tailored for the resource-constrained project scheduling problem incorporating transfer time constraints [21]. Zolfaghari et al. proposed a new linear-structured mixed integer programming model and introduced a new solution method based on triangular interval-valued fuzzy random variables, incorporating fuzziness and random uncertainty into the mathematical programming model for project portfolio selection and scheduling, while considering resource management, cash flow, delay costs, and multi-project robustness [22].
For approximate methods, Hou et al. developed a collaborative evolutionary NSGA-III framework integrated with Deep Reinforcement Learning (DRL), which embeds novel gene operation mechanisms into the NSGA architecture. This design allows the Reinforcement Learning (RL) agent to directly derive optimal gene combinations from chromosomes and feed them back to the NSGA-III algorithm, thereby accelerating the learning process through real-time strategy updates [17]. Kong et al. put forward a Discrete Improved Grey Wolf Optimization (DIGWO) aiming at the optimization problem regarding the makespan and critical machine load in the FJSP [23]. Wang et al. transformed the multi-objective FJSP into a single-objective optimization problem, which was subsequently tackled using the Hybrid Adaptive Differential Evolution (HADE) algorithm [24]. Shao et al. established the multi-objective FJSP in the context of shipbuilding enterprises and used a Multi-Objective Imperialist Competition Algorithm (MOICA) to solve it [25].
- (3)
- Research applications
The practical application scenarios for the workshop scheduling problem are gradually increasing and have been widely applied in various fields of production and daily life.
For example, Du et al. considered the processing problems of piano companies and solved the mathematical models of batch optimization, processing tasks, and task sequencing based on the genetic algorithm (GA), further improving the working efficiency of piano processing [26]. Zeng et al., taking the paper mill industry as an example, optimized and solved the multi-objective model with makespan, power consumption, and material loss by using the improved GA, obtaining a more efficient workshop job scheduling method compared to manual scheduling [27]. Jiang et al. modeled and analyzed the energy-saving scheduling problem in the production and manufacturing process of aerospace components. According to the specific characteristics of the products, they proposed a batch production scheduling model for aerospace components, taking into account energy consumption, cost, and makespan [28]. Nouiri et al. proposed a batch production scheduling model based on GA for the problem of production and Internet of Things scheduling [29]. Wu et al. proposed the Multi-objective Dynamic Partial-re-entrant Hybrid Flow shop Scheduling Problem (MDPR-HFSP) to supplement the FJSP. They considered partial re-entrant processing, dynamic interference events, green manufacturing requirements, and machine workload in the problem, and proposed Modified Multi-agent Proximal Policy Optimization (MMAPPO) to solve it [30]. Hu et al. conducted a study on the dynamic scheduling of unexpected events under cloud manufacturing. Taking actual workshop resource scheduling as the background, they considered random arrival tasks, resource decomposition, and resource maintenance, and proposed a dynamic scheduling method based on game theory to solve it [31].
In summary, scholars from different research areas have conducted extensive studies on multi-objective problems. The existing research on workshop scheduling mainly focuses on production efficiency and costs, while there are relatively few studies on production quality and the vehicle power battery production workshop. If the optimization model from other backgrounds is directly applied, the specific characteristics and unique processing constraints of the automotive power battery production process will be ignored, which will eventually lead to poor or unrealistic scheduling results. There are many ways to solve the FJSP, both exact and approximate algorithms. Exact algorithms are more effective in solving the small-scale static FJSP, but approximate algorithms have a larger application background and solving capabilities. When solving complex and large-scale problems, the heuristic algorithm in the approximation algorithm is able to quickly find an approximate solution.
Particle Swarm Optimization (PSO) is one of the common heuristic algorithms, which is often used to solve optimization problems in various scenarios [32]. Energy Valley Optimization (EVO) and PSO are both particle-based optimization algorithms, which have a certain similarity in the background, and some structures of the algorithm can be skillfully integrated to ensure the rationality of the algorithm. Therefore, considering the actual needs of enterprises for production activities, this study takes the vehicle power battery manufacturing workshop as the research object, focuses on the production efficiency problem of vehicle power batteries, takes the total machine load, makespan, and processing quality as optimization indicators, and constructs a vehicle power battery workshop scheduling model. Aiming to solve the scheduling problem of the vehicle power battery production workshop, a Multi-objective Particle Swarm Energy Valley Optimization (MPSEVO) is proposed to solve the solution set of Pareto optimization. For the solution of benchmarks and examples, the MPSEVO results are similar to the Pareto frontiers of other traditional algorithms. The results of each algorithm are evaluated by using the indicators of consistency, convergence, and diversity, and it is found that most of the indicators of MPSEVO are better.
Compared to existing methods, the MPSEVO innovatively integrates the advantageous features of PSO and EVO. By constructing a particle stability grading mechanism and employing a differentiated updating strategy, MPSEVO achieves a dynamic balance between convergence performance and population diversity. Meanwhile, its designed adaptive updating mechanism and local search strategy effectively alleviate the issues of getting trapped in local optima and a lack of population diversity. The proposal of MPSEVO not only provides a new pathway for EVO to solve the multi-objective optimization problem, but also provides a theoretical reference for the improvement of PSO.
The organization of this paper is as follows: Section 2 provides a description of the problem and establishes a mathematical model. Section 3 introduces the details of MPSEVO. Section 4 conducts computational experiments and comparative analysis of the algorithms. Section 5 validates the performance of the proposed method using a case from a real vehicle power battery production workshop. Section 6 summarizes the conclusion and several directions for future research.
2. Scheduling Optimization Model
2.1. Problem Description
Existing research has insufficiently focused on the processing quality of batteries in terms of scheduling objectives, and has not adequately considered the multi-mapping characteristics of the “operation–machine” system in the battery manufacturing scenario [33]. In addition, the scheduling decision-making method of manufacturing production management is the key to ensuring high efficiency, high quality, high flexibility, and low cost of the vehicle power battery process. Therefore, this section aims to address the scheduling problem in power battery workshops, clarifying the problem boundaries and constructing a multi-objective optimization model with the goals of maximizing makespan, total machine load, and processing quality.
The scheduling problem within a vehicle power battery manufacturing workshop can be depicted in the following ways: workpieces in the workpiece set are machined on machines in the machine set . Each workpiece contains operations, and the sequence of operations is predetermined. The -th operation of the workpiece can be processed on any machine in the set; the processing time of the operation varies depending on the different machines used for processing.
The scheduling result is derived from the selection of the most suitable machine for each process, the determination of the optimal processing sequence for each process on each machine, and the determination of the start-up time, so that the objective function of the whole system is optimized. To better establish the scheduling model for a vehicle power battery manufacturing workshop, the parameters and variables used in the problem are introduced and explained in Table 1.

Table 1.
Explanation of parameters and variables.
2.2. Optimization Indicators
- (1)
- Makespan Indicator
The makespan of a workpiece, denoted as , refers to the moment when the final operation on the processed workpiece is completed. The overall makespan of an order is determined by the maximum makespan among all individual workpieces. This makespan order serves as an important indicator of production efficiency within a manufacturing system and plays a critical role as a performance metric.
- (2)
- Total Machine Load Indicator
Implementing different scheduling plans will lead to different machine selection plans. In order to improve machine utilization, the number of operations undertaken by each device should be roughly the same, and the machine load can be expressed by the sum of the machine processing time.
- (3)
- Processing Quality Indicator
The processing quality of the same workpiece processed by different machines is also different. In order to improve the processing quality, the defective rate should be kept to a minimum. Since the power battery manufacturing process is an automated production, the failure rate of each process is low, and the processing quality is expressed by the sum of the failure rates of each process.
In summary, the objective function of the vehicle power battery manufacturing workshop scheduling optimization model can be expressed as follows:
In the actual production process, there is a batch of workpieces that need to be processed in the workshop, and each workpiece requires multiple processing operations. It should be noted that for the same workpiece, the subsequent operation must be processed after the previous operation, which is a real-world constraint. There are many such constraints in this problem, and the existence of these constraints ensures the normal operation of the workshop. In order to establish an accurate model, the constraints existing in the power battery manufacturing workshop need to be incorporated into the mathematical model to ensure the accuracy of the model. The constraints can be expressed as follows:
where
where
where
where
where
where
Equation (5) indicates that there are sequence constraints in different processing operations of the same workpiece, which must be processed on machines in a sequential order. Equation (6) shows that a certain processing operation of a workpiece can only be processed once. Equation (7) means that the sum of the starting processing time and the required processing time of each operation shall not exceed the final processing time of that operation. Equation (8) implies that the makespan of any workpiece must be less than the maximum makespan. Equation (9) indicates that any machine can only process one operation at any time. Equation (10) shows that the start and makespan of each workpiece must be greater than or equal to 0.
3. Algorithm
The above power battery manufacturing workshop scheduling model contains three optimization objectives and multiple constraints, which belongs to the high-dimensional multi-objective discrete optimization problem. Traditional exact algorithms are difficult to solve in a reasonable time, but the PSO shows good convergence efficiency in discrete problems. Therefore, this section integrates the EVO idea on the basis of the PSO and proposes the MPSEVO method adapted to this model.
3.1. PSO
Kennedy et al. proposed the PSO optimization algorithm in 1995 and demonstrated the stability and convergence of the algorithm from a theoretical level [34]. The PSO algorithm simulates the foraging activities of birds in nature, and maps the location of food to the optimal solution set of the optimization problem. The flight direction and position of birds correspond to the speed and position of the particles, respectively. Through the information interaction between the global optimal solution (gbest) and the individual historical optimal solution (pbest), the position and velocity of the particle are continuously updated. This process can improve search efficiency and effectively guide the population to converge. The specific update mechanism is as follows:
where is the update generation, is the inertia weight, and are learning factors, and are independent random numbers between (0, 1), is the velocity of particle in the -th dimension when iterating to the -th generation, and is the position of particle in the -th dimension when iterating to the -th generation.
As an optimization method based on collective intelligence, PSO has been widely applied in the field of optimization due to its simplicity of principles [35]. Such problems are prevalent in various scenarios, including industrial production, engineering design, and management decision-making.
3.2. MOPSO
For the application of multi-objective optimization scenarios, a Multi-Objective Particle Swarm Optimization (MOPSO) is proposed. Compared with PSO, MOPSO adds out-of-bounds processing and a shrinkage factor when updating the particle velocity. In addition, the construction and maintenance of external archives are also introduced, and the non-inferior solutions of each round are stored according to the dominance relationship, and the inferior solutions are eliminated. It screens and stores the Pareto optimal solutions of each generation by setting an external archive and selects the gbest of each generation from the external archive. These features make it uniquely advantageous in multi-objective optimization scenarios.
MOPSO has a strong ability to search for the optimal solution globally, and its advantages include easy implementation, fast convergence speed, and applicability to various types of problems due to its unique particle update method. It is now widely applied in fields such as engineering design, energy system optimization, and financial investment.
3.3. Encoding and Decoding
In order to enable each particle to better express the solution of the FJSP, two levels of coding are used for each chromosome, and combined together, and this type of coding is widely used in GA to solve the FJSP. Operation Sequence (OS): Each gene in this layer characterizes the sequential processing order relationship between different processing processes of all the workpieces to be processed. Machine Assignment (MA): In the FJSP, each process corresponds to multiple processing machines, and each gene in this layer of encoding represents the corresponding processing machine that has been selected.
In this study, a two-layer integer coding method is adopted, in which each particle in the solution space contains two gene segments, MA and OS, and they are spliced back and forth to form a particle of length 2 in the coding process, where denotes the sum of the number of all the processes of the workpiece, and thus the particles in the solution space can be expressed as “MA + OS”. To better illustrate this encoding method, an example is provided in Table 2 to demonstrate the coding process.

Table 2.
Coding example.
The encoding form of the particles is shown in Figure 1; the length of the MA and the OS are both equal to 5, and the total length of the particles is 10. The OS is composed of some numbers “1” and “2”, representing the workpieces and . The occurrence frequency of the same value implies different processes within the workpiece. The frequency with which a number is presented suggests different processes within the workpiece. For example, the initial occurrence of the value “1” corresponds to process , while its subsequent appearance is associated with process . This principle is applied to other values in the same manner. Additionally, the sequence within the MA segment follows the chronological order of the processes in the workpiece, as demonstrated in Figure 1. The numerical information at the third position is “2”, according to Table 1; it represents the machine selected for the first process of workpiece 2. The second machine () is selected in the machine set that can process it. The same principle is applied to other positions, and using this encoding method on machine segments can effectively avoid infeasible solutions.
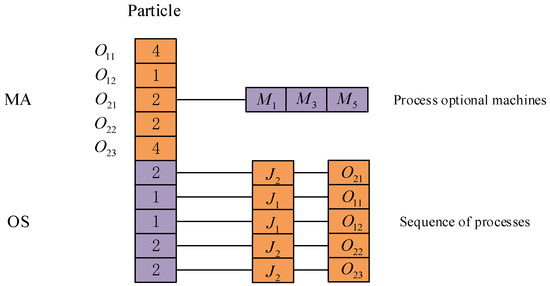
Figure 1.
Particle encoding.
In this paper, the decoding operation adopted primarily involves two steps. Firstly, the processing machine for each workpiece operation should be identified based on the coded particles. Subsequently, it is necessary to compare the makespan of the previous operation of the current operation with the makespan of the last workpiece on the current machine. Meanwhile, the start and end times of the current operation on the machine are determined based on the processing sequence. Ultimately, the scheduling scheme for all the workpieces to be processed is generated.
3.4. MPSEVO
Although MOPSO has many advantages, it still has shortcomings, such as susceptibility to being trapped in local optima. To overcome these shortcomings, it is necessary to improve algorithms and develop appropriate update strategies to help achieve better solution results.
The EVO is a metaheuristic algorithm proposed by Mahdi et al. in 2023 [36], which is inspired by different decay modes in the process of particle stabilization and still has certain effectiveness in the high-dimensional search space. PSO and EVO are optimized by taking particles as individuals, which have a certain correlation in the background, and the solution performance can be improved by hybridizing the optimization strategies of EVO and PSO. Thus, EVO is integrated into MOPSO to enhance its stability and performance. Finally, an MPSEVO is proposed to solve the scheduling problem in the vehicle power battery manufacturing workshop. Additionally, several strategies, including external archive maintenance, local search, and adaptive parameter update mechanisms, are implemented to improve the convergence and accuracy of MOPSO.
3.4.1. Initialization and Fitness Function
- (1)
- Normalization
First, the minimum value on each target dimension is calculated, , and the set of constitutes an ideal set. For each individual in the population , the regularized target function value of the -th dimension is expressed as follows:
- (2)
- Initialization
In the MPSEVO algorithm, it is assumed that there are particles in the search space, and each particle is a -dimensional decision variable. The initialization population is generated by randomly selecting the operation sequencing part and randomly initializing the machine allocation vector globally and locally, represented as follows:
where . denotes the -th decision variable of the -th particle.
- (3)
- Fitness function
In MPSEVO, the stability of a particle is determined by the number of neutrons it contains. To evaluate the stability of each particle, the Enrichment Boundary () is introduced, which allows for the assessment of the particle’s stability based on its neutron count. This information is then used to update the particle according to its neutron level. The of the particle is utilized to depict the difference between neutron-rich and neutron-poor situations, and it is expressed as follows:
where is the Neutron Enrichment Level () of the -th particle, represented by the value of the objective function corresponding to the distribution results. The is the Enrichment Boundary of the particle in the solution space. Similarly, the stability level of the particle is defined using the Neutron Enrichment Level:
where is the stability level of the -th particle; and , respectively, represent the optimal and worst stability levels of the current particle.
3.4.2. Update Strategy
The main part of MPSEVO is MOPSO, which adopts the basic particle swarm update method as in Equations (10) and (11). At the same time, it is combined with the EVO algorithm for updating. The particle update strategy adopts a fusion mechanism of MOPSO and EVO, which is specifically divided into two progressive stages. First, a basic update is completed based on the core rules of MOPSO: particles update their velocity and position by tracking pbest and gbest, integrating adaptive inertia weights and learning factors, which generate the initial next-generation particles. On this basis, an EVO particle stability control mechanism is introduced for secondary optimization, calculating each particle’s and stability level . High instability particles ( > and > ) are subjected to decay updates (where some decision variables are replaced with genes from optimal stable particles or neighborhood particles), while medium instability particles ( ≤ ) undergo decay updates (making jumps towards the population center or the optimal particle direction), achieving precise optimization of particles in the solution space.
This layered update strategy retains the global search efficiency of MOPSO while enhancing population diversity through EVO’s differentiated stability control, effectively avoiding local optima. In the end, this results in the algorithm outperforming traditional MOPSO in both convergence speed and solution diversity, with specific performance improvements to be validated by subsequent experiments.
In terms of particle stability, when > , the ratio of neutrons to protons in the particle is large, and the particle is likely to undergo , or decay to increase its stability level. Next, a random number between [0, 1] is taken as the Stability Boundary () of the particle swarm. When > , the particle will undergo and decay. The updated equation of the particle at this time is as follows:
where represents the distance between the i-th particle and its -th neighboring particle, while (,) and (,) denote the coordinates of the particles within the search space. The vector refers to the new position of the -th particle after undergoing α decay, and represents the particle with the best stability. Alpha Index I is a random integer within the range [1, d], and Alpha Index II is another random integer within the range [1, Alpha Index I]. Similarly, denotes the updated position vector of the i-th particle after γ decay, while represents the position vector of the neighboring particles, determined by . The definitions of Gamma Index I and Gamma Index II are the same as those of Alpha Index I and Alpha Index II.
When , the particle undergoes decay. Since decay occurs in more unstable particles, such particles emit rays and jump significantly in space. At this time, the particle is updated with the following equations:
where represents the center of the particle, and denotes the new position vector of the -th particle after it undergoes decay. The particle moves towards and , and and are random numbers within the range [0, 1], which are used to determine the movement of the particle. For balancing the exploration and development phases of the EVO, another position update process is implemented for the particles that undergo decay, at which time the new position vector of the -th particle after undergoing decay is . This particle moves towards and in a controlled manner while has no impact on the movement process, and and are random numbers within the range [0, 1].
3.4.3. Particle Velocity Update Methods
As can be seen in Equations (11) and (12), the velocity update equation of the basic MOPSO consists of the velocity inertia of the particles themselves in the previous generation, individual cognition, and social cognition. Its fixed velocity update mode leads to high blindness in solving problems, making it easy to fall into local optima. The MPSEVO algorithm introduces the population clustering degree to define the exponent for real-time monitoring of the particles’ flight states, and its calculation method is as follows:
where
where refers to the Euclidean distance between particle and the global optimal particle , while and represent the minimum and maximum distances among all particles across all populations, respectively. represents the population size. is the index of the population clustering degree when the iteration reaches generation .
As can be seen in Equation (21), the value range of is [0, 1]. To facilitate algorithm convergence, the value of is designed to exhibit a decreasing trend with the increase in iteration.
In the early stage of iteration, the algorithm adopts the basic particle swarm velocity update method, namely Equation (11). Subsequently, the population enters the search and optimization stage. After each iteration, the algorithm updates the population clustering degree once. When the population clustering degree in the -th generation is smaller than the historical minimum population clustering degree, it indicates that the population diversity of the current generation is good, but the convergence is poor. Therefore, it is necessary to improve the local exploitation accuracy, and the velocity update method in Equation (24) is used to help the population converge.
When the population clustering degree in the -th generation is greater than the historical minimum population clustering degree, it indicates that the evolutionary state of the current generation tends to converge. The algorithm uses the exponent as a probability to adopt the Levy flight strategy to enhance the global exploitation ability of the algorithm and escape from local optima. The particle velocity update equation based on the Levy flight is as follows:
In Equations (24) and (25), is the inertial weight, , , and are learning factors, and , , and are mutually independent random numbers. The step size of the Levy flight follows a Levy distribution, which is often simulated using the Mantegna algorithm, and its calculation equation is as follows:
where the value of is 1, represents the gamma function, , is the random step size, and is the power exponent.
In summary, suppose that Equation (11) used in the initial stage of the algorithm is defined as , Equation (24) is adopted when the population clustering degree in -th generation is smaller than the historical minimum population clustering degree and is defined as , and Equation (25), with a probability of being selected to enhance global exploitation capability when the population clustering degree in -th generation is greater than the historical minimum population clustering degree, is defined as . Then, the particle velocity update equation of the MPSEVO algorithm is as follows:
where is a random number, and the position update mode adopts Equation (12). By using different particle velocity update strategies, the MPSEVO algorithm can monitor and intervene in the optimization search mode of the algorithm in real time, balancing the global search and local exploitation capabilities of the algorithm. This enables the solution to maintain good diversity while improving the accuracy of finding the optimal solution, meeting the convergence requirements of the algorithm.
3.4.4. Adjustment Strategies for Parameters
In Equation (11), the cognitive parameters in the speed update equation include inertia weight , individual cognitive parameter , social cognitive parameter , and cognitive parameters of Levy flight . Combined with the concept of population clustering degree proposed in the literature, the adaptive parameters of MPSEVO are shown as follows:
where
where denotes the maximum values of the individual cognitive coefficients, and denotes the minimum values of the individual cognitive coefficients. Similarly, represents the maximum values of the social cognitive coefficients, and represents the minimum values of the social cognitive coefficients. indicates the maximum values of the inertia weights, and indicates the minimum values of the inertia weights. is the maximum number of iterations of the algorithm.
In Equations (31) and (35), the values of each cognitive parameter are related to the population clustering degree of the particles and the current number of iterations. To guarantee that the convergence of the algorithm is continuously strengthened as the number of iterations increases, both and are required to demonstrate an overall downward tendency. Meanwhile, since the algorithm will keep converging during the iterative process, it is essential to enhance its global optimization ability in the later iterations to avoid getting trapped in the local optimum. Consequently, should keep an overall upward trend.
3.4.5. Local Search and External Archive Maintenance
The external archive filters and stores Pareto optimal solutions generated by the population during iterative evolution. Different from MOPSO, MPSEVO employs a local search strategy on the population at each iteration to update the external archive. Then, it combines and deduplicates the solution sets of the population, external archive, and local search. Based on Pareto dominance relationships, a new set of nondominated solutions is selected. If the number of nondominated solutions exceeds the size of the external archive, the crowded distance strategy is used to select each Pareto solution to form a new external archive, realizing the update and maintenance of the external archive.
- (1)
- Local search strategy
Let archive be the external archive with capacity . Referring to the selection, crossover, and mutation operations of the GA, each individual is regarded as a chromosome, and genetic operations are performed on the population. Firstly, the population popm and the previous generation’s external archive archivet−1 are combined to form a new temporary population popm′. Then, the chromosomes of popm′ are randomly combined in pairs. Subsequently, a segment of the two chromosomes in each group is randomly intercepted to carry out the crossover operation. Finally, individuals are selected according to the set mutation probability to perform the mutation operation, that is, a segment of genes on the target chromosome is randomly marked and recoded. In this way, a local search operation is completed. The obtained solution set popm″ has a greater ability to escape from the local optimum, allowing the algorithm to search in the potential solution space.
- (2)
- Crowded Distance Screening Strategy
The previous generation’s external archive archivet-1 is merged and deduplicated with contemporary updated popm and local search output popm″. After the non-dominated solution judgment, it is filtered to the prospective time selection set E. If the number of Pareto solutions exceeds the set value of the external archive, the algorithm uses the crowding distance screening strategy. Let be the -th objective function value of Pareto optimal solution , and sort the temporary candidate sets separately in three target spaces. The distances between the maximum and minimum solutions in the sorting are both assigned infinite values, and the distances of the remaining solutions are calculated from the two adjacent positions in their sequences. Then, the sum of the distances in the three dimensions is the crowding distance of each Pareto solution. The specific calculation method is defined as follows:
where is the congestion distance of in the first objective spaces, and and represent the maximum and minimum values that can be achieved by the objective function in the solution space, respectively. After finding the congestion distance of each Pareto optimal solution in E, they are arranged in descending order, and the first solutions with the largest congestion distance form a new generation of external archive archivet.
3.4.6. Algorithm Flow
Finally, the calculation process of MPSEVO is summarized and designed as follows:
Input: Power cell processing process, processing time, and processing machine information, population size , objective function ( = 1, 2, 3), and iteration number .
Output: Non-dominated solution set external archive archive.
Step 1: Initialization of the algorithm parameters; set initial values of parameters and the external archive archive.
Step 2: Initialize the population by employing a global randomization method.
Step 3: Calculate the objective function value of each particle as the fitness value from Equation (5); initialize the pbest of each particle and the gbest of the population; and calculate the stability boundaries and the stability level of each particle from Equations (15) and (16).
Step 4: Calculate the contemporary population clustering degree of each particle, and update each cognitive parameter of the algorithm according to Equations (31) and (35).
Step 5: Update the population and the particle velocity according to the different strategies in Equation (30), and update the position of the particle using Equation (12).
Step 6: Update the stability level based on individual particles, calculate α, β, or γ decays according to different stability levels, and update the particles using Equations (17) and (20).
Step 7: Evaluate the fitness of the new population popmt and compare it with the previous one, popmt-1. If the new solution dominates the old one, update the pbest. If the old solution dominates the new one, keep the previous pbest. If neither dominates the other, randomly decide whether to replace the pbest.
Step 8: Merge popm and archivet-1, conduct a local search strategy, merge the obtained popm″ again with the current population along with the external archive from the previous generation; after removing the duplicate solutions, perform a congestion distance judgment on E according to Equation (36); sort and crop the external archive of the new generation archivet; and update gbest.
Step 9: Judge whether the current iteration number t of the algorithm reaches the maximum iteration number . If it reaches the number, output the solution set archive and the algorithm terminates; otherwise, turn to step 4.
The flowchart of MPSEVO for solving the scheduling problem of flexible operation on the vehicle power battery is shown in Figure 2.
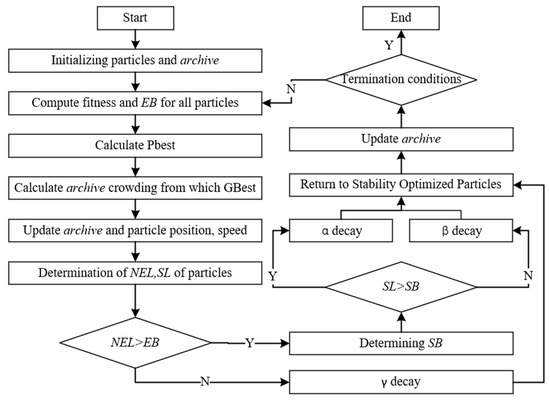
Figure 2.
Algorithm flowchart.
3.5. Parameter Determination
In MPSEVO, different parameters have a large impact on the performance of the algorithm, so the parameters should be selected first before conducting experiments. Here, the orthogonal method is used to select the optimal parameter values, considering the maximum number of iterations , population size , external archive capacity , individual cognitive coefficients , and social cognitive coefficients , and each parameter is set to four levels, and the orthogonal matrices are generated, as shown in the table. The advantage of using the orthogonal matrix is that it can effectively reduce the number of experimental groups. Traditional methods usually require control variables, i.e., changing one variable while keeping the other parameters constant. If there are parameters, each with choices, then a total of experiments are required, which is 1024 in this experiment. In contrast, using the orthogonal approach allows the effects of several parameters to be studied simultaneously while reducing the number of experiments, which can be reduced to 16 in this experiment. Each column of the orthogonal matrix shows the setting level of the parameter, and each row represents a set of experiments with different parameter levels. Because determines the running time of the algorithm and the final convergence state, affects the diversity in the initial search scope and iterations and determines the diversity of solutions in external archives. The balance between and directly determines the ability of the algorithm to “optimize” and “converge”, which is the core contradiction of MPSEVO, so these five parameters are selected for orthogonal experiments. Individual experiments were performed on MPSEVO using the 16 groups of parameters shown in Table 3, while the other parameters shown in Table 4 were set and kept constant, with parameter settings referencing previous studies [37].

Table 3.
Orthogonal experimental design table.

Table 4.
The values of other parameters.
The orthogonal experimental table is shown in Table 3, with a total of 16 experiments. The experimental data uses the Brandimarte standard dataset case Mk01. In Mk01, the processing quality (failure rate) of the operation on the machine follows a uniform distribution of .
The quality of solutions for three-dimensional optimization problems cannot be directly observed from graphical representations; therefore, the Inverted Generational Distance () metric is employed to evaluate the performance of solution sets. computes the average distance from the individuals within the true Pareto optimal solution set PFtrue to the non-dominated solution set PFknown, which is calculated by the optimization methods. The metric is calculated as follows:
Due to the lack of a true Pareto optimal solution set, it is necessary to generate an approximate reference set via optimization methods for calculating the metric. The specific approach is as follows: First, collect the non-dominated solution sets obtained by running several high-performance algorithms (NSGA-III, MOPSO, and MOEA/D) independently 2000 times on the same problem. Then, apply non-dominance filtering to the merged set by removing points dominated by others and retaining the final non-dominated subset. Finally, perform uniformity pruning on the filtered set using K-means clustering to retain points with a more uniform distribution, thereby avoiding an excessively dense or sparse approximate reference set.
The algorithms are implemented in Python 3.7 on a Windows 11 operating system, with a hardware configuration consisting of an Intel Core i5-10400F processor (2.90 GHz) and 16 GB RAM. For each group, the algorithm was run independently 30 times and then averaged. The values and comparison of Pareto optimal fronts obtained from each group of experiments are shown in Table 5 and Figure 3.

Table 5.
values for each group.
Figure 3.
Comparison of Pareto optimal fronts for each group.
Figure 3 shows the distribution of Pareto fronts for each set of experiments, and the results of each set of solutions are well balanced between multiple optimization objectives. It can be found that the solution set of the 13th set of results covers a wider range of target spaces, and this diversity makes the solutions of this set of solutions more adaptable. As can be seen in Table 5, the 13th group of experiments obtained the smallest value, indicating that the Pareto optimal frontier has better diversity and convergence than other experiments, and the parameter set of group 13 has stronger optimization search ability and better optimization effect. Therefore, this paper selects the 13th set of parameters for MPSEVO.
Based on the results of the orthogonal experiment, the algorithm’s maximum number of iterations is 500; the population size is 90; the individual cognitive coefficient was initially set as 1, with = 2, = 1; the social cognitive coefficient was initially set as 2, with = 2, = 1; and the external archive capacity is 50. In other comparative algorithms, the maximum number of iterations , population size , and external archive capacity are the same as the parameters in MPSEVO. In MOPSO, the individual cognitive coefficient is 2, the social cognitive coefficient is 2, and the inertia weight decreases linearly from 0.9 to 0.3. In NSGA-II and NSGA-III, the crossover probability is fixed at 0.5, and the variance probability is 0.2.
4. Computational Experiments
4.1. Experimental Design
MPSEVO enhances convergence and diversity through particle stability classification, local search, and other strategies, but its performance needs to be verified by standardized experiments. In this study, 10 commonly used FJSP test cases are selected to compare the capability of different algorithms, aiming to examine the optimization capability of the proposed algorithm. MK1-MK10 is a test case of the FJSP designed by Brucker et al. [38], and it is also a classic standard test set in the field of FJSP, which is widely used for general verification of algorithm performance. Its parameters cover typical scenarios from small to medium scale, which can systematically evaluate the convergence, diversity, and stability of the algorithm under different problem complexities. Due to the absence of processing quality data in the 10 test cases from Mk01 to Mk10, the processing quality (failure rate) of the operation on the machine conforms to a uniform distribution across all algorithms. NSGA-III, NSGA-II, and MOPSO are chosen as candidate algorithms in the comparison. Considering that the visual graphics cannot directly judge the quality of each solution, in order to compare the strengths and weaknesses of the solutions obtained by each optimization method, two calculation indicators, and Hypervolume (), are used to evaluate them.
is an effective indicator for evaluating the convergence and diversity of solutions obtained by optimization methods. It refers to the volume of the hypercube enclosed by each solution in the solution set and the reference point in the search space as follows:
where represents the Lebesgue measure, stands for the number of non-dominated solution sets, and represents the volume of the hypercube enclosed by the -th solution in the optimal solution set and the reference point.
4.2. Experimental Results
For each test problem, the different algorithms were run independently 30 times. Taking and as performance indicators, the and values obtained from 30 runs were averaged, the confidence level was set as 0.05, and the Wilcoxon rank sum test was performed. The algorithms are implemented in Python 3.7 on a Windows 11 operating system, with a hardware configuration consisting of an Intel Core i5-10400F processor (2.90 GHz) and 16 GB RAM. The mean is expressed as M-value, and the probability value (PR-value) is a statistic used to measure the significance of the difference between sample data and the null hypothesis. In the calculation results, the values that outperform those of other algorithms by a significant margin are highlighted in bold. Table 6 and Table 7 show that the PR-values of all algorithms in all cases are less than the confidence level 0.05, indicating that the obtained and index values are valid. Furthermore, the performance index values obtained by the MPSEVO method outperform NSGA-III, MOPSO, and NSGA-II. When solving the three-dimensional multi-objective FJSP, the MPSEVO algorithm improves convergence and diversity. MPSEVO can solve high-quality production scheduling schemes.

Table 6.
Output value of indicators.

Table 7.
Output value of indicators in computational experiments.
Table 6 and Table 7 indicate that MPSEVO can handle the three-objective FJSP with great flexibility, and the solutions obtained demonstrate good diversity and convergence. In this issue of low diversity, the congestion-based update operation adopted by NSGA-II cannot keep the diversity of solutions at a high level. However, iterative operation in NSGA-III based on reference points can also avoid this problem. In terms of convergence, NSGA-III emphasizes diversity while neglecting population convergence during the environment selection. Moreover, as the number of target dimensions increases, there is insufficient selection pressure for NSGA-III based on the Pareto dominance relation. However, MPSEVO, aside from utilizing the traditional pbest and gbest, also incorporates the particle energy level. Compared to the vertical distance in NSGA-III, which only represents diversity, MPSEVO can balance convergence and diversity. For the multi-objective scheduling optimization problem, MOPSO selects individuals using the crowding degree. This causes the algorithm to fall into a local optimum since the obtained solutions are not uniformly distributed across the non-dominated layers. In terms of diversity, MPSEVO adds the energy valley selection strategy on the basis of MOPSO. By assigning energy levels to particles, it effectively prevents rapid convergence and improves the population diversity. Additionally, the particles adopt different update strategies within different energy intervals.
In summary, after comparing the MPSEVO algorithm with other algorithms across various benchmark cases, it demonstrates not only better optimization results but also preferable diversity and convergence in its output Pareto optimal solution set. This allows it to explore potential solution spaces that are unreachable by other algorithms, making it less susceptible to being dominated by their solutions.
The MPSEVO algorithm can monitor the iteration progress in real time by utilizing population clustering metrics, enabling reasonable adjustments to its iterative parameters and updating methods. Throughout the iterations, it continuously refines the convergence and diversity trends guiding particle optimization. By introducing update strategies within EVO, it assigns stability level labels to particles and performs two updates, followed by a design for a local search strategy. It additionally conducts a further optimization based on GA in an external archive, which aids particles in escaping local optima. Finally, a rational external archive maintenance strategy is implemented, ensuring the MPSEVO algorithm exhibits superior performance in solving the FJSP.
Due to the fact that EVO was proposed two years ago, there has been relatively little research on its introduction to multi-objective optimization. The integration of EVO with MOPSO enhances the possibility of using EVO to solve multi-objective problems and provides a practical pathway. By incorporating particle stability level classification and differentiated update strategies into PSO, it balances the convergence and diversity of the solution. Additionally, it offers new insights for the performance improvement of MOPSO and expands the application boundaries of EVO.
5. Case Analysis
The above benchmark experiments verify the advantages of MPSEVO in the general FJSP, but there are unique constraints in the power battery workshop, such as strong process correlation and high processing quality requirements, and the performance of the algorithm in a real case still needs to be verified. Therefore, this section uses the real scheduling data of a power battery manufacturing workshop as input to further verify the engineering practicability of the algorithm.
5.1. Problem Background
The experiment of the benchmark instance aims to eliminate industry-specific interferences, focusing on the optimization performance of the algorithm itself and verifying its universality in the general FJSP. The real cases further test the algorithm’s adaptability to actual production constraints. The combination of the two forms a progressive logic of “universal performance validation to practical scenario implementation.”
Taking the production scheduling problem of a vehicle power battery production line as the application background, this workshop produces various types of power batteries, and the received production orders typically involve multiple varieties and large quantities. In order to verify the effectiveness of MPSEVO in solving practical workshop scheduling problems, it is used to schedule the production of five types of workpieces in factories. The scheduling objectives for this problem include the maximum processing quality, machine load, and makespan. This represents a typical high-dimensional multi-objective workshop scheduling problem. The original data collected during the manufacturing process for the workpieces to be processed includes various process information, as shown in Table 8. This case typically includes the product workpiece type, operations to be performed, processing machine, processing time, and processing quality.

Table 8.
Parameters of vehicle power battery products.
To evaluate the optimization performance of the proposed MPSEVO algorithm for the vehicle power battery workshop scheduling problem, it is compared with the multi-objective genetic algorithms, NSGA-II and NSGA-III, and MOPSO. The values of each objective function in the obtained solution sets are analyzed, and various performance indicators are designed to assess the convergence, uniformity, diversity, and mutual dominance of the Pareto solution set. These indicators allow for a comprehensive evaluation of the applicability and superiority of MPSEVO. The parameters for all algorithms are consistent with those described in Section 3.5, ensuring a fair comparison. The goal is to demonstrate the superior optimization performance of the MPSEVO algorithm across different evaluation dimensions.
5.2. Results Analysis
5.2.1. Optimization Results
The algorithms are implemented in Python 3.7 on a Windows 11 operating system, with a hardware configuration consisting of an Intel Core i5-10400F processor (2.90 GHz) and 16 GB RAM. For the production scheduling problem of a vehicle power battery production workshop, each algorithm in the test uses the same input data. The average values are obtained by running each algorithm 50 times independently, and the optimal and average values of the three optimization objectives in the Pareto optimal solution set obtained by each algorithm are presented. The optimization scheduling results for each algorithm are summarized in Table 9, with the better optimization results highlighted in bold within the scheduling solutions.

Table 9.
Optimal values and mean values for each algorithm.
Table 9 shows that MPSEVO has obvious advantages in three optimization objectives compared with other algorithms. It has the optimal average value in the task, and its optimal values in the makespan and processing quality objectives are also better than other algorithms. Although MPSEVO does not obtain the optimal value in the machine load objective, it is slightly lower than NSGA-III. At the same time, its average value is remarkably better than that of NSGA-III. The reason is that MPSEVO has good solution performance due to its advantage in dealing with discrete problems. Notably, all algorithms can search for the same optimal value in the makespan objective, and the average value of MPSEVO in this objective is significantly better, which also reflects that MPSEVO has better stability while exhibiting strong search ability.
The better performance of MPSEVO over commonly used multi-objective algorithms (such as NSGA-II, NSGA-III, and MOPSO) derives from its integration mechanism: it introduces particle stability classification by incorporating EVO, categorizing particles based on NEL and SL to balance exploration and exploitation capabilities. This effectively addresses the issues of uneven distribution in NSGA-II, fixed reference points in NSGA-III, and premature convergence in MOPSO. Additionally, its adaptive speed update based on population clustering can dynamically switch modes to avoid local optima, while the combination of local search and refined external archive maintenance enhances the quality and distribution of solutions. The integration of MOPSO and EVO ensures that the algorithm can rapidly converge to the Pareto frontier while maintaining a wide distribution of solutions. Thus, it demonstrates better performance in scheduling a vehicle power battery workshop.
Figure 4 shows the convergence of the Pareto solution sets obtained by each algorithm and their distribution in the solution space. It can be seen in Figure 4 that the solution set of the MPSEVO algorithm performs well in terms of convergence and distribution, and can search for Pareto fronts that are difficult for other algorithms to reach.
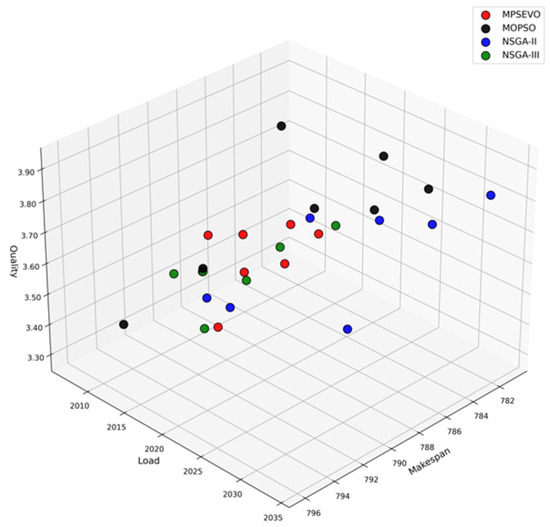
Figure 4.
Distribution of Pareto solution sets of each algorithm in the objective space.
5.2.2. Uniformity Index Analysis
Furthermore, the average space distance index is used to evaluate the uniformity of the solution set obtained by the algorithm in the solution space. Its mathematical essence is to calculate the coefficient of variation (discreteness) of the solution set, which helps to observe the degree of dispersion of the sample data within the solution set. The calculation equation for the average space distance index is defined as follows:
where , the value represents the minimum Euclidean distance between the -th Pareto solution and all other solutions in the solution set, while denotes the total number of solutions in the Pareto set. The index indicates the degree of uniformity in the distribution of the Pareto solutions within the solution space, with smaller values signifying better distribution uniformity.
Table 10 presents the mean and variance of the index for each algorithm after 20 independent runs under the same conditions. The optimization results with the best performance are highlighted in bold. In the table, it is evident that the mean and variance of the S values achieved by NSGA-II and MOPSO are relatively poor. In terms of the mean, the results of MPSEVO and NSGA-III are quite similar, although NSGA-III performs slightly better. Regarding variance, MPSEVO significantly outperforms the other algorithms, indicating that the Pareto optimal solution set produced by MPSEVO is the most uniformly distributed. This suggests that MPSEVO demonstrates high adaptability and robustness across different input data.

Table 10.
Results of the S index for each algorithm.
5.2.3. Convergence Index Analysis
Subsequently, the index is employed to assess the convergence performance of the Pareto optimal solution set obtained by the algorithm. It demonstrates how close the solution set acquired by the algorithm is to the true Pareto front. As a comprehensive index, it can also reflect the diversity of the solution set to a certain degree.
Table 11 shows the mean and variance of the index of each optimization algorithm after 20 independent runs. The better optimization results in the solution are shown in bold. Due to the introduction of the particle energy level as an index, MPSEVO has a better update strategy, and its convergence ability is remarkably stronger than that of other algorithms. It can search for the Pareto front that other algorithms cannot reach in the solution space. In terms of variance, MPSEVO is also significantly better than most algorithms, although it is slightly lower than NSGA-III; but the difference is very small, showing its excellent convergence and solution stability.

Table 11.
Results of for each algorithm.
Figure 5 illustrates the evolution iterations of the performance index for four algorithms in solving the workshop scheduling problem of a vehicle power battery production line, as the number of function evaluations increases. It is evident that the performance index for all four algorithms decreases gradually with more function evaluations, suggesting stable convergence performance. However, the evolution curve of NSGA-II exhibits significant fluctuations, indicating that this algorithm struggles with problems involving more than two objectives. In contrast, the other three algorithms show relatively stable evolution trends. Notably, the evolution curve for MPSEVO remains consistently lower than the others, demonstrating that MPSEVO yields better evolution results.
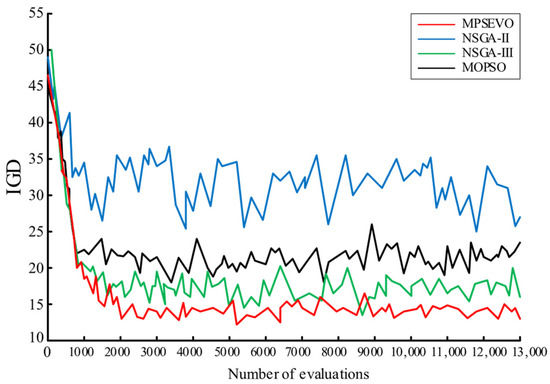
Figure 5.
Evolution curve of metrics for each algorithm.
5.2.4. Diversity Index Analysis
Next, the diversity index can evaluate the distribution and extensibility of the calculated solution set [39]. Since it is limited to two-dimensional objective optimization problems and cannot be applied to cases involving three optimization objectives, we adopt the index introduced by Zhou et al. [40]. The index is defined as follows:
where denotes the minimum Euclidean distance between the solution set and the boundary points of the true Pareto front on the -th objective, where represents the total number of objectives. A smaller value of indicates better diversity in the obtained Pareto solution set.
Table 12 presents the mean and variance of the index for each algorithm after 20 independent runs under different warehousing scales. The best optimization results are highlighted in bold. It can be observed that the mean and variance values for MPSEVO are significantly superior to those of the other algorithms. This can be attributed to the use of the crowding distance strategy in the external archive maintenance process, along with the incorporation of the energy performance index, which enhances particle stability. This approach interferes with the selection of the global optimal solution, resulting in a solution set that not only exhibits excellent distribution and extensibility but also provides enhanced stability in the algorithm performance.

Table 12.
Output value of indicators in case analysis.
5.2.5. Dominance Index Analysis
The Degree of Pareto Optimality () index is used to evaluate the extent to which the non-dominated solution set obtained by each algorithm is dominated by solutions from other algorithms. Its calculation formula is defined as follows:
where denotes the solution set obtained by algorithm , which is not dominated by any solutions from other algorithms, and represents the number of non-dominated solutions identified. A higher value indicates better solution quality.
Table 13 presents the mean and variance of the index for each algorithm after 20 independent runs under different warehousing scales. The best optimization results are highlighted in bold. It can be observed that the non-dominated rate of the solution set obtained by MPSEVO is significantly higher than that of the other algorithms, placing it in a dominant position. This further demonstrates that MPSEVO exhibits superior optimization performance, with the obtained solution set being closer to the true Pareto front.

Table 13.
Results of for each algorithm.
5.2.6. Comprehensive Index Analysis
The is used to measure the volume of the objective space that is enclosed by the non-dominated solution set produced by the algorithm, along with the reference points. This indicator is commonly employed to evaluate the performance of multi-objective optimization algorithms, as it helps to assess the quality of the generated solution set. The index considers both the distribution and diversity of the solutions. A higher value generally signifies superior overall performance of the algorithm.
Figure 6 shows the evolution trajectory of the performance index for the four algorithms when solving the workshop scheduling problem on a vehicle power battery production line. It can be observed that the performance index for all four algorithms increases gradually as the function evaluation increases, indicating their strong robustness. Among them, the evolution curve of the NSGA-II algorithm is the lowest and fluctuates significantly, suggesting that this algorithm performs poorly in handling high-dimensional multi-objective problems. In contrast, the other three algorithms tend to stabilize after reaching a certain point. The evolution curve of the MPSEVO algorithm is the highest, indicating that MPSEVO demonstrates better performance.
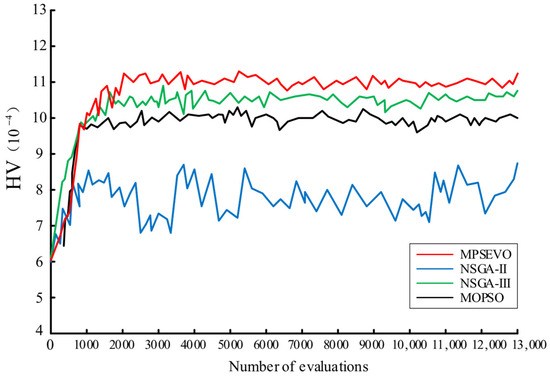
Figure 6.
Evolution curve of for each algorithm.
In summary, compared to other algorithms in the operation of the discrete vehicle power battery workshop scheduling problem, the MPSEVO algorithm shows good optimization effects. At the same time, the optimal solution set obtained by MPSEVO exhibits better diversity, distribution, and convergence than those produced by other algorithms. MPSEVO can search for potential solution spaces of other algorithms and is not easily dominated by the solutions of other algorithms.
The MPSEVO algorithm can optimize the iteration ability of the algorithm by adding the particle energy level as an index. During the iteration process, it continuously corrects and guides the convergence and diversity of the particle optimization trend, and on this basis, we design a local search strategy to further help the particle jump out of the local optimum. Finally, a reasonable external archive maintenance strategy is formulated to ensure that the MPSEVO algorithm shows excellent performance in solving the discrete vehicle power battery workshop scheduling problem.
5.3. Algorithm Improvement Effectiveness Analysis
In this paper, the improvement strategy of the algorithm can be roughly divided into three points: the first one is to integrate EVO into PSO, which enriches the update strategy of the algorithm, classifies particles according to their stability level, and adopts different update strategies for different particles, which helps to improve the diversity and convergence of the solution set. Second, based on the population clustering degree and the need to balance convergence and diversity, an adaptive particle velocity update mode is designed, in which the Levy flight stage and the parameter can ensure that the algorithm has more possibilities to jump out of the local optimum in the late iteration. The third is to carry out an additional local search strategy for the archiving stage of external archives, which is an additional global search without affecting the evolution of the population, which is helpful to improve the diversity of the solution set.
Defining MPSEVO-no-Levy means that the algorithm is not affected by parameter and its corresponding Levy flight phase during the particle velocity update phase, MPSEVO-no-ls, means that the algorithm does not use a local search strategy, and MOPSO-Levy-ls indicates that the algorithm does not hybridize EVO. In the context of the actual power battery manufacturing workshop, MPSEVO, after introducing the above improved strategy, is compared with the algorithm before the improvement.
Table 14 shows the comparison of the mean values of each of the indicators obtained after 50 repeated solutions, and the algorithm of unhybridized EVO is inferior to MPSEVO in convergence and diversity. The convergence of the algorithm without the Levy flight speed update strategy is significantly reduced, the diversity of the algorithm without the local search strategy is significantly reduced, and the evaluation indexes of the improved algorithm are optimized to varying degrees. It can be seen that hybrid EVO can improve the quality of the solution to a certain extent, the global search strategy of Levy flight can avoid the population converging in a certain part of the solution space, and the local search strategy based on genetics is of great significance in improving the diversity of the solution.

Table 14.
Results of algorithm improvement effectiveness analysis.
Although MSPEVO achieves better solution results compared to common multi-objective algorithms, it has a higher preparation cost. The improved algorithm involves many parameters, requiring the use of methods such as orthogonal experiments to determine parameters before solving optimization problems in different scenarios. Furthermore, the structure of MPSEVO is also relatively complex, resulting in longer iteration times, which means its solving speed is not as excellent as that of common multi-objective algorithms.
5.4. Scheduling Scheme
There are a few studies on the scheduling scenario of a power battery manufacturing workshop. This paper aims to solve its complex process and multi-objective optimization requirements to avoid the problem of general models ignoring the characteristics of the industry. It also provides theoretical support and decision-making solutions for power battery workshop scheduling, and helps lean management in intelligent manufacturing.
Since workshop production values comprehensive performance, weights of 40%, 30%, and 30% are assigned to the total makespan, machine load, and processing quality, respectively. The optimal compromise solution is selected from the Pareto solution set. Table 15 presents the optimal compromise solutions obtained after running the four methods. The optimal function values in the table are indicated in bold, and the figure gives the Gantt chart of the scheduling scheme of each method. In Table 15, it can be seen that the optimal compromise solution obtained by the MPSEVO method is better than the other methods, and only the processing quality is slightly lower; the other objective function values are better than the other methods. Although the processing quality index of MPSEVO is not optimal, it is only 0.01 less than the optimal value. At present, the manufacturing workshop adopts automated production, and the failure rate of each operation is maintained at a low level, resulting in little difference in the processing quality indicators solved by each algorithm.

Table 15.
Optimal solution.
Figure 7 presents the scheduling Gantt chart generated by each algorithm. In the chart, different colors represent the various types of batteries being processed, and the numbers indicate the workpiece IDs. It is evident that the scheduling scheme obtained using the MPSEVO method outperforms those generated by NSGA-III and NSGA-II. The MPSEVO method effectively reduces the makespan, improves the quality of vehicle power battery processing, and lowers the machine load, offering a more efficient production guide. The results shown in Figure 7 demonstrate the feasibility, effectiveness, and advantages of the MPSEVO method.
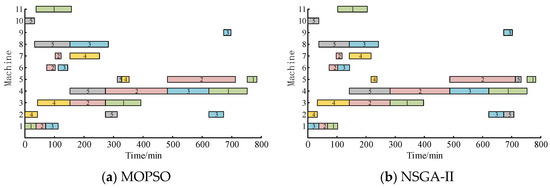
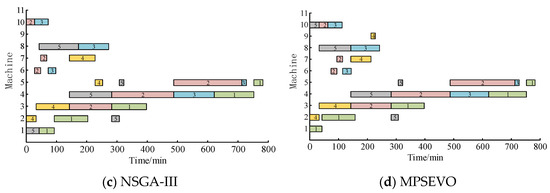
Figure 7.
Gantt chart of different methods.
6. Conclusions
This study addresses the practical problem of scheduling decision optimization in vehicle power battery manufacturing workshops, analyzes the basic workshop layout and operation flow, and studies the processing sequence and machine allocation for different types of batteries. Three objectives, including makespan, machine load, and processing quality, are proposed to evaluate the workshop scheduling scheme. Accordingly, MPSEVO is designed to solve the scheduling problem, which provides the particle stability on the basis of MOPSO, and adopts different updating strategies for particles with different stability to improve the convergence and diversity of the solution. Furthermore, the local search strategy is designed to further prevent the algorithm from getting trapped in a local optimum. In the ten benchmark instances and one real case study of this paper, the optimization performance of MPSEVO (convergence, diversity, and practical scheduling metrics) is better than comparison algorithms, providing a feasible method for scheduling optimization in similar scenarios. Ablation experiments were also carried out to demonstrate the effectiveness of the improvement strategies in MPSEVO. MPSEVO is not limited to workshop scheduling issues. It is applicable to various optimization scenarios that involve multi-objective conflicts, high-dimensional decision spaces, and the need to balance convergence and diversity. Essentially, it achieves efficient exploration of complex solution spaces by integrating the global search capability of swarm intelligence algorithms with the stability regulation concepts of Energy Valley Optimization. This framework can be transferred to other fields.
Based on the real manufacturing environment of vehicle power batteries, this study discusses the theoretical scheduling results of a manufacturing workshop, and the research conclusions have practical application value. However, there are still several unaddressed limitations, such as the lack of analysis and demonstration of feasibility in the actual workshop scheduling process. In the future, we can consider large-scale production scheduling problems and integrate this research into the Manufacturing Execution System (MES) to increase its executability. In addition, the production process is a dynamic process, and some emergencies are inevitable. These situations need to be dynamically scheduled to ensure production efficiency. Finally, the Automated Guided Vehicle (AGV) scheduling problem can also be introduced into workshop scheduling in future studies.
Author Contributions
Conceptualization, J.T.; Methodology, J.T., T.D. and T.Y.; Software, T.D. and F.W.; Validation, F.W.; Formal analysis, F.W.; Investigation, L.H.; Data curation, L.H. and T.Y.; Writing—original draft, T.D.; Writing—review & editing, J.T.; Visualization, T.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Key R&D Program of Hunan Province (No. 2023GK2014), Hunan Provincial Natural Science Foundation of China (No. 2023JJ40731).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, J. The Official Release of the Technology Roadmap for Energy-saving and New-energy Vehicles. Auto Rev. 2016, 11, 82–85. (In Chinese) [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H.; Tao, S. Retired electric vehicle (EV) batteries: Integrated waste management and research needs. Environ. Sci. Technol. 2017, 51, 10927–10929. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Cai, T.; Xu, W. Exploring the technology changes of new energy vehicles in China: Evolution and trends. Comput. Ind. Eng. 2024, 191, 110178. [Google Scholar] [CrossRef]
- Gao, Y.; Jin, T. Analysis of the International Competitiveness of China’s New Energy Vehicles under the New Situation. Int. Econ. Coop. 2021, 4, 65–76. Available online: https://kns.cnki.net/kcms2/article/abstract?v=JEPDQvKdoqJ5dOwDWQK708RM-uU47va2fba_ONle5dZr25-7W1FmHaUTmFNQBRUTkQMbmDZMk7zIY0_PcMoyZI3F-pgVP-YlC1OH7pP1O6kGdiJUI2gx9wzjc9PWJcdgfs1NDsFDkCTen3EfX2lhAipuPtLChDG5c8ojT6G_OKA=&uniplatform=NZKPT&language=CHS (accessed on 29 July 2021). (In Chinese).
- Ma, J.; Gao, W.; Tong, W. A deep reinforcement learning assisted adaptive genetic algorithm for flexible job shop scheduling. Eng. Appl. Artif. Intell. 2025, 149, 110447. [Google Scholar] [CrossRef]
- Alcaraz, J.; Anton-Sanchez, L.; Saldanha-da-Gama, F. Bi-objective resource-constrained project scheduling problem with time-dependent resource costs. J. Manuf. Syst. 2022, 63, 506–523. [Google Scholar] [CrossRef]
- Gui, L.; Li, X.; Zhang, Q.; Gao, L. Domain knowledge used in meta-heuristic algorithms for the job-shop scheduling problem: Review and analysis. Tsinghua Sci. Technol. 2024, 29, 1368–1389. [Google Scholar] [CrossRef]
- Schütte, M.; Degen, F.; Walter, H. Reducing energy consumption and greenhouse gas emissions of industrial drying processes in lithium-ion battery cell production: A qualitative technology benchmark. Batteries 2024, 10, 64. [Google Scholar] [CrossRef]
- Johansson, B.; Despeisse, M.; Bokrantz, J.; Braun, G.; Cao, H.; Chari, A.; Fang, Q.; Chávez, C.A.G.; Skoogh, A.; Söderlund, H.; et al. Challenges and opportunities to advance manufacturing research for sustainable battery life cycles. Front. Manuf. Technol. 2024, 4, 1360076. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Z.; Wu, C.; Hua, L.; Zhu, D. Towards region-based robotic machining system from perspective of intelligent manufacturing: A technology framework with case study. J. Manuf. Syst. 2023, 70, 451–463. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, G.; Bao, Q.; Yu, L. Flexible job-shop green scheduling considering transportation time and machine preventive maintenance. Comput. Integr. Manuf. Syst. 2024, 30, 3111–3124. [Google Scholar] [CrossRef]
- Wei, G.; Ye, C. Multi-objective dual resource constrained flexible job shop energy-efficient scheduling with transfer time. Comput. Integr. Manuf. Syst. 2025, 31, 67–88. [Google Scholar] [CrossRef]
- Aqil, S.; Allali, K. On a bi-criteria flow shop scheduling problem under constraints of blocking and sequence dependent setup time. Ann. Oper. Res. 2021, 296, 615–637. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, D.; Song, H.; Cheng, Z.; Lang, X.; Yuan, W.; Wang, J. Hybrid genetic algorithm with variable neighborhood search for flexible job shop scheduling problem in a machining system. Expert Syst. Appl. 2023, 215, 119359. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y. A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 2018, 172, 3249–3264. [Google Scholar] [CrossRef]
- Zhang, B.; Pan, Q.K.; Meng, L.L.; Lu, C.; Mou, J.H.; Li, J.Q. An automatic multi-objective evolutionary algorithm for the hybrid flowshop scheduling problem with consistent sublots. Knowl.-Based Syst. 2022, 238, 107819. [Google Scholar] [CrossRef]
- Hou, Y.; Liao, X.; Chen, G.; Chen, Y. Co-Evolutionary NSGA-III with deep reinforcement learning for multi-objective distributed flexible job shop scheduling. Comput. Ind. Eng. 2025, 203, 110990. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, M.; Yang, M.; Wang, D. Hybrid quantum particle swarm optimization and variable neighborhood search for flexible job-shop scheduling problem. J. Manuf. Syst. 2024, 73, 334–348. [Google Scholar] [CrossRef]
- Ham, A.; Park, M.J.; Kim, K.M. Energy-Aware Flexible Job Shop Scheduling Using Mixed Integer Programming and Constraint Programming. Math. Probl. Eng. 2021, 2021, 8035806. [Google Scholar] [CrossRef]
- Soto, C.; Dorronsoro, B.; Fraire, H.; Cruz-Reyes, L.; Gomez-Santillan, C.; Rangel, N. Solving the multi-objective flexible job shop scheduling problem with a novel parallel branch and bound algorithm. Swarm Evol. Comput. 2020, 53, 100632. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, J.; Lim, A.; Hu, Q. A tree search heuristic for the resource constrained project scheduling problem with transfer times. Eur. J. Oper. Res. 2023, 304, 939–951. [Google Scholar] [CrossRef]
- Zolfaghari, S.; Mousavi, S.M. A novel mathematical programming model for multi-mode project portfolio selection and scheduling with flexible resources and due dates under interval-valued fuzzy random uncertainty. Expert Syst. Appl. 2021, 182, 115207. [Google Scholar] [CrossRef]
- Kong, X.; Yao, Y.; Yang, W.; Yang, Z.; Su, J. Solving the flexible job shop scheduling problem using a discrete improved grey wolf optimization algorithm. Machines 2022, 10, 1100. [Google Scholar] [CrossRef]
- Wang, G.; Gao, D.; Pedrycz, W. Solving multi-objective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans. Ind. Inform. 2022, 18, 8519–8528. [Google Scholar] [CrossRef]
- Shao, Q.; Xu, P.; Ding, R.; Deng, B.; Yang, Z.; Wang, P. A multi-target flexible workshop scheduling algorithm for shipbuilding. In Eighth International Conference on Electromechanical Control Technology and Transportation (ICECTT 2023); SPIE: Bellingham, Washington, USA, 2023; Volume 12790, pp. 1030–1037. [Google Scholar] [CrossRef]
- Xuan, D.U.; Tian-yi, L.I.A.O.; Bao-wan, L.I. Research on Piano Batch Scheduling Method Based on Constraint Model. J. Phys. Conf. Ser. 2021, 1750, 012015. [Google Scholar] [CrossRef]
- Zeng, Z.; Hong, M.; Man, Y.; Li, J.; Zhang, Y.; Liu, H. Multi-object optimization of flexible flow shop scheduling with batch process—Consideration total electricity consumption and material wastage. J. Clean. Prod. 2018, 183, 925–939. [Google Scholar] [CrossRef]
- Jiang, X.; Tian, Z.; Liu, W.; Suo, Y.; Chen, K.; Xu, X.; Li, Z. Energy-efficient scheduling of flexible job shops with complex processes: A case study for the aerospace industry complex components in China. J. Ind. Inf. Integr. 2022, 27, 100293. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Trentesaux, D. An energy-efficient scheduling and rescheduling method for production and logistics systems. Int. J. Prod. Res. 2020, 58, 3263–3283. [Google Scholar] [CrossRef]
- Wu, J.; Liu, Y. A modified multi-agent proximal policy optimization algorithm for multi-objective dynamic partial-re-entrant hybrid flow shop scheduling problem. Eng. Appl. Artif. Intell. 2025, 140, 109688. [Google Scholar] [CrossRef]
- Hu, Y.; Pan, L.; Pan, X. Dynamic scheduling of workshop resource in cloud manufacturing environment. Eng. Appl. Artif. Intell. 2024, 138, 109405. [Google Scholar] [CrossRef]
- Abualigah, L.; Sheikhan, A.; Ikotun, A.M.; Zitar, R.A.; Alsoud, A.R.; Al-Shourbaji, I.; Hussien, A.G.; Jia, H. Particle swarm optimization algorithm: Review and applications. In Metaheuristic Optimization Algorithms; Morgan Kaufmann: Burlington, MA, USA, 2024; pp. 1–14. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, H.J. Single machine scheduling with variable maintenance in the battery manufacturing. Int. J. Prod. Res. 2025, 1–21. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, K.; Lu, S.; Lu, C.; Li, X. Modeling and optimization of energy consumption, surface quality and relative density in GH3625 superalloy by laser powder bed melting via RSM MOPSO and CRITIC-TOPSIS. Opt. Laser Technol. 2025, 184, 112411. [Google Scholar] [CrossRef]
- Brucker, P.; Schlie, R. Job-shop scheduling with multipurpose machines. Computing 1990, 45, 369–375. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI, Proceedings of the 6th International Conference, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar] [CrossRef]
- Zhou, A.; Jin, Y.; Zhang, Q.; Sendhoff, B.; Tsang, E. Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion. In 2006 IEEE International Conference on Evolutionary Computation, Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; IEEE: Singapore, 2006; pp. 892–899. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).