Zero-Shot Learning for S&P 500 Forecasting via Constituent-Level Dynamics: Latent Structure Modeling Without Index Supervision

Abstract

Market indices, such as the S&P 500, serve as compressed representations of complex constituent-level dynamics. This study proposes a zero-shot forecasting framework capable of predicting index-level trajectories without direct supervision from index data. By leveraging a Variational AutoEncoder (VAE), the model learns a latent mapping from constituent-level price movements and macroeconomic factors to index behavior, effectively bypassing the need for aggregated index labels during training. Using hourly OHLC data of S&P 500 constituents, combined with the U.S. 10-Year Treasury Yield and the CBOE Volatility Index, the model is trained solely on disaggregated inputs. Experimental results demonstrate that the VAE achieves superior accuracy in index-level forecasting compared to models trained directly on index targets, highlighting its effectiveness in capturing the implicit generative structure of index formation. These findings suggest that constituent-driven latent representations can provide a scalable and generalizable approach to modeling aggregate market indicators, offering a robust alternative to traditional direct supervision paradigms.

1. Introduction

The financial market is in a constant state of flux due to the dynamics of various assets and policy decisions, as well as the influence of unpredictable external factors [1]. Consequently, investors are continually exposed to uncertainty in their decision-making processes. In response, market participants regard indices such as the S&P 500 as benchmarks for assessing overall market trends, upon which they formulate strategies for portfolio construction, risk hedging, and capital allocation [2,3]. From this perspective, financial market indices are not merely passive references of market performance but serve as key indicators that guide market sentiment and shape overall investment strategies. For this reason, forecasting major indices has long been a core challenge in financial engineering and quantitative finance.

For decades, Autoregressive Conditional Heteroskedasticity (ARCH) [4] models and Generalized ARCH models [5] have played a central role in modeling the conditional variance of return time series and in forecasting financial market volatility. Subsequently, functional models [6,7] have been introduced to model conditional variance structures in function spaces, aiming to capture fine-grained market microstructures and temporal patterns. However, these classical time-series models simplify market-intrinsic dynamics through linear or quasi-linear assumptions, which limits their ability in capturing nonlinear interactions and the complex effects of exogenous variables. In contrast, modern deep learning techniques offer more flexibility for modeling nonlinear patterns. Their strength in automatically extracting predictive features from large-scale financial data has led to a methodological shift, with deep learning emerging as a dominant paradigm in the field of financial forecasting.

One common approach is to integrate Long Short-term Memory (LSTM) [8] networks with other methods to exploit the complementary strengths of individual models. The authors of [9] proposed a hybrid wavelet-AGA-LSTM model that integrates wavelet transforms for denoising with an LSTM optimized by an Adaptive Genetic Algorithm. Similarly, ref. [10] highlights the effectiveness of ensemble learning and time-series decomposition. By breaking index data into simpler components and automatically tuning hyperparameters, their MEMD-AO-LSTM model—which combines Multivariate Empirical Mode Decomposition and the Aquila Optimizer—outperforms conventional single models. Other studies likewise combine LSTM with domain-specific enhancements. For instance, ref. [11] introduced an ETICA-LSTM approach—merging an External Trend and Internal Components Analysis decomposition with an LSTM—to improve index forecasts. Beyond numerical data, LSTM models have also been enriched with textual sentiment features. The authors of ref. [12] combined a FinBERT-based sentiment analyzer with an LSTM, leveraging sentiment scores generated by FinBERT from daily news as additional inputs.

Conversely, the success of attention mechanisms [13] in sequence modeling has led many researchers to adopt Transformer-based architectures for stock index forecasting. The authors of [14] addressed the challenges of multi-step stock forecasting with Galformer, which introduces a generative-style decoder to predict entire output sequences in a single forward pass, eliminating recursive decoding. To better capture the dynamics of volatile financial time series, they proposed a hybrid loss function that combines the mean squared error with trend direction accuracy. The authors of ref. [15] proposed a Deep Convolutional Transformer that combines Convolutional Neural Networks (CNNs) and Transformer layers using multi-head attention, incorporating inception-style convolutional token embedding and separable fully connected layers to capture both local and global dependencies. Another innovative direction is hybridizing with Large Language models (LLMs). The authors of ref. [16] proposed MambaLLM, a dual-branch architecture that integrates micro-level stock data modeled through state-space techniques with macroeconomic signals captured via DeepSeek R1, which generates textual summaries encoded by FinBERT into sentiment-rich embeddings.

Another stream of recent research focuses on leveraging generative models—such as Generative Adversarial Networks (GANs) [17] and diffusion models [18]—to enhance stock index forecasting. These approaches often augment training data through synthetic sample generation or improve prediction stability by modeling uncertainty in volatile market conditions. The authors of ref. [19] proposed a GAN-assisted model that integrates the attention mechanism. The GAN generates synthetic stock price sequences conditioned on market sentiment and volatility, thereby expanding the training set with plausible scenarios. In contrast, ref. [20] Introduced a GAN-enhanced nonlinear fusion model featuring a hybrid generator: an attention-based CNN for technical patterns, an LSTM for temporal dynamics, and an Autoregressive Integrated Moving Average Model component for linear trends. The discriminator, implemented as a CNN, evaluates the realism of the generated sequence. The authors of ref. [21] proposed a framework that models asset price dynamics by generating OHLC chart images from simulated data based on the Geometric Brownian Motion model, and training diffusion models on these images. This approach enables the generation of synthetic price paths and demonstrates effectiveness in option pricing through Monte Carlo simulation.

Collectively, these studies reflect key trends in financial market modeling. By addressing challenges such as nonlinearity, multi-step dependencies, and multi-modal inputs, these approaches substantially outperform traditional time-series models in both accuracy and reliability. However, stock indices are fundamentally derived from a mapping function over their constituent assets, each of which is influenced in different ways by broader macroeconomic conditions. Despite this, most existing studies on index prediction rely primarily on the index’s own time series as training input. While some incorporate macroeconomic indicators for additional context, the core data typically remain centered on the index itself. Although recent advances in AI have improved generalization, such models remain prone to overfitting to the training data on which they were built [22,23].

Yet, despite these advances in other domains, such generalizable approaches have seen limited application in financial modeling. This highlights the need to explore zero-shot learning for index prediction—a direction that remains largely underexplored. Zero-shot learning is a paradigm in which a model leverages generalized representations to make predictions on tasks or inputs that were not explicitly included during training [24]. This capability, known as zero-shot inference, enables models to perform novel tasks without labeled examples. High zero-shot performance indicates that the model has captured truly generalizable patterns rather than memorizing task-specific data. Recent advances in natural language processing and computer vision, exemplified by GPT models [25] and CLIP [26], demonstrate strong zero-shot inference capabilities.

In response, our study proposes a deep learning framework for structural inference of stock indices, capable of forecasting the S&P 500 without direct exposure to index-level data during training. The model is trained solely on time-series data from the S&P 500’s 503 constituent stocks, along with key macroeconomic indicators such as the U.S. 10-Year Treasury Yield (10YY) and the CBOE Volatility Index (VIX). Crucially, the index itself is never used as a training target. Instead, the model is evaluated on its ability to predict the index’s full price trajectory one day ahead—specifically, the hourly open, high, low, and close (OHLC) values for the next trading day. This design implements a zero-shot forecasting scenario that allows us to assess whether the model has implicitly learned the underlying structural relationships between constituent assets and index-level dynamics.

We select the S&P 500 as the focal benchmark for several reasons. First, it provides a highly diverse sectoral composition and a capitalization-weighted structure, making it representative of broad U.S. equity market dynamics. Second, the index’s global relevance, liquidity, and rich data availability make it an ideal candidate for evaluating whether constituent-level dynamics can effectively reconstruct aggregate index behavior. Finally, the S&P 500 has been extensively studied in both academic and industry contexts, which reinforces its suitability as a benchmark for testing novel forecasting methodologies. Our empirical analysis relies on disaggregated OHLC data from all S&P 500 constituents, ensuring that the extracted signals are both representative and robust for evaluating the proposed zero-shot framework under realistic market conditions. Accordingly, the S&P 500 provides a rigorous testbed for assessing whether constituent-level dynamics can effectively reconstruct aggregate market behavior and for evaluating novel forecasting methodologies.

This study aims to investigate whether an index’s future behavior can be effectively inferred from its components and macroeconomic context alone, without relying on direct supervision from the index itself. Accordingly, we present a novel zero-shot forecasting framework that diverges from conventional index modeling paradigms. Rather than merely enhancing predictive accuracy, this approach emphasizes structural abstraction and generalization—enabling the model to internalize the formation principles of stock indices. The proposed framework offers practical value in scenarios where index-level data are delayed, restricted, or inaccessible. In such cases, it enables the approximation of index dynamics or the construction of surrogate benchmarks using only asset-level time-series data.

In summary, our contributions are threefold: (1) a novel zero-shot index forecasting framework without index-level supervision training, (2) empirical validation of constituent-driven forecasting capability, and (3) practical applicability in real-world settings with limited index access. This structural abstraction not only improves generalization but also opens new avenues for interpreting index formation through learned representations. The remainder of this paper is organized as follows: Section 2 details the dataset, research design, methodologies, and evaluation metrics used for performance comparison. Section 3 presents the experimental results. Section 4 discusses key findings and their implications, and Section 5 concludes this paper with final remarks.

2. Materials and Methods

2.1. Dataset

We constructed a time-series dataset from hourly OHLC data of the 503 constituent stocks of the S&P 500 and two macroeconomic indicators: the 10YY and VIX. The dataset spans 1 April 2023 to 20 June 2025 (551 trading days), with seven hourly trading intervals per day. Data from different sources were aligned to a unified UTC-based market calendar, and only common timestamps were retained to ensure temporal consistency.

The forecasting task is framed as a sequence-to-sequence problem: the model receives five consecutive trading days (35 hourly steps) as input and predicts the full-day OHLC trajectory for the next trading day (7 hourly steps). Each sample is structured as a three-channel tensor—target stock, 10YY, and VIX—of shape (3, 4, 35), and the label tensor has shape (1, 4, 7). We generated these samples using a five-day sliding window with a one-day shift, and partitioned the data chronologically into training, validation, and test sets in an 8:1:1 ratio, inserting a five-day buffer between splits to prevent temporal leakage. The final dataset comprises 433 training days and 54 days each for validation and testing. All features were min–max normalized using statistics from the training set only, with the same parameters applied to validation and test sets. To preserve the zero-shot setting, S&P 500 index data were entirely excluded from training and used only for evaluation.

Table 1. Dataset overview, including time span, input structure, and data splits.

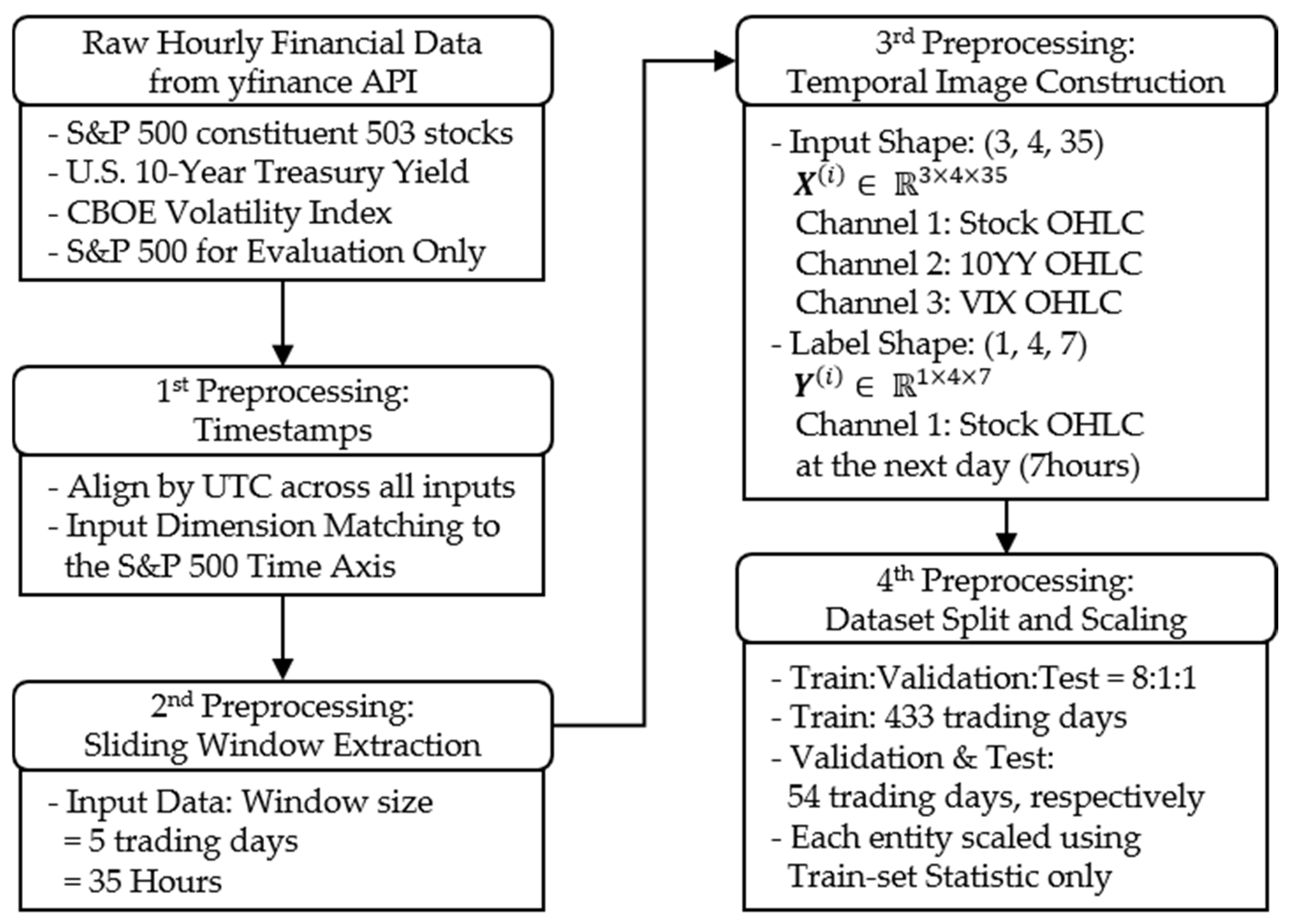
Category	Description
Time Span	1 April 2023–20 June 2025
Trading Days	551
Input Window	5 Days (35 hourly steps)
Tensor Shape	Input: (3, 4, 35); Label: (1, 4, 7)
Features	OHLC for Stock, 10YY, VIX and S&P 500 1
Stock Samples (Train/Val/Test)	208,248/27,162/27,131
Macro/Index Samples (Train/Val/Test)	433/54/54
Scaling Method	Min–max per entity, using training set statistics

¹ S&P 500 index data were collected for evaluation purposes only and excluded from training.

summarizes the dataset composition and tensor dimensions used throughout this study.

This design allows us to rigorously evaluate the model’s ability to infer the structural dynamics of the market index based solely on constituent-level and macroeconomic information, without any exposure to index-level data during training. Figure 1 illustrates the preprocessing workflow in detail.

To develop a model capable of zero-shot index forecasting, we employ input data that jointly capture micro-level asset behavior and macro-level market dynamics. In addition to the OHLC time series of each constituent stock in the S&P 500, we incorporate two market-level indicators: the 10YY and the VIX.

The 10YY serves as a benchmark risk-free rate and reflects market expectations regarding monetary policy, economic growth, and inflation [27,28]. It plays a critical role in equity valuation through the discounting of expected future cash flows, a factor particularly influential for growth-oriented sectors that are heavily represented in the S&P 500 [29]. The VIX, by contrast, quantifies expected short-term volatility derived from S&P 500 options and serves as a proxy for market uncertainty and risk sentiment [30]. Elevated VIX levels are often associated with heightened market stress, sharp drawdowns, and increased volatility in equity indices [31].

Together, these macroeconomic indicators provide complementary information to the asset-level OHLC data. While individual stock price series primarily capture localized and recent trends, the 10YY and the VIX can capture macroeconomic expectations and forward-looking risk sentiment that are not directly observable in stock-level price movements. By integrating these dimensions, the model is able to form a richer representation of the structural forces underlying index formation—even without direct supervision from the index itself during training.

In addition to the asset- and macro-level inputs, we also collect the S&P 500 index OHLC data exclusively for evaluation. This index-level data are withheld during training and used only at inference to assess the model’s ability to generalize to an aggregate-level target in a strict zero-shot setting. By treating the index as an unseen synthetic asset, we can directly test whether the model has internalized the latent structural relationships governing index formation.

Table 2. Summary statistics of S&P 500 index data across evaluation spans. The statistics are computed over the same chronological periods as those used for training (span-1), validation (span-2), and testing (span-3) of the constituent-level model. Although the index-level data were never seen during training, these figures serve as reference points to compare the distributional characteristics of the model’s zero-shot predictions against the true index values. All values are normalized via min–max scaling using statistics derived from the training set of each respective entity.

Span	Type	Count	Mean	Std	Min	25%	50%	75%	Max
span-1	Input	433	0.4486	0.2931	0.0000	0.1815	0.4579	0.6980	1.0000
	Label	433	0.4561	0.2933	0.0007	0.1876	0.4690	0.7015	1.0000
span-2	Input	54	0.9152	0.0839	0.7139	0.8580	0.9387	0.9835	1.0279
	Label	54	0.9096	0.0865	0.7139	0.8384	0.9336	0.9835	1.0279
span-3	Input	54	0.7919	0.1445	0.3862	0.6808	0.7960	0.9176	0.9814
	Label	54	0.8022	0.1488	0.3862	0.6808	0.8627	0.9303	0.9814

summarizes the normalized mean, standard deviation, and quantiles of the S&P 500 index across the training, validation, and test span, separately for input and label values.

2.2. Study Design

We aim to investigate whether the structural dynamics of a market index can be inferred and forecasted without any direct supervision from index-level data. To this end, we define a zero-shot forecasting task, in which the model is trained exclusively on time-series data from the 503 constituent stocks of the S&P 500 and two macroeconomic indicators: 10YY and the VIX. The S&P 500 index itself is withheld during training and used only during inference to evaluate generalization performance on an unseen aggregate-level target. At inference, the S&P 500 index is fed into the model using the exact same input structure as in training, with a channel-wise concatenation of the corresponding 10YY and VIX series on a shared time axis to form a three-channel input tensor. The overall study design, including data processing, training configuration, and evaluation, is illustrated in Figure 2.

The forecasting problem is framed as a sequence-to-sequence task. Each input sample consists of five consecutive trading days (35 hourly steps) of OHLC data, and the model predicts the full-day OHLC trajectory of the next trading day (7 hourly steps). Inputs are structured as three-channel tensors—one channel each for the target stock, the 10YY, and the VIX—yielding a shape of (3, 4, 35), while outputs have a shape of (1, 4, 7). Samples are constructed using a five-day sliding window and split chronologically into training, validation, and test sets at an 8:1:1 ratio, with five-day buffer zones to avoid temporal leakage. Training samples are randomly shuffled at each epoch to reduce order-related bias.

We evaluate four distinct model architectures representing generative, probabilistic, and transformer-based paradigms:

(1)

a Variational AutoEncoder for supervised learning;

(2)

a Conditional Denoising Diffusion Probabilistic Model (cDDPM);

(3)

a spatial Transformer with an encoder–decoder (Transformer-ED);

(4)

a spatial Transformer with an encoder only (Transformer-E).

2.3. Methodologies

2.3.1. OHLC Order-Consistency Loss

Among OHLC, the daily high price must always be greater than or equal to all other price levels, and the daily low price must always be less than or equal to the others. To enforce this structural property during training, we introduce an order-consistency loss that is applied uniformly across all models.

Let the predicted output tensor be ${\widehat{Y}}^{\left(i\right)}\in {\mathbb{R}}^{B\times 1\times C\times T}$, where B is the batch size, C = 4 for {O, H, L, C} channels corresponding to OHLC, and T = 7 for the number of hourly timesteps. For each timestep t, the loss enforces the following constraints: the predicted high value should be larger than the open, low, and close values by at least a margin m: ${\widehat{Y}}_{H,t}\ge {\widehat{Y}}_{x,t}+m$, $x\in \{O,L,C\}$; the predicted low value should be smaller than the open, high, and close values by at least a margin m: ${\widehat{Y}}_{L,t}\le {\widehat{Y}}_{x,t}+m$, $x\in \{O,H,C\}$.

$${\mathcal{L}}_m={\displaystyle \frac{1}{BT}}\sum _{i=1}^B\sum _{t=1}^T\left[\sum _{x\in \{O,L,C\}}{({\widehat{Y}}_{x,t}-{\widehat{Y}}_{H,t}+m)}_{+}+\sum _{x\in \{O,H,C\}}{({\widehat{Y}}_{L,t}-{\widehat{Y}}_{x,t}+m)}_{+}\right],$$

(1)

where ${\left(z\right)}_{+}$ = max(z, 0), reflecting the hinge loss formulation [32].

The final loss function is defined as follows: $\mathcal{L}={\mathcal{L}}_{pred}+{\mathcal{L}}_m$, where ${\mathcal{L}}_{pred}$ denotes the primary prediction loss of model and ${\mathcal{L}}_m$ controls the contribution of the OHLC order-consistency. This loss regularizes predictions to maintain realistic OHLC relationships, reducing structurally implausible forecasts.

2.3.2. Variational AutoEncoder for Supervised Learning

We employed a supervised VAE [33] architecture to model the distribution of the input data while incorporating supervised learning signals into the forecasting process. The proposed model is a variant of the standard VAE, designed to predict structured outputs with explicit attention to specific sub-regions in the output space. The encoder network is composed of a series of five convolutional blocks, where each block consists of a convolution layer, batch normalization, and a LeakyReLU [34] activation function. The encoder output is flattened and projected into the latent space through two parallel linear layers to estimate the mean and log-variance vectors of the latent Gaussian distribution. The decoder network first projects the latent vector back into a high-dimensional feature space using a linear layer. It then employs a series of transposed convolutional blocks with asymmetric strides and output paddings to sequentially upsample the spatial dimensions.

The model optimizes a composite loss function composed of three components: (1) reconstruction loss: the reconstruction loss is computed as the mean squared error (MSE) between the predicted and target “temporal images”, which are a shape of (1, 4, 7) label tensors. (2) Kullback–Leibler divergence (KLD) loss [35]: to regularize the latent space, a standard KLD loss is computed between the posterior distribution q(z|x) and the prior p(z) ~ $\mathcal{N}$(0, I). The KLD term is scaled by a hyperparameter $\mathsf{\beta }$ = 0.00025 to balance the trade-off between reconstruction fidelity and latent space regularization. (3) OHLC order-consistency loss.

2.3.3. Conditional Denoise Diffusion Probabilistic Model

The model architecture extends the classical Denoising Diffusion Probabilistic Model (DDPM) [18] by integrating supervised conditions directly into the denoising process, enabling structured generation conditioned on auxiliary inputs. The backbone of our diffusion model is a UNet-based denoising network [36], modified to accept conditional inputs via self-conditioning. The model receives a primary input data X_t and, when self-conditioning is enabled, concatenates it with an auxiliary condition label along the channel dimension. Each block in the encoder and decoder paths of the UNet is composed of ResNet [37] blocks with time-dependent feature modulation.

Given an input sample X_t,0, the forward diffusion process gradually corrupts the data with Gaussian noise through a series of timesteps $ts\in$ [0, 1000]. The reverse process is parameterized by the UNet, which predicts the noise residual at each timestep. We adopt a Sigmoid Beta Schedule to define the variance in the noise added at each diffusion step. The primary objective of the model is to minimize the MSE between the predicted and true noise, scaled by a time-dependent weighting factor. Additionally, we leverage an OHLC order-consistency loss to enforce relational structures within specific regions of the predicted outputs. The trained model enables generation via two methods: a stochastic iterative denoising process using the learned posterior distributions and a deterministic variant allowing faster sampling at the cost of slight diversity reduction. For conditional prediction, during inference, the conditioning input is fed directly into the network at each timestep via the self-conditioning mechanism, ensuring the generated samples adhere to the provided structure.

2.3.4. Spatial Transformer: Encoder–Decoder Structure and Encoder-Only Configuration

We implement a spatial Transformer architecture to model structured spatial dependencies in multi-dimensional spatial data. The model processes inputs of shape (C, H, W), where C is the number of channels, and H $\times$ W defines the spatial dimension. Both variants of the model share the following architectural components. (1) Patch embedding: Each spatial position is linearly projected into a high-dimensional embedding space of dimension D_model using a shared linear transformation. This produces a tensor of shape (N, H, W, D). (2) Row-group positional encoding: To inject spatial priors, each row is assigned a unique embedding, and columns are grouped with shared group embeddings—in segments of five days. This structured positional encoding allows the model to differentiate between row-wise semantics and localized column-group patterns. (3) Transformer encoder layers: the positionally encoded patch embeddings are reshaped into a sequence of length T = H $\times$ W and passed through a stack of multi-head self-attention layers [13] and feedforward networks. (4) Final projection layer: the outputs from the encoder (or decoder) are projected back to the output channels through a linear layer, followed by reshaping into the spatial shape of (1, H, W).

In the Transformer-ED, we incorporate an additional Transformer decoder block on top of the encoder output. This design exploits a set of learnable query embeddings that interact with the encoder’s memory through cross-attention mechanisms. Specifically, a learnable query tensor of shape (1, T, D) is initialized and expanded across the batch, and the decoder layers attend over the encoder memory, enabling explicit query-driven reconstruction of spatial output. The decoder allows the model to iteratively refine the output representation, guided by latent query embeddings, effectively introducing a mechanism similar to sequence-to-sequence translation in spatial domains. Conversely, the Transformer-E simplifies the architecture by removing the decoder block and directly projecting the encoder’s output back to the target spatial dimension.

2.4. Metrics: Average RMSE and Average MAE

We evaluate predictive accuracy using two complementary error metrics: the average Root Mean Squared Error (aRMSE) and the average Mean Absolute Error (aMAE). Let the predicted label for the ith sample be ${\widehat{Y}}^{\left(i\right)}\in {\mathbb{R}}^{C\times T}$ and the ground truth label be as $Y^{\left(i\right)}\in {\mathbb{R}}^{C\times T}$, where C = 4 (OHLC channels) and T = 7 (hourly steps). For N total samples, the metrics are defined as follows:

$$aRMSE ={\displaystyle \frac{1}{n}}{\sum }_{n=1}^N\sqrt{{\displaystyle \frac{1}{CT}}{\sum }_{c=1}^C{\sum }_{t=1}^T{\left({\widehat{Y}}^{\left(i\right)}-Y^{\left(i\right)}\right)}^2,}$$

(2)

$$\mathrm{and} aMAE={\displaystyle \frac{1}{n}}{\sum }_{n=1}^N{\displaystyle \frac{1}{CT}}{\sum }_{c=1}^C{\sum }_{t=1}^T\left|{\widehat{Y}}^{\left(i\right)}-Y^{\left(i\right)}\right|.$$

(3)

The aRMSE penalizes large deviations more heavily, highlighting catastrophic prediction failures, while aMAE measures the typical absolute deviation regardless of direction. We report both metrics to capture complementary aspects of predictive performance.

3. Results

3.1. Experiment Settings

We evaluated the proposed model’s performance on index-level forecasting, focusing on its ability to generalize under a zero-shot setting. In response, we design two experimental conditions.

(1)

Direct-supervision setting: The models are trained directly on the S&P 500 index data together with the 10YY and the VIX, allowing it to learn index-level dynamics under explicit supervision. Each model’s weights were selected at the epoch corresponding to the minimum validation loss.

(2)

Zero-shot setting (core of our study): The zero-shot models are trained exclusively on the individual constituent stocks, without any access to index-level data, and is subsequently evaluated on the S&P 500 using its OHLC sequence combined with the responding macroeconomic inputs. The zero-shot model—trained without access to the S&P 500 index—was evaluated using the weights from the epoch with the lowest validation loss on constituent-level and macro input.

This comparison allows us to test whether a model that has never been exposed to the index during training can still infer its structural behavior from the learned representations of its components and macro-level context. Performance is evaluated using the aRMSE and aMAE calculated on the predicted intra-day OHLC trajectories of the S&P 500.

3.2. Quantitative Experiment Results

3.2.1. Direct-Supervision Forecasting

Table 3. Performance of directly trained models on S&P 500 index forecasting. Evaluation results for models directly trained using S&P 500 index OHLC hourly data along with 10YY and VIX. The table reports average RMSE (aRMSE) and average MAE (aMAE) across the train validation, and test sets. Validation loss was used for optimal epoch selection.

	Train		Validation		Test
Models 1	aRMSE	aMAE	aRMSE	aMAE	aRMSE	aMAE
VAE	0.0020	0.0357	0.0028	0.0438	0.0059	0.0566
cDDPM	0.2829	0.4418	0.0215	0.0985	0.0648	0.1990
Transformer-ED	0.0024	0.0366	0.0099	0.0846	0.0111	0.0922
Transformer-E	0.0023	0.0353	0.0139	0.1122	0.0164	0.1204

¹ VAE refers to a Variational AutoEncoder for supervised learning; cDDPM denotes a Conditional Denoising Diffusion Probabilistic Model; Transformer-ED refers to a spatial Transformer with an encoder–decoder architecture; and Transformer-E denotes a spatial Transformer using only the encoder.

presents the performance of models directly trained on the S&P 500 index using additional macroeconomic inputs. The VAE achieved the lowest test error overall, with an aRMSE of 0.0059 and an aMAE of 0.0566, indicating high consistency between training and inference performance. The Transformer-ED followed, with a test aRMSE and aMAE of 0.0111 and 0.0922, respectively. In contrast, both the cDDPM and Transformer-E exhibited divergent behaviors. cDDPM showed relatively high training errors, with an aRMSE of 0.2829, while its validation and test error were substantially lower. This pattern indicates that the model has experienced unstable optimization during training. Transformer-E, conversely, displayed clear signs of overfitting, although it achieved a very low training error of 0.0023 in terms of aRMSE. This discrepancy suggests that the model failed to generalize effectively and has relied too heavily on memorized index-level patterns during training.

3.2.2. Zero-Shot Forecasting

Table 4. Zero-shot forecasting results using constituent stocks and macroeconomic indicators. Performance of models trained solely on constituent stocks, 10YY, and VIX, without any exposure to S&P index data during training and validation. The table shows aRMSE and aMAE across three evaluation spans (span-1 to span-3), corresponding to the training, validation, and test periods used in Table 3. The models demonstrate the ability to generalize to an unseen aggregate-level target under a zero-shot forecasting scenario.

	Span-1		Span-2		Span-3
Zero-Shot Models 1	aRMSE	aMAE	aRMSE	aMAE	aRMSE	aMAE
VAE (Best)	0.0006	0.0187	0.0032	0.0486	0.0033	0.0437
cDDPM	0.3788	0.5408	0.0156	0.0926	0.0612	0.1973
Transformer-ED	0.0051	0.0508	0.0251	0.1513	0.0268	0.1533
Transformer-E	0.0084	0.0656	0.0436	0.2061	0.0471	0.2079

¹ The zero-shot model—trained without access to the S&P 500 index—was evaluated using the weights from the epoch with the lowest validation loss on constituent-level and macro input.

reports the zero-shot forecasting results. Across all three evaluation spans, the VAE consistently outperformed other models. Its aRMSE on span-3 (the test-equivalent period) was 0.0033, and aMAE was 0.0437, both of which are lower than its own performance in the directly supervised setting. Importantly, since the S&P 500 index was never exposed during training, both span-2 and span-3 represent true zero-shot inference conditions for the VAE. The model maintained stable performance across these two temporally distinct spans, with only marginal differences in both aRMSE of 0.0001 and aMAE of 0.0049. Transformer-ED also maintained stable performance, although its errors increased relative to the direct setup. Specifically, its aRMSE and aMAE on span-3 were 0.0268 and 0.1533, respectively, compared to 0.0111 and 0.0922 in Table 3. Meanwhile, cDDPM and Transformer-E suffered greater degradation in zero-shot performance, showing limited transferability to unseen aggregate-level targets.

3.3. Qualitative Visualization

Figure 3 illustrates the inference sequences of each model across the training, validation, and test spans. The visualization enables a span-wise qualitative assessment of how well each model captures the underlying index dynamics under both direct supervision and zero-shot conditions.

Among the models, the zero-shot VAE shows the closest alignment to the actual price trajectory, maintaining consistent trend-following behavior with minimal phase lag. Despite not having seen index-level data during training, its predictions exhibit smooth transitions and effectively track both upward and downward movements of the S&P 500. The direct VAE, which was trained with index-level supervision, also follows the general pattern of the ground truth. However, subtle deviations are observed in certain segments. In contrast, the Transformer-ED models, both in direct and zero-shot settings, display noticeable discrepancies. The direct Transformer-ED underestimates the amplitude of index movements, while the zero-shot variant exhibits fragmented and step-like patterns, failing to capture the smooth progression of the index trajectory. Overall, the qualitative results demonstrate that the VAE architecture generalizes better to unseen index-level forecasting tasks, while Transformer-based models are more prone to structural inconsistencies, especially in zero-shot scenarios.

4. Discussion

4.1. Analysis and Insights

In the zero-shot test span, the VAE model achieved a lower aRMSE and aMAE in the zero-shot test span compared to its direct test performance, suggesting robust latent abstraction that can compensate for the absence of index-level training. VAE is a powerful generative model that learns probabilistic latent representations of the training data [33], modeling the underlying distribution of the data. By learning a low-dimensional latent representation of the index’s constituents, the VAE effectively performs a feature extraction that abstracts the market’s state. This process can filter out noise and emphasize the co-movements and interactions that truly drive the index, thereby improving the signal-to-noise ratio in forecasting. As [38] noted, VAE can be adept at capturing the joint distribution of multiple inputs, which in finance translates to capturing how stocks move together under certain market conditions. In addition, the probabilistic nature of the VAE introduces regularization through its reconstruction objective and latent space prior, reducing overfitting. This could explain why the VAE model’s error actually decreased in the zero-shot test span: freed from fitting the quirks of the training index series, the model’s latent understanding generalizes to new data.

Conversely, models like Transformer-E experienced an aMAE increase of +0.0875 in the zero-shot setting compared to direct supervision, highlighting a significant generalization gap. Transformer-ED also exhibited noticeable degradation in zero-shot performance, though the encoder–decoder architecture mitigated overfitting to some extent compared to Transformer-E. Despite sharing the same encoder architecture, Transformer-E and Transformer-ED exhibit markedly different generalization performance under distribution shifts between validation and test spans. Transformer-E, which directly projects encoder outputs into the target spatial domain, exhibited sharp performance degradation. This weakness can be attributed to its architectural reliance on positional encodings for aligning input and output tokens. Without an additional mechanism to reinterpret encoder representations, the model essentially learns a one-to-one mapping tied to training distributions, making it brittle when exposed to unseen spans or structural shifts in the temporal–spatial grid. In contrast, Transformer-ED introduces a decoder block with learnable queries that interact with encoder memory through cross-attention. These queries provide an inductive bias for reassembling encoder features into output space, effectively functioning as a sequence-to-sequence translation step. By decoupling input representation from output reconstruction, the decoder improves robustness against distributional drift and enables a more flexible adaptation to novel spatial configurations. This contrast highlights the critical role of query-driven decoding in enhancing zero-shot generalization beyond the limits of encoder-only designs.

Meanwhile, the cDDPM failed to achieve sufficient optimization during training, limiting its forecasting capacity in the both scenarios. This approach focuses on progressively reconstructing data through iterative denoising steps using a large number of samples [18], which can cause the model to specialize in reconstructing specific structures observed during training and struggle to generalize to unseen patterns in a zero-shot setting. In other words, cDDPM relies on a repeated sampling procedure, which makes both the training objective and inference process inherently unstable. In contrast to models such as VAE that explicitly learn a structured latent space, cDDPM lacks an explicit latent abstraction mechanism, relying instead on iterative denoising that is highly sensitive to training distributional noise. Without a compressed probabilistic representation to regularize learning, the model overfits to local structures seen during training, which undermines its zero-shot generalization compared to the VAE. Transformer encoder–decoder architectures, conversely, leverage a query–memory mechanism that provides resilience against distribution shifts across validation and test spans. Finally, the strict reliance of DDPM on the training distribution makes it particularly vulnerable to cascading failures during sampling when exposed to distribution shifts, ultimately leading to severe performance degradation. These results suggest that zero-shot inference may yield comparable or superior performance when using models capable of capturing underlying structure through constituent and macroeconomic data.

In addition, the experimental results provide critical insights into the structural nature of stock indices and the efficacy of constituent-level learning in index forecasting tasks. The observed performance gap between zero-shot and direct-supervision models indicates that the proposed approach enables the model to internalize the generative structure of the index. Stock indices, such as the S&P 500, are fundamentally constructed as market-capitalization-weighted aggregates of their constituent securities. When models are trained directly on the index time series, they risk overfitting to the surface-level patterns of a compressed and information-reduced signal, limiting their ability to generalize beyond the specific temporal characteristics of the training data [39]. In contrast, the model trained exclusively on individual stock tickers and macroeconomic indicators outperforms the directly supervised counterpart, suggesting that it has captured a more generalizable understanding of the latent rules governing index formation.

This empirical observation underscores a key insight: an index is not an independent signal but a deterministic function of its underlying components. The S&P 500 index is, by design, a highly compressed representation that aggregates the complex, multivariate dynamics of its constituent stocks. Training a model solely on these aggregates obscures valuable intra-component relationships that are critical to understanding the market’s structural behavior [40]. By learning from the disaggregated source signals (tickers and macroeconomic variables), the model gains access to a richer, more granular feature space, enhancing its ability to generalize.

4.2. Limitations and Future Works

While this study introduces a novel zero-shot forecasting framework that predicts index-level trajectories using only constituent stock data and key macroeconomic indicators, certain limitations offer opportunities for further enhancement. The empirical evaluation in this study is based on data from a relatively recent period, from 2023 to 2025, selected to reflect the prevailing financial environment and to assess the framework under contemporary market conditions. While this design choice allows the analysis to capture recent structural dynamics, it also constrains the ability to assess generalizability across different historical regimes. Extending the framework to longer time horizons and to alternative markets, such as the Euro Stoxx 50 or Nikkei 225, represents an important direction for future research, and would provide a more comprehensive evaluation of its scalability and robustness.

Notably, the current model does not explicitly incorporate the capitalization-based weighting scheme inherent in index construction. Indices like the S&P 500 aggregate constituent dynamics use market-capitalization weights, where larger companies exert greater influence. The proposed framework adopts an equal-weighted approach to capture constituent-level dynamics, whereas real-world indices such as the S&P 500 are capitalization-weighted by construction. While our design emphasizes the extraction of latent cross-sectional signals without imposing index-level constraints, it is plausible that the integration of capitalization-weighted adjustments into the latent representation could enhance zero-shot forecasting accuracy.

Additionally, the macroeconomic context is limited to the 10YY and the VIX. While these variables capture essential aspects of monetary expectations and market sentiment, broader exogenous factors—such as policy rates, labor market indicators, and geopolitical risks—were not incorporated. An additional consideration concerns the role of macro-financial regimes in shaping the joint dynamics. For example, during economic slowdowns, capital reallocation from equities to bonds is often accompanied by heightened volatility and option-hedging demand, both of which amplify the VIX. Provided that such dynamics are present in the training data, the framework should remain capable of generalizing to these conditions. We note, however, that our current dataset is concentrated in a high-rate, growth-oriented regime, and we acknowledge this limitation in the manuscript.

While the 10YY serves as a widely accepted proxy for interest rate expectations, its behavior under zero lower bound (ZLB) conditions introduces distinct challenges. At the ZLB, marginal policy adjustments tend to translate disproportionately into yield movements, amplifying the sensitivity of bond markets to even small policy shifts. Such dynamics might be not well captured by the rising-rate narrative implicit in our current model. Consequently, there is a risk that the 10YY–equity relationship becomes overstated in certain environments, particularly within growth-heavy sectors that are highly sensitive to discount rate assumptions. This can undermine the zero-shot generalization capacity of the model by making latent mappings overly dependent on specific macro-financial episodes. To mitigate this vulnerability, future extensions of the framework could incorporate a broader set of macroeconomic aggregates that better capture the structural transmission mechanisms shaping equity index dynamics across regimes.

Although our study simplifies certain aspects of index construction and macroeconomic context, the framework’s strong zero-shot generalization demonstrates that constituent-level learning provides a robust foundation for modeling aggregate market behavior. Incorporating additional structural information—such as capitalization-based weighting schemes or sectoral hierarchies—into the model architecture could further enhance its fidelity to real-world index dynamics, especially in replicating the aggregation logic inherent in indices like the S&P 500. Moreover, broadening the macroeconomic feature set to include variables such as monetary policy rates, inflation expectations, employment data, and geopolitical risk factors would enrich the contextual inputs, potentially improving the model’s adaptability to regime shifts and external shocks. Extending this zero-shot inference approach to a wider array of financial indices—including international equities, fixed-income benchmarks, and sector-specific aggregates—would also offer valuable insights into the generalizability and practical relevance of constituent-driven forecasting methodologies. Furthermore, extending the framework beyond purely financial variables represents an important avenue for future research. Broader drivers such as labor market conditions, inflation expectations, fiscal policy signals, geopolitical risks, and exogenous non-financial shocks can critically influence investor sentiment and cross-asset correlations. Incorporating these factors would allow the model to capture structural transmission mechanisms with greater fidelity and enhance its robustness across diverse macro-financial environments.

While the proposed framework demonstrates strong zero-shot forecasting robustness, future research could extend its applicability through targeted fine-tuning strategies. Specifically, once a robust zero-shot baseline is established, limited index-level data could be incorporated to refine the latent representations and enhance domain-specific accuracy. In addition, parameter-efficient tuning methods, such as adapters, Low-rank Adaptation [41], or latent space conditioning [42], would allow the well-trained zero-shot base model to learn from new data while minimizing any degradation to its existing weights. Such approaches could preserve the model’s generalization ability while improving its sensitivity to latent market patterns, ultimately bridging the gap between pure zero-shot inference and fully supervised index forecasting.

5. Conclusions

This study introduces a zero-shot index forecasting framework that predicts index-level trajectories without direct supervision from index data. Rather than approaching index forecasting as a sequence-matching problem against an aggregated target, we propose a probabilistic mapping perspective, wherein the model learns to approximate the latent function that governs how constituent-level price dynamics and macroeconomic conditions jointly shape index behavior. This paradigm shift reframes index forecasting as the task of internalizing the generative mechanism by which aggregate market indicators emerge from micro-level interactions, rather than merely regressing towards a compressed summary signal.

Empirical results demonstrate that a model trained solely on constituent-level data, when equipped with a structurally informed learning objective, can infer index-level dynamics with accuracy that rivals, and in some cases surpasses, models trained with direct index supervision. This finding underscores the efficacy of constituent-driven learning in capturing structural properties of financial aggregates, while also mitigating the risk of overfitting to surface-level patterns present in index-level time series. Beyond index forecasting, the proposed approach highlights the broader potential of modeling aggregated phenomena through disaggregated source signals.