Existence and Uniqueness of Solutions for Cohen–Grossberg BAM Neural Networks with Time-Varying Leakage, Neutral, Distributed, and Transmission Delays
Abstract
1. Introduction
2. Problem Description
3. Existence and Uniqueness of Solutions
- then for any given initial conditions and , the CGBAMNN (1) has a unique solution:
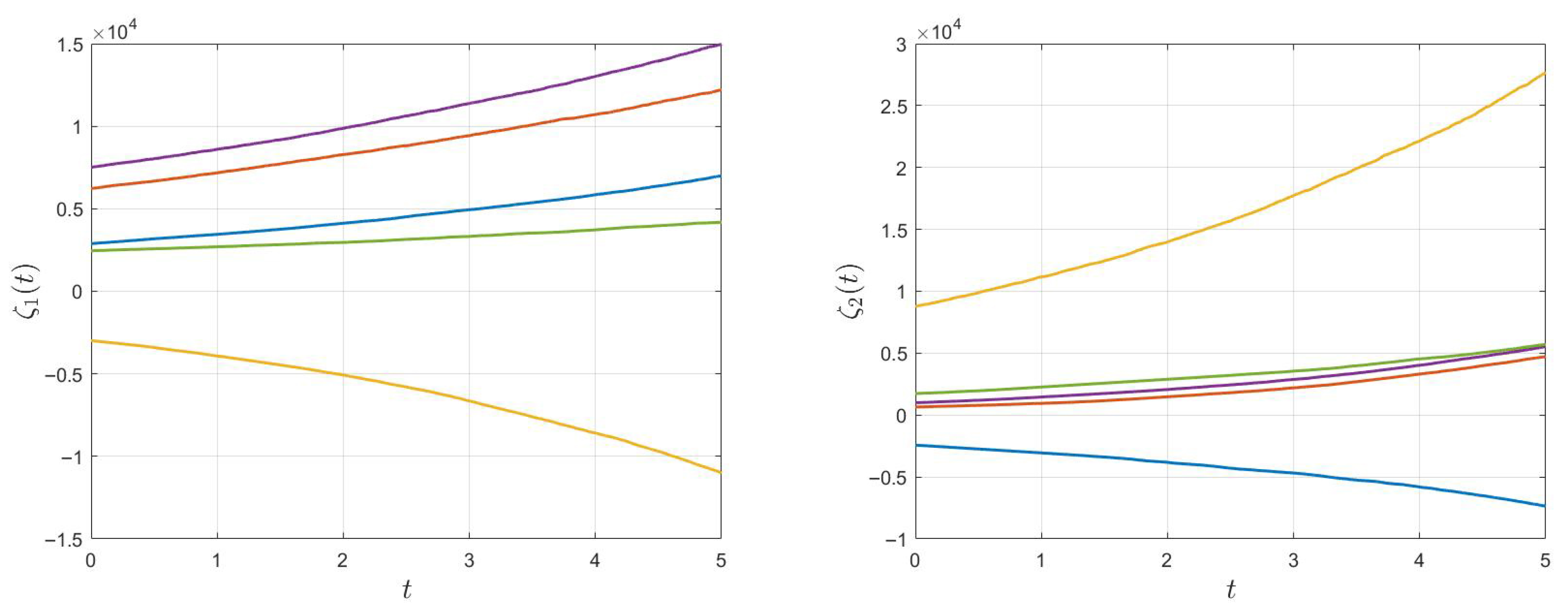
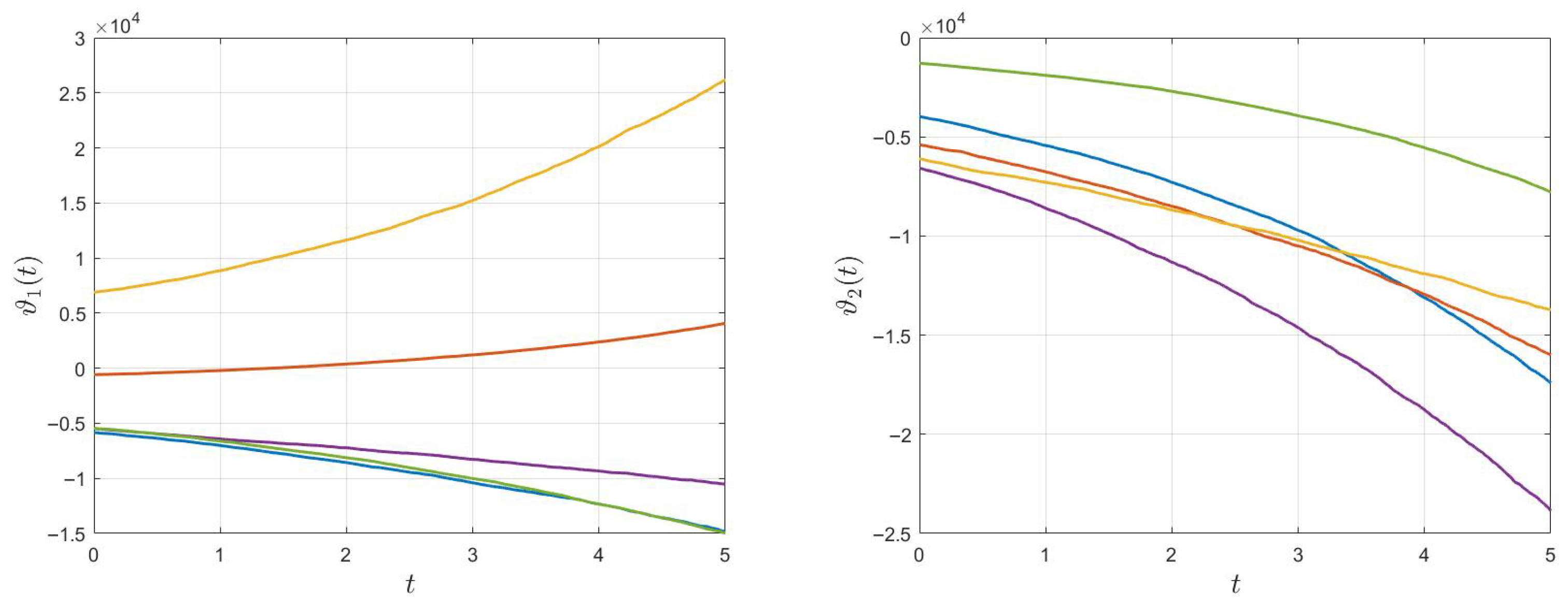
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Townsend, J.; Chaton, T.; Monteiro, J.M. Extracting relational explanations from deep neural networks: A survey from a neural-symbolic perspective. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3456–3470. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, X.; Zhang, X.; Hu, M.; Dinh, T.N. Global exponential synchronization of discrete-time high-order switched neural networks and its application to multi-channel audio encryption. Nonlinear Anal. Hybrid Syst. 2023, 47, 101291. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.; Liu, G.P.; Zhang, H.; Navaratne, R. A prediction-based approach to distributed filtering with missing measurements and communication delays through sensor networks. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2021, 51, 7063–7074. [Google Scholar] [CrossRef]
- Hu, J.; Liu, G.; Zhang, H.; Liu, H. On state estimation for nonlinear dynamical networks with random sensor delays and coupling strength under event-based communication mechanism. Inf. Sci. 2020, 511, 265–283. [Google Scholar] [CrossRef]
- Thangarajan, S.K.; Chokkalingam, A. Integration of optimized neural network and convolutional neural network for automated brain tumor detection. Sens. Rev. 2021, 41, 16–34. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Xue, Y. Global exponential synchronization of high-order quaternion Hopfield neural networks with unbounded distributed delays and time-varying discrete delays. Math. Comput. Simul. 2022, 193, 173–189. [Google Scholar] [CrossRef]
- Cohen, M.A.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. Syst. 1983, 13, 815–826. [Google Scholar] [CrossRef]
- Kosko, B. Adaptive bidirectional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef]
- Kosko, B. Bi-directional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Cao, J.; Liang, J.; Lam, J. Exponential stability of high-order bidirectional associative memory neural networks with time delays. Phys. D Nonlinear Phenom. 2004, 199, 425–436. [Google Scholar] [CrossRef]
- Ho, D.W.C.; Liang, J.; Lam, J. Global exponential stability of impulsive high-order BAM neural networks with time-varying delays. Neural Netw. 2006, 19, 1581–1590. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, M. Global exponential stability of high-order bidirectional associative memory (BAM) neural networks with time delays in leakage terms. Neurocomputing 2016, 177, 515–528. [Google Scholar] [CrossRef]
- Yang, W.; Yu, W.; Cao, J.; Alsaadi, F.E.; Hayat, T. Almost automorphic solution for neutral type high-order Hopfield BAM neural networks with time-varying leakage delays on time scales. Neurocomputing 2017, 267, 241–260. [Google Scholar] [CrossRef]
- Li, X.; Fu, X.; Balasubramaniam, P.; Rakkiyappan, R. Existence, uniqueness and stability analysis of recurrent neural networks with time delay in the leakage term under impulsive perturbations. Nonlinear Anal. Real World Appl. 2010, 11, 4092–4108. [Google Scholar] [CrossRef]
- Xi, Q.; Si, J. Existence, Uniqueness, and Stability Analysis of Impulsive Neural Networks with Mixed Time Delays. Abstr. Appl. Anal. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, L.; Wang, Y. Existence-uniqueness and stability of reaction-diffusion stochastic Hopfield neural networks with S-type distributed time delays. Neurocomputing 2018, 275, 470–477. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. Basic theorem and global exponential stability of differential-algebraic neural networks with delay. Neural Netw. 2021, 140, 336–343. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Hioual, A.; Ouannas, A.; Sawalha, M.M.; Alshammari, S.; Alshammari, M. On Variable-Order Fractional Discrete Neural Networks: Existence, Uniqueness and Stability. Fractal Fract. 2023, 7, 118. [Google Scholar] [CrossRef]
- Alzabut, J.; Tyagi, S.; Martha, S.C. On the stability and Lyapunov direct method for fractional difference model of BAM neural networks. J. Intell. Fuzzy Syst. 2020, 38, 2491–2501. [Google Scholar] [CrossRef]
- Li, P.; Lu, Y.; Xu, C.; Ren, J. Bifurcation Phenomenon and Control Technique in Fractional BAM Neural Network Models Concerning Delays. Fractal Fract. 2023, 7, 7. [Google Scholar] [CrossRef]
- Li, P.; Lu, Y.; Xu, C.; Ren, J. Insight into Hopf Bifurcation and Control Methods in Fractional Order BAM Neural Networks Incorporating Symmetric Structure and Delay. Cogn. Comput. 2023, 15, 1825–1867. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Huang, J.; Gorbachev, S.; Aravind, R.V. Exploration on bifurcation for an incommensurate five-neuron fractional-order BAM neural network involving multiple delays. Phys. D Nonlinear Phenom. 2024, 460, 134047. [Google Scholar] [CrossRef]
- Fang, W.; Xie, T.; Li, B. Robustness Analysis of BAM Cellular Neural Network with Deviating Arguments of Generalized Type. Discret. Dyn. Nat. Soc. 2023, 2023, 9570805. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, E.-Y.; Zhang, X.; Zhu, L. Existence and Uniqueness of Solutions for Cohen–Grossberg BAM Neural Networks with Time-Varying Leakage, Neutral, Distributed, and Transmission Delays. Mathematics 2025, 13, 2723. https://doi.org/10.3390/math13172723
Cong E-Y, Zhang X, Zhu L. Existence and Uniqueness of Solutions for Cohen–Grossberg BAM Neural Networks with Time-Varying Leakage, Neutral, Distributed, and Transmission Delays. Mathematics. 2025; 13(17):2723. https://doi.org/10.3390/math13172723
Chicago/Turabian StyleCong, Er-Yong, Xian Zhang, and Li Zhu. 2025. "Existence and Uniqueness of Solutions for Cohen–Grossberg BAM Neural Networks with Time-Varying Leakage, Neutral, Distributed, and Transmission Delays" Mathematics 13, no. 17: 2723. https://doi.org/10.3390/math13172723
APA StyleCong, E.-Y., Zhang, X., & Zhu, L. (2025). Existence and Uniqueness of Solutions for Cohen–Grossberg BAM Neural Networks with Time-Varying Leakage, Neutral, Distributed, and Transmission Delays. Mathematics, 13(17), 2723. https://doi.org/10.3390/math13172723





