Abstract
Trapezoidal-valued intuitionistic fuzzy numbers (TrVIFNs) are the real generalizations of intuitionistic fuzzy numbers, interval-valued intuitionistic fuzzy numbers, and triangular intuitionistic fuzzy numbers, which effectively model real-life problems that consist of imprecise and incomplete data. This study incorporates the Aczel-Alsina aggregation operators (which consist of parameter-based flexibility) for solving any group of decision-making problems modeled in a trapezoidal-valued intuitionistic fuzzy (TrVIF) environment. In this study, we first define new operations on TrVIFNs based on the Aczel-Alsina operations. Secondly, we introduce new trapezoidal-valued intuitionistic fuzzy aggregation operators, such as the TrVIF Aczel-Alsina weighted averaging operator, the TrVIF Aczel-Alsina ordered weighted averaging operator, and the TrVIF Aczel-Alsina hybrid averaging operator, and we discuss their fundamental mathematical properties by examining various theorems. This study also includes a new algorithm named ‘three-stage multi-criteria group decision-making’, where we obtain the criteria weights using the newly proposed TrVIF-MEREC method. Additionally, we introduce a new modified algorithm called TrVIF-WASPAS to solve the multi-criteria decision-making (MCDM) problem in the trapezoidal-valued intuitionistic fuzzy environment. Then, we apply this proposed method to solve a model case study problem involving location selection for a wind power plant project. Then, we discuss the proposed algorithm’s sensitivity analysis by changing the criteria weights concerning different parameter values. Finally, we compare our proposed methods with various existing methods, like some subclasses of TrVIFNs such as IVIFWA, IVIFWG, IVIFEWA, and IVIFEWG, and also with some MCGDM methods of TrVIFNs, such as the Dombi aggregation operator-based method in TrVIFNs and the TrVIF-Topsis method-based MCGDM, to show the efficacy of our proposed algorithm. This study has many advantages, as it consists of a total ordering principle in ranking alternatives in the newly proposed TrVIF-MCGDM techniques and TrVIF-WASPAS MCDM techniques for the first time in the literature.
Keywords:
trapezoidal-valued intuitionistic fuzzy Aczel-Alsina weighted averaging aggregation operator (TrVIFAAWA); three-stage multi-criteria group decision-making method; TrVIF-MEREC; TrVIF-WASPAS; renewable energy site selection; multi-criteria decision-making MSC:
03B52; 03E72; 26E50
1. Introduction
Multi-criteria group decision-making (MCGDM) techniques play a vital role in modeling and solving many real-life problems. The modeling of real-life problems involves a mixture of data in many scenarios. Sometimes, it is difficult for an expert to use crisp (real-number) values instead of fuzzy numbers. For this, Zadeh [1] introduced fuzzy set (FS) theory by increasing the range of crisp sets from to the unit interval (). Later, in 1986, Atanassov and Stoeva [2] introduced the extension concept of the traditional fuzzy set into intuitionistic fuzzy sets (IFSs). Still, in the case of a traditional fuzzy set, the sum of membership and non-membership values is exactly one, which shows that the membership value is one minus the value of non-membership, and vice versa. However, in the case of IFSs, this may not always be true. Similar to IFSs, Atanassov [3] suggested the theory of interval-valued intuitionistic fuzzy sets (IVIFSs). Nehi and Maleki [4] have suggested the theory of trapezoidal intuitionistic fuzzy sets (TrIFSs) as an extension of triangular intuitionistic fuzzy sets (TIFSs). However, this is not a real generalization of real-valued intuitionistic fuzzy sets. The actual generalization of real-valued intuitionistics fuzzy sets, interval-valued intuitionistic fuzzy sets (IVIFSs), and triangular intuitionistic fuzzy sets (TIFSs) were properly discussed by Jeevaraj et al. [5] in the year 2023, which is known as trapezoidal-valued intuitionistic fuzzy numbers (TrVIFNs), defined in the form of with .
Regarding aggregation operators, Xu and Yager [6] presented the theory of some geometric aggregation operators for intuitionistic fuzzy numbers (IFN). They also explained the idea of weighted arithmetic and geometric average operators to aggregate the performances of alternatives concerning criteria. The information systems field has two leading aggregation operators: the weighted arithmetic and geometric average operators. Xu [7] defined some operational laws of interval-valued intuitionistic fuzzy numbers (IVIFNs) and then established the interval-valued intuitionistic fuzzy weighted arithmetic and interval-valued intuitionistic fuzzy weighted geometric aggregation operators. Jianqiang and Zhong [8] proposed the idea of trapezoidal intuitionistic fuzzy weighted geometric and weighted arithmetic averaging operators.
The theory of the Aczel-Alsina (AA) aggregation operator using t-norm and t-conorm was proposed by Aczel and Alsina [9]. The AA aggregation operator in the IFS environment was introduced by Senapati et al. [10], and Senapati et al. [11] proposed the idea of Aczel-Alsina in an IVIF environment. Further, Senapati et al. [12] introduced the triangular norm-based Aczel-Alsina geometric operators on IFNs and discussed their application to MADM. Many authors have introduced the Aczel-Alsina operator in different fuzzy environments. Some of them are listed as follows: Khan et al. [13] introduced the AA operator in q-rung orthopair fuzzy sets, Garg et al. [14] presented the AA operator in a bipolar fuzzy environment, and Wang et al. [15] proposed the AA operator for T-spherical fuzzy sets. Very recently, Meher and Jeevaraj [16] introduced the concept of the Aczel-Alsina aggregation operator in the interval-valued Fermatean fuzzy set environment and its application to group decision-making problems. Demir et al. [17] established a wind farm site selection tool using a geographic information system and a fuzzy decision-making model. Very recently, Meher and Jeevaraj [18] proposed a trapezoidal-valued intuitionistic fuzzy Aczel-Alsina weighted geometric aggregation operator in the group decision-making problem for the selection of an e-learning platform using TrVIF-TOPSIS techniques. Jawad Ali [19] proposed the idea of the Aczel-Alsina prioritized aggregation operator in T-spherical fuzzy sets. Shit and Ghorai [20] established the theory of a novel Aczel-Alsina aggregation operator-based multi-criteria group decision-making approach under a hesitant fuzzy set. Senapati [21] presented an Aczel-Alsina aggregation-based outranking method for multiple attribute decision-making using single-valued neutrosophic numbers. In addition, Meher et al. [22] established the trapezoidal-valued intuitionistic fuzzy Dombi weighted geometric aggregation operator and studied its application to group decision making for photovoltaic site selection for the first time in the literature.
Zavadskas et al. [23] established the WASPAS (Weighted Aggregated Sum Product Assessment) algorithm. It is a promising method in MCDM. It offers several advantages over other approaches, such as simplicity in calculation, the ability to select the most preferred alternative using aggregated operators, and enhanced accuracy due to its combination of the Weighted Sum Model (WSM) and Weighted Product Model (WPM) elements. Additionally, its capability to provide highly accurate estimates is valuable in decision-making scenarios where precision is crucial. Later on, many authors extended the concept to different fuzzy environments. Al-Barakati et al. [24] introduced the concept of WASPAS in an interval-valued Pythagorean fuzzy environment. Keshavarz-Ghorabaee et al. [25] first introduced the MEREC method. This method is a technique used to calculate criteria weights in MCDM algorithms/ problems. This method determines the relative importance or significance of different criteria in decision-making. Many authors like Shang et al. [26] used the MEREC method to calculate the criteria weights of their MCDM problem. In addition to that, Tripura et al. [27] presented a picture fuzzy aggregation operator-based integrated MEREC-WASPAS technique for video conferencing tool selection.
From the literature, we have carefully observed that Aczel-Alsina aggregation operators play a vital role in aggregating fuzzy numbers. Also, the operational laws of Aczel-Alsina are more general and superior to the algebraic operational laws due to the presence of parameters. Inspired by this operator, we investigate these operators for the class of TrVIFNs in this work, which has not been done so far. The important aims of this article are to:
- introduce AA-based arithmetic laws in the environment of TrVIFNs.
- present the TrVIFAAWA aggregation operator, the TrVIFAAOWA aggregation operator, and the TrVIFAAHA aggregation operator and study their properties.
- establish a new three-stage multi-criteria group decision-making algorithm by proposing the TrVIF-MEREC method for calculating the criteria weights to solve an MCDM problem.
- introduce the TrVIF-WASPAS method (by extending the WASPAS approach to the class of TrVIFNs) to solve the MCGDM problem modeled in a TrVIF environment.
- perform a comparative and sensitivity analysis to demonstrate the presented method’s reliability, strength, and effectiveness.
The remainder of this article is as follows: Section 2 clearly describes the basic preliminaries and the scoring function to evaluate the alternative’s ranking. Section 3 introduces the operational rule of AA in the environment of TrVIFNs. Section 4 proposes the TrVIFAAWA, TrVIFAAOWA, and TrVIFAAHA aggregation operators and establishes their properties using theorems. Section 5 establishes two decision-making algorithms to solve the MCGDM problem modeled under a trapezoidal-valued intuitionistic fuzzy (TrVIF) environment. Section 6 deals with the model case study problem involving the location selection process for a wind power plant project. We solve the case study problem using the two proposed decision-making algorithms in Section 6. In Section 7, we describe the sensitivity analysis of the presented decision-making algorithms, looking into the ranking of alternatives by changing different weights for the criteria. To examine the comparative analysis correctly, we consider a different numerical problem and compare the results of the proposed decision-making algorithm with a few existing MCGDM/MCDM approaches in Section 8. Finally, conclusions are given in Section 9. The list of important symbols and abbreviations is presented in Table 1.

Table 1.
List of important symbols and abbreviations.
2. Preliminaries
Here, we consider the various important definitions, score functions, and some examples related to the proposed aggregation operator.
Definition 1
([2]). Let us consider a nonempty set . An intuitionistic fuzzy set (IFS) in is defined by , where and with the conditions . The numbers denote the degree of membership and non-membership of to lie in , respectively. For each intuitionistic fuzzy subset in , is said to be the hesitancy degree of to occur in .
Definition 2
([5]). Let be the set of all trapezoidal fuzzy numbers in . A trapezoidal-valued intuitionistic fuzzy set on a set is an expression given by where with the condition .
TrVIFNs and denote, respectively, the degree of membership and non-membership of the element present in the set . Thus, for each , and are TrVIFNs and are described by their legs , , , and , , , . We denote
where .
The set of TrVIFN in is described by TrVIFN(). In general, any TrVIFN is represented by with for convenience. This paper considers both membership and non-membership functions of TrVIFNs as finite.
Definition 3.
Let = , and = be two TrVIFNs. Then, the relations between and are defined by
- (i)
- = if and only if = , = , = , = , and = , = , = , = .
- (ii)
- ≤ if and only if ≤ , ≤ , ≤ , ≤ , and ≥ , ≥ , ≥ , ≥ .
Definition 4
([5]). Let = ∈ TrVIFN. Then, the score functions of are defined as below:
Definition 5
([5]). Let = , and = ∈ TrVIFN. Then, the “<” relation in the environment of the TrVIFNs is described below.
- If < then < (or)
- If = and > then < (or)
- If = , = , and < then < (or)
- If = , = , = , and > then < (or)
- If = , = , = , = , and < then < (or)
- If = , = , = , = , = , and > then < (or)
- If = , = , = , = , = , = , and < then < (or)
- If = , = , = , = , = , = , = , and
- > then < .
Definition 6
([28]). T: × → , defined in such a way that the following axioms are satisfied ():
- (1)
- Symmetric: ;
- (2)
- Monotonic: if ;
- (3)
- Associative: ;
- (4)
- Identity element (as one):
Definition 7
([28]). S: × → , defined in such a way that the following axioms are satisfied ():
- (1)
- Symmetric: ;
- (2)
- Monotonic: if ;
- (3)
- Associative: ;
- (4)
- Identity element (as zero):
Definition 8
([9,29]). The AA t-norms are defined as follows:
The Aczel-Alsina t-conorms are defined as follows:
After introducing the basic preliminaries and some important definitions, we will discuss the Aczel-Alsina operations on TrVIFNs in the next Section 3 below.
3. Aczel-Alsina Operations on TrVIFNs
This section describes the basic definitions of Aczel-Alsina (AA) operations, such as the sum, product, and scalar multiplication of AA in the environment of TrVIFNs. These operations are essential for introducing and studying the mathematical properties.
Definition 9.
Let = , = , and = , be three TrVIFNs, , and . Following that, the AA t-NM and t-CM operations of TrVIFNs are summarized as follows:
⊕
=
⊗
=
=
Below are some numerical examples that are defined in Definition 9.
Example 1.
Let = , = , and = be three TrVIFNs. As per Definition 9, using AA operations on TrVIFNs for and , we can write the following:
⊕
=
=
Similarly, we can calculate the following:
⊗
=
=
=
=
Theorem 1 discusses the basic results of AA in TrVIFNs that will be used in the upcoming sections.
Theorem 1.
Let = , = , and = be three TrVIFNs. Then, we have the following:
- (i)
- ⊕ = ⊕ ;
- (ii)
- = ;
- (iii)
- = , ;
- (iv)
- = , ;
- (v)
- = , ;
- (vi)
- = , .
Proof.
The proof of the above theorem is obvious, and thus it has been skipped. □
By using the above Definition 9 and Theorem 1, we will define a few new aggregation operators (TrVIFAAWA, TrVIFAAOWA, and TrVIFAAHA) in Section 4.
4. A New Set of Aggregation Operators in the Environment of TrVIFS
This section presents a series of new aggregation operators such as TrVIFAAWA, TrVIFAAOWA, and TrVIFAAHA on TrVIFNs and studies their properties using various theorems.
Definition 10 describes our proposed TrVIFAAWA operator.
Definition 10.
Let = be a collection of TrVIFNs, and are the weighting vector of such that and . Then, a TrVIFAAWA operator is a function such that TrVIFAAWA: defined as follows: = = .
Theorem 2 shows that if we take the n-tuples of TrVIFNs (as an input) and aggregate them using the AA operations, then it returns a single TrVIFN (as an output).
Theorem 2.
Let = be a set of TrVIFNs. Then, its value after aggregation using TrVIFAAWA operations is again a TrVIFN:
= =
where the weight vector of is with and .
Proof.
Hence, , which shows that the proposed TrVIFAAWA operator defined in the Equation (9) is a TrVIFN. □
The above theorem can be proved using the method of mathematical induction, i.e., for , we have the following:
= =
=
⊕
=
Let us assume that the result is true for . Then, we have the following:
=
=
,
,
Now, for the value of , we have the following:
=
=
=
,
⊕
,
=
,
Thus, Equation (9) is true for . Hence, we can conclude based on the method of induction that the result in Equation (9) is true ∀.
Also, let , and .
Additionally, we need to show .
We know that (based on the definition of TrVIFN).
Therefore, we can now write the following:
Now, we replace the value of in the above Equation (10). Then, we have the following:
Theorems 3–5 show that the TrVIFAAWA aggregation operator satisfies the aggregation properties like idempotency, boundedness, and monotonicity, respectively. Proof of the theorem is also given below.
Theorem 3
(Idempotency). If all = are equal—that is, = for all ℘—then .
Proof.
Since for —that is, , , , and , , , —we have the following based on Equation (9):
=
=
,
=
=
= = . □
Theorem 4
(Boundedness). Let = be a collection of TrVIFNs, and let and . Then, ≤ ≤ .
Proof.
Let = be a collection of TrVIFNs and = and = , where we have , , , , and , , , , and , , , , and , , , ,
Also, we can write the following:
Similarly, we can write the rest of the inequalities as follows.
Then, we have the following inequalities:
≤
≤
≤
≤
≤
≤
≤
≤
and
≤ ≤
≤ ≤
≤ ≤
≤ ≤
Therefore, ≤ ≤ . □
Theorem 5
(Monotonicity). Let and be two sets of TrVIFNs, if , ∀℘, then , where and .
Proof.
; that is, , , , and , , , . Therefore, we can write it as follows:
≤ ,
≤ ,
≤ ,
≤ ,
and
≥ ,
≥ ,
≥ ,
≥ .
Therefore, based on the above conditions, we can write the following:
. □
Now, we define the TrVIFAAOWA operator in Definition 11.
Definition 11.
Suppose = is a series of TrVIFNs. A TrVIFAAOWA operator of dimension σ is a mapping TrVIFAAOWA: with the equivalent weight vector, such that and , defined as follows:
=
= ,where the permutations of are , for which ≥ for all .
We can prove the following theorem in the TrVIF environment based on the Aczel-Alsina operations.
Theorem 6.
Suppose = is a set of TrVIFNs. A TrVIFAAOWA operator of dimension σ is a mapping of TrVIFAAOWA: with the corresponding weight vector as such that and . Then,
=
=
The following properties of aggregation can be easily proven using the TrVIFAAOWA operator:
Theorem 7
(Idempotency). If all = are equal—that is, = for all ℘— then .
Theorem 8
(Boundedness). Let = be a collection of TrVIFNs and let and . Then, ≤ ≤ .
Theorem 9
(Monotonicity). Let and be two sets of TrVIFNs. If for all ℘, then , where and
.
Theorem 10
(Commutativity). Let and be two sets of TrVIFNs. Then, = , where is any permutation of .
Now, we propose a new operator named the “trapezoidal-valued intuitionistic fuzzy Aczel-Alsina hybrid averaging (TrVIFAAHA) operator” as the generalization of TrVIFAAWA and TrVIFAAOWA to visualize both the operators using a single function, discussing more variation when we compare it with the individual operators.
Definition 12.
Let = be a series of TrVIFNs. A TrVIFAAHA operator of dimension σ is a function TrVIFAAHA: with the related weight vector being such that and , defined as follows:
=
=
Let be the weighting vector for the TrVIFAAHA operator, , and ; , . is any permutation of a collection of the weighted TrVIFNs such that ≥ . denotes the weight vector of , with and , and is the balancing coefficient, which serves a role of balance.
Theorem 11.
Let = be a collection of TrVIFNs. Therefore, the aggregated output using the TrVIFAAHA operator is again a TrVIFN, i.e.,
=
=
Proof.
Similar to Theorem 2, we can prove Theorem 11. □
Theorem 12.
The TrVIFAAWA and TrVIFAAOWA operators are special cases of the TrVIFAAHA operator.
Proof.
(1) Let . Then
=
= ,
=
=
=
(2) Let . Then, and
= ,
= ,
=
Hence, the proof is complete. □
In the upcoming sections, we show the applicability of our proposed aggregation operators defined in Section 4 by proposing two decision-making algorithms and solving a real-life model case study problem to show the efficacy and applicability of the proposed aggregation operators in decision science.
5. Novel MCGDM Methods for Solving Problem Modeled in TrVIF Environment
This section establishes two decision-making approaches to dealing with uncertainty in MCGDM problems modeled in the TrVIF environment. We adequately describe the two algorithms to solve the MCGDM problem in a stepwise manner. In Section 1, we explain the stepwise procedures of our first decision-making method using our presented aggregation operator. In the first decision-making method, we utilize the weights (for calculating the criteria’s weight from the aggregated decision matrix) computed using the TrVIF-MEREC method. In Section 2, we discuss our second decision-making method, which is the extended version of the WASPAS method available in the literature.
5.1. A Three-Stage Multi-Criteria Group Decision-Making Method
This subsection establishes a three-stage multi-criteria group decision-making method that utilizes our proposed aggregation operator. Firstly, we discuss any TrVIF decision-making problem mathematically, then we discuss the algorithm’s step-by-step procedure. As the name suggests, this algorithm works in three stages. In Stage 1, we convert the obtained GDM into a single DM. This step converts the group MCDM problem into an MCDM problem. In Stage 2, we obtain the criteria weights by proposing a modified TrVIF-MEREC method. In Stage 3, we obtain the final ranking of the alternatives using the decision matrix obtained in Stage 1 and the weights from Stage 2.
Let be a set of alternatives, be a set of criteria, be a set of decision makers, and is known as the weight vector of decision makers, where , and . Let be a TrVIF decision matrix presented by the decision makers . Here, = is a TrVIF for alternative w.r.t. the criterion by the decision maker . The weight vector of the criteria can be calculated using the MEREC method.
The algorithm utilizes the presented TrVIFAAWA aggregation operator for solving the MCGDM problem, which is illustrated in the following steps.
The flowchart of the proposed Algorithm 1 is shown in Figure 1.
| Algorithm 1 A novel 3-stage MCGDM algorithm |
Stage 1: Conversion of group decision matrix into a decision matrix.
|
Stage 2: Determination of criteria weight using TrVIF-MEREC Method After finding the single aggregated decision matrix from the original group decision matrix, we now calculate the criteria weights using the TrVIF-MEREC method. The TrVIF-MEREC method is described as follows: The MEREC method will be applied to TrVIFNs to find the criteria weights. Also, we determine the score matrix using the total ordering principle defined in Definitions 4 and 5, which is more logical, realistic, and applicable to finding the score value of every type of TrVIFN. In the following section, we present the procedure for the TrVIF-MEREC method.
|
Stage 3: Final Score matrix and the ranking: Based on the criteria weights of the TrVIF-MEREC method, we find out the final aggregated matrix again by using Equation (9) of the TrVIFAAWA operator, and we calculate the final aggregated alternative values.
|
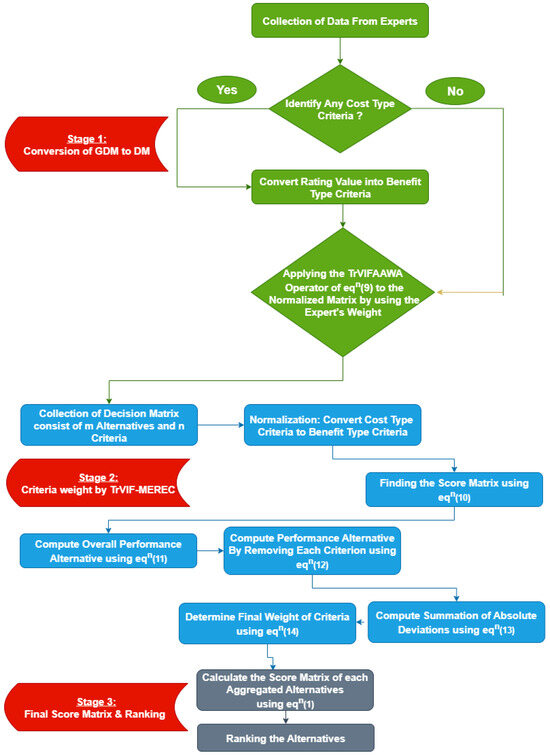
Figure 1.
Flowchart of the 3-stage MCGDM Algorithm 1.
5.2. A TrVIF-WASPAS Algorithm
We establish the TrVIF-WASPAS algorithm in this subsection by extending the traditional WASPAS MCDM method to the TrVIF environment. Also, the flowchart of the proposed TrVIF-WASPAS algorithm is given in Figure 2.
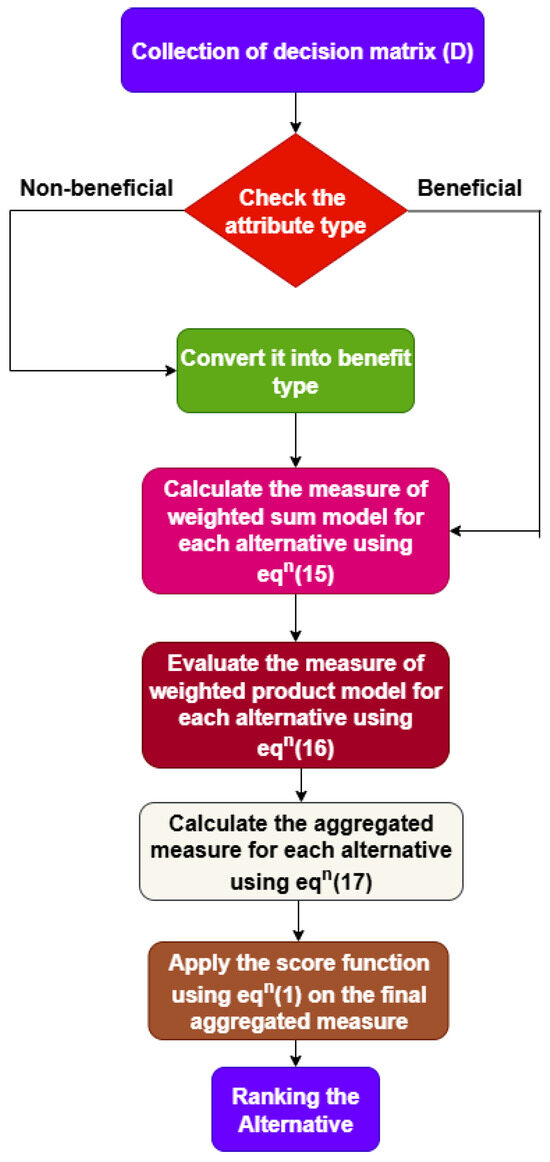

Figure 2.
Flowchart of TrVIF-WASPAS Algorithm 2.
| Algorithm 2 Stepwise procedure of the TrVIF-WASPAS algorithm |
|
6. Location Selection for a Wind Power Plant Project
In this section, we consider an example related to practicality for the location selection for a wind power plant project. Here, we solve the model case study problem using two decision-making methods proposed in the previous section. In Section 6.2.1, we solve the location selection problem using the three-stage (3-stage) MCGDM method proposed in Section 5.1 (Algorithm 1). In Section 6.2.2, we solve the same location selection problem using the TrVIF-WASPAS approach (Algorithm 2) proposed in Section 5.2. Before proceeding with the solution, we first discuss the crucial criteria that play a significant role in selecting a location for a wind power plant project in Section 6.1.
6.1. Criteria for Selection Process for a Wind Power Plant Project
Here, we consider the eleven possible criteria that are crucial in the location selection for a wind power plant project. Also, we clearly describe the role of every criterion in detail below. We chose all the possible criteria from the literature presented by Yeh and Huang [30], Shafiee [31], Nasehi et al. [32], Lee et al. [33], and Tegou et al. [34].
- High annual average wind speed ():The power generated by a wind turbine, such as a windmill, depends on the cube of the wind velocity, and a slight increase in wind speed can significantly impact the power output of a wind turbine. This is why selecting a site for wind energy conversion systems (WECSs) with high and consistent wind speed is essential.
- Availability of anemometry data ():Anemometry data, which measures wind speeds and directions, is crucial for making informed decisions about the location of wind energy conversion systems (WECS) such as wind turbines.
- Availability of wind curve at the proposed site ():The curve is a foundational component of wind energy project planning and evaluation. It helps ensure that WECSs are sited and designed in locations with adequate and reliable wind resources, which is essential for their long-term success and economic viability.
- Wind structure at the proposed site ():Wind turbine designs and control systems are developed to handle the non-ideal characteristics of the wind. They include features like variable pitch blades, yaw control, and mechanisms to protect the turbine during high winds.
- Altitude of the proposed site ():The altitude at which a Wind Energy Conversion System (WECS) is located can significantly impact the air density, wind power, and the resulting electric power output. Air density, wind velocity, and altitude are interconnected factors that influence wind turbines’ performance and power output.
- Terrain and its aerodynamics ():The terrain of the chosen site is a critical factor in the placement and operation of Wind Energy Conversion Systems (WECSs). The local topography can substantially impact wind conditions and energy production. However, the choice of terrain and the specific location within that terrain can considerably impact the energy output and efficiency of wind energy projects.
- Local Ecology ():Surface conditions, such as bare rock, vegetation, or other obstacles, can significantly impact the hub height and overall system costs for Wind Energy Conversion Systems (WECSs).
- Distance to road or railways ():The logistical aspects of moving heavy machinery, materials, and all the necessary components to a chosen Wind Energy Conversion System (WECS) site are critical considerations in the system engineering and project planning process.
- Nearness of site to local center/users ():Minimizing the length of the transmission lines is a key criterion in the site selection process for Wind Energy Conversion Systems (WECSs) and other energy generation facilities.
- Nature of ground ():Ground conditions at a Wind Energy Conversion System (WECS) site are critical factors to consider. A stable and secure foundation is essential to the long-term success and safety of the WECS.
- Favorable land cost ():Land cost is indeed a significant factor to consider in the total cost of a Wind Energy Conversion System (WECS) project.
6.2. Illustrative Example
Below, we calculate the ranking of alternatives by taking the very important class of problems related to practicality. We collected the possible data in TrVIF form from the various decision-makers.
Let us consider an organization that intends to evaluate the selection process of a location for a wind power plant project. A team of experts chose the best location for a wind power plant. In this problem, we analyze the selection of a site in which six alternative locations, , are chosen to introduce the problem, and we must select the appropriate one. Therefore, eleven criteria are from to (defined in Section 6). There are six decision makers, which are represented by to . The weights of the criteria can be calculated using the TrVIF-MEREC method. Suppose that the weight vectors for experts (decision makers) are .
Now, we solve the considered Example Section 6.2 to show the applicability of the proposed Algorithms 1 and 2.
6.2.1. Solving Example Section 6.2 Using the Proposed Algorithm 1
Here, we solve Example Section 6.2 using our proposed TrVIFAAWA operator and also using the extended TrVIF-MEREC method for calculating the weight of criteria.
Stage 1: Conversion of GDM into a DM
- Step 1(a): Six alternatives have to be evaluated based on eleven criteria. The six decision-makers use the linguistic variables shown in Table 2 for rating. Table 3 provides the set of decision matrices given by different decision makers.
 Table 2. Conversion scale of linguistic variables & TrVIFNs.
Table 2. Conversion scale of linguistic variables & TrVIFNs. Table 3. Decision matrix given by six different experts w.r.t. alternatives versus criteria.
Table 3. Decision matrix given by six different experts w.r.t. alternatives versus criteria. - Step 1(b): Among the eleven criteria, the criterion is the only cost criterion. Therefore, in the normalization process, we use the formula given in Step 1(b) in Algorithm 1 above.
- Step 1(c): Now, we apply our proposed trapezoidal-valued intuitionistic fuzzy Aczel-Alsina weighted averaging aggregation operators given in Equation (9) to the normalized form obtained in Step 1(b) above. First, we aggregate alternatives one and two, like that of each decision maker, by taking the corresponding weights of each decision maker. Therefore, we obtain the aggregated matrix, which is shown in Table 4 and Table 5. We will now calculate the criteria’s weight using the proposed TrVIF-MEREC method below.
 Table 4. A single aggregated decision matrix w.r.t. nine criteria for six alternatives.
Table 4. A single aggregated decision matrix w.r.t. nine criteria for six alternatives. Table 5. A single aggregated decision matrix w.r.t. last two criteria for six alternatives.
Table 5. A single aggregated decision matrix w.r.t. last two criteria for six alternatives.
Stage 2: Determination of criteria weight using TrVIF-MEREC Method
- Step 2(b): Here, the criterion is the cost criterion. In the process of normalization, we interchange the membership values with non-membership values, and vice versa.
- Step 2(c): Now, we calculate the score matrix using the formulas in Equation (11). The score matrix of normalized aggregated TrVIFNs is shown in Table 6.
 Table 6. Score matrix of normalized aggregated TrVIFNs for the determination of the criteria weight of the TrVIF-MEREC method.
Table 6. Score matrix of normalized aggregated TrVIFNs for the determination of the criteria weight of the TrVIF-MEREC method. - Step 2(d): Using the formula given in Equation (12), we compute the overall performance of alternatives based on the score values obtained in the previous Step M3. Therefore,.Similarly, we get , , , , .
- Step 2(e): Using Equation (13), we calculate the performance of the alternatives by removing each criterion. Table 7 represents the values of for all , and . For example,
 Table 7. The values of that are used for the determination of the criteria weight of the TrVIF-MEREC method..
Table 7. The values of that are used for the determination of the criteria weight of the TrVIF-MEREC method.. - Step 2(f): Using the result given in Equation (14), we can calculate the absolute deviations , which are given below:, , , , , , , , , , .
- Step 2(g): Now, we determine the final weights of the criteria using Equation (15). Thus, the values of the final weights are as follows:, , , , , , , , , , .
Stage 3: Final score matrix and the ranking
Now, again, we apply the TrVIFAAWA aggregation operator from Equation (9) in the aggregated Table 4 and Table 5 with the help of the criteria weights determined in Step 3(g) to obtain the final aggregated values of each alternative in the form of TrVIFN. The values of each alternative in the form of TrVIFNs are as follows:
,
,
,
,
,
- Step 3(a): By incorporating the score function presented in Equation (1), we determine the score value of all alternative locations; that is, , , , , , and ,
- Step 3(b): According to Definition (5), we observes that . Thus, based on the proposed Algorithm 1, we determined that “location 6” is the best location.
6.2.2. Solving Example Section 6.2 Using the Proposed TrVIF-WASPAS Algorithm 2
Here, we solve Example Section 6.2 using our proposed TrVIF-WASPAS algorithm defined in Section 2.
- Step W1: In this step, we collect the initial decision matrix, which is obtained after applying our proposed aggregation operator defined in Equation (9). We obtain a single aggregated decision matrix from the group decision matrix. Table 4 and Table 5 represent the single aggregated decision matrix.
- Step W2: After solving Step W1 above, in this step, we apply the process of normalization. Here, all the criteria except the criterion are of the benefit type. Therefore, we will use the the criterion only in Step W2(b) (that is, changing the information value from membership to non-membership and vice versa). For all other benefit criteria from to , the data are same as given in aggregated Table 4 and Table 5.
- Step W3: Using Equation (16), we can calculate the WSM for each alternative, which can be written as follows:,,,,,.
- Step W4: Using Equation (17), we compute the WPM for each alternative as follows:,,,,..
- Step W5: The aggregated measure of the WASPAS method for each alternative using Equation (18) is obtained as follows:
- Step W6: Now, we apply the score function given in Equation (1) according to Definitions 4 and 5 to . For each alternative, we get, , , , ,Thus, the ranking of alternatives is . Therefore, using the proposed Algorithm 2, we again identified “location 6” as the best location.
Thus, using both proposed Algorithms 1 and 2 (that have been thoroughly solved in Section 6.2.1 and Section 6.2.2), we identify “location 6” as the optimal location. Hence, “location 6” is the optimal location for wind power plant projects. In the next Section 7, we will discuss and examine variations in location via slight changes in the criteria weights. Also, we see which location will come at maximum times and which will be preferred more after implementing various subtle changes in the criteria weights instead of fixing a particular weight.
7. Sensitivity Analysis
Firstly, we consider the eleven criteria, then we take various criteria weights like increasing, decreasing, and random weights. Here, we deal with ten different weights from sets S1 to S10 for each criterion, which are given in Table 8.

Table 8.
Various sets of different criteria weights.
Here, we apply our proposed TrVIFAAWA aggregation operator to the same numerical Example Section 6.2 for the different sets of criteria weights from Table 8. For different parameters , we can easily observe the ranking in Table 9, Table 10, Table 11, and Table 12. For example, if we choose the set of criteria S1 and the value of parameters to , , and , we obtain the best alternative as . Similarly, in most cases, with little changes in the criteria weights, the best alternative locations are always ranging between , , and , while the alternatives locations , , and are in the worst cases. But in most cases, 96 out of 120 cases, we found that the alternative —that is, “location 1”—was the best alternative. We found that the alternative —that is, “location 6”—was the best in only 24 out of the 120 cases. Overall, we can say that “location 1” is the best location. Therefore, one can choose “location 1” for selecting the best site for wind power plant projects.

Table 9.
Ranking of alternatives for different values of parameter for sets , , and .

Table 10.
Ranking of alternatives for different values of parameter for sets and .

Table 11.
Ranking of alternatives for various values of parameter for different sets ( to ) of criteria weights.

Table 12.
Ranking order of alternatives for different values of parameter for sets and .
Figure 3 below shows a diagrammatic representation of the sensitivity analysis of our proposed TrVIFAAWA aggregation operator for distinct combinations of criteria weights for the parameter . In the figure, we can clearly see that the alternative , that is, “location 1”, is the best.
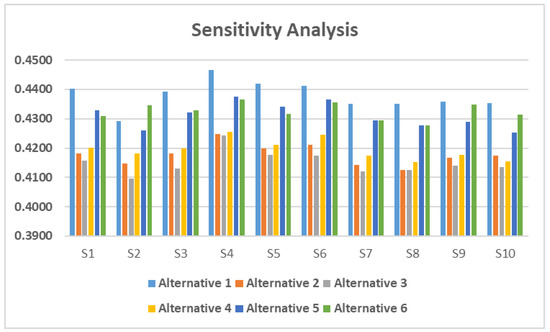
Figure 3.
Sensitivity analysis for parameter in TrVIFAAWA operator w.r.t. various criteria weights from S1 to S10.
Figure 4 below shows a diagrammatic representation of the sensitivity analysis of our proposed TrVIFAAWA aggregation operator for ten sets (S1 to S10) of criteria weights (given in Table 8) for the parameter . Also, from the figure, we can clearly see that the alternative , that is, “location 1”, is the best.
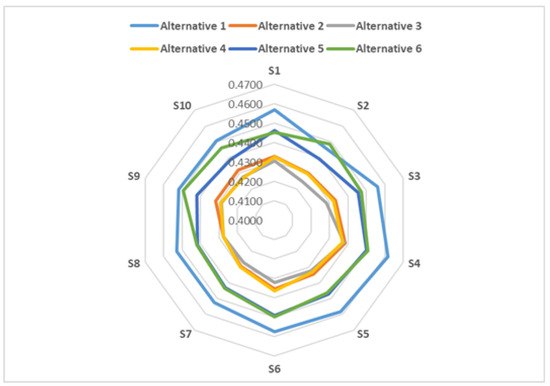
Figure 4.
Sensitivity analysis for parameter in TrVIFAAWA operator w.r.t. various criteria weights from S1 to S10.
8. Comparative Study
In this section, we compare our proposed methods with various existing methods. Here, we consider a numerical problem and solve it using the proposed decision-making methods and the existing methods to show the effectiveness of the proposed method with various existing approaches.
Example 2.
Let us consider an MCDM problem that deals with four different criteria that are of the benefit type, say , , , and . There are five alternatives, say , , , , and . The matrix below represents the data given by the decision-maker for each alternative with respect to the corresponding criteria. Here, the weights of the criteria can be calculated using our proposed TrVIF-MEREC method, and they are found to be , , , and for the criteria , , , and , respectively.
8.1. Solving Example 2 Using Our Proposed TrVIF-WASPAS Defined in Algorithm 2
- Step W1: Here, in the given decision matrix above, the entries of IVIFN can be converted into the TrVIFN, as TrVIFN is an extension of IVIFN. For example, is the same as.
- Step W2: All of the criteria presented here are of the benefit type, so in the process of normalization, they are the same as the original data.
- Step W3: Using Equation (16), we can calculate the WSM for each alternative, which can be written as follows:,,,,.
- Step W4: Using Equation (17), we compute the WPM for each alternative. The values are as follows:,,,,.
- Step W5: The aggregated measure of the WASPAS method for each alternative using Equation (18) is obtained as follows:
- Step W6: Now, we apply the score function given in Equation (1) to for each alternative, and we get, , , , .Thus, the ranking of alternatives is .
8.2. Solving Example 2 Using Different Prevailing Techniques
Here, we compare our proposed method with different types of existing methods—for example, Xu [35]: IVIFWA and IVIFWG operators, Wang and Liu [36]: IVIFEWA and IVIFEWG operators, Ye [37]: IVIFWA and IVIFWG operators, Sahin [38]: IVIFWA and IVIFWG operators, Nayagam et al. [39]: IVIFWA and IVIFWG operators, Meher et al. [22]: TrVIFDWG operator, and Meher and Jeevaraj [18]: TrVIFAAWG operator—to validate the effectiveness of the developed method.
The ranking outcomes obtained from Xu [35]: IVIFWA operator, Wang and Liu [36]: IVIFEWA operator, Ye [37]: IVIFWA operator, Ye [37]: IVIFWG operator, Sahin [38]: IVIFWA operator, and Nayagam et al. [39]: IVIFWA operator are identical to the results of our proposed method, TrVIFAAWA and TrVIF-WSM. Similarly, Xu [35]: IVIFWG operator, Wang and Liu [36]: IVIFEWG operator, Sahin [38]: IVIFWG operator, and Meher and Jeevaraj [18]: TrVIFAAWG operator are identical to the proposed method, TrVIF-WPM. Nayagam et al. [39]: IVIFWG operator ranks the same as our proposed TrVIF-WASPAS. In addition, the ranking obtained from Meher et al. [22]: TrVIFDWG operator is slightly different. However, the alternative always remains the optimal choice.
Table 13 represents our proposed methods and existing techniques with their score values and rankings of alternatives. Also, Figure 5 provides a diagrammatic representation of the ranking of alternatives, which shows that the alternative is the best alternative. Also, Tech 1 to Tech 10 in Table 13 use no parameter flexibility condition, but they use their score functions defined in their methodology. However, Tech 11, i.e., the TrVIFDWG aggregation operator-based method, sets the Dombi flexible parameter as 1. Similarly, Tech 12, i.e., the TrVIFAAWG aggregation operator-based method, consists of TrVIF-Topsis techniques to solve the group decision-making problem, and the Aczel-Alsina flexible parameter is 1. Also, our proposed method from Tech 13 to Tech 16 uses the total ordering principle in ranking, and the Aczel-Alsina flexible parameter is 1.

Table 13.
Comparative analysis with various existing methods.
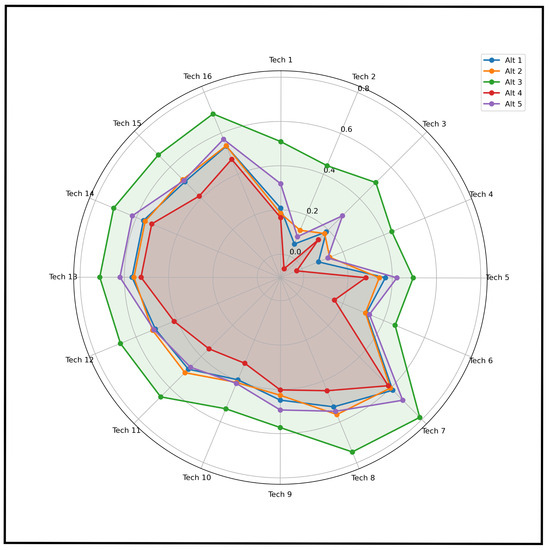
Figure 5.
Comparative analysis of rankings given in Table 13.
The main advantages and motivations for considering a different numerical Example 2 and providing a comparative analysis with popular existing techniques are based on the novelty of the proposed method in the environment of trapezoidal-valued intuitionistic fuzzy number (TrVIFN), which was introduced for the first time in the literature by Jeevaraj et al. [5] in the year 2023. There are only very few aggregation operators defined in this TrVIF environment of the fuzzy class, and we have compared our proposed method with all of those methods in this study. In addition, for comparative analysis, we chose a few existing approaches from the particular classes of trapezoidal-valued intuitionistic fuzzy numbers (TrVIFNs), such as real-valued IFNs and IVIFNs, since the class of TrVIFN is the generalized class of IFNs and IVIFNs.
8.3. Statistical Analysis
A statistical analysis was performed to check the ranking consistency between two variables. This is a non-parametric measure, as it does not require the data to follow a normal distribution, but it operates on ranked values instead of the original data points. Here, we present the statistical analysis to check the ranking consistency of Example 2. We use Spearman’s rank correlation coefficient [41] to calculate the consistency of the ranking. The formula for calculating Spearman’s rank correlation coefficient () is given as follows:
where ‘m’ indicates the number of observations and ‘’ represents the differences in ranks between the results. Also, we can say that = ranking scenario i—ranking scenario j. We can notice from Table 13 that we have four scenarios of ranking outcomes from the comparative analysis of the different techniques. The four ranking scenarios of outcomes (also illustrated in Table 14) are , , , and . Furthermore, we discuss the correlations between these four ranking scenarios. We apply the Spearman rank correlation coefficient using Equation (19) and obtain the following result.

Table 14.
Different ranking scenarios for numerical Example 2 for calculation of Spearman’s rank correlation coefficient.
By using the formula for the Spearman rank correlation coefficient given in Equation (19), we have , , , , , and . This shows that the Spearman’s correlation coefficeint between ranking scenario 1 (i.e., ) and ranking scenario 2 (i.e., ) is −0.3. That is, they are not correlated with each other. Similarly, the Spearman’s rank correlation coefficient values are reported in Table 15. Finally, we can say that ranking scenarios 1 and 3 are 90 % correlated with each other, which indicates that the methods whose ranking comes under ranking scenario 1 and scenario 3 are 90 % correlated.

Table 15.
Spearman’s rank correlation coefficient () between different ranking scenarios.
9. Conclusions
The concept of Aczel-Alsina operations on TrVIFN is introduced in this study by using the Aczel-Alsina (AA) t-norm and t-conorm concept. Several novel TrVIF aggregation operators are proposed for aggregating TrVIF data, including the TrVIFAAWA operator, the TrVIFAAOWA operator, and the TrVIFAAHA operator. TrVIFAAWA and TrVIFAAOWA aggregation operators are a special case of the TrVIFAAHA aggregation operator. However, all three proposed aggregation operators have their own importance. For example, the TrVIFAAWA aggregation operator considers only the TrVIFNs, whereas the TrVIFAAOWA aggregation operator deals only with the ordered position of TrVIFNs. Both the TrVIFAAWA and TrVIFAAOWA aggregation operators represent their weights in different forms. The properties of such aggregation operators are also examined. A practical numerical problem in the selection of a wind power plant project was solved to investigate the viability of the new TrVIFAAWA operator, and two decision-making Algorithms 1 and 2 were developed in consideration of the TrVIFAAWA operator on TrVIFNs. Our method consists of a total ordering principle in ranking and a new criterion weight finding method in TrVIFNs, for which the ranking consistency rate and performance are better than all the existing methods presented in the comparative analysis section. In addition, statistical analysis was performed to calculate the percentage correlation among the methods. No methods other than our proposed method, mentioned in the comparative section, introduce a new algorithm for determining the weights of the criteria; instead, all others assign random weights to the criteria. Sensitivity analysis is then performed to study how changes in criteria weights affect the ranking.
Limitations and Future Research Directions
As every aggregation operator is defined in the specific class of fuzzy numbers, and it is formulated with different types of combinations of functions, this leads the pathway to develop new types of aggregation operators in a new environment. Every aggregation operator consists of both merits and limitations. The limitations of our proposed method include the following. Our method does not apply to other classes of fuzzy numbers, like spherical fuzzy numbers and interval-valued q-rung orthopair fuzzy numbers. Additionally, computational complexity may occur for large-scale datasets. Secondly, in the case of a parameter sensitivity analysis, small variations can lead to notable changes in ranking results. Thirdly, different experts may interpret the same criteria differently, leading to variations in the final ranking results.
In the future, we intend to apply this proposed aggregation operator to a new class of fuzzy sets and apply it to various case studies and real-life problems. In addition, we can define some new aggregation operators in the TrVIFN class, since the TrVIFN class was introduced in 2023. Additionally, we will try to enhance the computational efficiency of the proposed aggregation operator to handle large-scale multi-attribute group decision-making (MAGDM) problems, possibly through algorithmic optimizations or approximation techniques. Also, our proposed method can be improved by integrating an operator with advanced machine learning methods for automatic weight determination.
Author Contributions
Conceptualization, B.B.M. and J.S.; Methodology, B.B.M., J.S. and M.A.; Validation, B.B.M., J.S. and M.A.; Formal analysis, B.B.M., J.S. and M.A.; Investigation, J.S.; Resources, J.S. and M.A.; Data curation, B.B.M., J.S. and M.A.; Writing—original draft, B.B.M. and J.S.; Writing—review & editing, B.B.M., J.S. and M.A.; Visualization, B.B.M., J.S. and M.A.; Supervision, J.S.; Funding acquisition, J.S. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU252938].
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Stoeva, S. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval valued intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets: Theory and Applications; Physica-Verlag: Heidelberg, Germany, 1999; pp. 139–177. [Google Scholar]
- Nehi, H.M.; Maleki, H.R. Intuitionistic fuzzy numbers and it’s applications in fuzzy optimization problem. In Proceedings of the 9th WSEAS International Conference on Systems, Athens, Greece, 11–13 July 2005; pp. 1–5. [Google Scholar]
- Jeevaraj, S.; Rajesh, R.; Lakshmana Gomathi Nayagam, V. A complete ranking of trapezoidal-valued intuitionistic fuzzy number: An application in evaluating social sustainability. Neural Comput. Appl. 2023, 35, 5939–5962. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 22, 215–219. [Google Scholar]
- Jianqiang, W.; Zhong, Z. Aggregation operators on intuitionistic trapezoidal fuzzy number and its application to multi-criteria decision making problems. J. Syst. Eng. Electron. 2009, 20, 321–326. [Google Scholar]
- Aczél, J.; Alsina, C. Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Math. 1982, 25, 313–315. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Yager, R.R. Aczel–Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int. J. Intell. Syst. 2022, 37, 1529–1551. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Mesiar, R.; Yager, R.R. Novel Aczel–Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int. J. Intell. Syst. 2022, 37, 5059–5081. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Mesiar, R.; Yager, R.R. Intuitionistic fuzzy geometric aggregation operators in the framework of Aczel-Alsina triangular norms and their application to multiple attribute decision making. Expert Syst. Appl. 2023, 212, 118832. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Karamti, H.; Khan, Q.; Mahmood, T. Multi-attribute group decision-making based on q-rung orthopair fuzzy Aczel–Alsina power aggregation operators. Eng. Appl. Artif. Intell. 2023, 126, 106629. [Google Scholar] [CrossRef]
- Garg, H.; Mahmood, T.; ur Rehman, U.; Nguyen, G.N. Multi-attribute decision-making approach based on Aczel-Alsina power aggregation operators under bipolar fuzzy information & its application to quantum computing. Alex. Eng. J. 2023, 82, 248–259. [Google Scholar]
- Wang, H.; Xu, T.; Feng, L.; Mahmood, T.; Ullah, K. Aczel–Alsina Hamy mean aggregation operators in T-spherical fuzzy multi-criteria decision-making. Axioms 2023, 12, 224. [Google Scholar] [CrossRef]
- Meher, B.B.; Jeevaraj, S. Interval-valued fermatean fuzzy Aczel-Alsina geometric aggregation operators and their applications to group decision-making. Phys. Scr. 2024, 99, 095027. [Google Scholar] [CrossRef]
- Demir, G.; Riaz, M.; Deveci, M. Wind farm site selection using geographic information system and fuzzy decision making model. Expert Syst. Appl. 2024, 255, 124772. [Google Scholar] [CrossRef]
- Meher, B.B.; Jeevaraj, S. Trapezoidal-valued intuitionistic fuzzy Aczel-Alsina weighted geometric aggregation operator and its applications to selection of e-learning platform. Comput. Appl. Math. 2025, 44, 285. [Google Scholar] [CrossRef]
- Ali, J. Multi-criteria decision-making method based on an integrated model using T-spherical fuzzy aczel-alsina prioritized aggregation operators. Comput. Appl. Math. 2025, 44, 181. [Google Scholar] [CrossRef]
- Shit, C.; Ghorai, G. A novel Aczel-Alsina aggregation operators based multi-criteria group decision making approach under Hesitant fuzzy set for the selection of best brand in Educational Institution. Eng. Appl. Artif. Intell. 2025, 158, 111464. [Google Scholar] [CrossRef]
- Senapati, T. An Aczel-Alsina aggregation-based outranking method for multiple attribute decision-making using single-valued neutrosophic numbers. Complex Intell. Syst. 2024, 10, 1185–1199. [Google Scholar] [CrossRef]
- Meher, B.B.; S, J.; Alrasheedi, M. Dombi weighted geometric aggregation operators on the class of trapezoidal-valued intuitionistic fuzzy numbers and their applications to multi-attribute group decision-making. Artif. Intell. Rev. 2025, 58, 205. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Al-Barakati, A.; Mishra, A.R.; Mardani, A.; Rani, P. An extended interval-valued Pythagorean fuzzy WASPAS method based on new similarity measures to evaluate the renewable energy sources. Appl. Soft Comput. 2022, 120, 108689. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of objective weights using a new method based on the removal effects of criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Shang, C.; Jiang, J.; Zhu, L.; Saeidi, P. A decision support model for evaluating risks in the digital economy transformation of the manufacturing industry. J. Innov. Knowl. 2023, 8, 100393. [Google Scholar] [CrossRef]
- Tripura, C.; Chakraborty, S.; Bhattacharya, B. Picture Fuzzy Aggregation Operator-Based Integrated MEREC-WASPAS Technique for Video Conferencing Tool Selection. J. Uncertain Syst. 2024, 17, 2450003. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper III: Continuous t-norms. Fuzzy Sets Syst. 2004, 145, 439–454. [Google Scholar] [CrossRef]
- Alsina, C.; Schweizer, B.; Frank, M.J. Associative Functions: Triangular Norms and Copulas; World Scientific: Singapore, 2006. [Google Scholar]
- Yeh, T.M.; Huang, Y.L. Factors in determining wind farm location: Integrating GQM, fuzzy DEMATEL, and ANP. Renew. Energy 2014, 66, 159–169. [Google Scholar] [CrossRef]
- Shafiee, M. Wind energy development site selection using an integrated fuzzy ANP-TOPSIS decision model. Energies 2022, 15, 4289. [Google Scholar] [CrossRef]
- Nasehi, S.; Karimi, S.; Jafari, H. Application of fuzzy GIS and ANP for wind power plant site selection in East Azerbaijan Province of Iran. Comput. Res. Prog. Appl. Sci. Eng. 2016, 2, 116–124. [Google Scholar]
- Lee, A.H.; Chen, H.H.; Kang, H.Y. Multi-criteria decision making on strategic selection of wind farms. Renew. Energy 2009, 34, 120–126. [Google Scholar] [CrossRef]
- Tegou, L.I.; Polatidis, H.; Haralambopoulos, D.A. Environmental management framework for wind farm siting: Methodology and case study. J. Environ. Manag. 2010, 91, 2134–2147. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Interval-valued intuitionistic fuzzy hybrid weighted averaging operator based on Einstein operation and its application to decision making. J. Intell. Fuzzy Syst. 2013, 25, 279–290. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 2009, 36, 6899–6902. [Google Scholar] [CrossRef]
- Şahin, R. Fuzzy multicriteria decision making method based on the improved accuracy function for interval-valued intuitionistic fuzzy sets. Soft Comput. 2016, 20, 2557–2563. [Google Scholar] [CrossRef]
- Nayagam, V.L.G.; Jeevaraj, S.; Dhanasekaran, P. An intuitionistic fuzzy multi-criteria decision-making method based on non-hesitance score for interval-valued intuitionistic fuzzy sets. Soft Comput. 2017, 21, 7077–7082. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. The multi-attribute decision making method based on interval-valued intuitionistic fuzzy Einstein hybrid weighted geometric operator. Comput. Math. Appl. 2013, 66, 1845–1856. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).