On Solving the Knapsack Problem with Conflicts

Abstract

A variant of the well-known Knapsack Problem is studied in this paper. In the classic problem, a set of items is given, with each item characterized by a weight and a profit. A knapsack of a given capacity is provided, and the problem consists of selecting a subset of items such that the total weight does not exceed the capacity of the knapsack, while the total profit is maximized. In the variation considered in the present work, pairs of items are conflicting, and cannot be selected at the same time. The resulting problem, which can be used to model several real applications, is considerably harder to approach than the classic one. In this paper, we consider a mixed-integer linear program representing the problem and we solve it with a state-of-the-art black-box software. A vast experimental procedure on the instances available from the literature, and adopted in the last decade by the community, indicates that the approach we propose achieves results comparable with, and in many cases better than, those of state-of-the-art methods, notwithstanding that the latter are typically based on more complex and problem-specific ideas and algorithms than the idea we propose.

1. Introduction

The classic Knapsack Problem [1] consists of selecting items from a given set, where each item is associated with a profit and a weight, in such a way that the total weight of the objects selected is below a given threshold and the total profit is maximized. In this work a generalization of the problem, known as the Knapsack Problem with Conflicts (KPC), where pairs $(i,j)$ of conflicting items are given, and for each pair at most one item can be part of the final solution. The capacity constraint and the objective remain unchanged.

The KPC arises as a subproblem in several algorithms in the Operations Research domain. For example, it is solved within branch-and-price methods for the Bin-Packing Problem [2] and the Bin-Packing Problem with Conflicts [3]. However, the KPC can be used to model in mathematical terms some real-world applications. For example, in the scheduling domain, where there are tasks that cannot be executed in parallel due to conflicting resources, the problem maps directly into a KPC.

The KPC was originally introduced in [4], where a local-search heuristic and a branch-and-bound method based on Lagrangian relaxation are discussed. In [5] the authors proposed some preprocessing techniques and a different branch-and-bound algorithm. Heuristic methods for the KPC were discussed in [6,7], the latter method being a matheuristic algorithm. Other metaheuristic approaches were finally presented in [8] (scatter search) and [9] (rounding heuristic). The KPC was proven to be $\mathcal{NP}$-hard in [10], where some special cases solvable in polynomial time are also highlighted. Finally, a branch-and-bound exact method based on binary branching was proposed in [3], while another branch-and-bound schema based on an n-ary branching was developed and tested in [11].

In the literature of Graph Theory and Algorithms, several classic optimization problems have been studied in one or more variants involving conflict constraints, demonstrating an increasing popularity of the topic, motivated by the number of related real-world applications. For example, theoretical results, heuristics, and exact algorithms were proposed for the Assignment Problem with Conflicts [12,13,14,15,16]; for the Set-Covering Problem with Conflicts [17,18,19,20]; for the Spanning Tree Problem with Conflicts—The MSTC [12,21,22,23,24,25,26]; for the Shortest-Path Problem with Conflicts [27,28,29,30,31]; and for the Maximum-Flow Problem with Conflicts [32,33,34,35,36,37].

In this paper, a mixed-integer linear programming model for the KPC is considered and solved by the open-source solver CP-SAT, which is part of the Google OR-Tools [38] optimization suite. The aim of the work is to understand if mixed-integer linear programs purely characterized by binary variables (like the one we consider) can be efficiently attacked by a solver (CP-SAT) mainly based on logical reasoning and Lazy Clause Generation [39]. Notice that successful applications of this solver on different optimization problems have been recently proposed [37,40,41]. An extensive experimental campaign on the benchmark instances previously proposed in the recent literature is finally presented and discussed.

The implications of the work are twofold: first, from a theoretical point of view, it extends the understanding of the potentials of the CP-SAT solver on binary linear programming models; second, from a practical point of view, a new approach to attack the real applications that can be model as a KPC is proposed. This approach is simpler to implement than most of those that previously appeared in the literature, since it relies on a black-box solver.

The overall organization of the paper can be summarized as follows. The Knapsack Problem with Conflicts is formally defined in Section 2. Section 3 discusses a mixed-integer linear programming model to represent the problem. In Section 4, the performances of the model are evaluated experimentally on the benchmark instances adopted in the literature in the last decade. The approach we propose is thoughtfully compared with recent state-of-the-art methods from the literature. Conclusions are finally drawn in Section 5.

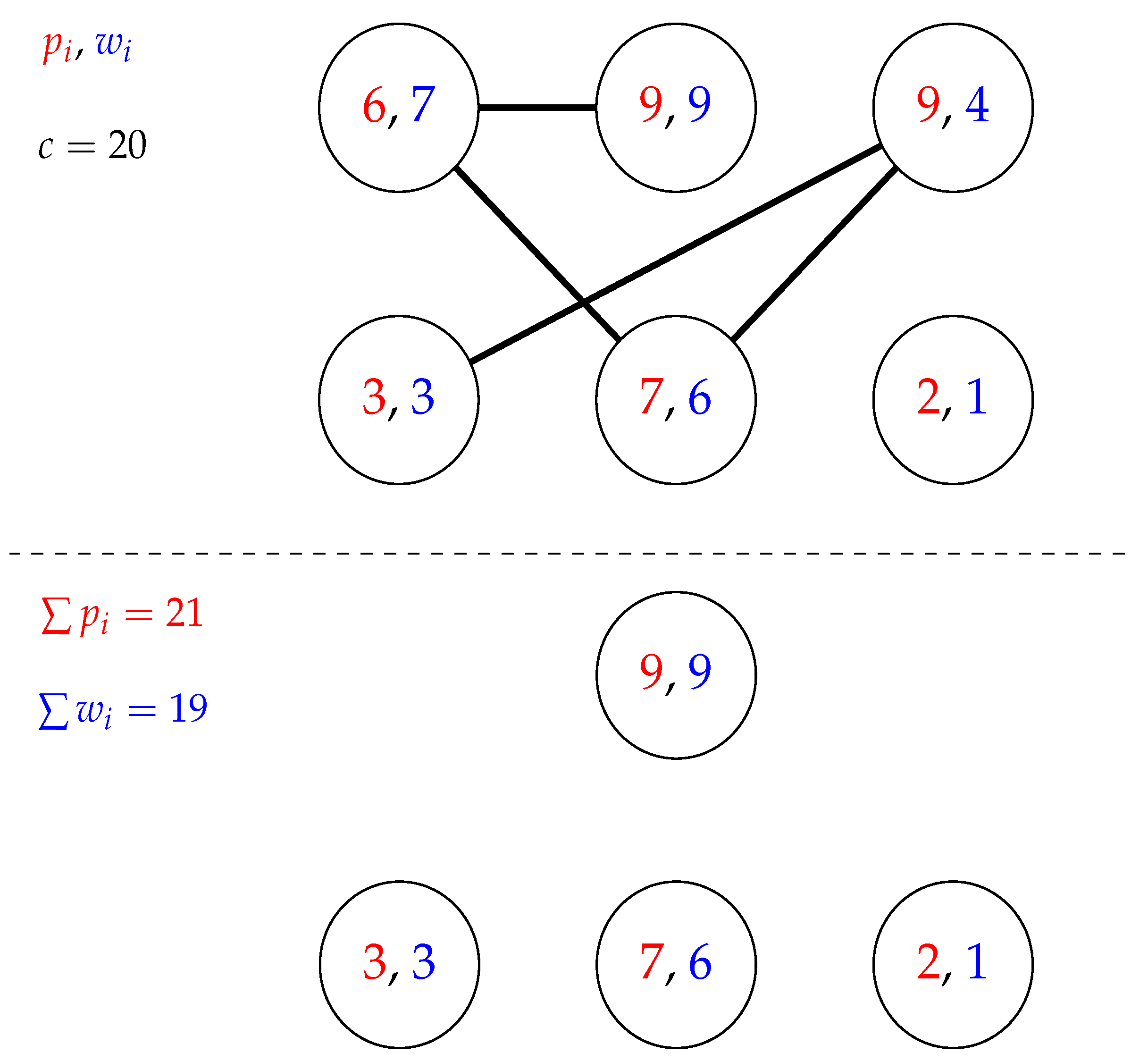
2. Formal Problem Description

The KPC can be formally defined as follows. Let $G=(V,E)$ be a graph where each vertex $i\in V$ is associated with an item, and each edge $\{i,j\}\in E$ models a conflict between the items i and j of V. A profit $p_i$ and a weight $w_i$ are provided for each item $i\in V$, and a capacity c of the knapsack is provided. The aim of the problem is to select a subset S of the items of V such that the total weight of the items of S is not greater than c, and no conflict is violated, which means $\forall i,j\in S,\{i,j\}\notin E$, and the total profit of the selected items is maximized.

An example of a KPC instance and a related optimal solution are depicted in Figure 1.

3. A Mixed-Integer Linear Programming Model

In this section, a mixed-integer linear programming model for the KPC, inspired by that discussed in [3], is presented. Once the model is defined, it fully describes the original optimization problem, and can be solved by black-box solvers to obtain the optimal solution, or at least approximations for it in case the model is too complex.

A variable $x_i$ is defined for each item $i\in V$. It takes a value of 1 if the item i is selected, 0 otherwise. The optimization problem will therefore search for an assignment of the x variables that maximizes the profit of the selected items, while respecting all the operational constraints. The objective of the optimization and the constraints are formally described through the following model:

$$\begin{array}{ccc}\hfill max& \sum _{i\in V}{p}_i{x}_i\hfill & \end{array}$$

(1)

$$\begin{array}{ccc}\hfill s.t.& \sum _{i\in V}{w}_i{x}_i\le c\hfill & \end{array}$$

(2)

$$\begin{array}{ccc}\hfill & x_i+x_j\le 1\hfill & \hspace{1em}\hspace{1em}\{i,j\}\in E\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill & x_i\in \{0,1\}\hfill & \hspace{1em}\hspace{1em} j\in V\hfill \end{array}$$

(4)

The objective function (1) imposes the maximization of the profit of the items selected. The operational constraints are imposed as flows. The inequalities (2) force the total weight of the selected items to be lower than or equal to the given capacity c. Observe that so far the model coincides with that of the classic Knapsack Problem. Inequalities (3) model the conflicts, imposing that at most one of a conflicting pair of items can be selected to be part of the solution. The latter constraints characterize the variant of the classic problem studied in the present work, and make the overall problem substantially more difficult from a computational point of view (see, for example, ref. [3]). To complete the formal model, the domain of the x variables has to be finally specified, and this is carried out in (4).

4. Computational Experiments

In Section 4.1, we describe the benchmark instances previously introduced in the literature for validating the algorithms presented in the last decade, and used for the present study. In Section 4.2, the approach we propose is compared from an experimental viewpoint against the other methods available in the literature, and positioned consequently.

4.1. Benchmark Instances

The first benchmark set adopted for the experiments was proposed in [3]. The instances are derived from those originally introduced in [42] for the Bin-Packing Problem. They consist of eight classes, each composed by 10 instances; in the first four classes, the items have weights that follow a uniform distribution in the range $[20,100]$ and the capacity c is 150. The number n of items is 120, 250, 500, and 1000, respectively. The last four classes have weights sampled with a uniform distribution in the range $[250,500]$ and a capacity of 1000. The instances have 60, 120, 349, and 501 items, respectively. A random conflict graph is generated for each instance, with density values in the range from 0.1 to 0.9, making a total of 90 instances for each class. A profit is associated with each item. Profits are either uniformly distributed in the interval $[1,100]$ (R instances, random), or defined as $p_i=w_i+10$ for each item i (C instances, correlated). Three copies of each instance are obtained by considering the original capacity ($C1$, $R1$), or a capacity obtained by multiplying the original one by 3 ($C3$, $R3$) or 10 ($C10$, $R10$). Overall, 4320 instances compose the first dataset.

The second group of instances—again first introduced in [3]—considers very sparse conflict graphs, with the densities 0.001, 0.002, 0.005 and 0.01. Capacities are either 1000 or 2000 and the number of items is 500 or 1000. Ten instances with random profits and ten with correlated profits were generated for each combination of parameters, for a total of 480 instances.

We refer the interested reader to [3] for a comprehensive description of the instances.

4.2. Experimental Results

The model discussed in Section 3 has been solved with the Google OR-Tools CP-SAT solver [38], version 9.12. The experiments have been run on a computer equipped with an Intel Core i7 12700F CPU. The experiments for the methods previously discussed in [3,11], and against which we compare, were run on an a machine equipped with an Intel Xeon CPU E5-2690, which according to [43] is approximately 10% slower than our machine. Moreover, in [11] the experiments were run on a single core, while we let the solver use all the potentialities of the processor. These two factors give an advantage to the approach we propose, although this will not change the outcome of the general experiments.

In details, the methods involved in the presented comparison are:

• CFS: a combinatorial branch-and-bound algorithm, introduced in [11];
• BCM: a branch-and-bound algorithm based on binary branching and a strong upper-bounding procedure, introduced in [3];
• ILP: three integer linear programming models discussed in [11] and solved with ILOG CPLEX 12.8 [44]. For each dataset, the results of the best of the three models are presented (notice that this gives a clear theoretical advantage to the method);
• CP-SAT: the mixed-integer linear program presented in Section 3 is solved with Google OR-Tools CP-SAT solver 9.12 [38].

Following the trend of the previous literature [3,11], all the methods considered were run for a maximum of 600 s on each instance. This allows for a fair comparison. We decided, however, to also consider longer runs of 3600 s on selected instances for CP-SAT, in order to better understand the behaviour of the solver and its potential. For each group of instances, the number of proven optimal solutions and the average time to find such optimal solutions are reported. For the method CP-SAT, the average optimality gap is also reported for the second benchmark set, in order to also measure the quality of the solutions when optimality could not be proven (this information was unfortunately not available for the other methods). Results in bold highlight improvements of CP-SAT over the state of the art.

The results on the first benchmark set are aggregated by class and type and presented in

Table 1. Results on the first benchmark set, correlated instances. Aggregation by class and type.

Instances		CFS [11]		BCM [3]		ILP [11]		CP-SAT
Class	Type	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Sec
C1	1	90	0.0	90	0.0	90	0.2	90	0.1
	2	90	0.0	90	0.0	90	1.1	90	0.3
	3	90	0.0	90	0.0	90	8.2	90	1.7
	4	90	0.0	90	0.0	90	24.2	90	14.4
	5	90	0.0	90	0.0	90	0.0	90	0.0
	6	90	0.0	90	0.0	90	0.1	90	0.1
	7	90	0.0	90	0.0	90	0.5	90	0.2
	8	90	0.0	90	0.0	90	3.6	90	0.7
C3	1	90	0.0	90	0.0	90	1.5	90	0.0
	2	90	0.0	90	0.1	90	25.8	90	0.1
	3	90	0.1	90	1.3	54	162.8	90	0.2
	4	90	1.6	90	27.3	21	141.9	90	1.9
	5	90	0.0	90	0.0	90	0.2	90	0.0
	6	90	0.0	90	0.0	90	2.0	90	0.0
	7	90	0.0	90	0.1	90	46.5	90	0.1
	8	90	0.0	90	0.6	59	35.3	90	0.2
C10	1	90	0.1	90	1.6	90	3.5	90	0.1
	2	90	25.2	73	31.9	68	126.2	90	0.3
	3	61	15.9	50	18.2	22	166.0	90	1.6
	4	50	47.2	40	108.8	1	575.1	90	14.5
	5	90	0.0	90	0.0	90	0.2	90	0.0
	6	90	0.5	90	6.8	90	5.3	90	0.1
	7	86	35.9	70	24.5	65	143.1	90	0.2
	8	60	7.3	49	17.4	20	156.4	90	0.7
Average		85.7	5.6	83.0	9.9	72.9	67.9	90.0	1.6

(correlated instances) and

Table 2. Results on the first benchmark set, random instances. Aggregation by class and type.

Instances		CFS [11]		BCM [3]		ILP [11]		CP-SAT
Class	Type	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Sec
R1	1	90	0.0	90	0.0	90	0.1	90	0.1
	2	90	0.0	90	0.0	90	0.8	90	0.2
	3	90	0.0	90	0.0	90	4.8	90	1.0
	4	90	0.0	90	0.1	90	10.1	90	9.0
	5	90	0.0	90	0.0	90	0.0	90	0.0
	6	90	0.0	90	0.0	90	0.1	90	0.1
	7	90	0.0	90	0.0	90	0.4	90	0.2
	8	90	0.0	90	0.1	90	2.7	90	0.8
R3	1	90	0.0	90	0.0	90	0.4	90	0.0
	2	90	0.0	90	0.0	90	5.0	90	0.1
	3	90	0.0	90	0.2	90	55.1	90	0.2
	4	90	0.1	90	2.3	50	127.2	90	1.9
	5	90	0.0	90	0.0	90	0.1	90	0.0
	6	90	0.0	90	0.0	90	0.5	90	0.0
	7	90	0.0	90	0.0	90	5.0	90	0.1
	8	90	0.0	90	0.2	90	64.7	90	0.2
R10	1	90	0.0	90	0.1	90	1.6	90	0.1
	2	90	0.8	90	9.1	87	107.4	90	0.2
	3	89	49.9	69	57.0	33	100.0	90	1.0
	4	51	23.2	40	25.0	8	333.6	90	9.0
	5	90	0.0	90	0.0	90	0.1	90	0.0
	6	90	0.0	90	0.2	90	1.5	90	0.1
	7	90	1.5	90	17.7	80	91.7	90	0.2
	8	79	19.5	69	43.2	30	77.0	90	0.8
Average		87.9	4.0	86.2	6.5	79.5	41.2	90.0	1.1

(random instances), and are aggregated by class and density in

Table 3. Results on the first benchmark set, correlate instances. Aggregation by class and density.

Instances		CFS [11]		BCM [3]		ILP [11]		CP-SAT
Class	Density	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Sec
C1	0.1	80	0.0	80	0.0	80	0.1	80	0.2
	0.2	80	0.0	80	0.0	80	0.2	80	0.4
	0.3	80	0.0	80	0.0	80	0.4	80	0.7
	0.4	80	0.0	80	0.0	80	0.6	80	1.2
	0.5	80	0.0	80	0.0	80	1.3	80	1.5
	0.6	80	0.0	80	0.0	80	2.7	80	3.2
	0.7	80	0.0	80	0.0	80	5.5	80	3.3
	0.8	80	0.0	80	0.0	80	14.4	80	5.2
	0.9	80	0.0	80	0.0	80	17.5	80	4.0
C3	0.1	80	0.2	80	0.3	77	11.2	80	0.2
	0.2	80	0.1	80	2.4	79	26.7	80	0.4
	0.3	80	0.4	80	6.6	72	27.7	80	0.7
	0.4	80	0.5	80	9.1	66	41.3	80	1.2
	0.5	80	0.5	80	9.6	52	74.6	80	1.6
	0.6	80	0.2	80	3.9	50	41.9	80	3.3
	0.7	80	0.1	80	1.0	50	11.0	80	3.3
	0.8	80	0.0	80	0.2	66	68.4	80	5.2
	0.9	80	0.0	80	0.0	72	27.2	80	3.9
C10	0.1	47	41.4	33	37.3	47	53.3	80	0.1
	0.2	50	79.0	30	4.4	30	4.5	80	0.1
	0.3	50	1.6	50	64.7	30	3.7	80	0.1
	0.4	70	11.5	50	3.7	48	169.0	80	0.2
	0.5	80	28.8	69	23.6	50	106.4	80	0.4
	0.6	80	1.2	80	52.5	50	38.2	80	0.4
	0.7	80	0.1	80	3.7	50	12.4	80	0.5
	0.8	80	0.0	80	0.3	70	75.8	80	0.5
	0.9	80	0.0	80	0.0	71	28.7	80	0.6
Average		76.2	6.1	73.8	8.3	64.8	32.0	80.0	1.6

(correlated instances) and

Table 4. Results on the first benchmark set, random instances. Aggregation by class and density.

Instances		CFS [11]		BCM [3]		ILP [11]		CP-SAT
Class	Density	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Sec
R1	0.1	80	0.0	80	0.0	80	0.1	80	0.3
	0.2	80	0.0	80	0.0	80	0.2	80	0.4
	0.3	80	0.0	80	0.0	80	0.3	80	0.8
	0.4	80	0.0	80	0.0	80	0.6	80	1.2
	0.5	80	0.0	80	0.0	80	0.9	80	1.5
	0.6	80	0.0	80	0.0	80	1.6	80	1.8
	0.7	80	0.0	80	0.0	80	4.8	80	2.1
	0.8	80	0.0	80	0.0	80	5.3	80	2.6
	0.9	80	0.0	80	0.0	80	7.2	80	2.2
R3	0.1	80	0.0	80	0.1	80	0.1	80	0.3
	0.2	80	0.0	80	0.1	80	1.0	80	0.4
	0.3	80	0.0	80	0.4	80	10.9	80	0.8
	0.4	80	0.0	80	0.7	78	35.6	80	1.2
	0.5	80	0.0	80	0.8	70	23.3	80	1.6
	0.6	80	0.0	80	0.6	70	46.3	80	1.8
	0.7	80	0.0	80	0.3	70	53.4	80	2.1
	0.8	80	0.0	80	0.1	74	45.2	80	2.5
	0.9	80	0.0	80	0.0	78	31.2	80	2.3
R10	0.1	71	11.2	69	59.9	72	16.0	80	0.1
	0.2	59	47.9	50	39.5	43	85.1	80	0.1
	0.3	70	42.8	50	3.9	44	139.2	80	0.1
	0.4	70	2.0	70	38.9	50	53.8	80	0.2
	0.5	80	7.2	70	3.9	50	51.6	80	0.4
	0.6	80	0.4	80	11.6	50	16.2	80	0.4
	0.7	80	0.1	80	1.3	54	38.5	80	0.5
	0.8	80	0.0	80	0.2	70	40.4	80	0.5
	0.9	79	0.0	79	0.0	75	44.6	80	0.6
Average		78.1	4.1	76.6	6.0	70.7	27.9	80.0	1.1

(random instances).

The results on the first benchmark set clearly highlight the superiority of the approach we propose, based on CP-SAT. The dominance does not appear to be affected by the details of the instances, and suggests that for these densities that are not in any non-extreme range, the CP-SAT solver firmly outperforms the others. It is the only method able to solve all the instances to optimality, and with computation times orders of magnitude lower than most of the competitors. It is worth observing that the ILP method seems to suffer more than the others when changing the types of instances. In particular, it faces trouble generally on instances of Type 3 and 4, especially for classes C10 and R10. When examining densities, once again problems seem to emerge for the ILP method, especially for values around 0.5, although the main issues seem to be related to class more than density.

The results on the second benchmark set are presented in

Table 5. Results on the second benchmark set, correlated instances. Aggregation by number of items/capacity and density.

Instances			CFS [11]		BCM [3]		ILP [11]		CP-SAT 600 s			CP-SAT 3600 s
Items	Capacity	Density	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Gap %	Sec	# Opt	Gap %	Sec
500	1000	0.001	10	0.0	10	0.0	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.002	10	0.0	10	0.6	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.005	10	0.2	10	6.7	10	0.0	10	0.00	13.1	10	0.00	13.1
		0.01	10	0.8	9	103.3	10	0.0	9	0.02	30.4	10	0.00	73.6
		0.02	10	56.7	1	272.7	10	0.3	10	0.00	24.8	10	0.00	24.8
		0.05	1	165.8	0	-	10	90.6	9	0.09	204.0	10	0.00	218.8
500	2000	0.001	10	4.2	10	0.4	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.002	10	0.1	10	5.2	10	0.0	10	0.00	0.2	10	0.00	0.2
		0.005	10	7.3	8	199.6	10	0.0	9	0.01	100.9	10	0.00	362.9
		0.01	7	49.8	0	-	10	0.0	6	0.04	5.3	8	0.02	296.9
		0.02	0	-	0	-	9	6.1	9	0.01	12.2	10	0.00	136.9
		0.05	0	-	0	-	0	-	0	2.77	-	0	1.97	-
1000	1000	0.001	10	0.1	10	5.4	10	0.0	10	0.00	0.3	10	0.00	0.3
		0.002	10	0.2	10	11.1	10	0.0	10	0.00	0.5	10	0.00	0.5
		0.005	10	5.9	5	379.9	10	0.0	7	0.05	22.5211	10	0.00	456.6
		0.01	7	163.9	0	-	10	0.1	2	0.14	84.5555	4	0.10	522.1
		0.02	0	-	0	-	7	2.4	5	0.11	2.8536	6	0.08	153.0
		0.05	0	-	0	-	0	-	0	4.72	-	0	3.44	-
1000	2000	0.001	10	3.1	9	84.7	10	0.0	10	0.00	8.7	10	0.00	8.7
		0.002	10	45.8	7	210.3	10	0.0	8	0.02	36.9609	9	0.01	188.2
		0.005	7	182.0	0	-	10	0.0	6	0.03	159.758	8	0.02	405.8
		0.01	4	0.0	0	-	9	0.1	6	0.04	100.436	7	0.03	196.0
		0.02	0	-	0	-	5	193.8	1	0.82	388.104	8	0.11	1697.2
		0.05	0	-	0	-	0	-	0	8.21	-	0	7.08	-
Average			6.5	38.1	4.5	98.5	8.3	14.0	7.0	0.71	56.9	7.9	0.54	226.5

for the correlated instances and in

Table 6. Results on the second benchmark set, random instances. Aggregation by number of items/capacity and density.

Instances			CFS [11]		BCM [3]		ILP [11]		CP-SAT 600 s			CP-SAT 3600 s
Items	Capacity	Density	# Opt	Sec	# Opt	Sec	# Opt	Sec	# Opt	Gap %	Sec	# Opt	Gap %	Sec
500	1000	0.001	10	0.0	10	0.0	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.002	10	0.0	10	0.1	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.005	10	0.0	10	0.4	10	0.0	10	0.00	0.2	10	0.00	0.2
		0.01	10	0.1	10	2.1	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.02	10	1.2	10	32.8	10	0.0	10	0.00	0.2	10	0.00	0.2
		0.05	9	132.7	3	133.2	10	1.2	10	0.00	1.2	10	0.00	1.2
500	2000	0.001	10	0.0	10	0.1	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.002	10	0.0	10	0.3	10	0.0	10	0.00	0.2	10	0.00	0.2
		0.005	10	0.1	10	2.4	10	0.0	10	0.00	0.2	10	0.00	0.2
		0.01	10	10.4	9	190.7	10	0.0	10	0.00	0.1	10	0.00	0.1
		0.02	3	116.5	1	39.6	10	0.1	10	0.00	0.2	10	0.00	0.2
		0.05	0	-	0	-	10	81.2	6	1.61	228.895	10	0.00	471.9
1000	1000	0.001	10	0.0	10	0.4	10	0.0	10	0.0	0.2	10	0.0	0.2
		0.002	10	0.0	10	1.6	10	0.0	10	0.0	0.4	10	0.0	0.4
		0.005	10	0.1	10	16.8	10	0.0	10	0.0	0.3	10	0.0	0.3
		0.01	10	15.0	8	152.6	10	0.1	10	0.0	0.2	10	0.0	0.2
		0.02	4	125.7	1	468.8	10	0.6	10	0.0	0.4	10	0.0	0.4
		0.05	0	-	0	-	9	255.0	3	2.9	139.3	10	0.00	943.3
1000	2000	0.001	10	0.0	10	2.3	10	0.0	10	0.00	0.3	10	0.00	0.3
		0.002	10	0.0	10	20.3	10	0.0	10	0.00	0.6	10	0.00	0.6
		0.005	9	69.5	2	189.9	10	0.0	10	0.00	0.3	10	0.00	0.3
		0.01	1	565.8	0	-	10	0.1	10	0.00	0.3	10	0.00	0.3
		0.02	0	-	0	-	10	2.1	10	0.00	10.2	10	0.00	10.2
		0.05	0	-	0	-	0	-	0	12.45	-	0	10.51	-
Average			7.3	51.9	6.4	66.0	9.5	14.8	9.1	0.71	16.7	9.6	0.44	62.2

for the random instances, with data aggregated by items/capacity and density in both the tables. For these experiments, the results of CP-SAT are reported for both a maximum computation time of 600 and 3600 s.

The results on both correlated and random instances of the second benchmark set suggest that on these problems, characterized by extreme low densities of the conflict graph, the method we propose remains competitive but is slightly inferior to the ILP approach when a maximum computation time of 600 s is considered. We remind the reader, however, that in the ILP column, the best of three different models is reported. It appears that the most critical values of densities are those around 0.02 and 0.05 for all methods. Larger instances with higher capacities are, on the other hand, the most difficult ones for all the approaches, although ILP appears to undergo slightly less critical degradation than the others.

When a longer computation time of 3600 s is considered, CP-SAT enhances its results, showing results comparable to that collected under the ILP column (the best of the three models). This suggests that the approach we propose requires more time on the critical instances where the density of the conflicts is 0.02 or 0.05. For other problems [37], it has been previously observed that CP-SAT could be slower than other methods on the most difficult instances, and this might be motivated by the more complex logical inference associated with larger or more difficult instances. This behaviour appears to be confirmed for the KPC.

Concerning CP-SAT, the method we propose, it is worth observing that even when optimality is not proven, the gap at the end of the computation is always extremely low (apart from the largest instances with density 0.05), demonstrating the effectiveness of the approach.

In conclusion, CP-SAT performs better than the other methods on most of the instances, but under very particular settings such as instances with densities of 0.02 and 0.05, and large instances in general, its superiority vanishes in favor of ILP, probably also due to the slower convergence that appears to characterize CP-SAT.

5. Conclusions

The Knapsack Problem with Conflicts, a problem used to represent, directly or indirectly, several real-world applications, has been studied in this paper.

A formulation based on a mixed-integer linear formulation for the problem has been considered and solved via the open-source solver CP-SAT, part of the Google OR-Tools computational suite.

An extensive experimental procedure has been run to compare the new method with those already available in the literature, and the results indicate that the approach we propose achieves a performance comparable with, and often better than, those of the state-of-the-art solvers available in the literature. Several instances were closed for the first time in the present study, notwithstanding the several other exact approaches developed in the last decade for the problem. However, the approach we propose sometimes appears to converge slower than the best of the other methods. This is especially evident for the largest and most challenging instances.

Lastly, it is important to observe that the good performance of the new approach is achieved in spite of the substantially smaller implementation effort required for the solution we propose when compared with the more complex and problem-dependent methods that appear in the existing literature.