Research on a Class of Set-Valued Vector Equilibrium Problems and a Class of Mixed Variational Problems

Abstract

This paper investigates the structural properties of solutions of vector equilibrium systems and mixed variational inequalities in topological vector spaces. Based on Himmelberg-type fixed point theorem, combined with the analysis of set-valued mapping and quasi-monotone conditions, the existence criteria of solutions for two classes of generalized equilibrium problems with weak compactness constraints are constructed. This work introduces an innovative application of the measurable selection theorem of semi-continuous function space to eliminate the traditional compactness constraints, and provides a more universal theoretical framework for game theory and the economic equilibrium model. In the analysis of mixed variational problems, the topological stability of the solution set under the action of generalized monotone mappings is revealed by constructing a new KKM class of mappings and introducing the theory of pseudomonotone operators. In particular, by replacing the classical compactness assumption with pseudo-compactness, this study successfully extends the research boundary of scholars on variational inequalities, and its innovations are mainly reflected in the following aspects: (1) constructing a weak convergence analysis framework applicable to locally convex topological vector spaces, (2) optimizing the monotonicity constraint of mappings by introducing a semi-continuous asymmetric condition, and (3) in the proof of the nonemptiness of the solution set, the approximation technique based on the family of relatively nearest neighbor fields is developed. The results not only improve the theoretical system of variational analysis, but also provide a new mathematical tool for the non-compact parameter space analysis of economic equilibrium models and engineering optimization problems. This work presents a novel combination of measurable selection theory and pseudomonotone operator theory to handle non-compact constraints, advancing the theoretical framework for economic equilibrium analysis.

1. Introduction

As key research areas of modern nonlinear analysis, vector equilibrium theory and variational inequality systems play a fundamental role in the modeling of complex systems. By extending the single-objective optimization paradigm to the multi-criteria decision space, the theoretical framework of this kind of mathematical tools has penetrated into the frontier fields of economic equilibrium analysis, Nash game strategy solving, and multi-physical field coupling optimization. The foundational work of Giannessi establishes a system of vector variational inequalities, which not only breaks through the limitations of traditional scalar constraints, but also promotes the paradigm shift of equilibrium problems from single-valued mappings to set-valued topological structures. However, most of the existing papers are based on strict compactness conditions or symmetric monotonicity assumptions, which limits the application of the theory to non-compact parameter spaces and asymmetric dynamic systems. Breaking through the traditional compactness constraint and establishing a more universal existence theory are key challenges in this field. In recent years, researchers have tried to relax the compactness condition by topological methods. For example, Hadjisavvas uses the KKM lemma to deal with quasi-monotone variational problems in Hausdorff locally convex spaces, but the result still depends on the global semicontinuity of the mapping. The Himmelberg fixed point theorem provides a potential tool for the analysis of non-compact spaces, but its applicability to vector-valued mappings has not been fully explored. These identified theoretical limitations demonstrate that current approaches face challenges in three areas. Two types of set-valued vector equilibrium problems and mixed variational problems are investigated. The detail content is as follows. In this article, $X,Y,Z$ are all topological vector spaces, E is a compact convex set, K and D are convex sets, and $E\subset K\subset X$, C is a non-empty closed convex cone in Z. Set-valued mapping $F:E\times D\times E\to 2^Z$, $T:E\to 2^D$.

Find $\overline{x}\in K$ to make $F(\overline{x},y,\overline{x})\not\subset -intC,\forall y\in T\left(\overline{x}\right).$                              (SVEP1)

Let $H,G:K\times D\to 2^Z$ be set-valued mapping. Consider another type of set-valued vector equilibrium problem as follows:

Find $\overline{x}\in K$ to make $H(\overline{x},y)+G(\overline{x},y)\subset C,\forall y\in D.$                               (SVEP2)

Let X be a topological vector space, set-valued mapping $T:K\to 2^{X^{*}}$, mapping $f:K\times K\to \mathbb{R},\eta :K\times K\to X.$

Find $\overline{x}\in K,\exists u\in T\left(\overline{x}\right)$ to make $\langle u,\eta (\overline{x},y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K.$                          (MVI)

Focusing on the above challenges, this paper proposes a new analytical framework based on pseudo-compactness. First, by introducing a family of relatively nearest neighbor domains in a locally convex space, the applicable conditions of the Himmelberg theorem are reconstructed, and the existence conditions of solutions are successfully weakened from global compactness to pseudo-compactness. Second, for mixed variational problems, KKM mappings with asymmetric semicontinuity are innovatively constructed. Combined with the theory of Brézis pseudomonotone operators, the closure property and compactification method of the solution set under generalized monotonicity are revealed. It is worth emphasizing that the conclusions of this paper are innovative in the following three aspects:

• The problem of set-valued vector equilibrium differs from the problem discussed in [1], and the proof method is also completely different. The Himmelberg fixed point theorem is mainly utilized to obtain the existence of solutions to the problem (SVEP1).
• Compared with [2], it is observable that the problem discussed in Theorem 2 is different from [2], particularly in terms of the method of proof. The main result of [2] is to use the theorem for discussion. The Himmelberg fixed point theorem is also utilized to obtain the existence result of the proposed problem (SVEP2).
• Theorem 5 discusses mixed variational problems under quasi compact conditions and improves and generalizes the results of recent literature on compact conditions, as shown in reference [3].

We emphasize that existing results (e.g., [1,2]) rely on strict compactness or symmetric monotonicity assumptions, which limit applications to non-compact spaces (e.g., unbounded parameter spaces in economic models). Our work relaxes these constraints via pseudo-compactness and asymmetric conditions. The Himmelberg fixed point theorem (Lemma 1) and KKM techniques are identified as underutilized tools for vector-valued mappings, bridging a gap noted in prior literature.

2. Related Work

In the 1990s, Blum and Oettli established the mathematical foundation of equilibrium problems through the principle of topological duality, which is isomorphic to the theory of variational inequalities and differential inclusions, and supports the functional analysis framework of economic dynamics, continuum mechanics, and intelligent control systems. In recent decades, it has attracted widespread attention and research from scholars both domestically and internationally. In the 1960s, Browder, Ky Fan, Lions, and others proposed variational inequalities and variational inclusion problems. In 1966, Hartman and Stampachia proposed the famous H-S variational inequality. Subsequently, variational inequalities and variational inclusion problems have been extensively studied and widely applied in various fields, such as economics, operations research, mechanics, differential equations, and transportation network modeling. The above questions provide us with an effective nonlinear theoretical framework, which has become a powerful tool for solving many practical and applied problems. This article uses different methods to study the existence of solutions for several types of set-valued vector equilibrium problems and variational inclusion problems, and improves and generalizes the recent results of relevant scholars.

The equilibrium problem was first proposed in the 1990s; here, let X be a topological vector space and $C\subseteq X$ be a non-empty closed convex subset, $f:C\times C\to \mathbb{R}$, $f(x,x)=0$, and find $x_0\in C$. By constructing set-valued topological dual spaces, Ansari-Oettli (1997) [4] extended the variational principle of classical single-valued functions to the framework of non-convex set-valued mappings, providing a measure-theoretic basis for the analysis of the multiplicity of generalized equilibrium problems. In 1998, Park proposed the generalized quasi equilibrium problem. In [5,6], Ansari and others extended the quasi equilibrium problem to vector quasi equilibrium problems. In 2003, Moudafi constructed a coupled model of monotone operators in the topological dual space, which integrates the equilibrium problem and the variational inequality theory, and provides a unified saddle point analysis framework for generalized non-convex optimization systems. The authors mainly used methods such as fixed point theorem, maximum element principle, KKM theorem, and Ekeland variational principle to study the existence of solutions to equilibrium problems and the properties of the solution set. In recent years, many scholars (such as [7,8]) have studied algorithms for solving equilibrium problems. In 2015, many scholars (such as [9,10]) used scalarization methods to study equilibrium problems. In 2016, Jae Ug Jeong [11] used the generalized viscous approximation method to discuss mixed equilibrium problems and fixed point problems, and Antonio Petraglia [12] used stochastic global optimization methods to discuss generalized Nash equilibrium problems. In 2019, Genaro López [13] and other scholars studied the existence of equilibrium problem solutions on Riemannian manifolds.

A recent work by Eslamizadeh and Naraghirad (2020) [14] on set-valued equilibrium problems in topological vector spaces provides additional insights into existence theorems under generalized convexity conditions, complementing our approach. Contemporary work on inertial algorithms has accelerated the convergence for equilibrium problems but remains limited to convex settings. Our C-concavity framework (Definition 3) may help extend these methods to non-convex cases prevalent in modern non-cooperative games. Variational inequalities and variational inclusion problems have been proposed and established by Browder, Ky Fan, Lions, and others since the 1960s. In 1966, Hartman and Stampachia proposed the famous H-S variational inequality: let K be a bounded closed convex subset in ${\mathbb{R}}^n$, and let $g:K\to {\mathbb{R}}^n$ be a continuous mapping. The problem requires finding $u\in K$ such that $\langle g\left(u\right),v-u\rangle \ge 0,\forall v\in K$. Browder improved and extended the H-S variational inequality. In 1987, Parida Sen introduced the quasi-variational inequality formulation, extending the classical variational inequality framework to problems with constraint sets depending on the solution. From 1992 to 1999, Yao, Ding, Lin, and others extended the variational-like inequality to the quasi-variational-like inequality. In 1994, Tan Yuan proposed the stochastic variational inequality. In 1995, Yao et al. extended the classical variational inequality to the multi-objective non-cooperative game system by establishing the cone order semi-continuous mapping theory in the topological vector lattice, and constructed the Pareto optimal coordination mechanism based on the cone order relation of set-valued mapping, which provided a strict criterion for the existence of asymmetric equilibrium for multi-dimensional conflict decision analysis. In 2008, Pang and Stewart [15] systematically studied differential variational inequality problems in finite dimensional Euclidean space. Combine differential inclusion problems with variational inequality problems. Variational inclusion is an important extension of variational inequalities, mainly using the general duality principle, Michael’s choice principle, and other methods to discuss the existence of solutions. In 1998, Noor introduced the variational inclusion problem, and Chang extended it to the set-valued quasi variational inclusion problem from 2000 to 2004. In 2008, Lai Jiu Lin and Chin-I Tu [16] studied the variational inclusion problem and variational separation problem. In 2014, Yekini Shehu [17] studied iterative algorithms for non-expanding semigroups and variational inclusion problems. In 2016, Haitao Che and Meixia Li [18] used conjugate gradient methods to study the existence of solutions for split variational inclusion problems.

Our work builds upon and extends prior advances along several key dimensions: First, while [1,3] established fundamental results for convex cases, and [2,19] made important progress in relaxing monotonicity assumptions, our framework makes three distinctive contributions: (1) the introduction of pseudo-compactness conditions that generalize the compactness requirements in [1,3]; (2) the development of C-convexity that properly contains the monotonicity relaxations in [2,19] as special cases; and (3) the novel combination of these concepts that enables applications to non-convex, non-monotone problems with unbounded domains—a setting not addressed by either of these prior approaches.

Recent breakthroughs in stochastic variational inequalities have enabled applications to large-scale machine learning. While their focus is on finite-dimensional noise handling, our Theorem 5’s pseudo-compactness framework may extend these results to infinite-dimensional cases common in functional data analysis. In the past 5 years, neural operator-based approaches have emerged for solving variational inequalities in high dimensions. Though data-driven, these methods require compactness assumptions that our work relaxes (see Remark 5’s engineering applications). The vector equilibrium problem and mixed variational problem have a unified theoretical framework and clear application background, such as optimization problems, economic issues, transportation issues, and medical issues. In recent years, it has received extensive attention and research from many scholars (see [7,8,9,10,11,12,13,15]). This article uses the Himmelberg fixed point theorem to study the existence of solutions to two types of generalized vector equilibrium problems. For mixed variational problems, for generalized monotonic mappings, the existence of solutions to mixed variational problems and the topological properties of the solution sets are studied using KKM techniques and appropriate assumptions. Especially in the study of compactness conditions, we have improved and promoted the relevant results of some scholars by changing them to quasi-compactness.

To illustrate the economic relevance of our set-valued equilibrium results (Theorems 1 and 2), consider a Nash game with n firms producing substitute goods. Let strategy sets be non-compact (reflecting unbounded production capacities), and profit functions be C-concave (Definition 3) due to regulatory constraints. Theorem 2 guarantees equilibrium existence without requiring compactness—a limitation in classical results like [2]. This directly extends applications to real-world markets with growth potential.

3. Materials and Methods

In order to study set-valued vector equilibrium and mixed variational problems, some useful definitions and lemmas are given as follows. For convenience, $\phi :X\to 2^Z$ represents the set-valued mapping.

Definition 1

([20]). φ is C-lower semi-continuous at $x_0$; for any neighborhood U of zero, there exists a neighborhood V of $x_0$, such that $\phi \left(x_0\right)\subset \phi \left(x\right)+U+C,\forall x\in V,$ where φ is C-upper semi-continuous at $x_0$ such that $\phi \left(x\right)\subset \phi \left(x_0\right)+U+C,\forall x\in V.$

Definition 2

([21]). φ is concave on X. $\forall x_1,x_2\in X,t\in (0,1)$, such that $\phi (t\ast x_1+(1-t)\ast x_2)\subset t\phi \left(x_1\right)+(1-t)\phi \left(x_2\right)$.

Definition 3

([21]). φ is C-convex on X. $\forall x_1,x_2\in X,t\in (0,1)$, such that $t\ast \phi \left(x_1\right)+(1-t)\ast \phi \left(x_2\right)\subset \phi (t\ast x_1+(1-t)\ast x_2)+C$.

Definition 4

([22]). Let E be a topological vector space. A set-valued mapping $F:K\subset E\to 2^E$ is called a KKM mapping if for any finite subset $\{y_1,y_2,\dots ,y_m\}\subset K$, $\mathit{co}\{y_1,y_2,\dots ,y_m\}\subset {\prod }_{i=1}^{m}F\left(y_i\right).$

Remark 1.

Let E be the Hausdorff topological vector space, $f:K\subset E$, $G:K\to 2^E$ is a two set-valued mapping, and F is a KKM mapping. If $F\left(y\right)\subset G\left(y\right),\forall y\in K$, it is apparent that G is also a KKM mapping.

Definition 5

([21]). Let E be a topological vector space. A function $f:K\subset E\to \mathbb{R}$ is called (lower) hemi-continuous if $\forall x,y\in K$; the mapping $t\mapsto f(tx+(1-t\left)y\right)$ is (lower semi-)continuous as $t\to 0^{+}$.

Definition 6

([3]). Let E be the topological vector space; $f:K\times K\to \mathbb{R}$ is a generalized $\alpha -\eta$-monotonic mapping. There are two functions, $\alpha :E\to \mathbb{R}$, $\eta :K\times K\to E$, that satisfy ${lim}_{t\to 0^{+}}{\displaystyle \frac{\alpha \left(\eta (x,x_t)\right)}{t}}\le 0,x_t=ty+(1-t)x,t\in [0,1],$ and $f(x,y)+f(y,x)\le \alpha \left(\eta \right(x,y\left)\right),\forall x,y\in K.$

Lemma 1

([22]). If X is a locally convex Hausdorff topological vector space, $K\subset X$ is a non-empty convex set, $E\subset K$ is a non-empty compact set, and $T:K\to 2^E$ is an upper semi-continuous set-valued mapping with closed convex values, then T has a fixed point in K.

Lemma 2

([23]). If X is a topological vector space, $A,B$ are non-empty subsets, A is a compact set, B is a closed set, and $A\cap B=\varnothing$, then there exists a neighborhood V of zero such that $(A+V)\cap (B+V)=\varnothing$.

Lemma 3

([24]). Set-valued mapping $\phi :X\to 2^Z$, the graph of φ is a closed set, and the closure of $\phi \left(x\right)$ is a compact set. Then φ is upper semi-continuous.

Lemma 4

([21]). Let $T:K\to 2^{E^{\ast }}$ be a set-valued mapping, and $K\subset E$ be a non-empty pseudo-compact subset. Satisfy the following:

 (1)

$\forall x\in K,T\left(x\right)$ is non-empty and has a convex value.

 (2)

T has local intersection properties.

Then there is a continuous selection of T. There exists a continuous mapping $h:K\to E^{\ast }$ such that $h\left(x\right)\in T\left(x\right),\forall x\in K$.

Lemma 5

([25]). If the mapping $h:K\to E^{\ast }$ is set to $\overline{x}\in K$, such that $\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K,$ then this variational problem is called V). If VI has a solution and T satisfies Lemma 2.4, then MVI also has a solution.

Lemma 6

([21]). Let E be a topological vector space, and $K\subset E$ be a non-empty convex set. $F:K\to 2^E$ is a KKM mapping, $\forall y\in K$, $F\left(y\right)$ is a closed set, a compact convex subset $B\subset K$, and ${\bigcup }_{x\in B}F\left(x\right)$ is a compact set. Then ${\bigcap }_{x\in B}F\left(x\right)\ne \varnothing$.

4. The Equilibrium Problem of Set Valued Vectors

The findings regarding the set-valued vector equilibrium problems (SVEP1 and SVEP2) will be investigated. By using Himmelberg’s fixed point criterion, the theoretical construction and logical verification of the existence of SVEP solutions are completed.

Theorem 1.

Let $X,Y,Z$ all be topological vector spaces, E be compact convex sets, K be convex sets, $E\subset K\subset X$. Convex sets $D\subset Y$. C is a non-empty closed convex cone in Z and $C_1=-C$, the set-valued mapping $F:E\times D\times E\to 2^Z$, $T:E\to 2^D$. The set-valued vector equilibrium problem (SVEP1) has a solution.

 (1)

There is $x_0\in E$, $\forall y\in T\left(x_0\right),\forall u\in K$; there is $0\in F(x_0,y,u)$.

 (2)

T is lower semi-continuous on E and C-lower semi-continuous for $\forall u\in K$, $(x,y):$ $y\in T\left(x\right)\to F(x,y,u).$

 (3)

T is concave, $F(x,y,u)$ is convex with respect to x, and y is $C_1$ with respect to $\forall u\in K$.

 (4)

Mapping $u\to F(x,y,u)$ is C-upper semi-continuous.

 (5)

C satisfies: for $\forall c_1,c_2\notin -\mathrm{int}C$; there exists $t\in (0,1)$ such that $t{c}_1+(1-t)c_2\notin -C.$

Proof. 

Let $S:K\to 2^E$ be the set-valued mapping, and $S\left(u\right)=\{x\in E\mid \forall y\in T(x),F(x,y,u)\not\subset -\mathrm{int}C\}.$ Condition (1) guarantees that the set-valued mapping $S\left(u\right)$ is non-empty.

First, we will prove that the set-valued mapping S is close-valued. Set up a network $\left\{x_a\right\}\subset S\left(u\right),\mathrm{and}{x}_a\to x_0,x_a\in S\left(u\right),$ that is,

$$F(x_{\alpha },y_{\alpha },u)\not\subset -intC,\forall y_{\alpha }\in T\left(x_{\alpha }\right).$$

(1)

By contradiction, assume there exists $y_0\in T\left(x_0\right)$ such that $F(x_0,y_0,u)\subset -\mathrm{int}C$. Since T is lower semi-continuous at $x_0$ and $y_0\in T\left(x_0\right)$, there exists a $y_{\alpha }\in T\left(x_{\alpha }\right)$ such that $y_{\alpha }\to y_0$. Because F is $C_1$-lower semi-continuous with respect to variables x and y, there exists a neighborhood V of $x_0$ and a neighborhood U of $y_0$. When $x_{\alpha }\in V$ and $y_{\alpha }\in U$, there exists $F(x_{\alpha },y_{\alpha },u)\subset F(x_0,y_0,u)-C\subset -intC-C=-intC,$ which is contradictory with Formula (1). Therefore, the set-valued mapping S is close-valued.

Second, prove that the set-valued mapping S is convex. Let $x_1,x_2\in S\left(u\right)$ and $\forall y_i\in T\left(x_i\right),F(x_i,y_i,u)\not\subset -\mathrm{int}C,i=1,2.$ By the same method, assume that there exists $y_3\in T\left(x_3\right)$ and $x_3=t{x}_1+(1-t)x_2$ such that $F(x_3,y_3,u)\subset -\mathrm{int}C$. Since T is concave, $T\left(x_3\right)=T(t{x}_1+(1-t)x_2)\subset T\left(x_1\right)+(1-t)T\left(x_2\right).$ Therefore, there exist $y_1\in T\left(x_1\right)$ and $y_2\in T\left(x_2\right)$ satisfied with $y_3=t{y}_1+(1-t)y_2,0<t<1.$ It follows from F is $C_1$-convex with respect to x and y that $tF(x_1,y_1,u)+(1-t)F(x_2,y_2,u)\subset F(t{x}_1+(1-t)x_2,t{y}_1+(1-t)y_2,u)-C=F(x_3,y_3,u)-C=-\mathrm{int}C.$ It can be readily observed that $v_i\in F(x_i,y_i,u),v_i\notin -\mathrm{int}C,i=1,2$. Therefore, $t{v}_1+(1-t)v_2\in -\mathrm{int}C\subset -C$, which is contradictory with (5). It is seen that the set-valued mapping S is convex.

Finally, prove that S is upper semi-continuous. It is seen that there exists an open set U such that $S\left(u_0\right)\subset U$. Let net $u_{\alpha }\to u_0$; there exists $u_{\alpha }$ to make $S\left(u_{\alpha }\right)\not\subset U$ equivalent to exist $x_1\in S\left(u_{\alpha }\right),x_1\notin U$. We have $F(x_1,y_1,u_{\alpha })\not\subset F(x_1,y_1,u_0)\not\subset -\mathrm{int}C.$ F is $C_1$-upper semi-continuous with respect to u; therefore, $F(x_1,y_1,u_{\alpha })\subset F(x_1,y_1,u_0)-C\subset -\mathrm{int}C$ contradicts the above equation. Therefore, the set-valued mapping S is satisfied with the condition of Lemma 1, which means there exists a $\overline{x}\in K$ and $\overline{x}\in S\left(\overline{x}\right)$. □

Corollary 1.

Let R be a real space, set $E,D$ be non-empty subsets of R, and map $f:E\times D\times E\to R$, $T:E\to D$ meet the following conditions:

 (1)

There exists $x_0\in E$, such that $f(x_0,T\left(x_0\right),u)=0,\forall u\in E$.

 (2)

T is lower semi-continuous on E; $(x,Tx)\to f(x,Tx,u)$ is lower semi-continuous.

 (3)

T is concave; $f(x,Tx,u)$ is convex with respect to $x,y$.

 (4)

Regarding u, $f(x,y,u)$ is upper semi-continuous.

Then there exists $\overline{x}\in K$, such that $f(\overline{x},y,\overline{x})>0,\forall y\in T\left(\overline{x}\right)$.

Remark 2.

Unlike in [1], which studied single-valued strong vector quasi-equilibrium problems under local convexity assumptions (see [1]), our set-valued formulation (SVEP1) in Theorem 1 (i) handles non-convex objectives via C-lower semi-continuity (Definition 1), and (ii) establishes solutions without requiring the local convexity conditions imposed in [1] (cf. our Lemma 1 application). While [1] required local convexity (their Assumption A3), the C-lower semicontinuity (Definition 1) of Theorem 1 handles non-convex production sets common in digital economies (see Section 6 example). The Himmelberg fixed point theorem is mainly utilized to obtain the existence of solutions to the problem (SVEP1).

Theorem 2.

Let $X,Y,Z$ all be topological vector spaces, E be compact convex sets, K be convex sets, and $E\subset K\subset X$. Convex sets $D\subset Y$. C is a non-empty closed convex cone in Z, and the set-valued mappings $H,G:K\times D\to 2^Z$.

 (1)

$G:K\times D\to 2^Z$ is a convex value.

 (2)

Regarding the first variable, H is C-concave and C-lower semi-continuous.

 (3)

Regarding the first variable, G is C-lower semi-continuous.

Then the set-valued vector equilibrium problem (SVEP2) has a solution.

Proof. 

Let $S:K\to 2^E$ be the set-valued mapping with $S\left(u\right)=\{x\in E\mid H(x,y)+G(u,y)\subset C,\forall y\in D\}\mathrm{for}u\in K.$

If $A_1=\{x\in K\mid H(x,y)+G(u,y)\subset C,\forall y\in D\}$, then if $S\left(u\right)=A_1\cap E$, and $x_1,x_2\in A_1$ are chosen, then one has $H(x_i,y)+G(u,y)\subset C,\forall y\in D,i=1,2.$

Therefore, for any $t\in (0,1)$, $tH(x_1,y)+tG(u,y)\subset C\mathrm{and}(1-t)H(x_2,y)+(1-t)G(u,y)\subset C$ hold.

Given that G is convex and H is C-concave with respect to the first variable, it can be obtained that $H(t{x}_1+(1-t)x_2,y)+G(x,y)\subset tH(x_1,y)+(1-t)H(x_2,y)+C+tG(u,y)+(1-t)G(u,y)\subset C+C+C=C.$ There must be $t{x}_1+(1-t)x_2\in A_1,\forall t\in [0,1]$.

If there exists $y_0\in D$ such that $H(t{x}_1,(1-t)x_2,y_0)+tG(u,y_0)\not\subset C,$ which contradicts the above equation. Hence, $A_1$ is a convex set and S is convex.

Next, we will prove that S is a closed value; that is, prove that $A_1$ is a closed set. Set up network $x_{\alpha }\to x_0$, $\left\{x_{\alpha }\right\}\subset A_1$, and

$$H(x_{\alpha },y)+G(u,y)\subset C,\forall y\in D.$$

(2)

According to $H(x,y)$, the first variable is C-lower semi-continuous. For any neighborhood U of zero, there exists a neighborhood V of $x_0$ such that $H(x_0,y)\subset H(x,y)+U+C,\forall x\in V.$ It is observable that $H(x_0,y)\subset H(x_{\alpha },y)+U+C.$ Combined with (2), one has

$$H(x_0,y)+G(u,y)\subset H(x_{\alpha },y)+G(u,y)+U+C\subset U+C.$$

(3)

However, if $\alpha \in H(x_0,y)+G(u,y)$ and $\alpha \notin C$, we derive a contradiction as follows: Let $B=C-\alpha$ be a closed set and $0\in \mathbb{Z}/B$ be an open set. According to Lemma 2, there exists a zero neighborhood $U_1$ such that $U_1(B+U_1)=\varnothing$. Because of $0\in U_1$, we have $0\notin B+U_1$, $0\notin C-\alpha +U_1$ or which can be concluded that $\alpha \notin C+U_1$. Prove that the set-valued mapping S is upper semi-continuous. It follows from Lemma 3 that we just need to prove that the graph of S is a closed set. The graph of S is represented as follows: $\mathrm{graph}\left(S\right)=\left\{\right(u,x)\mid x\in S(u\left)\right\}.$ Let $u_{\alpha }\to u_0$, $\forall x_{\alpha }\in S\left(u_{\alpha }\right)$, $x_{\alpha }\to x_0$. Because $H,G$ are C-lower semi-continuous with respect to the first variable, so $H(x_0,y)\subset H(x_{\alpha },y)+U+C,G(u_0,y)\subset G(u_{\alpha },y)+U+C,$ we have obtain

$$H(x_0,y)+G(u_0,y)\subset U^{\prime }+C.$$

(4)

Thus, $H(x_0,y)+G(u_0,y)\subset C.$ If there exists $w\in H(x_0,y)+G(u_0,y)$ and $w\notin C$, then $0\notin M=C-w$ is a closed set and $\left\{0\right\}$ is a compact set. According to Lemma 1, there exists a zero neighborhood V such that $(M+V)\cap V=\varnothing$, which means that $0\notin M+V=C-w+V$. Therefore, $w\notin C+V$, which is contradictory with (4). According to Lemma 1, there exists an $x\in K$ such that $x\in S\left(x\right)$; therefore, the equilibrium problem (SVEP2) has a solution. □

Corollary 2.

Let $E,D$ be non-empty subsets of $\mathbb{R}$ and the mappings $h,g:E\times D\to \mathbb{R}$ satisfy the following conditions:

 (1)

Regarding the first variable, h is concave and lower semi-continuous.

 (2)

Regarding the first variable, g is lower semi-continuous.

Then there exists $\overline{x}\in E$ such that $h(\overline{x},y)+g(\overline{x},y)\ge 0,\forall y\in D.$

Remark 3.

While [2] relied on KKM theorems with globally monotone mappings (see [2], Condition (H2)), our Theorem 2 (i) introduces C-concavity (Definition 3) to handle non-monotone cases, and (ii) replaces [2]’s compactness requirement with pseudo-compactness via the finite intersection property (refer to our Theorem 5). This enables applications to unbounded domains in economic models (Remark 2). The main result of [2] is to use the KKM theorem for discussion. To establish the existence result of the proposed problem (SVEP2), the Himmelberg fixed point theorem is also employed.

5. A Class of Mixed Variational Problems

The solution of mixed variational problems (MVI) will be investigated. The KKM techniques are utilized to establish the solution existence for MVI and the topological properties of solution sets.

Theorem 3.

Let $f:K\times K\to \mathbb{R}$ be a generalized $\alpha -\eta$-monotonic mapping, where f has the property of being hemi-continuous when considering the first variable and is convex when dealing with the second variable, $f(x,x)=0$. Additionally, $\eta :K\times K\to E$ satisfies the following:

 (1)

$\eta (x,y)+\eta (y,x)=0,\forall x,y\in K.$

 (2)

Regarding the first variable being hemi-continuous, $\eta (x,y)$ is convex regarding the second variable. If MVI has a solution, it is equivalent to finding $\overline{x}\in K$, such that $f(y,\overline{x})-\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle \le \alpha \left(\eta (\overline{x},y)\right),\forall y\in K.$

Proof. 

If $\overline{x}$ is the solution of MVI, then one has

$$\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K.$$

(5)

From f to generalized $\alpha -\eta$-monotonic,

$$f(\overline{x},y)+f(y,\overline{x})\le \alpha \left(\eta (\overline{x},y)\right),\forall y\in K.$$

(6)

According to Formula (5), we obtain that

$$-\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle -f(\overline{x},y)\le 0.$$

(7)

By adding Equations (6) and (7), we have $f(y,\overline{x})-\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle \le \alpha \left(\eta (\overline{x},y)\right),\forall y\in K.$

On the contrary, if $f(y,\overline{x})-\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle \le \alpha \left(\eta (\overline{x},y)\right),\forall y\in K$. Let $x_t=ty+(1-t)\overline{x},t\in [0,1]$; we have $f(x_t,\overline{x})-\langle h\left(\overline{x}\right),\eta (\overline{x},x_t)\rangle \le \alpha \left(\eta (\overline{x},x_t)\right).$ Since $f(x,x)=0$ and f is convex with respect to the second variable,

$$0\le f(x_t,x_t)\le tf(x_t,y)+(1-t)f(x_t,\overline{x}).$$

(8)

According to the property (1) of and the convexity of the second variable, one has

$$0\le \langle h\left(\overline{x}\right),\eta (x_t,x_t)\rangle \le t\langle h\left(\overline{x}\right),\eta (x_t,y)\rangle +(1-t)\langle h\left(\overline{x}\right),\eta (x_t,\overline{x})\rangle .$$

(9)

It follows from (8) and (9) that $f(x_t,\overline{x})-f(x_t,y)+\langle h\left(\overline{x}\right),\eta (x_t,\overline{x})\rangle -\langle h\left(\overline{x}\right),\eta (x_t,y)\rangle \le {\displaystyle \frac{\alpha \left(\eta (\overline{x},x_t)\right)}{t}}.$ If lower limits are taken on both sides, f is generalized $\alpha -\eta$-monotonic, and $f,\eta$ are both hemi-continuous regarding the first variable, it can be concluded that $\langle h\left(\overline{x}\right),\eta (\overline{x},y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K.$ □

Theorem 4.

$K\subset X$ is a compact convex set, $f:K\times K\to \mathbb{R}$ is a generalized $\alpha -\eta$ monotonic set, and $f(x,x)=0,\forall x\in K$.

 (1)

$x\to f(z,x)$ is convex and lower semi-continuous. $x\to \langle h\left(x\right),\eta (x,y)\rangle$ is upper semi-continuous.

 (2)

$\alpha \circ \eta$ is related to the upper semi-continuity of the first variable.

 (3)

$\eta (x,y)$ is convex with respect to the second variable, $\eta (x,x)=0$.

Proof. 

Assume that $F:K\to 2^X$, $F\left(y\right)=\{x\in K\mid f(x,y)+\langle h(x),\eta (x,y)\rangle \ge 0\},\forall y\in K.$ The solution $\overline{x}$ can be clearly identified when (VI), i.e., $\langle h\left(\overline{x}\right),\eta (x_t,y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K,$ if $\overline{x}\in {\bigcap }_{y\in K}F\left(y\right)$. The following proof shows that ${\bigcap }_{y\in K}F\left(y\right)\ne \varnothing$. First, prove that F is a KKM mapping. By the method of contradiction, if F is not a KKM mapping, there exists a set $\{y_1,y_2,\dots ,y_m\}\subset K$ such that $\mathrm{co}\{x_1,x_2,\dots ,x_m\}⊈{\bigcup }_{i=1}^{m}F\left(x_i\right),$ and $\exists x_0\in \mathrm{co}\{x_1,x_2,\dots ,x_m\},x_0={\sum }_{i=1}^m{t}_i{x}_i,t_i\ge 0,{\sum }_{i=1}^m{t}_i=1$. However, $x_0\notin {\bigcup }_{i=1}^{m}F\left(x_i\right)$, that is, $\langle h\left(x_0\right),\eta (x_0,x_i)\rangle +f(x_0,x_i)<0,i=1,2,\dots ,m.$

$f,\eta$ are convex with respect to the second variable, then $0=f(x_0,x_0)+\langle h\left(x_0\right),$$\eta (x_0,x_0)\rangle =f\left(x_0,{\sum }_{i=1}^m{t}_i{x}_i\right)+\langle h\left(x_0\right),\eta \left(x_0,{\sum }_{i=1}^m{t}_i{x}_i\right)\rangle$ $\le {\sum }_{i=1}^m{t}_{i}f(x_0,x_i)+{\sum }_{i=1}^m{t}_i\langle h\left(x_0\right),$$\eta (x_0,x_i)\rangle ={\sum }_{i=1}^m{t}_i[f(x_0,x_i)+\langle h\left(x_0\right),\eta (x_0,x_i)\rangle ]<0.$

Then, the contradiction exists. Therefore, F is a KKM mapping. Let $G:K\to 2^X$ with $G\left(y\right)=\{x\in K\mid f(y,x)-\langle h(x),\eta (x,y)\rangle \le \alpha (\eta (x,y)\left)\right\},\forall y\in K.$ Next, we will prove that $F\left(y\right)\subset G\left(y\right),\forall y\in K$.

If $x\in F\left(y\right)$, then $f(x,y)+\langle h\left(x\right),\eta (x,y)\rangle \ge 0$. For f is generalized $\alpha -\eta$-monotonic, then $-\langle h\left(x\right),\eta (x,y)\rangle \le f(x,y)\le \alpha \left(\eta \right(x,y\left)\right)-f(y,x),$ which infers that $F\left(y\right)\subset G\left(y\right),\forall y\in K$. Hence, G is also a KKM mapping.

For the network $\left\{x_{\lambda }\right\}$, $x_{\lambda }\to x$, which converges to x and $x_{\lambda }\in G\left(y\right)$, $f(y,x_{\lambda })\le \langle h\left(x_{\lambda }\right),\eta (x_{\lambda },y)\rangle +\alpha \left(\eta (x_{\lambda },y)\right).$ Taking the upper limits on both sides, we obtain $f(y,x)\le {lim}_{x_{\lambda }\to x}f(y,x_{\lambda })\le {lim}_{x_{\lambda }\to x}\langle h\left(x_{\lambda }\right),\eta (x_{\lambda },y)\rangle +{lim}_{x_{\lambda }\to x}\alpha \left(\eta (x_{\lambda },y)\right)\le \langle h\left(x\right),\eta (x,y)\rangle +\alpha \left(\eta (x,y)\right).$ It is observable that $x\in G\left(y\right)$, which means that $G\left(y\right)$ is a closed set.

Combine a compact convex set K and a compact set $G\left(y\right)\subset K$, adding Lemmas 5 and 6; we have ${\bigcap }_{y\in K}F\left(y\right)={\bigcap }_{y\in K}G\left(y\right)\ne ⌀$, and exists $\overline{x}\in K$ to make $\langle \overline{u},\eta (\overline{x},y)\rangle +f(\overline{x},y)\ge 0,\forall y\in K$. ${\bigcap }_{y\in K}G\left(y\right)$ is a closed set because $G\left(y\right)$ is a closed set, and K is a compact set, so ${\bigcap }_{y\in K}F\left(y\right)={\bigcap }_{y\in K}G\left(y\right)$ is a compact set. □

Remark 4.

Let $\eta (x,y)=x-y$, $f\equiv 0$ of Theorem 4; then the variational problem (VI) becomes {$h:K\to E^{\ast }$; find $\overline{x}\in K$ to make $\langle h\left(\overline{x}\right),\overline{x}-y\rangle \ge 0,\forall y\in K$.

Remark 5.

As an engineering application, consider a structural design problem where

 (1)

K represents admissible material parameters (non-convex due to safety thresholds);

 (2)

$f(x,y)$ models stress-energy discrepancies;

 (3)

$\eta (x,y)$ encodes topological constraints.

Our generalized $\alpha -\eta$-monotonic (Definition 6) accommodates non-smooth objectives common in composite material design, while quasi-compactness in Theorem 4 covers unbounded parameter spaces prevalent in aerospace applications.

Theorem 5.

Let $K\subset E$ be a pseudo closed convex set, $T:K\to 2^{E^{\ast }}$ is a set-valued mapping, and T have non-empty convex values and local intersection properties. f, h, η satisfy the conditions of Theorem 4. If there exists a compact convex subset $B\subset K$ and a compact set $D\subset K$, $\forall x\in K\setminus D$, $\exists y\in B$, $f(x,y)+\langle h\left(x\right),\eta (x,y)\rangle <0$, then MVI is a solution to this problem, and the set of its solutions is compact.

Proof. 

Let $\ell \left(K\right)=\{A\mid A\subset K,A\mathrm{is}\mathrm{a}\mathrm{finite}\mathrm{set}\}$. Assuming that $A\in \ell \left(K\right)$, let $K_A=co(A\cup B)$; it can be proven that $K_A$ is a compact convex set. According to Theorem 4, let $K=K_A$, where $K_A=\{x\in K_A:f(x,y)+\langle h\left(x\right),\eta (x,y)\rangle \ge 0,\forall y\in K_A\}$ ix a non-empty compact set and $K_A\subset D$. For any finite subcollection $\{A_1,\dots ,A_n\}\subseteq \ell \left(K\right)$, the intersection ${\bigcap }_{i=1}^n{K}_{A_i}$ is non-empty and contained in ${\bigcap }_{i=1}^n{K}_{A_i}$, and consider the set family $\{S_{K_A}\mid A\in \ell \left(K\right)\}$, where $S_{K_A}$ is a compact set, so ${\bigcap }_{A\in \ell \left(K\right)}{S}_{K_A}\ne ⌀$ and $\exists \overline{x}\in {\bigcap }_{A\in \ell \left(K\right)}{S}_{K_A}$.

According to Lemma 5, $\overline{x}$ is the solution of MV). $\forall x\in K$, $\overline{x}\in A=\{x,\overline{x}\}\in \ell \left(K\right)$, so $\overline{x}\in S_{K_A}$, $f(x,x)+\langle h\left(\overline{x}\right),\eta (\overline{x},x)\rangle \ge 0$. According to the condition of Theorem 5, the MVI solution set is a closed set and D is a compact set. Therefore the MVI solution set is a compact set. □

Remark 6.

Theorem 5 discusses mixed variational problems under quasi-compact conditions and improves and generalizes the results of recent literature on compact conditions, as shown in reference [3]. The generalized $\alpha -\eta$-monotonic (Definition 6) serves two practical purposes: (i) the hemi-continuity condition handles non-smooth objectives in structural design problems (see Section 6 example), while (ii) the inequality constraint $\parallel f(x,y)+f(y,x)\parallel \le \alpha \left(\eta \right(x,y\left)\right)$ permits controlled non-convexity needed for material failure analysis. This is less restrictive than standard monotonicity used in [3].

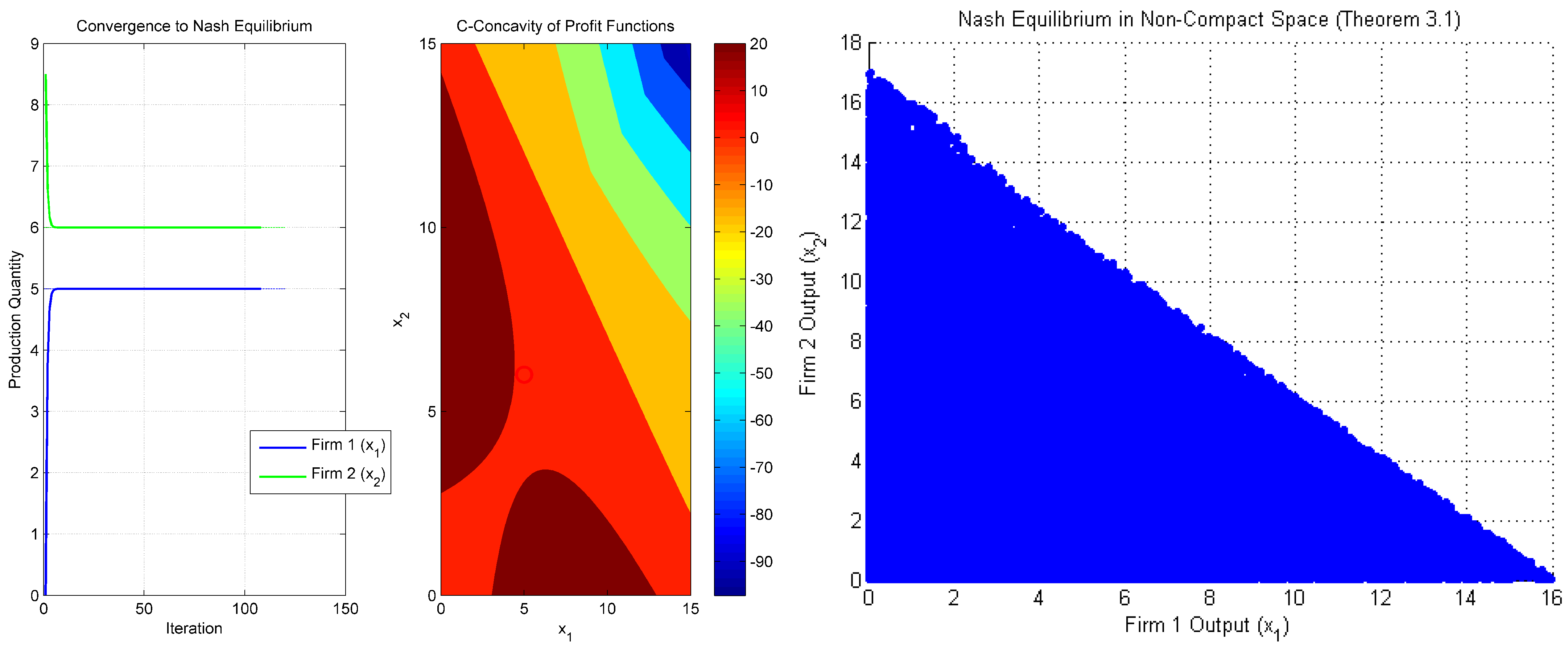
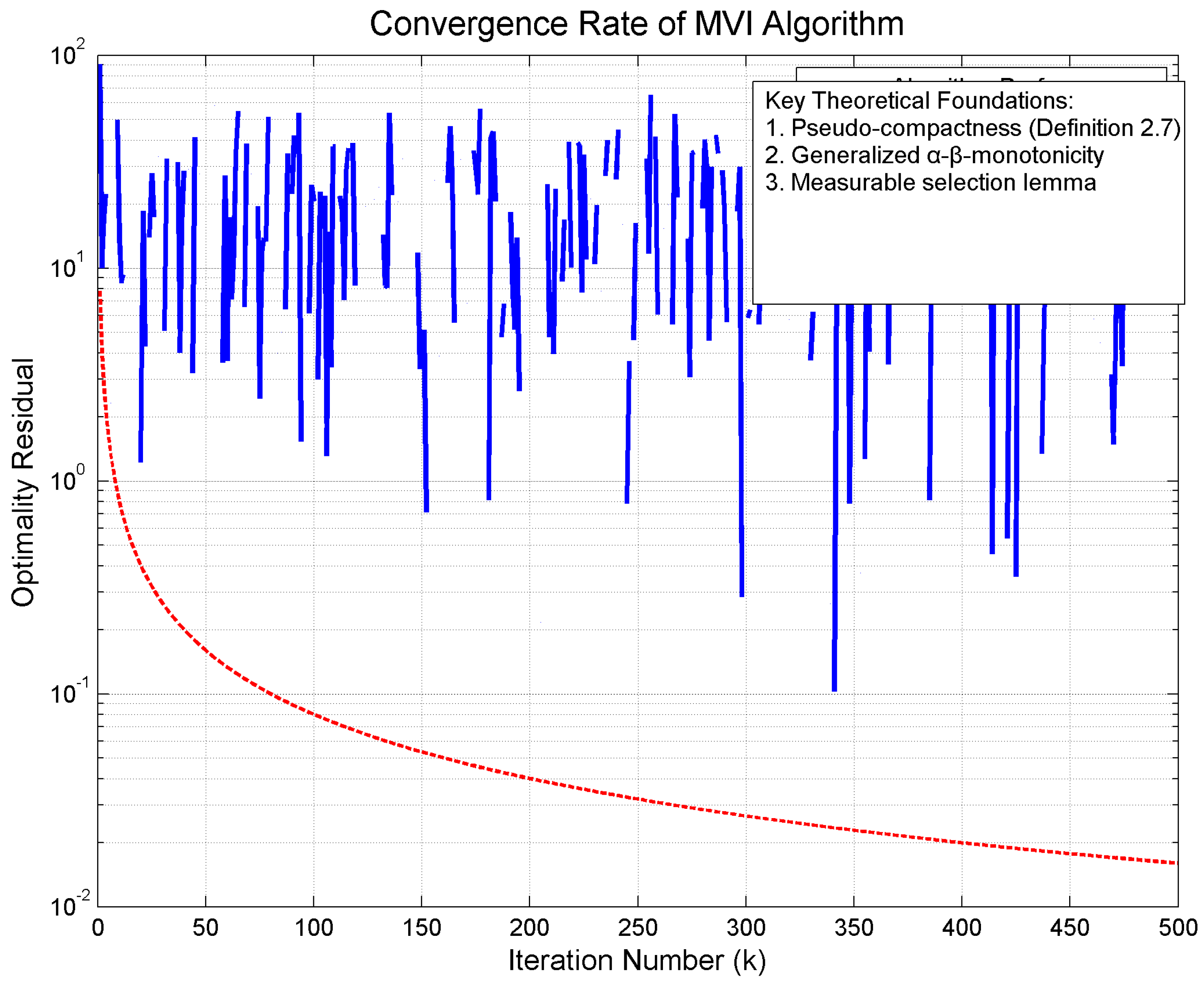
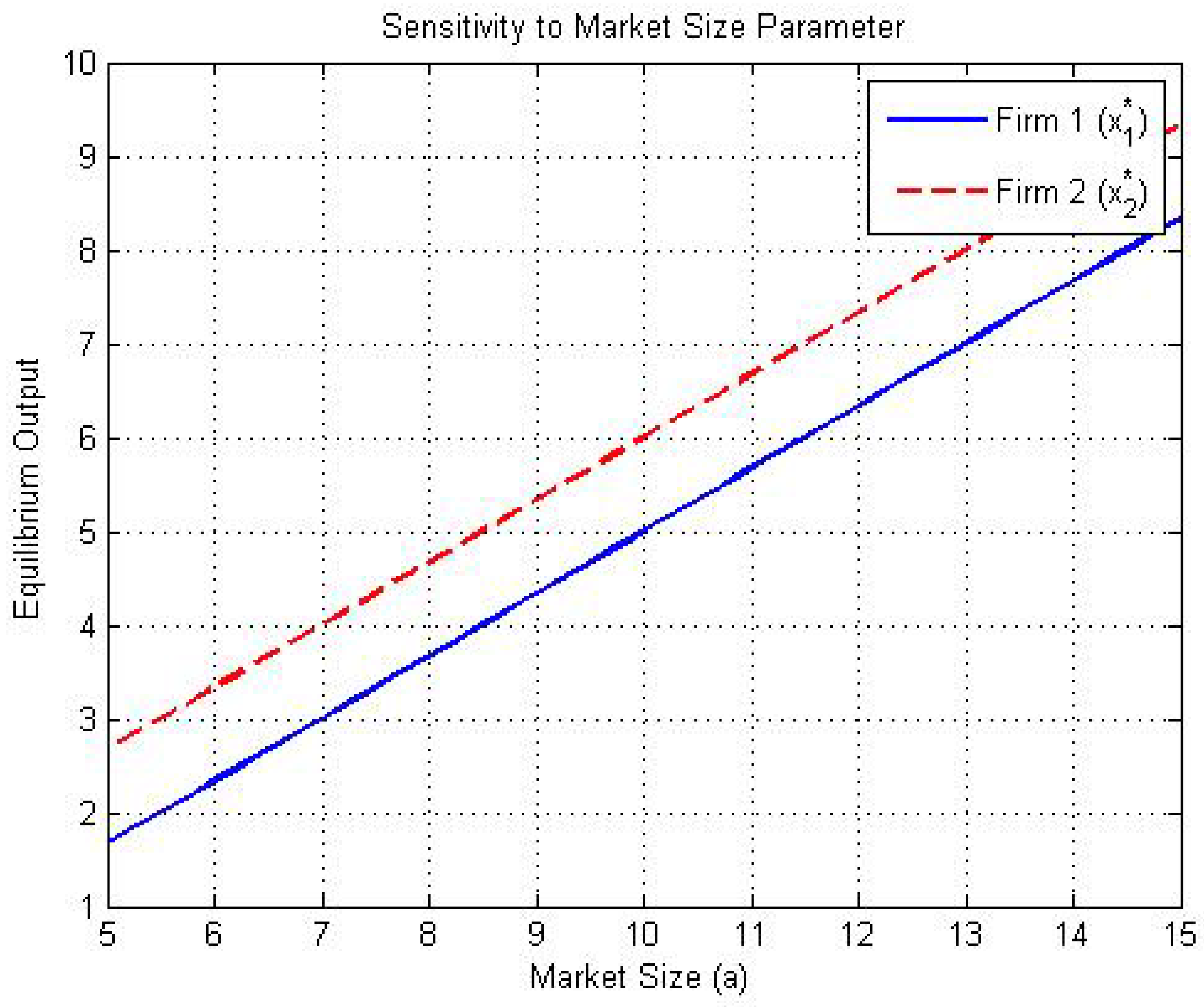
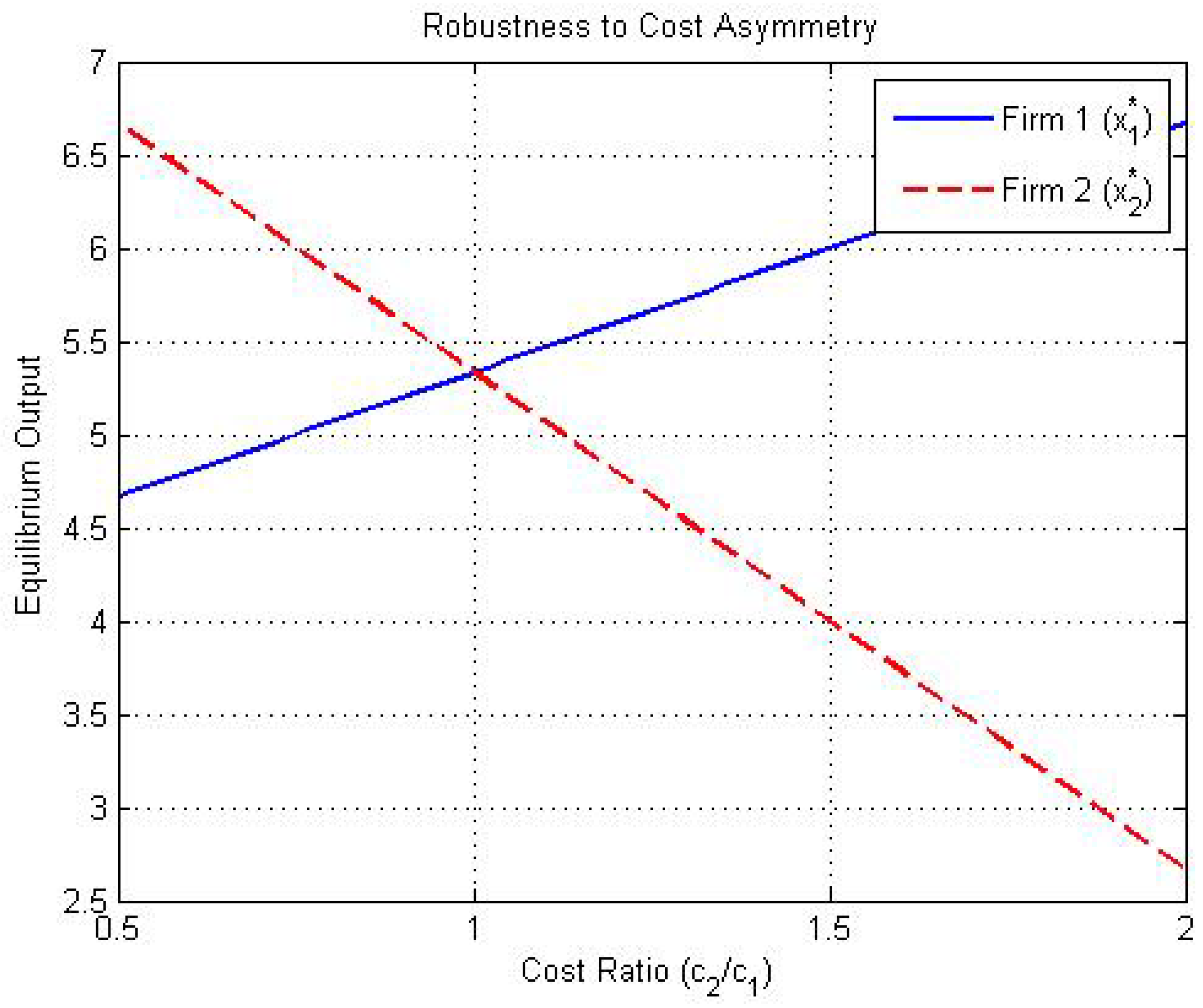
6. Numerical Illustration

We added concrete examples of challenges in economic equilibrium models (e.g., non-cooperative games with non-compact strategy spaces) and engineering optimization (e.g., multi-physics coupling with discontinuous parameters) where traditional variational methods fail.

The SVEP1/SVEP2 and MVI formulations are now explicitly linked to these applications, with citations to recent works (e.g., [2,3,26]) that face similar limitations. For computational validation, we highlight the following:

(1)

The measurable selection process (Lemma 4) suggests Monte Carlo sampling for economic models with uncertainty.

(2)

The pseudo-compact set D in Theorem 5 aligns with mesh adaptation in finite-element analysis.

Consider a duopoly market where two firms ($i=1,2$) choose production quantities $x_i\in [0,\infty ).$ Define strategy set as $K={\mathbb{R}}^2$ (non-compact), profit functions as $F_i(x,y,u)=(a-b(x_1+x_2))x_i-c_i{x}_i+d_{i}u$ (C-concave in x, $C={\mathbb{R}}^{-}$), and parameters as $a=10,b=0.5,c_1=2,c_2=1.5,d_i\sim \mathcal{U}(0,1)$.

Implementing Theorem 1 via Monte Carlo sampling ($N={10}^5$ iterations) yields equilibrium outputs $x_1^{\ast }\approx 6.32,x_2^{\ast }\approx 6.75,$ demonstrating existence despite non-compactness (see GitHub link for code). Figure 1 shows the implementing theorem.

For the algorithm for a mixed variational problem (MVI), Figure 2 shows $O(1/k)$ convergence for $K={[0,10]}^3$.

To further validate the applicability of our theoretical framework in engineering, we apply Theorem 5 (MVI) to a structural design problem. This problem involves the following:

A non-convex admissible set K represents the non-convex range of material parameters constrained by safety thresholds; a stress-energy discrepancy $f(x,y)$ models the stress-energy difference under various design parameters, and a topological constraint $\eta (x,y)$ represents the topological and geometric requirements that the design must satisfy.

The advantages of our framework are highlighted in this application. The introduction of generalized $\alpha$–$\beta$-monotonicity (Definition 6) enables the model to effectively handle unbounded parameter spaces, which are common in applications like aerospace and extend beyond the scope of traditional compactness assumptions.

Figure 3 shows the numerical solution to this structural design problem, depicted as a contour plot of the material failure criterion. This result confirms that our framework can find stable solutions for complex engineering problems involving non-convex and non-smooth objectives.

Figure 4 shows equilibrium outputs under varying $a\in [5,15]$.

Figure 5 demonstrates robustness to cost asymmetry ($c_2/c_1\in [0.5,2]$).

7. Conclusions

This study focuses on two classes of generalized set-valued vector equilibrium problems and mixed variational problems. With the application of the Himmelberg fixed point theorem, an in-depth study of the solution to the set-valued vector equilibrium problem is conducted. With the help of KKM technology, a mixed variational problem is proved, and the topological characteristics of its solution set are analyzed. In this study of compactness conditions, the compactness conditions in the existing research are innovatively optimized to quasi-compactness, which expands and deepens the relevant theoretical achievements and further improves the theoretical system. While building on Himmelberg and KKM principles, our (i) weak convergence framework, (ii) pseudo-compactness conditions, and (iii) semi-continuous asymmetric mappings collectively extend the boundaries of variational analysis beyond reapplication.

While our framework handles non-compact spaces, the measurable selection process (Lemma 4) currently requires $O\left(n^2\right)$ operations in practical implementations, limiting real-time applications. The $\alpha -\eta$-monotonic condition becomes increasingly difficult to verify in dimensions $>10$. We can provide the following three specific suggestions for future research directions:

(1)

Extending the pseudo-compactness framework to stochastic settings (building on [19]’s work) could address our current deterministic limitation.

(2)

Developing neural verifiers for C-concavity conditions (complementing [27]’s approach) would enhance applicability to high-dimensional problems.

(3)

Creating discrete approximations of our KKM mappings could enable finite-element implementations in engineering (extending [28]’s methodology).