Existence, Stability, and Numerical Methods for Multi-Fractional Integro-Differential Equations with Singular Kernel
Abstract
1. Introduction
- Sumudu–Adomian decomposition method (Sumudu-ADM)
- Shehu–Adomian decomposition method (Shehu-ADM)
- We present the Two-Step ADM (TSADM), a modified form of the ADM that can yield exact solutions in a single iteration.
- We introduce two transform-based ADM variations, the Sumudu-ADM and Shehu- ADM techniques, which improve accuracy and convergence while preserving computational simplicity.
- These transform-based methods significantly improve the performance of ADM without requiring initial guesses or assumptions about the solution.
- The U-H stability [57] of the solutions is analyzed in depth, reinforcing the reliability of the proposed methods.
- We perform detailed error and convergence analysis and validate the methods using illustrative examples supported by comparative plots and error norm tables.
2. Preliminaries
3. Analytical Method
4. Numerical Methods
4.1. Adomian Decomposition Method (ADM)
4.2. Sumudu–Adomian Decomposition Method (Sumudu-ADM)
- The term corresponds to the Sumudu image of the second derivative composed of the Caputo integral;
- The term arises from the image of the nested RL integral term;
- The function can represent a known function or a non-linear function expressed as a series of decompositions.
4.3. Shehu–Adomian Decomposition Method (Shehu-ADM)
- is the initial approximation,
- incorporates the effect of , the second derivative, and the fractional integral of ,
- higher-order terms are obtained iteratively using Equation (27).
5. Error Estimate and Convergence Analysis
6. Existence and Uniqueness of Solutions
- (a)
- ,
- (b)
- ,
- (a)
- For the Caputo fractional derivativewhere , which bounds the Caputo derivative on . Suppose ; then
- (b)
- For the RL fractional integral:where , which bounds the RL integral on .
Error Propagation
- (i)
- (ii)
- is a strict contraction on η, that is, there exists a such that
- (iii)
- is continuous on η and is a relatively compact subset of
7. Stability
Mittag–Leffler Bound for Establishing Ulam–Hyers Stability
- (i)
- for all ,
- (ii)
- for all .
8. Illustrative Examples and Discussion
- (i)
- The suggested approach is universal and can be used for any interval , , even if the numerical examples are given on the interval . Because fractional-order operators have a memory effect that can affect accuracy and computational cost, the method might need finer time discretization for larger T.
- (ii)
- The exact solution, such as , where n depends on the order of the fractional derivative and the numerical approach, is assumed to be sufficiently smooth for the convergence analysis. This regularity assumption guarantees the validity of the observed convergence rates and the computed error estimates. The equation studied in Equation (1) is a problem in the literature due to its relevance in modeling systems with memory effects and its analytical tractability, allowing for comparison with exact solutions.
- (iii)
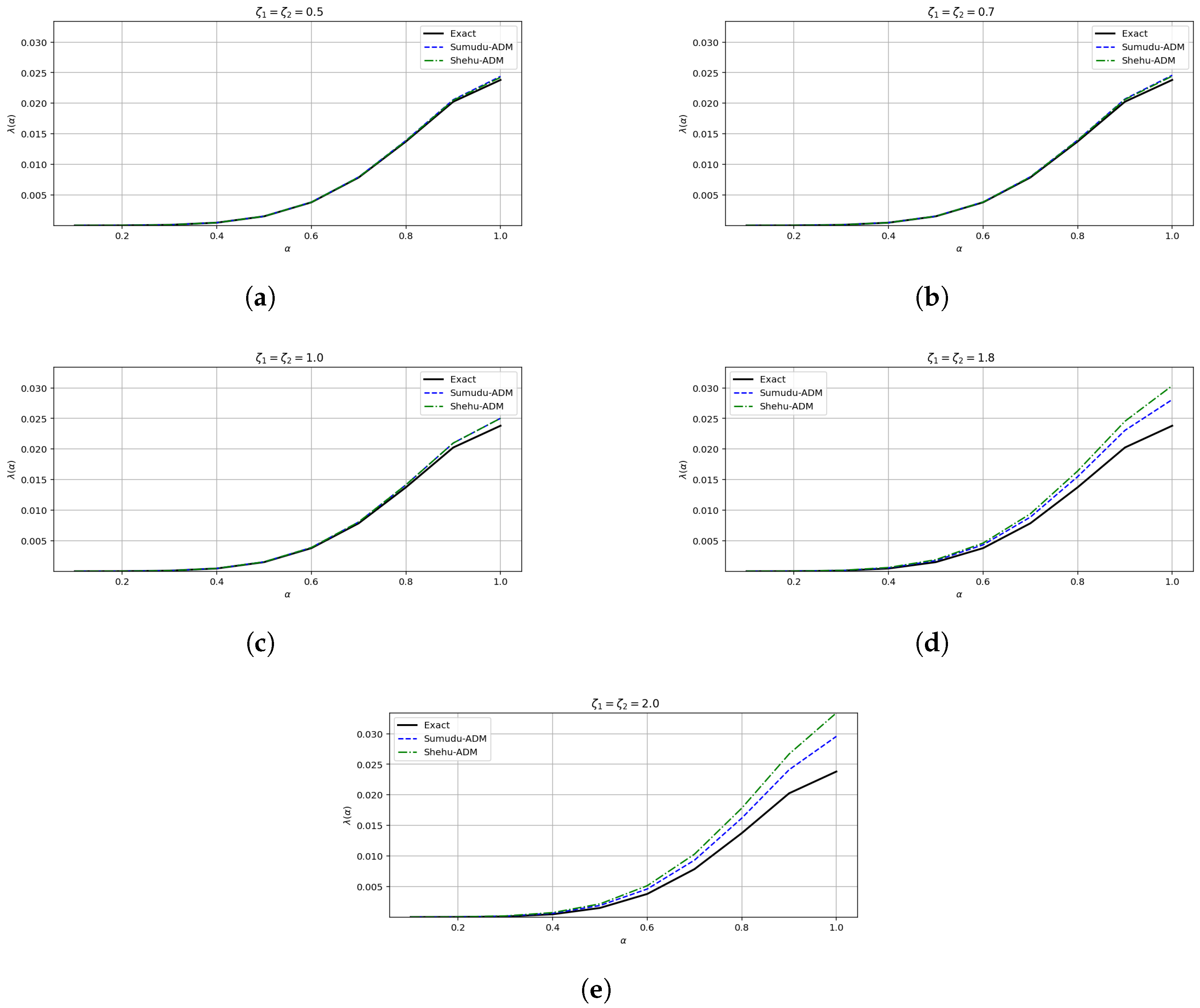
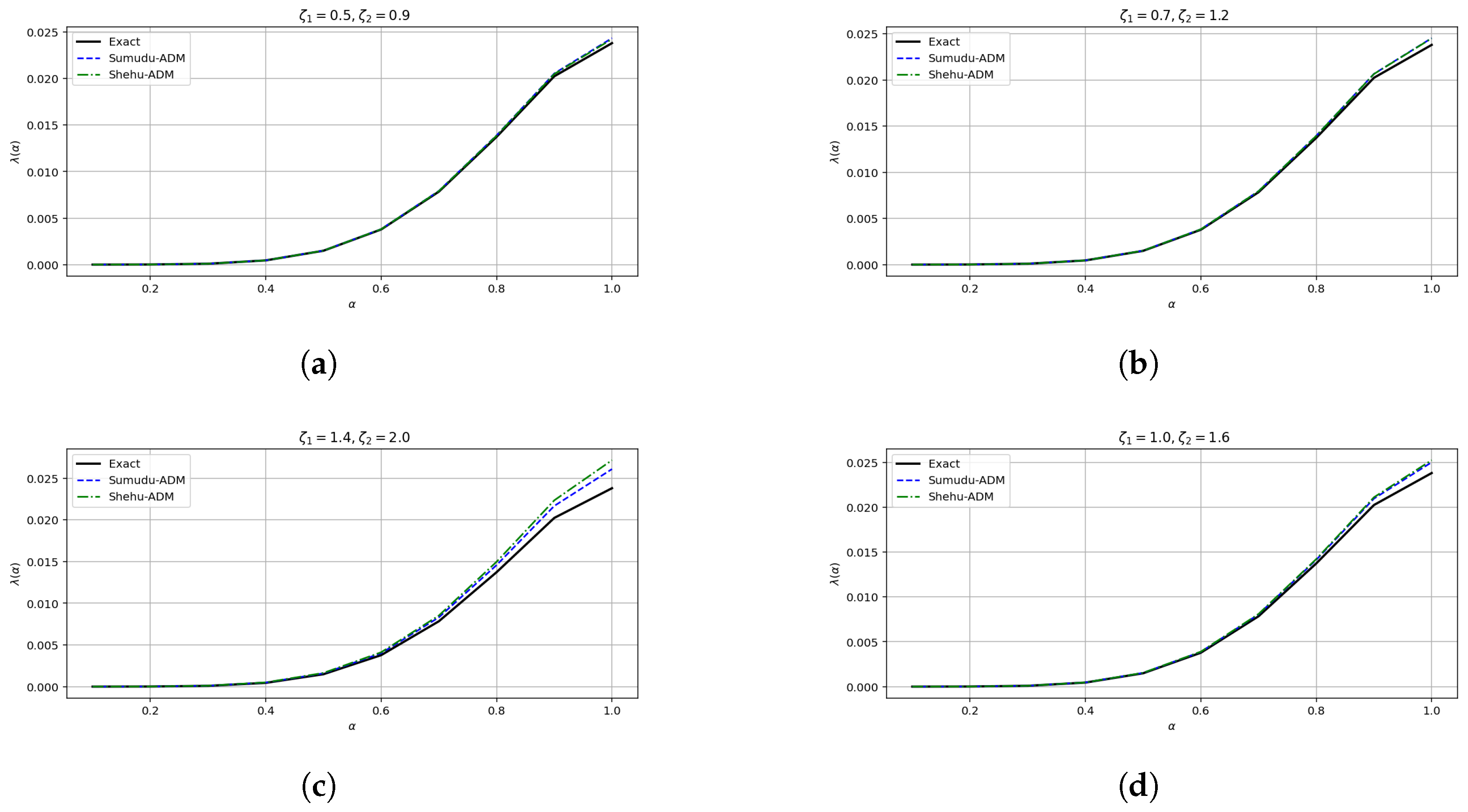
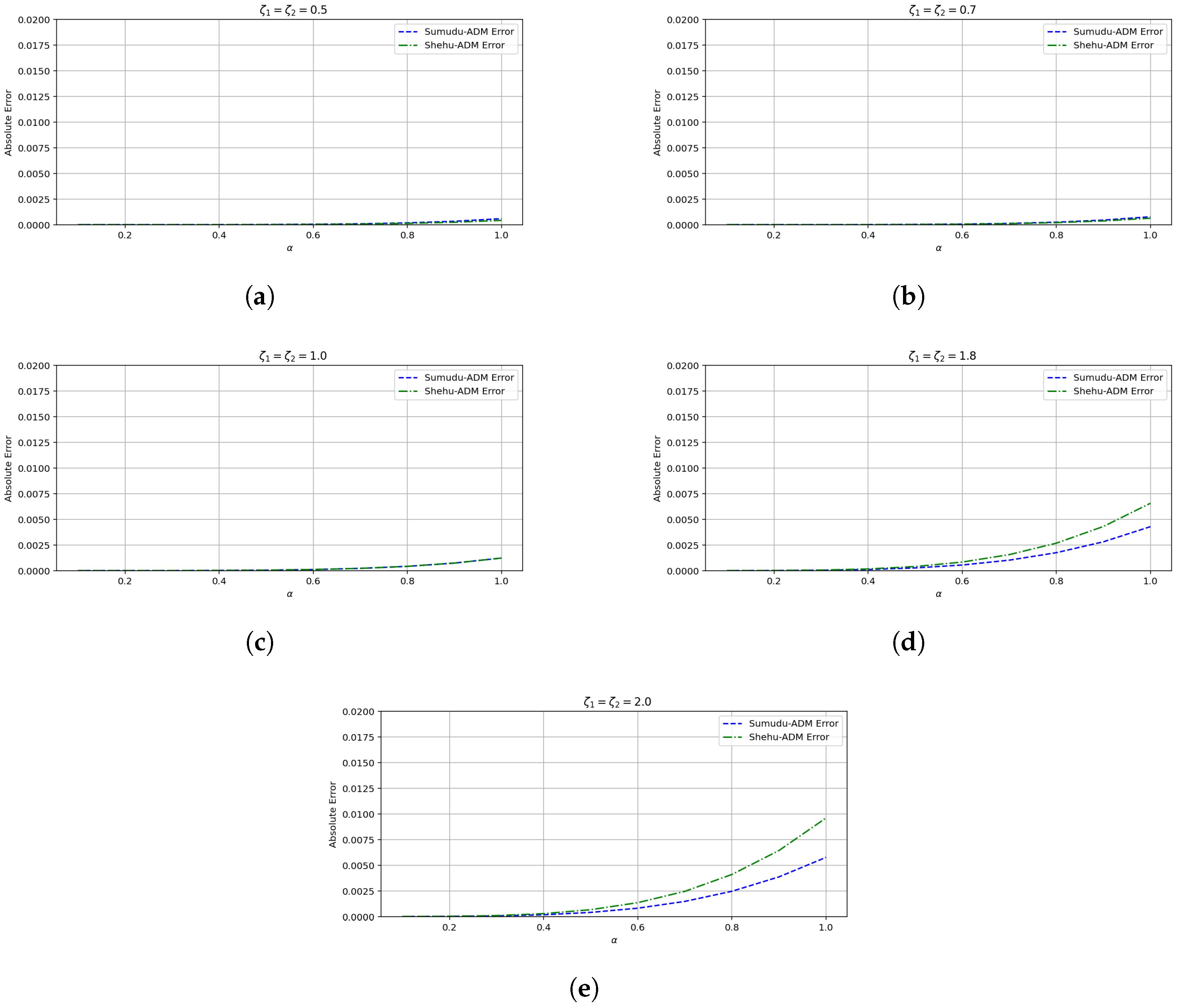
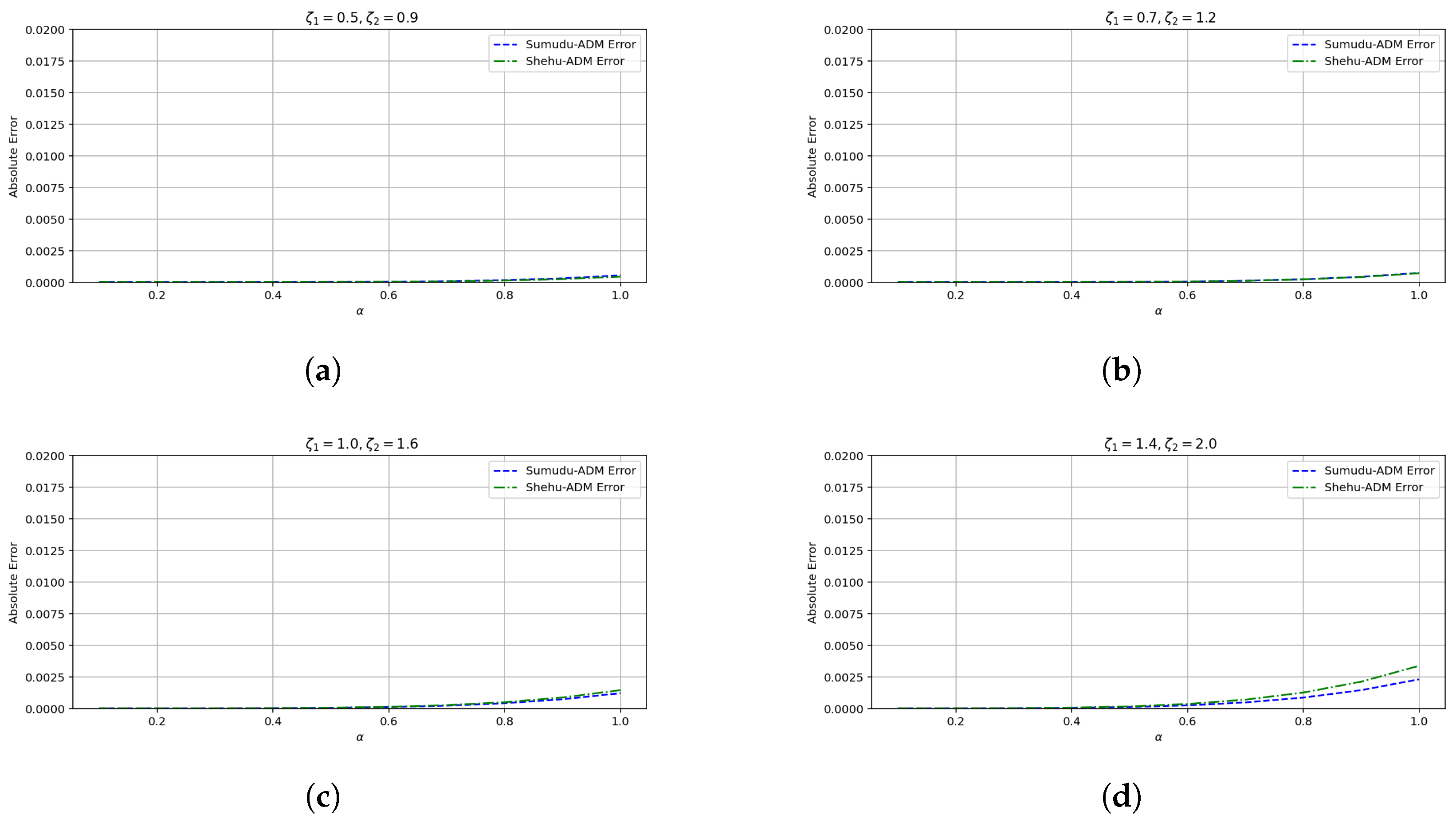
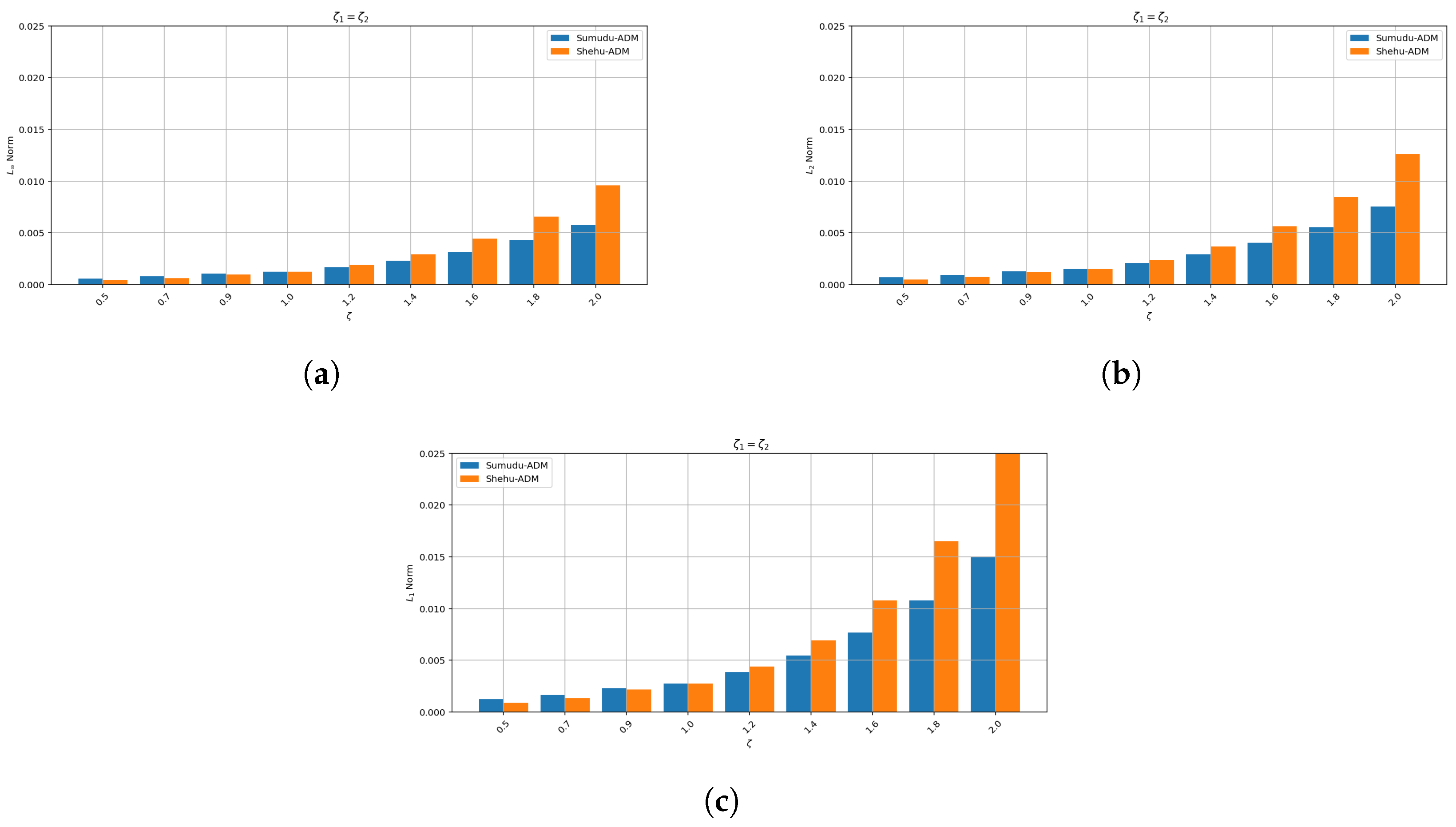
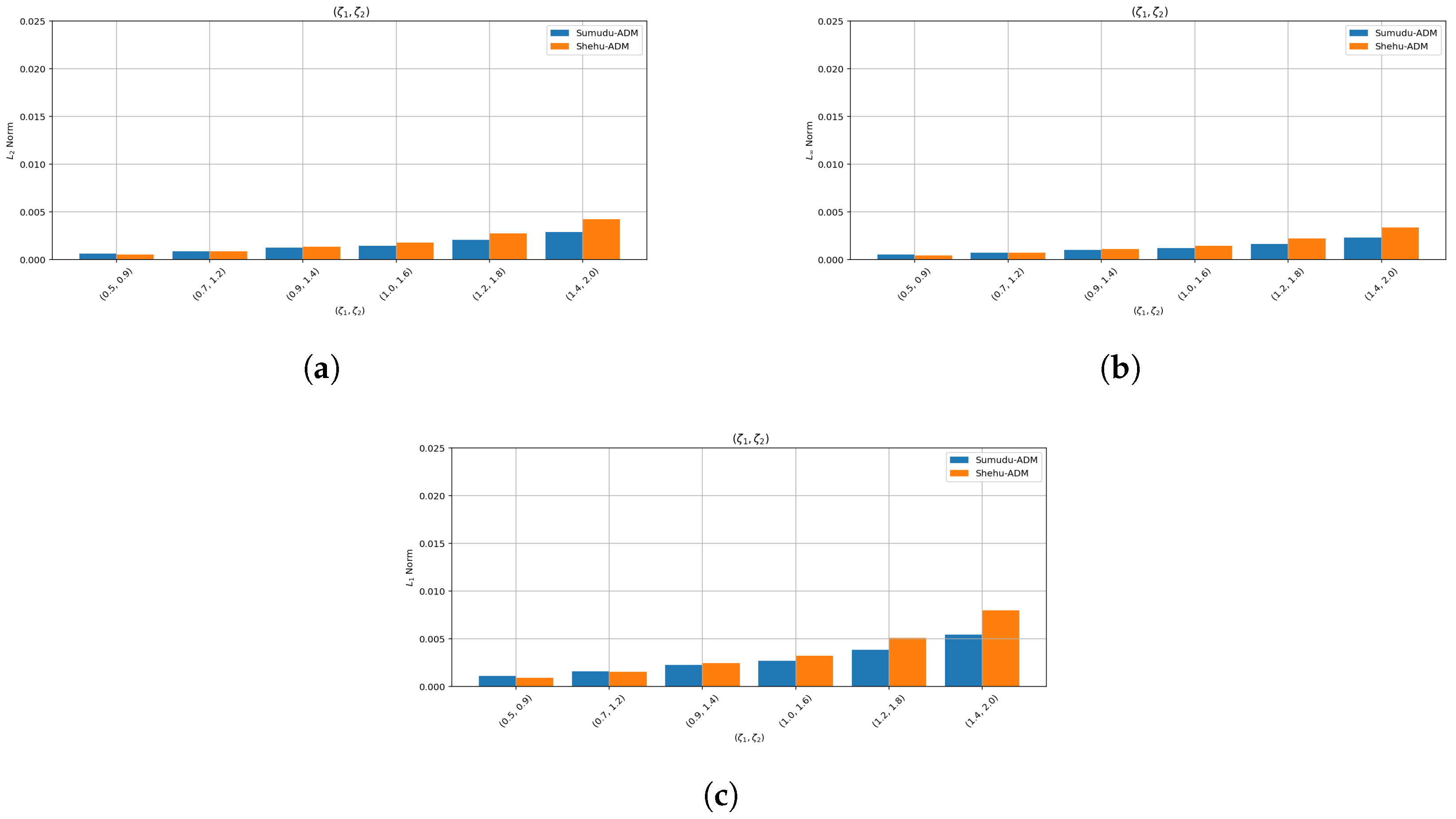
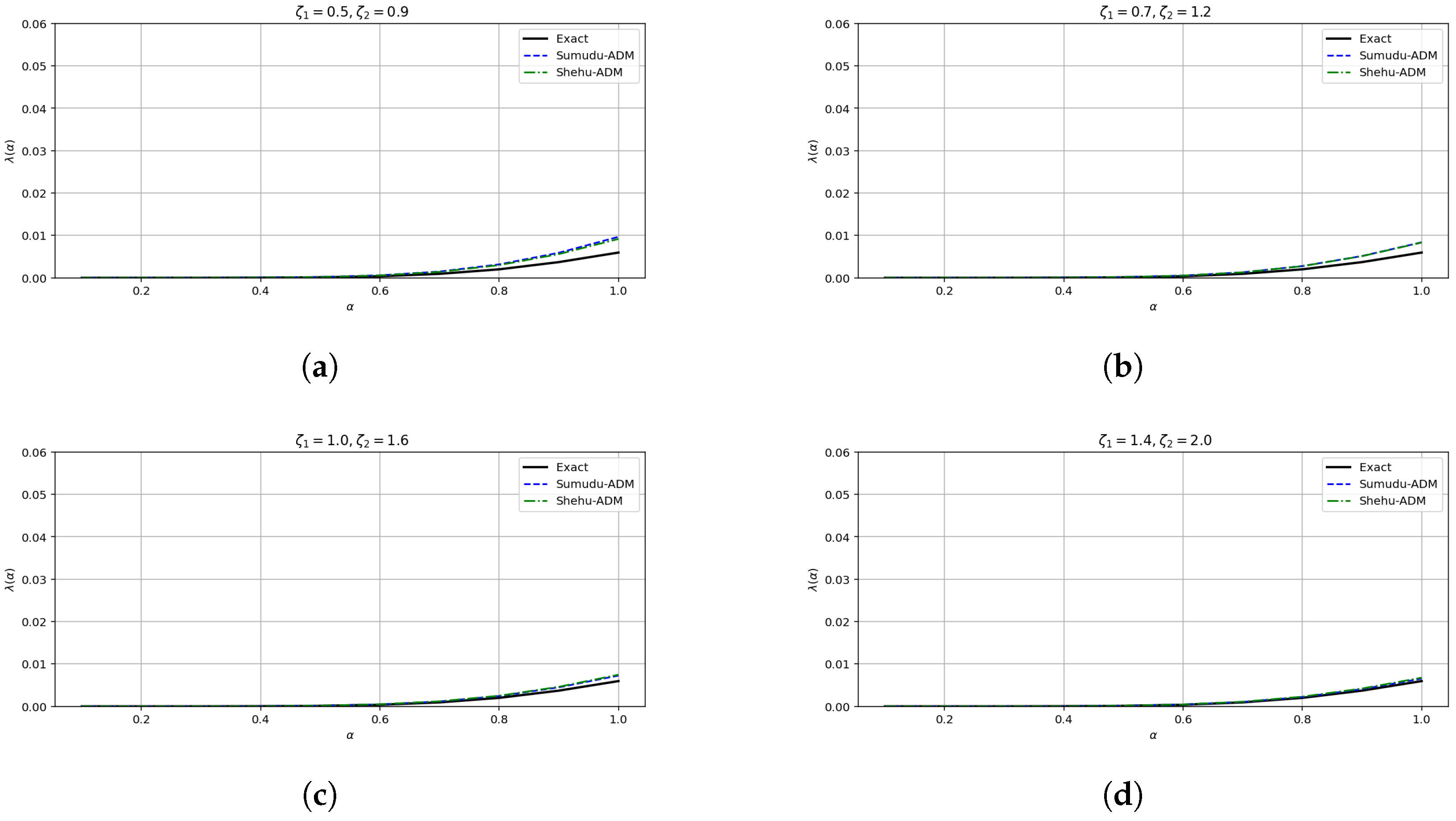
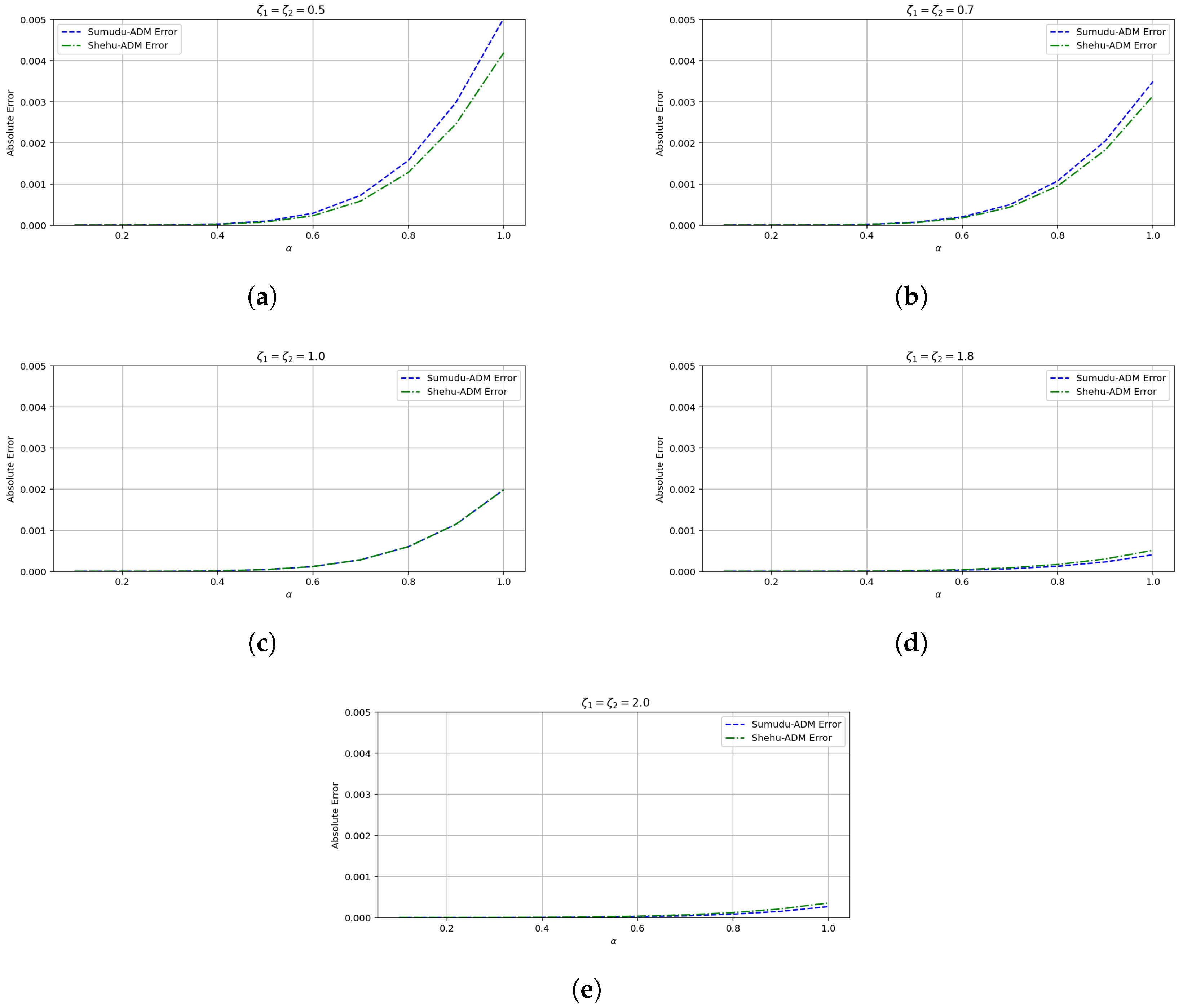
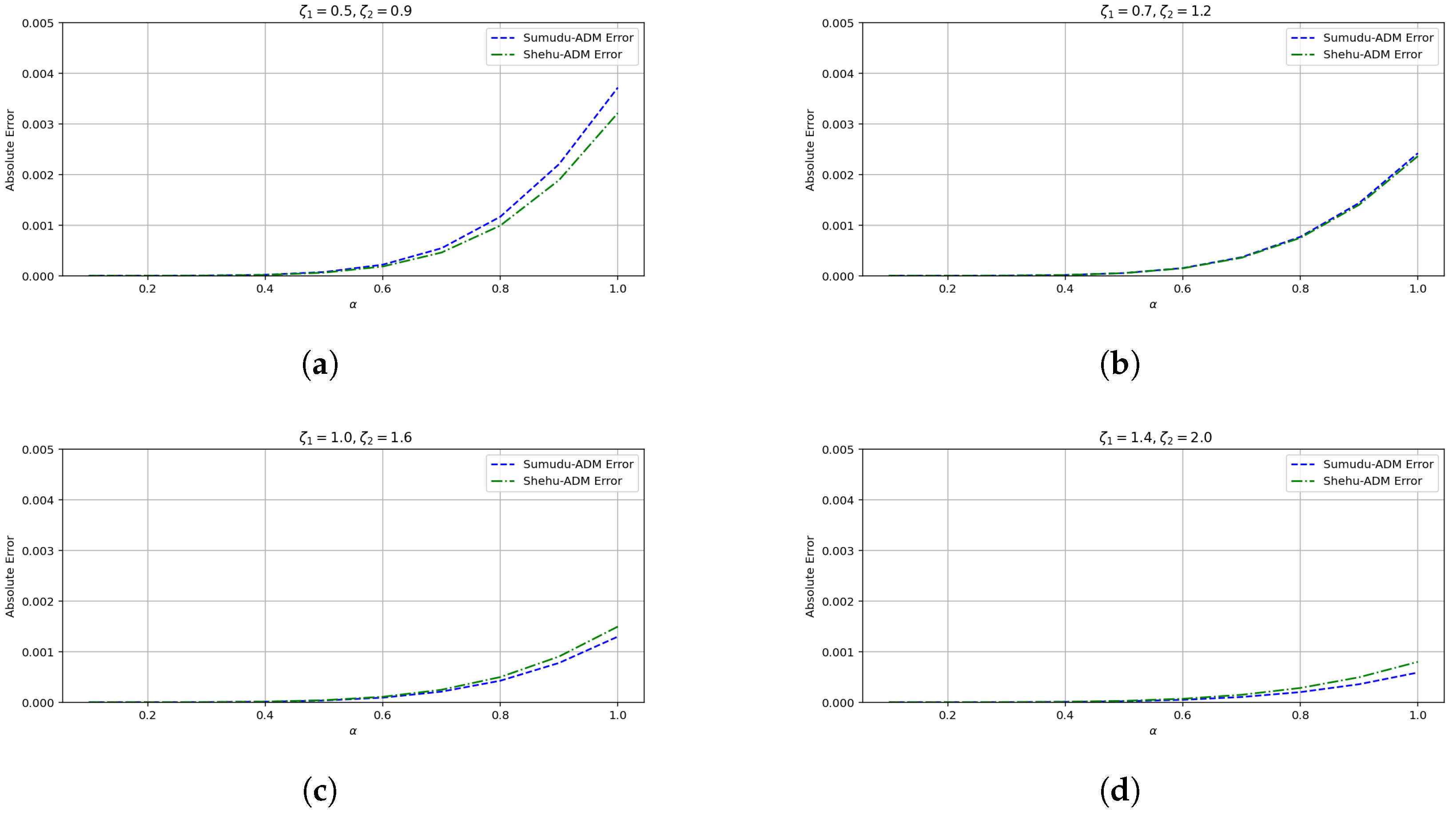
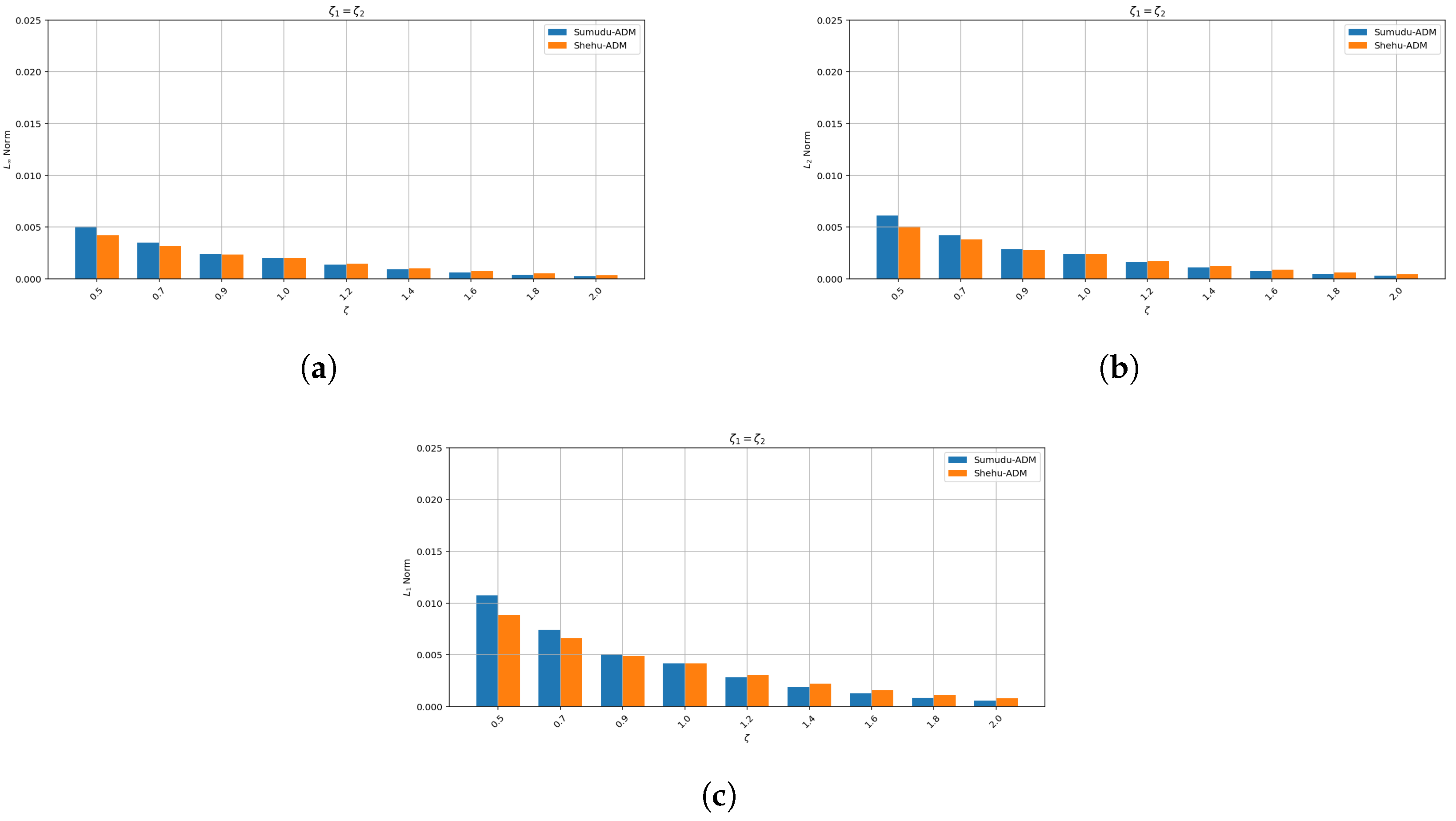
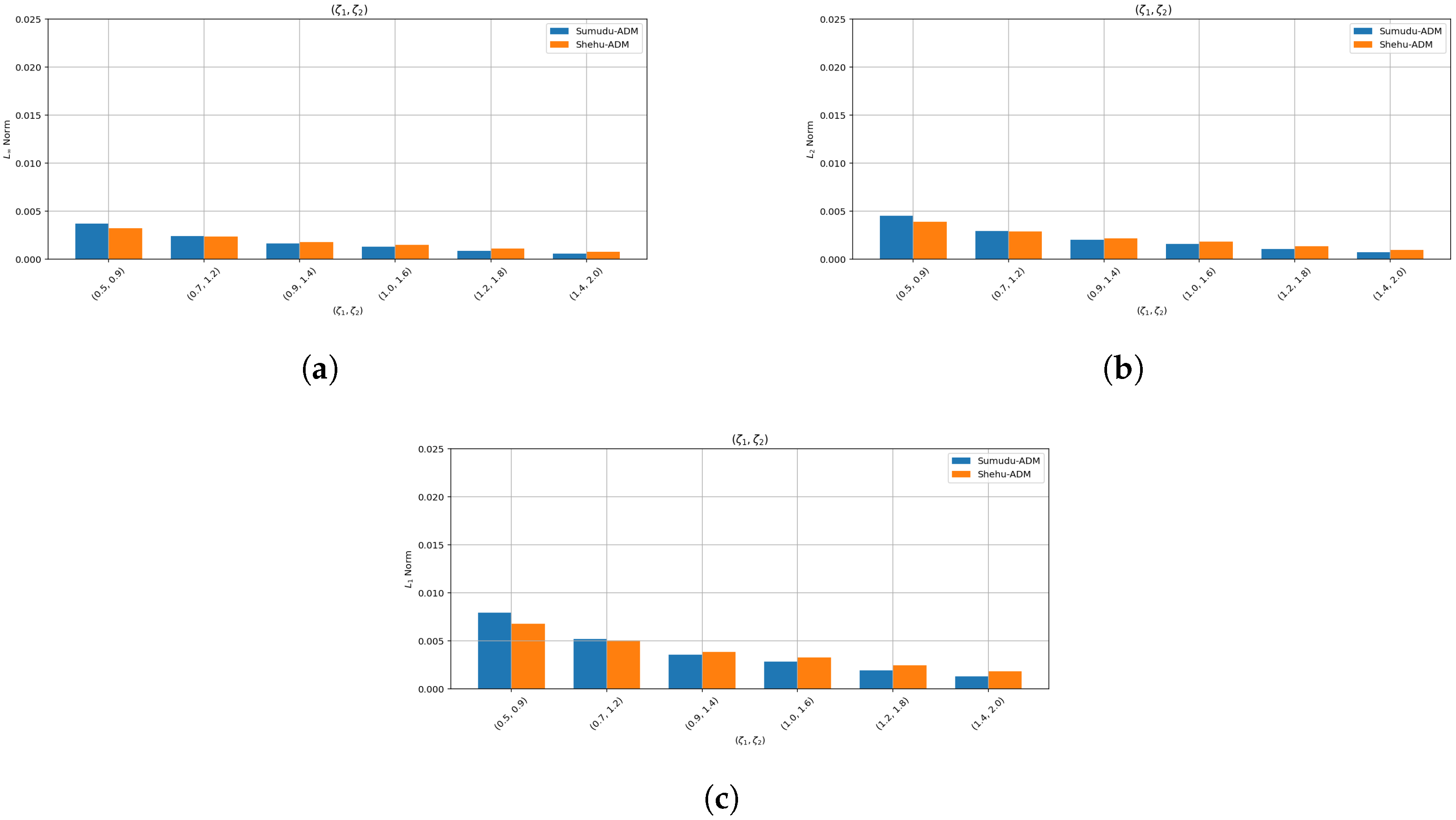
- The convergence behavior established in this Section 5 is supported by the numerical results presented in Section 8. In particular, the error plots and tables based on the , , and norms (see Table 1 and Table 2 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 for Example 1, and Table 3 and Table 4 and Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 for Example 2) demonstrate a decreasing trend in the error values, consistent with the theoretical convergence expectations. These results confirm the practical effectiveness and reliability of the proposed method.
Results and Discussion
9. Comparative Analysis
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| Symbol | Description |
| Unknown solution function | |
| Known source term | |
| Caputo fractional derivative of order [59,64] | |
| , | Riemann–Liouville fractional integral of order [59,64] |
| Initial condition; is a real constant | |
| Initial condition; is a real constant | |
| Problem (1) domain | |
| nth iteration in ADM-based schemes [59] | |
| Orders of fractional operators | |
| Shehu transform operator [67,68] | |
| Variable for Shehu transform | |
| Sumudu transform operator | |
| w | Variable for Sumudu transform [65] |
| Banach space of continuous functions on the interval [58] | |
| Partial sum of the series , defined as |
References
- Jia, Y.; Xu, M.; Lin, Y.; Jiang, D. An efficient technique based on least-squares method for fractional integro-differential equations. Alex. Eng. J. 2023, 64, 97–105. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E. Numerical solution of nonlinear fractional differential equations by spline collocation methods. J. Comput. Appl. Math. 2024, 255, 216–230. [Google Scholar] [CrossRef]
- Li, X.; Wu, B. A new reproducing kernel collocation method for nonlocal fractional boundary value problems with non-smooth solutions. Appl. Math. Lett. 2018, 86, 194–199. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Neural Ordinary Differential Equations for robust parameter estimation in dynamic systems with physical priors. Appl. Soft Comput. 2025, 169, 112649. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Khan, H.; Shah, K.; Khan, A. Fractional order mathematical modeling of COVID-19 transmission. Chaos Solitons Fractals 2020, 139, 110256. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. A fractional differential equation model for the COVID-19 transmission by using the Caputo-Fabrizio derivative. Adv. Differ. Equ. 2020, 2020, 299. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Sumelka, W.; Łuczak, B.; Gajewski, T.; Voyiadjis, G.Z. Modelling of AAA in the framework of time-fractional damage hyperelasticity. Int. J. Solids Struct. 2020, 206, 30–42. [Google Scholar] [CrossRef]
- Caballero, J.; Lopez, B.; Sadarangani, K. Existence of positive solutions in the space of Lipschitz functions for a fractional boundary problem with nonlocal boundary condition. J. Fixed Point Theory Appl. 2021, 23, 27. [Google Scholar] [CrossRef]
- Bougoffa, L.; Rach, R.C. An adaptation of the modified decomposition method in solving nonlinear initial-boundary value problems for ODEs. J. Appl. Math. Comput. 2021, 68, 2787–2802. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y. Hahn wavelets collocation method combined with Laplace transform method for solving fractional integro-differential equations. Math. Sci. 2024, 18, 463–477. [Google Scholar] [CrossRef]
- Meng, Z.; Yi, M.; Huang, J.; Song, L. Numerical solutions of nonlinear fractional differential equations by alternative Legendre polynomials. Appl. Math. Comput. 2018, 336, 454–464. [Google Scholar] [CrossRef]
- Masti, I.; Sayevand, K. On collocation-Galerkin method and fractional B-spline functions for a class of stochastic fractional integro-differential equations. Math. Comput. Simul. 2024, 216, 263–287. [Google Scholar] [CrossRef]
- Chandel, V.S.; Wang, G.; Talha, M. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Bouallala, M.; Essoufi, E.L.H.; Nguyen, V.T.; Pang, W. A time-fractional of a viscoelastic frictionless contact problem with normal compliance. Eur. Phys. J. Spec. Top. 2023, 232, 2549–2558. [Google Scholar] [CrossRef]
- Bouallala, M.; Ouafik, Y. Analysis and Numerical Simulation for a Time-Fractional Contact Problem with History-Dependent Operator in Thermo-Viscoelasticity. New Math. Nat. Comput. 2025. [Google Scholar] [CrossRef]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20200050. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M. A new wavelet method for fractional integro-differential equations with ψ-Caputo fractional derivative. Math. Comput. Simul. 2024, 217, 97–108. [Google Scholar] [CrossRef]
- Azarnavid, B. A kernel-based method for fractional integro-differential equations with a weakly singular kernel in multi-dimensional complex domains. Eng. Anal. Bound. Elem. 2024, 159, 1–10. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics. Int. Cent. Mech. Sci. 1997, 378, 223–276. [Google Scholar] [CrossRef]
- Abbas, S.; Un Nisa, Z.; Nazar, M.; Amjad, M.; Ali, H.; Jan, A.Z. Application of heat and mass transfer to convective flow of Casson fluids in a microchannel with Caputo–Fabrizio derivative approach. Arab. J. Sci. Eng. 2024, 49, 1275–1286. [Google Scholar] [CrossRef]
- Ullah, S.; Arif, M.S.; Din, R.U.; Ullah, I. Stability and numerical analysis of SEIVR COVID-19 fractional and integral order model under saturated incidence rate. Int. J. Appl. Comput. Math. 2025, 11, 105. [Google Scholar] [CrossRef]
- Adiguzel, R.S.; Aksoy, U.; Karapinar, E.; Erhan, I.M. On the solution of a boundary value problem associated with a fractional differential equation. Math. Methods Appl. Sci. 2024, 47, 10928–10939. [Google Scholar] [CrossRef]
- Wanassi, O.K.; Bourguiba, R.; Torres, D.F.M. Existence and uniqueness of solution for fractional differential equations with integral boundary conditions and the Adomian decomposition method. Math. Methods Appl. Sci. 2024, 47, 3582–3595. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y. A Fractional Adams Method for Caputo Fractional Differential Equations with Modified Graded Meshes. Mathematics 2025, 13, 891. [Google Scholar] [CrossRef]
- Selvam, A.; Sabarinathan, S.; Nisar, K.S.; Ravichandran, C.; Kumar, B.V.S. Results on Ulam-type stability of linear differential equation with integral transform. Math. Methods Appl. Sci. 2024, 47, 2311–2323. [Google Scholar] [CrossRef]
- Mohammed, M.O.; Rafeeq, A.S. New Results for Existence, Uniqueness, and Ulam Stable Theorem to Caputo–Fabrizio Fractional Differential Equations with Periodic Boundary Conditions. Int. J. Appl. Comput. Math. 2024, 10, 109. [Google Scholar] [CrossRef]
- Vijayalakshmi, G.M.; Ariyanatchi, M.; Govindan, V.; Byeon, H.; Pimpunchat, B. Stability and Hopf Bifurcations Analysis in a Three-Phase Dengue Diffusion Model with Time Delay in Fractional Derivative and Laplace–Adomian Decomposition Numerical Approach. Math. Methods Appl. Sci. 2025, 48, 11630–11651. [Google Scholar] [CrossRef]
- Yunus, A.O.; Olayiwola, M.O.; Omoloye, M.A.; Oladapo, A.O. A fractional order model of Lassa disease using the Laplace-Adomian Decomposition Method. Healthc. Anal. 2023, 3, 100167. [Google Scholar] [CrossRef]
- Yunus, A.O.; Olayiwola, M.O.; Adedokun, K.A.; Adedeji, J.A.; Alaje, I.A. Mathematical analysis of fractional-order Caputo’s derivative of coronavirus disease model via Laplace Adomian decomposition method. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 144. [Google Scholar] [CrossRef]
- Cai, X.; Wang, Y. A Novel Fourth-Order Finite Difference Scheme for European Option Pricing in the Time-Fractional Black-Scholes Model. Mathematics 2024, 12, 3343. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Y. A difference method for solving the q-fractional differential equations. Appl. Math. Lett. 2019, 98, 292–299. [Google Scholar] [CrossRef]
- Kumari, T.; Roul, P. An efficient computational technique for solving a time-fractional reaction-subdiffusion model in 2D space. Comput. Math. Appl. 2024, 160, 191–208. [Google Scholar] [CrossRef]
- Khader, M.M. Introducing an efficient modification of the homotopy perturbation method by using Chebyshev polynomials. Arab. J. Math. Sci. 2012, 18, 61–71. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions. J. Math. Chem. 2021, 59, 1139–1150. [Google Scholar] [CrossRef]
- Liao, S. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Hemeda, A.A. Modified Homotopy Perturbation Method for Solving Fractional Differential Equations. J. Appl. Math. 2014, 2014, 594245. [Google Scholar] [CrossRef]
- Gusu, D.M.; Wegi, D.; Gemechu, G.; Gemechu, D. Fractional Order Airy’s Type Differential Equations of Its Models Using RDTM. ZAMM-Math. Probl. Eng. 2021, 2021, 3719206. [Google Scholar] [CrossRef]
- Ali, K.; Faridi, A.A.; Khan, N.; Nisar, K.S.; Ahmad, S. On the suitability of differential transform method for solving the self-similar channel flow problems. ZAMM-Math. Probl. Eng. 2023, 103, e202100358. [Google Scholar] [CrossRef]
- Rysak, A.; Gregorczyk, M. Differential Transform Method as an Effective Tool for Investigating Fractional Dynamical Systems. Appl. Sci. 2021, 11, 6955. [Google Scholar] [CrossRef]
- Gassem, F.; Almalahi, M.; Osman, O.; Muflh, B.; Aldwoah, K.; Kamel, A.; Eljaneid, N. Nonlinear Fractional Evolution Control Modeling via Power Non-Local Kernels: A Generalization of Caputo–Fabrizio, Atangana–Baleanu, and Hattaf Derivatives. Fractal Fract. 2025, 9, 104. [Google Scholar] [CrossRef]
- Li, C.; Zheng, L.; He, T. Fractional-order rate-dependent porous-thermo-elasticity model based on new fractional derivatives with non-singular kernels and 1D transient dynamic response analysis of magnesium-based porous half-space with voids. Arch. Appl. Mech. 2025, 95, 30. [Google Scholar] [CrossRef]
- Szajek, K.; Sumelka, W. Discrete mass-spring structure identification in nonlocal continuum space-fractional model. Eur. Phys. J. Plus 2019, 134, 448. [Google Scholar] [CrossRef]
- Shiri, B.; Guang, Y.; Baleanu, D. Inverse problems for discrete Hermite nabla difference equation. Appl. Math. Sci. Eng. 2025, 33, 2431000. [Google Scholar] [CrossRef]
- Wu, G.C.; Shiri, B.; Fan, Q.; Feng, H.R. Terminal Value Problems of Non-homogeneous Fractional Linear Systems with General Memory Kernels. J. Nonlinear Math. Phys. 2023, 30, 303–314. [Google Scholar] [CrossRef]
- Kelil, A.S.; Appadu, A.R. Shehu-Adomian Decomposition Method for Dispersive KdV-Type Equations. Math. Anal. Appl. 2021, 381, 103–129. [Google Scholar]
- Liaqat, M.I.; Khan, A.; Alam, M.A.; Pandit, M.K.; Etemad, S.; Rezapour, S. Approximate and Closed-Form Solutions of Newell-Whitehead-Segel Equations via Modified Conformable Shehu Transform Decomposition Method. Math. Probl. Eng. 2022, 2022, 6752455. [Google Scholar] [CrossRef]
- Chu, Y.M.; Bani Hani, E.H.; El-Zahar, E.R.; Ebaid, A.; Shah, N.A. Combination of Shehu Decomposition and Variational Iteration Transform Methods for Solving Fractional Third Order Dispersive Partial Differential Equations. Numer. Methods Partial. Differ. Equ. 2024, 40, e22755. [Google Scholar] [CrossRef]
- Kapoor, M.; Shah, N.A.; Weera, W. Analytical Solution of Time-Fractional Schrödinger Equations via Shehu Adomian Decomposition Method. Aims Math. 2022, 7, 19562–19596. [Google Scholar] [CrossRef]
- Bildik, N.; Deniz, S. The Use of Sumudu Decomposition Method for Solving Predator-Prey Systems. Math. Sci. Lett. 2016, 5, 285–289. [Google Scholar] [CrossRef]
- Eltayeb, H.; Kılıçman, A. Application of Sumudu Decomposition Method to Solve Nonlinear System of Partial Differential Equations. In Abstract and Applied Analysis 2021, 2021, 412948. [Google Scholar] [CrossRef]
- Richard, M.; Zhao, W. Padé-Sumudu-Adomian Decomposition Method for Nonlinear Schrödinger Equation. J. Appl. Math. 2021, 2021, 6626236. [Google Scholar] [CrossRef]
- Jia, H.; Nie, Y.; Zhao, Y. General Conformable Fractional Double Laplace-Sumudu Transform and Its Application. J. Appl. Anal. Comput. 2025, 15, 9–20. [Google Scholar] [CrossRef]
- Das, A.; Rabbani, M.; Mohiuddine, S.A.; Deuri, B.C. Iterative algorithm and theoretical treatment of existence of solution for (k, z)-Riemann-Liouville fractional integral equations. J. Pseudo-Differ. Oper. Appl. 2022, 13, 39. [Google Scholar] [CrossRef]
- Das, A.; Mohiuddine, S.A.; Alotaibi, A.; Deuri, B.C. Generalization of Darbo-type theorem and application on existence of implicit fractional integral equations in tempered sequence spaces. Alex. Eng. J. 2022, 61, 2010–2015. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Mirgani, S.M.; Tellab, B.; Amara, A.; Mezabia, M.E.H.; Zennir, K.; Bouhali, K. Hyers-Ulam Stability Results of Solutions for a Multi-Point ϕ-Riemann-Liouville Fractional Boundary Value Problem. Mathematics 2025, 13, 1450. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Switzerland; Philadelphia, PA, USA, 1993. [Google Scholar]
- Verma, P.; Kumar, M. Analytical solution with existence and uniqueness conditions of non-linear initial value multi-order fractional differential equations using Caputo derivative. Eng. Comput. 2022, 38, 661–678. [Google Scholar] [CrossRef]
- Verma, P.; Kumar, M. Exact solution with existence and uniqueness conditions for multi-dimensional time-space tempered fractional diffusion-wave equation. Eng. Comput. 2022, 38, 271–281. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Janev, M.; Konjik, S.; Pilipovic, S. Wave equation for generalized Zener model containing complex order fractional derivatives. Contin. Mech. Thermodyn. 2017, 29, 569–583. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Janev, M.; Pilipovic, S. Non-linear boundary value problems involving Caputo derivatives of complex fractional order. Appl. Math. Comput. 2018, 334, 326–342. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Numerical methods for nonlinear partial differential equations of fractional order. Appl. Math. Model. 2008, 32, 28–39. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holl. Math. Stud. 2006, 204, 1–523. [Google Scholar]
- Alomari, A.K. Homotopy-Sumudu transforms for solving system of fractional partial differential equations. Adv. Differ. Equ. 2020, 2020, 222. [Google Scholar] [CrossRef]
- Bekela, A.S.; Deresse, A.T. An Efficient Numerical Method for Nonlinear Time Fractional Hyperbolic Partial Differential Equations Based on Fractional Shehu Transform Iterative Method. J. Appl. Math. 2025, 22, 7007124. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. Homotopy analysis Shehu transform method for solving fuzzy differential equations of fractional and integer order derivatives. Comput. Appl. Math. 2021, 40, 86. [Google Scholar] [CrossRef]
- Areshi, M.; Zidan, A.M.; Shah, R.; Nonlaopon, K. A Modified Techniques of Fractional-Order Cauchy-ReactionDiffusion Equation via Shehu Transform. J. Funct. Spaces 2021, 15, 5726822. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; ISBN 9780125588409. [Google Scholar]
- Verma, P.; Kumar, M. Hyers-Ulam Stability and Existence of Solution for Nonlinear Variable Fractional Differential Equations with Singular Kernel. Int. J. Appl. Comput. Math. 2021, 7, 147. [Google Scholar] [CrossRef]
- Verma, P.; Kumar, M.; Shukla, A. Ulam-Hyers stability and analytical approachfor m-dimensional Caputo space-time variable fractional order advection-dispersion equation. Int. J. Model. Simul. Sci. Comput. 2022, 13, 2250004. [Google Scholar] [CrossRef]
- Verma, P.; Kumar, M.; Shukla, A. Analysis on Krasnoselskii’s fixed point theorem of fuzzy variable fractional differential equation for a novel coronavirus (COVID-19) model with singular operator. Int. J. Model. Simul. Sci. Comput. 2021, 12, 2150034. [Google Scholar] [CrossRef]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1955; Volume 3. [Google Scholar]
- Ali, Z.; Zada, A.; Shah, K. On Ulam’s Stability for a Coupled Systems of Nonlinear Implicit Fractional Differential Equations. Bull. Malays. Math. Sci. Soc. 2018, 42, 2681–2699. [Google Scholar] [CrossRef]
- Hassani, H.; Avazzadeh, Z. Novel operational matrices for solving 2-dim nonlinear variable order fractional optimal control problems via a new set of basis functions. Appl. Numer. Math. 2021, 166, 26–39. [Google Scholar] [CrossRef]
- Zhao, J.; Qin, S.; Wang, J.; Liu, S. Variational problem containing psi-RL complex-order fractional derivatives. Asian J. Control 2021, 23, 1792–1802. [Google Scholar] [CrossRef]
- Mohammadizadeh, S.; Rashidinia, J.; Ezzati, R.; Khumalo, M. C3-spline for solution of second order fractional integro-differential equations. Alex. Eng. J. 2020, 59, 3535–3641. [Google Scholar] [CrossRef]
- Xu, M.; Niu, J.; Tohidi, E.; Hou, J.; Jiang, D. A new least-squares-based reproducing kernel method for solving regular and weakly singular Volterra-Fredholm integral equations with smooth and nonsmooth solutions. Math. Methods Appl. Sci. 2021, 44, 10772–10784. [Google Scholar] [CrossRef]
- Kolmanovskii, V.; Myshkis, A. Introduction to the Theory and Applications of Functional Differential Equations; Mathematics and Its Applications; Springer Science+Business Media: Dordrecht, The Netherlands, 1999; Volume 463. [Google Scholar] [CrossRef]
- Hai, X.; Yu, Y.; Xu, C.; Ren, G. Stability analysis of fractional differential equations with the short-term memory property. Fract. Calc. Appl. Anal. 2022, 25, 962–994. [Google Scholar] [CrossRef]
- Gao, G.H.; Sun, Z.Z.; Zhang, H.W. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of Fractional Calculus to the Theory of Viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Liao, Z.; Peng, C.; Peng, Y. Subspace identification in time-domain for fractional order systems based on short memory principle. J. Appl. Sci. 2011, 29, 209–215. [Google Scholar]
- Al-Jamel, A.; Al-Jamal, M.F.; El-Karamany, A. A memory-dependent derivative model for damping in oscillatory systems. J. Vib. Control 2016, 24, 2221–2229. [Google Scholar] [CrossRef]
- Guo, T.; Nikan, O.; Avazzadeh, Z.; Qiu, W. Efficient alternating direction implicit numerical approaches for multi-dimensional distributed-order fractional integro differential problems. Comput. Appl. Math. 2022, 41, 236. [Google Scholar] [CrossRef]
- Wang, Z.; Cen, D.; Mo, Y. Sharp error estimate of a compact L1-ADI scheme for the two-dimensional time-fractional integro-differential equation with singular kernels. Appl. Numer. Math. 2021, 159, 190–203. [Google Scholar] [CrossRef]
- Qiao, L.; Xu, D.; Yan, Y. High-order ADI orthogonal spline collocation method for a new 2D fractional integro-differential problem. Math. Methods Appl. Sci. 2020, 43, 5162–5178. [Google Scholar] [CrossRef]
- Qiao, L.; Xu, D.; Wang, Z. An ADI difference scheme based on fractional trapezoidal rule for fractional integro-differential equation with a weakly singular kernel. Appl. Math. Comput. 2019, 354, 103–114. [Google Scholar] [CrossRef]

| 0.5 | 0.000581 | 0.001810 | 0.010145 | 0.000541 | 0.001698 | 0.009503 |
| 0.7 | 0.000767 | 0.002435 | 0.013888 | 0.000732 | 0.002341 | 0.013386 |
| 0.9 | 0.001017 | 0.003276 | 0.019148 | 0.000987 | 0.003203 | 0.018734 |
| 1.0 | 0.001220 | 0.003992 | 0.023371 | 0.001199 | 0.003942 | 0.023015 |
| 1.2 | 0.001757 | 0.006017 | 0.035532 | 0.001761 | 0.006027 | 0.035609 |
| 1.4 | 0.002405 | 0.008461 | 0.051930 | 0.002498 | 0.008778 | 0.053857 |
| 1.6 | 0.003163 | 0.011340 | 0.072578 | 0.003379 | 0.012107 | 0.077822 |
| 1.8 | 0.004030 | 0.014652 | 0.097478 | 0.004379 | 0.015913 | 0.106326 |
| 2.0 | 0.005004 | 0.018395 | 0.126631 | 0.005569 | 0.020568 | 0.141598 |
| (0.5, 0.9) | 0.000539 | 0.000644 | 0.001129 | 0.000438 | 0.000523 | 0.000916 |
| (0.7, 1.2) | 0.000733 | 0.000887 | 0.001580 | 0.000709 | 0.000858 | 0.001528 |
| (0.9, 1.4) | 0.001019 | 0.001245 | 0.002254 | 0.001119 | 0.001369 | 0.002477 |
| (1.0, 1.6) | 0.001199 | 0.001475 | 0.002690 | 0.001437 | 0.001768 | 0.003224 |
| (1.2, 1.8) | 0.001665 | 0.002070 | 0.003836 | 0.002218 | 0.002758 | 0.005112 |
| (1.4, 2.0) | 0.002297 | 0.002892 | 0.005444 | 0.003367 | 0.004239 | 0.007982 |
| (0.3, 0.7) | 0.000367 | 0.000523 | 0.001194 | 0.000366 | 0.000520 | 0.001183 |
| (0.6, 1.1) | 0.000625 | 0.000794 | 0.001527 | 0.000619 | 0.000780 | 0.001490 |
| (0.8, 1.5) | 0.000919 | 0.001176 | 0.002155 | 0.000989 | 0.001278 | 0.002359 |
| (1.0, 1.8) | 0.001291 | 0.001667 | 0.003035 | 0.001515 | 0.001982 | 0.003675 |
| (1.3, 2.0) | 0.002069 | 0.002747 | 0.005008 | 0.002901 | 0.003884 | 0.007263 |
| (0.4, 1.0) | 0.000447 | 0.000625 | 0.001348 | 0.000443 | 0.000612 | 0.001313 |
| (0.9, 1.6) | 0.001101 | 0.001372 | 0.002465 | 0.001304 | 0.001668 | 0.003102 |
| (1.1, 1.7) | 0.001456 | 0.001897 | 0.003422 | 0.001835 | 0.002421 | 0.004575 |
| (0.5, 0.9) | 0.003715 | 0.006381 | 0.015866 | 0.003212 | 0.005497 | 0.013609 |
| (0.6, 1.0) | 0.003090 | 0.003751 | 0.006604 | 0.002811 | 0.003403 | 0.005972 |
| (0.7, 1.2) | 0.002419 | 0.004162 | 0.010406 | 0.002361 | 0.004059 | 0.010142 |
| (0.8, 1.3) | 0.002002 | 0.002437 | 0.004319 | 0.002051 | 0.002497 | 0.004429 |
| (0.9, 1.4) | 0.001654 | 0.002849 | 0.007158 | 0.001774 | 0.003061 | 0.007710 |
| (1.0, 1.6) | 0.001295 | 0.001584 | 0.002834 | 0.001493 | 0.001834 | 0.003294 |
| (1.1, 1.7) | 0.001011 | 0.001230 | 0.002189 | 0.001214 | 0.001485 | 0.002673 |
| (1.2, 1.8) | 0.000876 | 0.001068 | 0.001931 | 0.001087 | 0.001337 | 0.002356 |
| (1.3, 1.9) | 0.000679 | 0.000826 | 0.001493 | 0.000888 | 0.001102 | 0.001940 |
| (1.4, 2.0) | 0.000585 | 0.000721 | 0.001311 | 0.000797 | 0.000991 | 0.001819 |
| (0.5, 1.5) | 0.003414 | 0.004062 | 0.007204 | 0.002976 | 0.003540 | 0.006337 |
| (0.6, 1.8) | 0.002525 | 0.003105 | 0.005511 | 0.002384 | 0.002946 | 0.005152 |
| (0.5, 0.5) | 0.005030 | 0.006108 | 0.010714 | 0.004191 | 0.005066 | 0.008833 |
| (0.7, 0.7) | 0.003492 | 0.004221 | 0.007385 | 0.003143 | 0.003786 | 0.006592 |
| (0.9, 0.9) | 0.002401 | 0.002892 | 0.005053 | 0.002321 | 0.002792 | 0.004869 |
| (1.0, 1.0) | 0.001984 | 0.002387 | 0.004169 | 0.001984 | 0.002387 | 0.004169 |
| (1.2, 1.2) | 0.001346 | 0.001616 | 0.002825 | 0.001436 | 0.001729 | 0.003036 |
| (1.4, 1.4) | 0.000912 | 0.001096 | 0.001973 | 0.001084 | 0.001304 | 0.002348 |
| (1.6, 1.6) | 0.000639 | 0.000767 | 0.001392 | 0.000841 | 0.001013 | 0.001825 |
| (1.8, 1.8) | 0.000460 | 0.000551 | 0.001000 | 0.000671 | 0.000806 | 0.001470 |
| (2.0, 2.0) | 0.000344 | 0.000411 | 0.000745 | 0.000552 | 0.000663 | 0.001203 |
| Method | Transform Inversions per Iteration | Convergence Behavior |
|---|---|---|
| Standard ADM | - | Not applicable (fails to converge) |
| Laplace-ADM | - | Diverges or produces inaccurate results |
| Sumudu-ADM | 2 | Converges slowly |
| Shehu-ADM | 2 | Stable and accurate due to weighted formulation |
| Two-Step ADM (TSADM) | 1 | Yields exact results |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, P.; Sumelka, W. Existence, Stability, and Numerical Methods for Multi-Fractional Integro-Differential Equations with Singular Kernel. Mathematics 2025, 13, 2656. https://doi.org/10.3390/math13162656
Verma P, Sumelka W. Existence, Stability, and Numerical Methods for Multi-Fractional Integro-Differential Equations with Singular Kernel. Mathematics. 2025; 13(16):2656. https://doi.org/10.3390/math13162656
Chicago/Turabian StyleVerma, Pratibha, and Wojciech Sumelka. 2025. "Existence, Stability, and Numerical Methods for Multi-Fractional Integro-Differential Equations with Singular Kernel" Mathematics 13, no. 16: 2656. https://doi.org/10.3390/math13162656
APA StyleVerma, P., & Sumelka, W. (2025). Existence, Stability, and Numerical Methods for Multi-Fractional Integro-Differential Equations with Singular Kernel. Mathematics, 13(16), 2656. https://doi.org/10.3390/math13162656







