Abstract
In recent years, computational intelligence techniques have significantly contributed to the automation and optimization of trading strategies. Despite the increasing sophistication of predictive models, classical technical indicators such as dual Simple Moving Averages (2-SMA) remain popular due to their simplicity and interpretability. This work proposes an adaptive trading system that combines the 2-SMA strategy with a learning-based metaheuristic optimizer known as the Learning-Based Linear Balancer (). The objective is to dynamically adjust the strategy’s parameters to maximize returns in the highly volatile cryptocurrency market. The proposed system is evaluated through simulations using historical data of the BTCUSDT futures contract from the Binance platform, incorporating real-world trading constraints such as transaction fees. The optimization process is validated over 34 training/test splits using overlapping 60-day windows. Results show that the -optimized strategy achieves an average return on investment (ROI) of 7.9% in unseen test periods, with a maximum ROI of 17.2% in the best case. Statistical analysis using the Wilcoxon Signed-Rank Test confirms that our approach significantly outperforms classical benchmarks, including Buy and Hold, Random Walk, and non-optimized 2-SMA. This study demonstrates that hybrid strategies combining classical indicators with adaptive optimization can achieve robust and consistent returns, making them a viable alternative to more complex predictive models in crypto-based financial environments.
Keywords:
automated trading systems; technical analysis; cryptocurrency; optimization; learning-based optimization MSC:
91G60
1. Introduction
Over the last decade, cryptocurrencies have emerged as increasingly prominent assets in global financial markets, primarily due to their rapid capitalization and growing popularity [1]. As of today, thousands of cryptocurrencies are actively traded, with Bitcoin standing out as the first and most capitalized digital asset since its inception in 2009 [2,3]. However, the extreme volatility and limited predictability of cryptocurrency prices, especially Bitcoin, have posed significant challenges for analysts and researchers alike [4,5,6]. This uncertainty has prompted the development of advanced tools and strategies aimed at reducing risk and improving trading outcomes. While fundamental analysis has traditionally been used to evaluate the intrinsic value of financial assets, its limitations in highly volatile markets have led experts to increasingly rely on technical analysis [7,8]. Within this context, the use of moving averages (MAs) has gained popularity as a basic yet effective strategy for trend identification. To improve its performance, optimization techniques have been integrated into technical indicators, offering adaptive mechanisms for better decision-making.
In this work, we propose a hybrid automatic trading system that combines a dual Simple Moving Average (2-SMA) strategy with the Learning-Based Linear Balancer () optimization framework [9]. The 2-SMA component serves as the signal generator, while dynamically adjusts its parameters to maximize profitability over time. This optimization framework leverages population-based metaheuristics and learning-based feedback to balance intensification and diversification during the search process. The use of is further motivated by recent findings in the literature, which highlight the advantages of hybrid optimization schemes over traditional single-metaheuristic approaches [10,11]. By integrating learning-based components, enables adaptive control of the search dynamics based on real-time feedback from the optimization process. This flexibility improves the algorithm’s ability to respond to changes in the search space and enhances overall performance. Such hybrid strategies have shown superior results when tackling complex, noisy, and dynamic optimization problems, conditions frequently encountered in financial trading environments. Beyond its empirical performance, the proposed system introduces several methodological innovations. First, it models the 2-SMA strategy as a finite-state machine with six tunable parameters, including stop–loss and stop–win thresholds for both long and short positions—extending the classical crossover approach. Second, the objective function integrates transaction costs and realistic position management logic, simulating the compound effect of sequential trades over historical market periods. Finally, the adoption of for adaptive parameter tuning represents a novel application of learning-based hybrid optimization in the context of algorithmic trading, enabling a more robust and data-driven configuration process.
The system proposed in this work is tested on historical BTCUSDT data (a Bitcoin-based perpetual futures instrument) obtained from the Binance platform, covering the period from August 2020 to January 2022. The simulations replicate real-world trading conditions, including transaction fees and position management rules. The results demonstrate consistent positive returns, reinforcing the practicality of combining technical analysis with adaptive optimization in volatile markets such as cryptocurrencies.
The central challenge addressed in this work lies in the rigidity of traditional technical trading strategies, such as 2-SMA, which rely on fixed parameters and lack adaptation to rapidly changing market dynamics [12]. In highly volatile markets like cryptocurrencies, static configurations often lead to inconsistent performance, overfitting to past trends, or exposure to avoidable risks [13]. Although 2-SMA strategies are widely used for their simplicity and interpretability [14], their effectiveness depends heavily on parameter tuning, which is rarely optimized in practice. This highlights the need for intelligent optimization frameworks capable of adapting to different market conditions [15,16]. Our work aims to fill this gap by integrating a learning-based optimization mechanism that adaptively tunes 2-SMA parameters to maximize performance while maintaining generalizability.
The main contributions of this work are summarized as follows:
- We design and implement a hybrid trading system combining the 2-SMA strategy with the optimizer.
- The system is validated on real historical data under realistic trading constraints (Binance Futures platform).
- Performance is evaluated across multiple temporal windows, showing consistency in returns and robustness to volatility.
- A comparison with baseline strategies and statistical validation is provided to strengthen the empirical assessment.
While our study focuses on BTCUSDT, a liquid, highly volatile cryptocurrency pair, many of the behavioral patterns captured by technical indicators such as moving average crossovers are shared with other major cryptocurrencies (e.g., ETH, LTC). In particular, their decentralized structure, 24/7 trading availability, and heightened sensitivity to investor sentiment result in frequent trend reversals and short-lived patterns, which are precisely the types of dynamics that crossover-based systems aim to capture [17]. In contrast, fiat currency pairs (Forex) tend to exhibit lower volatility and stronger influence from macroeconomic events and centralized monetary policies. Consequently, similar strategies may require longer time frames or additional filters to perform effectively in traditional markets. Regarding regional differences, centralized exchanges such as Binance operate globally, creating a relatively uniform trading environment. However, time zone effects (e.g., higher volatility during overlapping U.S. and European sessions) can impact short-term patterns. Since our system is data-driven and optimized over multiple historical periods, it inherently adapts to such fluctuations without being explicitly tied to any regional market structure. Finally, we note that BTC’s high liquidity, dominance in the crypto market, and tendency to lead broader market trends make it an appropriate candidate for initial testing [18]. However, future work could extend our methodology to multi-asset or cross-market scenarios to further explore its generalization capabilities.
The remainder of this paper is organized as follows: Section 2 reviews the main research directions in automated trading systems and optimization methods. Section 3 introduces the core concepts underlying metaheuristics, the optimization framework, and technical trading indicators. Section 4 presents the methodology used in this work. Section 5 formally defines the trading problem, including the decision variables, constraints, and objective function. Section 6 outlines the proposed simulation and optimization workflow. Section 7 details the experimental setup, reports performance outcomes, and compares the proposed approach against classical trading benchmarks. Finally, Section 8 summarizes the main contributions and discusses potential avenues for future research.
2. Related Works
In recent years, the interest in automated trading systems has grown significantly, particularly in the context of cryptocurrency markets. This surge is driven by the increasing complexity of trading environments and the potential for high returns. Research efforts in this field have primarily focused on three main areas: portfolio optimization [19,20,21,22], the application of deep learning models for price forecasting [23,24,25,26], and, though to a lesser extent, the use of metaheuristics to optimize rule-based strategies derived from technical indicators [27,28,29,30,31].
The present work is aligned with the third line of research. It proposes a hybrid architecture that integrates a classical technical analysis method (dual Simple Moving Average, or 2-SMA) with a metaheuristic optimization framework (LB2). This approach aims to enhance the profitability of traditional indicators by adaptively tuning their parameters using machine learning-assisted metaheuristics. Although the integration of technical analysis and metaheuristics has received limited attention, a growing number of studies have explored this intersection. For example, in [31], Ant Colony Optimization (ACO) was applied to dynamically adjust decision thresholds in a Pairs Trading strategy on the Forex market. Similarly, ref. [29] presented a trading model based on three moving averages optimized by Particle Swarm Optimization (PSO), where trading signals were generated based on predicted price movements. Other studies have compared the performance of different optimization algorithms in financial contexts. In [27], PSO and Genetic Algorithms (GAs) were evaluated for designing market timing strategies using Moving Average Convergence Divergence (MACD), Relative Strength Index (RSI), and CHAIKIN indicators. The results showed that optimized strategies outperformed static configurations across varying market conditions. Furthermore, ref. [28] implemented and analyzed the Fireworks Algorithm (FA) and PSO for optimizing Bollinger Band-based strategies on the S&P 500 index, focusing on the balance between exploration and exploitation. These works collectively highlight the potential of metaheuristic optimization in enhancing trading strategies. However, only a few studies have applied such techniques specifically to the cryptocurrency market, where price volatility and rapid regime changes present additional challenges. Moreover, the majority of previous approaches rely on static or purist optimization schemes. In contrast, our proposed method leverages a hybrid learning-based optimizer, LB2, which dynamically adjusts the exploration–exploitation trade-off in real time.
In summary, this work contributes to the growing body of research on intelligent trading systems by (i) applying metaheuristic optimization to a classical indicator under real-world trading conditions and (ii) demonstrating the advantages of using hybrid, adaptive optimization strategies in volatile financial markets such as cryptocurrencies.
3. Background
This section presents the core algorithms and methods employed in the proposed trading system. First, we introduce relevant concepts from the field of optimization, including population-based metaheuristics and the hybrid optimization framework known as . Then, we describe the classical technical indicator used in this work, the dual Simple Moving Average (2-SMA), commonly applied in algorithmic trading strategies.
3.1. Optimization
Optimization has become a highly relevant and attractive research area within the field of Artificial Intelligence (AI) [32,33]. Its primary goal is to model real-world problems, design abstract representations, and implement algorithms that can find high-quality solutions efficiently. Numerous industrial applications have benefited from optimization techniques, including manufacturing cell design [34], the knapsack problem [35], crew scheduling [36], set covering [37], and vehicle routing [38], among others.
To address these complex real-life problems, researchers have developed both exact and approximate methods. Exact methods search exhaustively through the solution space to identify the global optimum. While they guarantee optimality, they are typically computationally expensive and suitable only for small-scale or well-structured instances. In contrast, approximate methods focus on exploring promising regions of the solution space without exhaustively evaluating every possibility. These methods do not guarantee optimal solutions but can often find near-optimal results within reasonable computational time. Among the most prominent approximate techniques are metaheuristics, which have proven effective across a wide range of optimization problems.
3.1.1. Metaheuristics
Metaheuristics are high-level optimization strategies designed to guide subordinate heuristics in efficiently exploring the solution space. Over the years, they have gained significant attention in AI due to their success in solving complex and diverse problems across multiple domains. Metaheuristics can be broadly categorized based on their search dynamics. For example, single-solution metaheuristics modify a single candidate solution iteratively; typical examples include local search [39] and simulated annealing [40]. In contrast, population-based metaheuristics operate on a set of solutions simultaneously, allowing interaction and information exchange among individuals during the search process. Prominent algorithms in this category include the Shuffle Frog Leaping Algorithm (SFLA) [41], Ant Colony Optimization (ACO) [42], Gray Wolf Optimizer (GWO) [43], and Spotted Hyena Optimizer (SHO) [44]. The SHO, in particular, is inspired by the hunting strategies of hyenas in nature. It integrates four mechanisms, encircling prey, cooperative hunting, attacking, and global search, to balance exploration and exploitation effectively. These characteristics make it a suitable choice for tackling high-dimensional and nonlinear optimization tasks, such as those found in financial strategy design.
3.1.2. Hybrid Approaches
In recent years, numerous state-of-the-art approaches have emerged from the combination of techniques across different domains. These hybrid strategies typically integrate diverse methods or paradigms, such as metaheuristics and machine learning, to take advantage of their complementary strengths. Compared to purist algorithms, hybrid approaches have demonstrated superior performance in solving complex, real-world optimization problems [10,11,45].
Learning-Based Linear Balancer ()
The Learning-Based Linear Balancer () is a hybrid optimization framework designed to improve the adaptive behavior of population-based metaheuristics [9]. It aims to dynamically balance two fundamental search mechanisms: intensification (exploitation of promising areas) and diversification (exploration of new regions). Traditional metaheuristics such as PSO or GA typically rely on fixed parameter settings or manually tuned weights, which often limit robustness in dynamic or uncertain optimization landscapes. Unlike these approaches, uses a lightweight online learning strategy to guide the selection of search strategies. Specifically, it incorporates simple linear regression models that collect real-time feedback on the effectiveness of different combinations of intensification and diversification levels, adjusting their selection probabilities adaptively as the search progresses. This adaptive mechanism allows to better respond to changes in the fitness landscape, a key requirement in highly volatile domains such as cryptocurrency trading. Hybrid strategies combining metaheuristics with machine learning feedback have been shown to provide superior performance and convergence properties in complex optimization scenarios [11].
In the framework, three levels of intensification and diversification (Soft, Medium, Hard) are defined, and their combinations are applied as search strategies during the optimization process (see Table 1). Initially, all strategies are assigned equal selection probabilities. As the algorithm iterates, the regression models update these probabilities based on observed performance, reinforcing the most effective search behaviors. The learning mechanism operates as follows:

Table 1.
Scheme configuration for based on intensification and diversification levels.
Intensification:
Diversification:
The predictions are used to identify the best-performing schemes for the next iterations:
These weights then influence a Monte Carlo-style selection mechanism that adjusts the application frequency of each strategy.
3.2. Trading
Trading refers to the process of exchanging financial assets and has existed for centuries in various forms. In modern financial markets, trading decisions must account for numerous uncertain variables and external influences. This complexity makes the process well-suited for computational models that can assist with decision-making under uncertainty.
3.2.1. High-Frequency Trading
Recent advancements in technology have led to the development of automated and high-frequency trading systems. These systems are designed to execute large volumes of transactions within extremely short time frames, often capitalizing on small price fluctuations. Their efficiency and profitability have made them a popular area of research in algorithmic trading.
3.2.2. Trading Algorithm
One of the most widely used technical indicators in algorithmic trading is the moving average (MA). This technique smooths time series data to highlight trends by averaging past values. The general formula for a Simple Moving Average (SMA) is
where represents the asset price at time t and n is the size of the averaging window. By increasing n, the resulting series becomes smoother and less reactive to short-term volatility.
In this work, we employ a dual moving average (2-SMA) strategy, which uses two SMAs with different window lengths. Trading signals are generated based on crossover points between the fast and slow averages, a technique commonly used to identify trend reversals and entry/exit points.
3.2.3. Cryptocurrency Market Characteristics
Unlike traditional markets such as equities or Forex, cryptocurrency trading presents unique operational and behavioral features. First, these markets operate continuously, 24/7, without centralized oversight, which increases intraday volatility and requires dynamically adaptable systems [17]. Second, cryptocurrencies like Bitcoin often exhibit substantially higher volatility than conventional financial instruments, with daily price swings regularly exceeding 5% [46]. Their speculative nature and sensitivity to external news amplify short-term fluctuations. Additionally, perpetual futures contracts such as BTCUSDT, traded on platforms like Binance, allow for leveraged positions with no expiration. This constant exposure heightens risk and necessitates robust position management. These structural differences, high volatility, 24/7 operation, and leveraged trading make Bitcoin a suitable initial testbed for crossover-based and adaptive strategies such as 2-SMA optimized with . While the method may generalize to other crypto pairs like Ethereum (ETH) or Litecoin (LTC), it would likely require recalibration to account for asset-specific volatility regimes. Forex, by contrast, typically requires different tuning due to its lower volatility and influence from centralized policy decisions.
4. Methodology
The core objective of this study is to implement an automatic trading strategy based on a dual Simple Moving Average (2-SMA) system, whose parameters are optimized using the Learning-Based Linear Balancer (). The strategy is applied to the BTCUSDT trading pair using historical data extracted from the Binance Futures platform.
The foundation of the system lies in computing two Simple Moving Averages (SMAs) with different time windows over the closing prices of the financial instrument. The longer-period SMA reflects a broader market trend and reacts more slowly to recent changes, while the shorter-period SMA captures more recent price movements with greater sensitivity (Figure 1).
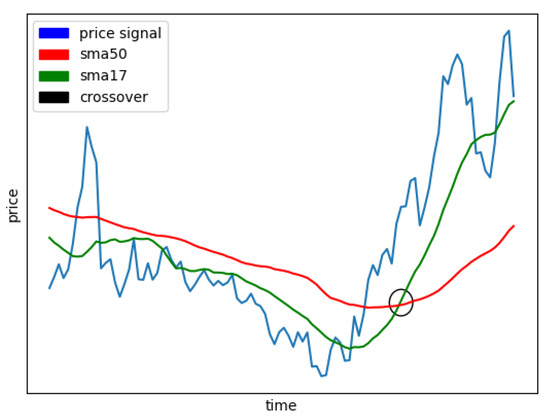
Figure 1.
Graphical representation of 2-SMA crossover.
Trading signals are generated based on crossover events. A long position (buy signal) is initiated when the short-term SMA crosses above the long-term SMA, suggesting a potential upward trend. Conversely, a short position (sell signal) is triggered when the short-term SMA crosses below the long-term SMA, indicating a downward trend. To manage open positions and mitigate risks, the system incorporates two additional mechanisms: trailing stop–loss bands and fixed stop–win thresholds. These bands are applied differently for long and short positions:
- Trailing Stop–Loss: A dynamic threshold that adjusts with market movement and is designed to limit losses. If the market moves against the currently open position beyond a specified tolerance, the system automatically closes the position.
- Stop–Win: A fixed threshold (expressed as a percentage of the entry price) that locks in profits if the price reaches a predefined favorable point. This helps prevent reversals from eroding potential gains.
Figure 2 illustrates a case where a long position is opened after a crossover signal, but the price does not increase as expected. The stop–loss mechanism triggers an exit before greater losses occur. Similarly, if the price had increased beyond a certain percentage, the stop–win mechanism would have secured profits.
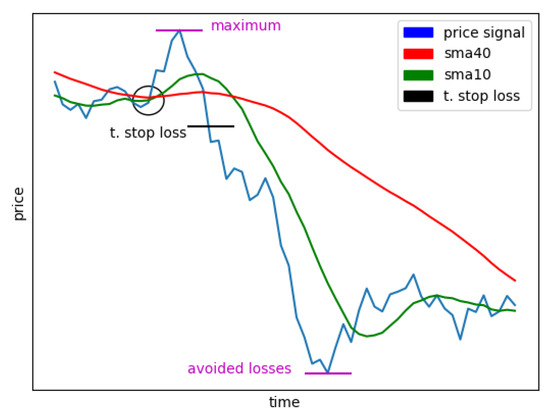
Figure 2.
An illustration of a trailing stop–loss mechanism in a long position.
The complete strategy, therefore, combines trend detection (via 2-SMA crossovers) with dynamic position management to reduce risk and capture gains. The parameters of the moving averages and stop bands are then optimized using the framework, as detailed in the following subsection.
5. Problem Model
The 2-SMA trading strategy is modeled as a four-state finite-state machine. The states represent whether the system is (i) waiting to open a long position, (ii) waiting to open a short position, (iii) holding a long position, or (iv) holding a short position. Transitions between states are triggered by crossover events between the short-term and long-term moving averages. Specifically, when in a waiting state, a transition to an open position occurs if the short-term moving average crosses above (long signal) or below (short signal) the long-term moving average. Positions are closed based on predefined thresholds using either trailing stop–loss or fixed stop–win rules, depending on the current position type (Figure 3).
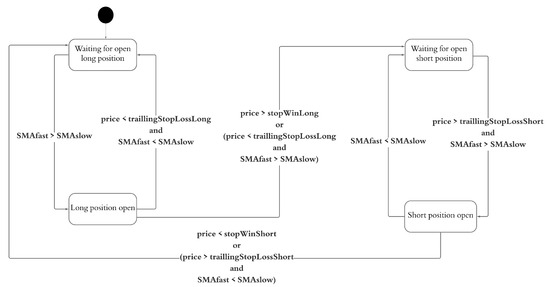
Figure 3.
A state diagram of the 2-SMA trading strategy.
The model involves six key parameters:
- : number of time intervals for the fast (short-term) SMA, with .
- : number of intervals for the slow (long-term) SMA, with and .
- : multiplier for the minimum asset value to define the short trailing stop–loss (range: ).
- : multiplier for the maximum asset value for the long trailing stop–loss (range: ).
- : multiplier of entry price for the short stop–win threshold ().
- : multiplier of entry price for the long stop–win threshold ().
The profit or loss of a single trading period i is defined as
where is the gain or loss of a position at time t in period i and denotes the transaction costs applied when opening and closing trades.
The objective function used in this work is based on net profit accumulation over multiple simulation periods. This approach is conceptually aligned with previous applications in high-frequency trading systems, such as that of Crawford et al. (2018) [30], where performance is measured by accumulated returns across discrete trading intervals. However, our model extends prior work by incorporating two additional decision variables (stop–loss and stop–win thresholds) and a state-driven control architecture. While alternative formulations using logarithmic or geometric returns are common in portfolio theory, we deliberately avoid them here to ensure consistency with discrete capital simulation and practical interpretability under real-world trading rules.
6. Proposed Approach
The evaluation of the proposed trading system is carried out through simulation-based experiments, where the 2-SMA strategy is optimized and tested across multiple historical periods. As described in Equation (11), the optimization objective is to maximize the average logarithmic return over several independent periods. The simulation framework uses historical closing prices of the BTCUSDT trading pair, with a time frame of 15 min per data point. Each simulation starts with an initial capital of one monetary unit and applies the trading decisions derived from the 2-SMA strategy, including opening and closing positions based on crossover signals and stop–band thresholds. The entire simulation environment follows the conventions and trading rules of the Binance Futures platform, including transaction fees and leverage settings. This ensures that the results are representative of a real-world trading environment. The parameters of the 2-SMA strategy, specifically the moving average windows and stop–band thresholds, are optimized using the metaheuristic. The optimizer searches for the parameter configuration that maximizes the objective function described previously. Once a parameter configuration is identified during the training phase, its performance is validated on a different set of unseen time periods. To ensure statistical robustness and mitigate the effects of overfitting, this train/test process is repeated 34 times, each with different combinations of training and test periods drawn from the dataset.
Figure 4 illustrates the interaction between the components of the system, including the optimization loop, the trading simulator, and the evaluation metrics.
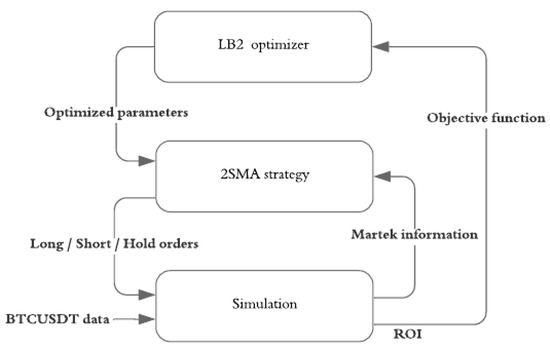
Figure 4.
Interaction between system components.
7. Experimental Results
This section presents the experimental evaluation of the proposed trading strategy. We assess the performance of the 2-SMA model optimized by the framework using historical market data under realistic trading constraints. The experiments are designed to examine the profitability, robustness, and consistency of the strategy across multiple temporal windows. Additionally, we compare the proposed approach against three classical baselines and apply statistical tests to validate the significance of the observed results.
7.1. Data Employed
The dataset used in this work consists of the historical closing prices of the BTCUSDT instrument from the Binance Futures platform, covering the period from August 2020 to January 2022. The data uses a 15 min time frame. To enable robust performance evaluation, the data was segmented into overlapping 60-day periods, each consisting of 5760 time intervals. A new simulation period is created every 30 days, resulting in 23 training periods and 8 distinct testing periods. This overlapping scheme reduces the risk of performance distortion due to short-term extreme gains. For instance, high returns in a single month will not overshadow consistent losses throughout the remaining year, thus promoting fairness and robustness in model evaluation. The optimization process is conducted over the training periods, and the resulting parameter configurations are evaluated on the separate testing set. The final metric to optimize is the geometric mean of investment returns across all simulation periods, as discussed in Section 5.
7.2. Results and Comparison
To facilitate interpretation, the figures and tables presented in this section provide both aggregated metrics and detailed visualizations of the trading system’s behavior. The capital accumulation plots represent compounded returns over time, while the tabulated ROI values indicate gains relative to the initial capital invested. Values greater than 1.0 denote net profits; values below 1.0 represent losses.
Table 2 summarizes the return on investment (ROI) and execution time for 34 repeated simulations using different training/test splits. The optimizer used in all experiments is . As shown, the strategy achieved consistently positive results in both training and testing scenarios, with the best configurations yielding an average ROI of 11.6% in training and 7.9% in testing periods. The duration of the experiments ranged from approximately 6 to 11 min per run, depending on the complexity of each instance, confirming the computational feasibility of the proposed approach even when applied across multiple rolling windows.

Table 2.
Performance summary of 34 experiments using 2-SMA + .
We further analyze the best-performing configuration, identified in 31 simulations. This configuration achieved a 17.2% ROI on the test set. Out of the 23 training periods, it yielded profits in 17 cases (approximately 74%), while on the 8 test periods it was profitable in 7 (87.5%). These results indicate a consistent performance profile. Figure 5 shows the capital evolution of this configuration from January 2020 to September 2022. The y-axis represents accumulated capital in relative units, while the x-axis reflects the simulated trading time frame. The curve starts from an initial capital of 1.0 and illustrates the compound effect of applying the 2-SMA strategy optimized by over sequential trades. The figure reveals both periods of moderate drawdowns and strong recoveries, culminating in a final capital value exceeding 5.0, which supports the long-term profitability and robustness of the system under volatile conditions. From a financial perspective, the performance of this strategy is highly promising. While the system may incur short-term losses (up to 10.5% in certain 2-month periods), the average gains and win rate across multiple windows suggest it can deliver consistent long-term returns.
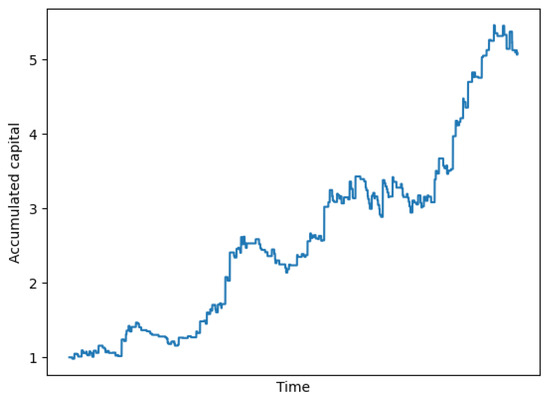
Figure 5.
Capital growth over time using the best-performing configuration (Run 31). The x-axis represents the simulation time frame from January 2020 to September 2022, and the y-axis shows accumulated capital in relative units. Initial capital is set to 1.0. The curve illustrates the compound effect of sequential trades under the LB2-optimized 2-SMA strategy.
Table 3 details the specific parameter values that produced this optimal performance, including the window sizes of the moving averages and the stop–loss/stop–win thresholds. Table 4 further characterizes the return profile of this configuration, reporting the number of profitable and loss periods, the geometric mean ROI, and the range of observed returns over discrete 2-month windows. Together, these results demonstrate generalization attributes and reliability of the proposed strategy under realistic market conditions.

Table 3.
Parameter values for the best-performing strategy.

Table 4.
Return profile of the best-performing configuration. The ROI (return on investment) is shown per 2-month period, where a value greater than 1.0 indicates a net gain (e.g., ROI = 1.172 implies a 17.2% return).
7.3. Comparison with Classical Strategies
To contextualize the effectiveness of the proposed strategy, we compare it against two classical benchmarks commonly used in financial trading:
- Buy and Hold: A passive strategy where a long position is opened at the beginning of each test period and closed at the end, without any intermediate intervention.
- Fixed-Parameter 2-SMA: A standard technical analysis strategy using non-optimized parameters: , , with fixed thresholds , , , and .
- Random Walk Model: A stochastic baseline that assumes asset price changes follow a random walk process, with each step determined by a random direction and magnitude sampled from a normal distribution estimated from historical returns. This model serves as a neutral benchmark that incorporates volatility but lacks any market-timing capability.
These benchmarks are evaluated over the same eight test periods used in the experiments, using the same capital initialization and trading simulation framework. Thus, Table 5 summarizes the average performance of each strategy on the test set.

Table 5.
A comparison of the proposed approach with classical benchmark strategies on the test set.
The results indicate that the proposed strategy outperforms all benchmark models in terms of average ROI and consistency across test periods. Buy and Hold, while intuitive, fails to capture market fluctuations and often underperforms in volatile markets. The fixed-parameter 2-SMA approach performs slightly better, but still lacks the adaptability of the -optimized strategy. When compared to a Random Walk baseline, which represents a naive, non-informative model of price movement, the proposed system shows clear superiority in both mean returns and stability. Although the Random Walk occasionally yields higher returns in isolated periods due to favorable stochastic paths, its high variance and lack of trend exploitation result in lower overall reliability for systematic trading. These improvements can be attributed to two key aspects of the proposed method. First, the framework allows for adaptive tuning of parameters across multiple time windows, enabling the strategy to respond to evolving market dynamics, an advantage not present in static strategies like fixed-parameter 2-SMA or in purely stochastic approaches like Random Walk. Second, the integration of both trailing stop–loss and stop–win mechanisms provides finer control over risk and profit capture, contributing to capital preservation during unfavorable conditions. However, some limitations must be acknowledged. The proposed system is reactive rather than predictive, as it relies on historical crossover events without directly forecasting future price trends. Moreover, its computational requirements are higher than those of baseline strategies, due to the iterative optimization process and evaluation over multiple training/test splits. Despite these costs, our results show that this trade-off yields significantly better and more consistent returns, a finding consistent with previous studies advocating the use of learning-assisted or hybrid metaheuristic strategies in financial decision-making [16,30]. To statistically validate the improvement, we conducted a Wilcoxon Signed-Rank Test comparing the ROI per test period between our strategy and each baseline. The p-values obtained are summarized in Table 6.

Table 6.
Wilcoxon Signed-Rank Test results comparing test ROI distributions.
In all cases, the p-values are below the 0.05 significance threshold, allowing us to reject the null hypothesis of no difference in performance. This provides statistical evidence that the -optimized strategy offers significantly better returns than classical alternatives and the Random Walk model. These findings reinforce the importance of parameter tuning and adaptive optimization in financial strategy design. The framework not only improves raw performance but also enhances robustness and consistency across different market conditions, which is essential in real-world applications where volatility and regime shifts are common.
8. Conclusions
In this work, we proposed an automated trading system based on the dual Simple Moving Average (2-SMA) strategy, optimized using the Learning-Based Linear Balancer () metaheuristic framework. The strategy was evaluated through simulations using historical data of the BTCUSDT trading pair on the Binance Futures platform. The simulation environment replicated real-world trading conditions, including transaction fees, enhancing the practical relevance of the results. The optimizer was applied across 34 different training/test splits, achieving an average return on investment (ROI) of 7.9% on unseen test periods. In the best configuration, the system achieved up to 17.2% ROI over a 2-month period. These results confirm the ability of the proposed system to consistently generate profits under volatile market conditions, surpassing both Buy and Hold and traditional fixed-parameter strategies.
Despite these promising results, some variability was observed across different periods, with occasional drawdowns in performance. To address this, future work could explore the construction of diversified portfolios across multiple futures instruments, reducing the risk of asset-specific downturns. Additionally, incorporating alternative technical indicators could enhance robustness and capture a wider range of market dynamics. Another avenue for extension is the reformulation of the optimization problem in a multi-objective framework, balancing return maximization with risk control or variance minimization. This would enable a more comprehensive assessment of performance, especially in risk-sensitive applications. Furthermore, an interesting direction for future research involves extending our framework to support the modeling of derivative instruments with early-exercise features, such as American-style futures. While our study is centered on European-styled perpetual futures typical of cryptocurrency markets, incorporating optimal stopping behavior and free boundary formulations could enable meaningful comparisons with classical pricing approaches. In particular, the recent work by Zaevski provides a comprehensive analytical treatment of American futures contracts that could serve as a theoretical benchmark for such extensions [47]. Bridging adaptive trading strategies with formal pricing models represents a promising avenue for unifying practice-oriented and theory-driven approaches in algorithmic trading. Finally, to evaluate the universality and robustness of the proposed approach, future work will involve applying the LB2-optimized 2-SMA strategy to traditional financial markets such as the S&P 500 and the Shanghai Composite Index. These markets exhibit markedly different characteristics compared to cryptocurrencies, including fixed trading hours, lower volatility, and tighter regulatory oversight. By testing the method across diverse asset classes and geographic regions, we aim to assess its adaptability and generalization capacity in broader financial contexts.
Beyond its technical and methodological contributions, this study offers practical implications for risk management and investment strategy design. The use of trailing stop–loss and stop–win mechanisms allows for dynamic position control, helping to limit downside exposure while capturing profitable opportunities. Additionally, the adaptive nature of the optimizer supports real-time adjustment of strategy parameters, enabling more responsive decision-making in high-volatility environments. These features make the system suitable for integration into automated investment pipelines or as a decision-support tool for traders seeking consistent, risk-aware performance under uncertainty. Overall, this study demonstrates the effectiveness of combining classical technical analysis with adaptive optimization. The results open promising directions for building more intelligent, robust, and adaptive trading systems in high-volatility markets like cryptocurrencies.
Author Contributions
Formal analysis, E.V., A.R. and R.S.; investigation, E.V., A.R. and A.S.; resource, R.S. and B.C.; software, E.V., M.B.-R. and A.R.; validation, R.S. and B.C.; writing—original draft, E.V., R.S., M.B.-R. and A.R.; writing—review and editing, E.V. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available online at the binance website.
Conflicts of Interest
The authors declare no conflicts of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
List of Acronyms
A list of acronyms and abbreviations used in the paper:
| 2-SMA | Dual Simple Moving Average |
| ACO | Ant Colony Optimization |
| AI | Artificial Intelligence |
| BTCUSDT | Bitcoin/Tether (Cryptocurrency Trading Pair) |
| FA | Fireworks Algorithm |
| GA | Genetic Algorithm |
| GWO | Gray Wolf Optimizer |
| LB2 | Learning-Based Linear Balancer |
| MACD | Moving Average Convergence Divergence |
| MA | Moving Average |
| PNL | Profit and Loss |
| PSO | Particle Swarm Optimization |
| ROI | Return on Investment |
| RSI | Relative Strength Index |
| SFLA | Shuffle Frog Leaping Algorithm |
| SHO | Spotted Hyena Optimizer |
| SMA | Simple Moving Average |
References
- Grobys, K.; Ahmed, S.; Sapkota, N. Technical trading rules in the cryptocurrency market. Financ. Res. Lett. 2020, 32, 101396. [Google Scholar] [CrossRef]
- Fry, J.; Cheah, E.T. Negative bubbles and shocks in cryptocurrency markets. Int. Rev. Financ. Anal. 2016, 47, 343–352. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Decentralized Business Review. 2008. Available online: https://ssrn.com/abstract=3440802 (accessed on 4 February 2025).
- Resta, M.; Pagnottoni, P.; De Giuli, M.E. Technical analysis on the bitcoin market: Trading opportunities or investors’ pitfall? Risks 2020, 8, 44. [Google Scholar] [CrossRef]
- Nadarajah, S.; Chu, J. On the inefficiency of Bitcoin. Econ. Lett. 2017, 150, 6–9. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Jana, R.K.; Das, D.; Roubaud, D. Informational efficiency of Bitcoin—An extension. Econ. Lett. 2018, 163, 106–109. [Google Scholar] [CrossRef]
- Corbet, S.; Lucey, B.; Urquhart, A.; Yarovaya, L. Cryptocurrencies as a financial asset: A systematic analysis. Int. Rev. Financ. Anal. 2019, 62, 182–199. [Google Scholar] [CrossRef]
- Gradojevic, N.; Kukolj, D.; Adcock, R.; Djakovic, V. Forecasting Bitcoin with technical analysis: A not-so-random forest? Int. J. Forecast. 2023, 39, 1–17. [Google Scholar] [CrossRef]
- Vega, E.; Soto, R.; Crawford, B.; Peña, J.; Castro, C. A learning-based hybrid framework for dynamic balancing of exploration-exploitation: Combining regression analysis and metaheuristics. Mathematics 2021, 9, 1976. [Google Scholar] [CrossRef]
- Karimi-Mamaghan, M.; Mohammadi, M.; Meyer, P.; Karimi-Mamaghan, A.M.; Talbi, E.G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur. J. Oper. Res. 2022, 296, 393–422. [Google Scholar] [CrossRef]
- Talbi, E.G. Machine learning into metaheuristics: A survey and taxonomy. ACM Comput. Surv. (CSUR) 2021, 54, 1–32. [Google Scholar] [CrossRef]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Bouri, E.; Molnár, P.; Azzi, G.; Roubaud, D.; Hagfors, L.I. On the hedge and safe haven properties of Bitcoin: Is it really more than a diversifier? Financ. Res. Lett. 2017, 20, 192–198. [Google Scholar] [CrossRef]
- Achelis, S.B. Technical Analysis from A to Z; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Lin, J.H.; Yeh, C.H. Mining stock data to predict the best time to buy and sell using integrated GA and ANN. Appl. Soft Comput. 2009, 9, 231–238. [Google Scholar]
- Akyildirim, E.; Goncu, A.; Sensoy, A. Prediction of cryptocurrency returns using machine learning. Ann. Oper. Res. 2021, 297, 3–36. [Google Scholar] [CrossRef]
- Sebastião, H.; Godinho, P. Forecasting and trading cryptocurrencies with machine learning under changing market conditions. Financ. Innov. 2021, 7, 3. [Google Scholar] [CrossRef]
- Katsiampa, P. Volatility estimation for Bitcoin: A comparison of GARCH models. Econ. Lett. 2017, 158, 3–6. [Google Scholar] [CrossRef]
- Morteza, H.; Jameii, S.M.; Sohrabi, M.K. An improved learning automata based multi-objective whale optimization approach for multi-objective portfolio optimization in financial markets. Expert Syst. Appl. 2023, 224, 119970. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Z.G.; Zhan, Z.H.; Kwong, S.; Zhang, J. Multiple populations co-evolutionary particle swarm optimization for multi-objective cardinality constrained portfolio optimization problem. Neurocomputing 2021, 430, 58–70. [Google Scholar] [CrossRef]
- Ahmad, F.; Hasan, F.; Shahid, M.; Chauhan, J.; Imran, M. Cardinality Constrained Portfolio Selection Strategy Based on Hybrid Metaheuristic Optimization Algorithm. In Proceedings of the International Conference on Data Science and Applications: ICDSA 2022, Kolkata, India, 26–27 March 2022; Springer Nature: Singapore, 2023; Volume 1, pp. 853–862. [Google Scholar]
- Li, J.; Zhang, Y.; Yang, X.; Chen, L. Online portfolio management via deep reinforcement learning with high-frequency data. Inf. Process. Manag. 2023, 60, 103247. [Google Scholar] [CrossRef]
- Ayyappa, Y.; Siva Kumar, A.P. Optimized long short-term memory-based stock price prediction with sentiment score. Soc. Netw. Anal. Min. 2022, 13, 13. [Google Scholar] [CrossRef]
- Goutte, S.; Le, H.V.; Liu, F.; Von Mettenheim, H.J. Deep learning and technical analysis in cryptocurrency market. Financ. Res. Lett. 2023, 54, 103809. [Google Scholar] [CrossRef]
- Gajamannage, K.; Park, Y.; Jayathilake, D.I. Real-time forecasting of time series in financial markets using sequentially trained dual-LSTMs. Expert Syst. Appl. 2023, 223, 119879. [Google Scholar] [CrossRef]
- Seabe, P.L.; Moutsinga, C.R.B.; Pindza, E. Forecasting cryptocurrency prices using LSTM, GRU, and bi-directional LSTM: A deep learning approach. Fractal Fract. 2023, 7, 203. [Google Scholar] [CrossRef]
- Mohamed, I.; Otero, F.E. Using population-based metaheuristics and trend representative testing to compose strategies for market timing. In Proceedings of the 11th International Joint Conference on Computational Intelligence, Vienna, Austria, 17–19 September 2019. [Google Scholar]
- Pizzi, C.; Bitto, I.; Corazza, M. Exploration and Exploitation in Optimizing a Basic Financial Trading System: A Comparison Between FA and PSO Algorithms. In Progresses in Artificial Intelligence and Neural Systems; Springer: Singapore, 2021; pp. 293–303. [Google Scholar]
- Papatsimpas, M.G.; Lykogiorgos, I.; Parsopoulos, K.E. Forex trading model based on forecast aggregation and metaheuristic optimization. In Proceedings of the 11th Hellenic Conference on Artificial Intelligence, Athens, Greece, 2–4 September 2020; pp. 215–223. [Google Scholar]
- Crawford, B.; Soto, R.; San Martín, M.A.; De La Fuente-Mella, H.; Castro, C.; Paredes, F. Automatic high-frequency trading: An application to emerging chilean stock market. Sci. Program. 2018, 2018, 8721246. [Google Scholar] [CrossRef]
- Cerda, J.; Rojas-Morales, N.; Minutolo, M.C.; Kristjanpoller, W. High frequency and dynamic pairs trading with ant colony optimization. Comput. Econ. 2022, 59, 1251–1275. [Google Scholar] [CrossRef]
- Cuevas, E.; Fausto, F.; González, A. New Advancements in Swarm Algorithms: Operators and Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; CambridgeUniversity Press: New York, NY, USA, 2004. [Google Scholar]
- Soto, R.; Crawford, B.; Vega, E.; Paredes, F. Solving manufacturing cell design problems using an artificial fish swarm algorithm. In Mexican International Conference on Artificial Intelligence; Springer: Cham, Switzerland, 2015; pp. 282–290. [Google Scholar]
- García, J.; Crawford, B.; Soto, R.; Castro, C.; Paredes, F. A k-means binarization framework applied to multidimensional knapsack problem. Appl. Intell. 2018, 48, 357–380. [Google Scholar] [CrossRef]
- Smith, B.M. Impacs-a bus crew scheduling system using integer programming. Math. Program. 1988, 42, 181–187. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Olivares, R.; Embry, G.; Flores, D.; Palma, W.; Castro, C.; Paredes, F.; Rubio, J.M. A binary monkey search algorithm variation for solving the set covering problem. Nat. Comput. 2019, 19, 825–841. [Google Scholar] [CrossRef]
- Elshaer, R.; Awad, H. A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants. Comput. Ind. Eng. 2020, 140, 106242. [Google Scholar] [CrossRef]
- Crama, Y.; Kolen, A.W.; Pesch, E.J. Local search in combinatorial optimization. In Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1995; pp. 157–174. [Google Scholar]
- Kirkpatrick, S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Song, H.; Triguero, I.; Özcan, E. A review on the self and dual interactions between machine learning and optimisation. Prog. Artif. Intell. 2019, 8, 143–165. [Google Scholar] [CrossRef]
- Kim, J.M.; Jun, C.; Lee, J. Forecasting the volatility of the cryptocurrency market by GARCH and Stochastic Volatility. Mathematics 2021, 9, 1614. [Google Scholar] [CrossRef]
- Zaevski, T. On the American style futures contracts. Croat. Oper. Res. Rev. 2024, 15, 39–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).