Rule-Based Generation of de Bruijn Sequences: Memory and Learning
Abstract
1. Introduction
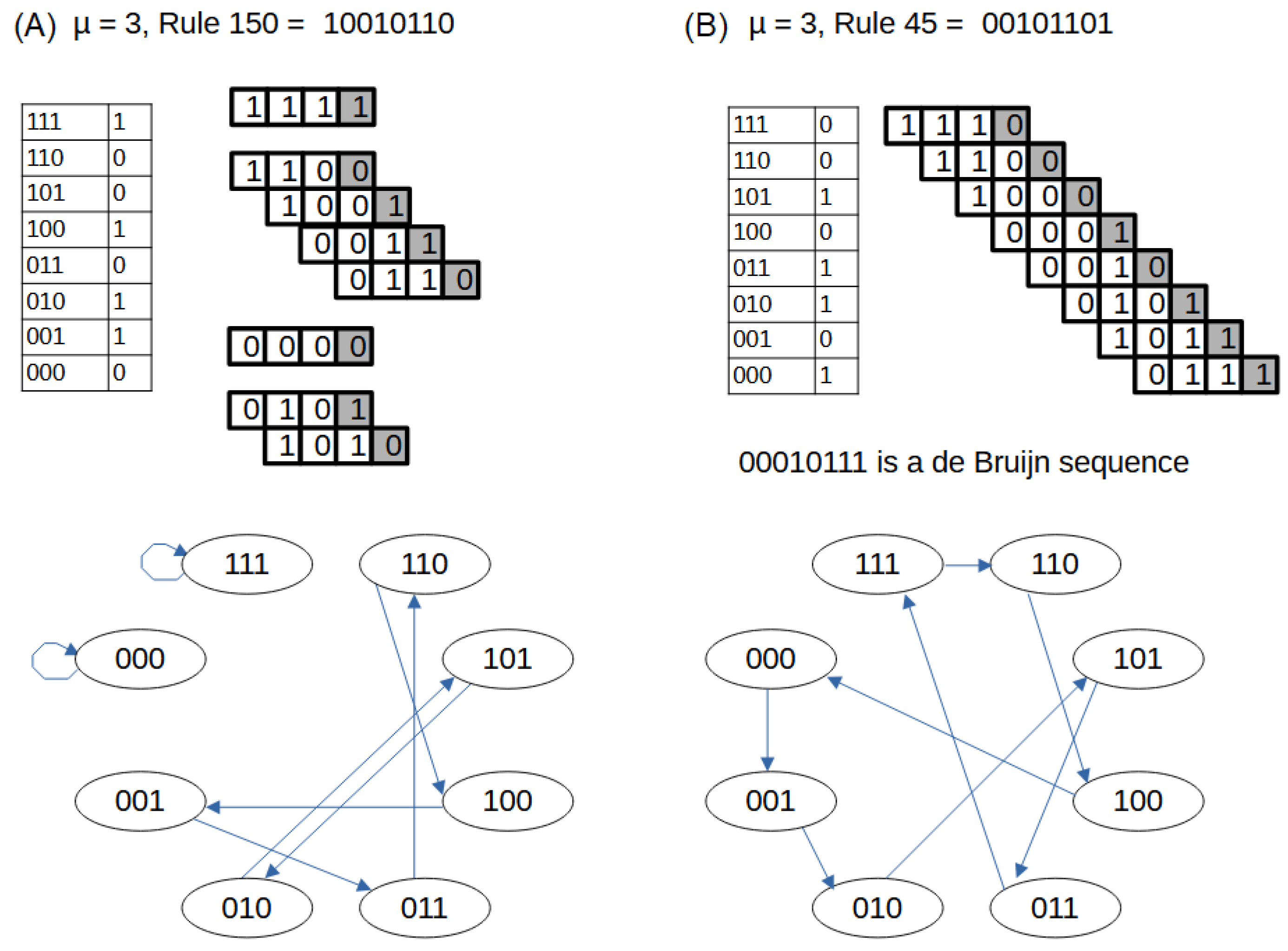
2. 0-Dimensional CA
3. Rules That Generate Maximum Period Sequences: De Bruijn Rules
4. Characterization of de Bruijn Rules
- Boundary Conditions: The binary representations of de Bruijn rules must start with 0 and end with 1. This condition arises from the convention in rule ordering, which arranges input strings from the highest binary value () to the lowest () and from the necessity to avoid fixed points (e.g., if , the sequence remains constant). This constraint immediately reduces the number of candidate rules by a factor of 4. For example, for , the number of potentially valid rules is reduced from = 65,536 to 16,384.
- Symmetry and Parity: The binary representations of de Bruijn rules are symmetric with respect to their midpoint, such that each half is the complement of the other. This symmetry ensures parity: the number of 0s equals the number of 1s, although the balance may be broken within each half. Under this constraint, valid de Bruijn rules correspond to multiples of certain Numbers derived from sequences of Evil Odd numbers [20], multiplied by factors denoted as (see Appendix A). Let be a rule for a given . Then,In Appendix A, we show that the factor isFor instance, , , , and = 65,535. The consideration of this property causes a huge reduction in the feasible set of the de Bruijn rules, from 16,384 to 64 for the case .
- Evil Odd Number divisibilityIt is also empirical evidence that factor in Equation (5) must be an Evil Odd Number for to be a de Bruijn rule. For each , there is a unique that divides , which results in multiple remainders that are Evil Odd Numbers. To consider that, it is convenient to denote this factor as , representing the Evil Odd Numbers for . For instance,Table 2 presents all de Bruijn rules for whose decimal representations are products of an Evil Odd Number and the corresponding . Note, however, that not all Evil Odd Numbers yield valid de Bruijn rules, and the problem of determining which ones do remains open for larger values of . For , applying these conditions reduce the feasible set of de Bruijn rules to 32.
- Constrained Position Pairs: There exist pairs of positions in the binary representation of de Bruijn rules that cannot simultaneously take the same value (1 for even -values and 0 for odd ones). This condition is applied only to the first half of the binary string for symmetry (according to the previous item) and depends on according to a recursive pattern.Let be the binary value of the j position in a de Bruijn rule of memory . For , the constrained positions are and , and
- −
- If , then and .
- −
- If , then and .
for .This structural condition eliminates of the remaining candidates. For example, for , these positions are and . For , and , and for , and .Remarkably, for , the final count of feasible de Bruijn rules after applying all constraints is 24. In general, for all values of , the feasible set exceeds the actual number of de Bruijn rules (see Table 3). - Symmetric Rule Invariance: If a rule of the formis a de Bruijn rule, then its mirrored versionis also a de Bruijn rule.This property reflects the inherent symmetry and reversibility in de Bruijn rule structure. It ensures that for each valid de Bruijn rule constructed in this way, a corresponding reverse-complement rule also exists within the de Bruijn set.
- After applying the boundary conditions, 16,384 rules remain feasible.
- Applying symmetry, i.e., dividing by , 64 rules remain.
- The requirement that the remainder is an Evil Odd Number reduces the previous number to 32 rules.
- Verifying the constrained position pairs reduces the feasible set to 24 rules.
5. Neural Networks to Classify de Bruijn Rules
- Data loading and preprocessing: The input data consisted of a character string representing a binary sequence and a binary integer label.
- Feature extraction: Each rule was split into individual bits transforming the strings into a matrix where each column corresponds to a bit (bit1 to ). According to the necessary properties of de Bruijn rules (see Section 4), only the first bits were retained for further analysis. The first and the bits were also removed because they are necessarily 0.
- Dataset splitting: The data were randomly split into training (80%) and testing (20%) subsets to evaluate model performance on unseen data. The validation set was chosen to be of the training set in all cases.
- An input layer with 14 features (bits);
- A hidden dense layer with 32 units and ReLU activation;
- A second hidden dense layer with 16 units and ReLU activation;
- An output layer with 1 unit and sigmoid activation for binary classification.
- Three hidden dense layers with 64, 64, and 8 units, respectively;
- ReLU activations in all hidden layers;
- A sigmoid output unit for binary classification.
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- .
- .
- .
- .
Appendix B
| 39 | 2599 | 3751 | 6245 | 7565 | 9127 | 10,203 | 12,729 | 13,977 | 16,431 | 18,993 | 20,127 | 22,689 | 23,941 | 25,531 | 26,573 | 29,173 | 30,311 |
| 43 | 2605 | 3763 | 6255 | 7571 | 9139 | 10,205 | 12,771 | 13,983 | 16,433 | 18,999 | 20,143 | 22,695 | 23,951 | 25,533 | 26,585 | 29,177 | 30,323 |
| 45 | 2611 | 3789 | 6257 | 7573 | 9141 | 10,221 | 12,777 | 13,999 | 16,439 | 19,003 | 20,155 | 22,701 | 23,963 | 25,581 | 26,659 | 29,223 | 30,341 |
| 51 | 2617 | 3801 | 6263 | 7589 | 9199 | 10,233 | 12,785 | 14,011 | 16,551 | 19,053 | 20,175 | 22,713 | 23,965 | 25,593 | 26,665 | 29,229 | 30,353 |
| 57 | 2623 | 3807 | 6267 | 7593 | 9211 | 10,403 | 12,837 | 14,021 | 16,555 | 19,065 | 20,187 | 22,719 | 23,969 | 25,601 | 26,683 | 29,235 | 30,359 |
| 63 | 2671 | 3823 | 6309 | 7599 | 9213 | 10,409 | 12,849 | 14,031 | 16,557 | 19,071 | 20,231 | 22,755 | 23,975 | 25,607 | 26,727 | 29,241 | 30,375 |
| 165 | 2683 | 3835 | 6313 | 7601 | 9219 | 10,427 | 12,855 | 14,033 | 16,563 | 19,111 | 20,237 | 22,757 | 23,981 | 25,613 | 26,731 | 29,247 | 30,387 |
| 169 | 2725 | 3845 | 6319 | 7611 | 9225 | 10,471 | 12,903 | 14,039 | 16,569 | 19,117 | 20,243 | 22,767 | 23,987 | 25,625 | 26,733 | 29,285 | 30,407 |
| 175 | 2735 | 3855 | 6321 | 7613 | 9243 | 10,475 | 12,915 | 14,043 | 16,575 | 19,123 | 20,245 | 22,769 | 23,989 | 25,631 | 26,739 | 29,295 | 30,419 |
| 177 | 2737 | 3857 | 6327 | 7619 | 9255 | 10,477 | 12,967 | 14,055 | 16,679 | 19,129 | 20,249 | 22,775 | 23,993 | 25,635 | 26,745 | 29,297 | 30,469 |
| 183 | 2743 | 3867 | 6369 | 7625 | 9259 | 10,483 | 12,973 | 14,067 | 16,683 | 19,135 | 20,261 | 22,779 | 24,001 | 25,637 | 26,751 | 29,303 | 30,479 |
| 293 | 2747 | 3869 | 6379 | 7633 | 9261 | 10,489 | 12,979 | 14,087 | 16,685 | 19,183 | 20,273 | 22,823 | 24,007 | 25,647 | 26,913 | 29,307 | 30,481 |
| 297 | 2797 | 3885 | 6387 | 7649 | 9267 | 10,495 | 12,985 | 14,099 | 16,691 | 19,195 | 20,303 | 22,827 | 24,013 | 25,649 | 26,923 | 29,349 | 30,491 |
| 303 | 2809 | 3897 | 6435 | 7655 | 9273 | 10,657 | 12,991 | 14,101 | 16,693 | 19,239 | 20,315 | 22,829 | 24,019 | 25,655 | 26,937 | 29,361 | 30,493 |
| 305 | 2815 | 3917 | 6437 | 7661 | 9279 | 10,667 | 13,029 | 14,117 | 16,805 | 19,245 | 20,317 | 22,835 | 24,021 | 25,659 | 26,981 | 29,367 | 30,509 |
| 315 | 2853 | 3929 | 6447 | 7667 | 9287 | 10,681 | 13,039 | 14,129 | 16,809 | 19,251 | 20,333 | 22,837 | 24,025 | 25,669 | 26,985 | 29,415 | 30,521 |
| 317 | 2863 | 3975 | 6459 | 7669 | 9291 | 10,725 | 13,041 | 14,149 | 16,815 | 19,253 | 20,345 | 22,883 | 24,077 | 25,673 | 26,991 | 29,427 | 30,535 |
| 423 | 2865 | 3981 | 6461 | 7673 | 9293 | 10,729 | 13,047 | 14,161 | 16,817 | 19,257 | 20,357 | 22,889 | 24,089 | 25,679 | 26,993 | 29,477 | 30,541 |
| 427 | 2875 | 3987 | 6497 | 7685 | 9299 | 10,735 | 13,051 | 14,213 | 16,827 | 19,311 | 20,367 | 22,897 | 24,095 | 25,681 | 27,003 | 29,487 | 30,547 |
| 429 | 2877 | 3989 | 6503 | 7697 | 9305 | 10,737 | 13,095 | 14,223 | 16,829 | 19,323 | 20,369 | 22,947 | 24,111 | 25,687 | 27,005 | 29,489 | 30,549 |
| 435 | 2925 | 3993 | 6509 | 7703 | 9311 | 10,747 | 13,107 | 14,225 | 16,941 | 19,325 | 20,379 | 22,949 | 24,123 | 25,703 | 27,175 | 29,499 | 30,553 |
| 437 | 2937 | 4005 | 6515 | 7719 | 9345 | 10,749 | 13,109 | 14,235 | 16,953 | 19,365 | 20,381 | 22,959 | 24,133 | 25,707 | 27,181 | 29,501 | 30,565 |
| 559 | 2983 | 4017 | 6517 | 7731 | 9351 | 10,919 | 13,157 | 14,237 | 16,959 | 19,375 | 20,397 | 22,971 | 24,143 | 25,709 | 27,187 | 29,543 | 30,577 |
| 571 | 2989 | 4047 | 6521 | 7751 | 9357 | 10,925 | 13,169 | 14,253 | 17,071 | 19,377 | 20,409 | 22,973 | 24,145 | 25,715 | 27,193 | 29,549 | 30,599 |
| 685 | 2995 | 4059 | 6567 | 7763 | 9369 | 10,931 | 13,221 | 14,265 | 17,083 | 19,387 | 20,429 | 23,009 | 24,151 | 25,721 | 27,199 | 29,555 | 30,611 |
| 697 | 2997 | 4061 | 6571 | 7821 | 9375 | 10,937 | 13,231 | 14,279 | 17,199 | 19,389 | 20,441 | 23,015 | 24,155 | 25,727 | 27,247 | 29,557 | 30,613 |
| 703 | 3001 | 4077 | 6573 | 7833 | 9379 | 10,943 | 13,233 | 14,285 | 17,211 | 19,437 | 20,513 | 23,021 | 24,167 | 25,731 | 27,259 | 29,561 | 30,629 |
| 813 | 3055 | 4089 | 6579 | 7839 | 9381 | 10,991 | 13,243 | 14,291 | 17,213 | 19,449 | 20,523 | 23,027 | 24,179 | 25,737 | 27,429 | 29,607 | 30,641 |
| 825 | 3067 | 4131 | 6581 | 7855 | 9391 | 11,003 | 13,245 | 14,293 | 17,325 | 19,457 | 20,531 | 23,029 | 24,197 | 25,755 | 27,439 | 29,619 | 30,661 |
| 943 | 3069 | 4133 | 6627 | 7867 | 9393 | 11,173 | 13,287 | 14,297 | 17,337 | 19,467 | 20,643 | 23,033 | 24,209 | 25,767 | 27,441 | 29,621 | 30,673 |
| 955 | 3075 | 4143 | 6633 | 7877 | 9399 | 11,183 | 13,293 | 14,309 | 17,413 | 19,475 | 20,645 | 23,085 | 24,215 | 25,771 | 27,451 | 29,669 | 30,753 |
| 957 | 3081 | 4145 | 6641 | 7887 | 9403 | 11,185 | 13,299 | 14,321 | 17,417 | 19,491 | 20,655 | 23,097 | 24,231 | 25,773 | 27,453 | 29,681 | 30,759 |
| 1031 | 3099 | 4151 | 6693 | 7889 | 9413 | 11,195 | 13,301 | 14,497 | 17,423 | 19,493 | 20,657 | 23,103 | 24,243 | 25,779 | 27,501 | 29,699 | 30,765 |
| 1035 | 3111 | 4155 | 6705 | 7895 | 9417 | 11,197 | 13,305 | 14,503 | 17,425 | 19,503 | 20,663 | 23,141 | 24,263 | 25,785 | 27,513 | 29,705 | 30,777 |
| 1037 | 3115 | 4257 | 6711 | 7899 | 9423 | 11,245 | 13,313 | 14,509 | 17,431 | 19,505 | 20,667 | 23,151 | 24,275 | 25,791 | 27,651 | 29,723 | 30,783 |
| 1043 | 3117 | 4267 | 6759 | 7911 | 9425 | 11,257 | 13,319 | 14,521 | 17,447 | 19,511 | 20,771 | 23,153 | 24,335 | 25,799 | 27,657 | 29,735 | 30,819 |
| 1049 | 3123 | 4275 | 6771 | 7923 | 9431 | 11,395 | 13,325 | 14,527 | 17,451 | 19,515 | 20,777 | 23,159 | 24,347 | 25,803 | 27,675 | 29,739 | 30,821 |
| 1055 | 3129 | 4385 | 6829 | 7943 | 9447 | 11,401 | 13,337 | 14,563 | 17,453 | 19,525 | 20,785 | 23,163 | 24,349 | 25,805 | 27,687 | 29,741 | 30,831 |
| 1157 | 3135 | 4391 | 6841 | 7955 | 9451 | 11,419 | 13,343 | 14,565 | 17,459 | 19,529 | 20,897 | 23,205 | 24,365 | 25,811 | 27,691 | 29,747 | 30,833 |
| 1161 | 3143 | 4397 | 6847 | 7957 | 9453 | 11,431 | 13,347 | 14,575 | 17,465 | 19,535 | 20,903 | 23,217 | 24,377 | 25,817 | 27,693 | 29,753 | 30,839 |
| 1167 | 3147 | 4403 | 6885 | 7973 | 9459 | 11,435 | 13,349 | 14,577 | 17,471 | 19,537 | 20,909 | 23,223 | 24,391 | 25,823 | 27,699 | 29,759 | 30,843 |
| 1169 | 3149 | 4405 | 6895 | 7985 | 9465 | 11,437 | 13,359 | 14,583 | 17,543 | 19,543 | 20,915 | 23,271 | 24,397 | 25,859 | 27,705 | 29,761 | 31,011 |
| 1175 | 3155 | 4409 | 6897 | 8005 | 9471 | 11,443 | 13,361 | 14,587 | 17,547 | 19,559 | 20,917 | 23,283 | 24,403 | 25,861 | 27,711 | 29,771 | 31,013 |
| 1191 | 3161 | 4515 | 6903 | 8017 | 9473 | 11,449 | 13,367 | 14,755 | 17,549 | 19,563 | 20,921 | 23,343 | 24,405 | 25,871 | 27,719 | 29,779 | 31,023 |
| 1195 | 3167 | 4521 | 6907 | 8079 | 9483 | 11,455 | 13,371 | 14,757 | 17,555 | 19,565 | 21,029 | 23,355 | 24,409 | 25,883 | 27,723 | 29,795 | 31,035 |
| 1197 | 3201 | 4529 | 6951 | 8091 | 9497 | 11,463 | 13,379 | 14,767 | 17,561 | 19,571 | 21,039 | 23,357 | 24,421 | 25,885 | 27,725 | 29,797 | 31,037 |
| 1203 | 3211 | 4647 | 6963 | 8093 | 9509 | 11,467 | 13,381 | 14,779 | 17,567 | 19,577 | 21,041 | 23,399 | 24,433 | 25,889 | 27,731 | 29,807 | 31,073 |
| 1209 | 3219 | 4659 | 6965 | 8109 | 9513 | 11,469 | 13,391 | 14,781 | 17,671 | 19,583 | 21,047 | 23,405 | 24,455 | 25,895 | 27,737 | 29,809 | 31,079 |
| 1215 | 3235 | 4773 | 7013 | 8121 | 9519 | 11,475 | 13,393 | 14,817 | 17,675 | 19,587 | 21,051 | 23,411 | 24,467 | 25,901 | 27,743 | 29,815 | 31,085 |
| 1285 | 3237 | 4783 | 7025 | 8135 | 9521 | 11,481 | 13,399 | 14,823 | 17,677 | 19,593 | 21,159 | 23,413 | 24,469 | 25,907 | 27,905 | 29,819 | 31,091 |
| 1289 | 3247 | 4785 | 7087 | 8141 | 9531 | 11,487 | 13,403 | 14,829 | 17,683 | 19,611 | 21,171 | 23,417 | 24,485 | 25,909 | 27,915 | 29,825 | 31,093 |
| 1295 | 3249 | 4791 | 7099 | 8147 | 9533 | 11,649 | 13,443 | 14,835 | 17,685 | 19,623 | 21,287 | 23,463 | 24,497 | 25,913 | 27,929 | 29,831 | 31,097 |
| 1297 | 3255 | 4795 | 7101 | 8149 | 9541 | 11,659 | 13,449 | 14,837 | 17,701 | 19,627 | 21,293 | 23,475 | 24,517 | 25,927 | 27,941 | 29,837 | 31,269 |
| 1307 | 3259 | 4901 | 7143 | 8153 | 9545 | 11,673 | 13,467 | 14,841 | 17,705 | 19,629 | 21,299 | 23,477 | 24,529 | 25,931 | 27,945 | 29,849 | 31,281 |
| 1309 | 3269 | 4913 | 7149 | 8165 | 9551 | 11,685 | 13,479 | 15,013 | 17,711 | 19,635 | 21,301 | 23,525 | 24,609 | 25,933 | 27,951 | 29,855 | 31,287 |
| 1415 | 3273 | 5031 | 7155 | 8177 | 9553 | 11,689 | 13,483 | 15,025 | 17,713 | 19,641 | 21,305 | 23,537 | 24,615 | 25,939 | 27,953 | 29,859 | 31,335 |
| 1419 | 3279 | 5037 | 7157 | 8227 | 9563 | 11,695 | 13,485 | 15,031 | 17,723 | 19,647 | 21,413 | 23,557 | 24,621 | 25,941 | 27,963 | 29,861 | 31,347 |
| 1421 | 3281 | 5043 | 7161 | 8233 | 9565 | 11,697 | 13,491 | 15,079 | 17,725 | 19,655 | 21,425 | 23,561 | 24,633 | 25,957 | 27,965 | 29,871 | 31,527 |
| 1427 | 3287 | 5045 | 7169 | 8251 | 9603 | 11,707 | 13,497 | 15,091 | 17,797 | 19,659 | 21,505 | 23,567 | 24,639 | 25,961 | 27,973 | 29,873 | 31,539 |
| 1429 | 3303 | 5049 | 7175 | 8295 | 9605 | 11,709 | 13,503 | 15,271 | 17,801 | 19,661 | 21,515 | 23,569 | 24,677 | 25,967 | 27,977 | 29,879 | 31,541 |
| 1445 | 3307 | 5123 | 7181 | 8299 | 9615 | 11,717 | 13,505 | 15,283 | 17,807 | 19,667 | 21,523 | 23,575 | 24,681 | 25,969 | 27,983 | 29,883 | 31,589 |
| 1449 | 3309 | 5125 | 7193 | 8301 | 9627 | 11,721 | 13,515 | 15,285 | 17,809 | 19,673 | 21,539 | 23,591 | 24,687 | 25,979 | 27,985 | 29,891 | 31,601 |
| 1455 | 3315 | 5135 | 7199 | 8307 | 9629 | 11,727 | 13,523 | 15,333 | 17,819 | 19,679 | 21,541 | 23,595 | 24,689 | 25,981 | 27,995 | 29,893 | 31,745 |
| 1457 | 3321 | 5137 | 7203 | 8313 | 9633 | 11,729 | 13,539 | 15,345 | 17,821 | 19,715 | 21,551 | 23,597 | 24,695 | 25,985 | 27,997 | 29,903 | 31,751 |
| 1467 | 3327 | 5143 | 7205 | 8319 | 9639 | 11,739 | 13,541 | 15,489 | 17,933 | 19,721 | 21,553 | 23,603 | 24,739 | 25,995 | 28,167 | 29,905 | 31,757 |
| 1469 | 3329 | 5147 | 7215 | 8353 | 9645 | 11,741 | 13,551 | 15,495 | 17,945 | 19,729 | 21,559 | 23,609 | 24,745 | 26,009 | 28,173 | 29,911 | 31,769 |
| 1551 | 3339 | 5249 | 7217 | 8359 | 9651 | 11,911 | 13,553 | 15,501 | 17,951 | 19,745 | 21,563 | 23,615 | 24,763 | 26,021 | 28,179 | 29,915 | 31,775 |
| 1563 | 3353 | 5259 | 7223 | 8365 | 9653 | 11,917 | 13,559 | 15,513 | 17,967 | 19,751 | 21,635 | 23,617 | 24,807 | 26,025 | 28,185 | 29,953 | 31,779 |
| 1677 | 3365 | 5267 | 7227 | 8377 | 9657 | 11,923 | 13,563 | 15,519 | 17,979 | 19,757 | 21,637 | 23,627 | 24,811 | 26,031 | 28,191 | 29,963 | 31,781 |
| 1689 | 3369 | 5283 | 7235 | 8383 | 9671 | 11,929 | 13,571 | 15,523 | 18,063 | 19,763 | 21,647 | 23,635 | 24,813 | 26,033 | 28,207 | 29,977 | 31,791 |
| 1695 | 3375 | 5285 | 7237 | 8421 | 9675 | 11,935 | 13,573 | 15,525 | 18,075 | 19,765 | 21,649 | 23,651 | 24,819 | 26,043 | 28,219 | 29,989 | 31,793 |
| 1711 | 3377 | 5295 | 7247 | 8425 | 9677 | 11,951 | 13,583 | 15,535 | 18,191 | 19,769 | 21,655 | 23,653 | 24,825 | 26,045 | 28,239 | 29,993 | 31,799 |
| 1723 | 3387 | 5297 | 7249 | 8431 | 9683 | 11,963 | 13,595 | 15,537 | 18,203 | 19,783 | 21,659 | 23,663 | 24,831 | 26,053 | 28,251 | 29,999 | 31,803 |
| 1805 | 3389 | 5303 | 7255 | 8433 | 9685 | 11,983 | 13,597 | 15,543 | 18,205 | 19,787 | 21,763 | 23,665 | 24,867 | 26,057 | 28,421 | 30,001 | 31,811 |
| 1817 | 3397 | 5307 | 7259 | 8439 | 9701 | 11,995 | 13,601 | 15,547 | 18,221 | 19,789 | 21,769 | 23,671 | 24,869 | 26,063 | 28,431 | 30,011 | 31,813 |
| 1935 | 3401 | 5377 | 7301 | 8481 | 9705 | 12,165 | 13,607 | 15,555 | 18,233 | 19,795 | 21,777 | 23,675 | 24,879 | 26,065 | 28,433 | 30,013 | 31,823 |
| 1947 | 3407 | 5383 | 7305 | 8491 | 9711 | 12,175 | 13,613 | 15,557 | 18,317 | 19,797 | 21,793 | 23,681 | 24,891 | 26,075 | 28,443 | 30,019 | 31,825 |
| 1949 | 3409 | 5389 | 7311 | 8505 | 9713 | 12,177 | 13,619 | 15,567 | 18,329 | 19,813 | 21,799 | 23,687 | 24,893 | 26,077 | 28,445 | 30,025 | 31,831 |
| 1965 | 3419 | 5395 | 7313 | 8549 | 9723 | 12,187 | 13,621 | 15,569 | 18,465 | 19,817 | 21,805 | 23,693 | 24,935 | 26,117 | 28,461 | 30,033 | 31,835 |
| 1977 | 3421 | 5397 | 7319 | 8553 | 9725 | 12,189 | 13,625 | 15,575 | 18,475 | 19,823 | 21,811 | 23,705 | 24,939 | 26,129 | 28,473 | 30,049 | 32,003 |
| 2083 | 3459 | 5401 | 7335 | 8559 | 9735 | 12,205 | 13,633 | 15,579 | 18,483 | 19,825 | 21,813 | 23,711 | 24,941 | 26,135 | 28,493 | 30,055 | 32,005 |
| 2089 | 3465 | 5507 | 7339 | 8561 | 9741 | 12,217 | 13,639 | 15,747 | 18,533 | 19,835 | 21,817 | 23,715 | 24,947 | 26,151 | 28,505 | 30,061 | 32,015 |
| 2107 | 3473 | 5513 | 7341 | 8571 | 9747 | 12,237 | 13,645 | 15,749 | 18,537 | 19,837 | 21,889 | 23,717 | 24,949 | 26,163 | 28,707 | 30,067 | 32,027 |
| 2151 | 3489 | 5521 | 7347 | 8573 | 9753 | 12,249 | 13,651 | 15,759 | 18,543 | 19,841 | 21,895 | 23,727 | 24,993 | 26,189 | 28,713 | 30,069 | 32,029 |
| 2155 | 3495 | 5537 | 7353 | 8611 | 9759 | 12,321 | 13,653 | 15,771 | 18,545 | 19,851 | 21,901 | 23,729 | 25,003 | 26,201 | 28,731 | 30,073 | 32,033 |
| 2157 | 3501 | 5543 | 7359 | 8613 | 9775 | 12,327 | 13,657 | 15,773 | 18,551 | 19,865 | 21,907 | 23,735 | 25,017 | 26,207 | 28,769 | 30,083 | 32,039 |
| 2163 | 3507 | 5549 | 7361 | 8623 | 9787 | 12,333 | 13,697 | 15,777 | 18,595 | 19,877 | 21,909 | 23,739 | 25,061 | 26,223 | 28,779 | 30,085 | 32,045 |
| 2169 | 3509 | 5555 | 7371 | 8635 | 9807 | 12,345 | 13,707 | 15,783 | 18,601 | 19,881 | 21,913 | 23,747 | 25,065 | 26,235 | 28,787 | 30,095 | 32,051 |
| 2175 | 3513 | 5557 | 7379 | 8637 | 9819 | 12,351 | 13,721 | 15,789 | 18,619 | 19,887 | 22,021 | 23,749 | 25,071 | 26,247 | 28,833 | 30,107 | 32,053 |
| 2209 | 3527 | 5561 | 7395 | 8679 | 9861 | 12,387 | 13,733 | 15,795 | 18,663 | 19,889 | 22,031 | 23,759 | 25,073 | 26,253 | 28,839 | 30,109 | 32,057 |
| 2219 | 3531 | 5639 | 7397 | 8683 | 9873 | 12,389 | 13,737 | 15,797 | 18,667 | 19,899 | 22,033 | 23,761 | 25,083 | 26,259 | 28,845 | 30,113 | 32,065 |
| 2227 | 3533 | 5651 | 7407 | 8685 | 9879 | 12,399 | 13,743 | 15,801 | 18,669 | 19,901 | 22,039 | 23,767 | 25,085 | 26,265 | 28,857 | 30,119 | 32,071 |
| 2277 | 3539 | 5765 | 7409 | 8691 | 9895 | 12,401 | 13,745 | 15,809 | 18,675 | 19,909 | 22,043 | 23,771 | 25,125 | 26,271 | 28,863 | 30,125 | 32,077 |
| 2281 | 3541 | 5775 | 7415 | 8693 | 9907 | 12,407 | 13,755 | 15,815 | 18,681 | 19,913 | 22,055 | 23,815 | 25,137 | 26,287 | 28,899 | 30,131 | 32,083 |
| 2287 | 3557 | 5777 | 7419 | 8743 | 9933 | 12,411 | 13,757 | 15,821 | 18,687 | 19,919 | 22,067 | 23,819 | 25,143 | 26,299 | 28,901 | 30,133 | 32,085 |
| 2289 | 3561 | 5783 | 7427 | 8749 | 9945 | 12,451 | 13,763 | 15,827 | 18,723 | 19,921 | 22,151 | 23,821 | 25,197 | 26,319 | 28,911 | 30,137 | 32,089 |
| 2295 | 3567 | 5787 | 7429 | 8755 | 9951 | 12,457 | 13,769 | 15,829 | 18,729 | 19,931 | 22,163 | 23,827 | 25,209 | 26,331 | 28,913 | 30,145 | 32,261 |
| 2337 | 3569 | 5799 | 7439 | 8761 | 9967 | 12,475 | 13,777 | 15,833 | 18,737 | 19,933 | 22,279 | 23,829 | 25,215 | 26,375 | 28,919 | 30,151 | 32,273 |
| 2347 | 3579 | 5811 | 7451 | 8767 | 9979 | 12,513 | 13,793 | 16,005 | 18,791 | 19,973 | 22,285 | 23,845 | 25,255 | 26,387 | 28,923 | 30,157 | 32,279 |
| 2361 | 3581 | 5893 | 7453 | 8815 | 9989 | 12,523 | 13,799 | 16,017 | 18,795 | 19,983 | 22,291 | 23,849 | 25,261 | 26,389 | 28,961 | 30,163 | 32,295 |
| 2405 | 3591 | 5905 | 7457 | 8827 | 9999 | 12,531 | 13,805 | 16,023 | 18,797 | 19,985 | 22,293 | 23,855 | 25,267 | 26,405 | 28,971 | 30,165 | 32,307 |
| 2409 | 3597 | 6023 | 7463 | 8869 | 10,001 | 12,579 | 13,811 | 16,039 | 18,803 | 19,991 | 22,297 | 23,857 | 25,273 | 26,417 | 28,985 | 30,169 | 32,327 |
| 2415 | 3603 | 6029 | 7469 | 8881 | 10,011 | 12,581 | 13,813 | 16,051 | 18,805 | 19,995 | 22,309 | 23,867 | 25,279 | 26,447 | 29,027 | 30,215 | 32,339 |
| 2417 | 3609 | 6035 | 7475 | 8887 | 10,013 | 12,591 | 13,817 | 16,071 | 18,849 | 20,007 | 22,321 | 23,869 | 25,327 | 26,459 | 29,033 | 30,221 | 32,519 |
| 2427 | 3615 | 6037 | 7477 | 8941 | 10,029 | 12,603 | 13,829 | 16,083 | 18,859 | 20,019 | 22,405 | 23,875 | 25,339 | 26,461 | 29,041 | 30,227 | 32,531 |
| 2429 | 3631 | 6041 | 7481 | 8953 | 10,041 | 12,605 | 13,841 | 16,263 | 18,873 | 20,045 | 22,417 | 23,881 | 25,383 | 26,477 | 29,091 | 30,233 | 32,533 |
| 2467 | 3643 | 6053 | 7489 | 8959 | 10,061 | 12,641 | 13,847 | 16,275 | 18,917 | 20,057 | 22,565 | 23,889 | 25,395 | 26,489 | 29,093 | 30,239 | 32,549 |
| 2473 | 3663 | 6065 | 7495 | 8997 | 10,073 | 12,647 | 13,863 | 16,277 | 18,921 | 20,063 | 22,569 | 23,905 | 25,397 | 26,501 | 29,103 | 30,255 | 32,561 |
| 2481 | 3675 | 6177 | 7501 | 9007 | 10,119 | 12,653 | 13,875 | 16,293 | 18,927 | 20,079 | 22,575 | 23,911 | 25,455 | 26,511 | 29,115 | 30,267 | 32,581 |
| 2535 | 3717 | 6183 | 7507 | 9009 | 10,131 | 12,659 | 13,895 | 16,305 | 18,929 | 20,091 | 22,577 | 23,917 | 25,467 | 26,513 | 29,117 | 30,277 | 32,593 |
| 2539 | 3727 | 6189 | 7509 | 9019 | 10,133 | 12,661 | 13,907 | 16,325 | 18,939 | 20,103 | 22,583 | 23,923 | 25,469 | 26,523 | 29,153 | 30,287 | |
| 2541 | 3729 | 6201 | 7513 | 9021 | 10,149 | 12,665 | 13,959 | 16,337 | 18,941 | 20,109 | 22,625 | 23,925 | 25,509 | 26,525 | 29,159 | 30,289 | |
| 2547 | 3735 | 6207 | 7559 | 9069 | 10,161 | 12,705 | 13,965 | 16,421 | 18,981 | 20,115 | 22,635 | 23,929 | 25,519 | 26,541 | 29,165 | 30,295 | |
| 2549 | 3739 | 6243 | 7563 | 9081 | 10,191 | 12,715 | 13,971 | 16,425 | 18,991 | 20,121 | 22,643 | 23,939 | 25,521 | 26,553 | 29,171 | 30,299 |
Appendix C
References
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Wolfram, S. Computation Theory of Cellular Automata. Commun. Math. Phys. 1984, 96, 15–57. [Google Scholar] [CrossRef]
- Li, W. Phenomenology of Noniocal Cellular Automata. J. Stat. Phys. 1992, 68, 829–882. [Google Scholar] [CrossRef]
- Alonso-Sanz, R. Discrete Systems with Memory; World Scientific Series on Nonlinear Science Series A; World Scientific Publishing: Singapore, 2011; Volume 75. [Google Scholar]
- Jin, W.; Chen, F. Symbolic Dynamics of Cellular Automata. In Advances in Cellular Automata; Springer: Berlin/Heidelberg, Germany, 2025; pp. 375–397. [Google Scholar]
- Etzion, T. Sequences and the de Bruijn Graph: Properties, Constructions, and Applications; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- OEIS Foundation Inc. A000215 in the On-Line Encyclopaedia of Integer Sequences. Available online: https://oeis.org/A000215 (accessed on 3 August 2025).
- Fredricksen, H. A Survey of Full Length Nonlinear Shift Register Cycle Algorithms. SIAM Rev. 1982, 24, 195–221. [Google Scholar] [CrossRef]
- Golomb, W. Shift Register Sequences; Holden-Day: San Francisco, CA, USA, 1967; pp. 118–122. [Google Scholar]
- Zhao, X.-X.; Qi, W.-F.; Wang, Z.-X.; Zheng, Q.-X.; Tang, D. The decomposition of cascade connections of NFSRs: Old and New results. IEEE Trans. Inf. Theory 2025. [CrossRef]
- Gao, Z.; Feng, J. Status of Nonlinear Feedback Shift Register Based on Semi-Tensor Product. Mathematics 2022, 10, 3538. [Google Scholar] [CrossRef]
- De Bruijn, G. A combinatorial problem. Nederl. Akad. Wetensch. Proc. 1946, 49, 758–764. [Google Scholar]
- Ralston, A. De Bruijn Sequences: A Model Example of the Interaction of Discrete Mathematics and Computer Science. Math. Mag. 1982, 55, 131–143. [Google Scholar] [PubMed]
- Huang, S.; Zhang, H.; Bao, E. A Comprehensive Review of the de Bruijn Graph and Its Interdisciplinary Applications in Computing. Eng. Sci. 2024, 28, 1061. [Google Scholar] [CrossRef]
- Miroschnyk, M.; Korytchinko, T.; Demihev, O.; Krylova, V.; Karaman, D.; Filippenko, I. Practical methods for de Bruijn sequences generation using non-linear feedback shift registers. In Proceedings of the 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; pp. 1157–1161. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1; Pearson Education: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- OEIS Foundation Inc. A016031 in the On-Line Encyclopaedia of Integer Sequences. Available online: https://oeis.org/A016031 (accessed on 3 August 2025).
- Hall, M. Combinatorial Theory; Blaisdell: Waltham, MA, USA, 1967. [Google Scholar]
- De Bruijn Sequence and Universal Cycle Constructions. 2024. Available online: http://debruijnsequence.org (accessed on 3 August 2025).
- OEIS Foundation Inc. A129771 in the On-Line Encyclopaedia of Integer Sequences. Available online: https://oeis.org/A129771 (accessed on 3 August 2025).
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 11 August 2025).
- Kalinowski, T.; Falbel, D.; Allaire, J.J.; Chollet, F.; Tang, Y.; Bijl, W.V.D.; Studer, M.; Keydana, S. Keras: R Interface to ’Keras’. R Package Version 2.16.0. 2024. Available online: https://CRAN.R-project.org/package=keras (accessed on 11 August 2025).
| Initial Sequence | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0000 | 36,096 | 3304 | 4944 | 4734 | 5836 | 3758 | 2472 | 1846 | 1120 | 758 | 332 | 144 | 80 | 48 | 48 | 16 |
| 0001 | 12,912 | 6608 | 9888 | 9468 | 9624 | 6492 | 3920 | 2924 | 1728 | 1068 | 440 | 208 | 96 | 80 | 64 | 16 |
| 0010 | 11,800 | 8976 | 11,780 | 8457 | 8976 | 5697 | 3552 | 2803 | 1634 | 995 | 412 | 200 | 94 | 80 | 64 | 16 |
| 0011 | 15,368 | 5320 | 9490 | 9252 | 9296 | 6397 | 3702 | 2981 | 1756 | 1067 | 444 | 207 | 96 | 80 | 64 | 16 |
| 0100 | 14,568 | 5524 | 11,588 | 8860 | 9190 | 5851 | 3570 | 2834 | 1672 | 1011 | 414 | 200 | 94 | 80 | 64 | 16 |
| 0101 | 10,520 | 16,384 | 8458 | 6494 | 8542 | 5755 | 3620 | 2572 | 1438 | 919 | 406 | 192 | 80 | 76 | 64 | 16 |
| 0110 | 12,032 | 6428 | 12,398 | 9128 | 9438 | 6043 | 3486 | 2975 | 1714 | 1019 | 422 | 199 | 94 | 80 | 64 | 16 |
| 0111 | 21,376 | 4956 | 7416 | 8125 | 8242 | 5637 | 3580 | 2641 | 1648 | 1025 | 426 | 208 | 96 | 80 | 64 | 16 |
| 1000 | 21,376 | 4956 | 7416 | 8125 | 8242 | 5637 | 3580 | 2641 | 1648 | 1025 | 426 | 208 | 96 | 80 | 64 | 16 |
| 1001 | 12,032 | 6428 | 12,398 | 9128 | 9438 | 6043 | 3486 | 2975 | 1714 | 1019 | 422 | 199 | 94 | 80 | 64 | 16 |
| 1010 | 10,520 | 16,384 | 8458 | 6494 | 8542 | 5755 | 3620 | 2572 | 1438 | 919 | 406 | 192 | 80 | 76 | 64 | 16 |
| 1011 | 14,568 | 5524 | 11,588 | 8860 | 9190 | 5851 | 3570 | 2834 | 1672 | 1011 | 414 | 200 | 94 | 80 | 64 | 16 |
| 1100 | 15,368 | 5320 | 9490 | 9252 | 9296 | 6397 | 3702 | 2981 | 1756 | 1067 | 444 | 207 | 96 | 80 | 64 | 16 |
| 1101 | 11,800 | 8976 | 11,780 | 8457 | 8976 | 5697 | 3552 | 2803 | 1634 | 995 | 412 | 200 | 94 | 80 | 64 | 16 |
| 1110 | 12,912 | 6608 | 9888 | 9468 | 9624 | 6492 | 3920 | 2924 | 1728 | 1068 | 440 | 208 | 96 | 80 | 64 | 16 |
| 1111 | 36,096 | 3304 | 4944 | 4734 | 5836 | 3758 | 2472 | 1846 | 1120 | 758 | 332 | 144 | 80 | 48 | 48 | 16 |
| Evil Odd Number | Rule in Decimal | Rule in Binary | de Bruijn Sequence | ||
|---|---|---|---|---|---|
| 1 | - | - | 1 | 01 | 01 |
| 2 | - | 3 | 3 | 0011 | 0011 |
| 3 | 3 | 15 | 45 | 00101101 | 00010111 |
| 3 | 5 | 15 | 75 | 01001011 | 00011101 |
| 4 | 3 | 255 | 765 | 0000001011111101 | 0000101101001111 |
| 4 | 9 | 255 | 2295 | 0000100011110111 | 0000110100101111 |
| 4 | 15 | 255 | 3825 | 0000111011110001 | 0000100110101111 |
| 4 | 17 | 255 | 4335 | 0001000011101111 | 0000111100101101 |
| 4 | 27 | 255 | 6885 | 0001101011100101 | 0000101111001101 |
| 4 | 29 | 255 | 7395 | 0001110011100011 | 0000110101111001 |
| 4 | 43 | 255 | 10,965 | 0010101011010101 | 0000101001101111 |
| 4 | 57 | 255 | 14,535 | 0011100011000111 | 0000110111100101 |
| 4 | 65 | 255 | 16,575 | 0100000010111111 | 0000111101001011 |
| 4 | 71 | 255 | 18,105 | 0100011010111001 | 0000100111101011 |
| 4 | 75 | 255 | 19,125 | 0100101010110101 | 0000101111010011 |
| 4 | 83 | 255 | 21,165 | 0101001010101101 | 0000101100111101 |
| 4 | 85 | 255 | 21,675 | 0101010010101011 | 0000111101011001 |
| 4 | 89 | 255 | 22,695 | 0101100010100111 | 0000110010111101 |
| 4 | 99 | 255 | 25,245 | 0110001010011101 | 0000101001111011 |
| 4 | 113 | 255 | 28,815 | 0111000010001111 | 0000111101100101 |
| # Feasible | # de Bruijn | Feasible/Total | de Bruijn/Total | de Bruijn/Feasible | ||
|---|---|---|---|---|---|---|
| 2 | 16 | 1 | 0.0625 | |||
| 3 | 256 | 2 | 2 | 0.0078125 | 0.0078125 | 1 |
| 4 | 65,536 | 24 | 16 | 0.000366211 | 0.00024414 | 0.66666667 |
| 5 | 4,294,967,296 | 6144 | 2048 | 1.4305 × 10 | 4.7683 × 10 | 0.33333333 |
| 6 | 1.84467 × 1019 | 402,653,184 | 67,108,864 | 2.1827 × 10 | 3.6379 × 10 | 0.16666667 |
| 7 | 3.40282 × 1038 | 1.7293 × 1018 | 1.4411 × 1017 | 5.0820 × 10 | 4.2351 × 10 | 0.08333333 |
| 8 | 1.15792 × 1077 | 3.1901 × 1037 | 1.3292 × 1036 | 2.7550 × 10 | 1.1479 × 10 | 0.04166667 |
| 9 | 1.3408 × 10154 | 1.0855 × 1076 | 2.2615 × 1074 | 8.0964 × 10 | 1.6867 × 10 | 0.02083333 |
| Metric, Definition | ||
|---|---|---|
| True Positives (TP) | 397 | 198,563 |
| False Positives (FP) | 3 | 19,839 |
| True Negatives (TN) | 820 | 180,668 |
| False Negatives (FN) | 9 | 930 |
| Accuracy, (TP + TN)/Total | 0.9902 | 0.9481 |
| Sensitivity (Recall), TP/(TP + FN) | 0.9778 | 0.9953 |
| Specificity, TN/(TN + FP) | 0.9964 | 0.9011 |
| Precision (PPV), TP/(TP + FP) | 0.9925 | 0.9092 |
| Negative Predictive Value (NPV), TN/(TN + FN) | 0.9891 | 0.9949 |
| Balanced Accuracy, (Sens. + Spec.)/2 | 0.9871 | 0.9482 |
| Detection Rate, TP/Total | 0.3230 | 0.4964 |
| Detection Prevalence, (TP + FP) / Total | 0.3255 | 0.5460 |
| True Prevalence, (TP + FN) / Total | 0.3303 | 0.4987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, F.J.; Nuño, J.C. Rule-Based Generation of de Bruijn Sequences: Memory and Learning. Mathematics 2025, 13, 2598. https://doi.org/10.3390/math13162598
Muñoz FJ, Nuño JC. Rule-Based Generation of de Bruijn Sequences: Memory and Learning. Mathematics. 2025; 13(16):2598. https://doi.org/10.3390/math13162598
Chicago/Turabian StyleMuñoz, Francisco J., and Juan Carlos Nuño. 2025. "Rule-Based Generation of de Bruijn Sequences: Memory and Learning" Mathematics 13, no. 16: 2598. https://doi.org/10.3390/math13162598
APA StyleMuñoz, F. J., & Nuño, J. C. (2025). Rule-Based Generation of de Bruijn Sequences: Memory and Learning. Mathematics, 13(16), 2598. https://doi.org/10.3390/math13162598






