Abstract
Decision-making plays a pivotal role in data-driven optimization, aiming to achieve optimal results by identifying the most effective combination of input variables. Traditionally, in multi-objective data-driven optimization problems, decision-making relies solely on the Pareto front derived from the training data, as provided by the optimizer. This approach limits consideration to a subset of solutions and often overlooks potentially superior solutions on test set within the optimizer’s final population. What if we include the entire final population in the decision-making process? This paper is the first to systematically explore the potential of utilizing the entire final population, rather than relying solely on the optimization Pareto front, for decision-making in data-driven multi-objective optimization. This novel perspective reveals overlooked yet potentially superior solutions that generalize better to unseen data and help mitigate issues such as overfitting and training-data bias. This paper highlights the use of the entire final population of the optimizer for final decision-making in multi-objective optimization. Using feature selection as a case study, this method is evaluated on two key objectives: minimizing classification error rate and reducing the number of selected features. We compare the proposed test Pareto front, derived from the final population, with traditional test Pareto fronts based on training data. Experiments conducted on fifteen large-scale datasets reveal that some optimal solutions within the entire population are overlooked when focusing solely on the optimization Pareto front. This indicates that the solutions on the optimization Pareto front are not necessarily the optimal solutions for real-world unseen data. There may be additional solutions in the final population yet to be utilized for decision-making.
Keywords:
data-driven optimization; multi-objective optimization; feature selection; final population; overfitting; decision-making MSC:
68T05
1. Introduction
Effectively addressing complex optimization problems is crucial in diverse fields, such as healthcare, engineering, and computational biology [1]. One of the most effective approaches to tackling these problems is data-driven optimization [2,3], which utilizes insights from existing data to guide the optimization process. This approach has become invaluable for solving real-world challenges, such as feature selection in machine learning, where the optimization process plays a key role in enhancing algorithmic performance.
However, several challenges persist when implementing data-driven optimization in machine learning. These challenges include managing distributed, noisy, or heterogeneous data, dealing with sparse data, and combating overfitting [4,5]. Overfitting occurs when optimization solutions perform well on training data but fail to generalize to unseen scenarios [6]. This issue is exacerbated when multi-objective optimization decisions rely solely on Pareto fronts derived from the training data, which limits the ability to effectively address broader problem spaces. Overfitting is particularly problematic when decisions are based solely on training-derived Pareto fronts. Our approach mitigates this by evaluating the final population on test data, thereby identifying solutions that generalize better to unseen scenarios.
In parallel with these challenges, data-driven decision-making [7] has become central to modern industrial operations [8,9]. With the rapid increase in data availability and advancements in analytics, decision-making processes have undergone profound transformations. By utilizing real-time data, businesses are able to make informed, adaptable decisions that respond to evolving market conditions, thereby improving efficiency and fostering innovation.
In traditional, non-data-driven optimization [10], the Pareto front from the final population is often computed to identify the best possible trade-offs between conflicting objectives. This serves as a powerful tool for decision-making, allowing decision-makers to evaluate and select solutions that align with their preferences. This approach makes sense in regular real-world optimization problems because the solutions on the Pareto front represent the only analytically derived trade-offs and are generally optimal within the defined problem space. However, in data-driven optimization problems, these solutions are not necessarily the best. The reliance on training data and model approximations means that the Pareto front may overlook better solutions that generalize well to unseen scenarios, as it is often influenced by overfitting and the inherent biases of the data.
Accordingly, a persistent challenge in data-driven evolutionary optimization is overfitting [6,11], where solutions may perform well on training data but fail to generalize effectively to new, unseen data. This issue becomes particularly problematic when decisions are made based solely on the optimization Pareto front, causing the optimization process to miss potentially more optimal solutions within the final population. Hence, it becomes critical to explore the entire final population of solutions to ensure effective decision-making.
In conventional data-driven multi-objective optimization [12], optimization is performed using the training dataset, and the Pareto front is constructed based on this data. A solution is then chosen from the optimization Pareto front and evaluated on unseen test data. However, this method often suffers from overfitting, leading to poor generalization on test data. Limiting decision-making to the optimization Pareto front ignores other potentially promising solutions within the optimizer’s final population. To overcome this limitation, we propose a different strategy: instead of relying solely on the optimization Pareto front, we evaluate the full final population generated by the optimizer. Unlike traditional methods that rely solely on the optimization of the Pareto front derived from training data, our work introduces the idea of evaluating the entire final population to uncover high-performing, generalizable solutions. This approach represents a paradigm shift in data-driven optimization, enhancing decision quality while mitigating the risks of overfitting. This approach allows us to identify solutions with superior performance on the test data that might otherwise be overlooked.
Within this framework, all solutions may have equal potential to perform well on unseen data, making it impractical to rely solely on the Pareto front derived from training data. This limitation underscores the importance of developing decision-making strategies that consider the entire population of solutions rather than focusing exclusively on the optimization Pareto front. By doing so, decision-making processes become more robust and capable of addressing real-world challenges, ensuring better alignment between optimization objectives and practical applications.
This paper highlights the advantage of using the entire final population for decision-making in data-driven evolutionary computation, rather than relying solely on the output of the optimizer. Unlike traditional approaches that focus on individual solutions derived from the optimizer, our method emphasizes the collective potential of the final population to identify optimal solutions, particularly in test scenarios. We illustrate the effectiveness of this approach through a case study on multi-objective feature selection, demonstrating how utilizing the full population can lead to more robust decision-making and a better identification of optimal solutions. It is worth mentioning that even in single-objective data-driven optimization, evaluating the entire population is often more effective than relying solely on the best individual solution. Additionally, incorporating validation data can play a crucial role in decision-making, whether in single- or multi-objective scenarios. Whether the decision is made by an automated system or a human expert, considering the full population can lead to better generalization and improved performance on the test data.
Feature selection as a data-driven optimization task [13,14] plays a crucial role in enhancing the performance of machine learning algorithms. It involves selecting an optimal subset of features that improves both the efficiency and accuracy of the learning process [15]. While feature selection is often treated as a single-objective optimization task, it is essential to recognize that this process involves balancing multiple conflicting objectives, such as maximizing classification accuracy while minimizing the number of selected features [16]. To address this complexity, multi-objective optimization techniques are employed, which yield a set of Pareto-optimal solutions, each representing a different trade-off between the objectives [17].
In the field of multi-objective feature selection [18,19,20], many published studies compare their proposed methods to existing approaches by evaluating the test Pareto front derived from the optimization Pareto front. However, this approach is not ideal, as it may not accurately reflect the true performance or generalizability of the methods being assessed.
The structure of this paper is as follows: Section 2 provides background information on multi-objective optimization and feature selection. Section 3 presents the conducted investigation of the entire final population. Section 4 discusses the experimental results and analysis. Finally, Section 5 concludes the paper and suggests future research directions.
2. Background Review
In the following subsections, we provide a detailed review of multi-objective optimization (MOO), including an explanation of the GDE3 and NSGA-II algorithms, which serve as the basis for our case studies to examine the effectiveness of the proposed strategy. Furthermore, we discuss the role of feature selection within MOO.
2.1. Multi-Objective Optimization (MOO)
Multi-objective optimization [21,22] involves the simultaneous optimization of two or more objectives that may conflict with each other. To assess how optimal a solution is multiple evaluation methods are used, which typically involve making trade-offs between competing objectives. Instead of focusing on a single solution, these methods aim to select a group of solutions that represent the best possible trade-offs. This group of solutions is known as the Pareto front [23], which consists of solutions that are not dominated by any others.
The Pareto front is generated based on the concept of dominance, which is used as the fundamental criterion for comparing solutions. A multi-objective optimization problem is formally defined in Equation (1) [24]:
In this equation, M is the number of objectives, d is the number of variables or dimensions, and represents an individual solution. Each variable is bounded within the range [, ]. The objective functions, represented by , are the ones that need to be minimized.
To compare two vectors, and , within the decision space, x dominates () if, and only if, the following conditions are true:
Non-Dominated Sorting is an essential method used to categorize solutions based on their dominance relationships. A solution is considered non-dominated if no other solution surpasses it in all objective functions. The resulting Pareto front is made up of solutions that represent the best trade-offs between the conflicting objectives. Once Non-Dominated Sorting is completed, the algorithm calculates the crowding distance for each solution within the Pareto front. This metric gauges the degree of “crowding” or density around a particular solution compared to the others in the front, serving as an indicator of diversity.
Generalized Differential Evolution (GDE3): To solve our feature selection optimization problem, we utilized the GDE3 algorithm. Various Differential Evolution (DE)-based algorithms [25] have been developed for solving multi-objective optimization problems, with GDE3 being a notable variant. Designed to handle multiple objectives and constraints, GDE3 enhances the basic DE framework by generating offspring using three randomly selected vectors [26].
In GDE3, solution selection is guided by feasibility and Pareto dominance. Infeasible solutions are compared based on constraint violation, while feasible solutions are preferred over infeasible ones. When both solutions are feasible, Pareto dominance determines the choice; if neither dominates, both are retained, temporarily increasing the population size, which is then trimmed. Inspired by NSGA-II, GDE3 uses non-dominated sorting and crowding distance to rank and select solutions for the next generation, ensuring diversity and progress in the evolutionary process.
Non-Dominated Sorting Genetic Algorithm (NSGA-II): The NSGA-II algorithm [27] starts by generating a randomly initialized parent population, which is then organized using a non-dominated sorting process. Each individual is assigned a fitness rank based on its level of non-domination, where a lower rank indicates a better solution. To generate the offspring population, the algorithm employs binary tournament selection, along with crossover and mutation operators. Elitism is integrated into the process by preserving high-quality non-dominated solutions discovered in earlier generations, resulting in a modified procedure following the initial iteration.
To implement elitism, a combined population is formed by merging the current and previous populations. Non-Dominated Sorting (NDS) [28] is applied to this combined group to identify the best individuals, prioritizing solutions that are not outperformed across all objectives. If the number of top-ranked non-dominated solutions is less than the target population size, all are included. A solution is considered non-dominated if no other solution is superior in all objectives, and the set of such solutions forms the Pareto front, representing optimal trade-offs between conflicting objectives.
To promote diversity among solutions, the crowding distance is calculated for each individual within the Pareto front. This metric assesses the proximity of neighboring solutions and helps preserve diversity by favoring those in less crowded regions. Individuals with higher crowding distances are preferred, as they contribute to a more spread-out and comprehensive search of the solution space [29]. The algorithm then selects the top N solutions with the highest crowding distances for the next generation.
If the desired population size has not yet been reached, additional members are selected from subsequent non-dominated fronts in order of rank until the population is fully restored.
2.2. Multi-Objective Feature Selection
Feature selection in multi-objective optimization (MOO) [30,31] plays a crucial role in improving machine learning models by balancing two core goals: enhancing classification accuracy and minimizing the number of selected features. These two objectives often conflict, as optimizing one may negatively impact the other. The objective of feature selection is to identify a subset of features that achieves both high classification performance and low dimensionality.
Each feature is represented by a binary variable indicating whether it is included in the subset or not. Classification performance is evaluated using metrics such as Precision, Recall, and the F1-score. The F1-score is the harmonic mean of Precision and Recall, and it is defined as Equation (3):
To calculate the classification error, we use the inverse of the F1-score as defined in Equation (4):
The second objective in feature selection is to minimize the number of the selected features. This is represented by the ratio of selected features to the total number of available features, which is computed as Equation (5):
By optimizing these two objectives simultaneously, the goal is to find feature subsets that achieve both good classification performance and reduced dimensionality. Non-dominated solutions are identified through dominance relationships, where a solution is considered better if it is at least as good in all objectives and strictly better in at least one. The crowding distance measure helps maintain diversity within the Pareto front, ensuring that selected feature subsets are not only optimal but also diverse, preventing premature convergence and promoting a comprehensive exploration of the solution space.
3. Beyond the Optimization Pareto Front: Investigation of Entire Final Population
In traditional data-driven multi-objective optimization [12], the optimization is typically performed using the training set, and the Pareto front is derived from this training data. A solution is then selected from the optimization Pareto front and evaluated on the test set. However, this approach can lead to suboptimal results on the test data, mainly due to overfitting. Overfitting may occur on some solutions of the Pareto front, but not on all solutions or the entire population. The decision-making process, when restricted to the Pareto front of the training data, fails to account for potentially better solutions that exist within the broader population. In this paper, we propose an alternative approach: instead of limiting decision-making to the optimization Pareto front, we leverage the entire final population produced by the optimizer. This allows us to uncover better-performing solutions that may not be captured in the optimization Pareto front.
In real-world scenarios, test data is typically unavailable during the optimization process, necessitating decision-making based on the training data. However, our study shows that there are potentially better solutions within the population that are ignored when decisions rely solely on the optimization Pareto front. These overlooked solutions may offer more favorable trade-offs between objectives, but can only be discovered by considering the entire population. It is important to clarify that this paper does not propose a new method for decision-making, nor does it introduce a new approach to multi-objective feature selection. Instead, we investigate the impact of considering the full population on test data, highlighting how this broader perspective may lead to improved outcomes.
For multi-objective feature selection as a case study, we focus on two key objectives: minimizing the classification error rate and reducing the number of selected features. The classification error is measured using the F1-score, a standard metric ranging from 0 to 1, as defined in Equation (4).
To begin, we split the dataset into two parts: training set and test set. The optimization process is carried out using evolutionary algorithms (GDE3 and NSGA-II), which identify optimal feature subsets by iteratively refining a population of candidate solutions. Each individual in the population represents a potential feature subset and is evaluated against the two objectives using the training data.
The optimization process begins by generating an initial random population of candidate solutions, where each solution represents a potential feature subset. These solutions are then evaluated based on the two objectives.
Similar to other population-based optimization algorithms, new solutions are generated using generative operators such as crossover and mutation. The best set of solutions is carried forward to the next generation, and this iterative process continues until the stopping criteria are met.
In traditional approach, after completing the optimization process, the Pareto front (i.e., optimization Pareto front) is derived from the population as the optimal solutions. We evaluate the final population on the test data by computing the classification error for each solution while retaining the same selected features. This evaluation produces two sets of solutions: one for the training data and another for the test data. Each solution in both sets is characterized by its classification error and the number of selected features.
To investigate the potential of the final population against the optimization Pareto front, we compare two Pareto fronts for the test data. The first, referred to as the test-training Pareto front, is derived from the Pareto front of the training data. We perform non-dominated sorting (NDS) on the training solutions to compute their Pareto front. For each solution on this front, we calculate its classification error on the test set while keeping the selected features fixed. These test evaluations are then subjected to NDS to form the test-training Pareto front. This approach mirrors traditional data-driven optimization methods.
The second Pareto front, referred to as the test-population Pareto front, is constructed by performing NDS directly on the test evaluations of the final population. This generates a new Pareto front that reflects the best trade-offs present in the broader solution space explored by the optimizer. Unlike the test-training Pareto front, this front captures solutions that may not have been represented in the optimization Pareto front but perform well on the test data. In essence, it allows us to compare the traditional Pareto front obtained during optimization with one derived from evaluating the final solutions on unseen test data.
We compare the two test Pareto fronts to evaluate the effectiveness of our approach. This includes analyzing hypervolume (HV) metrics to assess their coverage and diversity in the objective space, as well as identifying the extreme points, particularly the minimum classification error (MCE points), on each front. The MCE point represents the solution with the lowest classification error, and we analyze its performance in terms of both error rate and the number of selected features.
The comparison highlights that relying solely on the optimization Pareto front is insufficient for identifying the best test solutions. By leveraging the final population, we uncover solutions that are absent from the optimization Pareto front but offer superior performance on the test data. This demonstrates the advantages of population-based decision-making, as it provides a more reliable basis for identifying optimal solutions.
By analyzing both Pareto fronts and their respective MCE points, we establish that decision-making based on the population set results in superior outcomes in multi-objective optimization tasks. This paper emphasizes the necessity of moving beyond the optimization Pareto front and leveraging the final population to achieve enhanced performance, particularly in real-world scenarios where test data is unavailable during the optimization process. However, discovering those points still requires some innovative decision-making methods.
To ensure reproducibility, we provide Algorithm 1, which outlines the main implementation steps of our approach, including how the population is generated, evaluated, and used to construct both the training-based and population-based test Pareto fronts. This algorithm outlines our main strategy, detailing the steps for evaluating solutions and constructing Pareto fronts.
| Algorithm 1 Investigation of the entire final population beyond the optimization pareto front |
|
4. Experimental Results
In the following subsections, we present experimental results encompassing datasets, experimental settings, and numerical results along with their analysis.
4.1. Datasets
To emphasize the effectiveness of decision-making based on population data rather than training data for data-driven optimization tasks, we utilized 15 datasets from various domains, including biological data, face image data, and mass spectrometry. These datasets exhibit variations in sample sizes, feature dimensions, and label complexities, with the number of classes ranging from 2 to 40 and the number of features varying from 1024 to 19,993. Detailed information about each dataset is provided in Table 1.

Table 1.
Datasets description.
4.2. Experimental Settings
To emphasize the role of population data in decision-making for multi-objective optimization problems, each dataset was split into 80% training data and 20% test data. The optimization process was conducted solely on the training data, ensuring that the test data remained completely independent and uninvolved. This partitioning was performed at the start of each run to preserve the integrity of the evaluation. The well-known GDE3 and NSGA-II algorithms were employed for multi-objective feature selection, each run 15 times using a consistent population size and 100 iterations per run.
To perform data classification based on the number of features and the classification error (treated as one of the objectives), the k-Nearest Neighbors (k-NN) algorithm [32] is employed. A uniform value of k = 5 is used consistently across both the training and test datasets.
The experimental setup for the GDE3 algorithm includes a mutation scale factor (F) that varies between 0.0 and 0.9, enabling extensive exploration of the solution space. A crossover rate (CR) of 0.5 is applied to govern the probability of crossover between trial and parent individuals. To ensure that all generated individuals stay within the feasible solution space, a “bounce-back” repair mechanism is implemented.
For NSGA-II, two-point crossover is used to recombine parent solutions, while bit-flip mutation introduces diversity by flipping individual bits.
The comparison of test Pareto fronts derived from population data and training data is performed using the HV indicator. This metric evaluates the quality and diversity of solutions in multi-objective optimization, offering a quantitative assessment of how effectively an algorithm explores the Pareto front. The analysis examines the Pareto fronts produced by each approach across all datasets.
Alongside hypervolume analysis, the Wilcoxon Signed-Rank Test is applied as a statistical method to evaluate performance metrics such as hypervolume, MCE, the number of features associated with the MCE, and the number of solutions on each Pareto front. This statistical test identifies significant differences in overall performance between the two approaches, shedding light on how the population set enhances decision-making compared to the training set.
4.3. Numerical Results and Analysis
As previously discussed, our main goal is to demonstrate that the final population from the last generation contains solutions that cannot be obtained by relying solely on decision-making based on the training data Pareto front in multi-objective optimization problems. We show that when decision-making for test data is guided by population data rather than the training set, it leads to improved performance on new, unseen data. We examined this superiority from different perspectives.
4.3.1. Results on GDE3
Table 2 provides a comprehensive overview, including the average MCE across all Pareto fronts and the average number of features for the solution associated with MCE for the test data and the number of solutions on each Pareto front. Additionally, Table 2 presents insights into the hypervolume of the test data, and the results are highlighted alongside the Wilcoxon Signed-Rank Test to further illustrate the statistical significance of the observed differences. This experimental analysis highlights the effectiveness of population-based decision-making compared to traditional decision-making methods that rely solely on training data.

Table 2.
Comparison of Test Pareto front derived from Training data (Train) and final population (Population) across four metrics using GDE3 algorithm: Minimum classification error rates (MCE), Number of Features at MCE Points (NF-MCE), hypervolume (HV), and number of solutions on Pareto front (#Solution on Test PF).
First, we compare the differences between the extreme points of the two test Pareto fronts obtained using population data and training data. As shown in Table 2, the Pareto front derived from the population achieves a lower error rate at the extreme points (i.e., at the MCE points) compared to the Pareto front obtained from the training data. The “avg” row in Table 2 supports this, indicating that the average MCE error of the test data obtained from the population across 15 datasets is lower than that from the training data Pareto front. In terms of win/tie/loss (w/t/l), the population-based solutions is still superior with a score of 15 wins, 0 ties, and 0 losses. This indicates that the solutions on the optimization Pareto front are not necessarily the optimal solutions for real-world data. There are better solutions discovered during the optimization process that should be considered in decision-making.
Since we are dealing with a multi-objective optimization problem, we must also consider the second objective, which is the number of features. In terms of the number of features for the MCE points, population-based decision-making does not perform as well. However, except for two datasets (orlraws10P and lymphoma), the number of features for both decision-making methods is the same, with a score of (1/13/1). This is an exceptional result, as in multi-objective feature selection, it is common for the number of features to increase when trying to reduce the error rate, since selecting more features can improve the model’s accuracy. Even though the number of features for the MCE points is the same for both methods, we still prefer the population-based decision-making approach, as it results in better performance in terms of the error rate at the MCE points.
Third, as shown in Table 2, we compare the number of solutions on each Pareto front. A greater number of solutions on the Pareto front indicates a more diverse set of optimal solutions, suggesting a better exploration of the solution space in a multi-objective optimization problem. This often reflects a trade-off between different objectives, offering a wider range of possible solutions that balance competing goals. In terms of the number of solutions on the Pareto fronts, population provides more options, with a score of 13 wins, 2 ties, and no losses.
Finally, we compare the HVs of the two Pareto fronts. As shown in Table 2, the hypervolume of the population-based Pareto front is superior to that of the training-based Pareto front, with a score of 15 wins, no ties, and no losses, and an average HV of 0.99 versus 0.95. This indicates the necessity of considering the entire population for decision making rather than the optimization Pareto front as the set of optimal solutions.
In Figure 1, we present the Pareto front obtained from the training data (blue), the final test Pareto front produced by the population (orange), and the test Pareto front derived from the training data (red) for the CLL-SUB-111, CARCINOM, lung, lymphoma, SMK-CAN-187, and colon datasets using the GDE3 algorithm. The population-based Pareto front generally outperforms the training-based front. This difference arises because certain solutions discovered by the population are not attainable when relying solely on the Pareto front generated from the training data.
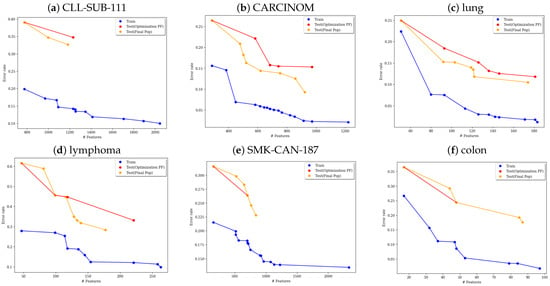
Figure 1.
Comparison of Pareto fronts for the CLL-SUB-111, CARCINOM, lung, lymphoma, SMK-CAN-187, and colon datasets: The figure illustrates the Pareto front for the training data (blue), and two Pareto fronts for the test data—one obtained from the final population (orange) and the other from the optimization Pareto front (red) using GDE3 algorithm.
The results summarized in Table 2 are illustrated in Figure 1. For example, a higher number of Pareto-optimal solutions and greater diversity are evident in the figures for the CLL-SUB-111, CARCINOM, lung, lymphoma, SMK-CAN-187, and colon datasets. Additionally, a lower minimum classification error (MCE) is observed across all datasets. The figures for CLL-SUB-111, CARCINOM, lung, and lymphoma also show that the MCE points correspond to solutions with fewer selected features.
We also observe a greater number of solutions on the Pareto front of the population-based test Pareto, and a higher HV in the figures. Additionally, the figure highlights that when comparing the MCE points for the training and population sets, the population set is preferred due to its lower error rates at the MCE points.
4.3.2. Results on NSGA-II
Table 3 presents a comprehensive summary of the results, including the minimum classification error (MCE) across all Pareto fronts, the average number of features corresponding to MCE points on the test set, and the number of solutions found on each Pareto front. Additionally, it reports hypervolume (HV) values for the test set and includes Wilcoxon Signed-Rank Test results to assess the statistical significance of the observed differences. These results highlight the superiority of population-based decision-making over traditional approaches that rely solely on training-based Pareto fronts.

Table 3.
Comparison of Test Pareto front derived from Training data (Train) and final population (Population) across four metrics using NSGA-II algorithm: Minimum classification error rates (MCE), Number of Features at MCE Points (NF-MCE), hypervolume (HV), and number of solutions on Pareto front (#Solution on Test PF).
We begin by comparing the extreme points (i.e., MCE points) of the two test Pareto fronts obtained from population-based and training-based decision-making. As seen in Table 3, the population-derived Pareto fronts consistently achieve lower error rates at the MCE points. This trend aligns with the average MCE values reported in the “avg” row of Table 3, where population-based methods outperform training-based ones across 15 datasets. In terms of win/tie/loss (w/t/l) comparison, population-based solutions achieve 14 wins, 1 tie, and 0 losses, demonstrating a clear advantage.
These findings indicate that the solutions present on the optimization (training-based) Pareto front do not necessarily translate into the best outcomes on real-world test data. Valuable solutions discovered during the evolutionary process may be excluded from the training-derived front but should still be considered in the final decision-making phase.
Regarding the number of features at the MCE points, population-based decision-making performs similarly to the training-based approach. In 12 out of 15 datasets, both methods select the same number of features, with differences observed only in CARCINOM, colon, and leukemia (score: 0/12/3). This is notable, as multi-objective feature selection often involves a trade-off where lower error rates are achieved at the cost of selecting more features. Despite similar feature counts, the lower error rates provided by the population-based approach make it preferable for model selection.
We also compare the number of solutions on each Pareto front, as shown in Table 3. A higher number of Pareto-optimal solutions indicates better diversity and exploration of the objective space. In this regard, the population-based approach again performs better, with 10 wins, 5 ties, and 0 losses. This richer set of trade-off solutions offers broader flexibility in model selection.
Further, hypervolume (HV) analysis, which measures both convergence and diversity, also favors the population-based approach. As reported in Table 3, it achieves 14 wins, 1 tie, and 0 losses, with an average HV of 1.03 compared to 0.99 for the training-based method. This emphasizes the value of using the entire population for final decision-making, rather than relying solely on the optimization Pareto front.
Figure 2 visualizes the test Pareto fronts generated using the NSGA-II algorithm for the ORL, CLL-SUB-111, lung, nci9, warpAR10P, and warpPIE10P datasets. The population-based Pareto front (orange) clearly outperforms the training-based one (red). This performance gap arises because certain high-quality solutions discovered during the evolutionary process are not captured by the training-data Pareto front.
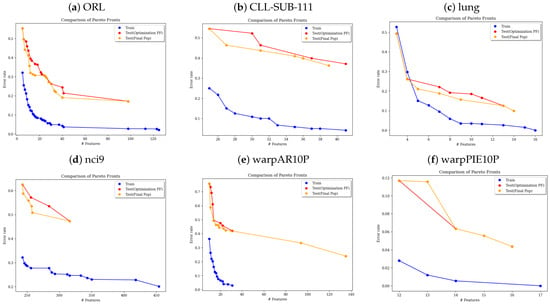
Figure 2.
Comparison of Pareto fronts for the ORL, CLL-SUB-111, lung, nci9, warpAR10P, and warpPIE10P datasets: The figure illustrates the Pareto front for the training data (blue), and two Pareto fronts for the test data: one obtained from the final population (orange) and the other from the optimization Pareto front (red) using NSGA-II algorithm.
These patterns are further illustrated in Figure 2, which corresponds to the data in Table 3. For instance, datasets such as CLL-SUB-111, nci9, ORL, warpAR10P, and warpPIE10P show a higher number of Pareto-optimal and more diverse solutions. Lower MCE values are evident in datasets like CLL-SUB-111, lung, warpAR10P, and warpPIE10P. Notably, in the CLL-SUB-111 dataset, the MCE point corresponds to a solution with fewer selected features, reinforcing the benefits of population-based selection.
Furthermore, the population-based test Pareto fronts consistently contain more solutions and achieve higher hypervolume values. When comparing MCE points across the training and population-based fronts, the latter consistently yields lower error rates, further supporting its superiority. Compared to methods relying solely on training-based Pareto fronts, our approach uncovers superior trade-offs on test data (Table 2 and Table 3), with consistent improvements in hypervolume, minimum classification error, and solution diversity. Our findings show that population-based decision-making yields lower error rates and higher diversity on test data, effectively reducing the risk of overfitting that arises when only training-based Pareto fronts are considered.
Overall, these results confirm that leveraging the entire population during decision-making offers substantial advantages. While the training-based Pareto front captures good solutions for the training set, it often misses better-performing solutions for unseen data. Many promising candidates exist outside the optimization Pareto front but within the broader population. Therefore, adopting decision-making strategies that consider the entire population can enhance the robustness and generalizability of multi-objective optimization outcomes, making them more suitable for real-world applications.
It is worth mentioning that although our approach provides a richer solution space, we acknowledge the cognitive limitations and biases that human decision-makers may face when selecting among many options. Future work could explore decision-support tools, such as visual filtering or interactive ranking, to help users manage complexity and avoid suboptimal choices. Our results suggest that even with better solutions available, behavioral biases such as those predicted by prospect theory may influence decision-making. This highlights the need to integrate behavioral-aware Multi-Criteria Decision Analysis (MCDA) frameworks in future work to align optimization outputs with realistic human decision behavior. Furthermore, bounded rationality imposes cognitive limits on human decision-makers. Future research should investigate simplified selection mechanisms or surrogate-guided recommendations to make population-based decision-making more practical and accessible. In summary, In data-driven optimization, the quality of selected solutions is closely tied to how well they generalize to unseen data. While the optimization process generates a population of candidate solutions, relying solely on the best-performing individual based on training data can lead to overfitting. Validation plays a crucial role in this context, serving as an intermediate evaluation step to guide the selection of solutions that are more likely to perform well on test data. By incorporating validation data into the selection process, one can make more informed decisions and improve the generalization ability of the final solution. This approach is particularly valuable in both single- and multi-objective optimization, where choosing from the entire population, rather than just the top-ranked candidate, can significantly enhance robustness and real-world performance. This issue deserves special attention from researchers working in data-driven optimization.
5. Conclusions Remarks
In conclusion, this paper highlights the importance of considering the entire population as a more valuable resource for decision-making in data-driven optimization, rather than relying solely on the Pareto front derived from training data. Most existing approaches focus on this narrow view, guiding decision-making and performance evaluation on test data. However, our study shows that solutions within the final population can outperform those on the Pareto front, offering superior hypervolume, more solutions on the Pareto front, and better error rates with fewer selected features. Traditional methods, by restricting the search to the Pareto front, may miss these better alternatives. Through experiments using the multi-objective optimization algorithms GDE3 and NSGA-II on 15 datasets, we found that utilizing the entire population results in lower error rates, higher hypervolume (HV) values, and more robust Pareto fronts compared to conventional approaches. This underscores the need for further research into strategies for identifying these superior solutions, especially when test data is unavailable during optimization. Addressing this issue presents an opportunity for innovation, where methods that integrate test-set insights or explore the full population could improve decision-making. Future work could focus on searching for promising solutions beyond the optimization Pareto front, uncovering valuable regions of the solution space. Additionally, applying this approach to single-objective optimization problems by considering the entire population rather than just the best solution may enhance exploration and drive advancements in optimization. Incorporating post-optimization validation or hybrid approaches that balance Pareto optimality with test set performance metrics could further improve decision-making by enhancing robustness and generalization.
Author Contributions
Conceptualization, S.R.; Methodology, P.D., A.A.B. and S.R.; Software, P.D.; Validation, A.A.B.; Writing—original draft, P.D.; Writing—review & editing, A.A.B. and S.R.; Visualization, P.D.; Supervision, A.A.B. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in https://jundongl.github.io/scikit-feature/datasets.html (accessed on 1 June 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhan, Z.H.; Shi, L.; Tan, K.C.; Zhang, J. A survey on evolutionary computation for complex continuous optimization. Artif. Intell. Rev. 2022, 55, 59–110. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, Y.; Ligeti, P.; Jin, Y. A secure federated data-driven evolutionary multi-objective optimization algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 191–205. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Yao, X. A data-driven evolutionary transfer optimization for expensive problems in dynamic environments. IEEE Trans. Evol. Comput. 2023, 28, 1396–1411. [Google Scholar] [CrossRef]
- Bejani, M.M.; Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artif. Intell. Rev. 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
- Cheng, M.; Zhao, X.; Dhimish, M.; Qiu, W.; Niu, S. A Review of Data-driven Surrogate Models for Design Optimization of Electric Motors. IEEE Trans. Transp. Electrif. 2024, 10, 8413–8431. [Google Scholar] [CrossRef]
- Fisher, O.J.; Watson, N.J.; Escrig, J.E.; Witt, R.; Porcu, L.; Bacon, D.; Rigley, M.; Gomes, R.L. Considerations, challenges and opportunities when developing data-driven models for process manufacturing systems. Comput. Chem. Eng. 2020, 140, 106881. [Google Scholar] [CrossRef]
- Rinat, K.; Koli, S.; Sobti, R.; Ledalla, S.; Arora, R. Data-Driven Decision Making: Real-world Effectiveness in Industry 5.0—An Experimental Approach. BIO Web Conf. 2024, 86, 01061. [Google Scholar] [CrossRef]
- Coronado, E.; Kiyokawa, T.; Ricardez, G.A.G.; Ramirez-Alpizar, I.G.; Venture, G.; Yamanobe, N. Evaluating quality in human-robot interaction: A systematic search and classification of performance and human-centered factors, measures and metrics towards an industry 5.0. J. Manuf. Syst. 2022, 63, 392–410. [Google Scholar] [CrossRef]
- Gladysz, B.; Tran, T.a.; Romero, D.; van Erp, T.; Abonyi, J.; Ruppert, T. Current development on the Operator 4.0 and transition towards the Operator 5.0: A systematic literature review in light of Industry 5.0. J. Manuf. Syst. 2023, 70, 160–185. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, Y.; Zuo, G.; Fan, S.; Yu, H.; Shaikh, Z.A.; Wen, Z. Addressing Overfitting Problem in Deep Learning-Based Solutions for Next Generation Data-Driven Networks. Wirel. Commun. Mob. Comput. 2021, 2021, 8493795. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Sun, C. Data-Driven Evolutionary Optimization; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Bidgoli, A.A.; Rahnamayan, S. Large-scale Multi-objective Feature Selection: A Multi-phase Search Space Shrinking Approach. arXiv 2024, arXiv:2410.21293. [Google Scholar]
- Zanjani Miyandoab, S.; Rahnamayan, S.; Asilian Bidgoli, A. Compact NSGA-II for Multi-objective Feature Selection. arXiv 2024, arXiv:2402.12625. [Google Scholar]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the IEEE 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 372–378. [Google Scholar]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef]
- Bidgoli, A.A.; Ebrahimpour-Komleh, H.; Rahnamayan, S. An evolutionary decomposition-based multi-objective feature selection for multi-label classification. PeerJ Comput. Sci. 2020, 6, e261. [Google Scholar] [CrossRef]
- Jiao, R.; Nguyen, B.H.; Xue, B.; Zhang, M. A survey on evolutionary multiobjective feature selection in classification: Approaches, applications, and challenges. IEEE Trans. Evol. Comput. 2023, 28, 1156–1176. [Google Scholar] [CrossRef]
- Jiao, R.; Xue, B.; Zhang, M. Learning to Preselection: A Filter-Based Performance Predictor for Multiobjective Feature Selection in Classification. In IEEE Transactions on Evolutionary Computation; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Espinosa, R.; Jiménez, F.; Palma, J. Multi-surrogate assisted multi-objective evolutionary algorithms for feature selection in regression and classification problems with time series data. Inf. Sci. 2023, 622, 1064–1091. [Google Scholar] [CrossRef]
- Bidgoli, A.A.; Ebrahimpour-Komleh, H.; Rahnamayan, S. Reference-point-based multi-objective optimization algorithm with opposition-based voting scheme for multi-label feature selection. Inf. Sci. 2021, 547, 1–17. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A comprehensive review on multi-objective optimization techniques: Past, present and future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Dowlatshahi, M.; Hashemi, A. Multi-objective Optimization for Feature Selection: A Review. In Applied Multi-Objective Optimization; Springer Nature: Singapore, 2024; pp. 155–170. [Google Scholar]
- Asilian Bidgoli, A.; Rahnamayan, S.; Erdem, B.; Erdem, Z.; Ibrahim, A.; Deb, K.; Grami, A. Machine learning-based framework to cover optimal Pareto-front in many-objective optimization. Complex Intell. Syst. 2022, 8, 5287–5308. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Asilian Bidgoli, A.; Rahnamayan, S.; Ebrahimpour-Komleh, H. Opposition-based multi-objective binary differential evolution for multi-label feature selection. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, East Lansing, MI, USA, 10–13 March 2019; Springer: Cham, Switzerland, 2019; pp. 553–564. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, X.; Zhou, Y.; Liu, Y.; Zhou, X.; Chen, H.; Zhao, H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022, 585, 441–453. [Google Scholar] [CrossRef]
- Miyandoab, S.Z.; Rahnamayan, S.; Bidgoli, A.A.; Ebrahimi, S.; Makrehchi, M. Enhancing Diversity in Multi-Objective Feature Selection. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Almutairi, M.S. Evolutionary Multi-Objective Feature Selection Algorithms on Multiple Smart Sustainable Community Indicator Datasets. Sustainability 2024, 16, 1511. [Google Scholar] [CrossRef]
- Zanjani Miyandoab, S.; Rahnamayan, S.; Asilian Bidgoli, A. Multi-objective Binary Coordinate Search for Feature Selection. In Proceedings of the 2023 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Honolulu, HI, USA, 1–4 October 2023. [Google Scholar]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN model-based approach in classification. In On the Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE, Proceedings of the OTM Confederated International Conferences, CoopIS, DOA, and ODBASE 2003, Catania, Italy, 3–7 November 2003; Springer: Berlin/Heidelberg, Germay, 2003; pp. 986–996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).