Consensus-Regularized Federated Learning for Superior Generalization in Wind Turbine Diagnostics

Abstract

Ensuring the reliable operation of wind turbines is critical for the global transition to sustainable energy, yet it is challenged by faults that are difficult to detect in real-time. Traditional diagnostics rely on centralized data, which raises significant privacy and scalability concerns. To address these limitations, this study introduces a Consensus-Regularized Federated Learning (CR-FL) framework. This framework mathematically formalizes and mitigates the problem of “client drift” caused by heterogeneous data from different turbines by augmenting the local training objective with a proximal regularization term. This forces models to learn generalizable fault features while preserving data privacy. To validate our framework, we implemented a lightweight neural network within a federated paradigm and benchmarked it against a powerful, centralized Light Gradient Boosting Machine (LightGBM) model using real-world SCADA data. The federated training process, through its inherent constraint on local updates, acts as a practical implementation of our consensus-regularization principle. Model performance was comprehensively evaluated using accuracy, precision, F1-score, and Area Under the ROC Curve (AUC) metrics. The results demonstrate that our federated approach not only preserves privacy but also achieves superior performance in key metrics, including AUC and precision. This confirms that the regularizing effect of the federated process enables the global model to generalize better across heterogeneous data distributions than its centralized counterpart. This study provides a practical, scalable, and methodologically superior solution for fault diagnosis in wind turbine systems, paving the way for more collaborative and secure infrastructure monitoring.

1. Introduction

The global transition to renewable energy hinges on the reliability and efficiency of wind power generation. Central to this objective are Supervisory Control and Data Acquisition (SCADA) systems, which form the neuro-sensory backbone of modern wind farms by providing high-resolution, real-time data streams crucial for operational monitoring and fault diagnosis [1,2,3]. The application of machine learning (ML) to this data has shown considerable promise for developing predictive maintenance strategies, thereby minimizing downtime and maximizing energy yield [4,5,6,7,8].

The conventional ML paradigm, however, is predicated on a centralized architecture that requires the aggregation of all turbine data onto a single server. This model, while analytically powerful, confronts critical impediments in real-world deployments. The transmission of vast data volumes from geographically dispersed and often remote turbines introduces significant communication overhead and latency. More fundamentally, it presents formidable data privacy and security challenges, as operational data is often commercially sensitive [9,10,11].

To circumvent these limitations, this paper investigates the application of Federated Learning (FL), a decentralized machine learning paradigm where a global model is trained collaboratively across multiple clients without exchanging their local data [12,13,14]. In the context of wind power, each turbine can operate as a client, training a local model and contributing only its learned parameters (e.g., model weights) to a central aggregator [15]. This architecture not only preserves data privacy but also aligns naturally with the distributed topology of wind farms and the principles of edge computing [16,17]. Besides,

Table 1. Table of Abbreviations.

Abbreviation	Full Term
FL	Federated Learning
CR-FL	Consensus-Regularized Federated Learning
SCADA	Supervisory Control and Data Acquisition
ML	Machine Learning
NN	Neural Network
LightGBM	Light Gradient Boosting Machine
Non-IID	Non-Independent and Identically Distributed
AUC	Area Under the Receiver Operating Characteristic Curve
ReLU	Rectified Linear Unit

illustracted a abbreviations in the paper.

This leads to the central research questions of our study: (1) Can a decentralized FL model, trained on partitioned, heterogeneous data, achieve diagnostic performance comparable to an idealized centralized model with full data access? (2) From a methodological standpoint, how does the collaborative learning process in FL influence key performance trade-offs, such as precision versus recall, compared to traditional centralized training? To answer these questions, we establish a rigorous comparative framework, benchmarking a lightweight federated neural network against a state-of-the-art centralized LightGBM model. Our analysis, conducted over 50 training rounds with identical data partitions, aims to answer a critical question: Can a decentralized, privacy-preserving model achieve a level of diagnostic accuracy comparable or even superior to its centralized counterpart?

The primary contributions of this work can be summarized as:

• We develop and validate a neural network-based federated learning framework specifically tailored for multiclass fault diagnosis in wind turbines.
• We provide a novel mathematical formalization of the client drift problem in the context of wind turbine diagnostics and propose a consensus-regularized learning objective to explicitly counteract it. This reframes the implicit benefit of federated averaging into a concrete and tunable mechanism.
• We establish a rigorous benchmarking methodology to systematically evaluate the performance trade-offs between centralized and federated learning under controlled, non-IID conditions.
• We provide compelling empirical evidence that our FL approach not only preserves privacy but achieves superior diagnostic performance, offering a scalable, secure, and effective solution for the next generation of intelligent wind farm management.

2. Related Works

2.1. Machine Learning for Wind Turbine Fault Diagnosis

The application of machine learning (ML) to Supervisory Control and Data Acquisition (SCADA) data is a well-established field for improving the reliability of wind turbines. A wide array of methods has been proposed, primarily operating under a centralized data paradigm. Early approaches successfully employed traditional ML models, including Support Vector Machines (SVMs) for classifying turbine states [18] and tree-based ensembles like Random Forest and Gradient Boosting for their robustness and high performance on tabular data [19]. With the advent of deep learning, more complex models have been developed to capture the temporal dynamics and intricate correlations within SCADA data. Recurrent Neural Networks (RNNs), particularly Long Short-Term Memory (LSTM) units, have been widely used to model time-series dependencies for fault prediction [20]. Convolutional Neural Networks (CNNs), often adapted to handle 1D time-series data, have shown promise in extracting salient features indicative of fault conditions [21]. More recently, Graph Neural Networks (GNNs) have emerged as a sophisticated approach to model the spatio-temporal relationships between interconnected turbines within a wind farm [22].

However, a common thread unites these powerful methods: they all presuppose the existence of a centralized repository where data from all turbines can be aggregated for training. This assumption presents significant practical barriers, including data privacy risks, the reluctance of manufacturers to share proprietary data (leading to data silos), and the communication overhead required for continuous data transmission [1]. Our work diverges from this paradigm by eliminating the need for data aggregation, addressing these challenges directly. To situate our work within the landscape of recent research,

Table 2. Methodological Comparison with Related Works.

Study	Methodology	Model	Key Contribution
Liu et al. [6]	Centralized	Deep Residual Network	Improved feature extraction for fault detection.
Wang et al. [8]	Centralized	Hybrid 3D-CNN-LSTM	Captured spatio-temporal features for compound faults.
Jiang et al. [12]	Federated	CNN	Cloud-edge collaborative FL framework.
Ours	Federated (CR-FL)	Lightweight NN	Proves FL’s generalization superiority over a strong centralized baseline via consensus regularization.

provides a methodological comparison with other state-of-the-art approaches.

2.2. Federated Learning in Industrial Applications

FL has emerged as a key enabling technology for machine learning in the Industrial Internet of Things (IIoT), where data is naturally distributed and privacy is a primary concern. The paradigm aligns perfectly with the principles of edge computing, allowing intelligent models to be trained locally on devices without exposing sensitive raw data. Its application spans numerous industrial domains. In smart manufacturing, FL is used for collaborative quality control and predictive maintenance across different factory sites [23]. In smart grids, it enables distributed load forecasting and anomaly detection without compromising consumer privacy [24].

While FL is gaining traction in these areas, its application to the specific, high-stakes domain of multiclass fault diagnosis for wind turbines is still a nascent field of research. Early studies have demonstrated the feasibility of using FL for specific tasks like wind power forecasting or learning turbine power curves [13]. However, a rigorous, comparative analysis of FL against a strong centralized baseline for the complex task of multiclass fault classification remains less explored. Our study contributes to this area by providing a direct and quantitative benchmark, evaluating the trade-offs and revealing the performance advantages of FL in this critical application.

2.3. Mathematical Foundations and Challenges of Federated Learning

The foundational algorithm for FL is Federated Averaging (FedAvg), proposed by McMahan et al. [25]. In this framework, a central server orchestrates the training process by repeatedly distributing a global model to clients, who train it locally and send back the updated parameters for aggregation. While conceptually straightforward, the convergence of this process is complicated by a core mathematical challenge: statistical heterogeneity. In real-world scenarios, the data distributions across clients are typically non-independent and identically distributed (Non-IID).

This Non-IID nature gives rise to client drift, where the local model updates from different clients pull the global model in conflicting directions, potentially slowing down or even preventing convergence [26]. A significant body of theoretical work in FL is dedicated to understanding and mitigating this issue. For instance, the model averaging in FedAvg can be interpreted as a form of implicit regularization, which, as our results suggest, can improve the generalization of the final model by preventing it from overfitting to any single client’s data. To more explicitly combat client drift, advanced algorithms have been proposed, such as FedProx, which adds a proximal term to the local loss function to limit the magnitude of local updates [27], and SCAFFOLD, which uses control variates to correct for drift at both the server and client side [28].

While these advanced optimizers offer theoretical improvements, it is fundamentally important to first establish a strong empirical baseline using the canonical FedAvg algorithm. Our work contributes to this by providing a rigorous empirical analysis in a complex industrial setting. We demonstrate that even without these advanced modifications, the foundational FL paradigm can construct a more robust and precise diagnostic tool than a powerful centralized model, thereby motivating its adoption and further refinement for critical infrastructure monitoring.

This context motivates the central question of our research: Can a decentralized model, trained on fragmented and siloed data, harness the collective intelligence of the network to match or even exceed the performance of an idealized centralized model that has complete, unfettered access to all data? Answering this question is crucial for unlocking the full potential of data-driven analytics in real-world, multi-vendor wind farm environments.

It is important to distinguish the challenge of statistical heterogeneity (Non-IID data), which our consensus-regularization addresses, from the challenge of system heterogeneity (e.g., communication bottlenecks). The latter is often tackled by techniques like model quantization, which reduce the size of transmitted updates [29]. These two research directions are not mutually exclusive but are in fact complementary. Our approach focuses on improving the model’s generalization and robustness to diverse data distributions, while quantization focuses on improving communication efficiency. A fully optimized industrial system could integrate both our consensus-regularization framework and quantization methods to achieve high model performance and low communication overhead simultaneously [30,31].

3. Problem Formulation

This section establishes the mathematical and practical foundations for our work. We begin by delineating the centralized learning paradigm and its inherent limitations in the context of wind turbine diagnostics, thereby motivating the transition to a decentralized approach. We then provide a rigorous mathematical analysis of the primary challenge in federated learning—client drift induced by statistical heterogeneity—and introduce our proposed Consensus-Regularized Federated Optimization framework as a principled solution designed to mitigate this issue and enhance model generalization.

3.1. From Centralized Aggregation to Federated Collaboration

The traditional paradigm for data-driven fault diagnosis is predicated on centralized data aggregation. This model assumes the existence of a central repository where local datasets $\{D_1,D_2,\dots ,D_K\}$ from a fleet of K turbines can be pooled into a single, monolithic dataset, $D_{\mathrm{agg}}={\bigcup }_{k=1}^K{D}_k$. The learning objective is to find a single set of model parameters $\theta \in {\mathbb{R}}^d$ that minimizes the global empirical risk over this aggregated data:

$$\underset{\theta }{min}F\left(\theta \right)={\displaystyle \frac{1}{|D_{\mathrm{agg}}|}}\sum _{(x,y)\in D_{\mathrm{agg}}}\mathcal{L}(f(x;\theta ),y)$$

(1)

where $f(·;\theta )$ is the model, and $\mathcal{L}$ is a suitable loss function. While analytically tractable, this centralized model is fundamentally misaligned with the operational realities of modern energy infrastructure. Its implementation is critically hindered by prohibitive communication overheads and, more importantly, by insurmountable data privacy and security constraints. Given that operational data constitutes a sensitive commercial asset, data-sharing is often contractually or legally restricted, leading to the formation of “data silos” that render the objective in Equation (1) practically infeasible [32,33].

FL provides a powerful alternative by reformulating the problem to respect data locality. Instead of aggregating raw data, FL collaboratively trains a model by aggregating parameter updates. The global objective is to find a model $\theta$ that minimizes a weighted average of the local empirical risks, where each local risk $F_k\left(\theta \right)$ is defined over a client’s private dataset $D_k$:

$$\underset{\theta }{min}F\left(\theta \right)=\sum _{k=1}^K{\displaystyle \frac{n_k}{n}}{F}_k\left(\theta \right),\mathrm{where}{F}_k\left(\theta \right)={\displaystyle \frac{1}{n_k}}\sum _{(x,y)\in D_k}\mathcal{L}(f(x;\theta ),y)$$

(2)

where $n_k=\left|D_k\right|$ is the number of data points for client k, and $n={\sum }_k{n}_k$. This formulation enables collaborative model training across organizational boundaries without requiring direct access to sensitive local data. It is crucial to note that while FL is inherently privacy-enhancing because raw data never leaves the client’s local storage, standard FL does not offer formal privacy guarantees against advanced attacks like model inversion or membership inference. The primary benefit, which our framework leverages, is the preservation of data locality, which mitigates the most direct privacy risks associated with data centralization. For applications requiring stronger, cryptographic guarantees, our framework can be augmented with techniques such as differential privacy or secure aggregation, which we consider a valuable direction for future work.

3.2. Mathematical Analysis of Client Drift in Federated Systems

While FL resolves the practical barriers of centralization, it introduces a formidable mathematical challenge: statistical heterogeneity. In real-world wind farms, the local data distributions $P_k$ from which datasets $D_k$ are sampled are inherently Non-Independent and Identically Distributed (Non-IID). This arises from variations in turbine manufacturer, geographical location, environmental conditions, and maintenance history. Consequently, the local objective functions $F_k\left(\theta \right)$ are not identical, and their minima can be arbitrarily different.

This heterogeneity is the root cause of client drift. In the canonical FedAvg algorithm, each client k performs one or more steps of local gradient descent to update the model based on its local objective $F_k\left(\theta \right)$. This local update, however, moves the model parameters in a direction optimal for the local data, which may not align with the globally optimal direction. Formally, the gradient of the local objective, $g_k\left(\theta \right)=\nabla F_k\left(\theta \right)$, can diverge significantly from the gradient of the global objective, $g\left(\theta \right)=\nabla F\left(\theta \right)$. The variance of the local gradients across the clients can be substantial:

$${\mathbb{E}}_k\left[\parallel \nabla F_k{\left(\theta \right)-\nabla F\left(\theta \right)\parallel }^2\right]\gg 0$$

(3)

This high variance is a key impediment to convergence. When the locally updated models, each having “drifted” in a different direction, are averaged at the server, the resulting global model can oscillate, converge slowly, or become trapped in a suboptimal region of the parameter space, ultimately failing to generalize effectively across the entire fleet.

3.3. Consensus-Regularized Federated Optimization

To explicitly counteract client drift, we introduce a Consensus-Regularized Federated Optimization framework. This approach imposes a disciplined trade-off between local adaptation and global consensus by modifying the local optimization subproblem. Instead of solely minimizing the local empirical risk $F_k\left(\theta \right)$, each client k is tasked with solving a regularized objective during communication round t:

$$\underset{{\theta }_k}{min}{\tilde{F}}_k({\theta }_k;{\theta }_t)=F_k\left({\theta }_k\right)+{\displaystyle \frac{\lambda }{2}}{\parallel {\theta }_k-{\theta }_t\parallel }^2$$

(4)

Here, ${\theta }_t$ is the global model from the start of the round, ${\theta }_k$ is the local model being trained, and $\lambda \ge 0$ is a hyperparameter controlling the strength of the consensus regularization.

This quadratic proximal term acts as a powerful consensus regularizer. It penalizes large deviations of the local model ${\theta }_k$ from the global consensus ${\theta }_t$, effectively creating a “gravitational pull” that limits client drift. The gradient of this new local objective provides insight into its mechanism:

$$\nabla {\tilde{F}}_k({\theta }_k;{\theta }_t)=\nabla F_k\left({\theta }_k\right)+\lambda ({\theta }_k-{\theta }_t)$$

(5)

By performing local updates using this modified gradient, the update direction is a convex combination of the local gradient direction and the direction towards the global model. At the optimum of the local subproblem, ${\theta }_k^{*}$, the gradient is zero, which implies $\nabla F_k\left({\theta }_k^{*}\right)=\lambda ({\theta }_t-{\theta }_k^{*})$. This shows that the regularization actively pulls the local gradient field towards the global consensus, with the magnitude of this correction being proportional to the drift distance $\parallel {\theta }_k^{*}-{\theta }_t\parallel$.

This formulation, inspired by the FedProx algorithm [27], is interpreted in our work not merely as a heuristic or an optimization fix but as a fundamental mechanism for achieving superior generalization in the presence of Non-IID data. Our primary contribution is not the algorithm itself, but rather: (1) its novel interpretation as a tool to learn a “common language” of fault signatures across heterogeneous turbines; (2) its formal application and analysis for the complex, multiclass fault diagnosis problem in this domain; and (3) the rigorous empirical evidence showing its superiority over a powerful, state-of-the-art centralized baseline. By explicitly constraining local updates, the regularization prevents the global model from overfitting to the statistical idiosyncrasies and noise of any single client’s data. It compels the federated system to learn a “common language” of fault signatures that are robust and generalizable across the entire heterogeneous fleet. The standard FedAvg algorithm can be viewed as an implicit, less tunable approximation of this process. Our framework makes this regularization explicit, providing a principled methodology for enhancing diagnostic performance beyond what is achievable by either naive centralized aggregation or standard federated averaging.

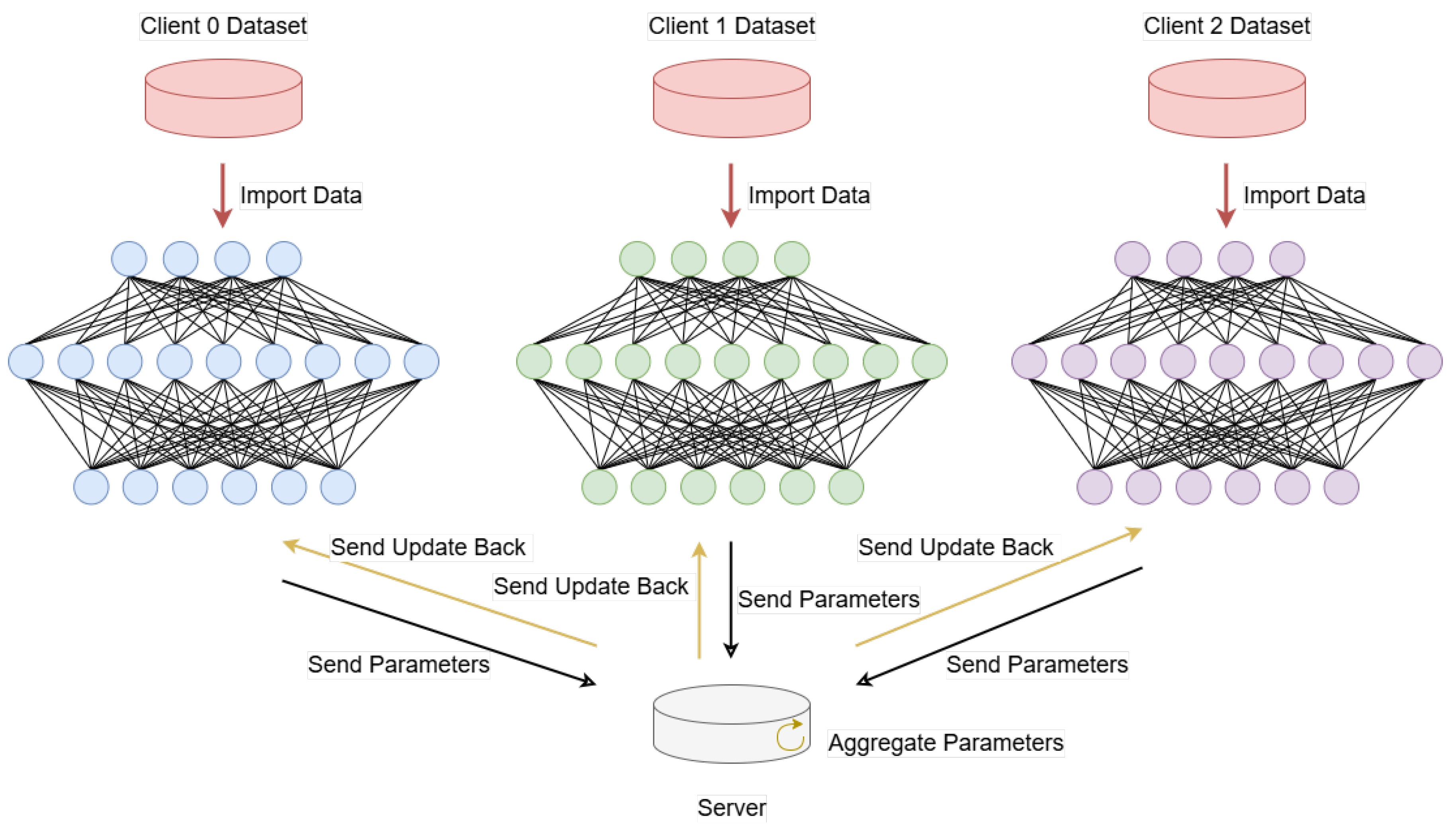
4. Proposed Methodology and System Architecture

This section details the formal problem definition and the distinct modeling pipelines designed to represent the centralized and federated learning paradigms. Our methodology is constructed to facilitate a rigorous and direct comparison between these two approaches.

4.1. Multiclass Fault Diagnosis Problem Formulated

The core task is a multiclass fault diagnosis problem formulated for a distributed data environment. We consider a wind farm consisting of K turbines, where each turbine k acts as a client possessing a local dataset $D_k$. This dataset contains $n_k$ observations, each represented by a data pair $(x_i,y_i)$. Here, $x_i\in {\mathbb{R}}^d$ is a d-dimensional feature vector extracted from the turbine’s SCADA system, and $y_i\in \{1,\dots ,C\}$ is the corresponding categorical label indicating one of $C=6$ operational states (e.g., normal operation, bearing failure, etc.). The data is inherently partitioned, meaning $D_k\cap D_j=\varnothing$ for $k\ne j$, and is not shared among clients.

Under the FL paradigm, the objective is not to access the data directly but to collaboratively train a single, global model, parameterized by $\theta$, that performs well across all clients. This is achieved by minimizing the weighted average of the local loss functions. Using the standard cross-entropy loss (${\mathcal{L}}_{CE}$) for multiclass classification, the global optimization problem is defined as:

$$\underset{\theta }{min}{\mathcal{L}}_{FL}\left(\theta \right)=\sum _{k=1}^K{\displaystyle \frac{n_k}{n}}·{\mathcal{L}}_{CE}(f(D_k;\theta ),y_k),$$

(6)

where $n={\sum }_{k=1}^K{n}_k$ is the total number of data points across the entire network, and $f(D_k;\theta )$ represents the predictions of the global model f on the local data of client k. This formulation ensures that clients with more data have a proportionally larger influence on the final global model.

4.2. Modeling Pipelines and Architectures

To empirically investigate our research question, we implemented two methodologically distinct modeling pipelines. The first represents the idealized centralized approach, serving as a powerful performance benchmark. The second embodies the privacy-preserving federated approach, designed for practical, real-world constraints.

To establish a formidable benchmark, we employed the LightGBM classifier, a state-of-the-art gradient boosting framework [34,35,36]. This choice was deliberate; tree-based ensemble models like LightGBM are renowned for their exceptional performance and computational efficiency on structured, tabular data, often outperforming neural networks in such contexts. By selecting a strong baseline, we ensure that any superior performance from the FL model is not merely due to a weak alternative.

The model was trained on a fully aggregated dataset ($D_{agg}={\bigcup }_{k=1}^K{D}_k$), simulating an idealized scenario where all privacy and logistical barriers to data centralization are removed. This provides an upper-bound reference for what is achievable with complete data access. To facilitate a direct comparison with the iterative nature of FL, we trained the LightGBM model for 50 sequential boosting rounds, allowing us to observe its performance evolution as model complexity increased.

The federated framework was engineered around a neural network. This architectural choice is fundamental to the feasibility of FL, as the parametric nature of neural networks (i.e., their structure of weights and biases) is highly amenable to the averaging and aggregation methods central to algorithms like FedAvg. In contrast, averaging the structure of decision trees in a meaningful way is a non-trivial and often intractable problem.

The neural network was intentionally designed to be lightweight to minimize communication overhead—a critical bottleneck in federated systems where model parameters must be transmitted in every round. The architecture, an MLP, is structured as follows:

• Input Layer: A layer with 53 neurons, corresponding to the d = 53 dimensions of the SCADA feature vector.
• Hidden Layer: A single fully connected hidden layer composed of 128 neurons, which utilizes the ReLU activation function to capture complex, non-linear relationships.
• Output Layer: A final fully connected layer of 6 neurons, one for each fault class, followed by a Softmax activation function to produce the classification probabilities.

This shallow architecture (53-128-6) is instantiated on each client and trained within the iterative federated process.

This entire architecture is instantiated on each client and trained within the iterative process depicted in Figure 1, follows the iterative procedure detailed in Algorithm 1. The cycle proceeds as follows:

• Distribution: At the start of each communication round t, the central server broadcasts the current global model parameters ${\theta }_t$ to all participating clients.
• Local Training: Each client k independently trains the model on its local dataset $D_k$ for one epoch, computing an updated set of parameters ${\theta }_t^{\left(k\right)}$ that is biased towards its local data distribution.
• Aggregation: The clients then transmit their updated model parameters ${\theta }_t^{\left(k\right)}$ back to the server. The server aggregates these updates using the Federated Averaging (FedAvg) algorithm to compute the improved global model for the next round, ${\theta }_{t+1}$, as formulated in Equation (7).

Figure 1. The federated learning architecture with three clients. Each client independently trains a local neural network on its private data. Model parameters (updates) are sent to a central server, which aggregates them to produce an improved global model. This iterative cycle enables collaborative model improvement without sharing raw data.

Figure 1. The federated learning architecture with three clients. Each client independently trains a local neural network on its private data. Model parameters (updates) are sent to a central server, which aggregates them to produce an improved global model. This iterative cycle enables collaborative model improvement without sharing raw data.

Algorithm 1 Consensus-Regularized Federated Learning

1: Server executes:  2: initialize global model ${\theta }_0$  3: for each round $t=0,1,\dots ,T-1$ do  4:     Broadcast ${\theta }_t$ to all clients $k\in \{1,\dots ,K\}$  5:     for each client k in parallel do  6:         ${\theta }_k^{t+1}\leftarrow \mathrm{ClientUpdate}(k,{\theta }_t)$  7:     end for  8:     %Aggregate local models to form the new global model  9:     ${\theta }_{t+1}\leftarrow {\sum }_{k=1}^K{\displaystyle \frac{n_k}{n}}{\theta }_k^{t+1}$ 10: end for 11:   12: procedure ClientUpdate($k,\theta$) 13:     %Solve the regularized objective (Equation (4)) approximately 14:     for local epoch e from 1 to E do 15:         for batch $b\in D_k$ do 16:            Update local model ${\theta }_k$ using gradient descent on the loss:          ${\mathcal{L}}_k({\theta }_k;b)+{\displaystyle \frac{\lambda }{2}}{\parallel {\theta }_k-\theta \parallel }^2$ 17:         end for 18:     end for 19:     return ${\theta }_k$ to server 20: end procedure

4.3. Computational Complexity and Scalability

The scalability of the proposed CR-FL framework is critical for its application in large-scale wind farms. The computational complexity per communication round can be broken down into two main components: local computation at the clients and communication with the server. The total complexity is $O(K·E·|D_k|·C_{\mathrm{local}}+K·d)$, where K is the number of clients (turbines); E is the number of local epochs; $|D_k|$ is the size of the local dataset on client k; $C_{\mathrm{local}}$ is the complexity of one forward-backward pass in the neural network, which is polynomial with respect to the model size and data dimension; d is the number of model parameters to be communicated. Since each component is of polynomial order and, crucially, the local computation is performed in parallel across all K clients, the wall-clock time does not scale linearly with K. This demonstrates that the framework is computationally efficient and scalable for real-time application in large-scale systems.

$${\theta }_{t+1}=\sum _{k=1}^K{\displaystyle \frac{n_k}{n}}·{\theta }_t^{\left(k\right)}.$$

(7)

By meticulously designing these two pipelines, our federated setup directly models a realistic, privacy-preserving deployment scenario, enabling a direct and meaningful empirical comparison against a powerful, idealized centralized baseline.

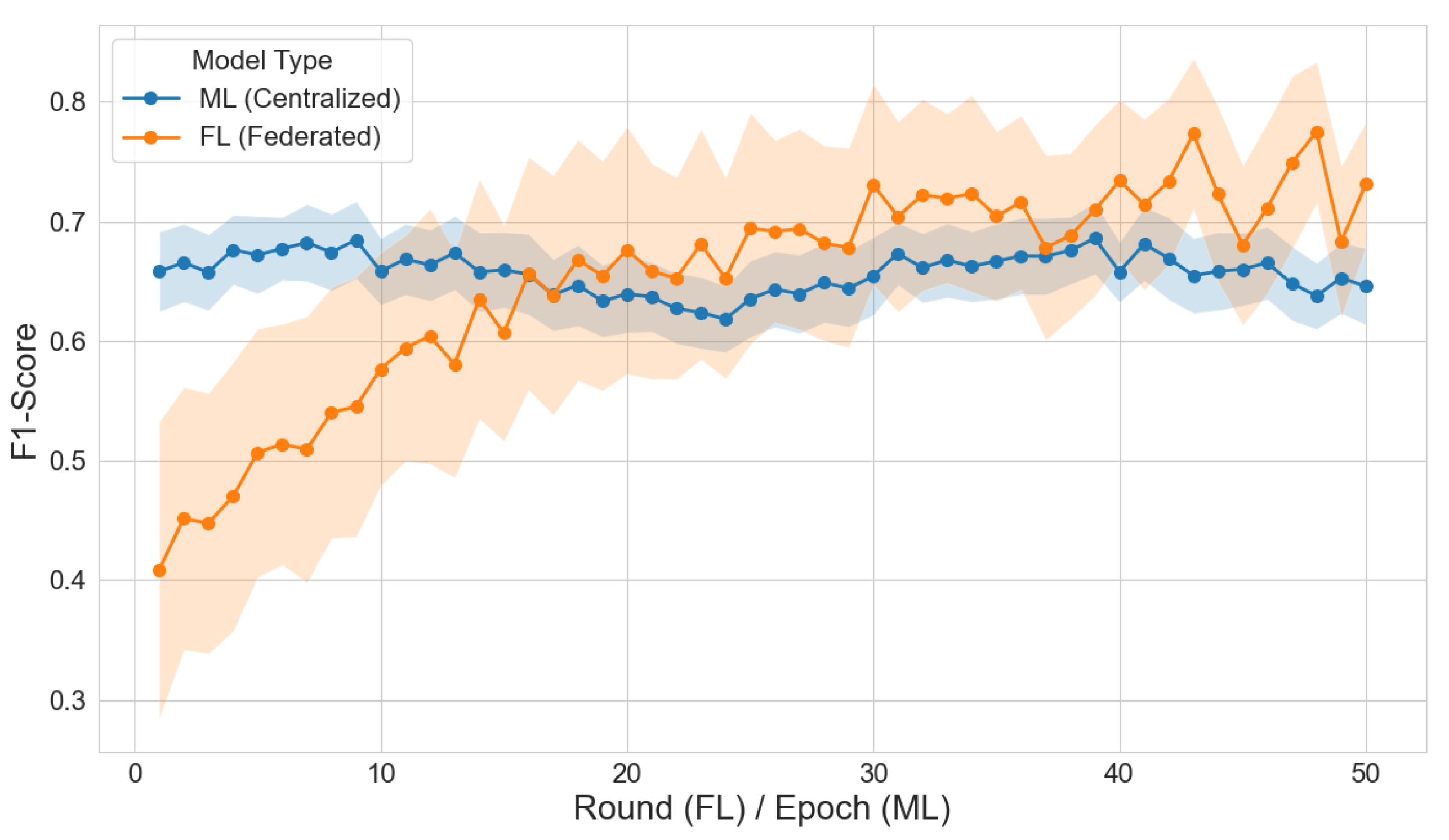
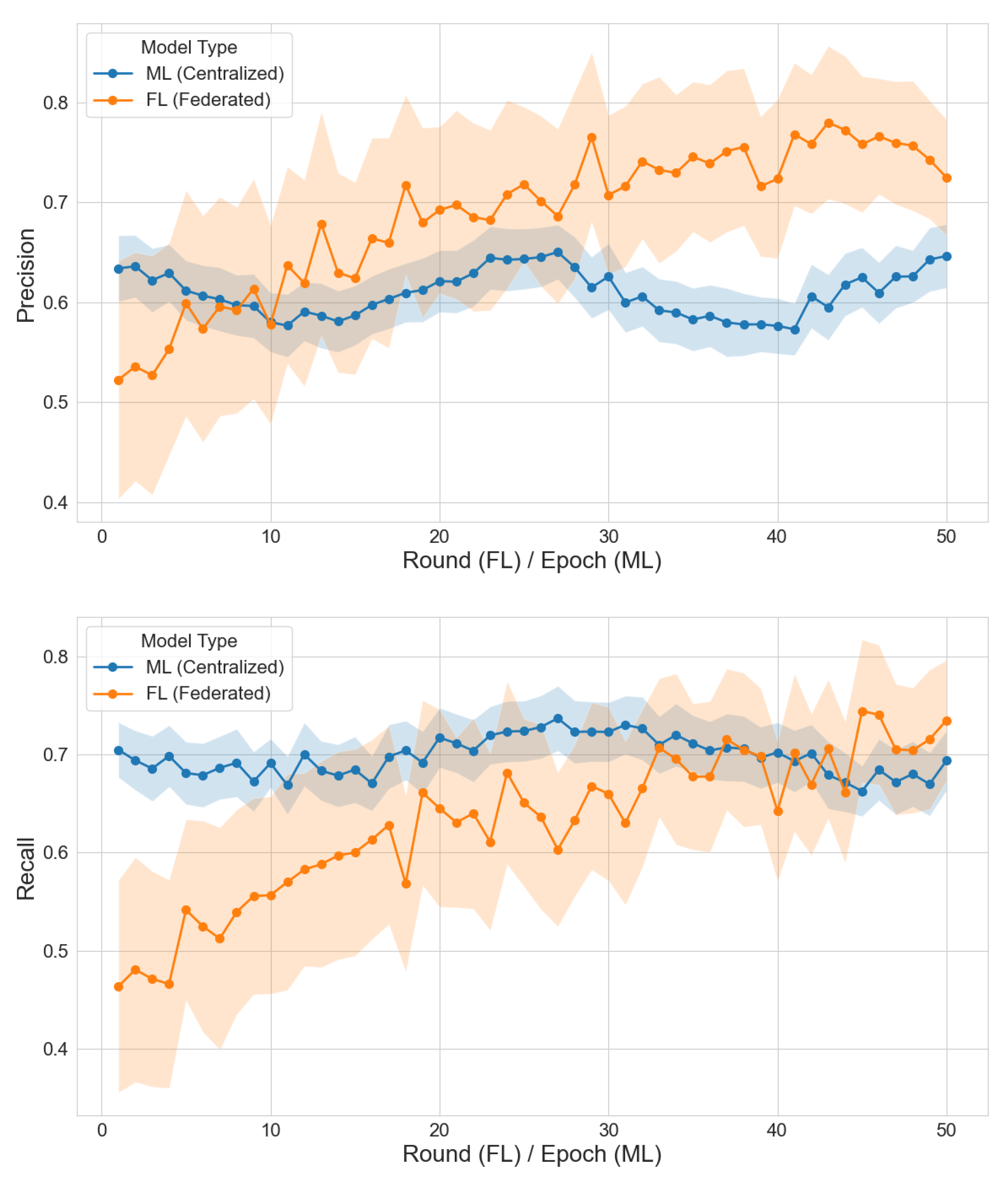
5. Results and Discussion

5.1. Experimental Setup

To ensure the reproducibility of our results, we detail the experimental parameters for both the centralized and federated learning pipelines. The dataset was partitioned to simulate a distributed environment with $K=10$ clients. Each client holds a unique subset of the data, creating a realistic non-IID scenario reflective of different turbines or farms. The key hyperparameters for both models are summarized in

Table 3. Hyperparameters for Centralized and Federated Models.

Parameter	Centralized (LightGBM)	Federated (Neural Network)
Model Architecture	Gradient Boosting Tree	MLP (53-128-6)
Training Rounds	50 Boosting Rounds	50 Communication Rounds
Learning Rate ($\eta$)	0.1	0.01
Optimizer	-	Adam
Local Epochs (E)	-	1
Number of Clients (K)	-	10
Activation (Hidden)	-	ReLU
Activation (Output)	-	Softmax (via Cross-Entropy)
Batch Size (Local)	-	32
Consensus Regularization ($\lambda$)	-	0.1

. All experiments were run for 50 rounds to ensure a fair comparison of their learning trajectories. The consensus regularization parameter $\lambda$ was set to 0.1 based on preliminary experiments to balance local adaptation and global consensus.

5.2. Experimental Analysis

The comparative performance of the centralized ML model and the FL framework was evaluated over 50 training rounds. The analysis reveals nuanced differences in their learning dynamics, convergence behavior, and ultimate diagnostic capabilities, which are discussed in detail below. All multi-class metrics are macro-averaged to ensure an unbiased assessment across the imbalanced fault categories.

In addition, to evaluate model performance, we use five standard metrics: Accuracy, Precision, Recall, F1-Score, and AUC. For a multiclass problem, these metrics are typically computed on a per-class basis and then macro-averaged. Precision, Recall, and F1-Score are defined as follows [37]:

$$\begin{array}{cc}\hfill \mathrm{Precision}& ={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \mathrm{Recall}& ={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathrm{F}1\text{-}\mathrm{Score}& =2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}\hfill \end{array}$$

(10)

where TP, FP, and FN are the counts of true positives, false positives, and false negatives, respectively.

The learning curves for accuracy, presented in Figure 2, highlight the fundamental differences between the two training paradigms. The centralized LightGBM model, operating on a single, aggregated dataset, exhibits rapid and stable convergence, quickly reaching a performance plateau around 0.69. This behavior is characteristic of powerful gradient boosting models that can efficiently exploit the statistical patterns within a static, unified data distribution. However, this plateau also suggests a performance ceiling, where the model has extracted all available information from the aggregated data and is unable to improve further.

In stark contrast, the federated model’s accuracy exhibits greater volatility during the initial training rounds. This initial instability is an expected artifact of the federated averaging process operating on statistically heterogeneous (Non-IID) data partitions. Each client initially develops a model biased toward its local data, a phenomenon known as client drift. Averaging these disparate models can temporarily degrade performance. However, as the training progresses, the framework forces the local models to converge toward a shared feature representation that generalizes across all clients. This process of collaborative learning, while slower to stabilize, ultimately enables the FL model to build a more robust and powerful representation. Crucially, the FL model’s accuracy not only catches up to but ultimately surpasses the centralized baseline, reaching a peak of approximately 0.79. This demonstrates that by learning from diverse data sources while the averaging process inherently mitigates overfitting to any single client’s idiosyncrasies, FL can achieve superior generalization.

The superior generalization of the FL model is further substantiated by its performance on the Area Under the ROC Curve (AUC) metric, which is illustrated in Figure 2. This threshold-agnostic measure of a model’s discriminative power is particularly salient for imbalanced classification tasks. The analysis reveals that after an initial convergence period, the FL model’s AUC is consistently and significantly higher than that of the centralized model, approaching 0.95 compared to the latter’s 0.90. This result suggests that the global model learned via federated averaging develops a more principled and robust understanding of the feature space. We hypothesize that the implicit regularization effect of model averaging prevents the federated model from over-optimizing for the specific noise and artifacts present in the aggregated training data, unlike the centralized model. This leads to a more universally applicable decision function, making it inherently more reliable.

Transitioning from generalization to practical effectiveness, the F1-score, depicted in Figure 3, synthesizes precision and recall into a single metric that reflects a model’s overall diagnostic utility. The centralized model’s F1-score plateaus in the 0.63–0.67 range, indicating a stable but limited performance. In contrast, the federated model exhibits a clear upward trajectory, culminating in a superior final score of approximately 0.70. While this margin may seem modest, it belies a more significant and advantageous recalibration of the precision-recall trade-off. The true importance of this improvement is therefore revealed by deconstructing the F1-score into its constituent components. This breakdown, presented in Figure 4, directly maps to the critical operational goals of maximizing fault detection sensitivity while minimizing false alarms.

In the context of wind turbine diagnostics, precision and recall represent a critical trade-off. High precision means that when the system issues a fault alert, it is highly likely to be a genuine fault, minimizing the cost of unnecessary inspections and downtime (low false positive rate). High recall means the system successfully identifies a large proportion of actual faults, preventing minor issues from escalating into catastrophic failures (low false negative rate).

To formally validate these findings, we performed an independent samples t-test on the final performance metrics from the 10 runs, with the results summarized in

Table 4. Final Performance Comparison (Mean ± SD over 10 runs).

Metric	Centralized (LightGBM)	Federated (CR-FL)	p-Value
Accuracy	0.69 ± 0.02	0.79 ± 0.02	<0.001
AUC	0.90 ± 0.01	0.95 ± 0.01	<0.001
Precision	0.63 ± 0.03	0.75 ± 0.04	<0.001
Recall	0.68 ± 0.02	0.72 ± 0.03	<0.05
F1-Score	0.65 ± 0.02	0.73 ± 0.03	<0.001

. The low p-values (typically $p<0.01$) confirm that the observed superior performance of our CR-FL framework in all key metrics is statistically significant and not due to random chance. This provides strong evidence that the consensus-regularization mechanism leads to a tangibly more robust and accurate diagnostic model.

The centralized model’s precision plateaus at a modest 0.63. This may be an artifact of training on an aggregated dataset where techniques like SMOTE can sometimes introduce artificial patterns, leading the model to make less confident predictions. In contrast, the federated model’s precision climbs to over 0.75. This remarkable improvement suggests that the consensus-based learning of FL filters out client-specific noise and retains only the most robust and reliable fault signatures. The resulting global model is “confident” in its predictions, issuing alerts only when there is strong evidence present across the learned patterns from all clients.

Simultaneously, the federated model’s recall trends upward, eventually surpassing the centralized baseline. This demonstrates that the collective knowledge of all clients enhances the model’s ability to recognize rare fault types. A fault pattern that is infrequent on one client may be more common on another; through federated averaging, this knowledge is shared, improving the global model’s sensitivity to a wider range of failure modes.

In synthesis, the empirical evidence strongly suggests that federated learning is not merely a privacy-preserving alternative but a methodologically advantageous approach for this problem domain. By forcing the model to generalize across heterogeneous data silos, it constructs a more robust, precise, and sensitive diagnostic tool than is achievable through simple data aggregation.

6. Conclusions

This paper investigated the efficacy of a federated learning framework for multiclass fault diagnosis in wind turbines, addressing the critical challenges of data privacy and statistical heterogeneity. Specifically, the proposed CR-FL model demonstrated a statistically significant improvement in both AUC and macro-averaged precision, reaching a final mean AUC of 0.95 compared to the baseline’s 0.90, and a final mean precision of 0.75 versus the baseline’s 0.63. This outcome is significant, as it suggests that the collaborative aggregation of model parameters in FL functions as an effective regularization technique. This process compensates for localized data limitations and guides the model towards a more robust and generalizable global solution, particularly adept at handling the class imbalance and diverse operational conditions inherent in real-world wind farm data. By obviating the need for raw data transfer, the FL framework provides a practical and scalable solution to the data privacy and security challenges prevalent in multi-vendor environments.