Elastic Curves and Euler–Bernoulli Constrained Beams from the Perspective of Geometric Algebra

Abstract

Elasticity is a well-established field within mathematical physics, yet new formulations can provide deeper insight and computational advantages. This study explores the geometry of two- and three-dimensional elastic curves using the formalism of geometric algebra, offering a unified and coordinate-free approach. This work systematically derives the Frenet, Darboux, and Bishop frames within the three-dimensional geometric algebra and employs them to integrate the elastica equation. A concise Lagrangian formulation of the problem is introduced, enabling the identification of Noetherian, conserved, multi-vector moments associated with the elastic system. A particularly compact form of the elastica equation emerges when expressed in the Bishop frame, revealing structural simplifications and making the equations more amenable to analysis. Ultimately, the geometric algebra perspective uncovers a natural correspondence between the theory of free elastic curves and classical beam models, showing how constrained theories, such as Euler–Bernoulli and Kirchhoff beam formulations, arise as special cases. These results not only clarify foundational aspects of elasticity theory but also provide a framework for future applications in continuum mechanics and geometric modeling.

1. Introduction

Elasticity is a mature branch of mathematical physics. The foundations of non-linear beam models date back to Euler’s elastica, which describes planar beams undergoing bending deformations, and were later extended by Kirchhoff to spatial beams also exhibiting torsional deformations. The elastica theory is one of the oldest branches of analytical mechanics, which can be traced back to the works of the Bernoulli brothers and Leonard Euler.

The elastica theory exhibits links to other physical disciplines. For example, Hasimoto discovered special solutions including Euler’s elastica in relation to the non-linear Schrödinger equation [1]. Tsuru also found special solutions of elastic rods in three-dimensional space in relation to the local induction equation [2]. Fukumoto investigated the relations between vortex filaments and elastic rods [3]. The Euler elastica is also connected to the modified Korteweg–de Vries (mKdV) equation through the geometric evolution of curves (see, for example, [4]). In particular, when an elastica is interpreted as a planar curve whose tangent angle evolves under certain geometric flows, the angle function can satisfy the mKdV equation. This connection becomes explicit in the framework of integrable systems, where the stationary solutions of the mKdV correspond to shapes of constant elastic energy. Furthermore, the filament or vortex filament equations, when projected onto a plane or constrained to elastic curves, lead to formulations where the curvature evolves according to variants of the mKdV equation, such as the focusing or sine-modified KdV (FSMKdV) equation. Thus, the Euler elastica emerges as a natural geometric context in which the FSMKdV arises as a governing equation for the deformation of elastic curves.

The closed-form solutions for the elastica, initially derived by Saalschütz in 1880 [5], rely on the theory of Jacobi’s elliptic functions [6]. A recent account can be found in [7]. Kirchhoff discovered that the equilibrium equations for a straight, prismatic, and unstressed elastic rod are analogous to the equations for a spinning top [8,9]. These results suggest that the kinetic analogy was a useful guideline in obtaining solutions [8]. The classical approach of Love [8] adopted a Lagrangian description, characterizing a filament by contiguous cross-sections that remain undeformed, perpendicular to the rod’s center line, and capable of turning relative to each other. Under the assumptions of Love, static beam theory is equivalent to the description of an elastic curve attached to the center line of the beam, as discussed by Langer and Singer ([10], Corr. 3).

The present contribution will nevertheless offer a different perspective on the study of elastic curves in two and three spatial dimensions. The proposed approach naturally extends to higher-dimensional settings due to the dimensionally co-variant nature of the underlying formalism. As a result, the approach lends itself to a clear and nearly algorithmic generalization for use in higher-dimensional settings. This generality stems from the use of geometric algebra (GA), which provides a coordinate-free framework and enables seamless transitions between coordinate systems, guided by computational convenience.

This paper is also intended to serve as a guide for readers unfamiliar with GA. I try to persuade readers that the GA formalism is no more difficult than the more familiar vector calculus. To this end, several well-known results from the differential geometry of curves are reformulated within the GA framework, as presented in Section 3. For a broader overview of GA and its applications—particularly in physics—readers are referred to the works of Hestenes, Sobczyk [11], Doran, and Lasenby [12].

The main contribution of this paper is a coordinate-free expression of the elastica equation using only the curvature and the local inertial reference frame (i.e., Bishop’s frame) as inputs. The conserved quantities of the theory—Hamiltonian, linear, and angular momentum—are concisely derived based on the Noether theorem and second-order Lagrangian formulation. This paper is organized as follows. Section 2 introduces the main concepts of geometric algebra. Section 3 introduces the Frenet, Gradient, and Bishop frames. Section 4 develops the Euler–Lagrange theory of the elastica. Section 5 presents the main applications of the theory.

2. Geometric Algebra

While Clifford algebra affords mixed signatures, here we restrict the discussion only to algebras with positive signatures, which will be called geometric algebras, i.e., ${\mathbb{G}}^n\equiv C{\ell }_{n,0}$ for the natural number n. The purpose of the present section is to give an extremely brief overview of the geometric algebra. Interested readers are directed to the textbook of MacDonald [13] for a more didactic overview. Clifford algebras are implemented in several Computer Algebra Systems (CAS) to facilitate symbolic and numerical computations in geometric algebra, physics, and engineering. Systems like Maple, Mathematica, and Maxima offer dedicated packages that support multi-vector operations, blade products, and grade projections. One of them has been implemented by the present author [14]. In the following we use the convention of denoting the scalars with Greek letters, the vectors with lowercase Latin letters, and multi-vectors and blades with capital Latin letters.

The planar Euclidean geometric algebra ${\mathbb{G}}^3\equiv C{\ell }_{3,0}\left(\mathbb{R}\right)$ is generated by the set of orthonormal basis vectors $E=\{e_1,e_2,e_3\}$, for which the associative, so-called geometric, product is defined with fundamental properties

$$e_i{e}_i=1$$

(1)

$$e_i{e}_j=-e_j{e}_i,i\ne j$$

(2)

The pseudoscalar is denoted by $I_3=e_{123}$ and commutes with all elements. The structure of the Euclidean algebra can be illustrated in the diagram below, which is produced by the action of the geometric product by the basis vectors.

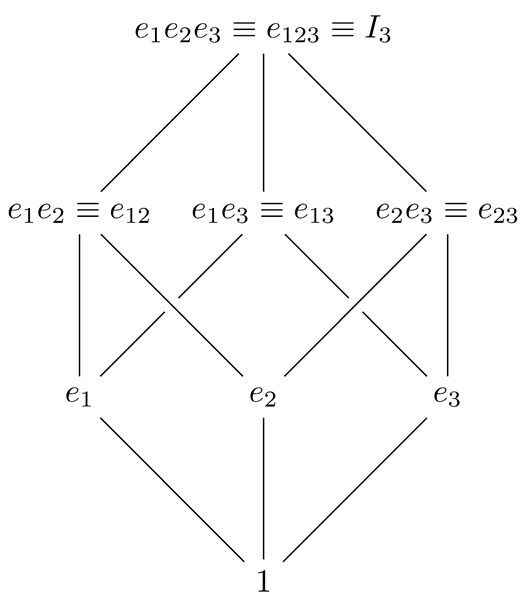
Definition 1.

The term blade will denote an ordered geometric product of basis vectors without index repetition. A blade containing k basis vectors will be called a blade of grade k. Blade composition will be denoted by index concatenation, as written in the diagram above.

From the diagram it can be read off that every row has a different grade and the upper two rows of elements are blades. Moreover, blades can be associated with geometric objects, such as planes and volumes.

A general element of the ${\mathbb{G}}^3$ algebra is written as

$$A=a_0+a_1{e}_1+a_2{e}_2+a_3{e}_3+a_{12}{e}_{12}+a_{13}{e}_{13}+a_{23}{e}_{23}+a_{123}{e}_{123}$$

and contains a scalar $a_0$, vector $A_1=a_1{e}_1+a_2{e}_2+a_3{e}_3$, bi-vector $A_2=a_{12}{e}_{12}+a_{13}{e}_{13}+a_{23}{e}_{23}$, and a pseudoscalar or tri-vector part $a_{123}{e}_{123}$. Blades in the above expression are the bi-vectors $e_{12},e_{13},e_{23}$ and the pseudoscalar $e_{123}$. Basis vectors square to 1, while blades square to −1 (see Appendix A.5). The grade extraction operation will be denoted by ⟨ ⟩_k so that $A_k={⟨A⟩}_k$.

2.1. Products in GA

Besides the fundamental geometric product, the GA formalism features several other products exhibiting useful properties. The geometric product of two vectors can be decomposed into a symmetrical scalar product and an anti-symmetrical wedge product:

$$ab=a\ast b+a\wedge b,a\ast b=b\ast a,a\wedge b=-b\wedge a$$

by the use of the polarization identity. The wedge product is also called "exterior" by some authors. Its properties are designed to match the properties of the exterior product of differential forms.

For higher-dimensional objects, the scalar product is defined simply as the scalar part of the geometric product of multi-vectors:

$$A\ast B:={⟨AB⟩}_0$$

(3)

where the notation ⟨ ⟩_k denotes the part of the multi-vector of grade k.

Furthermore, the wedge product is extended for blade a $A_k$ of grade k ([15], Chapter 1, p. 7) as

$$a\wedge A_k:={\displaystyle \frac{1}{2}}\left(a{A}_k+{(-1)}^k{A}_{k}a\right)$$

(4)

From this definition it is apparent that a blade can also be written as a wedge product of basis vectors as

$$A_k=e_1\wedge e_2\wedge \dots \wedge e_k$$

by the orthogonality of the generators of different indices. For scalars, the exterior product is identified with re-scaling—i.e., $\lambda \wedge a:=\lambda a$ for the scalar $\lambda$.

The interior product, also sometimes called Hestenes contraction (see the discussion in [16]), is an operation defined for multi-vectors as

$$A·B:=\sum _{r,l>0}^n{⟨{⟨A⟩}_r{⟨B⟩}_l⟩}_{|r-l|}$$

(5)

while for scalars $\alpha ·A=0$. Therefore, for vectors $a·b=a\ast b$, as expected from the vector calculus. It is noteworthy also that for any vector and blade ([15], Chapter 1, p. 7), the interior product can be extended as

$$a·A_k={\displaystyle \frac{1}{2}}\left(a{A}_k-{(-1)}^k{A}_{k}a\right)$$

(6)

assuming grade k for the blade $A_k$. The above formula also extends the geometric product decomposition to the products of vectors and blades:

$$a{A}_k=a·A_k+a\wedge A_k$$

(7)

A useful expansion formula for the vector a and blade $A_k$ is the sequential expansion ([15], Chapter 1, p. 7)

$$a·A_k=\sum _{j=1}^k{(-1)}^{j-1}{e}_1\wedge e_2\wedge \dots (a·e_j)\wedge \dots e_k$$

(8)

Another useful expansion formula for the vectors a and b and the blade $A_k$ is

$$(a\wedge b)·A_k=a·(b·A_k),k\ge 2$$

(9)

so that the following holds for the double product: $a·(a·A_k)=0$. In this way, the contraction $a·A_k$ becomes the subspace of $A_k$ orthogonal to a, which is one of the main applications of the contraction operation. It should be noted that unlike the scalar product the contraction is not associative in the general case.

Note that by the linearity of the so-defined products, the formulas also remain valid for generic expressions of a fixed grade k.

The familiar cross product for 3-dimensional space can be expressed as

$$a\times b=-I_3(a\wedge b)$$

(10)

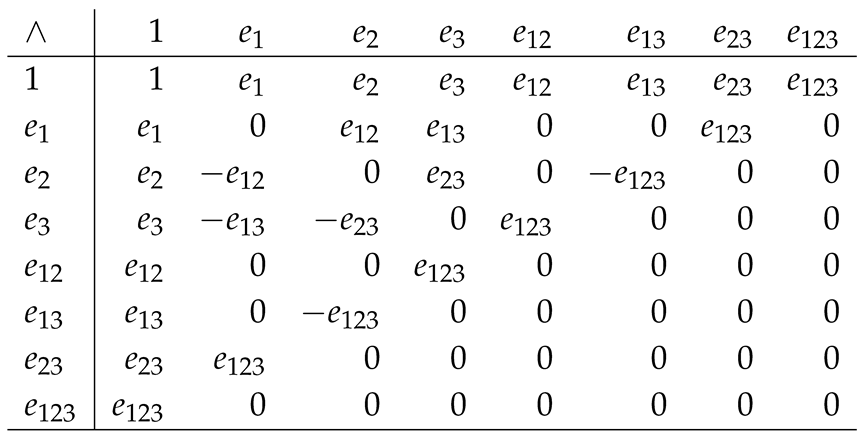
using the pseudoscalar $I_3\equiv e_{123}$. Therefore, all statements for cross products can be expressed in exterior products and vice versa. The distinct types of products in GA can be used to concisely represent geometric objects and operations. Readers are directed to [13] for an introductory exposition. Multiplication tables of geometric, inner, and outer products are presented for the reader’s convenience in Appendix A.5. They are computed using the Clifford package v 2.5 in CAS Maxima [17].

2.2. Principal Automorphisms

Three principle automorphisms can be identified in geometric algebra:

• Vector reflection: $v\mapsto -v$;
• Geometric product reversion: ${\left(ab\right)}^{\sim }:=ba$;
• Inverse blade, or Hermite, automorphism (IBA): $A^{\#}:=A^{-1}$ for the respective blade.

While the first two automorphisms are broadly recognized, the third one is less appreciated. The IBA is obviously defined only for non-nilpotent blades. Technically speaking, the reversion and IBA are anti-automorphisms [18]. For the positive signatures, i.e., in the Euclidean case, the IBA amounts to geometric product reversion $A^{\#}=A^{\sim }$.

2.3. Norm

For Clifford algebras with unspecified signatures, the norm of a multi-vector can be defined as

$$\left|\right|A\left|\right|:=\sqrt{A\ast A^{\#}}$$

(11)

For vectors we have the special case $\left|\right|v\left|\right|=\sqrt{v·v}=\sqrt{v^2}$, which recalls the formula for the absolute value of a scalar. For positive signatures, i.e., for ${\mathbb{G}}^3$, we have the equivalent formula

$$\left|\right|A\left|\right|=\sqrt{A\ast A^{\sim }}$$

This allows one to define the formula for the cosine, and, respectively, the angle, between two blades A and B as

$$cos\angle (A,B)={\displaystyle \frac{A\ast B^{\sim }}{\left|\right|A\left|\right|\left|\right|B\left|\right|}}$$

2.4. Elements of Geometric Calculus

The geometric derivative subsumes the divergence, curl, and gradient operations of the vector calculus. An introduction to the topic can be found in [19]. It is defined in the simplest way, under Einstein’s summation convention, as

$$\nabla f:=e^j{\partial }_{j}f,{\partial }_j\equiv {\displaystyle \frac{\partial }{\partial x_j}}$$

where $e^j$ are the components of the dual or reciprocal basis, such that

$$x=x_i{e}^j=x^i{e}_i$$

for an arbitrary vector x. For the dual basis, $e^i\ast x=x_i$ since $e^i{e}_j=e^i\ast e_j={\delta }_{ij}$, where $\delta$ denotes Kronecker’s symbol.

The geometric derivative is co-ordinate-independent. Moreover, it splits into grade-lowering and grade-increasing parts:

$$\nabla f=\nabla ·f+\nabla \wedge f$$

Therefore, in many cases ∇ can be treated as a vector.

3. Frenet, Gradient, and Inertial Frames in 3D

In the present section, the approach outlined above will be applied to the 3D Euclidean space. Differential geometry can be readily analyzed with the tools provided by geometric algebra. The approach pioneered by Hestenes, Sobczyk, Doran, and Lasenby is to use the shape operator as the main tool for the differential geometry in geometric algebra [11], ([12], Chapter 6), [20]. It uses the tangent vectors on the surface to build the pseudoscalar $I_n\left(x\right)$ at every point from the tangent vectors of the parameter curves on the surface. Although general in nature this approach is not very commonly used and can be simplified for curves and given an explicit form for engineering and physical applications.

In the subsequent discussion we work in ${\mathbb{G}}^3$. The pesudoscalar is denoted by $I_3$ and it commutes with all elements of the algebra. Consider the scalar equation $F(x,y,z)=0$, which defines a surface in 3D. We can also use it to specify a vector field-defining curve embedded in that surface in the following way.

Definition 2.

Define the curve specified by $F(x,y,z)=0$ by the vector field $\gamma \left(s\right)$, for which

$$F(x,y,z)=0\mapsto \gamma \left(s\right):=r{|}_{x=f\left(s\right),y=g\left(s\right),z=h\left(s\right)}=f\left(s\right)e_1+g\left(s\right)e_2+h\left(s\right)e_3$$

for suitable functions $f,g,h$, such that

$$F\left(f\right(s),g(s),h(s\left)\right)=0$$

holds identically.

Considering a curve in the 3D space, there is a parametrization by the length s, such that

$$\left|\right|{\gamma }^{\prime }\left(s\right)\left|\right|=1\Rightarrow s={\int }_0^s\left|\right|{\gamma }^{\prime }\left(t\right)\left|\right|dt={\int }_0^{s}dt$$

The assumption here is that $\gamma \left(s\right)$ is non-singular except at $s=0$.

Then define the tangent vector field as

$$t:={\gamma }^{\prime },\left|\right|{\gamma }^{\prime }\left(s\right)\left|\right|=1$$

Then obviously the radius vector can be reconstructed by curvature. Furthermore,

$$0=F^{\prime }=r^{\prime }\left(s\right)·\nabla F⟹t·{\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}=t·n=0$$

(12)

Therefore, the gradient $\nabla F$ is orthogonal to t, which will be used to define the gradient frame. We also obtain the equivalence

$${\displaystyle \frac{d}{ds}}=t·\nabla$$

Furthermore, identically

$$\nabla \wedge \gamma =\nabla \wedge r=e_i\wedge {\partial }_i{e}_k{x}_k{|}_{x_k=f\left(s\right)}=e_i\wedge e_i=0$$

Definition 3

(Frame bi-vector). A frame, or Darboux, bi-vector Ω is such that

$$t_i^{\prime }=\Omega ·i_i$$

for any basis vector $t_i$ of the mobile frame $\mathbf{E}$.

Except for the Frenet frame, all other frame bi-vectors will be indexed by the frame designation. Consider the identity

$$(t^{\prime }\wedge t)·t=t^{\prime }(t·t)=t^{\prime }$$

Therefore, we can identify an adapted frame bi-vector $\Omega$ up to an orthogonal bi-vector B with

$$\Omega =t^{\prime }\wedge t+B$$

such that $B·t=0$ and $t^{\prime }=\Omega ·t$. Different choices of B lead to different frames, as will be discussed in the next sections.

3.1. Frenet Frames

Consider the normalization constraint $t·t=1$. Differentiate the equation to obtain

$$t·t^{\prime }=0$$

Therefore, the acceleration field $t^{\prime }$ is orthogonal to t. Define the curve normal vector as

$$n:=t^{\prime }/\left|\right|t^{\prime }\left|\right|=t^{\prime }/\left|\kappa \right|$$

(13)

where the unsigned curvature is defined as the norm of the acceleration vector

$$\kappa :=\left|\right|t^{\prime }\left|\right|$$

(14)

so that $\kappa =t·n$. The bi-normal vector b is orthogonal to the osculating plane $t\wedge n$:

$$b:=-I_{3}tn=-I_3·(t\wedge n)=t\times n$$

(15)

without resorting to any specially constructed cross product. It also holds that

$$n^{\prime }·n=b^{\prime }·b=0$$

Define the torsion as

$$\tau :=b·n^{\prime }$$

(16)

The torsion measures the amount of rotation of the Frenet frame around the tangent t as the arc length increases (see Figure 1). Differentiating orthogonality relations

$$t·b=n·b=t·n=0$$

yields the anti-symmetric frame coefficient matrix

$$\mathbf{\Omega }=\left(\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right)$$

(17)

The frame derivative can be computed concisely from the matrix equation

$${\mathbf{E}}^{\prime }=\mathbf{\Omega }\mathbf{E},\mathbf{E}=\left(\begin{array}{c}t\\ n\\ b\end{array}\right)$$

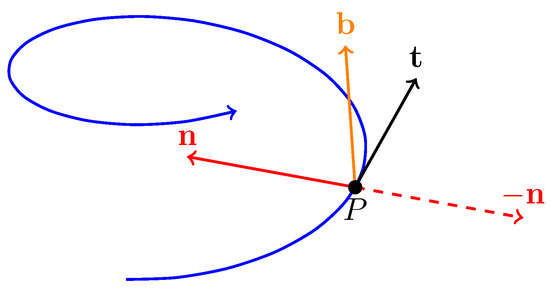
Figure 1. Frenet frame of a curve.

The Frenet frame bi-vector $\Omega$ can be completely specified as follows.

Proposition 1.

For the case of the Frenet frame, the Darboux or angular velocity bi-vector is

$$\Omega =t^{\prime }\wedge t+b^{\prime }\wedge b$$

(18)

and its dual Darboux vector is

$$\omega =\tau t+\kappa b$$

(19)

Proof. 

To demonstrate the statement we first compute the inner product

$$(b^{\prime }\wedge b)·t=(b·t)b^{\prime }-(b^{\prime }·t)b=\tau (n·t)b=0$$

Therefore,

$$\begin{array}{cc}\hfill \Omega ·b& =(t^{\prime }\wedge t)·b+(b^{\prime }\wedge b)·b=b^{\prime }=-\tau n\hfill \\ \hfill \Omega ·n& =\left(t^{\prime }\wedge t\right)·n+\left(b^{\prime }\wedge b\right)·n=-(t^{\prime }·n)t-(b^{\prime }·n)b=-\kappa t+\tau b\hfill \end{array}$$

Compute

$$\omega =\Omega I_3=(\kappa nt-\tau nb)tnb=\kappa b-\tau nbtnb=\kappa b-\tau t{\left(nb\right)}^2=\kappa b+\tau t$$

□

Therefore, the trajectory can be recovered by quadrature starting from the integral

$$t\left(s\right)=t\left(0\right)+{\int }_0^s\Omega ·tds=t\left(0\right)+{\int }_0^s\kappa (n\wedge t)·tds=t\left(0\right)+{\int }_0^s\kappa nds=t\left(0\right)+{\int }_0^s{t}^{\prime }ds$$

so that

$$t\left(s\right)=t\left(0\right)+{\int }_0^s\kappa nds$$

(20)

Remark 1.

The analogy between the frame matrix and frame bi-vector is not complete. The frame matrix Ω is singular since $\det \left(\mathbf{\Omega }\right)=0$. This is not the case for the frame bi-vector Ω, since the product ${\Omega }^{\sim }\Omega ={\kappa }^2+{\tau }^2$ results in a scalar, which is also the determinant of the bi-vector, so that its inverse is

$${\Omega }^{-1}={\Omega }^{\sim }/\left({\Omega }^{\sim }\Omega \right)$$

3.2. Gradient (Darboux) Frame

Define the surface normal vector as

$$n:={\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}$$

(21)

Remark 2.

The above relationship defines the Gauss map $G:\mathbb{R}\mapsto {⟨{\mathbb{G}}^3⟩}_1$ of the surface $F(x,y,z)$:

$$G:F\mapsto {\displaystyle \frac{\nabla F}{\left|\right|\nabla F\left|\right|}}$$

Define the osculating plane by the bi-vector $O:=t\wedge n$ and the tangent plane by $T_2:=I_3·n$. Define the bi-normal vector b to be orthogonal to the osculating plane O:

$$b:=-I_{3}tn=-I_3(t\wedge n)$$

(22)

Then $T_2=-t\wedge b$. It also holds that

$$t·t^{\prime }=n^{\prime }·n=b^{\prime }·b=0$$

as before. Differentiating the orthogonality relations

$$t·b=n·b=t·n=0$$

yields the anti-symmetric coefficient frame matrix as before.

We will look for a Darboux bi-vector as before starting from the identity

$$(n^{\prime }\wedge n)·n=n^{\prime }$$

Then

$$\Omega =(n^{\prime }\wedge n)+B$$

such that $n·B=0$ so that $\Omega ·n=n^{\prime }$ holds. Consider the constraint equation

$$\Omega ·t=(n^{\prime }\wedge n)·t+B·t=-(n^{\prime }·t)n+B·t=t^{\prime }$$

Therefore

$$n^{\prime }·t=n·t^{\prime }=0$$

(23)

Proposition 2.

For the case of the gradient frame, the Darboux, or angular velocity, bi-vector, is

$$\Omega =t^{\prime }\wedge t+n^{\prime }\wedge n$$

(24)

Proof. 

Consider the bi-vector specified in Equation (24). Compute

$$\begin{array}{c}{b}^{\prime }=-I_3(t^{\prime }n+t{n}^{\prime })=-I_3(t^{\prime }\wedge n+t\wedge n^{\prime })=n·\left(I_3{t}^{\prime }\right)-t·\left(I_3{n}^{\prime }\right)\hfill \\ \hfill =n·(I_3\Omega ·t)-t·(I_3\Omega ·n)=n·(\omega \wedge t)-t·(\omega \wedge n),\omega :=\Omega I_3\end{array}$$

in terms of the dual vector. Therefore,

$$b^{\prime }=(n·\omega )t-(t·\omega )n$$

(25)

Furthermore,

$$(n^{\prime }\wedge n)I_3=n^{\prime }·(n·(t\wedge n\wedge b)=-n^{\prime }·(t\wedge b)=(n^{\prime }·b)t-(n^{\prime }·t)b=(n^{\prime }·b)t$$

(26)

$$(t^{\prime }\wedge t)I_3=t^{\prime }·(t·(t\wedge n\wedge b)=t^{\prime }·(n\wedge b)=(t^{\prime }·n)b-(t^{\prime }·b)n=-(t^{\prime }·b)n$$

(27)

Therefore, the Darboux vector is

$$\omega =(n^{\prime }·b)t-(t^{\prime }·b)n$$

(28)

Therefore,

$$n·\omega =-(t^{\prime }·b),t·\omega =(n^{\prime }·b)$$

However,

$$\Omega ·b=-(n^{\prime }·b)n-(t^{\prime }·b)t$$

Therefore,

$$b^{\prime }=-(t^{\prime }·b)t-(n^{\prime }·b)n=\Omega ·b$$

Therefore, $\Omega$ is the Darboux bi-vector of the gradient frame. □

Define the coefficients

$$k_1:=t^{\prime }·b,k_2:=n^{\prime }·b$$

To determine explicitly $k_1$ and $k_2$, we use the following approach. Define the unit vector (i.e., the Frenet normal)

$$\eta :=t^{\prime }/\kappa$$

Then also $n·\eta =(n·t^{\prime })/\kappa =0$. On the other hand,

$$\eta \wedge b=-\eta \wedge \left(I_3(t\wedge n)\right)=-I_3(\eta ·(t\wedge n))=-I_3(n(\eta ·t)-t(\eta ·n))=I_{3}t(\eta ·n)=0$$

Therefore, $\eta$ and b are co-linear. Moreover, since both are unit vectors it follows that $\eta =\pm b$. Therefore, $k_1=t^{\prime }·(\pm \eta )=\pm \kappa$. Therefore, there are two possible combinations, $(k_1=\kappa ,\eta =b)$ and $(k_1=-\kappa ,\eta =-b)$. Considering the planar case we observe that the second option is realized. Therefore, $k_1=-\kappa$.

To obtain the transformation matrix between the Frenet and gradient frames, we proceed as follows. Define the dual vector

$$\beta :=-I_3(t\wedge \eta )$$

Then

$$n\wedge \beta =-n\wedge \left(I_3(t\wedge \eta )\right)=-I_3(n·(t\wedge \eta ))=I_{3}t(n·\eta )=0$$

Therefore, n and $\beta$ are co-linear. Furthermore,

$$n·\beta =-n·\left(I_3(t\wedge \eta )\right)=-I_3(n\wedge t\wedge (-b))=I_3(n\wedge t\wedge b)=-I_3{I}_3=1$$

Therefore, $n=\beta$ and $k_2=-n^{\prime }·\eta =-{\beta }^{\prime }·\eta$. Therefore,

$$\tau =\beta ·{\eta }^{\prime }=-{\beta }^{\prime }·\eta =k_2$$

To summarize, the Frenet and gradient frames are related by the transformation

$$\left(\begin{array}{c}t\\ -b\\ n\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right)\left(\begin{array}{c}t\\ n\\ b\end{array}\right),{\mathbf{U}}_g:=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right)$$

or in shortened matrix notation

$${\mathbf{E}}_g={\mathbf{U}}_g\mathbf{E}$$

(29)

From the above equation it is apparent that ${\mathbf{U}}_g$ is an orthogonal matrix—${\mathbf{U}}_g{\mathbf{U}}_g^T=\mathbf{I}$.

The two frame matrices are related by

$${\mathbf{\Omega }}_g={\mathbf{U}}_g\Omega {\mathbf{U}}_g^T$$

(30)

The frame matrix is

$${\mathbf{\Omega }}_g=\left(\begin{array}{ccc}0& 0& -\kappa \\ 0& 0& \tau \\ \kappa & -\tau & 0\end{array}\right)$$

(31)

Remark 3.

The name Darboux frame is justified since we can identify the plane as the surface “arena” where the equations evolve. Since the Darboux frame is represented by the matrix

$${\mathbf{\Omega }}_d=\left(\begin{array}{ccc}0& {\kappa }_g& {\kappa }_n\\ -{\kappa }_g& 0& \tau \\ -{\kappa }_n& -\tau & 0\end{array}\right)$$

Then for the plane ${\kappa }_g=0$; so up to the orientation of the normal vector one can identify ${\mathbf{\Omega }}_g$ with ${\mathbf{\Omega }}_d$.

The tangent field can be recovered by quadrature as

$$t\left(s\right)-t\left(0\right)={\int }_0^s\Omega ·tds=-{\int }_0^s\kappa bds$$

(32)

The gradient frame can be recognized as the Darboux frame for the plane, where the geodesic curvature ${\kappa }_g=0$.

Remark 4.

The gradient frame can be suitable for immersed elastic curves and also in the case where one wishes to characterize the interaction of the elastica with the medium. There, one could specify a normal forcing field as a constraint of the equations. Therefore, by duality, in a deformed body (under a strain field) the strength of interaction can be given by the value of ${\kappa }_g$.

3.3. Bishop (Inertial) Frames

The Bishop, or parallel transport, frame [21] is an alternative description that is well-defined even when the curve has vanishing acceleration. The Bishop frame ${\mathbf{E}}_b:={(t,\eta ,\beta )}^T$ is such that

$$t^{\prime }:=k_1\eta +k_2\beta$$

(33)

and, furthermore, the frame matrix has the form

$${\mathbf{\Omega }}_b=\left(\begin{array}{ccc}0& k_1& k_2\\ -k_1& 0& 0\\ -k_2& 0& 0\end{array}\right)$$

To connect with the approach discussed so far, we observe that for the first row the following holds:

$$\left|\right|t^{\prime }{\left|\right|}^2=k_1^2+k_2^2={\kappa }^2$$

Therefore, one can posit the rotation relationship

$$k_1=\kappa cos\varphi \left(s\right),k_2=\kappa sin\varphi \left(s\right),tan\varphi ={\displaystyle \frac{k_2}{k_1}}$$

for some phase function $\varphi \left(s\right)$ of the arc length to be determined further.

Therefore, the frame matrix becomes

$${\mathbf{\Omega }}_b=\kappa \left(s\right)\left(\begin{array}{ccc}0& cos\varphi \left(s\right)& sin\varphi \left(s\right)\\ -cos\varphi \left(s\right)& 0& 0\\ -sin\varphi \left(s\right)& 0& 0\end{array}\right)$$

(34)

To construct the frame we proceed as follows. Take the dot product with b

$$t^{\prime }·b=\kappa n·b=0=k_1\eta ·b+k_2\beta ·b$$

Therefore, up to sign (i.e., a reflection)

$$\eta ·b=k_2/\kappa =sin\varphi ,\beta ·b=-k_1/\kappa =-cos\varphi$$

On the other hand, taking the dot product with n results in

$$t^{\prime }·n=\kappa =k_1\eta ·n+k_2\beta ·n=\kappa cos\varphi \eta ·n+\kappa sin\varphi \beta ·n$$

Therefore,

$$\eta ·n=cos\varphi ,\beta ·n=sin\varphi$$

Therefore, the coordinate transformation can be identified with a rotation in the normal plane, or in matrix notation:

$$\left(\begin{array}{c}\eta \\ \beta \end{array}\right)=\left(\begin{array}{cc}sin\varphi \left(s\right)& cos\varphi \left(s\right)\\ -cos\varphi \left(s\right)& sin\varphi \left(s\right)\end{array}\right)\left(\begin{array}{c}b\\ n\end{array}\right)$$

(35)

A direct computation shows that the Bishop frame is related to the Frenet frame as

$$\left(\begin{array}{c}t\\ \eta \\ \beta \end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\varphi & sin\varphi \\ 0& sin\varphi & -cos\varphi \end{array}\right)\left(\begin{array}{c}t\\ n\\ b\end{array}\right),{\mathbf{U}}_b:=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\varphi & sin\varphi \\ 0& sin\varphi & -cos\varphi \end{array}\right)$$

(36)

which can be identified with a reflection at an angle $\varphi$. In shortened matrix notation

$${\mathbf{E}}_b={\mathbf{U}}_b\mathbf{E}$$

(37)

The Bishop frame matrix is related to the Frenet frame’s matrix as

$${\mathbf{\Omega }}_b={\mathbf{U}}_b^{\prime }{\mathbf{U}}_b^T+{\mathbf{U}}_b\mathbf{\Omega }{\mathbf{U}}_b^T$$

(38)

which can be demonstrated by a short computation by differentiating Equation (37).

We look for a Darboux bi-vector of the form

$$\Omega :=t^{\prime }\wedge t+B$$

Then

$$t^{\prime }=\Omega ·t=t^{\prime }+B·t⟶B·t=0$$

Furthermore

$${\eta }^{\prime }=\Omega ·\eta =-(t^{\prime }·\eta )t+B·\eta =-k_{1}t+B·\eta ⟶B·\eta =0$$

and finally

$${\beta }^{\prime }=\Omega ·\beta =-(t^{\prime }·\beta )t+B·\beta =-k_{2}t+B·\beta ⟶B·\beta =0$$

by hypothesis. Therefore, we can conclude that $B=0$ and the Darboux bi-vector has the especially simple form ([11], Chapter 6, p. 238)

$${\Omega }_b=t^{\prime }\wedge t$$

(39)

To determine the function $\varphi$ we proceed as follows. Using the Frenet frame we form the invariant volume

$$\omega :=t\wedge t^{\prime }\wedge t^{″}=\kappa t\wedge n\wedge ({\kappa }^{\prime }n+\kappa n^{\prime })=\kappa t\wedge n\wedge \underset{t^{″}}{\underbrace{({\kappa }^{\prime }n+\kappa (-\kappa t+\tau b))}}={\kappa }^2\tau I_3$$

(40)

Observe that

$$t^{″}\wedge t=(k_1^{\prime }\eta +k_1{\eta }^{\prime }+k_2^{\prime }\beta +k_2{\beta }^{\prime })\wedge t=k_1^{\prime }\eta \wedge t+k_2^{\prime }\beta \wedge t$$

Then under the orientation convention $I_3=t\wedge \eta \wedge \beta$ we have

$$\begin{array}{c}t\wedge t^{\prime }\wedge t^{″}=-(k_1{k}_2^{\prime }-k_2{k}_1^{\prime })\eta \wedge \beta \wedge t=\hfill \\ -(k_1{k}_2^{\prime }-k_2{k}_1^{\prime })I_3=-((\kappa cos\varphi ){(\kappa sin\varphi )}^{\prime }-(\kappa sin\varphi ){(\kappa cos\varphi )}^{\prime })I_3=-\\ (\kappa cos\varphi ({\kappa }^{\prime }sin\varphi +\kappa cos\varphi {\varphi }^{\prime })-\kappa sin\varphi ({\kappa }^{\prime }cos\varphi -\kappa sin\varphi {\varphi }^{\prime }))I_3=\\ \hfill -\left({\kappa }^2{cos}^2\varphi {\varphi }^{\prime }+{\kappa }^2{sin}^2\varphi {\varphi }^{\prime }\right)I_3=-{\kappa }^2{\varphi }^{\prime }{I}_3\end{array}$$

Therefore, from Equation (40) it follows that

$${\varphi }^{\prime }=-\tau$$

(41)

as also determined in [10]. In other words, $\varphi$ is the integral or cumulative torsion up to orientation of the pseudoscalar. It is a $2\pi$ multiple of the twisting number. From this presentation it is apparent that geometric algebra streamlines calculations.

3.4. Summary of the Frame Expressions

The above results can be summarized in the following Table 1.

Table 1. Summary of the frame expressions.

Frame	Darboux Bi-Vector	Frame Basis	Frame Matrix
Frenet	${\Omega }_f=t^{\prime }\wedge t+b^{\prime }\wedge b$	$\mathbf{E}={(t,n,b)}^T$	$\mathbf{\Omega }$
Gradient	${\Omega }_g=t^{\prime }\wedge t+n^{\prime }\wedge n$	${\mathbf{E}}_g={(t,-b,n)}^T={\mathbf{U}}_g\mathbf{E}$	${\mathbf{\Omega }}_g={\mathbf{U}}_g\mathbf{\Omega }{\mathbf{U}}_g^T$
Bishop	${\Omega }_b=t^{\prime }\wedge t$	${\mathbf{E}}_b={(t,\eta ,\beta )}^T={\mathbf{U}}_b\mathbf{E}$	${\mathbf{\Omega }}_b={\mathbf{U}}_b^{\prime }{\mathbf{U}}_b^T+{\mathbf{U}}_b\mathbf{\Omega }{\mathbf{U}}_b^T$

4. Euler–Lagrange Formulation of the Elastica Problem

A beam is defined to be a three-dimensional deformable body whose length is much larger than its other two dimensions. Such a body can be described by a curve threading its center line in $R^3$ and a cross-section at every point of the curve whose intersection is precisely the barycenter of the section. Variational analysis has been presented for the Kirchhoff rod in [10].

4.1. Free Elastica Equations

The elastica theory is the oldest variational model of elastic rods. The core of the presented approach is coordinate-free. The constrained Lagrangian energy density functional is identified as

$$\mathcal{L}(t,t^{\prime }):={\displaystyle \frac{1}{2}}{t}^{\prime 2}+{\displaystyle \frac{\lambda }{2}}\left(t^2-1\right)$$

(42)

where its independent variables are vectors and the multiplier is scalar, while t is not assumed a priori to be the tangent field. This Lagrangian is of first order in the variable t. However, if evaluated on the tangent field it becomes of second order in the radius vector field. Moreover, in this case it becomes manifestly translationally invariant. The above Lagrangian corresponds to the traditional definition given in [10,22] since

$$\mathcal{L}(t,t^{\prime })={\displaystyle \frac{1}{2}}{\kappa }^2+{\displaystyle \frac{\lambda }{2}}\left(t^2-1\right)={\displaystyle \frac{1}{2}}{\kappa }^2$$

where $\kappa =\left|\right|t\left|\right|$ is the curvature as defined above since t is taken to be the tangent vector field.

Remark 5.

In principle, anisotropy can be incorporated by modifying the scalar product to a symmetric positive-defined bi-linear form A

$$u\ast v\mapsto A(u,v)=u^T\mathbf{A}v$$

Since such a matrix can be put into a diagonal form, this would result in shear and scaling deformations compared to the homogeneous configuration.

Furthermore, assume that $t\in {\mathbb{G}}^n$, $n\ge 3$. The tangent field and its derivative are varied independently. To enact the variations we use the generalized partial gradient operator:

$${\nabla }_y:=\sum _{i=1}^n{e}^i{\partial }_{y_i}$$

(43)

The free elastica equation can be derived as follows. Observe the relations

$${\nabla }_{\gamma }\mathcal{L}=0,{\pi }_1:={\nabla }_t\mathcal{L}=\lambda t,{\pi }_2:={\nabla }_{t^{\prime }}\mathcal{L}=t^{\prime },{\partial }_{\lambda }\mathcal{L}=t^2-1$$

Therefore, the Euler–Lagrange equations in the variables $(\gamma ,t,t^{\prime },\lambda )$ are

$${\displaystyle \frac{d}{ds}}{\nabla }_t\mathcal{L}-{\displaystyle \frac{d^2}{d{s}^2}}{\nabla }_{t^{\prime }}\mathcal{L}={\nabla }_{\gamma }\mathcal{L},{\partial }_{\lambda }\mathcal{L}=0$$

That is, it holds that

$${\displaystyle \frac{d}{ds}}\lambda t-{\displaystyle \frac{d^2}{d{s}^2}}{t}^{\prime }={\pi }_1^{\prime }-{\pi }_2^{″}={\left(\lambda t\right)}^{\prime }-t^{‴}=0,t^2-1=0$$

(44)

4.2. Symmetries of the Lagrangian

The first equation integrates to the constant vector field J, which is also a Noether current, such that

$$J:=\lambda t-t^{″},J^{\prime }=0$$

(45)

up to sign. Furthermore, define the pseudoscalar

$$w:=t\wedge t^{\prime }\wedge J=-t\wedge t^{\prime }\wedge t^{″}$$

and differentiate it to obtain

$$w^{\prime }={(t\wedge t^{\prime }\wedge J)}^{\prime }={(t\wedge t^{\prime })}^{\prime }\wedge J=t\wedge t^{″}\wedge J=t\wedge (\lambda t-J)\wedge J=0$$

using the equation of motion. Therefore, w is also constant. Denote its magnitude by $c=\left|\right|w\left|\right|$. Observe that it is an invariant that does not depend on the used basis.

Furthermore, we establish the stronger result that

$$w\wedge t^{‴}=-t\wedge t^{\prime }\wedge t^{″}\wedge t^{‴}=-t\wedge t^{\prime }\wedge t^{″}\wedge ({\lambda }^{\prime }t+\lambda t^{\prime })=0$$

without explicitly using the dimensionality of Euclidean space. Therefore, we claim

Proposition 3.

An elastica is confined to a 3-dimensional subspace of ${\mathbb{G}}^n$.

Therefore, without loss of generality we assume further that $n=3$ so that we can use the approach developed in Section 3.

The Lagrangian is manifestly translationally and rotationally invariant, which assures the existence of Noether currents, as fully elaborated in Appendix A.6. As indicated above, $\mathcal{L}$ depends on the second derivative of the radius vector field $\gamma$. Therefore, by the Ostrogradsky principle for higher-order Lagrangians [23], the equation for the Hamiltonian, denoted by $\mathcal{H}$, is given by

$$\mathcal{H}=\left({\pi }_1-{\displaystyle \frac{d}{ds}}{\pi }_2\right)·t+{\pi }_2·t^{\prime }-\mathcal{L}={\pi }_3·t+{\pi }_2·t^{\prime }-\mathcal{L}=J·t+t^{\prime 2}-\mathcal{L},$$

(46)

where we have defined the extended canonical momentum as

$${\pi }_3:={\pi }_1-{\pi }_2^{\prime }$$

(47)

and observed that ${\pi }_3=J$. Differentiate the Hamiltonian and use the equations of motion to obtain

$${\mathcal{H}}^{\prime }=J·t^{\prime }+2t^{″}·t^{\prime }-{\mathcal{L}}^{\prime }=(\lambda t-t^{″})·t^{\prime }+t^{″}·t^{\prime }=-t^{″}·t^{\prime }+t^{″}·t^{\prime }=0$$

by the orthogonality of t and $t^{\prime }$. Therefore, it was just established that the Hamiltonian is a first integral of the system—i.e., a constant when evaluated on the solution curve.

Furthermore, the conservation of the Hamiltonian can be interpreted as the energy conservation law for the elastic energy density:

$$\mathcal{H}=J·t+{\displaystyle \frac{1}{2}}{t}^{\prime 2}-{\displaystyle \frac{1}{2}}\lambda (t^2-1)=\left(\lambda t-t^{″}\right)·t+{\displaystyle \frac{1}{2}}{t}^{\prime 2}=J·t+{\displaystyle \frac{1}{2}}{\kappa }^2\equiv H$$

(48)

applying the normalization of t and the definition of $\kappa$. Since the Hamiltonian is conserved, we use the Roman letter H to indicate its value on the solution curve.

Remark 6.

It is known that higher-derivatives Lagrangians lead to unbounded Hamiltonians and may lead to so-called Ostrogradsky instabilities. Ostrogradsky instability remains a central and actively studied issue in the context of higher-derivative theories. A recent application can be found in [24].

Observe that $\mathcal{H}$ is an affine function of the generalized momentum ${\pi }_3$ and may exhibit such an instability. Here the Ostrogradsky instability is avoided by virtue of the constant linear momentum ${\pi }_3=J$, which links the tangent vector field to its second derivative. On the solution curve the Hamiltonian is constant, $\mathcal{H}=H$. Since $t^{\prime }$ is assumed to exist almost everywhere in the configuration space, there is a number K, such that $\left|\kappa \right|<K$. Therefore,

$$H\in \left({\displaystyle \frac{1}{2}}{K}^2-j,{\displaystyle \frac{1}{2}}{K}^2+j\right)$$

where we denote $j\equiv \left|\right|J\left|\right|$. Further elaboration of the Hamiltonian formalism for the elastica problem is beyond the scope of the present paper but can be developed as outlined in [23].

The angular momentum can be identified with the bi-vector (see Appendix A.6)

$$\mathcal{M}=\gamma \wedge J+t\wedge t^{\prime }=\gamma \wedge J-{\Omega }_b$$

(49)

relating naturally to the Bishop frame bi-vector. Therefore,

$${\mathcal{M}}^{\prime }=t\wedge J+t\wedge t^{″}=-t\wedge t^{″}+t\wedge t^{″}=0$$

is the expression of the conservation law of angular momentum. Therefore, $\mathcal{M}$ can be identified with some constant M—i.e., $\mathcal{M}=M$. In an initial value setting, we also have $M=\gamma \left(0\right)\wedge J-{\Omega }_b\left(0\right)$.

One can summarize the above results in the following statement.

Proposition 4.

The free elastica system has two conserved momenta—the linear one J, given by Equation (45) and the angular one

$$M=\gamma \wedge J+t\wedge t^{\prime }$$

as well as conserved energy

$$H=J·t+{\displaystyle \frac{1}{2}}{\kappa }^2$$

Remark 7.

In order to account for distributed loads, the Lagrangian can be equipped with a scalar potential term $V\left(\gamma \right)$. In such a case, the Euler–Lagrange equations read

$$J^{\prime }=-{\nabla }_{\gamma }V,{\partial }_{\lambda }\mathcal{L}=t^2-1=0$$

Projecting the linear momentum J onto the tangent field results in a total derivative

$$t·J^{\prime }=-t·{\nabla }_{\gamma }V=-V^{\prime }$$

since V is a scalar. The Hamiltonian is

$$\mathcal{H}=J·t+t^{\prime 2}-\mathcal{L}$$

as before. Then

$${\mathcal{H}}^{\prime }=t·J^{\prime }+J·t^{\prime }+V^{\prime }+{\displaystyle \frac{1}{2}}{\left(t^{\prime 2}\right)}^{\prime }=-V^{\prime }+J·t^{\prime }+V^{\prime }+t^{\prime }·t^{″}=t^{\prime }·t^{″}-t^{\prime }·t^{″}=0$$

so that the Hamiltonian is conserved as before. The angular momentum can be identified as before as

$$\mathcal{M}=\gamma \wedge J+t\wedge t^{\prime }$$

Then

$${\mathcal{M}}^{\prime }=t\wedge J+\gamma \wedge J^{\prime }+t\wedge t^{″}=-t\wedge t^{″}+t\wedge t^{″}-\gamma \wedge {\nabla }_{\gamma }V=-\gamma \wedge {\nabla }_{\gamma }V$$

However, since V is a scalar the last term vanishes and the angular momentum is conserved, as before.

Remark 8.

We can define the generalized, multi-vector Hamiltonian, which combines both conservation laws, as an even element of the algebra as

$$\mathcal{F}:=\mathcal{H}+\mathcal{M}=J·t+{\displaystyle \frac{1}{2}}{t}^{\prime 2}+\gamma \wedge J+t\wedge t^{\prime }$$

(50)

In this formulation, $\mathcal{F}$ corresponds to a constant quaternion. Therefore, we have just established that an elastica can be suitably parametrizied, and therefore classified, by a quaternion up to a rigid motion.

Observe that

$$\mathcal{M}\wedge J=t\wedge t^{\prime }\wedge J=-t\wedge t^{\prime }\wedge t^{″}=-w=c{I}_3$$

up to sign and is also constant. Note that up to the last equation the approach is completely frame-independent. Thus, the choice of a specific frame and coordinates is a matter of utility guided by the need to simplify computations.

4.3. Derivation of the Curvature Equation Using the Frenet Frame

Observe that

$$J·t=\lambda -t^{″}·t=H-{\displaystyle \frac{1}{2}}{\kappa }^2$$

(51)

Furthermore, compute the pseudoscalar $w=t\wedge t^{\prime }\wedge J=-{\kappa }^2\tau I_3$ and identify the constraint

$${\kappa }^2\tau =c$$

(52)

coupling curvature and torsion.

Having derived the relevant symmetries of the system at this point, we specialize the discussion and employ Frenet frames to evaluate J.

$$t^{″}={\kappa }^{\prime }n+\kappa n^{\prime }={\kappa }^{\prime }n+\kappa (-\kappa t+\tau b)={\kappa }^{\prime }n-{\kappa }^{2}t+\kappa \tau b$$

(53)

Therefore,

$$J=({\kappa }^2+\lambda )t-{\kappa }^{\prime }n-\kappa \tau b$$

(54)

in the Frenet frame. The magnitude of the momentum vector can be calculated from the scalar product

$$J·J:=j^2={({\kappa }^2+\lambda )}^2+{\kappa }^{\prime 2}+{\left(\kappa \tau \right)}^2$$

(55)

for some constant j giving the norm of J. Observe that the above equation is also frame-independent.

Lastly, the Lagrange multiplier’s functional form is determined in the following way. Project J onto the tangent vector to obtain

$$J·t=\lambda -t^{″}·t=\lambda +{\kappa }^2\Rightarrow t^{″}·t=-{\kappa }^2$$

Substitute in Equation (51) to obtain the Lagrange multiplier

$$\lambda =H-{\displaystyle \frac{3}{2}}{\kappa }^2$$

(56)

Project J onto the normal vector to obtain

$$J·n=-t^{″}·n=-{\kappa }^{\prime }$$

Differentiate to obtain

$$J·n^{\prime }=J·(-\kappa t+\tau b)=-\kappa ({\kappa }^2+\lambda )-\kappa {\tau }^2=-{\kappa }^{″}$$

Substitute $\lambda$ from Equation (56) to obtain

$${\kappa }^{″}-{\kappa }^3-\left(H-{\displaystyle \frac{3}{2}}{\kappa }^2\right)\kappa ={\kappa }^{″}+{\displaystyle \frac{1}{2}}{\kappa }^3-H\kappa =\kappa {\tau }^2$$

(57)

agreeing with the result in [25].

Remark 9.

The traditional derivation of the elastic equation proceeds as follows [26]. Differentiate J and use the Frenet frame equations

$$(3\kappa {\kappa }^{\prime }+{\lambda }^{\prime })t-({\kappa }^{″}-{\kappa }^3-\lambda \kappa -\kappa {\tau }^2)n-(\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau )b=0$$

to obtain a system of three constraints:

$$3\kappa {\kappa }^{\prime }+{\lambda }^{\prime }=0,{\kappa }^{″}-{\kappa }^3-\lambda \kappa -\kappa {\tau }^2=0,\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau =0$$

Solve the constraint for the torsion

$$\kappa {\tau }^{\prime }+2{\kappa }^{\prime }\tau =0⟹{\tau }^{\prime }/\tau +2{\kappa }^{\prime }/\kappa =0⟹log\tau {\kappa }^2=logc⟹\tau ={\displaystyle \frac{c}{{\kappa }^2}}$$

and the Lagrange multiplier

$$3\kappa {\kappa }^{\prime }+{\lambda }^{\prime }=0⟹\lambda =H-{\displaystyle \frac{3}{2}}{\kappa }^2$$

Substitute the solutions into the remaining constraint. Observe that using the traditional approach the role of the constants H and c is not apparent and one has to solve two ODEs to obtain the sought relationship.

The advantage of the geometric algebraic approach is that one does not need to solve a differential equation for the torsion. Instead, the role of the invariant pseudoscalar is emphasized. From the present discussion it transpires that the choice of frame is a matter of convenience for the problem at hand.

The preceding discussion can be formulated concisely in the following theorem.

Theorem 1.

The 3-dimensional elastica system is equivalent to the first-order ODE

$${\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2+{\kappa }^{\prime 2}-j^2=-c\tau =-{\displaystyle \frac{c^2}{{\kappa }^2}}$$

(58)

which can be differentiated into the second-order differential equation

$${\kappa }^{″}+{\displaystyle \frac{1}{2}}{\kappa }^3-H\kappa =\kappa {\tau }^2={\displaystyle \frac{c^2}{{\kappa }^3}}$$

(59)

where H is the constant Hamiltonian energy density of the system, c is the torsion coupling, and j is the magnitude of the generalized momentum J. The vector field J can be expressed in the Frenet frame as

$$J=\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)t-{\kappa }^{\prime }n-\kappa \tau b,J^{\prime }=0$$

(60)

4.4. Classification of Elastic Curves Using Geometric Invariants

The geometrical meaning of the torsion coupling condition $\tau {\kappa }^2=c$ requires some attention. In the first place,

$$t^{″}={\kappa }^{\prime }n+\kappa n^{\prime }⟹t^{″}·b=\kappa \tau$$

Also $\kappa b=-\kappa I_3(t\wedge n)=-I_3(t\wedge t^{\prime })$. Therefore,

$${\kappa }^2\tau =\kappa t^{″}·b=-t^{″}·\left(I_3(t\wedge t^{\prime })\right)=-I_3(t\wedge t^{\prime }\wedge t^{″})$$

or equivalently,

$${\kappa }^2\tau I_3=c{I}_3=t\wedge t^{\prime }\wedge t^{″}=\omega$$

(61)

in terms of the volume invariant. Therefore, in the non-trivial case, linear dependence between the three vectors ($t\wedge t^{\prime }\wedge t^{″}=0$) implies that the curve is planar (i.e., $\tau =0$). Let $\sigma :=t\wedge t^{\prime }$. Obviously, whenever t and $t^{\prime }$ are linearly dependent, $\sigma =0$. On the other hand, suppose that only ${\sigma }^{\prime }=0$. Then

$$t\wedge t^{″}=0⟹t^{″}·b=0⟹\tau =0$$

Meanwhile

$${\sigma }^2=(t\wedge t^{\prime })·(t\wedge t^{\prime })=t·(t^{\prime }·(t\wedge t^{\prime }))=-t·\left(t{t}^{\prime 2}\right)=-{\kappa }^2$$

(62)

Furthermore, $t^{‴}$ is in the span of ($t,t^{\prime },t^{″}$) since $t\wedge t^{\prime }\wedge t^{″}\wedge t^{‴}={\kappa }^2\tau I_3\wedge t^{‴}=0$. The above results can be neatly summarized in the following diagram:

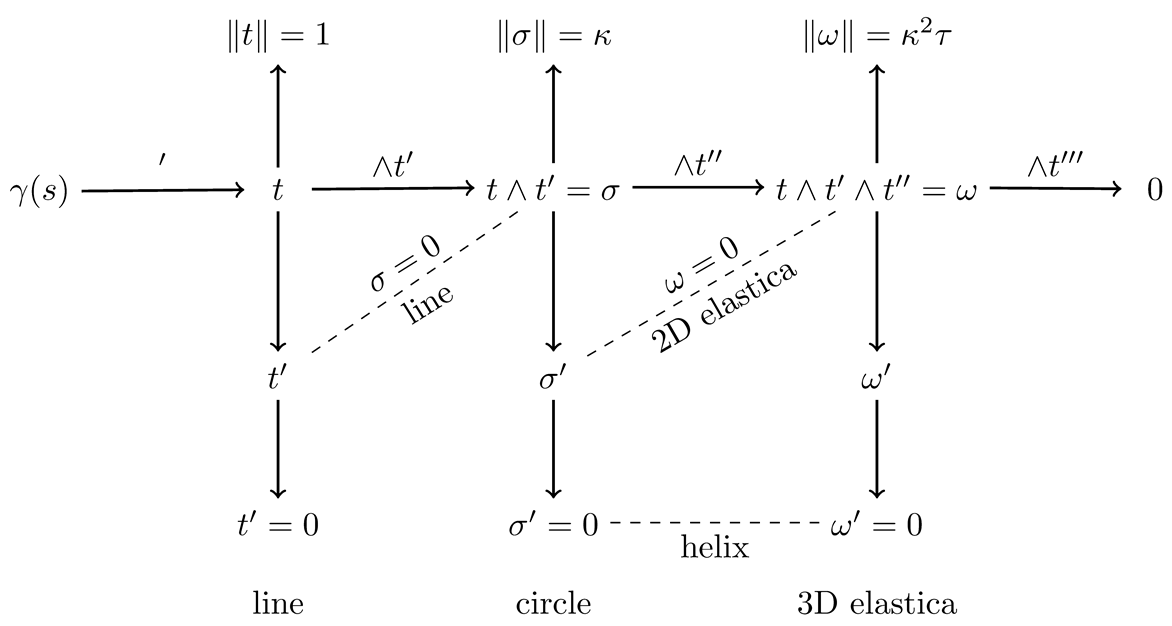
The above diagram is generated by the consecutive action of two operators—covariant arc length differentiation and exterior multiplication. The top row of the diagram summarizes the geometric invariants, which are the norms of the geometric objects, i.e., vectors, surfaces, and volumes, constructed by the covariant derivatives of the radius vector field in the middle row. The bottom row represents the limiting cases where the covariant derivatives of the respective objects vanish.

5. Applications

As already demonstrated, the elastica is confined to a subspace of ${\mathbb{G}}^n$ of maximal dimension 3. Therefore, there are only two non-trivial cases—a planar elastica and a 3D elastica.

5.1. Planar Elastica

In this section we assume that the elastica is confined to a plane. Then $\tau =c=0$. The curvature differential equation becomes

$${\kappa }^{\prime }=\pm \sqrt{j^2-{\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2}$$

(63)

The equation is resolved by variation of parameters using the generic ansatz

$$\kappa =A\mathrm{dn}\left(qs\right|m)$$

using the Jacobi delta amplitudinis function. In the formula A can be interpreted as a bending, q as a stretching, and m as a shape parameter. Some properties of the Jacobi functions and the associated elliptic integrals necessary for the present discussion are surveyed in Appendix A. This leads to the algebraic system for the undetermined parameters A, q, and m:

$$A^2{m}^2(4q^2-A^2)=0$$

(64)

$$A^{2}m(2m{q}^2+2H-A^2)=0$$

(65)

$$(2j-2H+A^2)(2j+2H-A^2)=0$$

(66)

The non-trivial solutions of the system are given by the set

$$\begin{array}{c}\left\{q=\pm \sqrt{{\displaystyle \frac{j+H}{2}}},m={\displaystyle \frac{2j}{j+H}},A=\mp \sqrt{2j+2H}\right\}\cup \hfill \\ \left\{q=\pm \sqrt{{\displaystyle \frac{j+H}{2}}},m={\displaystyle \frac{2j}{j+H}},A=\pm \sqrt{2j+2H}\right\}\cup \\ \left\{q=\pm \sqrt{{\displaystyle \frac{H-j}{2}}},m={\displaystyle \frac{2j}{j-H}},A=\mp \sqrt{2H-2j}\right\}\cup \\ \hfill \left\{q=\pm \sqrt{{\displaystyle \frac{H-j}{2}}},m={\displaystyle \frac{2j}{j-H}},A=\pm \sqrt{2H-2j}\right\}\end{array}$$

Observe that $A=\pm 2q$. Only the solutions with positive curvature are geometrically admissible, that is where A is positive. This leads to a general solution of the form

$$\kappa =2q\mathrm{dn}\left(qs\right|m),q>0$$

(67)

since $\mathrm{dn}\left(0\right|m)=1$. Therefore, $q=\kappa \left(0\right)/2$, fixing the interpretation of the parameter. The case $m=0$ corresponds to a circle since in this case $\mathrm{dn}\left(qs\right|0)=1$ and the curvature is constant. Therefore, one is left with the following two non-trivial cases:

$$\left\{q=\sqrt{{\displaystyle \frac{j+H}{2}}},m={\displaystyle \frac{2j}{j+H}}\right\}\cup \left\{q=\sqrt{{\displaystyle \frac{H-j}{2}}},m={\displaystyle \frac{2j}{j-H}}\right\}$$

(68)

The second set corresponds to $m<0$. Therefore, we restrict the first set to $m>0$.

This corresponds to the results given in [27] after a suitable reparametrization.

Furthermore, m is constrained by j since

$$m{q}^2=\pm j$$

Therefore, the shape of the elastica is determined by two factors—the initial value of the curvature and the magnitude of the linear momentum j.

The energy of the elastica is

$$H={\displaystyle \frac{1}{2}}{\kappa }^2\left(0\right)\pm j={\displaystyle \frac{1}{2}}{\kappa }^2\left(0\right)\pm m{q}^2={\displaystyle \frac{{\kappa }^2\left(0\right)}{2}}\left(1\pm {\displaystyle \frac{m}{2}}\right)$$

Observe that $m=2$ corresponds to vanishing energy—$H=0$.

5.2. Generic 3D Elastica

We follow the method described in [26], where the proposition stated below is proven.

Proposition 5.

The substitution $u={\kappa }^2$ results in an autonomous ODE for u:

$${\left({\displaystyle \frac{u^{\prime }}{2}}\right)}^2=u{j}^2-c^2-u{\left(H-{\displaystyle \frac{u}{2}}\right)}^2$$

(69)

Proof. 

Suppose that $u={\kappa }^2\ne 0$. Observe that wherever $\kappa \ne 0$

$${\kappa }^{\prime }={\displaystyle \frac{u^{\prime }}{2\kappa }}={\displaystyle \frac{u^{\prime }}{2\sqrt{u}}}$$

Therefore,

$${\left(H-{\displaystyle \frac{{\kappa }^2}{2}}\right)}^2+{\kappa }^{\prime 2}-j^2={\left(H-{\displaystyle \frac{u}{2}}\right)}^2+{\left({\displaystyle \frac{u^{\prime }}{2\sqrt{u}}}\right)}^2-j^2=-c\tau =-{\displaystyle \frac{c^2}{{\kappa }^2}}=-{\displaystyle \frac{c^2}{u}}$$

and multiplying by u yields

$$u{\left(H-{\displaystyle \frac{u}{2}}\right)}^2+{\left({\displaystyle \frac{u^{\prime }}{2}}\right)}^2-u{j}^2=-c^2$$

□

This equation can be integrated in elliptic functions as follows [10,25,28,29]. We make the ansatz

$${\kappa }^2=u=p-Am{\mathrm{sn}}^2\left(\sqrt{q}s\right|m)=p-A+A{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

for the parameters p, A, m, and q, which are to be determined further.

Observe that the 2D case corresponds to $A=p$. Using some identities for the elliptic functions, one arrives at the following system of polynomial equations for the parameters:

$$A^2{m}^3\left(4q-A\right)=0$$

(70)

$$A^2{m}^2\left(4mq+4q-3p+4H\right)=0$$

(71)

$$Am\left(4Amq-3p^2+8Hp+4j^2-4H^2\right)=0$$

(72)

$$p^3-4H{p}^2+4(H^2-j^2)p+4c^2=0$$

(73)

Therefore, a non-trivial constraint is $A=4q\ne 0$. This leads to a parametric solution of the form

$${\kappa }^2=p-4q+4q{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

(74)

and furthermore

$${\kappa }^2\left(0\right)=p-A+A{\mathrm{dn}}^2\left(0\right|m)=p$$

(75)

fixing the interpretation of p. The case $m=0$ as before leads to a circle since ${\kappa }^2=p$. Therefore, we can further assume $m\ne 0$.

Equation (73) contains only the integration constants H, c, and j besides the parameter p. Therefore, the solutions can be parameterized by the roots of the equation for p. Then

$$\begin{array}{cc}\hfill m_1& ={\displaystyle \frac{(3p-4H)\sqrt{-3p^2+8Hp+16j^2}+3p^2-8Hp+8j^2+8H^2}{2\left(3p^2-8Hp-4j^2+4H^2\right)}},\hfill \\ \hfill q_1& =-{\displaystyle \frac{\sqrt{-3p^2+8Hp+16j^2}-3p+4H}{8}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill m_2& =-{\displaystyle \frac{(3p-4H)\sqrt{-3p^2+8Hp+16j^2}-3p^2+8Hp-8j^2-8H^2}{2\left(3p^2-8Hp-4j^2+4H^2\right)}},\hfill \\ \hfill q_2& ={\displaystyle \frac{\sqrt{-3p^2+8Hp+16j^2}+3p-4H}{8}}\hfill \end{array}$$

In another parametrization, eliminating A, we have the system of equations

$$p={\displaystyle \frac{4}{3}}(H+q(m+1))$$

(76)

$$mq(H^2+3j^2-4(1-m+m^2)q^2)=0$$

(77)

$$4H^3+27c^2-36H{j}^2+12(H^2+3j^2)(1+m)q+16{\left(1+m\right)}^3{q}^3=0$$

(78)

which couples the p an q parameters algebraically. The advantage here is the linear relationship between p and H. The positive solution for q is

$$q={\displaystyle \frac{\sqrt{H^2+3j^2}}{2\sqrt{1-m+m^2}}}$$

The denominator is always positive. Then the solutions are parametrized by the value of m. In the 2D case, as observed

$$4q={\displaystyle \frac{4}{3}}(H+q(m+1))⟹H=q(2-m)$$

Otherwise,

$${\kappa }^2={\displaystyle \frac{4}{3}}(H+q(m-2))+4q{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)=p+4q{\mathrm{dn}}^2\left(\sqrt{q}s\right|m)$$

(79)

and

$${\kappa }^2-{\kappa }^2\left(0\right)=4q\left({\mathrm{dn}}^2\left(\sqrt{q}s\right|m)-1\right)$$

Remark 10.

The torsion is

$$\tau ={\displaystyle \frac{c}{p-4qm{\mathrm{sn}}^2\left(\sqrt{q}s\right|m)}}={\displaystyle \frac{c}{{\kappa }^2\left(0\right)-4qm{\mathrm{sn}}^2\left(\sqrt{q}s\right|m)}}$$

which determines the Frenet frame. This can be integrated into an incomplete elliptical integral of the third kind:

$$\varphi \left(s\right)=-{\displaystyle \frac{c}{p\sqrt{q}}}\Pi \left({\displaystyle \frac{4qm}{p}},\mathrm{am}\left(\sqrt{q}s\right|m)|m\right)=-{\displaystyle \frac{\tau \left(0\right)}{\sqrt{q}}}\mathcal{P}\left({\displaystyle \frac{4qm}{{\kappa }^2\left(0\right)}},\sqrt{q}s|m\right)$$

allowing for calculation of the Bishop frame.

Example 1.

As an example consider a circular helix. Take the values of $\kappa =k$ and $\tau =T$ as inputs. Consider a concrete implementation

$$\gamma =acost{e}_1+asint{e}_2+gt{e}_3,a,g>0$$

Then the task is to determine the parameters a and g from the inputs. One proceeds as follows. Compute

$$\left|\left|{\displaystyle \frac{d}{dt}}\gamma \right|\right|=\sqrt{a^2+g^2}=:L⟹{\displaystyle \frac{d}{ds}}={\displaystyle \frac{1}{L}}{\displaystyle \frac{d}{dt}}$$

so that

$$t={\displaystyle \frac{1}{L}}\left(-asint{e}_1+acost{e}_2+g{e}_3\right)$$

(80)

and

$$t^{\prime }=-{\displaystyle \frac{a}{L^2}}\left(cost{e}_1+sint{e}_2\right)$$

(81)

The Bishop frame is easily computed as

$${\Omega }_b=-{\displaystyle \frac{1}{L^3}}\left(a^2{e}_{12}+agcost{e}_{13}+agsint{e}_{23}\right)$$

and it is dual to the binormal

$$b={\displaystyle \frac{L}{a}}{I}_3·{\Omega }_b={\displaystyle \frac{1}{kL}}{I}_3·{\Omega }_b$$

Furthermore, one can directly compute

$$k={\displaystyle \frac{a}{L^2}}$$

(82)

$$T={\displaystyle \frac{g}{L^2}}$$

(83)

According to Theorem 1 we have

$$H={\displaystyle \frac{k^2}{2}}-T^2$$

and

$$j^2={(H-k^2/2)}^2+cT=T^4+cT=T^4+k^2{T}^2,c=k^{2}T$$

so that $j=T\sqrt{T^2+k^2}$. Then one can compute the conserved momenta and energy

$$J=-{\displaystyle \frac{g}{L^3}}{e}_3=-{\displaystyle \frac{T}{L}}{e}_3$$

(84)

$$M={\displaystyle \frac{a^2}{L^3}}{e}_{12}=k^{2}L{e}_{12}$$

(85)

$$H={\displaystyle \frac{k^2}{2}}-T^2={\displaystyle \frac{1}{2}}{\displaystyle \frac{a^2-2g^2}{L^4}}$$

(86)

One can also identify

$$L={\displaystyle \frac{1}{\sqrt{k^2+T^2}}}$$

which completes the parametrization.

5.3. Integration of the Elastica in Terms of the Bishop Frame

Observe that Equation (48) can be integrated as

$$J·\gamma +{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds=Hs$$

(87)

Adding both conservation laws allows one to solve for the $\gamma$ field using the invertibility of the geometric product:

$$\gamma \left(s\right)=\left(Hs+M-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds-\sigma \right)J^{-1},\sigma =t\wedge t^{\prime }=\kappa t\wedge n=-{\Omega }_b$$

(88)

Observe that the above formulation is coordinate-free, demonstrating the advantage of the geometric algebra approach. Therefore, we establish that the elastica is a completely integrable system in terms of the Bishop frame.

The conserved momentum allows for aligning the solution to a global basis and identifying a preferred coordinate system. Such a convenient system is the cylindrical one [25,28], aligned with the momentum J (see Figure 2). We define the constant-altitude unit vector along the direction of J as

$$e_3:=J/j$$

(89)

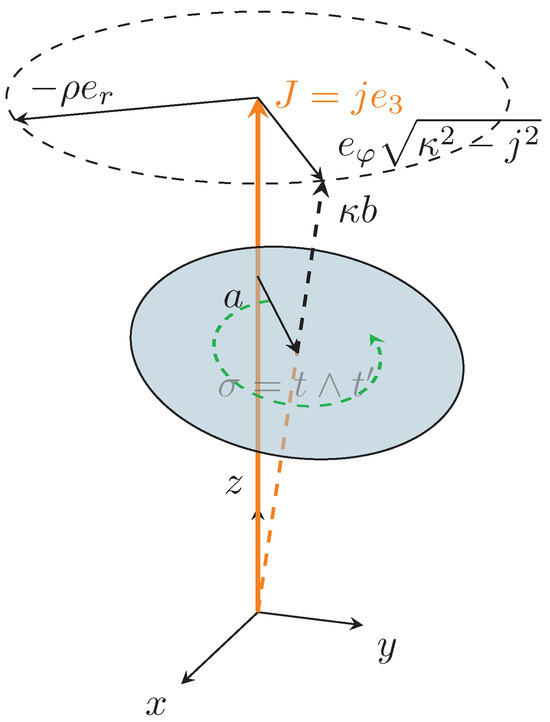
Figure 2. The preferred coordination system and Bishop frame configuration.

In summary, we can formulate following result.

Theorem 2.

Suppose that ${\Omega }_b$, J, H, and M are specified. Then the elastica curve can be reconstructed by quadrature as follows:

$$j\gamma \left(s\right)=\left(Hs-{\displaystyle \frac{1}{2}}{\int }_0^s{\kappa }^{2}ds\right)e_3+\left(M+{\Omega }_b\right)·e_3$$

(90)

under the compatibility condition

$${\Omega }_b^{\prime }=jt\wedge e_3=t\wedge J$$

Proof. 

Consider the identity $e_3\wedge (M-\sigma )=e_3\wedge \gamma \wedge J={⟨\gamma ⟩}_3=0$ (Equation (49)). Therefore, we are led to a new equation in terms of the preferred direction, which splits into translational and rotational components as follows:

$$j\gamma \left(s\right)=\left(Hs-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds\right)e_3+\left(M+{\Omega }_b\right)·e_3$$

Furthermore, the first term can be interpreted as a sum of translations while the second term as a sum of rotations.

Equation (88) implies the compatibility condition

$$jt{e}_3=H-{\displaystyle \frac{1}{2}}{\kappa }^2-{\sigma }^{\prime }⟹jt\wedge e_3=-{\sigma }^{\prime }={\Omega }_b^{\prime }$$

Therefore, formally the Bishop frame can be determined by quadrature as

$$\sigma =j\int e_3\wedge tds$$

from the tangent field, so the total angular momentum can be identified with the integration constant of the Bishop frame. □

Geometrically Equation (90) amounts to establishing a preferred orientation of the system (i.e., a global cylindrical symmetry). Using these coordinates, the solutions can be represented conveniently in a cylindrical coordinate system [28]. Then for the altitude we have

$$j{e}_3·\gamma =jz=Hs-{\displaystyle \frac{1}{2}}\int {\kappa }^{2}ds$$

So we can identify the altitude (i.e., the z-axis) with the direction of translation. Using Equation (74) one obtains directly

$$jz\left(s\right)=Hs-{\displaystyle \frac{1}{2}}(p-4q)s-2\sqrt{q}\mathcal{E}\left(\sqrt{q}s\right|m)={\displaystyle \frac{H}{3}}s-{\displaystyle \frac{2m}{3}}(q-2)s-2\sqrt{q}\mathcal{E}\left(\sqrt{q}s\right|m)$$

(91)

in terms of the Jacobi epsilon function.

Consider the identity

$$m_3\equiv M·e_3=-\underset{jz{e}_3}{\underbrace{j(\gamma ·e_3)e_3}}+\gamma j+\sigma ·e_3=j\rho e_r+\sigma ·e_3,m_3=M·J/j$$

We can solve for the radial component as

$$j\rho e_r=m_3-\sigma ·e_3$$

(92)

and furthermore,

$$j^2{\rho }^2=m_3^2+{(\sigma ·e_3)}^2-2m_3·\sigma ·e_3$$

To obtain the angular coordinate proceed as follows. Differentiate Equation (92) as

$$j\rho {\phi }^{\prime }{e}_{\phi }+j{\rho }^{\prime }{e}_r=e_3·{\sigma }^{\prime }$$

Take the inner products

$$j\rho {\phi }^{\prime }=e_3·{\sigma }^{\prime }·e_{\phi },j{\rho }^{\prime }=e_3·{\sigma }^{\prime }·e_r$$

Integrate to obtain the polar coordinates

$$j\rho \left(s\right)=e_3·\int {\sigma }^{\prime }·e_{r}ds$$

(93)

$$j\phi \left(s\right)=e_3·\int {\displaystyle \frac{{\sigma }^{\prime }·e_{\phi }}{\rho }}ds$$

(94)

The procedure is explicated in the next section.

5.4. Construction of the Preferred Coordinate System

The exposition follows the approach of [28], taking into account the differences in the employed formalism. Observe that $\kappa I_{3}b=\kappa tn=t\wedge t^{\prime }=\sigma =-{\Omega }_b$ so that $\kappa b=I_3\sigma$ (see Figure 2). The solid angle subtended between the planes $\sigma$ and $R=I_{3}J=j{e}_r\wedge e_{\phi }$ is given by

$$cos\theta ={\displaystyle \frac{\sigma ·R}{\left|\right|R\left|\right|\left|\right|\sigma \left|\right|}}=I_3{\displaystyle \frac{\sigma \wedge J}{j\left|\kappa \right|}}={\displaystyle \frac{I_{3}w}{j\left|\kappa \right|}}={\displaystyle \frac{c}{j\kappa }}$$

To construct $e_{\phi }$ compute the rejection vector for b in the plane $e_3\wedge b$ (see Figure 3)

$$a:=e_3·(e_3\wedge b)=b-(e_3·b)e_3=b-(J·b)J/j^2=\left|\right|a\left|\right|e_{\phi }$$

Furthermore, we have the identity

$$a^2={(e_3·(e_3\wedge b))}^2=1-{(e_3·b)}^2={sin}^2\theta$$

Therefore, the norm of the vector a can be computed as

$$\left|\right|a\left|\right|=|sin\theta |={\displaystyle \frac{\sqrt{j^2-{\kappa }^2{\tau }^2}}{j}}={\displaystyle \frac{\sqrt{j^2{\kappa }^2-c^2}}{j\kappa }}=\sqrt{1-{\left({\displaystyle \frac{c}{j\kappa }}\right)}^2}$$

(95)

after substituting in Equation (54) since $J·b=-\kappa \tau$.

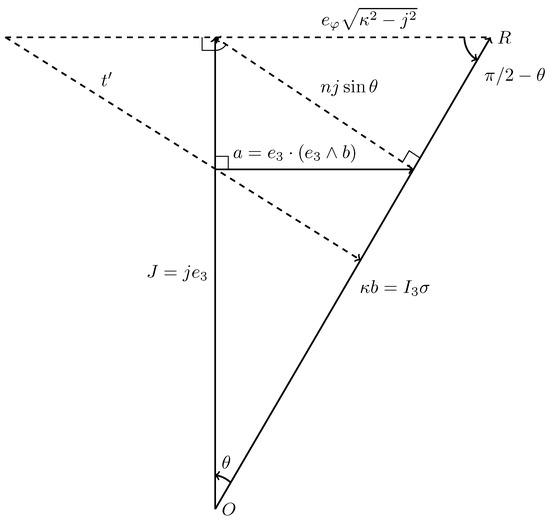
Figure 3. A section of the preferred coordination system with the Bishop frame.

Observe that in cylindrical coordinates $(\rho ,\phi ,z)$

$$r=\rho e_r+e_{3}z⟶t={\rho }^{\prime }{e}_r+\rho {\phi }^{\prime }{e}_{\phi }+z^{\prime }{e}_3$$

(96)

The two remaining coordinate equations can be obtained as the scalar products

$$t·e_r={\rho }^{\prime },t·e_{\phi }=\rho {\phi }^{\prime }$$

Direct representation of a in terms of the Frenet frame using Equation (60) results in

$$\begin{array}{c}a{j}^2=b{j}^2-(J·b)J=t\left({\kappa }^2+\lambda \right)\kappa \tau -n\kappa \tau {\kappa }^{\prime }+b\left(j^2-{\kappa }^2{\tau }^2\right)=\hfill \\ \hfill t\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)\kappa \tau -n\kappa \tau {\kappa }^{\prime }+b\left(j^2-{\kappa }^2{\tau }^2\right)\end{array}$$

(97)

Furthermore, the third basis vector can be computed as $e_r=R{e}_{\phi }=-I_3{e}_{\phi }{e}_3$.

$${\rho }^{\prime }=t·e_r=-t·\left(I_3{e}_{\phi }{e}_3\right)=-I_3(t\wedge e_{\phi }\wedge e_3)=-{\displaystyle \frac{I_3}{\left|\right|a\left|\right|j}}(t\wedge a\wedge J)$$

(98)

Then

$$a\wedge J=\left(b-{\displaystyle \frac{J·b}{j^2}}J\right)\wedge J=b\wedge J$$

so that

$$t\wedge a\wedge J=t\wedge b\wedge (\lambda t-t^{″})=t\wedge b\wedge t^{″}=t\wedge b\wedge ({\kappa }^{\prime }n-k{n}^{\prime })={\kappa }^{\prime }t\wedge b\wedge n=-{\kappa }^{\prime }{I}_3$$

Therefore,

$${\displaystyle \frac{I_3}{\left|\right|a\left|\right|j}}t\wedge a\wedge J={\displaystyle \frac{{\kappa }^{\prime }}{\left|\right|a\left|\right|j}}={\displaystyle \frac{j\kappa {\kappa }^{\prime }}{j\sqrt{j^2{\kappa }^2-c^2}}}={\rho }^{\prime }$$

from Equations (95) and (98), which directly integrates to

$$j^2\rho =\sqrt{j^2{\kappa }^2-c^2}=j\kappa \left|\right|a\left|\right|=j\kappa sin\theta$$

(99)

Furthermore,

$$\rho {\phi }^{\prime }=t·e_{\phi }=t·{\displaystyle \frac{a}{\left|\right|a\left|\right|}}={\displaystyle \frac{\kappa \tau ({\kappa }^2+\lambda )}{j\sqrt{j^2-{\kappa }^2{\tau }^2}}}={\displaystyle \frac{c(2H-{\kappa }^2)}{2j\sqrt{j^2{\kappa }^2-c^2}}}$$

so that

$${\phi }^{\prime }={\displaystyle \frac{jc(H-{\kappa }^2)}{2(j^2{\kappa }^2-c^2)}}=-{\displaystyle \frac{c}{2j}}+{\displaystyle \frac{c}{2j}}{\displaystyle \frac{(2H{j}^2-c^2)}{(j^2{\kappa }^2-c^2)}}$$

This can be integrated into

$$\phi \left(s\right)=-{\displaystyle \frac{cs}{2j}}+{\displaystyle \frac{c}{2j}}{\displaystyle \frac{(2H{j}^2-c^2)}{\sqrt{q}(j^{2}p-c^2)}}\Pi \left({\displaystyle \frac{4mq{j}^2}{j^{2}p-c^2}},\mathrm{am}\left(\sqrt{q}s|m\right)|m\right)$$

(100)

in terms of the incomplete elliptic integral of the third kind, corresponding to the result in [28]. This is, however, not the most convenient representation, as noted in [29]. It is produced here only to demonstrate the correspondence of the approach.

5.5. Specialization to 2D

To connect with the planar elastica, we use the frames {$e_1,e_3$} with the pseudoscalar $I_2=e_1\wedge e_3$. Observe that the Bishop frame is simply $\sigma =\kappa I_2=2q\mathrm{dn}\left(sq\right|m)I_2$ and the angular momentum bi-vector is $M=m_3{I}_2$ and $n=-I_2·t$. We can fix the origin of the curve at (0, 0); then $m_3=2q$. Then one immediately obtains the solution

$$j\gamma =\left(Hs-2q\mathcal{E}\left(qs\right|m)\right)e_3+2q\left(1-\mathrm{dn}\left(qs\right|m)\right)e_1$$

(101)

and $M=2q{I}_2$. From the parametric system m is constrained as $m=2-H/q^2$ and $j=m{q}^2$. The tangential field becomes

$$t={\displaystyle \frac{H-2q^2{\mathrm{dn}}^2\left(qs|m\right)}{m{q}^2}}{e}_3+2\mathrm{cn}\left(qs|m\right)\mathrm{sn}\left(qs|m\right)e_1$$

(102)

Furthermore, the linear momentum becomes

$$J=\left(H-{\displaystyle \frac{1}{2}}{\kappa }^2\right)t-{\kappa }^{\prime }n=(H-2q^2{\mathrm{dn}}^2\left(qs\right|m))t+2m{q}^2\mathrm{cn}\left(qs\right|m)\mathrm{sn}\left(qs\right|m)n=m{q}^2{e}_3=j{e}_3$$

which is constant, in agreement with the theory.

Example 2.

The solution for $m>0$ is the curve given by

$$\kappa \left(s\right)=\sqrt{2}\sqrt{j+H}\mathrm{dn}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)$$

(103)

$$x\left(s\right)={\displaystyle \frac{\sqrt{2}\sqrt{j+H}}{j}}\left(1-\mathrm{dn}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)\right)={\displaystyle \frac{\kappa \left(0\right)-\kappa \left(s\right)}{j}}$$

(104)

$$z\left(s\right)={\displaystyle \frac{Hs}{j}}-{\displaystyle \frac{\sqrt{2}\sqrt{j+H}}{j}}\mathcal{E}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j+H}}\right)$$

(105)

Example 3.

The solution for $m<0$ is the curve given by

$$\kappa \left(s\right)=\sqrt{2}\sqrt{-j+H}\mathrm{dn}\left({\displaystyle \frac{\sqrt{-j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j-H}}\right)$$

(106)

$$x\left(s\right)={\displaystyle \frac{\sqrt{2}\sqrt{-j+H}}{j}}\left(1-\mathrm{dn}\left({\displaystyle \frac{\sqrt{-j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j-H}}\right)\right)={\displaystyle \frac{\kappa \left(0\right)-\kappa \left(s\right)}{j}}$$

(107)

$$z\left(s\right)={\displaystyle \frac{Hs}{j}}-{\displaystyle \frac{\sqrt{2}\sqrt{-j+H}}{j}}\mathcal{E}\left({\displaystyle \frac{\sqrt{j+H}s}{\sqrt{2}}}|{\displaystyle \frac{2j}{j-H}}\right)$$

(108)

Note that in this case the analytical continuation identities must be used for computation.

6. Discussion

The present contribution considers the problem of 2D and 3D non-extendable elastic beams and rods from the perspective of geometric algebra. This allows for a great simplification of the problem due to the considerable expression power of the geometric algebra approach. Notably, the approach obviates the use of a non-Euclidean configuration space [9]. Instead, all calculations are performed in the physical Euclidean space.

Possible applications of the approach are inverse problems, image segmentation, Finite Element Modeling, FEM, or the Boundary Element Method, BEM. For example, Liu and Hong [30] and later Grigoriev and Yakovlev [31] explored applications of GA to elasticity. Liu and Hong constructed multiple-component spatial harmonic functions and developed a GA-valued BEM in order to solve numerically three-dimensional problems of elasticity for an arbitrary domain with complicated boundary conditions. Klimek et al. [32] achieve discretization of Maxwell’s equations for non-inertial observers using Space-Time Algebra. The main application that was demonstrated was the manifestation of Sagnac’s effect in a rotating ring resonator.

This paper demonstrates the forms of Frenet, Darboux, and Bishop frames in ${\mathbb{G}}^3$. Furthermore it offers a new Lagrangian formulation of the elastica theory. This allows for construction of the fundamental Notherian conserved quantities—energy and linear and angular momentum. The geometric algebra approach also enables an intuitive classification of the elastica system using its geometric invariants. Concise expressions of the elastica equations are found using the Bishop frame. The geometric algebra approach demonstrates natural correspondence of the free elastic problem with Kirchhoff beam theory. Finally, we have determined a new coordinate-free formulation of the solution (Theorem 2).

Appendix A.1. Elliptic Integrals of the First Kind

The following is an incomplete elliptic integral of the first kind:

$$\mathcal{F}\left(\varphi |m\right):={\int }_0^{\varphi }{\displaystyle \frac{du}{\sqrt{1-m{sin}^{2}u}}}$$

(A1)

where $m\le 1$ is the parameter. For $m>1$ the integral is analytically continued in the complex plane. The complete elliptic integral is defined as

$$\mathcal{F}\left({\displaystyle \frac{\pi }{2}}|m\right)=:\mathcal{K}\left(m\right)$$

(A2)

The Jacobi amplitude function is the inverse of the $\mathcal{F}$ integral:

$$u=\mathcal{F}\left(\varphi |m\right)⟹\mathrm{am}\left(u\right|m):=\varphi$$

(A3)

for all admissible values of m. The amplitude can be smoothly continued as

$$\mathrm{am}(u+2K|m)=\mathrm{am}(u\left|m\right)+\pi ,K=\mathcal{K}\left(m\right)$$

Its derivative is denoted by $\mathrm{dn}$:

$$\mathrm{dn}\left(x\right|m)={\displaystyle \frac{d}{dx}}\mathrm{am}\left(x\right|m)$$

The notation comes from the name delta amplitudinis.

The elliptic sine and cosine are defined by

$$\mathrm{sn}\left(x\right|m):=sin\mathrm{am}(x\left|m\right),\mathrm{cn}\left(x\right|m):=cos\mathrm{am}(x\left|m\right)$$

(A4)

Therefore, we have the identity

$$\mathrm{sn}{\left(x\right|m)}^2+{\mathrm{cn}}^2\left(x\right|m)=1$$

Furthermore,

$$\mathrm{dn}\left(x\right|m)=\sqrt{1-m{\mathrm{sn}}^2\left(x\right|m)}$$

Therefore, we have the identity

$$\mathrm{dn}{\left(x\right|m)}^2+m{\mathrm{sn}}^2\left(x\right|m)=1$$

Appendix A.2. Elliptic Integrals of the Second Kind

An incomplete elliptic integral of the second kind is defined as follows:

$$E\left(\varphi |m\right):={\int }_0^{\varphi }\sqrt{1-m{sin}^{2}u}du$$

(A5)

for $m\le 1$. For $m>1$ the integral is analytically continued in the complex plane. The complete elliptic integral is defined as $E\left({\displaystyle \frac{\pi }{2}}|m\right)=:E\left(m\right)$.

The Jacobi epsilon function $\mathcal{E}\left(x\right|m)$ is defined as

$$\mathcal{E}\left(x\right|m):={\int }_0^x{\mathrm{dn}}^2\left(t\right|m)dt$$

(A6)

The epsilon function is related to the incomplete elliptic integral of the second kind as

$$E\left(\mathrm{am}\right(x\left|m\right)\left|m\right)=\mathcal{E}\left(x\right|m)$$

(A7)

Appendix A.3. Elliptic Integrals of the Third Kind

The incomplete elliptic integral of the third kind is given by

$$\Pi \left(n,\varphi |m\right)={\int }_0^{\varphi }{\displaystyle \frac{1}{1-n{sin}^2\theta }}{\displaystyle \frac{d\theta }{\sqrt{1-m{sin}^2\theta }}}$$

(A8)

Furthermore, the integral can be analytically continued to a quasi-periodic function as

$$\Pi \left(n,\varphi |m\right)=\Pi \left(n,\left\{\varphi \right\}|m\right)+2⌊{\displaystyle \frac{\mathrm{Re}\left(\varphi \right)}{\pi }}⌋\Pi (n\mid m)$$

where $\left\{\varphi \right\}:=\varphi mod\pi$ denotes the fractional part of $\varphi$ modulo $\pi$. The integral is related to the elliptic functions by the integral equation

$$\Pi \left(n,\varphi |m\right)={\int }_0^z{\displaystyle \frac{du}{1-n{\mathrm{sn}}^2\left(u\right|m)}},z=\mathcal{F}\left(\varphi |m\right)$$

(A9)

This formula follows from the substitution $\theta =\mathrm{am}\left(u\right|m)$ so that $z=\mathcal{F}\left(\varphi |m\right)$ in the original argument. Therefore, we can also define the formula

$$\Pi \left(n,\mathrm{am}\left(\varphi \right|m\left)\right|m\right)={\int }_0^{\varphi }{\displaystyle \frac{du}{1-n{\mathrm{sn}}^2\left(u\right|m)}}=:\mathcal{P}(n,\varphi |m)$$

The complete elliptic integral of the third kind is given by

$$\Pi \left(n|m\right)=\Pi \left(n,{\displaystyle \frac{\pi }{2}}|m\right)={\int }_0^{{\displaystyle \frac{\pi }{2}}}{\displaystyle \frac{1}{1-n{sin}^2\theta }}{\displaystyle \frac{d\theta }{\sqrt{1-m{sin}^2\theta }}}$$

(A10)

Appendix A.4. Integral Identities

The following identities hold true:

$$\begin{array}{cc}\hfill {\int }_0^s\mathrm{sn}\left(u\right|m)\mathrm{cn}\left(u\right|m)du& =-{\displaystyle \frac{\mathrm{dn}\left(s\right|m)-1}{m}}\hfill \end{array}$$

(A11)

$$\begin{array}{cc}\hfill {\int }_0^s{\mathrm{cn}}^2\left(u\right|m)du& ={\displaystyle \frac{\mathcal{E}\left(s\right|m)-(1-m)s}{m}},\hfill \end{array}$$

(A12)

$$\begin{array}{cc}\hfill {\int }_0^s{\mathrm{sn}}^2\left(u\right|m)du& =-{\displaystyle \frac{\mathcal{E}\left(s\right|m)-s}{m}}\hfill \end{array}$$

(A13)

Appendix A.5. Inner and Outer Products in ${\mathbb{G}}^3$

Multiplication table of the geometric product:

Multiplication table of the symmetric inner product (i.e., Hestenes contraction):

Multiplication table of the anti-symmetric outer product:

Appendix A.6. Noether Symmetries of a Second-Order Lagrangian

Consider the action

$$\mathcal{A}[\gamma ,t,t^{\prime }]={\int }_0^L\mathcal{L}ds$$

A Noether current $\delta N$ comes from the first-order variation of boundary terms of the action,

$$\delta N=\delta \gamma ·\left({\nabla }_t-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\right)\mathcal{L}+\delta {\gamma }^{\prime }·{\nabla }_{t^{\prime }}\mathcal{L}=\delta \gamma ·\left({\nabla }_t-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\right)\mathcal{L}+\delta t·{\nabla }_{t^{\prime }}\mathcal{L}$$

(A14)

while the complete variation of the system is

$$\delta \mathcal{A}=\delta N{|}_0^L+{\int }_0^L\delta \gamma ·\left({\nabla }_{\gamma }\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_t\mathcal{L}+{\left({\displaystyle \frac{d}{ds}}\right)}^2{\nabla }_{t^{\prime }}\mathcal{L}\right)ds$$

(A15)

so that both terms vanish on shell.

To obtain the rotational symmetry, consider the infinitesimal virtual rotation of magnitude $\delta \varphi$ specified by the constant bi-vector $B=\delta \varphi /2U$. The resulting variations are

$$\begin{array}{cc}\hfill \delta \gamma & \mapsto exp\left(-{\displaystyle \frac{\delta \varphi }{2}}U\right)\gamma exp\left({\displaystyle \frac{\delta \varphi }{2}}U\right)-\gamma \hfill \\ \hfill \delta t& \mapsto exp\left(-{\displaystyle \frac{\delta \varphi }{2}}U\right)texp\left({\displaystyle \frac{\delta \varphi }{2}}U\right)-t\hfill \\ \hfill \delta t^{\prime }& \mapsto exp\left(-{\displaystyle \frac{\delta \varphi }{2}}U\right)t^{\prime }exp\left({\displaystyle \frac{\delta \varphi }{2}}U\right)-t^{\prime }\hfill \end{array}$$

For example, $\delta t$ is developed to first order as

$$\delta t=\left(1-{\displaystyle \frac{\delta \varphi }{2}}U\right)t\left(1+{\displaystyle \frac{\delta \varphi }{2}}U\right)-t+\mathcal{O}\left(\delta {\varphi }^2\right)=\delta \varphi t·U+\mathcal{O}\left(\delta {\varphi }^2\right)$$

In the same way

$$\delta t^{\prime }=\delta \varphi t^{\prime }·U+\mathcal{O}\left(\delta {\varphi }^2\right)$$

$$\delta \gamma =\delta \varphi \gamma ·U+\mathcal{O}\left(\delta {\varphi }^2\right)$$

Therefore, the Noether current becomes

$$\delta N=\delta \varphi \gamma ·U·J+\delta \varphi t·U·t^{\prime }=\delta \varphi \left(\gamma ·U·J+t·U·t^{\prime }\right)=\delta \varphi U·\left(\gamma \wedge J+t\wedge t^{\prime }\right)$$

Therefore, the bi-vector

$$\mathcal{M}:={\nabla }_U{\displaystyle \frac{\delta N}{\delta \varphi }}=\gamma \wedge J+t\wedge t^{\prime }$$

is conserved on shell, where the geometric derivative is also suitably extended as ${\nabla }_U=e_{ji}{\partial }_{u_{ij}}$.

To obtain the translational symmetry, consider an infinitesimal virtual translation in direction v and of magnitude $\delta h$. Then the variations are

$$\delta \gamma =\delta t=\delta hv+\mathcal{O}\left(\delta h^2\right),\delta t^{\prime }=0+\mathcal{O}\left(\delta h^2\right)$$

Then we have

$$\delta N=\delta hv·J$$

and in the same way the vector

$${\nabla }_v{\displaystyle \frac{\delta N}{\delta h}}=J$$

is conserved on shell.

To obtain the Hamiltonian consider an infinitesimal virtual stretch $s^{\prime }\mapsto s+\delta l$. Then the variations are

$$\delta \gamma =\delta lt+\mathcal{O}\left(\delta l^2\right),\delta t=\delta l{t}^{\prime }+\mathcal{O}\left(\delta l^2\right)$$

Then

$$\delta N=\delta lt·\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)+\delta l{t}^{\prime }·{\nabla }_{t^{\prime }}\mathcal{L}=:P\delta l$$

Differentiate P:

$$\begin{array}{c}{P}^{\prime }=t^{\prime }·\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)+t·{\displaystyle \frac{d}{ds}}\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)+t^{\prime \prime }·{\nabla }_{t^{\prime }}\mathcal{L}+t^{\prime }·{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}=\hfill \\ \hfill t^{\prime }·{\nabla }_t\mathcal{L}+t·{\displaystyle \frac{d}{ds}}\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)+t^{\prime \prime }·{\nabla }_{t^{\prime }}\mathcal{L}\end{array}$$

However,

$$t^{\prime }·{\nabla }_t\mathcal{L}+t^{″}·{\nabla }_{t^{\prime }}\mathcal{L}={\mathcal{L}}^{\prime }-t·{\nabla }_{\gamma }\mathcal{L}$$

Therefore,

$$P^{\prime }={\mathcal{L}}^{\prime }-t·{\nabla }_{\gamma }\mathcal{L}+t·{\displaystyle \frac{d}{ds}}\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)={\mathcal{L}}^{\prime }+t·\left(-{\nabla }_{\gamma }\mathcal{L}+{\displaystyle \frac{d}{ds}}\left({\nabla }_t\mathcal{L}-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\mathcal{L}\right)\right)$$

On shell the second term vanishes so that

$$P^{\prime }={\mathcal{L}}^{\prime }$$

Therefore, the scalar Hamiltonian

$$P-\mathcal{L}=t·\left({\nabla }_t-{\displaystyle \frac{d}{ds}}{\nabla }_{t^{\prime }}\right)\mathcal{L}+t^{\prime }·{\nabla }_{t^{\prime }}\mathcal{L}-\mathcal{L}=\mathcal{H}$$

is conserved along the lines of Ostrogradsky theory [23].