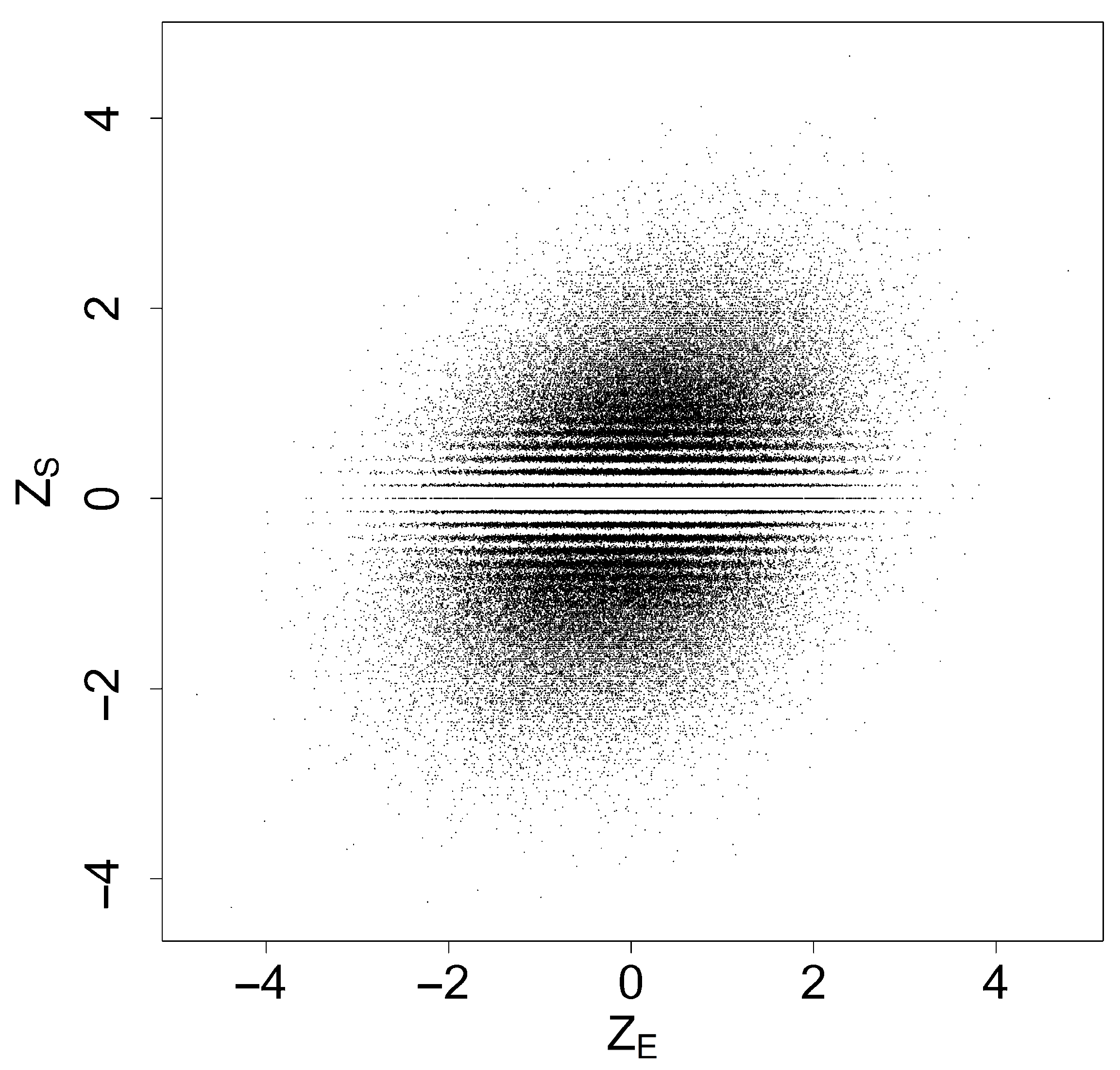Inflation of Familywise Error Rate in Treatment Efficacy Testing Due to the Reallocation of Significance Levels Based on Safety Data

Abstract

In randomized clinical trials comparing two standard treatments, a two-sided test for efficacy at a significance level $\alpha$ is typically used when neither treatment is expected to be superior at the design stage. This two-sided test comprises two one-sided tests, each conducted at a significance level of $\alpha /2$. If safety data later suggest that one treatment is not clinically acceptable due to a higher rate of adverse events, investigators may reallocate the $\alpha /2$ significance level originally assigned to the one-sided efficacy test for that treatment to the other one-sided test. This results in a two-stage procedure. We examine the impact of such reallocation on the familywise error rate (FWER). Using theoretical derivations and simulation studies, we show that FWER can exceed the nominal level $\alpha$ when the treatment with fewer adverse events tends to show greater efficacy. Therefore, the two-stage procedure should be avoided when strict control of FWER is a priority. These findings emphasize the need for caution when reallocating significance levels based on auxiliary information and have implications beyond clinical trials, particularly in adaptive statistical methodologies.

1. Introduction

This paper considers a randomized clinical trial comparing the efficacy of two standard treatments. When neither treatment is expected to be superior at the design stage, a two-sided test for efficacy at a significance level $\alpha$ is typically employed [1]. If one treatment is shown to be more effective than the other, it will continue to be the standard treatment, while the other will not be adopted as the standard treatment.

The two-sided test at a significance level of $\alpha$ consists of two one-sided tests, each assessing whether one treatment is superior to the other, with a significance level of $\alpha /2$. If, for some reason, one of the one-sided tests becomes irrelevant, the significance level of $\alpha /2$ assigned to that test will be wasted. Suppose that one treatment is found to have a very high rate of adverse events. Even though it has been shown to be more effective, clinicians may consider it unreasonable for that treatment to remain the standard while the other treatment does not. In such a case, investigators would not be interested in demonstrating that the treatment is more effective. Instead, they would seek to reallocate the significance level of $\alpha /2$, originally assigned to testing whether the treatment is more effective, to testing whether the other treatment is more effective.

This procedure consists of two stages: The first stage reviews safety data and determines the reallocation of the significance level, while the second stage conducts the efficacy test. Two-stage procedures in hypothesis testing, although different from the one described above, have been widely discussed in the statistical literature [2,3,4,5,6]. If the two stages are not properly considered, using these procedures can lead to an increased type I error rate or familywise error rate (FWER), defined as the probability of rejecting one or more true null hypotheses under any combination of true and false null hypotheses [7].

For example, seamless phase II/III trials use data from the phase II stage in the phase III stage, and the two-stage procedure involves decisions made at both stages [2]. Senn [3] introduced a different two-stage procedure in a cross-over trial, where a preliminary test on a carry-over effect guides the choice of a primary test for the treatment effect. Similarly, Kahan [4] considered a factorial design and used an interaction test to determine whether to compare individual treatment combinations or contrasts such as A vs. not-A and B vs. not-B. Campbell and Dean [5] considered a two-stage procedure for Cox models, selecting a test for regression coefficients based on a test of the proportional hazard assumption. A two-stage procedure for group-sequential designs with two endpoints was also described in [6].

To the best of our knowledge, the reallocation of significance levels in two-sided hypothesis testing problems has not been mathematically investigated in the existing literature. This paper examines the validity of the two-stage procedure in such settings in terms of controlling FWER. The remainder of the paper is organized as follows. Section 2 provides a formal analytic description of the problem, followed by the calculation of FWER in Section 3 and the calculation of power in Section 4. Section 5 presents a statistical model for individuals, which satisfies the requirements outlined in Section 2. Section 6 presents a concluding discussion.

2. Reallocation of Significance Levels Based on Safety Data

We present a formal analytic description of the problem discussed in the Introduction. Two treatments are represented by $T_1$ and $T_2$. For simplicity, we assume that the safety data used to determine the reallocation of significance levels relate to a single adverse event and are summarized by the difference in the proportions of patients experiencing the adverse event under treatments $T_1$ and $T_2$. In addition, a rule for determining the reallocation of significance levels based on these data is established when planning the trial. Let $\theta$ be an effect measure of efficacy, where $\theta >0$ indicates that $T_1$ is more efficacious than $T_2$, $\theta =0$ indicates that $T_1$ and $T_2$ have the same efficacy, and $\theta <0$ indicates that $T_2$ is more efficacious than $T_1$. One example of such a measure is $\theta =E\left(Y\right|T=T_1)-E(Y|T=T_2)$, where $Y$ is a continuous outcome and $T$ is the assigned treatment taking values $T_1$ and $T_2$. The null hypotheses of the two one-sided and one two-sided tests concerning $\theta$ are defined as $H_0^{T_1}:\theta \le 0$, $H_0^{T_1,T_2}:\theta =0$, and $H_0^{T_2}:\theta \ge 0$. Note that $H_0^{T_1,T_2}=H_0^{T_1}\cap H_0^{T_2}$.

Let $Z_E$ be a test statistic for $\theta$ that follows a normal distribution with mean $\theta$ and variance 1. Let $Z_S$ be the standardized difference between the proportions of patients experiencing an adverse event under treatments $T_1$ and $T_2$. Suppose that $(Z_E,Z_S)$ follows a two-dimensional normal distribution with mean vector $(\theta ,0)$, marginal variances of $1$, and correlation coefficient $r$. The mean of $Z_S$ is assumed to be 0 since it is not the focus of interest.

A two-stage procedure is determined with cutoff values $c_L$ and $c_U$ ($c_L\le c_U$) for safety data. If $c_L\le Z_S\le c_U$, the two-sided test for $H_0^{T_1, T_2}$ is conducted at the significance level of $\alpha$, which is equivalent to performing two one-sided tests for $H_0^{T_1}$ and $H_0^{T_2}$, each at the significance level of $\alpha /2$. If $Z_S>c_U$, the significance level of $\alpha /2$ assigned to the test for $H_0^{T_1}$ is reallocated to the test for $H_0^{T_2}$, so that only the test for $H_0^{T_2}$ is conducted at the significance level of $\alpha$. If $Z_S<c_L$, the significance level of $\alpha /2$ assigned to the test for $H_0^{T_2}$ is reallocated to the test for $H_0^{T_1}$, so that only the test for $H_0^{T_1}$ is conducted at the significance level of $\alpha$.

The two-stage procedure described above maintains a type I error rate of $\alpha$ for each test. However, due to the correlation $r=\mathrm{c}\mathrm{o}\mathrm{r}(Z_E,Z_S)$ between the efficacy test statistic and the safety index, it is unclear if the two-stage procedure adequately controls FWER. The next section mathematically evaluates FWER for the two-stage procedure.

3. Derivation of the Familywise Error Rate for the Two-Stage Procedure

This section evaluates FWER for the two-stage procedure. FWER for the two-stage procedure is a function of the effect measure $\theta$, the correlation coefficient $r$, the cutoff values $c_L$ and $c_U$, and the significance level $\alpha$. The function is denoted by FWER$(\theta ,r,c_L,c_U,\alpha )$. Let $\Phi \left(x\right)$ be the cumulative distribution function of the standard normal distribution, and let $z_{\alpha }$ be the critical value of the standard normal distribution cutoff probability $\alpha$ in the upper tail.

In the following, we evaluate FWER in three distinct cases: $\theta >0$, $\theta <0$, and $\theta =0$. When $\theta >0$, FWER is given by

$$\mathrm{FWER}\left(\theta ,r,c_L,c_U,\alpha \right)=P\left({c_U<Z}_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha /2}\right).$$

Since $-z_{\alpha /2}<-z_{\alpha },$ it follows that

$$\begin{gathered} P\left({c_U<Z}_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha /2}\right) \\ <P\left({c_U<Z}_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha }\right), \end{gathered}$$

which equals $P\left(c_L\le Z_S,Z_E<-z_{\alpha }\right).$ We then have

$${\displaystyle \begin{array}{l}\hspace{1em}P\left(c_L\le Z_S, Z_E<-z_{\alpha }\right)\hfill \\ \le P\left(Z_E<-z_{\alpha }\right)\\ =P\left(Z_E-\theta <{-z}_{\alpha }-\theta \right)\\ =\Phi \left(-z_{\alpha }-\theta \right)<\Phi \left({-z}_{\alpha }\right)\\ =\alpha .\end{array}}$$

Hence, for $\theta >0$, we conclude that FWER$\left(\theta ,r,c_L,c_U,\alpha \right)\le \alpha$.

When $\theta <0,$ FWER is given by

$$\mathrm{FWER}\left(\theta ,r,c_L,c_U,\alpha \right)=P\left(Z_S<c_L, z_{\alpha }<Z_E\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}{<Z}_E\right).$$

Since $z_{\alpha }<z_{\alpha /2},$ it follows that

$$\begin{gathered} P\left(Z_S<c_L, z_{\alpha }<Z_E\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}{<Z}_E\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<P\left(Z_S<c_L, z_{\alpha }<Z_E\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha }{<Z}_E\right), \end{gathered}$$

which equals $P\left(Z_S\le c_U,z_{\alpha }<Z_E\right).$ We then have

$$\begin{array}{l}\hspace{1em}P\left(Z_S\le c_U, z_{\alpha }<Z_E\right)\\ \le P\left(z_{\alpha }<Z_E\right)\\ =P\left(z_{\alpha }-\theta <Z_E-\theta \right)\\ =1-\Phi \left(z_{\alpha }-\theta \right)\\ <1-\Phi \left(z_{\alpha }\right)\\ =\alpha .\end{array}$$

Hence, for $\theta <0$, we conclude that FWER$\left(\theta ,r,c_L,c_U,\alpha \right)\le \alpha$.

When $\theta =0$, FWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ is given by

$$P\left(c_U<Z_S,Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}<\left|Z_E\right|\right)+P\left(Z_S<c_L,z_{\alpha }<Z_E\right).$$

When $\theta =0$ and $r=0$, $Z_E$ and $Z_S$ are independent since $\left(Z_E,Z_S\right)$ follows a two-dimensional normal distribution. Therefore, FWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ can be written as

$$\begin{gathered} P\left(c_U<Z_S\right)P\left(Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U\right)P\left(z_{\alpha /2}<\left|Z_E\right|\right) \\ +P\left(Z_S<c_L\right)P\left(z_{\alpha }<Z_E\right), \end{gathered}$$

which equals

$$\alpha \left(P\left(c_U<Z_S\right)+P\left(c_L\le Z_S\le c_U\right)+P\left(Z_S<c_L\right)\right)=\alpha .$$

Hence, when $\theta =0$ and $r=0$, we conclude that FWER$\left(\theta ,r,c_L,c_U,\alpha \right)=\alpha$.

When $\theta =0$ and $r\ne 0$, FWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ can be calculated via a numerical integration.

Table 1. FWERs of the two-stage procedure at $\theta =0$ and $\alpha =0.05.$

${\mathit{c}}_{\mathit{L}}$	${\mathit{c}}_{\mathit{U}}$	$\mathit{r}$
		−0.99	−0.80	−0.60	−0.40	−0.20	0.20	0.40	0.60	0.80	0.99
−0.1	0.1	0.100	0.099	0.093	0.081	0.066	0.034	0.019	0.006	0.000	0.000
−1.0	1.0	0.100	0.088	0.077	0.068	0.059	0.039	0.028	0.016	0.005	0.000
−1.5	1.5	0.097	0.073	0.065	0.060	0.055	0.044	0.037	0.027	0.014	0.000
−2.0	2.0	0.054	0.059	0.056	0.054	0.052	0.047	0.044	0.038	0.029	0.009
−2.5	2.5	0.050	0.052	0.052	0.051	0.051	0.049	0.048	0.045	0.042	0.038

FWER denotes the familywise error rate. $c_L$ and $c_U$ represent the lower and upper cutoff values for $Z_S$, respectively. $r$ denotes the correlation coefficient between $Z_E$ and $Z_S$.

presents the values of FWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ for $\alpha =0.05$ under various combinations of $r, c_L,$ and $c_U$. When $Z_E$ and $Z_S$ are negatively correlated, that is, when treatments with fewer adverse events tend to show better efficacy, FWER exceeds $\alpha$. In contrast, when $Z_E$ and $Z_S$ are positively correlated, that is, when treatments with more adverse events tend to show better efficacy, FWER remains below $\alpha$. When the absolute values of $c_L$ and $c_U$ are large (i.e., $\left|c_L\right|=\left|c_U\right|\ge 2.5$), the probability that no reallocation occurs is high, and as a result, FWER tends to be controlled at $\alpha$. In contrast, when the absolute values of $c_L$ and $c_U$ are small (i.e., $\left|c_L\right|=\left|c_U\right|\le 2.0$), the probability of reallocation increases, and as a result, the maximum FWER can reach $2\alpha =0.10$.

The observation regarding the maximum value of FWER can be formally proven. When $\theta =0$ and $r\ne 0$, the maximum value of FWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ is equal to $2\alpha$ since

$$\begin{array}{l}\hspace{1em}\mathrm{F}\mathrm{W}\mathrm{E}\mathrm{R}\left(\theta ,r,c_L,c_U,\alpha \right)\\ =P\left(c_U<Z_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}<\left|Z_E\right|\right)+P\left(Z_S<c_L,z_{\alpha }<Z_E\right)\\ =P\left(c_U<Z_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha /2}\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}<Z_E\right)+P\left(Z_S<c_L,z_{\alpha }<Z_E\right)\\ \le P\left(c_U<Z_S, Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha }<Z_E\right)+P\left(Z_S<c_L,z_{\alpha }<Z_E\right)\\ =P\left(c_L\le Z_S, Z_E<-z_{\alpha }\right)+P\left(Z_S\le c_U,z_{\alpha }<Z_E\right)\\ \le P\left( Z_E<-z_{\alpha }\right)+P\left(z_{\alpha }<Z_E\right)\\ =2\alpha .\end{array}$$

Equality holds if and only if the correlation coefficient $r=-1$ and the cutoff values satisfy $-z_{\alpha }\le c_L\le c_U\le z_{\alpha }$. We now provide a proof of this statement. Note that $\mathrm{F}\mathrm{W}\mathrm{E}\mathrm{R}\left(\theta ,r,c_L,c_U,\alpha \right)=2\alpha$ holds if and only if the following three equalities are satisfied:

$$P\left(c_L\le Z_S\le c_U, \left|Z_E\right|>z_{\alpha /2}\right)=P\left(c_L\le Z_S\le c_U, \left|Z_E\right|>z_{\alpha }\right),$$

(1)

$$P\left(c_L\le Z_S, Z_E<-z_{\alpha }\right)=P\left(Z_E<-z_{\alpha }\right),$$

(2)

$$P\left(Z_S\le c_U, z_{\alpha }<Z_E\right)=P\left(z_{\alpha }<Z_E\right) .$$

(3)

If $\left|r\right|<1$, then equalities (2) and (3) cannot hold. Therefore, we must have $\left|\mathrm{r}\right|=1.$ Suppose $\mathrm{r}=1$. Then, ${\mathrm{Z}}_{\mathrm{E}}={\mathrm{Z}}_{\mathrm{S}}$ and from (2) we have

$$P\left(c_L\le Z_E, Z_E<-z_{\alpha }\right)=P\left(Z_E<-z_{\alpha }\right),$$

which leads to a contradiction. Therefore, $r$ must be $-1$. In this case, from (2), we obtain

$$P\left(Z_E\le -c_L, Z_E<-z_{\alpha }\right)=P\left(Z_E<-z_{\alpha }\right),$$

which implies $-z_{\alpha }\le -c_L$, that is, $c_L\le z_{\alpha }$. Similarly, from (3) we obtain

$$P\left(-c_U\le Z_E, z_{\alpha }<Z_E\right)=P\left(z_{\alpha }<Z_E\right),$$

which implies $-c_U\le z_{\alpha }$, that is, $-z_{\alpha }\le c_U$. From (1), we have

$$P\left({-c}_U\le Z_E\le -c_L, \left|Z_E\right|>z_{\alpha /2}\right)=P\left({-c}_U\le Z_E\le -c_L, \left|Z_E\right|>z_{\alpha }\right),$$

which implies $-z_{\alpha }\le -c_U$ and $-c_L\le z_{\alpha }$, that is, $-z_{\alpha }\le c_L$ and $c_U\le z_{\alpha }$. Then, equalities (1)–(3) hold if and only if $r=-1$, and $-z_{\alpha }\le c_L\le c_U\le z_{\alpha }$. This completes the proof. The following theorem summarizes the discussion above.

Theorem 1.

FWER of the two-stage procedure satisfies the following properties: When $\theta \ne 0$, or $\theta =0$ and $r=0$, the FWER of the two-stage procedure can be controlled at $\alpha$. When $\theta =0$ and $r\ne 0$, FWER may exceed $\alpha$ and it can reach the maximum value of $2\alpha$ when $r=-1$ and $-z_{\alpha }\le c_L\le c_U\le z_{\alpha }$.

4. Derivation of Power for the Two-Stage Procedure

The power of the two-stage procedure to detect a true alternative hypothesis is a function of the effect measure $\theta$, the correlation coefficient $r$, the cutoff values $c_L$ and $c_U$, and the significance level $\alpha$. It is denoted by POWER$(\theta ,r,c_L,c_U,\alpha )$.

• When $\theta >0,$ POWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ is given by

$$P\left(Z_S<c_L,z_{\alpha }{<Z}_E\right)+P\left(c_L\le Z_S\le c_U,z_{\alpha /2}<Z_E\right).$$

When $\theta <0$, POWER$\left(\theta ,r,c_L,c_U,\alpha \right)$ is given by

$$P\left(c_U<Z_S,Z_E<-z_{\alpha }\right)+P\left(c_L\le Z_S\le c_U,Z_E<-z_{\alpha /2}\right).$$

When $\theta =0$, POWER$\left(\theta ,r,c_L,c_U,\alpha \right)=0$, as all alternative hypotheses are false. The power of the two-stage procedure can also be calculated via numerical integration.

Table 2. Power of the two-stage procedure at $\alpha =0.05.$

$\mathit{\theta }$	${\mathit{c}}_{\mathit{L}}$	${\mathit{c}}_{\mathit{U}}$	$\mathit{r}$
			−0.99	−0.80	−0.40	−0.20	0.20	0.40	0.80	0.99
3.0	−0.1	0.1	0.540	0.536	0.513	0.500	0.475	0.464	0.451	0.452
3.0	−1.5	1.5	0.851	0.836	0.811	0.803	0.795	0.794	0.795	0.786
3.0	−2.5	2.5	0.851	0.851	0.848	0.847	0.846	0.846	0.845	0.845
1.5	−0.1	0.1	0.428	0.367	0.293	0.261	0.198	0.164	0.078	0.001
1.5	−1.5	1.5	0.323	0.325	0.325	0.318	0.298	0.285	0.259	0.256
1.5	−2.5	2.5	0.323	0.323	0.323	0.323	0.320	0.318	0.317	0.317
0.5	−0.1	0.1	0.126	0.122	0.096	0.080	0.047	0.031	0.003	0.000
0.5	−1.5	1.5	0.077	0.084	0.079	0.076	0.065	0.058	0.036	0.010
0.5	−2.5	2.5	0.072	0.073	0.073	0.073	0.071	0.070	0.067	0.066
−0.5	−0.1	0.1	0.126	0.122	0.096	0.080	0.047	0.031	0.003	0.000
−0.5	−1.5	1.5	0.077	0.084	0.079	0.076	0.065	0.058	0.036	0.010
−0.5	−2.5	2.5	0.072	0.073	0.073	0.073	0.071	0.070	0.067	0.066
−1.5	−0.1	0.1	0.428	0.367	0.293	0.261	0.198	0.164	0.078	0.001
−1.5	−1.5	1.5	0.323	0.325	0.325	0.318	0.298	0.285	0.259	0.256
−1.5	−2.5	2.5	0.323	0.323	0.323	0.323	0.320	0.318	0.317	0.317
−3.0	−0.1	0.1	0.540	0.536	0.513	0.500	0.475	0.464	0.451	0.452
−3.0	−1.5	1.5	0.851	0.836	0.811	0.803	0.795	0.794	0.795	0.786
−3.0	−2.5	2.5	0.851	0.851	0.848	0.847	0.846	0.846	0.845	0.845

Power denotes the probability of detecting a true alternative hypothesis. $\theta$ represents the effect measure. $c_L$ and $c_U$ are the cutoff values for $Z_S$. $r$ denotes the correlation coefficient between $Z_E$ and $Z_S$.

presents the power of the two-stage procedure for $\alpha =0.05$ under various values of $r, c_L,$ and $c_U$. The two values of the power function for $\left|\theta \right|=3.0$ are identical, and this equality holds for other values of $\theta$ as well. This pattern arises from the symmetry of the bivariate normal distribution. When $\theta =3.0$ and $\left|c_L\right|=\left|c_U\right|=2.5$ or $1.5$, the probability of conducting the test for $H_0^{T_1}:\theta \le 0$ is high, resulting in high power. The same applies when $\theta =-3.0$, in which case the test for $H_0^{T_2}:\theta \ge 0$ is likely to be conducted. In contrast, when $\theta =3.0$and $\left|c_L\right|=\left|c_U\right|=0.1$, the probability of conducting the test for $H_0^{T_1}:\theta \le 0$ is low, resulting in low power. The same applies when $\theta =-3.0$, in which case the test for $H_0^{T_2}:\theta \ge 0$ is unlikely to be conducted. As the correlation coefficient $r$ increases, the power decreases since the probability of conducting the test for $H_0^{T_1}:\theta \le 0$ when $\theta >0$, and for $H_0^{T_2}:\theta \ge 0$ when $\theta <0$, decreases. The power of the two-sided test for $H_0^{T_1, T_2}:\theta =0$ is equal to $0.851$, $0.323$, $0.072$, $0.072$, $0.323$ and $0.851$, for $\theta =3.0, 1.5, 0.5,-0.5,-1.5,$ and $-3.0$, respectively. When $\left|\theta \right|=3.0$, the power of the two-stage procedure is, in some cases, lower than that of the two-sided test. This may be problematic. In contrast, when $\left|\theta \right|=1.5$, the power of the two-stage procedure, in some cases, exceeds that of the two-sided test. However, this improvement in power is a direct consequence of the failure to control the FWER under $\theta =0$; in other words, the gain in power reflects a loss of error rate control.

5. A Statistical Model Satisfying the Assumptions in Section 2

We present a statistical model for individuals that is appropriate for the setting described in Section 2. For $i,j=1,\dots ,n,$ let $L_i^{T_1}$ and $L_j^{T_2}$ denote latent variables for individuals receiving treatments $T_1$ and $T_2$, respectively. These variables are assumed to be independently and identically distributed as standard normal variables.

For a patient $i$ receiving $T_1$, the efficacy outcome $Y_{i,E}^{T_1}$ is given by $L_i^{T_1}+d$ for some positive value $d$, and the safety outcome $Y_{i,S}^{T_1}$ takes the value 0 (no adverse event) or 1 (adverse event) with probability

$$P\left(Y_{i,S}^{T_1}=1|L_i^{T_1}\right)=\exp \left(L_i^{T_1}-c\right)/\left\{1+\exp \left(L_i^{T_1}-c\right)\right\},$$

where we assume the logistic curve between the latent and response variable $L_i^{T_1}$ and $Y_{i,S}^{T_1}$. Here, $c$ is a constant term. Similarly, for patient $j$ receiving $T_2$, the efficacy outcome $Y_{j,E}^{T_2}$ is given by $L_j^{T_2}$, and the safety outcome $Y_{j,S}^{T_2}$ takes the value 0 (no adverse event) or 1 (adverse event) with probability

$$P\left(Y_{j,S}^{T_2}=1|L_j^{T_2}\right)=\exp \left(L_j^{T_2}-c\right)/\left\{1+\exp \left(L_j^{T_2}-c\right)\right\}.$$

When $c=1.0, 1.5,$and $2.0$, the probability that $Y_{i,S}^{T_1}$ or $Y_{j,S}^{T_2}$ equals 1 is $0.303$, $0.221$, and $0.115$, respectively. In this study, we set $c=2$.

In this setting, a test statistic for efficacy and a summary statistic for safety are given as

$$Z_E=\sqrt{{\displaystyle \frac{n}{2}}}\left({\displaystyle \frac{1}{n}}\sum _{i=1}^n{Y}_{i,E}^{T_1}-{\displaystyle \frac{1}{n}}\sum _{j=1}^n{Y}_{j,E}^{T_2}\right),$$

$$Z_S={\displaystyle \frac{\left(\frac{1}{n}{\sum }_{i=1}^n{Y}_{i,S}^{T_1}-\frac{1}{n}{\sum }_{j=1}^n{Y}_{j,S}^{T_2}\right)}{\sqrt{\left(\frac{1}{n}{\sum }_{i=1}^n{Y}_{i,S}^{T_1}\right)\left(1-\frac{1}{n}{\sum }_{i=1}^n{Y}_{i,S}^{T_1}\right)/n+\left(\frac{1}{n}{\sum }_{j=1}^n{Y}_{j,S}^{T_2}\right)\left(1-\frac{1}{n}{\sum }_{j=1}^n{Y}_{j,S}^{T_2}\right)/n}}}.$$

By the central limit theorem, the pair $\left(Z_E,Z_S\right)$ are asymptotically normally distributed and approximately satisfy the assumptions in Section 2. The mean of $Z_E$, denoted by $\theta$, is equal to $d/\sqrt{n/2}$, where $n$ is considered as a constant. The correlation coefficient between $Z_E$ and $Z_S$ was estimated via a Monte Carlo simulation. We generated data with $n=200$ and conducted ${10}^5$ repetitions under $\theta =0$, that is, $d=0$. This resulted in ${10}^5$ independent pairs of $\left(Z_E,Z_S\right)$, which are shown in the scatter plot in Figure 1. The correlation coefficient of $\left(Z_E,Z_S\right)$ was estimated to be 0.319, with a 95% confidence interval of $\left[0.314, 0.325\right]$.

Since the number of individuals in each treatment group is $n=200$, $Z_S$ can take at most $200\times 200=\mathrm{40,000}$ distinct values. As a result, certain values near zero are not represented in $Z_S$, leading to visible horizontal white lines in the scatterplot. As $n$ increases, these lines gradually disappear.

If the probability that $Y_{i,S}^{T_k}$ equals 1 is given by $\exp \left(-L_i^{T_k}-c\right)/\left\{1+\exp \left(-L_i^{T_k}-c\right)\right\}$ for $k=\mathrm{1,2}$, with $c=-2$, and all other settings remain as previously described, then the correlation coefficient between $Z_E$ and $Z_S$ was estimated to be $-0.319$, with a 95% confidence interval of $\left[-0.325, -0.314\right]$.

6. Concluding Discussion

In this paper, we consider a two-stage procedure in clinical trial settings comparing two standard treatments, in which a two-sided test for efficacy at a significance level of $\alpha$ is planned at the design stage. The $\alpha /2$ allocated to one of the two one-sided tests that constitute the two-sided test can potentially be reallocated as follows: the α/2 originally assigned to the one-sided test for the treatment with a higher rate of an adverse event is reallocated to the other one-sided test. In Theorem 1, we show that FWER for this two-stage procedure can exceed the nominal significance level $\alpha$ when the treatment associated with a lower rate of adverse event tends to demonstrate greater efficacy. Therefore, this procedure should be avoided when strict control of FWER is a priority.

Consider a clinical example in which cancer patients treated with anticancer drugs tend to experience greater treatment efficacy if they develop adverse events than if they do not [8]. In such a scenario, applying the two-stage procedure in a trial comparing two such anticancer drugs may control FWER at the nominal level $\alpha$; however, as demonstrated in this paper, it can result in reduced statistical power in some cases.

The main assumptions in Section 2 are as follows:

(1)

The test statistic for efficacy and the summary statistic for safety jointly follow a multivariate normal distribution.

(2)

The summary statistic for safety relates to a single adverse event and is determined by the difference in the proportions of patients experiencing the adverse event under treatments $T_1$ and $T_2$.

(3)

The cutoff values for the safety summary statistic are determined at the design stage and are used to guide the reallocation of the significance level.

Regarding Assumption (1), we consider it to be reasonable, as many commonly used test and summary statistics are asymptotically normally distributed under standard regularity conditions. Assumptions (2) and (3) were adopted to facilitate the theoretical derivation of the FWER. In practice, however, it may be difficult to pre-specify a single adverse event and fixed cutoff values at the design stage. More commonly, all safety data are reviewed after all data have been collected, but before efficacy data are analyzed, and the decision on whether to reallocate the significance level is taken following discussions among investigators. In such cases, the safety data may influence the choice of cutoff values, making the mathematical evaluation of FWER more complex. Therefore, for analytical tractability, we focused on a setting in which both the adverse event and the cutoff values are specified in advance. Given that our study demonstrated inflation of FWER even under this simplified setting—and that FWER control is not guaranteed under more flexible or data-driven reallocation procedures—we think that such procedures, including the one examined in this study, should be avoided when strict FWER control is required.

From a practical perspective, if a treatment is found to have a very high rate of adverse events, efficacy data may not be collected after patient dropout. In such cases, the sample sizes of both the intention-to-treat population and the full analysis set may become imbalanced between groups. In general, an imbalance in sample size can lead to reduced power in the two-stage procedure. However, this study focuses on fundamental theoretical aspects and does not address practical issues such as dropout-related sample size imbalance.

This study focused solely on a two-stage procedure. However, in three- or multi-stage procedures, inflation of FWER could also occur because correlations between the test statistic and other summary statistics, which drive the inflation, may also arise in these more complex settings.

The two-stage procedure examined in this study involves sequential decision-making and, therefore, bears some resemblance to group sequential designs and the associated bias correction for point estimation (e.g., [9,10]). However, a key difference is that group sequential designs involve repeated testing of a single null hypothesis, whereas our procedure conducts only a single hypothesis test in the second stage, guided by a decision taken in the first stage. The primary focus of this study is on controlling FWER in the second stage.

The implications of our findings extend beyond clinical trial settings. The issues addressed in this study commonly arise when significance levels are reallocated based on external or auxiliary information. Since intuitive reasoning about probabilities can be misleading, careful consideration is essential when employing complex testing procedures.