Viscoelectric and Steric Effects on Electroosmotic Flow in a Soft Channel
Abstract
1. Introduction
2. Problem Formulation
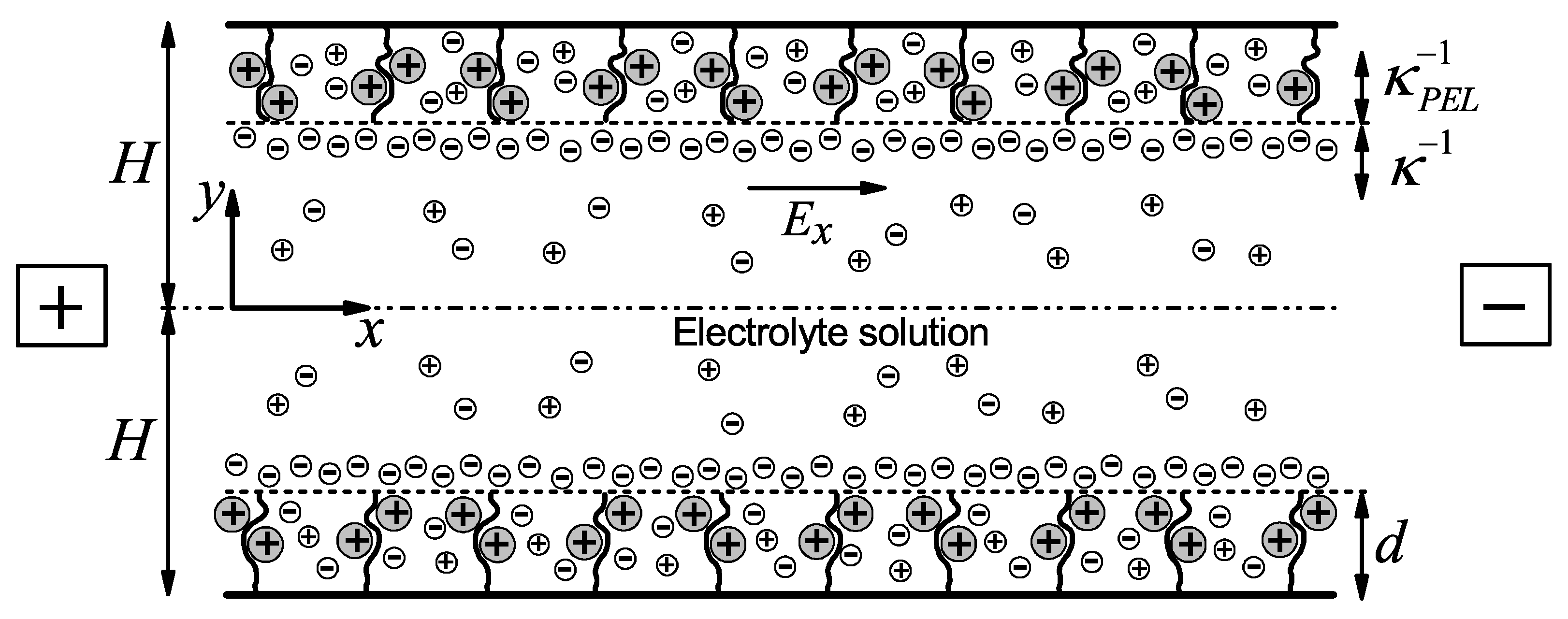
2.1. Physical Model
2.2. Governing Equations
2.3. Dimensionless Mathematical Model
3. Solution Methodology
4. Results and Discussion
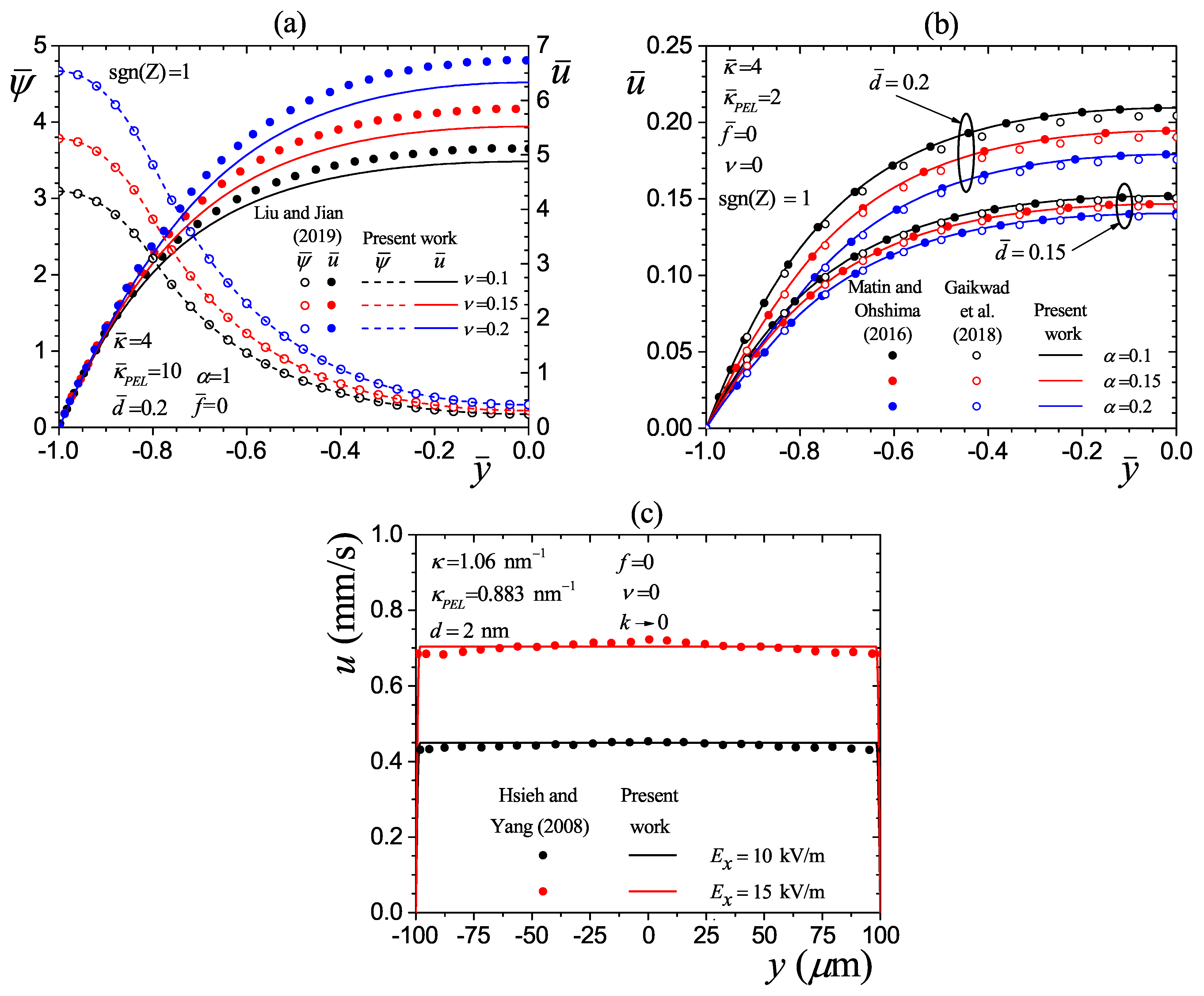
4.1. Validation
4.2. Electric Potential Distribution and Velocity Profiles
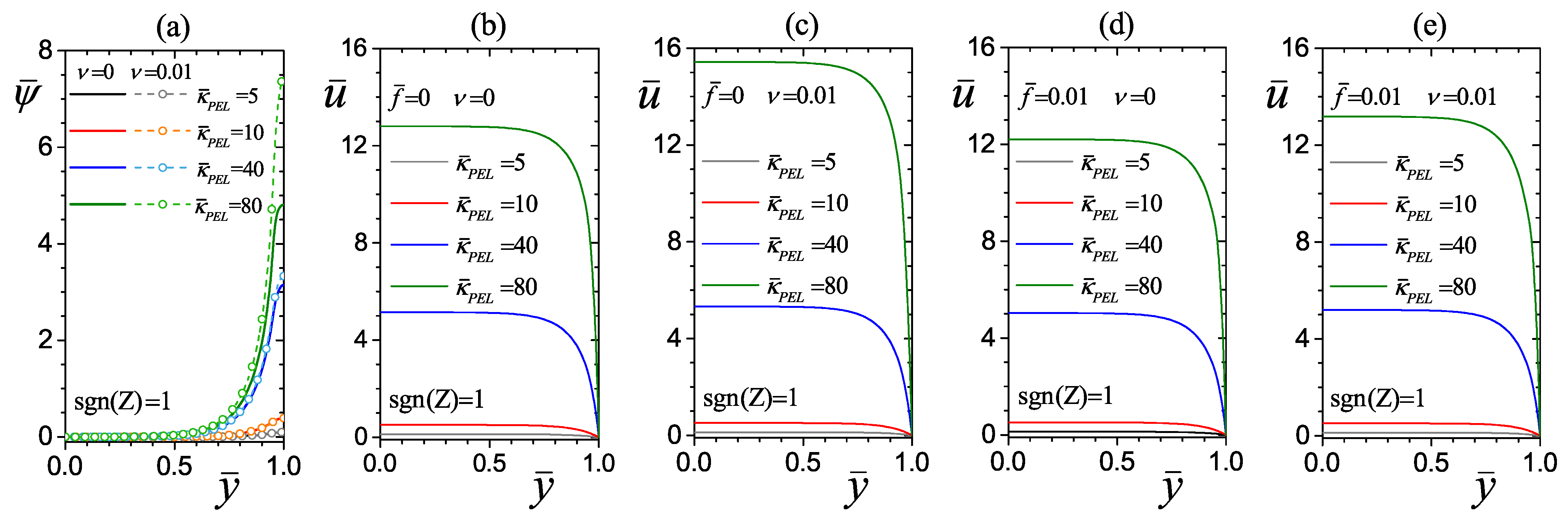
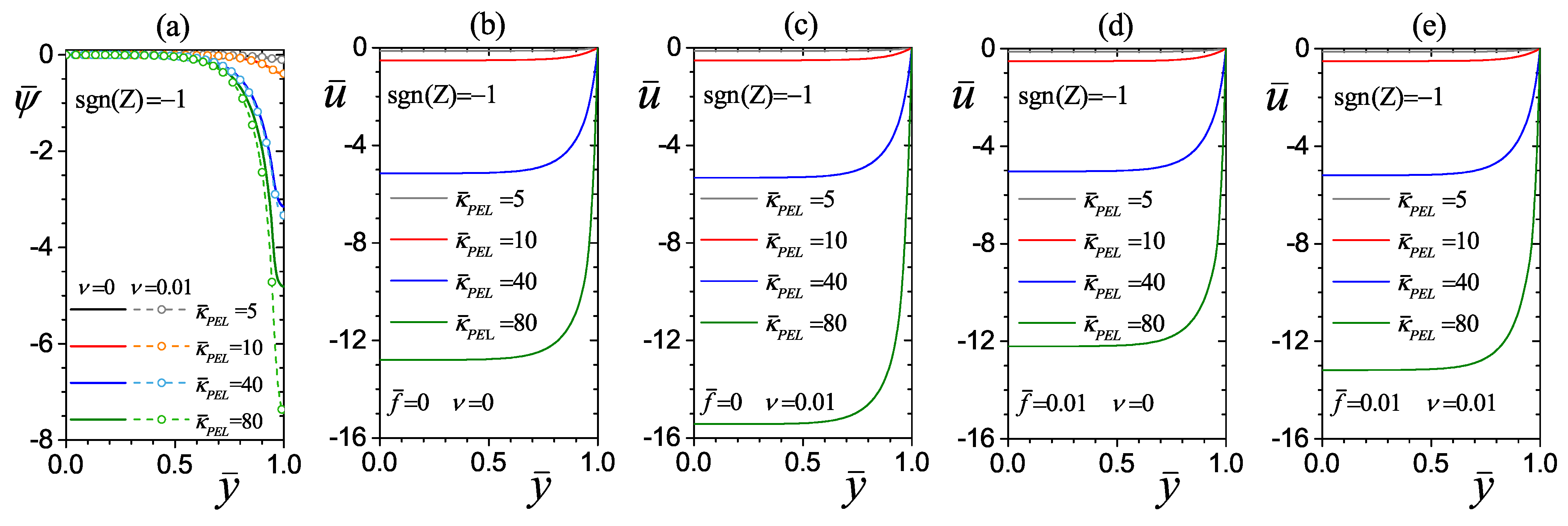
4.2.1. Effect of the Electrokinetic Parameter of the PEL
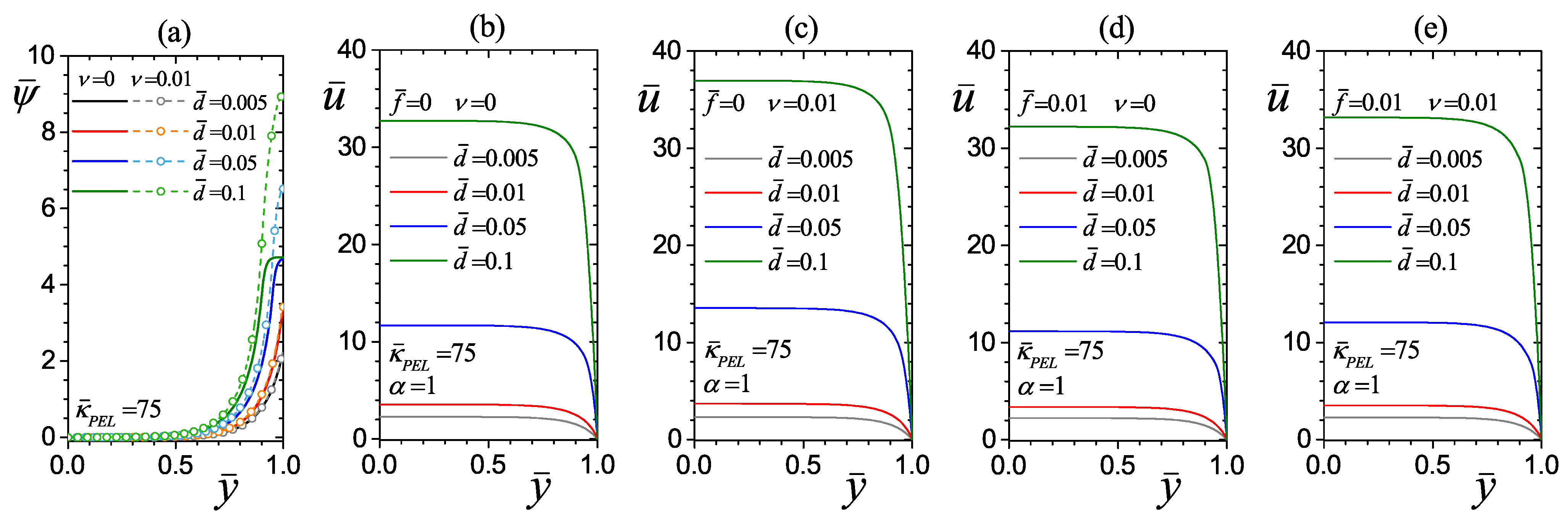
4.2.2. Effect of the PEL Thickness
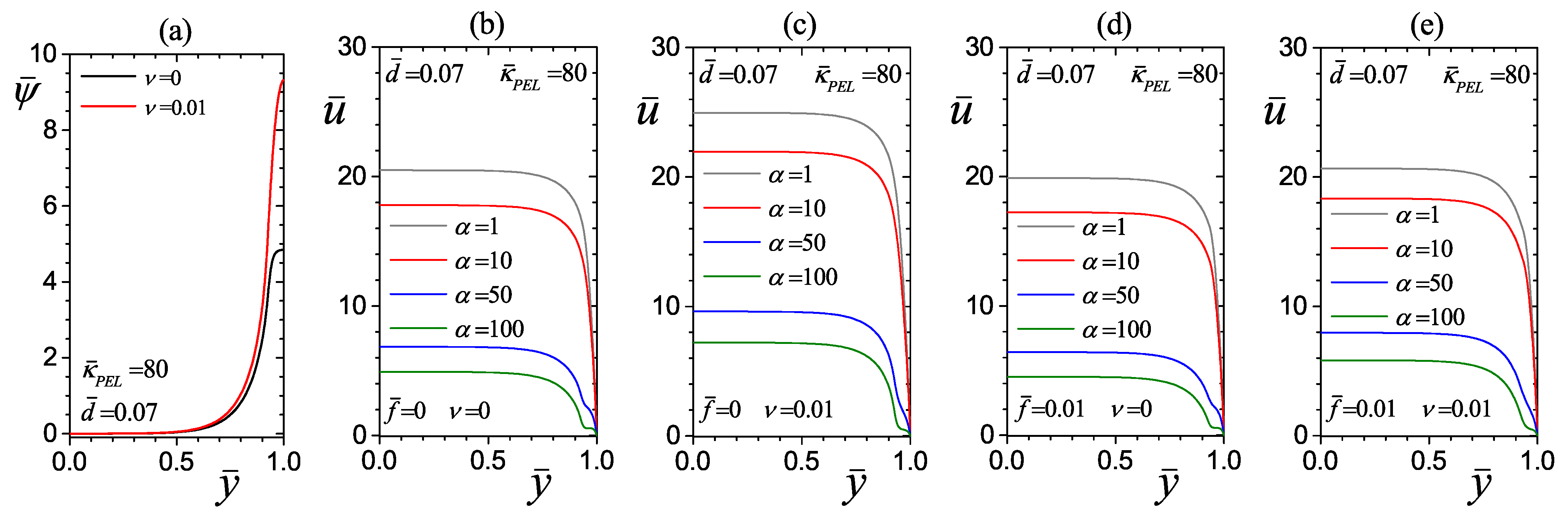
4.2.3. Effect of the Drag Parameter
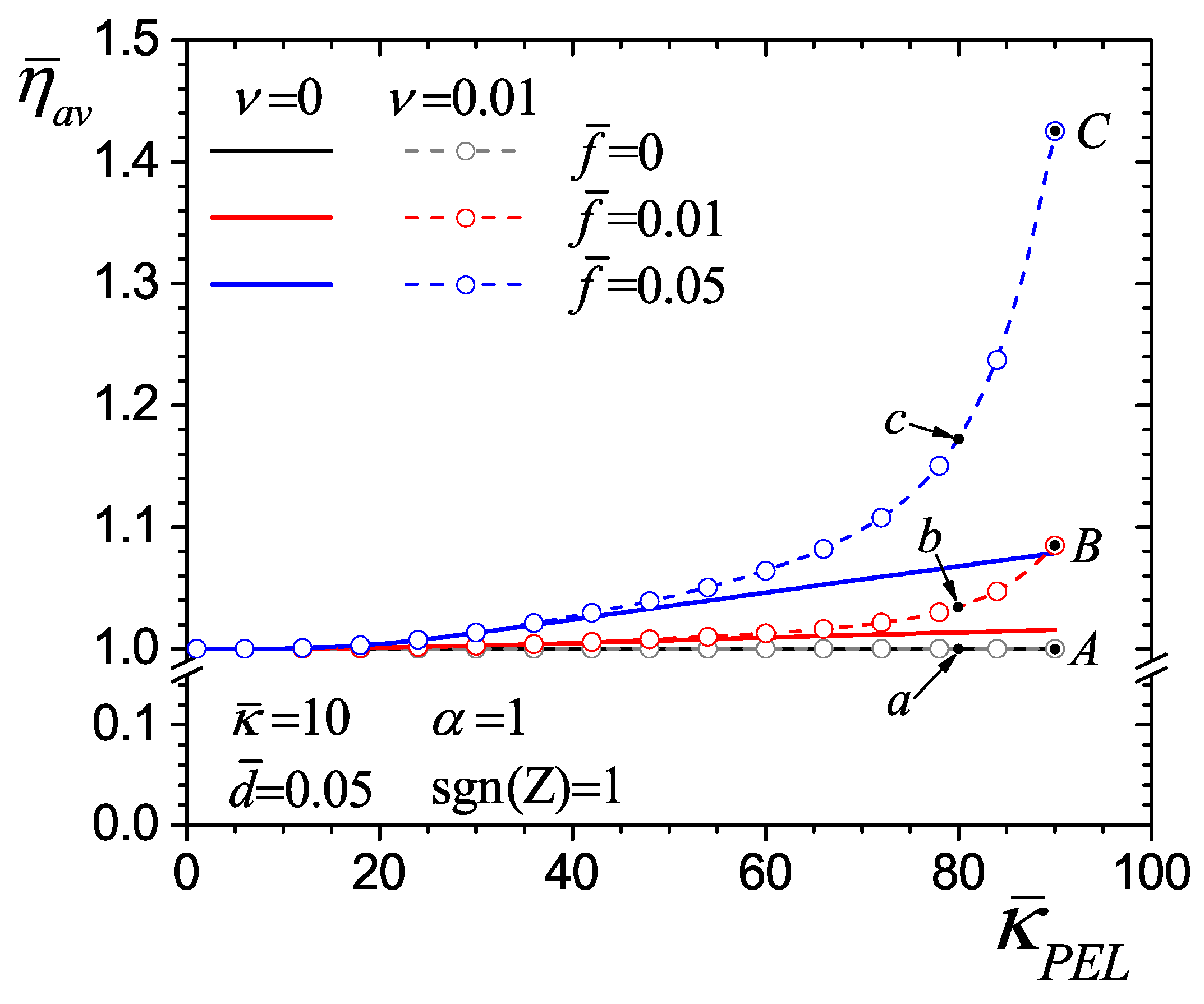
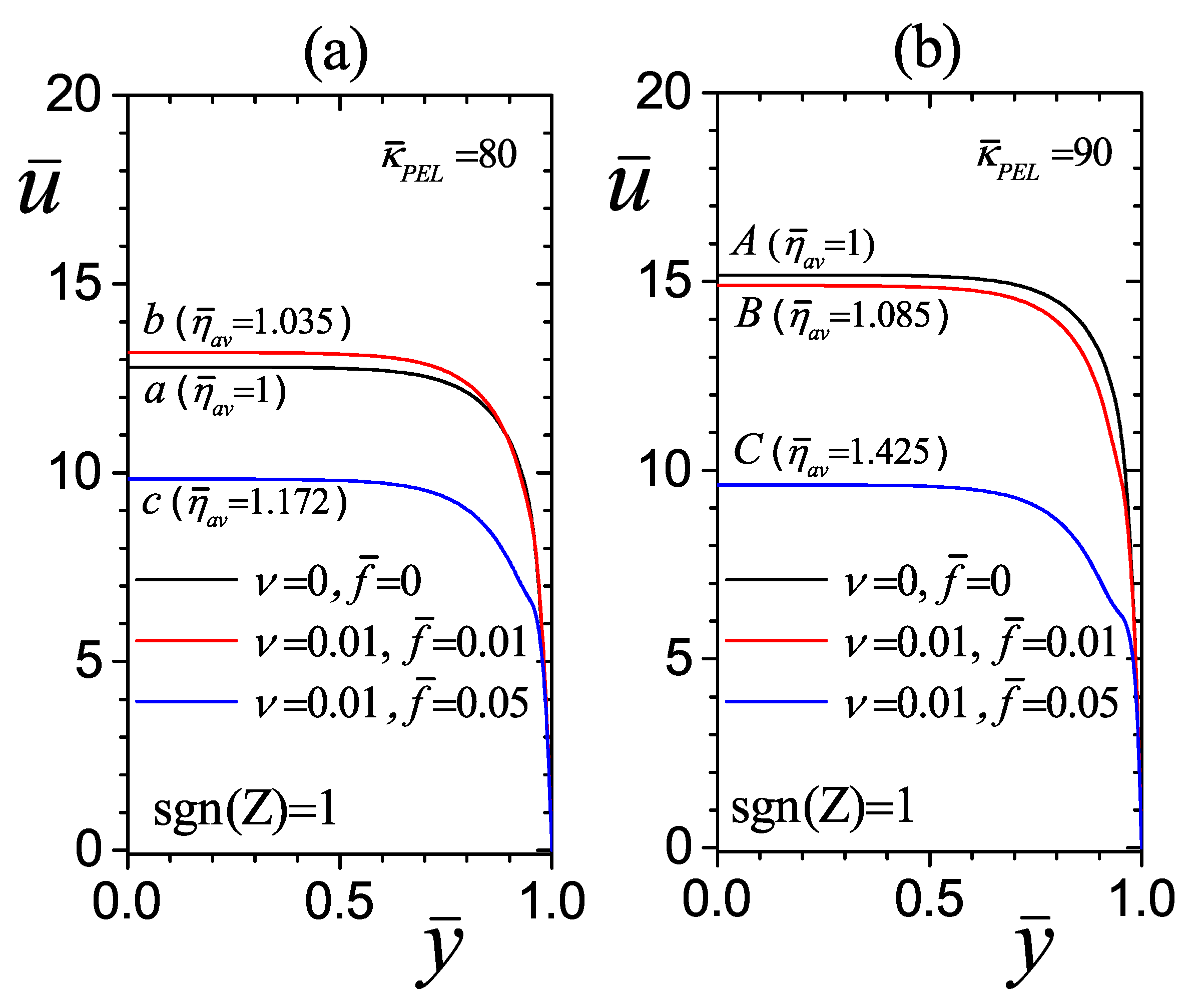
4.3. Effect of Average Dimensionless Viscosity on Flow Hydrodynamics
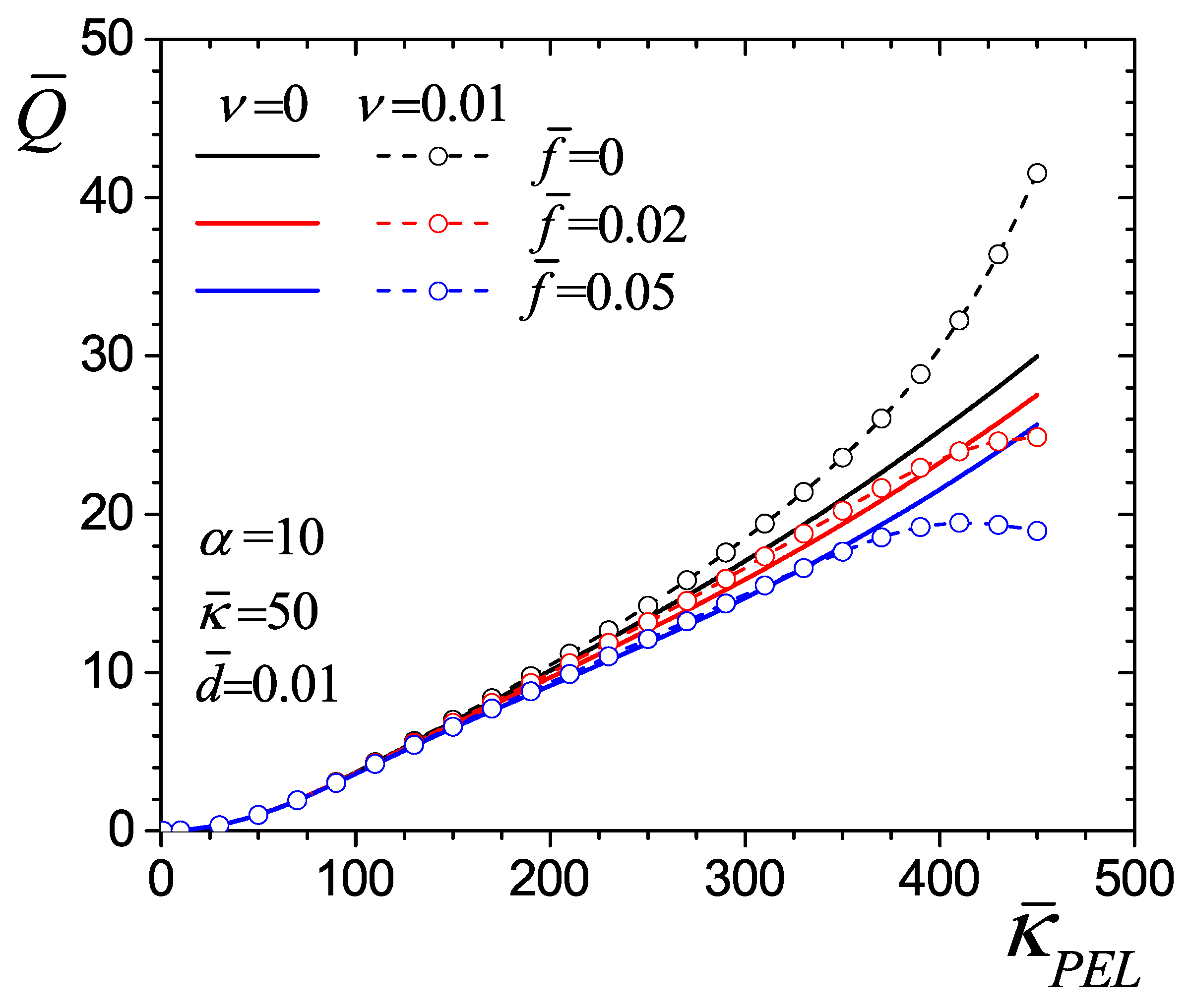
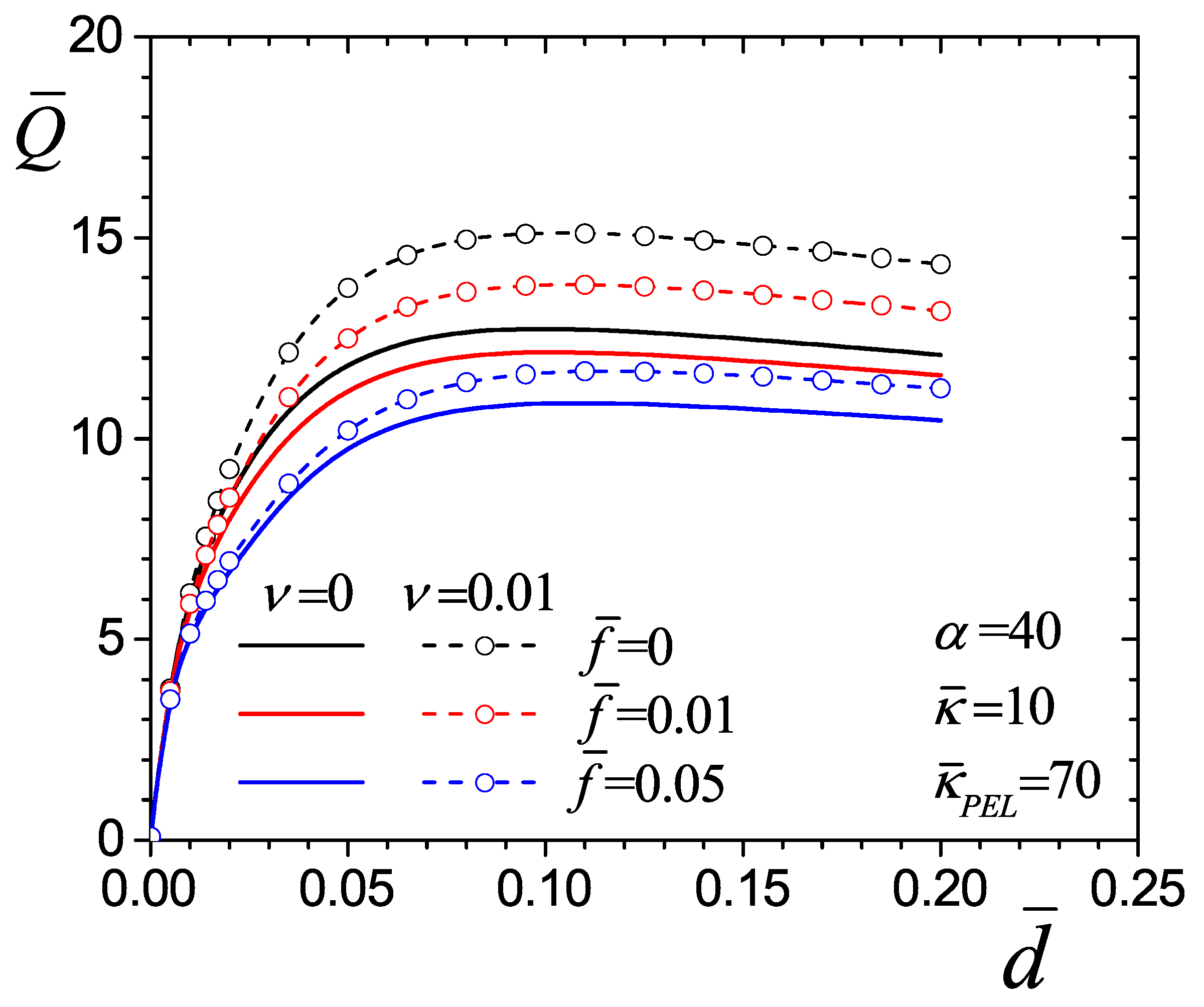
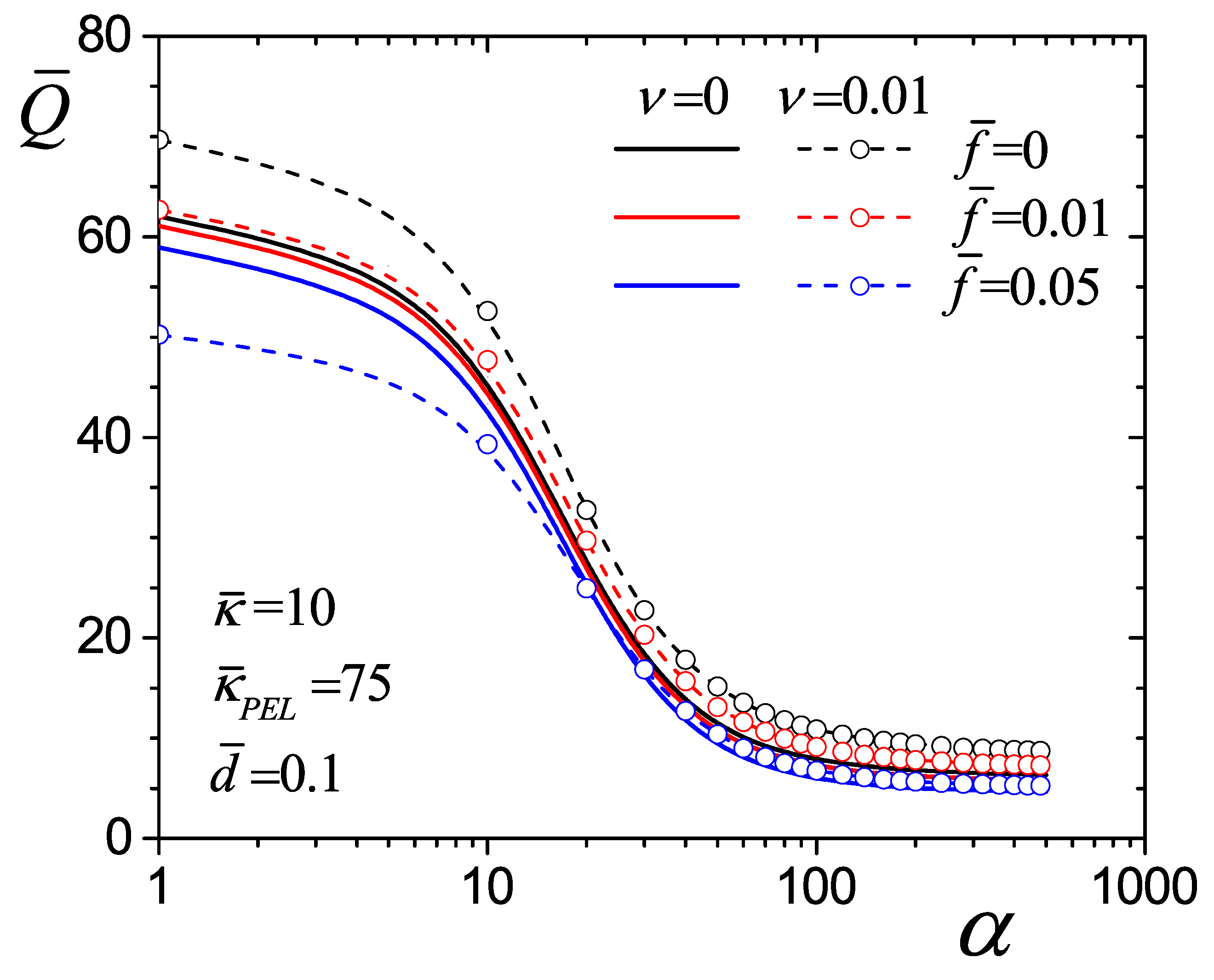
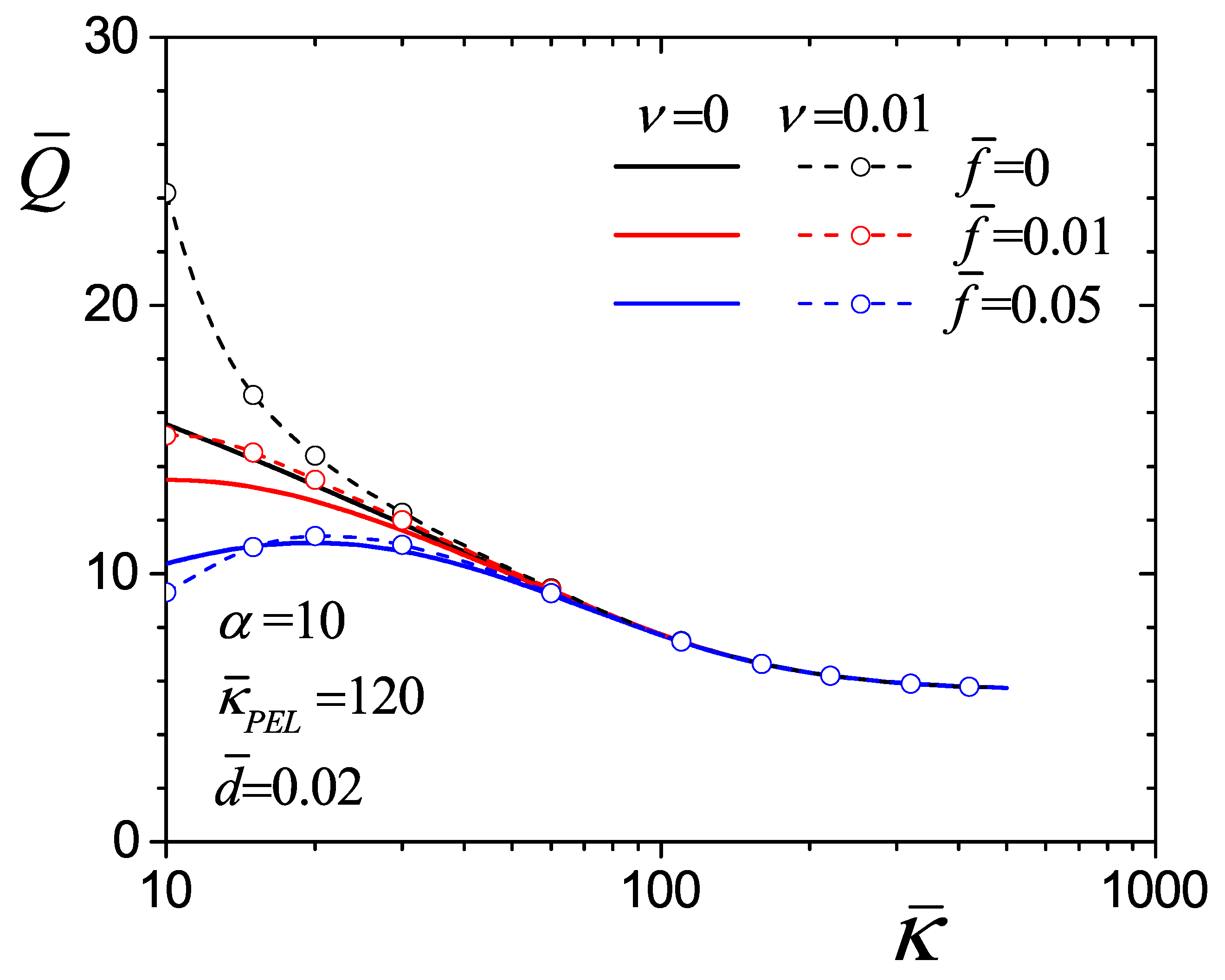
4.4. Flow Rate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Effective ionic size | m |
| d | PEL thickness | m |
| Dimensionless thickness of the PEL | - | |
| e | Elementary charge | C |
| Axial electric field | V m−1 | |
| Electric field vector | V m−1 | |
| Local electric field vector within the EDL | V m−1 | |
| f | Viscoelectric coefficient | m2 V−2 |
| Dimensionless viscoelectric coefficient | - | |
| Body force | N m−3 | |
| H | Half the height of the channel | m |
| Boltzmann constant | J K−1 | |
| k | Friction coefficient | Pa s m−2 |
| M | Molar concentration of an electrolyte solution | mol L−1 |
| m | Total number of data | - |
| Ionic number concentration in the bulk solution | m−3 | |
| number concentration of positive ions | m−3 | |
| number concentration of negative ions | m−3 | |
| N | Ionic number concentration of fixed charges within the PEL | m−3 |
| p | Pressure | Pa |
| Q | Flow rate per unit width of the channel | m2 s−1 |
| Characteristic flow rate per unit width of the channel | m2 s−1 | |
| Dimensionless flow rate per unit width of the channel | - | |
| Current dimensionless flow rate with mesh i | - | |
| Previous dimensionless flow rate with mesh j | - | |
| q | Nodal counter | - |
| T | Temperature | K |
| u | Axial velocity | m s−1 |
| Numerical velocity at node q | m s−1 | |
| Experimental velocity at node q | m s−1 | |
| Characteristic velocity | m s−1 | |
| Dimensionless axial velocity | - | |
| Velocity vector | m s−1 | |
| Cartesian coordinates | m | |
| Dimensionless Cartesian coordinates | - | |
| z | Absolute value of valency of a (z: z) electrolyte | - |
| Z | Absolute value of valency of the fixed ions within the PEL | - |
| Greek symbols | ||
| Drag parameter | - | |
| Dielectric permittivity of medium | C V−1 m−1 | |
| Approximate relative error | % | |
| Convergence rate | % | |
| Dynamic viscosity | Pa s | |
| Dynamic viscosity in the absence of an electric field | Pa s | |
| Average dimensionless viscosity | - | |
| Debye length in the electrolyte layer | m | |
| Electrokinetic parameter of the electrolyte layer | - | |
| Equivalent Debye length within the PEL | m | |
| Electrokinetic parameter of the PEL | - | |
| Fluid density | kg m−3 | |
| Volumetric free charge density | C m−3 | |
| Volumetric fixed charge density in the PEL | C m−3 | |
| Steric factor | - | |
| Electric potential within the EDL | V | |
| Dimensionless electric potential within the EDL | - |
References
- Alizadeh, A.; Hsu, W.-L.; Wang, M.; Daiguji, H. Electroosmotic flow: From microfluidics to nanofluidics. Electrophoresis 2021, 42, 834–868. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, C.; Huang, X. Analysis of the electroosmotic flow in a microchannel packed with homogeneous microspheres under electrokinetic wall effect. Int. J. Eng. Sci. 2004, 42, 2011–2027. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Pu, Q.; Liu, S. Advancement of electroosmotic pump in microflow analysis: A review. Anal. Chim. Acta 2019, 1060, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Haywood, D.G.; Harms, Z.D.; Jacobson, S.C. Electroosmotic flow in nanofluidic channels. Anal. Chem. 2014, 86, 11174–11180. [Google Scholar] [CrossRef] [PubMed]
- Deraney, R.N.; Schneider, L.; Tripathi, A. Synergistic use of electroosmotic flow and magnetic forces for nucleic acid extraction. Analyst 2020, 145, 2412–2419. [Google Scholar] [CrossRef]
- Silverio, V.; Canane, P.A.G.; Martins, T.A.; Afonso, R.; Cardoso, S.; Batista, E. Development of a microfluidic electroosmosis pump on a chip for steady and continuous fluid delivery. Biomed. Eng.-Biomed. Tech. 2023, 68, 79–90. [Google Scholar] [CrossRef]
- Jen, C.-P.; Amstislavskaya, T.G.; Liu, Y.-H.; Hsiao, J.-H.; Chen, Y.-H. Single-cell electric lysis on an electroosmotic-driven microfluidic chip with arrays of microwells. Sensors 2012, 12, 6967–6977. [Google Scholar] [CrossRef]
- Pramod, K.; Sen, A.K. Flow and heat transfer analysis of an electro-osmotic flow micropump for chip cooling. J. Electron. Packag. 2014, 136, 031012. [Google Scholar] [CrossRef]
- Plohl, O.; Zemljič, L.F.; Potrč, S.; Luxbacher, T. Applicability of electro-osmotic flow for the analysis of the surface zeta potential. RSC Adv. 2020, 10, 6777–6789. [Google Scholar] [CrossRef]
- Hsieh, S.-S.; Lin, H.-C.; Lin, C.-Y. Electroosmotic flow velocity measurements in a square microchannel. Colloid Polym. Sci. 2006, 284, 1275–1286. [Google Scholar] [CrossRef]
- Jiménez, E.; Escandón, J.; Bautista, O.; Méndez, F. Start-up electroosmotic flow of Maxwell fluids in a rectangular microchannel with high zeta potentials. J. Non–Newton. Fluid Mech. 2016, 227, 17–29. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S.; Zhao, M.; Xiao, Y. Electroosmotic flow of Maxwell fluid in a microchannel of isosceles right triangular cross section. Phys. Fluids 2021, 33, 123113. [Google Scholar] [CrossRef]
- Kwak, H.S.; Kim, H.; Hyun, J.M.; Song, T.-H. Thermal control of electroosmotic flow in a microchannel through temperature-dependent properties. J. Colloid Interface Sci. 2009, 335, 123–129. [Google Scholar] [CrossRef]
- Chen, L.-C.; Wu, C.-C.; Wu, R.-G.; Chang, H.-C. Electroosmotic flow control in microfluidic chips using a self-asssembled monolayer as the insulator of a flow field-effect transistor. Langmuir 2012, 28, 11281–11285. [Google Scholar] [CrossRef] [PubMed]
- Peng, R.; Li, D. Effects of ionic concentration gradient on electroosmotic flow mixing in a microchannel. J. Colloid Interface Sci. 2015, 440, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Seifollahi, Z.; Ashrafizadeh, S.N. Ionic-size dependent electroosmotic flow in ion-selective biomimetic nanochannels. Colloids Surf. B Biointerfaces 2022, 216, 112545. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Ren, Y.; Tao, Y.; Li, Y.; Wu, Q. On traveling-wave field-effect flow control for simultaneous induced-charge electroosmotic pumping and mixing in microfluidics: Physical perspectives and theoretical analysis. J. Micromech. Microeng. 2018, 28, 055004. [Google Scholar] [CrossRef]
- Liu, Y.-B. Effect of boundary slip on electroosmotic flow in a curved rectangular microchannel. Chin. Phys. B 2024, 33, 074101. [Google Scholar] [CrossRef]
- Tang, G.Y.; Yang, C.; Chai, J.C.; Gong, H.Q. Joule heating effect on electroosmotic flow and mass species transport in a microcapillary. Int. J. Heat Mass Transf. 2004, 47, 215–227. [Google Scholar] [CrossRef]
- Sadeghi, A.; Azari, M.; Hardt, S. Electroosmotic flow in soft microchannels at high grafting densities. Phys. Rev. Fluids 2019, 4, 063701. [Google Scholar] [CrossRef]
- Zhang, Z.; Zuo, C.; Cao, Q.; Ma, Y.; Chen, S. Modulation of electroosmotic flow using polyelectrolyte brushes: A molecular dynamics study. Macromol. Theory Simul. 2012, 21, 145–152. [Google Scholar] [CrossRef]
- Sadeghi, A. Theoretical modeling of electroosmotic flow in soft microchannels: A variational approach applied to the rectangular geometry. Phys. Fluids 2018, 30, 032004. [Google Scholar] [CrossRef]
- Matin, M.H.; Ohshima, H. Thermal transport characteristics of combined electroosmotic and pressure driven flow in soft nanofluidics. J. Colloid Interface Sci. 2016, 476, 167–176. [Google Scholar] [CrossRef]
- Chen, G.; Das, S. Electroosmotic transport in polyelectrolyte-grafted nanochannels with pH-dependent charge density. J. Appl. Phys. 2015, 117, 185304. [Google Scholar] [CrossRef]
- Kaushik, P.; Mondal, P.K.; Kundu, P.K.; Wongwises, S. Rotating electroosmotic flow through a polyelectrolyte-grafted microchannel: An analytical solution. Phys. Fluids 2019, 31, 022009. [Google Scholar] [CrossRef]
- Talebi, R.; Ashrafizadeh, S.N.; Sadeghi, A. Hydrodynamic dispersion by electroosmotic flow in soft microchannels: Consideration of different properties for electrolyte and polyelectrolyte layer. Chem. Eng. Sci. 2021, 229, 116058. [Google Scholar] [CrossRef]
- Gaikwad, H.S.; Mondal, P.K.; Wongwises, S. Softness induced enhancement in net throughput of non-linear biofluids in nanofuidic channel under EDL phenomenon. Sci. Rep. 2018, 8, 7893. [Google Scholar] [CrossRef]
- Yazdi, A.A.; Sadeghi, A.; Saidi, M.H. Steric effects on electrokinetic flow of non-linear biofluids. Colloids Surf. A Physicochem. Eng. Asp. 2015, 484, 394–401. [Google Scholar] [CrossRef]
- Liu, Y.; Jian, Y. The effects of finite ionic sizes and wall slip on entropy generation in electroosmotic flows in a soft nanochannel. J. Heat Transfer. 2019, 141, 102401. [Google Scholar] [CrossRef]
- Jimenez, E.; Escandón, J.; Méndez, F.; Bautista, O. Combined viscoelectric and steric effects on the electroosmotic flow in nano/microchannels with heterogeneous zeta potentials. Colloids Surf. A Physicochem. Eng. Asp. 2019, 577, 347–359. [Google Scholar] [CrossRef]
- Pabi, S.; Mehta, S.K.; Pati, S. Analysis of thermal transport and entropy generation characteristics for electroosmotic flow through a hydrophobic microchannel considering viscoelectric effect. Int. Commun. Heat Mass Transf. 2021, 127, 105519. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef] [PubMed]
- Bandopadhyay, A.; Chakraborty, S. Ionic size dependent electroosmosis in ion-selective microchannels and nanochannels. Electrophoresis 2013, 34, 2193–2198. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef]
- Dey, R.; Ghonge, T.; Chakraborty, S. Steric-effect-induced alteration of thermal transport phenomenon for mixed electroosmotic and pressure driven flows through narrow confinements. Int. J. Heat Mass Transf. 2013, 56, 251–262. [Google Scholar] [CrossRef]
- Jimenez, E.; Escandón, J.; Méndez, F.; Bautista, O. Combined viscoelectric and steric effects on the electroosmotic flow in a microchannel under induced high zeta potentials. Colloids Surf. A Physicochem. Eng. Asp. 2017, 531, 221–233. [Google Scholar] [CrossRef]
- Mehta, S.K.; Pati, S.; Baranyi, L. Steric effect induced heat transfer for electroosmotic flow of Carreau fluid through a wavy microchannel. Tech. Mech. 2023, 43, 2–12. [Google Scholar]
- Zheng, J.; Jia, B.; Jian, Y. Steric effects on space electroosmotic thrusters in soft nanochannels. Mathematics 2021, 9, 1916. [Google Scholar] [CrossRef]
- Hsu, W.-L.; Daiguji, H.; Dunstan, D.E.; Davidson, M.R.; Harvie, D.J.E. Electrokinetics of the silica and aqueous electrolyte solution interface: Viscoelectric effects. Adv. Colloid Interface Sci. 2016, 234, 108–131. [Google Scholar] [CrossRef]
- Hsu, W.-L.; Harvie, D.J.E.; Davidson, M.R.; Dunstan, D.E.; Hwang, J.; Daiguji, H. Viscoelectric effects in nanochannel electrokinetics. J. Phys. Chem. C 2017, 121, 20517–20523. [Google Scholar] [CrossRef]
- Lyklema, J.; Overbeek, J.T.G. On the interpretation of electrokinetic potentials. J. Colloid Sci. 1961, 16, 501–512. [Google Scholar] [CrossRef]
- Ramos, E.A.; Monsivais, I.G.; Méndez, F.; Lizardi, J.J. Viscoelectric effect analysis in an electroosmotic flow with microchannel wall slip. Phys. Scr. 2023, 98, 065022. [Google Scholar] [CrossRef]
- Marroquin-Desentis, J.; Méndez, F.; Bautista, O. Viscoelectric effect on electroosmotic flow in a cylindrical microcapillary. Fluid Dyn. Res. 2016, 48, 035503. [Google Scholar] [CrossRef]
- Huo, X.; Chen, X. A review on modeling, simulation and experiment of electrokinetic micromixers. J. Disper. Sci. Technol. 2020, 42, 1469–1481. [Google Scholar] [CrossRef]
- Höltzel, A.; Tallarek, U. Ionic conductance of nanopores in microscale analysis systems: Where microfluidics meets nanofluidics. J. Sep. Sci. 2007, 30, 1398–1419. [Google Scholar] [CrossRef]
- Cheng, L.J. Electrokinetic ion transport in nanofluidics and membranes with applications in bioanalysis and beyond. Biomicrofluidics 2018, 12, 021502. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.V.T.; Smadja, C.; Taverna, M.; Mousli, S.E.; Secret, E.; Siaugue, J.-M.; Nguyen, L.T.H.; Mai, T.D. Electroosmotic flow modulation for improved electrokinetic preconcentration: Application to capillary electrophoresis of fluorescent magnetic nanoparticles. Anal. Chim. Acta 2021, 1161, 338466. [Google Scholar] [CrossRef]
- Chanda, S.; Das, S. Effect of finite ion sizes in an electrostatic potential distribution for a charged soft surface in contact with an electrolyte solution. Phys. Rev. E 2014, 89, 012307. [Google Scholar] [CrossRef]
- Gaikwad, H.S.; Kumar, G.; Mondal, P.K. Efficient electroosmotic mixing in a narrow-fluidic channel: The role of a patterned soft layer. Soft Matter 2020, 16, 6304–6316. [Google Scholar] [CrossRef]
- Xing, J.; Jian, Y. Steric effects on electroosmotic flow in soft nanochannels. Meccanica 2018, 53, 135–144. [Google Scholar] [CrossRef]
- Zhao, G.; Jian, Y. Thermal transport of combined electroosmotically and pressure driven nanofluid flow in soft nanochannels. J. Therm. Anal. Calorim. 2019, 135, 379–391. [Google Scholar] [CrossRef]
- Sadeghi, A.; Amini, Y.; Saidi, M.H.; Chakraborty, S. Numerical modeling of surface reaction kinetics in electrokinetically actuated microfluidic devices. Anal. Chim. Acta 2014, 838, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Matin, M.H.; Ohshima, H. Combined electroosmotically and pressure driven flow in soft nanofluidics. J. Colloid. Interface Sci. 2015, 460, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Jian, Y. Electroosmotic thrusters in soft nanochannels for space propulsion. Phys. Fluids 2020, 32, 122005. [Google Scholar] [CrossRef]
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows. Fundamentals and Simulation; Springer: New York, NY, USA, 2005. [Google Scholar]
- Chun, B.; Chun, M.-S. Electrostatic potential analysis in polyelectrolyte brush-grafted microchannels filled with polyelectrolyte dispersion. Micromachines 2021, 12, 1475. [Google Scholar] [CrossRef]
- Hsieh, S.-S.; Yang, T.-K. Electroosmotic flow in rectangular microchannels with Joule heating effects. J. Micromech. Microeng. 2008, 18, 025025. [Google Scholar] [CrossRef]
- Andrews, J.; Das, S. Effect of finite ion sizes in electric double layer mediated interaction force between two soft charged plates. RSC Adv. 2015, 5, 46873–46880. [Google Scholar] [CrossRef]
- Patel, M.; Kruthiventi, S.S.H.; Kaushik, P. Polyelectrolyte layer grafting effect on the rotational electroosmotic flow of viscoplastic material. Microfluid. Nanofluidics 2021, 25, 11. [Google Scholar] [CrossRef]
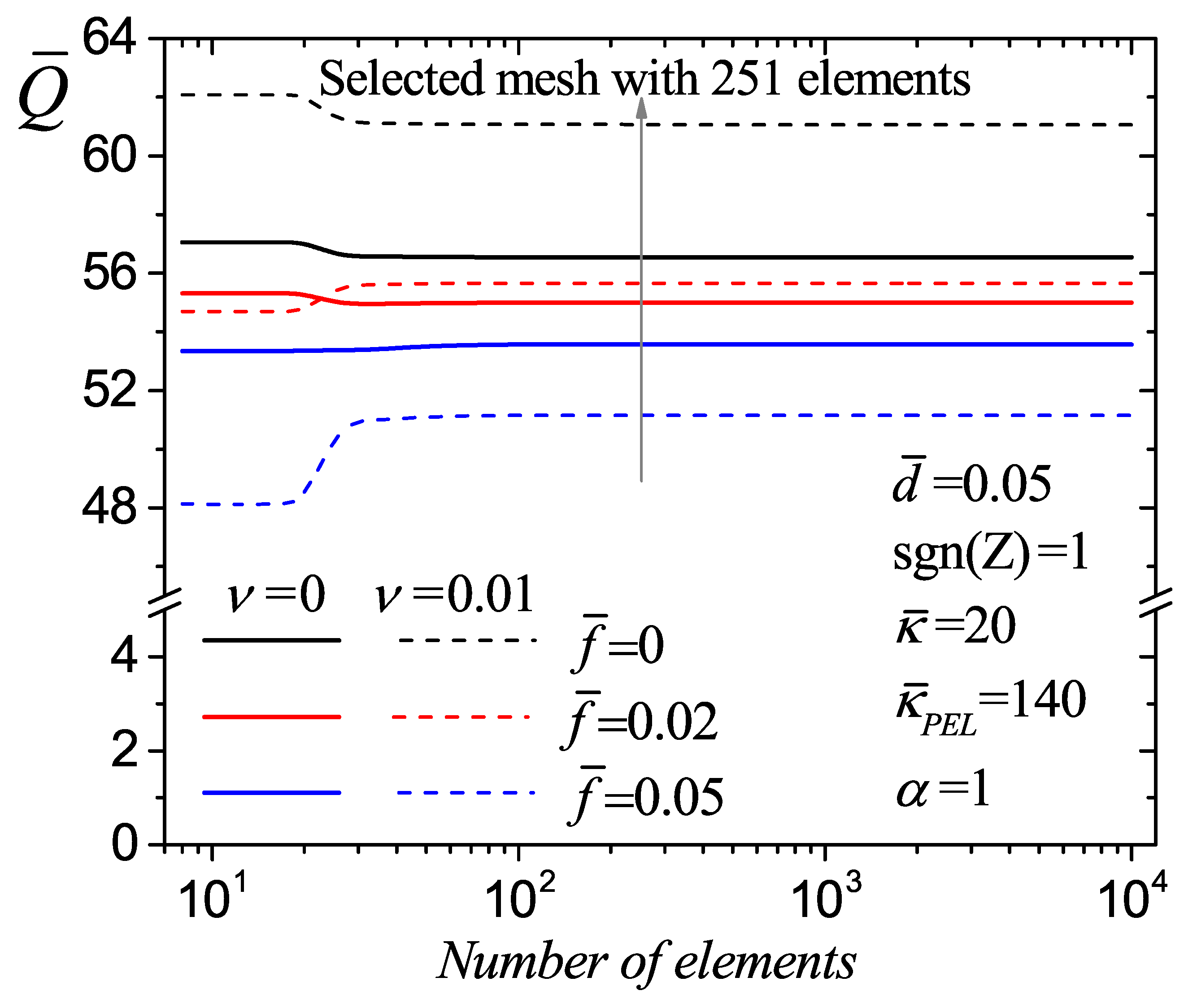
| Element Size | Number of Elements | (a) | (b) | ||
|---|---|---|---|---|---|
| 0.2 | 8 | 57.052004 | 48.130216 | ||
| 0.01 | 100 | 56.548255 | 0.89083 | 51.151099 | 5.90580 |
| 0.005 | 200 | 56.547887 | 0.00065 | 51.156773 | 0.01109 |
| 0.004 | 251 | 56.547861 | 0.00005 | 51.157141 | 0.00072 |
| 0.0001 | 10,000 | 56.547841 | 0.00004 | 51.157426 | 0.00056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jimenez, E.M.; Hernández, C.G.; Torres, D.A.; Ratkovich, N.; Escandón, J.P.; Gómez, J.R.; Vargas, R.O. Viscoelectric and Steric Effects on Electroosmotic Flow in a Soft Channel. Mathematics 2025, 13, 2546. https://doi.org/10.3390/math13162546
Jimenez EM, Hernández CG, Torres DA, Ratkovich N, Escandón JP, Gómez JR, Vargas RO. Viscoelectric and Steric Effects on Electroosmotic Flow in a Soft Channel. Mathematics. 2025; 13(16):2546. https://doi.org/10.3390/math13162546
Chicago/Turabian StyleJimenez, Edson M., Clara G. Hernández, David A. Torres, Nicolas Ratkovich, Juan P. Escandón, Juan R. Gómez, and René O. Vargas. 2025. "Viscoelectric and Steric Effects on Electroosmotic Flow in a Soft Channel" Mathematics 13, no. 16: 2546. https://doi.org/10.3390/math13162546
APA StyleJimenez, E. M., Hernández, C. G., Torres, D. A., Ratkovich, N., Escandón, J. P., Gómez, J. R., & Vargas, R. O. (2025). Viscoelectric and Steric Effects on Electroosmotic Flow in a Soft Channel. Mathematics, 13(16), 2546. https://doi.org/10.3390/math13162546








