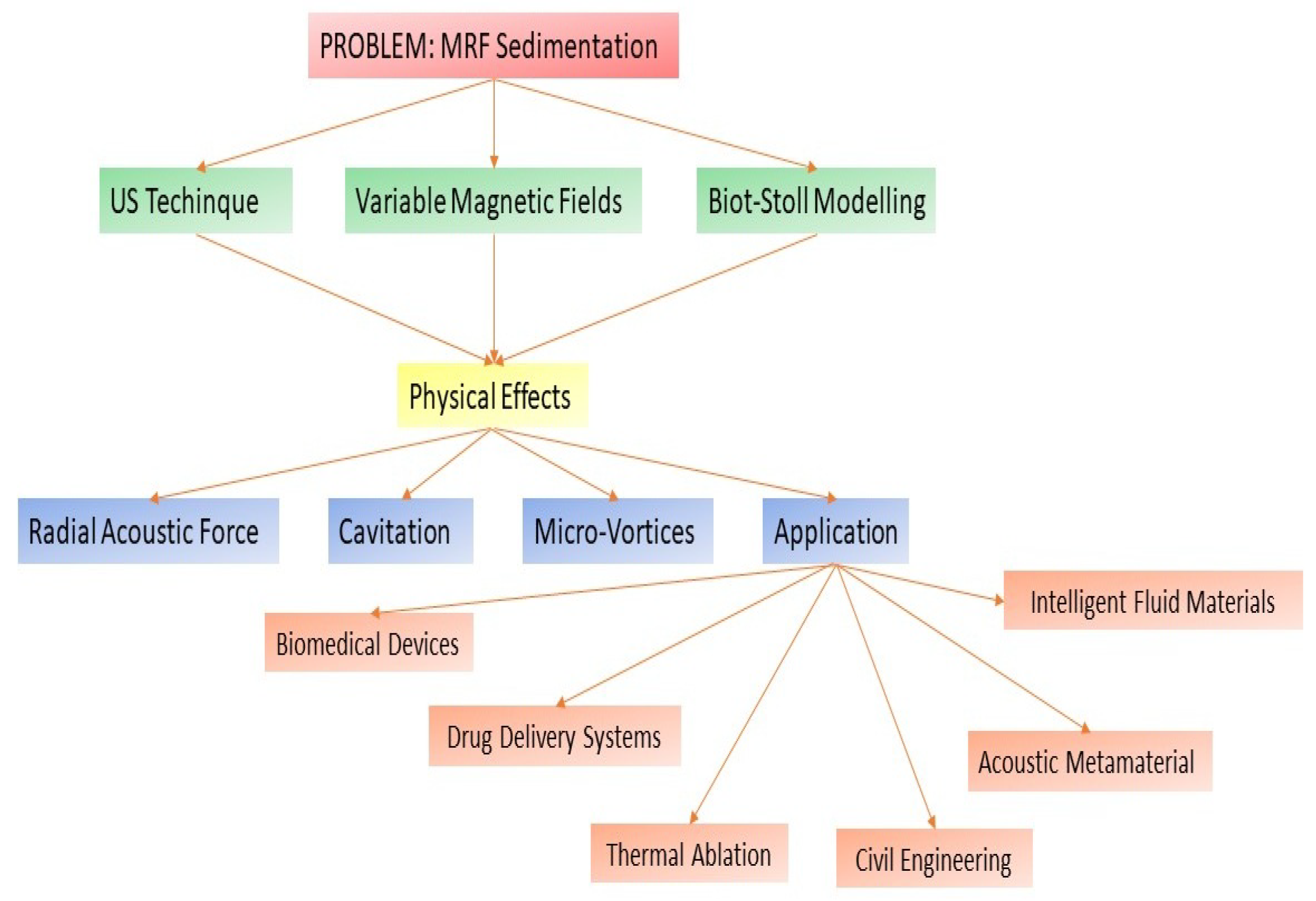
Controlling Sedimentation in Magnetorheological Fluids Through Ultrasound–Magnetic Field Coupling: Multiscale Analysis and Applications
Abstract
1. Introduction
- Radial Acoustic Pressure (ARP): generated by spherical or cylindrical waves, it induces a non-uniform pressure field that, through the acoustic radiation force (ARF), stabilizes the particles [42];
- Variable Magnetic Fields: when combined with US, they enhance the suspension effect through synergistic acoustic–magnetic configurations;
2. Radial Acoustic Pressure Theory
2.1. Propagation of Acoustic Waves in Fluids
2.1.1. Solution for Spherical Waves
2.1.2. Solution for Cylindrical Waves
2.2. Pressure Gradient and ARF for Spherical Waves
2.3. Effect of Acoustic Cavitation: The Case of Spherical US Waves
2.4. Effect of Acoustic Cavitation: The Case of Cylindrical US Waves
3. Industrial and Biomedical Applications: Recent Innovations in Particle Stabilization Through RAP Techniques
3.1. Optimization of the Rheological Response of MRF: Dynamic Control for Enhanced Stability and Performance in Damping Systems
3.2. Adaptive Materials for Acoustic Control: The Integration of US and Magnetic Fields to Optimize the Performance of MRFs
3.3. Tunable Acoustic Metamaterials: The Use of Programmable Acoustic Response for Advanced Sound Wave Control
3.4. ARF and US Techniques for Improving Concrete Properties
3.5. MRF and US: Advanced US Diagnostics
3.6. Effects of Acoustic Transparency on Phase Coherence and Scattering
3.7. MRF and US: US-Mediated Drug Delivery
3.8. Potential Energy Losses and Transducer Limitations
3.9. MRF and US: Localized Ablation (US-Assisted Magnetic Hyperthermia)
3.10. Limitations of Acousto-Magnetic Models in Biomedical Implants
3.11. MRF and US: Tissue Engineering
3.12. Challenges in the Implementation of the RAP Technique
4. Effect of the Time-Varying Magnetic Field
4.1. Sinusoidally Modulated
4.2. Stability Criteria and Physical Interpretation
5. Innovations and Industrial and Biomedical Applications of the Effect of Variable Magnetic Field on MRFs
5.1. Adaptive Rheological Control in High-Frequency Hydraulic Circuits
5.2. Intelligent and Reconfigurable Assembly of Microcomponents
5.3. Selective Hyperthermia and Non-Invasive Ablation of Tumor Tissues
5.4. Targeted Drug Delivery Mediated by US
6. MRF and US: Biot–Stoll
6.1. Fundamental Equations
6.2. Stoll’s Viscous Correction
6.3. Physical Interpretation and Comparative Perspective
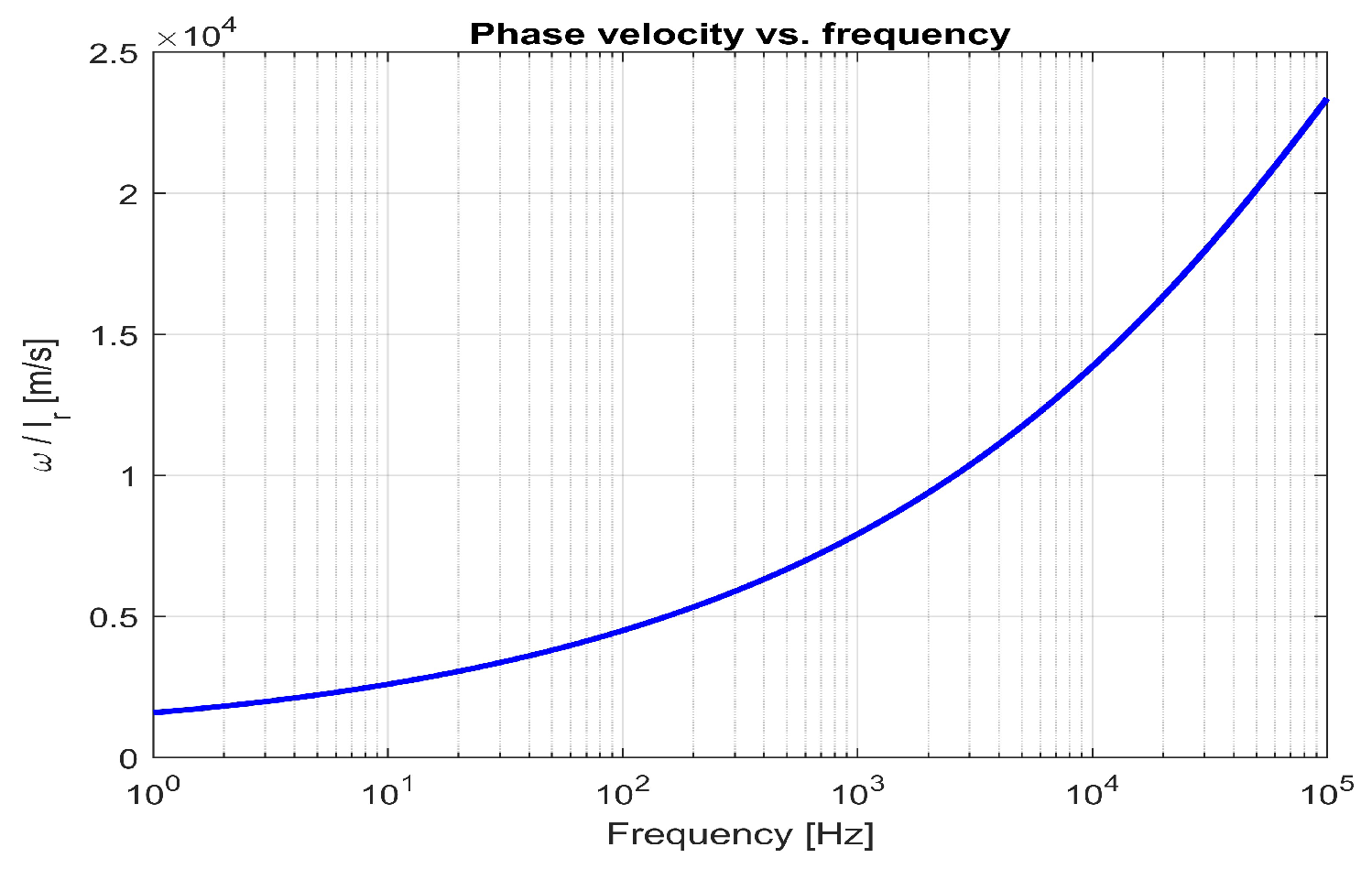
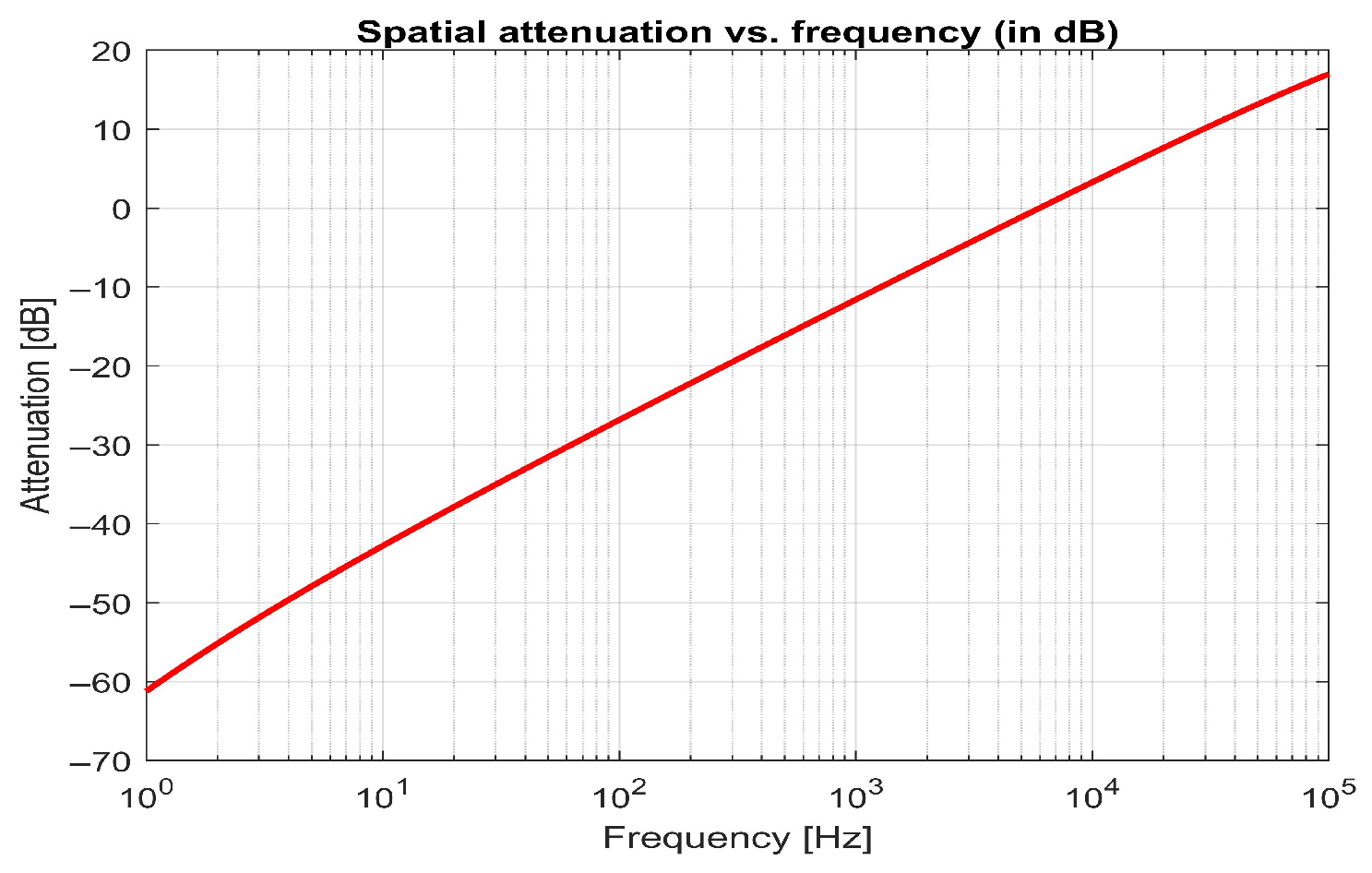
6.4. Frequency Equation
7. Industrial and Biomedical Applications of the Biot–Stoll Theory in MRF and US
7.1. Advanced Diagnostics in Composite Systems and Sandwich Structures
7.2. Adaptive Control of Sound Transmission in Industrial Ducts
7.3. Production and Quality Control in Multiphase 3D Printing
7.4. Non-Invasive Diagnosis of Pathological Soft Tissues
7.5. Real-Time Monitoring of Tissue Regeneration
7.6. Optimization of Targeted Delivery in Complex Tissues
8. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Acoustic Cavitation |
| AL | Acoustic Levitation |
| AMJ | Acoustic Micro-Jets |
| AOP | Acoustic oscillation of Particles |
| ARF | Acoustic Radiation Force |
| AS | Acoustic Streaming |
| MAR | Multimodal Acoustic Resonance |
| MRF | Magnetorheological Fluid |
| PDE | Partial Differential Equation |
| RAP | Radial Acoustic Pressure |
| US | Ultrasonics |
References
- Ginder, J.M. Behavior of Magnetorheological fluids. MRS Bull. 1998, 23, 26–29. [Google Scholar] [CrossRef]
- Muhammad, A.; Yao, X.L.; Deng, Z.C. Review of Magnetorheological (MR) Fluids and its Applications in Vibration Control. J. Mar. Sci. Appl. 2006, 5, 17–29. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Chen, L.; Li, X.; Liu, Q.; Wang, Y.; Wang, Z. Highly Sensitive Surface Acoustic Wave Magnetic Field Sensor Based on the Loss Mechanism. Smart Mater. Struct. 2024, 33, 055008. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. Magnetorheological Fluids: Qualitative Comparison between a Mixture Model in the Extended Irreversible Thermodynamiocs Framework and an Herschel-Bulkley Experimental Elastoviscoplastic Model. Int. J. Non-Linear Mech. 2020, 118, 103288. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. An Algorithm Proposal for the Qualitative Comparison Between the Chen-Yeh EIT Mixture Model and the Susan-Resiga GSMs Experimental Model for MR Fluids. In International Symposium on Intelligent and Distributed Computing; Springer International Publishing: Cham, Switzerland, 2020; pp. 309–318. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Fuzzy Time Series Approach for Disruption Prediction in Tokamak Reactors. IEEE Trans. Magn. 2003, 39, 1503–1506. [Google Scholar] [CrossRef]
- Morabito, C.F. Independent component analysis and feature extraction techniques for NDT data. Mater. Eval. 2000, 58, 85–92. [Google Scholar]
- Ginder, J.M.; Davis, L.C.; Elie, L.D. Rheology of Magnetorheological Fluids: Models and Measurements. Int. J. Mod. Phys. B 1996, 10, 3293–3303. [Google Scholar] [CrossRef]
- Chandra Shekhar, M.; Sarkar, C. Magnetorheological Fluids: A Comprehensive Review of Operational Modes and Performance Under Varied Circumstances. Rheol. Acta 2024, 63, 765–785. [Google Scholar] [CrossRef]
- Zhang, X.; Choi, Y.T.; Shou, M.; Zhu, G.; Wereley, N.M. Adaptive Magnetorheological Fluid Energy Absorption Systems: A Review. Smart Mater. Struct. 2024, 33, 033002. [Google Scholar] [CrossRef]
- Scarpa, F.; Smith, F.C. Passive and MR Fluid-Coated Auxetic PU Foam–Mechanical, Acoustic, and Electromagnetic Properties. J. Intell. Mater. Syst. Struct. 2004, 15, 973–979. [Google Scholar] [CrossRef]
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A Review of Challenges and Solutions in the Preparation and Use of Magnetorheological Fluids. Int. J. Mech. Mater. Eng. 2019, 14, 13. [Google Scholar] [CrossRef]
- Goncalves, F.D.; Koo, J.H.; Ahmadian, M. A Review of the State of the Art in Magnetorheological Fluid Technologies—Part I: MR Fluid and MR Fluid Models. Shock Vib. Dig. 2006, 38, 203–220. [Google Scholar] [CrossRef]
- Rinaldi, C.; Chaves, A.; Elborai, S.; He, X.T.; Zahn, M. Magnetic Fluid Rheology and Flows. Curr. Opin. Colloid Interface Sci. 2005, 10, 141–157. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Cacciola, M.; Morabito, F.C.; Polimeni, D.; Versaci, M. Fuzzy characterization of flawed metallic plates with eddy current tests. Prog. Electromagn. Res. 2007, 72, 241–252. [Google Scholar] [CrossRef]
- Zhu, W.; Li, P.; Hu, G.; Yu, L. Experimental and Numerical Analysis of Magnetorheological Valve Based on Herschel–Bulkley–Papanastasiou model. J. Magn. Magn. Mater. 2024, 602, 172169. [Google Scholar] [CrossRef]
- Claracq, J.; Sarrazin, J.; Montfort, J.P. Viscoelastic Properties of Magnetorheological Fluids. Rheol. Acta 2004, 43, 38–49. [Google Scholar] [CrossRef]
- Adeleke, A.I.; Waheed, M.A.; Sobamowo, G.M.; de Oliveira Siqueira, A.M. Viscoelastic Fluid Flow Model for Hydrodynamic Behavior of Magnetorheological Fluid in Valve and Shear Modes for a Damper System. J. Eng. Exact Sci. 2024, 10, 19082. [Google Scholar] [CrossRef]
- Hao, L.; Zhou, J. Experimental Study on the Rheological Properties of MF Lubricant Based on the Herschel-Bulkley Model. J. Supercond. Nov. Magn. 2022, 35, 3333–3346. [Google Scholar] [CrossRef]
- Kowol, P.; Sciuto, G.L.; Brociek, R.; Capizzi, G. Magnetic Characterization of MR Fluid by Means of Neural Networks. Electronics 2024, 13, 1723. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.J.; Ren, N.; England, R. Lubrication Subjected to Effects of Electric and Magnetic Fields: Recent Research Progress and a Generalized MEMT-Field Reynolds Equation. Front. Mech. Eng. 2024, 9, 1334814. [Google Scholar] [CrossRef]
- Versaci, M.; Cutrupi, A.; Palumbo, A. A Magneto-Thermo-Static Study of a Magneto-Rheological Fluid Damper: A Finite Element Analysis. IEEE Trans. Magn. 2020, 57, 4600210. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G. A FEMs Magnetic-Thermal Study for an MR Automotive Damper. In Proceedings of the Progress in Electromagnetics Research Symposium, Hangzhou, China, 21–25 November 2021; Institute of Electrical and Electronics Engineers Inc.: Interlaken, Switzerland, 2021; Volume 2021, pp. 2653–2660. [Google Scholar] [CrossRef]
- Pyle, R.J.; Bevan, R.L.; Hughes, R.R.; Rachev, R.K.; Ali, A.A.S.; Wilcox, P.D. Deep learning for ultrasonic crack characterization in NDE. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 68, 1854–1865. [Google Scholar] [CrossRef]
- Li, D.D.; Keogh, D.F.; Huang, K.; Chan, Q.N.; Yuen, A.C.Y.; Menictas, C.; Timchenko, V.; Yeoh, G.H. Modeling the Response of Magnetorheological Fluid Dampers under Seismic Conditions. Appl. Sci. 2019, 9, 4189. [Google Scholar] [CrossRef]
- Sodeyama, H.; Suzuki, K.; Sunakoda, K. Development of Large Capacity Semi-Active Seismic Damper Using Magneto-Rheological Fluid. J. Press. Vessel Technol. 2004, 126, 105–109. [Google Scholar] [CrossRef]
- Park, J.Y.; Oh, J.S.; Kim, Y.C. Design and Control of Multi-Plate MR Clutch Featuring Friction and Magnetic Field Control Modes. Sensors 2022, 22, 1757. [Google Scholar] [CrossRef] [PubMed]
- Kavlicoglu, B.M.; Gordaninejad, F.; Wang, X. Study of a Magnetorheological Grease Clutch. Smart Mater. Struct. 2013, 22, 125030. [Google Scholar] [CrossRef]
- Sohn, J.W.; Kim, G.-W.; Choi, S.-B. A State-of-the-Art Review on Robots and Medical Devices Using Smart Fluids and Shape Memory Alloys. Appl. Sci. 2018, 8, 1928. [Google Scholar] [CrossRef]
- Khanicheh, A.; Mintzopoulos, D.; Weinberg, B.; Tzika, A.A.; Mavroidis, C. Evaluation of Electrorheological Fluid Dampers for Applications at 3-T MRI Environment. IEEE/ASME Trans. Mechatron. 2008, 13, 286–294. [Google Scholar] [CrossRef]
- McDonald, K.J.; Kinnicutt, L.; Moran, A.M.; Ranzani, T. Modulation of Magnetorheological Fluid Flow in Soft Robots Using Electropermanent Magnets. IEEE Robot. Autom. Lett. 2022, 7, 3914–3921. [Google Scholar] [CrossRef]
- Hua, D.; Liu, X.; Sun, S.; Sotelo, M.A.; Li, Z.; Li, W. A Magnetorheological Fluid-Filled Soft Crawling Robot with Magnetic Actuation. IEEE/ASME Trans. Mechatron. 2020, 25, 2700–2710. [Google Scholar] [CrossRef]
- Lay-Ekuakille, A.; Palamara, I.; Caratelli, D.; Morabito, F.C. Experimental Infrared Measurements for Hydrocarbon Pollutant Determination in Subterranean Waters. Rev. Sci. Instrum. 2013, 84, 015103. [Google Scholar] [CrossRef]
- She, N.; Chen, B.; Lu, M.; Xu, Y.; Peng, X.; Hung, S. A Multi Particle Sedimentation Stability Investigation of Magnetorheological Fluid Using the DEM. Korea-Aust. Rheol. J. 2024, 36, 1–14. [Google Scholar] [CrossRef]
- Li, S.; Qi, S.; Liu, J.; Fu, J.; Li, Y.; Bai, L.; Wu, W.; Yu, M. Dimensional Analysis for Sedimentation Behavior of Magnetorheological Fluids. Phys. Fluids 2024, 36, 11–24. [Google Scholar] [CrossRef]
- Cvek, M.; Jamatia, T.; Suly, P.; Urbanek, M.; Torres-Mendieta, R. Stable Magnetorheological Fluids Containing Bidisperse Fillers with Compact/Mesoporous Silica Coatings. Int. J. Mol. Sci. 2022, 23, 11044. [Google Scholar] [CrossRef] [PubMed]
- Cacciola, M.; Calcagno, S.; Megali, G.; Morabito, F.C.; Pellicano, D.; Versaci, M.F.E.A. FEA Design and Misfit Minimization for In-Depth Flaw Characterization in Metallic Plates with Eddy Current Nondestructive Testing. IEEE Trans. Magn. 2009, 45, 1506–1509. [Google Scholar] [CrossRef]
- Choi, S.B. Sedimentation Stability of Magnetorheological Fluids: The State of the Art and Challenging Issues. Micromachines 2022, 13, 1904. [Google Scholar] [CrossRef]
- Maharani, E.T.; Lee, D.-H.; Kim, Y.-J.; Oh, J.-S.; Choi, S.-B. The Actuating Characteristics of Magnetorheological Fluids Subjected to Particle Sedimentation and Temperature Variation. Actuators 2024, 13, 277. [Google Scholar] [CrossRef]
- Ryapolov, P.; Vasilyeva, A.; Kalyuzhnaya, D.; Churaev, A.; Sokolov, E.; Shel’deshova, E. Magnetic Fluids: The Interaction between the Microstructure, Macroscopic Properties, and Dynamics under Different Combinations of External Influences. Nanomaterials 2024, 14, 222. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, Z.; Zhou, J.; Mao, A.; Bian, D. Modification of Magnetorheological Fluid and its Compatibility with Metal Skeleton: Insights from Multi-Body Dissipative Particle Dynamics Simulations and Experimental Study. Phys. Fluids 2024, 36, 1254. [Google Scholar] [CrossRef]
- Versaci, M.; Laganà, F.; Manin, L.; Angiulli, G. Soft Computing and Eddy Currents to Estimate and Classify Delaminations in Biomedical Device CFRP Plates. J. Electr. Eng. 2025, 2025 76, 72–79. [Google Scholar] [CrossRef]
- Laganà, F.; Pullano, S.A.; Angiulli, G.; Versaci, M. Optimized Analytical-Numerical Procedure for Ultrasonic Sludge Treatment for Agricultural Use. Algorithms 2024, 17, 592. [Google Scholar] [CrossRef]
- Gopinath, B.; Sathishkumar, G.K.; Karthik, P.; Charles, M.M.; Ashok, K.G.; Ibrahim, M.; Akheel, M.M. A Systematic Study of the Impact of Additives on Structural and Mechanical Properties of Magnetorheological Fluids. Mater. Today Proc. 2021, 37, 1721–1728. [Google Scholar] [CrossRef]
- Hoang, T.K.N.; Duong, H.Q.; Nguyen, Q.B.; Nguyen, D.B.T. Colloidal Stability and Rheological Properties of Bio-Ferrofluids of Polymer-Coated Single-Core and Multi-Core Nanoparticles. J. Magn. Magn. Mater. 2023, 579, 170838. [Google Scholar] [CrossRef]
- Guo, C.; Liu, J.; Li, X.; Yang, S. Effect of Cavitation Bubble on the Dispersion of Magnetorheological Polishing Fluid Under Ultrasonic Preparation. Ultrason. Sonochem. 2021, 79, 105782. [Google Scholar] [CrossRef] [PubMed]
- Gordeev, B.A.; Ivanov, E.G.; Okhulkov, S.N.; Ermolaev, A.I.; Plekhov, A.S. Production of Magnetorheological Suspensions by Cavitation. Russ. Eng. Res. 2023, 43, 962–967. [Google Scholar] [CrossRef]
- Leong, T.; Johansson, L.; Juliano, P.; McArthur, S.L.; Manasseh, R. Ultrasonic Separation of Particulate Fluids in Small and Large-Scale Systems: A Review. Ind. Eng. Chem. Res. 2013, 52, 16555–16576. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II Higher Frequency. J. Acoust. Soc. Am. 1955, 28, 179–191. [Google Scholar] [CrossRef]
- Hovem, J.M.; Ingram, C.D. Viscous Attenuation of Sound in Saturated Sand. J. Acoust. Soc. Am. 1979, 66, 812–1087. [Google Scholar] [CrossRef]
- Hovem, J.M. Viscous Attenuation of Sound in Suspension and High-Porosity Marine Sediments. J. Acoust. Soc. Am. 1980, 67, 1559–1563. [Google Scholar] [CrossRef]
- Ru, C.Q. Rotational Flow Field of a Particle-Laden Fluid on a Co-Rotating Disk. Phys. Fluids 2024, 36, 158–179. [Google Scholar] [CrossRef]
- Silva, R.C. Experimental Characterization Techniques for Solid-Liquid Slurry Flows in Pipelines: A Review. Processes 2022, 10, 597. [Google Scholar] [CrossRef]
- Pal, S.; Hanmaiahgari, P.R.; Karney, B.W. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water 2021, 13, 1597. [Google Scholar] [CrossRef]
- Eftekhari, K.; Parakhonskiy, B.V.; Grigoriev, D.; Skirtach, A.G. Advances in Nanoarchitectonics: A Review of “Static” and “Dynamic” Particle Assembly Methods. Materials 2024, 17, 1051. [Google Scholar] [CrossRef]
- Papanicolaou, G. (Ed.) Wave Propagation in Complex Media; Springer Science & Business Media: New York, NY, USA, 2012; Volume 96. [Google Scholar]
- Boccotti, P. Idraulica Marittima; UTET Università: Torino, Italy, 2004. [Google Scholar]
- Jia, B.; Soyama, H. Non-spherical cavitation bubbles: A review. Fluids 2024, 9, 249. [Google Scholar] [CrossRef]
- Ge, M.; Svennberg, U.; Bensow, R.E. Investigation on RANS Prediction of Propeller-Induced Pressure Pulses and Sheet-Tip Cavitation Interactions in Behind Hull Condition. Ocean Eng. 2020, 209, 107503. [Google Scholar] [CrossRef]
- Zhou, Y. Effect of microchannel protrusion on the bulk acoustic wave-induced acoustofluidics: Numerical investigation. Biomed. Microdevices 2022, 24, 7. [Google Scholar] [CrossRef]
- Oh, J.-S.; Choi, S.-B. A Review on the Development of Dampers Utilizing Smart Magnetorheological Fluids. Curr. Smart Mater. 2019, 4, 15–21. [Google Scholar] [CrossRef]
- Huang, H.; Chen, C.; Zhang, Z.C.; Zheng, J.N.; Li, Y.Z.; Chen, S.M. Design and Experiment of a New Structure of MR Damper for Improving and Self-Monitoring the Sedimentation Stability of MR Fluid. Smart Mater. Struct. 2020, 29, 075019. [Google Scholar] [CrossRef]
- Song, X. Design of Adaptive Vibration Control Systems with Application to Magneto-Rheological Dampers. Ph.D. Thesis, The University of Notre Dame, Notre Dame, IN, USA, 1999. [Google Scholar]
- Lam, A.H.-F.; Liao, W.-H. Semi-active control of automotive suspension systems with magneto-rheological dampers. Int. J. Veh. Des. 2003, 33, 50–75. [Google Scholar] [CrossRef]
- Ntella, S.L.; Duong, M.T.; Civet, Y.; Pataky, Z.; Pemard, Y. Design Optimization of Miniature Magnetorheological Valves with Self-Sensing Capabilities Used for a Wearable Medical Application. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 409–414. [Google Scholar] [CrossRef]
- Odenbach, S. Colloidal Magnetic Fluids: Basics, Development, and Application of Ferrofluids; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Amstad, E.; Zurcher, S.; Mashaghi, A.; Wong, J.Y.; Textor, M.; Reimhult, E. Surface functionalization of single superparamagnetic iron oxide nanoparticles for targeted magnetic resonance imaging. Small 2009, 5, 1334–1342. [Google Scholar] [CrossRef]
- Qian, B.; Zhao, Q.; Ye, X. Ultrasound and Magnetic Responsive Drug Delivery Systems for Cardiovascular Application. J. Cardiovasc. Pharmacol. 2020, 76, 414–426. [Google Scholar] [CrossRef]
- Cao, H.X.; Nguyen, V.D.; Park, J.O.; Choi, E.; Kang, B. Acoustic actuators for the manipulation of micro/nanorobots: State-of-the-art and future outlooks. Micromachines 2024, 15, 186. [Google Scholar] [CrossRef]
- Arowolo, M.O.; Fayose, F.T.; Ade-Omowaye, J.A.; Adekunle, A.A.; Akindele, S.O. Design and development of an energy-efficient audio-based repellent system for rice fields. Int. J. Emerg. Technol. Adv. Eng. 2022, 12, 82–94. [Google Scholar] [CrossRef] [PubMed]
- Postorino, M.N.; Versaci, M. A Neuro-Fuzzy Approach to Simulate the User Mode Choice Behavior in a Travel Decision Framework. Int. J. Model. Simul. 2008, 28, 64–71. [Google Scholar] [CrossRef]
- Bechtel, S.; Washington, G.; Ahmadkhanlou, F.; Wang, Y. Microstructural analysis and control of magneto-rheological fluid. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004; Volume 47004. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Z.; Zhao, Y.; Zhang, Q.; Wang, Z.; Liu, Q.; Zhao, J. Predictive Modeling and Experimental Investigation of Material Removal Profiles in Ultrasonic-Assisted Shear Thickening Polishing of 4H-SiC Crystals. Tribol. Int. 2025, 212, 110942. [Google Scholar] [CrossRef]
- García, A.; Espinosa, A.; Krawczyk, A. Targeted Drug Delivery Using Ultrasound-Magnetic Hybrid Systems. Nanomedicine 2022, 39, 102455. [Google Scholar]
- Manbachi, A.; Cobbold, R.S.C. Development and application of piezoelectric materials for ultrasound generation and detection. Ultrasound 2011, 19, 187–196. [Google Scholar] [CrossRef]
- Malik, V.; Pal, A.; Pravaz, O.; Crassous, J.J.; Granville, S.; Grobety, B.; Hirt, A.M.; Dietsch, H.; Schurtenberger, P. Hybrid magnetic iron oxide nanoparticles with tunable field-directed self-assembly. Nanoscale 2017, 9, 14405–14413. [Google Scholar] [CrossRef]
- Ashour, O.; Rogers, C.A.; Kordonsky, W. Magnetorheological fluids: Materials, characterization, and devices. J. Intell. Mater. Syst. Struct. 1996, 7, 123–130. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.G.; Fan, X.M.; Pang, J.L. Ultrasound-Responsive Smart Implantable Hydrogels for Targeted Delivery of Drugs. Int. J. Nanomed. 2021, 16, 6531–6546. [Google Scholar]
- Popa, B.-I.; Cummer, S.A. Non-reciprocal and highly nonlinear active acoustic metamaterials. Nat. Commun. 2013, 5, 3398. [Google Scholar] [CrossRef]
- Rodriguez-Lòpez, J.; Segura, L.E.; Montero de Espinosa Freijo, F. Ultrasonic Velocity and Amplitude Characterization of Magnetorheological Fluids under Magnetic Fields. J. Magn. Magn. Mater. 2012, 324, 222–230. [Google Scholar] [CrossRef]
- Sharath, S.S.; Ramu, J.; Nair, S.V.; Iyer, S.; Mony, U.; Rangasamy, J. Human adipose tissue derivatives as a potent native biomaterial for tissue regenerative therapies. Tissue Eng. Regen. Med. 2020, 17, 123–140. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jiang, Y.; Lan, L.; Ge, X.; Cheng, R.; Zhan, Y.; Chen, G.; Shi, L.; Wang, R.; Zheng, N.; et al. Optically-Generated Focused Ultrasound for Noninvasive Brain Stimulation with Ultrahigh Precision. arXiv 2022. [Google Scholar] [CrossRef] [PubMed]
- Zeroug, S.; Bose, S. Ultrasonic cement evaluation with the flexural wave imager: A new workflow to estimate cement wavespeeds. In SPE Annual Technical Conference and Exhibition; SPE: Houston, TX, USA, 2018; p. D021S017R001. [Google Scholar] [CrossRef]
- Ganjian, E.; Ehsani, A.; Mason, T.J.; Tyrer, M. Application of Power Ultrasound to Cementitious Materials: Advances, Issues, and Perspectives. Mater. Des. 2018, 160, 503–513. [Google Scholar] [CrossRef]
- Hasannejad, M.; Berenjian, J.; Pouraminian, M.; Sadeghi Larijani, A. Studying of Microstructure, Interface Transition Zone, and Ultrasonic Wave Velocity of High-Strength Concrete by Different Aggregates. J. Build. Pathol. Rehabil. 2022, 7, 9. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.L.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Utara, S.; Loykaew, A.; Khoonsap, S.; Mahakot, S.; Amnuaypanich, S. Natural rubber latex grafted with polyacrylamide as the cement admixture for improving flexural strength and toughness of cement pastes. Ind. Crops Prod. 2025, 224, 120310. [Google Scholar] [CrossRef]
- Vaitkevičius, V.; Šerelis, E.; Kerševičius, V. Effect of Ultrasonic Activation on Early Hydration Process in 3D Concrete Printing Technology. Constr. Build. Mater. 2018, 169, 354–363. [Google Scholar] [CrossRef]
- Bossis, G.; Volkova, O.; Lacis, S.; Meunier, A. Magnetorheology: Fluids, Structures and Rheology. In Ferrofluids; Springer: Vienna, Austria, 2002; pp. 202–230. [Google Scholar] [CrossRef]
- Odenbach, S. Recent progress in magnetic fluid research. J. Phys. Condens. Matter 2004, 16, R1135–R1150. [Google Scholar] [CrossRef]
- Shen, M.; Huang, Q.B. Acoustic properties of magnetorheological fluids under magnetic fields. Appl. Mech. Mater. 2015, 721, 818–823. [Google Scholar] [CrossRef]
- de Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Chauhan, V.; Kumar, A.; Sham, R. Magnetorheological fluids: A comprehensive review. Manuf. Rev. 2024, 11, 6. [Google Scholar] [CrossRef]
- Bruus, H. Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 2012, 12, 1014–1021. [Google Scholar] [CrossRef]
- Settnes, M.; Bruus, H. Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E 2012, 85, 016327. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Plesset, M.S.; Prosperetti, A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Deng, H.X.; Gong, X.L.; Wang, L.H. Development of an adaptive tuned vibration absorber with magnetorheological elastomer. Smart Mater. Struct. 2006, 15, N111–N116. [Google Scholar] [CrossRef]
- Wells, P.N.T. Medical ultrasonics. IEE Proc. A (Phys. Sci. Meas. Instrum.) 1984, 131, 225–232. [Google Scholar] [CrossRef]
- Singh Rajput, A.; Das, M.; Kapil, S. Surface properties and biocompatibility studies on bone plate by magnetorheological finishing. Surf. Eng. 2022, 38, 797–806. [Google Scholar] [CrossRef]
- Qian, E.; Zhang, X.; Wu, Y.; Li, M.; Zhao, J. Magnetic resonance fingerprinting based thermometry (MRFT): Application to ex vivo imaging near DBS leads. Phys. Med. Biol. 2023, 68, 17NT01. [Google Scholar] [CrossRef]
- Polat, E.O.; Cetin, M.M.; Tabak, A.F.; Bilget Güven, E.; Uysal, B.Ö.; Arsan, T.; Kabbani, A.; Hamed, H.; Gül, S.B. Transducer technologies for biosensors and their wearable applications. Biosensors 2022, 12, 385. [Google Scholar] [CrossRef] [PubMed]
- Horn, R.C. Determinação da Mutagenicidade e Atividade Citotóxica de Sedimentos em área Sujeita à Contaminação Petroquímica. Master’s Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2004. [Google Scholar]
- Soler, R. Magnetohydrodynamic waves in the partially ionized solar plasma. Philos. Trans. R. Soc. A 2024, 382, 20230223. [Google Scholar] [CrossRef]
- Persky, G. Effective Mass Theorems in Strained Moving Lattices with Application to Helicon-Acoustic Dispersion Relations. Ph.D. Thesis, Polytechnic Institute of Brooklyn, Brooklyn, NY, USA, 1968. [Google Scholar]
- Entzian, K.; Aigner, A. Drug delivery by ultrasound-responsive nanocarriers for cancer treatment. Pharmaceutics 2021, 13, 1135. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Wang, J.; Li, Y.; Liu, Y. A Novel Class of Bioinspired Composite via Ultrasound-Assisted Directed Self-Assembly Digital Light Processing. Addit. Manuf. 2022, 53, 102715. [Google Scholar]
- Fan, C.H.; Ho, Y.J.; Lin, C.W.; Wu, N.; Chiang, P.H.; Yeh, C.K. State-of-the-art of ultrasound-triggered drug delivery from ultrasound-responsive drug carriers. Expert Opin. Drug Deliv. 2022, 19, 997–1009. [Google Scholar] [CrossRef] [PubMed]
- Bommana, M.M.; Raut, S. Brain targeting of payload using mild magnetic field: Site specific delivery. In Nanostructures for the Engineering of Cells, Tissues and Organs; William Andrew: Norwich, NY, USA, 2018; pp. 167–185. [Google Scholar] [CrossRef]
- Volkova, O.; Bossis, G.; Guyot, M.; Bashtovoi, V.; Reks, A. Magnetorheology of magnetic holes compared to magnetic particles. J. Rheol. 2000, 44, 91–104. [Google Scholar] [CrossRef]
- Moradi Kashkooli, F.; Souri, M.; Tavakkoli, J.; Kolios, M.C. A spatiotemporal computational model of focused ultrasound heat-induced nano-sized drug delivery system in solid tumors. Drug Deliv. 2023, 30, 2219871. [Google Scholar] [CrossRef] [PubMed]
- Yazdan, M.; Naghib, S.M. Smart ultrasound-responsive polymers for drug delivery: An overview on advanced stimuli-sensitive materials and techniques. Curr. Drug Deliv. 2025, 22, 283–309. [Google Scholar] [CrossRef]
- Cavalieri, F.; Zhou, M.; Tortora, M.; Lucilla, B.; Ashokkumar, M. Methods of preparation of multifunctional microbubbles and their in vitro/in vivo assessment of stability, functional and structural properties. Curr. Pharm. Des. 2012, 18, 2135–2151. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; Huang, X.; Xu, J.; Guo, H.; Wang, H. Magnetic Hydrogel Scaffolds for Bone Regeneration: From Materials to Clinical Translation. Adv. Funct. Mater. 2021, 31, 2009583. [Google Scholar]
- Kim, Y.; Seo, Y.; Jeong, H.E.; Lee, J.B. Ultrasound-Stimulated Bioengineered Tissues: Advances in Regenerative Medicine. Trends Biotechnol. 2022, 40, 456–470. [Google Scholar] [CrossRef]
- Gao, F.; Li, Y.; Liu, M.; Wang, D.; Zhou, J. Magnetically Responsive Platforms for Orthopedic Applications: Therapeutic Strategies and Perspectives. Bioact. Mater. 2023, 20, 465–482. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Choi, D.; Kim, J.; Kim, H. Focused Ultrasound in Bone Repair and Regeneration: Current Status and Clinical Outlook. J. Orthop. Transl. 2023, 38, 113–125. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Y.; Chen, X.; Xu, F.; Zhang, Q.; Yin, Z.; Yuwen, L. Magnetic Field/Ultrasound-Responsive Microbubbles for Efficient Removal of MRSA Biofilms. Nanomaterials 2024, 14, 1830. [Google Scholar] [CrossRef]
- Al Refaai, K.A.; AlSawaftah, N.A.; Abuwatfa, W.; Husseini, G.A. Drug release via ultrasound-activated nanocarriers for cancer treatment: A review. Pharmaceutics 2024, 16, 1383. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-L.; Wu, M.-J. A Practical Risk Stratification System Based on Ultrasonography and Clinical Characteristics for Predicting the Malignancy of Soft Tissue Masses. Front. Oncol. 2024, 14, 1027. [Google Scholar] [CrossRef]
- Souri, M.; Moradi Kashkooli, F.; Soltani, M. Analysis of magneto-hyperthermia duration in nano-sized drug delivery system to solid tumors using intravascular-triggered thermosensitive-liposome. Pharm. Res. 2022, 39, 753–765. [Google Scholar] [CrossRef]
- Tanzi, M.C.; Bozzini, S.; Candiani, G.; Cigada, A.; De Nardo, L.; Fare, S.; Ganazzoli, F.; Gastaldi, D.; Levi, M.; Metrangolo, P.; et al. Trends in biomedical engineering: Focus on Smart Bio-Materials and Drug Delivery. J. Appl. Biomater. Biomech. 2011, 9, 87–97. [Google Scholar] [CrossRef]
- Terreno, E.; Uggeri, F.; Aime, S. Image guided therapy: The advent of theranostic agents. J. Control. Release 2012, 161, 328–337. [Google Scholar] [CrossRef]
- Ma, P.; Lai, X.; Luo, Z.; Chen, Y.; Loh, X.J.; Ye, E.; Wu, Y.L. Recent advances in mechanical force-responsive drug delivery systems. Nanoscale Adv. 2022, 4, 3462–3478. [Google Scholar] [CrossRef]
- Umemura, S. Focused ultrasound transducer for thermal treatment. Int. J. Hyperth. 2015, 31, 216–221. [Google Scholar] [CrossRef]
- Stride, E.; Coussios, C. Nucleation, mapping, and control of cavitation for drug delivery. Nat. Rev. Phys. 2019, 1, 495–509. [Google Scholar] [CrossRef]
- Yamakawa, R.; Onoe, H.; Kurashina, Y. Hydrogel Carrier with Bubble Vibration Enhancer for Ultrasound-Triggered Drug Release. Ultrason. Sonochem. 2024, 98, 106579. [Google Scholar] [CrossRef] [PubMed]
- Seemala, V.; King, R.; Williams, M.A.; Debnath, C.; Palit, A. Medical vs. MicroCT Based Finite Element Analysis: Exploring the Influence of Bone Heterogeneity and Bone Geometry. In Proceedings of the 2024 46th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 15–19 July 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Muñoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 607–614. [Google Scholar] [CrossRef]
- Baev, A.R.; Korobko, E.V.; Novikova, Z.A. Acoustical properties of magnetorheological fluids under applied magnetic field. J. Intell. Mater. Syst. Struct. 2015, 26, 1913–1919. [Google Scholar] [CrossRef]
- Shokrollahi, H. Structure, synthetic methods, magnetic properties and biomedical applications of ferrofluids. Mater. Sci. Eng. C 2013, 33, 2476–2487. [Google Scholar] [CrossRef]
- Ssimic, M.; Herakovic, N. Characterization of energy consumption of new piezo actuator system used for hydraulic on/off valves. J. Clean. Prod. 2021, 284, 124748. [Google Scholar] [CrossRef]
- Kazys, R.; Vaskeliene, V. High temperature ultrasonic transducers: A review. Sensors 2021, 21, 3200. [Google Scholar] [CrossRef]
- Cochran, S.; Bernassau, A.; Cumming, D.; Démoré, C.; Desmulliez, M.; Sweet, J. Future integration of silicon electronics with miniature piezoelectric ultrasonic transducers and arrays. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1108–1116. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Liu, M.; Chen, X. Study on Process Optimization of Ultrasound-Assisted Magnetorheological Finishing of Sapphire Hemisphere Surface. Precis. Eng. 2023, 84, 102345. [Google Scholar]
- Gharib, M.; Omran, A.; El-Bayoumi, G. Optimal vibration control for structural-acoustic coupling system. J. Vib. Control 2013, 19, 14–29. [Google Scholar] [CrossRef]
- Avirovik, D. System-Level Approach Towards Intelligent Healthcare Environment. Mathematics 2014. Available online: http://hdl.handle.net/10919/49581 (accessed on 3 August 2025).
- Sarath, S.; Paul, P.S. Application of Smart Fluid to Control Vibration in Metal Cutting: A Review. World J. Eng. 2021, 18, 458–479. [Google Scholar] [CrossRef]
- Kim, H.T.; Jeong, A.M.; Kim, H.Y.; An, J.W.; Kim, C.H.; Jin, K.C.; Choi, S.B. Lateral Vibration Control of a Precise Machine Using Magneto-Rheological Mounts Featuring Multiple Directional Damping Effect. Smart Mater. Struct. 2018, 27, 037001. [Google Scholar] [CrossRef]
- Luo, C.; Chen, Y.; Cao, H.; Al Sibahee, M.A.; Xu, W.; Zhang, J. Multi-modal autonomous ultrasound scanning for efficient human–machine fusion interaction. IEEE Trans. Autom. Sci. Eng. 2024, 22, 4712–4723. [Google Scholar] [CrossRef]
- Chen, S.H.; Lin, M.Y. Development and design of intelligent lubricating equipment for feed systems. Heliyon 2024, 10, e2402155. [Google Scholar] [CrossRef]
- Li, X.; Zhao, M.; Zhang, Y. Lubrication performance of magnetorheological fluid-lubricated rubber stern bearing test ring. Tribol. Int. 2021, 154, 106713. [Google Scholar] [CrossRef]
- Arul, K.; Kumar, V.S. Magnetorheological based minimum quantity lubrication (MR-MQL) with additive n-CuO. Mater. Manuf. Processes 2020, 35, 405–414. [Google Scholar]
- Žáček, J.; Strecker, Z.; Jeniš, F. Impact of magnetorheological fluid composition on their behaviour in gradient pinch mode. Sci. Rep. 2024, 14, 82752. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.S.; Silva, T.L.; Gomes, J.R.B. Synthetic oil gels with organoclays in the formulation of magnetorheological fluids. arXiv 2024, arXiv:2403.19774. [Google Scholar] [CrossRef]
- Masa’id, A.; Lenggana, B.W.; Ubaidillah, U.; Susilo, D.D.; Choi, S.-B. A Review on Vibration Control Strategies Using Magnetorheological Materials Actuators: Application Perspective. Actuators 2023, 12, 113. [Google Scholar] [CrossRef]
- Jahanbekam, S.; Mozafari, N.; Bagheri-Alamooti, A.; Mohammadi-Samani, S.; Daneshamouz, S.; Heidari, R.; Azadi, A. Ultrasound-responsive hyaluronic acid hydrogel of hydrocortisone to treat osteoarthritis. Int. J. Biol. Macromol. 2023, 240, 124449. [Google Scholar] [CrossRef]
- Rojek, I.; Mikołajewski, D.; Kempiński, M.; Galas, K.; Piszcz, A. Emerging applications of machine learning in 3D printing. Appl. Sci. 2025, 15, 1781. [Google Scholar] [CrossRef]
- Choi, C.M.K. Design, Fabrication, and Evaluation of Reconfigurable Acoustic Metamaterials. Doctoral Dissertation, UCL (University College London), London, UK, 2024. [Google Scholar]
- Wang, Y.; Qin, J. Advances in human organoids-on-chips in biomedical research. Life Med. 2023, 2, lnad007. [Google Scholar] [CrossRef]
- Abdul Aziz, M.; Mohtasim, S.M.; Ahammed, R. State-of-the-art Recent Developments of Large Magnetorheological Dampers. Korea-Aust. Rheol. J. 2022, 34, 105–136. [Google Scholar] [CrossRef]
- Vishwakarma, P.N.; Mishra, P.; Sharma, S.K. Characterization of a Magnetorheological Fluid Damper: A Review. Mater. Today Proc. 2021, 56, 2988–2994. [Google Scholar] [CrossRef]
- Hu, G.; Qi, H.; Zheng, K.; Yu, L. Design and Performance Evaluation of a Magnetorheological Valve with Mosquito-Coil-Plate Fluid Flow Channels. Sens. Actuators A Phys. 2022, 347, 113983. [Google Scholar] [CrossRef]
- Warke, V.; Kumar, S.; Bongale, A.; Kamat, P.; Kotecha, K.; Selvachandran, G.; Abraham, A. Improving the Useful Life of Tools Using Active Vibration Control Through Data-Driven Approaches: A Systematic Literature Review. Eng. Appl. Artif. Intell. 2024, 128, 107367. [Google Scholar] [CrossRef]
- Pi, Z.; Deng, D.; Chen, X.; Chen, S.; Lin, H.; Chen, M. Magneto-Acoustic Theranostic Approach: Integration of Magnetomotive Ultrasound Shear Wave Elastography and Magnetic Hyperthermia. J. Ultrasound Med. 2024, 43, 1819–1831. [Google Scholar] [CrossRef]
- Kim, W.S.; Min, S.; Kim, S.K.; Kang, S.; An, S.; Criado-Hidalgo, E.; Davis, H.; Bar-Zion, A.; Malounda, D.; Kim, Y.H.; et al. Magneto-Acoustic Protein Nanostructures for Non-Invasive Imaging of Tissue Mechanics In Vivo. Nat. Mater. 2024, 23, 290–300. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.; Galindo-Rosales, F.J.; Campo-Deaño, L. Magnetorheological Characterization of Blood Analogues Seeded with Paramagnetic Particles. arXiv 2025, arXiv:2504.09194. [Google Scholar] [CrossRef]
- Bhat, A.; Rao, V.S.; Jayalakshmi, N.S. Review of the Evolution of Magnetorheological Fluid-Based Rehabilitative Devices: From the Perspective of Modelling, Sensors, and Control Strategies. IEEE Access 2023, 11, 88759–88777. [Google Scholar] [CrossRef]
- Winkel, L.H.; Vriens, B.; Jones, G.D.; Schneider, L.S.; Pilon-Smits, E.; Bañuelos, G.S. Selenium cycling across soil-plant-atmosphere interfaces: A critical review. Nutrients 2015, 7, 4199–4239. [Google Scholar] [CrossRef]
- Darmani, G.; Ramezanpour, H.; Sarica, C.; Annirood, R.; Grippe, T.; Nankoo, J.-F.; Fomenko, A.; Santyr, B.; Zeng, K.; Vetkas, A.; et al. Individualized Non-Invasive Deep Brain Stimulation of the Basal Ganglia Using Transcranial Ultrasound Stimulation. Nat. Commun. 2025, 16, 2693. [Google Scholar] [CrossRef]
- Beisteiner, R.; Matt, E.; Fan, C.; Baldysiak, H.; Schönfeld, M.; Philippi Novak, T.; Amini, A.; Aslan, T.; Reinecke, R.; Lehrner, J.; et al. Transcranial Pulse Stimulation with Ultrasound in Alzheimer’s Disease—A New Navigated Focal Brain Therapy. Adv. Sci. 2023, 10, 2205634. [Google Scholar] [CrossRef]
- Labate, A.; Bertino, S.; Morabito, R.; Smorto, C.; Militi, A.; Cammaroto, S.; Anfuso, C.; Tomaiuolo, F.; Tonin, P.; Marino, S.; et al. MR Guided Focused Ultrasound for Refractory Epilepsy: Where Are We Now? J. Clin. Med. 2023, 12, 7070. [Google Scholar] [CrossRef]
- Meng, Y.; Hynynen, K.; Lipsman, N. Applications of Focused Ultrasound in the Brain: From Thermoablation to Drug Delivery. Nat. Rev. Neurol. 2025, 17, 7–22. [Google Scholar] [CrossRef] [PubMed]
- Park, G.; Kim, S.; Park, G.K.; Lee, N. Influence of carbon fiber on the electromagnetic shielding effectiveness of high-performance fiber-reinforced cementitious composites. J. Build. Eng. 2021, 35, 101982. [Google Scholar] [CrossRef]
- Xu, R.; Bestmann, S.; Treeby, B.E.; Martin, E. Strategies and Safety Simulations for Ultrasonic Cervical Spinal Cord Neuromodulation. arXiv 2024, arXiv:2402.14117. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wei, K.; Mei, M.; Yang, X. Ultrasound-Assisted Resin Transfer Molding to Improve the Impregnation and Balance Dual-Scale Flow in Composite Materials. Compos. Part A Appl. Sci. Manuf. 2024, 175, 107665. [Google Scholar] [CrossRef]
- Chircov, C.; Grumezescu, A.M.; Holban, A.M. Magnetic particles for advanced molecular diagnosis. Materials 2019, 12, 2158. [Google Scholar] [CrossRef]
- Qiao, K.; Luo, C.; Huang, R.; Xiang, J.; Pan, Y.; Zhang, S.; Ning, S. Ultrasound triggered tumor metabolism suppressor induces tumor starvation for enhanced sonodynamic immunotherapy of breast cancer. Int. J. Nanomed. 2023, 18, 3801–3811. [Google Scholar] [CrossRef]
- Rossi, A.; Bassi, G.; Cunha, C.; Baldisseri, C.; Ravaglia, N.; Giardini, D.; Molinari, F.; Lista, F.; Teran, F.J.; Piperno, A.; et al. Magnetically Induced Anisotropic Structure in an Injectable Hydrogel for Bone Tissue Engineering. J. Colloid Interface Sci. 2024, 650, 186–197. [Google Scholar] [CrossRef]
- Uthaman, S.; Huh, K.M.; Park, I.K. Tumor microenvironment-responsive nanoparticles for cancer theragnostic applications. Biomater. Res. 2018, 22, 22. [Google Scholar] [CrossRef]
- Inoue, S.; Li, C.; Hatakeyama, J.; Jiang, H.; Kuroki, H.; Moriyaman, H.; Kondo, K.; Nakamura, T. Higher-Intensity Ultrasound Accelerates Fracture Healing via Piezo1-Mediated Mechanotransduction. Bone 2023, 177, 116916. [Google Scholar] [CrossRef] [PubMed]
- Bordhan, P. Targeting Cancer Cell-Derived Small Extracellular Vesicles (sEVs) to Develop Nanoparticle-Integrated Detection Systems. Doctoral Dissertation, University of Technology Sydney, Ultimo, Australia, 2024. [Google Scholar]
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. A review on multi-physics numerical modelling in different applications of magnetorheological fluids. J. Intell. Mater. Syst. Struct. 2020, 31, 1855–1897. [Google Scholar] [CrossRef]
- Maiullari, S.; Cicirelli, A.; Picerno, A.; Giannuzzi, F.; Gesualdo, L.; Notarnicola, A.; Sallustio, F.; Moretti, B. Pulsed Electromagnetic Fields Induce Skeletal Muscle Cell Repair by Sustaining the Expression of Proteins Involved in the Response to Cellular Damage and Oxidative Stress. Int. J. Mol. Sci. 2023, 24, 16631. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.; Gao, H.; Liu, Y.; Sun, S.; Li, G. Application of Magnetism in Tissue Regeneration: Recent Progress and Future Prospects. Regen. Biomater. 2024, 11, rbae048. [Google Scholar] [CrossRef]
- Aw, M.S.; Paniwnyk, L.; Losic, D. The progressive role of acoustic cavitation for non-invasive therapies, contrast imaging, and blood-tumor permeability enhancement. Expert Opin. Drug Deliv. 2016, 13, 1383–1396. [Google Scholar] [CrossRef]
- Kline-Schoder, A.R.; Noel, R.L.; Phatnani, H.; Menon, V.; Konofagou, E.E. Focused Ultrasound-Mediated Blood–Brain Barrier Opening Best Promotes Neuroimmunomodulation through Brain Macrophage Redistribution. Neuroglia 2023, 4, 141–157. [Google Scholar] [CrossRef]
- Mehta, R.I.; Carpenter, J.S.; Mehta, R.I.; Haut, M.W.; Wang, P.; Ranjan, M.; Najib, U.; D’Haese, P.F.; Rezai, A.R. Ultrasound-Mediated Blood–Brain Barrier Opening Uncovers an Immediate, Brain-Wide Perivenous Fluid Efflux Pathway. Fluids Barriers CNS 2023, 20, 46. [Google Scholar] [CrossRef]
- Desmarais, S.; Ramos-Palacios, G.; Poree, J.; Lee, S.A.; Leconte, A.; Sadikot, A.F.; Provost, J. Equivalent-Time-Active-Cavitation-Imaging Enables Vascular-Resolution Blood–Brain Barrier Opening Therapy Planning. arXiv 2023, arXiv:2308.03287. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, M.; Zheng, J.; Ma, Z.; Yu, T.; Zhu, Y.; Nie, F. Ultrasound-responsive Nanocarriers delivering siRNA and Fe3O4 nanoparticles reprogram macrophages and inhibit M2 polarization for enhanced NSCLC immunotherapy. ACS Appl. Mater. Interfaces 2024, 16, 56634–56652. [Google Scholar] [CrossRef] [PubMed]
- Cattaneo, M.; Guerriero, G.; Shakya, G.; Krattiger, L.A.; Paganella, L.G.; Narciso, M.L.; Supponen, O. Cyclic Jetting Enables Microbubble-Mediated Drug Delivery. arXiv 2024, arXiv:2410.08990. [Google Scholar] [CrossRef]
- Fan, S.; Sun, R.; Zhao, X.; Wong, W.; Li, C. H∞ Design and Experimental Study of Two Types of Dynamic Vibration Absorbers with Tunable Damping. Chin. J. Theor. Appl. Mech. 2024, 56, 3324–3332. [Google Scholar] [CrossRef]
- Kawai, H.; Ito, A.; Kawaguchi, A.; Nagai-Tanima, M.; Nakahara, R.; Xu, S.; Kuroki, H. Ultrasound therapy for a week promotes regeneration and reduces pro-inflammatory macrophages in a rat sciatic nerve autograft model. Sci. Rep. 2023, 13, 11494. [Google Scholar] [CrossRef] [PubMed]
- Ezzat, M.A.; El-Bary, A.A.; Morsey, M.M. Space approach to the hydro-magnetic flow of a dusty fluid through a porous medium. Comput. Math. Appl. 2010, 59, 2868–2879. [Google Scholar] [CrossRef]
- Borowiec, M.; Litak, G.; Kasperek, R. Response of a Magneto-Rheological Fluid Damper Subjected to Periodic Forcing in a High Frequency Limit. arXiv 2006, arXiv:0610055. [Google Scholar] [CrossRef]
- Choi, Y.; Drake, K.; Jesik, M.; Hartzell, C.; Wereley, N. An Adaptive Magnetorheological Fluid-Based Robotic Claw with an Electro-Permanent Magnet Array. Actuators 2023, 12, 469. [Google Scholar] [CrossRef]
- Guan, R.; Zheng, H.; Liu, Q.; Ou, K.; Li, D.S.; Fan, J.; Fu, Q.; Sun, Y. DIW 3D Printing of Hybrid Magnetorheological Materials for Application in Soft Robotic Grippers. Compos. Sci. Technol. 2022, 223, 109409. [Google Scholar] [CrossRef]
- Gibaud, T.; Dagès, N.; Lidon, P.; Jung, G.; Ahouré, L.C.; Sztucki, M.; Poulesquen, A.; Hengl, N.; Pignon, F.; Manneville, S. Rheo-acoustic gels: Tuning mechanical and flow properties of colloidal gels with ultrasonic vibrations. arXiv 2019, arXiv:1905.07282. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M. A Neuro-Fuzzy Network for the Design of Circular and Triangular Equilateral Microstrip Antennas. Int. J. Infrared Millim. Waves 2002, 23, 1513–1520. [Google Scholar] [CrossRef]
- An, Y.; He, B.; Ma, Z.; Guo, Y.; Yang, G.-Z. Microassembly: A Review on Fundamentals, Applications, and Recent Developments. Engineering 2025, 48, 323–346. [Google Scholar] [CrossRef]
- Yuan, F.-Z.; Wang, H.-F.; Guan, J.; Fu, J.-N.; Yang, M.; Zhang, J.-Y.; Chen, Y.-R.; Wang, X.; Yu, J.-K. Fabrication of Injectable Chitosan-Chondroitin Sulfate Hydrogel Embedding Kartogenin-Loaded Microspheres as an Ultrasound-Triggered Drug Delivery System for Cartilage Tissue Engineering. Pharmaceutics 2021, 13, 1487. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Yu, J.; Vong, C.-I.; Chiu, P.W.Y.; Zhang, L. Magnetic Navigation of a Rotating Colloidal Swarm Using Ultrasound Images. arXiv 2018, arXiv:1809.06501. [Google Scholar] [CrossRef]
- Kumar, C.S.S.R.; Mohammad, F. Magnetic Nanomaterials for Hyperthermia-Based Therapy and Controlled Drug Delivery. Adv. Drug Deliv. Rev. 2011, 63, 789–808. [Google Scholar] [CrossRef] [PubMed]
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in Applications of Magnetic Nanoparticles in Biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Sun, W.; Zhao, X.; Li, Y. Ferrimagnetic Vortex Nanoring-Mediated Mild Magnetic Hyperthermia Imparts Potent Immunological Effect for Treating Cancer Metastasis. ACS Nano 2019, 13, 7800–7811. [Google Scholar] [CrossRef]
- Dutz, S.; Hergt, R. Magnetic Nanoparticle Heating and Heat Transfer on a Microscale: Basic Principles, Realities, and Physical Limitations of Hyperthermia for Tumor Therapy. Int. J. Hyperth. 2014, 29, 790–800. [Google Scholar] [CrossRef]
- Kennedy, J.E. High-Intensity Focused Ultrasound in the Treatment of Solid Tumors. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef]
- Cheng, Y.; Samia, A.C.; Meyers, J.D.; Panagopoulos, I.; Fei, B.; Burda, C. Highly Efficient Drug Delivery with Gold Nanoparticle Vectors for In Vivo Photodynamic Therapy of Cancer. J. Am. Chem. Soc. 2015, 137, 3076–3084. [Google Scholar] [CrossRef]
- Wilson, J.; Zhang, L.; Ramaswamy, S. Targeted Drug Release from Stable and Safe Ultrasound-Sensitive Nanocarriers. Front. Mol. Biosci. 2024, 11, 1408767. [Google Scholar] [CrossRef]
- Castle, J.; Butts, M.; Healey, A.; Kent, K.; Marino, M.; Feinstein, S.B. Ultrasound-Mediated Targeted Drug Delivery: Recent Success and Remaining Challenges. Am. J. Physiol. Heart Circ. Physiol. 2013, 304, H350–H357. [Google Scholar] [CrossRef]
- Fisher, D.G.; Price, R.J. Recent Advances in the Use of Focused Ultrasound for Magnetic Resonance Image-Guided Therapeutic Nanoparticle Delivery to the Central Nervous System. Front. Pharmacol. 2019, 10, 1348. [Google Scholar] [CrossRef]
- Han, H.; Kim, D.; Jang, Y.; Seo, M.; Kim, K. Focused Ultrasound-Triggered Chemo-Gene Therapy with Multifunctional Nanocomplex for Enhancing Therapeutic Efficacy. J. Control. Release 2020, 324, 303–315. [Google Scholar] [CrossRef]
- Rahman, M.; Rawat, S.; Yang, R.C.; Mahil, A.; Zhang, Y.X. A Comprehensive Review on Fresh and Rheological Properties of 3D Printable Cementitious Composites. J. Build. Eng. 2024, 91, 109719. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Park, H.; Choi, Y. Rheological Properties and 3D Printing Behavior of PCL and DMSO2 Composites. Materials 2024, 17, 2459. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Han, S.; Yang, J.; Li, Z.; An, M. Optimizing Printing and Rheological Parameters for 3D Printing with Cementitious Materials. Autom. Constr. 2025, 169, 105881. [Google Scholar] [CrossRef]
- Lin, W.; Wang, J.; Wang, S. Numerical and Experimental Investigation of Ultrasound Effects on Filtration Process in Wire-Wrapped Filter Tube. Ultrason. Sonochem. 2024, 109, 106991. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Lam, K.H.; Zheng, H.; Qiu, W.; Shung, K.K. Piezoelectric Single Crystal Ultrasonic Transducers for Biomedical Applications. Prog. Mater. Sci. 2014, 66, 87–111. [Google Scholar] [CrossRef]
- Xu, T.; Liu, Z.; Huang, L.; Jing, J.; Liu, X. Modulating the Tumor Immune Microenvironment with Nanoparticles: A Sword for Improving the Efficiency of Ovarian Cancer Immunotherapy. Front. Immunol. 2022, 13, 1057850. [Google Scholar] [CrossRef]
- Guo, F.; Cui, H.; Huang, X.; Du, C.; Mo, Z.; Lin, X. Mechanical Performance Enhancement of Self-Decoupling Magnetorheological Damper Enabled by Double-Graded High-Performance Magnetorheological Fluid. Appl. Sci. 2025, 15, 6305. [Google Scholar] [CrossRef]
- Hao, B.; Wang, X.; Zhang, L. Focused Ultrasound Enables Selective Actuation and Newton-Level Force Output of Untethered Soft Robots. Nat. Commun. 2024, 15, 49148. [Google Scholar] [CrossRef]
- Sebastian, A. Soft Robotics for Search and Rescue: Advancements, Challenges, and Future Directions. arXiv 2025, arXiv:2502.12373. [Google Scholar]
- Golecki, H.; Wu, Z.; Martínez, R.V. Soft Robots Built for Extreme Environments. Soft Sci. 2025, 5, 51. [Google Scholar] [CrossRef]
- Al-Dubooni, M.; Wong, C.; Althoefer, K. Hybrid Continuum-Eversion Robot: Precise Navigation and Decontamination in Nuclear Environments using Vine Robot. arXiv 2024, arXiv:2404.13135. [Google Scholar] [CrossRef]
- Tang, W.; Zhong, Y.; Zou, J. Self-Protection Soft Fluidic Robots with Rapid Large Area Self Healing Capabilities. Nat. Commun. 2024, 15, 49149. [Google Scholar] [CrossRef]
- Sheng, C. Hybrid Vibration Control Using Magnetorheological Dampers and Elastomers for Civil Structural Applications. AIP Adv. 2022, 12, 025222. [Google Scholar] [CrossRef]
- Fan, C.-H.; Ting, C.-Y.; Chang, Y.-C.; Wei, K.-C.; Liu, H.-L.; Yeh, C.-K. Drug-Loaded Bubbles with Matched Focused Ultrasound Excitation for Concurrent Blood–Brain Barrier Opening and Brain-Tumor Drug Delivery. Acta Biomater. 2023, 157, 290–300. [Google Scholar] [CrossRef]
- Aly, A.M. Vibration Control of Buildings Using Magnetorheological Damper: A New Control Algorithm. J. Eng. 2023, 2013, 596078. [Google Scholar] [CrossRef]
- Sapountzakis, I.E.; Tranakidis, P.G.; Antoniadis, I.A. Implementation of the KDamper Concept Using Disc Springs. arXiv 2017, arXiv:1705.05622. [Google Scholar] [CrossRef]
- Chauhdari, T.; Zaidi, S.A.; Su, J.; Ding, Y. Organoids Meet Microfluidics: Recent Advancements, Challenges, and Future of Organoids-on-Chip. Cell. Mol. Life Sci. 2025, 82, 86. [Google Scholar] [CrossRef]
- Zhu, J.; Ji, L.; Chen, Y.; Li, H.; Huang, M.; Dai, Z.; Wang, J.; Xiang, D.; Fu, G.; Lei, Z.; et al. Organoids and Organs-on-Chips: Insights into Predicting the Efficacy of Systemic Treatment in Colorectal Cancer. Cell Death Discov. 2023, 9, 72. [Google Scholar] [CrossRef]
- Berger, E.; Magliaro, C.; Paczia, N.; Monzel, A.S.; Linster, C.L.; Bolognin, S.; Ahluwalia, A.; Schwamborn, J.C. Millifluidic Culture Improves Midbrain Organoid Differentiation and Reduces Necrotic Core Formation. Lab A Chip 2018, 18, 3172–3183. [Google Scholar] [CrossRef]
- Schmidt, A.; Creason, W.; Law, B.E. Estimating Regional Effects of Climate Change and Altered Land Use on Biosphere Carbon Fluxes Using Distributed Time Delay Neural Networks with Bayesian Regularized Learning. Neural Netw. 2018, 108, 97–113. [Google Scholar] [CrossRef]
- Xing, X.; Tang, C.; Guo, Y.; Kurniawan, N.; Yang, G. Segment Anything Helps Microscopy Images Based Automatic and Quantitative Organoid Detection and Analysis. arXiv 2023, arXiv:2309.04190. [Google Scholar] [CrossRef]
- Bernert, C.; Assenbaum, S.; Bock, S.; Brack, F.-E.; Cowan, T.; Curry, C.B.; Garten, M.; Gaus, L.; Gauthier, M.; Gebhardt, R.; et al. ELBE Center for High-Power Radiation Sources. JLSRF 2024, 2. [Google Scholar] [CrossRef]
- Sharanya, V.; Ye, K.T.; Goh, J.; Teh, S.; Wong, C.; Goh, I.; Maier, A.B.; Kennedy, B.K.; Obregon, A.F. Brief, Weekly Magnetic Muscle Therapy Improves Mobility and Lean Mass in Postoperative Patients. Aging 2023, 15, 204597. [Google Scholar] [CrossRef]
- Liu, R.; Ma, R.; Liu, X.; Zhou, X.; Wang, X.; Yin, T.; Liu, Z. A Noninvasive Deep Brain Stimulation Method via Temporal Spatial Interference Magneto Acoustic Effect: Simulation and Experimental Validation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2474–2483. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Han, Y.; Li, Q.; Zou, Y.; Wang, S.; Jiao, X. Clinical Microfluidic Chip Platform for the Isolation of Versatile Circulating Tumor Cells. J. Vis. Exp. (JoVE) 2023, 200, e64674. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Li, W.; Lan, F.; Chen, S.; Chen, X.; Zhang, X.; Zhang, Y. DNA Nanotechnology in Tumor Liquid Biopsy: Enrichment and Determination of Circulating Biomarkers. Interdiscip. Med. 2024, 2, e20230043. [Google Scholar] [CrossRef]
- Meng, Y.; Kalia, L.V.; Kalia, S.K.; Hamani, C.; Huang, Y.; Hynynen, K.; Lipsman, N.; Davidson, B. Current Progress in Magnetic Resonance-Guided Focused Ultrasound to Facilitate Drug Delivery across the Blood-Brain Barrier. Pharmaceutics 2024, 16, 719. [Google Scholar] [CrossRef]
- Fan, C.-H.; Ting, C.-Y.; Lin, H.-J.; Wang, C.-H.; Liu, H.-L. SPIO-Conjugated, Doxorubicin-Loaded Microbubbles for Concurrent MRI and Focused-Ultrasound Enhanced Brain-Tumor Drug Delivery. Biomaterials 2013, 34, 3706–3715. [Google Scholar] [CrossRef] [PubMed]
- Tiryaki, M.E.; Dogangun, F.; Dayan, C.B.; Wrede, P.; Sitti, M. MRI-Powered Magnetic Miniature Capsule Robot with HIFU-Controlled On-Demand Drug Delivery. arXiv 2023, arXiv:2301.07197. [Google Scholar] [CrossRef]
- Ye, D.; Yuan, J.; Yue, Y.; Rubin, J.B.; Chen, H. Focused Ultrasound-Enhanced Delivery of Intranasally Administered Anti-Programmed Cell Death-Ligand 1 Antibody to an Intracranial Murine Glioma Model. Pharmaceutics 2021, 13, 1281. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Gupta, A.; Makabenta, J.M.; Park, J.; Amante, J.J.; Chattopadhyay, A.N.; Rotello, V.M. Ultrasound-Enhanced Antibacterial Activity of Polymeric Nanoparticles for Eradicating Bacterial Biofilms. Adv. Healthc. Mater. 2022, 11, 2201060. [Google Scholar] [CrossRef]
- Leulmi, S.; Joisten, H.; Grant, A.J.; Dieny, B.; Cowburn, R.P. Magneto-Mechanically Actuated Microstructures to Efficiently Prevent Bacterial Biofilm Formation. Sci. Rep. 2020, 10, 15470. [Google Scholar] [CrossRef]
- Król, J.E.; Ehrlich, G.D. Using Smart Magnetic Fluids and Gels for Prevention and Destruction of Bacterial Biofilms. Microorganisms 2023, 11, 1515. [Google Scholar] [CrossRef]
- Choi, V.; Carugo, D.; Stride, E. Repurposing Antimicrobials with Ultrasound-Triggered Nanoscale Systems for Targeted Biofilm Drug Delivery. npj Antimicrob. Resist. 2025, 3, 22. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Huang, Q. Acoustic Velocity and Attenuation Coefficient of Magnetorheological Fluids Under Electromagnetic Fields. Appl. Acoust. 2016, 107, 27–33. [Google Scholar] [CrossRef]
- Saridis, M.R.; Salmina, A.B.; Korsakova, S.A.; Yurchenko, S.O. Advances in Miniaturized Bioreactors: Bridging Biotechnology and Tissue Engineering for Enhanced Drug Development. Biotechnol. J. 2025, 20, e70065. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, V.; Kumar, A. Synthesis and Rheological Characterization of Magnetorheological Fluids. Mechanics 2025, 31, 199–210. [Google Scholar] [CrossRef]
- Mishra, H. Magnetic Field Sensor Based on Micro-Structured Magnetoelastic Surface Acoustic Wave Devices. Doctoral Dissertation, Université de Lorraine, Nancy and Metz, France, 2019. [Google Scholar]
- Song, F.; Huang, G.L.; Hu, G.K. Online Guided Wave-Based Debonding Detection in Honeycomb Sandwich Structures. AIAA J. 2012, 50, 284–293. [Google Scholar] [CrossRef]
- Skolekar, S.; Venkatesh, K.; Oh, J.S.; Choi, S.B. Vibration Controllability of Sandwich Structures with Smart Materials of Electrorheological Fluids and Magnetorheological Materials: A Review. J. Vib. Eng. Technol. 2019, 7, 359–377. [Google Scholar] [CrossRef]
- Hemmatian, M.; Sedaghati, R. Sound Transmission Analysis of MR Fluid based- Circular Sandwich Panels: Experimental and Finite Element Analysis. J. Sound Vib. 2017, 408, 43–59. [Google Scholar] [CrossRef]
- Fitzsimmons, J., II; Alyousef, A.; Dirksen, K.; Ware, N.; Miller, W. Soundproof, Fire-Resistant, Leak-Free, and Super-Insulated HVAC Ducts. Mathematics 2017, XX, 15–28. [Google Scholar]
- Forcinetti, R. Magneto-Fluid-Dynamic Energy Conversion Systems for Aerospace Applications. Ph.D Thesis, Università della Calabria, Arcavacata, Italy, 2017. [Google Scholar]
- Imaduddin, F.; Mazlan, S.A.; Zamzuri, H. A Design and Modelling Review of Rotary Magnetorheological Damper. Mater. Des. 2013, 51, 575–591. [Google Scholar] [CrossRef]
- Leonelli, C.; Mason, T.J. Microwave and Ultrasonic Processing: Now a Realistic Option for Industry. Chem. Eng. Process. Process Intensif. 2010, 49, 885–900. [Google Scholar] [CrossRef]
- Castillo, M.; Monroy, R.; Ahmad, R. A Cyber-Physical Production System for Autonomous Part Quality Control in Polymer Additive Manufacturing Material Extrusion Process. J. Intell. Manuf. 2024, 35, 3655–3679. [Google Scholar] [CrossRef]
- Sebaa, N.; Fellah, Z.E.A.; Fellah, M.; Ogam, E.; Mitri, F.G.; Depollier, C.; Lauriks, W. Application of the Biot Model to Ultrasound in Bone: Inverse Problem. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1516–1523. [Google Scholar] [CrossRef]
- Achunche, I.M. Acoustic Optimization and Prediction of Sound Propagation in Turbofan Engine Ducts. Doctoral Dissertation, University of Southampton, Southampton, UK, 2010. [Google Scholar]
- Gallot, T.; Perge, C.; Grenard, V.; Fardin, M.-A.; Taberlet, N.; Manneville, S. Ultrafast Ultrasonic Imaging Coupled to Rheometry: Principle and Illustration. arXiv 2013, arXiv:1301.6957. [Google Scholar] [CrossRef]
- Hashemi, H.S.; Mohammed, S.K.; Zeng, Q.; Zahiri Azar, R.; Rohling, R.N.; Salcudean, S.E. 3D Ultrafast Shear Wave Absolute Vibro-Elastography Using a Matrix Array Transducer. arXiv 2023, arXiv:2309.00002. [Google Scholar] [CrossRef]
- Grasland-Mongrain, P.; Miller-Jolicoeur, E.; Tang, A.; Catheline, S.; Cloutier, G. Contactless Remote Induction of Shear Waves in Soft Tissues Using a Transcranial Magnetic Stimulation Device. arXiv 2016, arXiv:1605.03032. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.G.; Fan, X.M.; Pang, J.L. Ultrasound Responsive Smart Implantable Hydrogels for Targeted Delivery of Drugs: Reviewing Current Practices. Int. J. Nanomed. 2022, 17, 5001. [Google Scholar] [CrossRef] [PubMed]
- de Lucas, B.; Pérez, L.M.; Bernal, A.; Gálvez, B.G. Ultrasound Therapy: Experiences and Perspectives for Regenerative Medicine. Genes 2020, 11, 1086. [Google Scholar] [CrossRef] [PubMed]
- Perra, E.; Hayward, N.; Pritzker, K.P.H.; Nieminen, H.J. An Ultrasonically Actuated Needle Promotes the Transport of Nanoparticles and Fluids. arXiv 2021, arXiv:2107.02601. [Google Scholar] [CrossRef]
- Paris, J.L.; Mannaris, C.; Cabañas, M.; Carlisle, R.; Manzano, M.; Vallet-Regí, M.; Coussios, C.C. Ultrasound-mediated Cavitation-enhanced Extravasation of Mesoporous Silica Nanoparticles for Controlled-release Drug Delivery. arXiv 2021, arXiv:2103.09554. [Google Scholar] [CrossRef]
- Ambartsumyan, I.; Ervin, V.J.; Nguyen, T.; Yotov, I. A Nonlinear Stokes-Biot Model for the Interaction of a Non-Newtonian Fluid with Poroelastic Media. arXiv 2018, arXiv:1803.00947. [Google Scholar] [CrossRef]
- Chiarelli, P.; Lanatà, A.; Domenici, C.; Carbone, M. High-Frequency Poroelastic Waves in Hydrogels. arXiv 2012, arXiv:1206.1221. [Google Scholar] [CrossRef]
- Fanelli, C.; Kaouri, K.; Phillips, T.N.; Myers, T.G.; Font, F. Magnetic Nanodrug Delivery in Non-Newtonian Blood Flows. arXiv 2021, arXiv:2102.03911. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, X.; Huang, B.; Liu, L.; Gao, S.; Zhou, H.; Liu, J.; Liu, B.; Zhang, C. Inversion of the Physical Properties of Seafloor Surface Sediments Based on AUV Sub-Bottom Profile Data in the Northern Slope of the South China Sea. Sci. Rep. 2021, 11, 6539. [Google Scholar] [CrossRef]
- Showalter, R.E.; Hosseinkhan, A. Biot-Pressure System with Unilateral Displacement Constraints. arXiv 2020, arXiv:2004.02885. [Google Scholar] [CrossRef]
- Berg, C.F. Permeability Description by Characteristic Length, Tortuosity, Constriction, and Porosity. arXiv 2015, arXiv:1505.02424. [Google Scholar] [CrossRef]
- Metcalfe, G.; Lester, D.; Trefry, M. A Primer on the Dynamical Systems Approach to Transport in Porous Media. arXiv 2022, arXiv:2202.13053. [Google Scholar] [CrossRef]
- Nissan, A.; Berkowitz, B. Inertial Effects on Flow and Transport in Heterogeneous Porous Media. Phys. Rev. Lett. 2018, 120, 054504. [Google Scholar] [CrossRef]
- Vanson, J.; Boutin, A.; Klotz, M.; Coudert, F.X. Transport and Adsorption Under Liquid Flow: The Role of Pore Geometry. Soft Matter 2017, 13, 875–885. [Google Scholar] [CrossRef]
- Theyab, M.A. Fluid Flow Assurance Issues: Literature Review. SciFed J. Pet. 2018, 2, 1–11. [Google Scholar]
- Papadakis, G.A. Major Hazard Pipelines: A Comparative Study of Onshore Transmission Accidents. J. Loss Prev. Process Ind. 1999, 12, 91–107. [Google Scholar] [CrossRef]
- Xu, T.; Teke, T.; Martynov, S.; Mahgerefteh, H. Monitoring Systems for CO2 Transport Pipelines: A Review of Optimization Problems and Methods. In Proceedings of the 17th Greenhouse Gas Control Technologies Conference (GHGT-17), Calgary, AL, Canada, 20–24 October 2024. [Google Scholar] [CrossRef]
- Brunner, A.J. Structural Health and Condition Monitoring with Acoustic Emission and Guided Ultrasonic Waves: What about Long-Term Durability of Sensors, Sensor Coupling and Measurement Chain? Appl. Sci. 2021, 11, 11648. [Google Scholar] [CrossRef]
- Kimura, M. Study on the Biot-Stoll Model for Porous Marine Sediments. Acoust. Sci. Technol. 2007, 28, 230–243. [Google Scholar] [CrossRef]
- Buchanan, J.L. An Assessment of the Biot-Stoll Model of a Poroelastic Seabed. In Naval Research Laboratory Memorandum Report; NRL/MR/7140-05-8885; U.S. Naval Research Laboratory: Washington, DC, USA, 2005. [Google Scholar]
- Agrawal, P.; Zhuang, S.; Dreher, S.; Mitter, S.; Ahmed, D. SonoPrint: Acoustically Assisted Volumetric 3D Printing for Composites. Adv. Mater. 2024, 36, 2408374. [Google Scholar] [CrossRef]
- Gianola, D.S.; Begley, M.R.; Ray, T.R. Recent Progress in Acoustic Field-Assisted 3D-Printing of Functional Composite Materials. MRS Adv. 2021, 6, 636–643. [Google Scholar] [CrossRef]
- Yeingst, T.J.; Arrizabalaga, J.H.; Hayes, D.J. Ultrasound-Induced Drug Release from Stimuli-Responsive Hydrogels. Gels 2022, 8, 554. [Google Scholar] [CrossRef] [PubMed]
- Melchert, D.S.; Collino, R.R.; Ray, T.R.; Dolinski, N.; Friedrich, L.; Begley, M.R.; Gianola, D.S. Flexible Conductive Composites with Programmed Electrical Anisotropy Using Acoustophoresis. arXiv 2019, arXiv:1902.08225. [Google Scholar] [CrossRef]
- Li, W.; Bing, C.; Dai, H.; Chopra, R.; Wang, Q.; Cheng, B. Prediction of Nanobubble-Assisted Focused Ultrasound-Induced Blood–Brain Barrier Opening with Machine Learning. arXiv 2023, arXiv:2306.04106. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, Z.; Li, Z.; Tang, H. Ultrasound-Assisted 3D Printing of Continuous Fiber-Reinforced Thermoplastic Composites. Int. J. Adv. Manuf. Technol. 2024, 122, 1–12. [Google Scholar] [CrossRef]
- Arulpragasam, A.R.; van’t Wout-Frank, M.; Barredo, J.; Faucher, C.R.; Greenberg, B.D.; Philip, N.S. Low Intensity Focused Ultrasound for Non-invasive and Reversible Deep Brain Neuromodulation—A Paradigm Shift in Psychiatric Research. Front. Psychiatry 2022, 13, 825802. [Google Scholar] [CrossRef]
- Blackmore, J.; Shrivastava, S.; Sallet, J.; Butler, C.R.; Cleveland, R.O. Ultrasound Neuromodulation: A Review of Results, Mechanisms, and Safety. Ultrasound Med. Biol. 2019, 45, 1509–1536. [Google Scholar] [CrossRef]
- Plaksin, M.; Shoham, S.; Kimmel, E. Intramembrane Cavitation as a Predictive Bio-Piezoelectric Mechanism for Ultrasonic Brain Stimulation. Phys. Rev. X 2014, 4, 011004. [Google Scholar] [CrossRef]
- Cain, J.A.; Visagan, S.; Johnson, M.A.; Crone, J.S.; Blades, R.; Spivak, N.M.; Bystritsky, A.; Yoo, S.S. Real-Time and Delayed Effects of Subcortical Low-Intensity Focused Ultrasound. Sci. Rep. 2021, 11, 6100. [Google Scholar] [CrossRef]
- Yoon, K.; Lee, W.; Lee, J.E.; Xu, L.; Croce, P.; Foley, L.; Yoo, S.S. Effects of Sonication Parameters on Transcranial Focused Ultrasound Brain Stimulation in an Ovine Model. PLoS ONE 2019, 14, e0224311. [Google Scholar] [CrossRef]
- Fomenko, A.; Neudorfer, C.; Dallapiazza, R.F.; Kalia, S.K.; Lozano, A.M. Low-Intensity Ultrasound Neuromodulation: An Overview of Mechanisms and Emerging Human Applications. Brain Stimul. 2018, 11, 1209–1217. [Google Scholar] [CrossRef]
- Tyler, W.J. Noninvasive Neuromodulation with Ultrasound? A Continuum Mechanics Hypothesis. Neuroscientist 2011, 17, 25–36. [Google Scholar] [CrossRef]
- Yoo, S.S.; Bystritsky, A.; Lee, J.H.; Zhang, Y.; Fischer, K.; Min, B.K.; McDannold, N.J.; Pascual-Leone, A.; Jolesz, F.A. Focused Ultrasound Modulates Region-Specific Brain Activity. NeuroImage 2011, 56, 1267–1275. [Google Scholar] [CrossRef] [PubMed]
- Remya, A.R.; Vishwash, B.; Lee, C.; Srinivasa Pai, P.; Espinoza Orías, A.A.; Ozevin, D.; Mathew, M.T. Hip Implant Performance Prediction by Acoustic Emission Techniques: A Review. Med. Biol. Eng. Comput. 2020, 58, 1637–1650. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zhang, L.; Morris, D.; Cheng, K.Y.; Ramachandran, R.A.; Barba, M.; Bijukumar, D.; Ozevin, D.; Mathew, M.T. Non-Invasive Early Detection of Failure Modes in Total Hip Replacements via Acoustic Emission. J. Mech. Behav. Biomed. Mater. 2021, 118, 104484. [Google Scholar] [CrossRef] [PubMed]
- Reulbach, M.; Meyer Zu Vilsendorf, M.; Yarcu, S.; Behrens, B.A.; Hübner, S.; Jakubowitz, E. Soft Tissue-Like Coupling Materials for In Vitro Acoustic Emission Studies in Total Hip Arthroplasty. J. Mech. Behav. Biomed. Mater. 2025, 164, 106905. [Google Scholar] [CrossRef]
- Patel, S.; Hecht, C.J.; Homma, Y.; Kamath, A.F. What Is the Clinical Utility of Acoustic and Vibrational Analyses in Uncemented Total Hip Arthroplasty? Arthroplasty 2024, 6, 59. [Google Scholar] [CrossRef]
- Zeitler, D.M.; Buchlak, Q.D.; Ramasundara, S.; Farrokhi, F.; Esmaili, N. Predicting Acoustic Hearing Preservation Following Cochlear Implant Surgery Using Machine Learning. Laryngoscope 2024, 134, 926–936. [Google Scholar] [CrossRef]
- Essaid, B.; Kheddar, H.; Batel, N.; Chowdhury, M.E.H.; Lakas, A. Artificial Intelligence for Cochlear Implants: Review of Strategies, Challenges, and Perspectives. arXiv 2024, arXiv:2403.15442. [Google Scholar] [CrossRef]
- Yeiser, A.J.; Wawrzynek, E.F.; Zhang, J.Z.; Graf, L.; McHugh, C.I.; Kymissis, I.; Olson, E.S.; Lang, J.H.; Nakajima, H.H. The UmboMic: A PVDF Cantilever Microphone. arXiv 2023, arXiv:2312.14339. [Google Scholar] [CrossRef]
- Ivani, A.S.; Barontini, F.; Catalano, M.G.; Grioli, G.; Bianchi, M.; Bicchi, A. VIBES: Vibro-Inertial Bionic Enhancement System in a Prosthetic Socket. arXiv 2023, arXiv:2312.13015. [Google Scholar] [CrossRef]
- Ijaz, N.; Banoori, F.; Koo, I. Reshaping Bioacoustics Event Detection: Leveraging Few-Shot Learning with Transductive Inference and Data Augmentation. Bioengineering 2024, 11, 685. [Google Scholar] [CrossRef]
- Nsugbe, E.; Olorunlambe, K.; Dearn, K. On the Early and Affordable Diagnosis of Joint Pathologies Using Acoustic Emissions, Deep Learning Decompositions, and Prediction Machines. Sensors 2023, 23, 4449. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Lin, X.; He, Q. Reconfigurable Assembly of Colloidal Motors Towards Interactive Soft Materials and Systems. J. Colloid Interface Sci. 2022, 612, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Wei, P.; Cornel, E.J.; Du, J. Ultrasound-responsive polymer-based drug delivery systems. Drug Deliv. Transl. Res. 2021, 11, 1323–1339. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, X.; Jones, E.; Bingham, P.A.; Scrimshire, A.; Thornton, P.D.; Tronci, G. An Injectable, Self-Healing, and MMP-Inhibiting Hyaluronic Acid Gel via Iron Coordination. arXiv 2021, arXiv:2101.02414. [Google Scholar] [CrossRef]
- Bajpayee, A.G.; Scheu, M.; Grodzinsky, A.J.; Porter, R.M. Electrostatic Interactions Enable Rapid Penetration, Enhanced Uptake, and Retention of Intra-Articular Injected Avidin in Rat Knee Joints. J. Orthop. Res. 2014, 32, 1044–1051. [Google Scholar] [CrossRef]
| Strengths | Highly effective technology for preventing particle sedimentation and maintaining uniform distribution, featuring flexible magnetic modulation and versatile applications while optimizing energy efficiency. |
| Weaknesses | The system’s effectiveness relies on accurate selection of operational parameters, as suboptimal choices may promote particle aggregation and complicate analysis due to the coexistence of stationary and oscillating components. |
| Opportunities | The development prospects for this technology are promising, with potential improvements in efficiency through the use of higher-susceptibility materials and real-time optimization. Its versatility makes it suitable for both industrial and biomedical applications. |
| Threats | The threats include sensitivity to environmental variations, mechanical degradation from cyclic stress, and competition from more widely adopted alternative technologies. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [108,110,111,112,113,125,126,127,128,129,140,141] | Field-guided microfabrication and assembly | Combined use of acoustic and magnetic fields to guide the controlled self-assembly of particles into functional three-dimensional structures. | and RAP enables precise, rapid, and reconfigurable particle assembly for advanced 3D structures in micro-robotics and bioengineering. |
| [142,143,144,145,146,147] | Intelligent lubrication in complex environments | MRF and US integration enables adaptive lubrication with improved stability and tribological performance. | Smart MRF-US lubrication adapts dynamically to improve efficiency and reduce wear. |
| [148,149,150,151,152,153,154,155,156] | Active control of vibrations and noise | MR devices with predictive models and algorithms enable active vibration control in industrial structures. | Actively controlled MR materials improve vibration damping, structural efficiency, and durability in advanced industries. |
| [146,157,158,159,160,161] | Advanced liquid treatment and magneto-acoustic separations | Magnetic fields and US enable precise control of MRF for imaging, localized heating, and liquid separation applications. | MRF and US coupling enables advanced liquid separation and fluid control for diagnostics and therapy. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [162,163,164,165,166,167] | Non-invasive focused neuro-stimulation | 3D-guided focused US enables precise, non-invasive deep brain stimulation. | Precise and safe technique with promising clinical applications in neurology and advanced neuro-therapy. |
| [168,169,170,171,172] | Dynamic control of the tumor microenvironment for immunotherapy | US-activated magnetic nano-carriers enhance tumor immunotherapy by locally modulating the microenvironment. | Localized tumor microenvironment modulation enhances immunotherapy efficacy in preclinical models. |
| [173,174,175,176,177,178] | Acceleration of bone and muscle healing | US, magnetic fields, and injectable hydrogels promote tissue regeneration via mechanotransduction and inflammation control. | Enhances bone and muscle healing by promoting cell growth and tissue repair. |
| [179,180,181,182,183,184,185] | Intracranial navigation and delivery across the blood-brain barrier | Focused US with microbubbles and AI enables precise blood-brain barrier opening for targeted drug delivery. | Safe, targeted blood-brain barrier opening improves drug delivery precision and efficacy. |
| Strengths | The theory of variable magnetic fields enables real-time, non-invasive modulation of material properties like viscosity and stiffness, offering energy-efficient and adaptable control in both industrial and biomedical systems, especially when integrated with smart materials. |
| Weaknesses | The theory of variable magnetic fields enables real-time, non-invasive modulation of material properties like viscosity and stiffness, offering energy-efficient and adaptable control in both industrial and biomedical systems, especially when integrated with smart materials. |
| Opportunities | Variable magnetic field-based systems offer strong potential for future applications, enabling precise control in targeted therapies, soft robotics, advanced manufacturing, and real-time structural health monitoring. |
| Threats | Despite their potential, magnetic field-based systems face challenges such as electromagnetic interference, strict biomedical regulations, high material and integration costs, and competition from more scalable alternative technologies. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [121,204,205,206,207] | 3D printing of rheologically adaptive materials | 3D printing and US activation enable controlled rheology and targeted release of functional materials. | 3D printing of rheologically adaptive materials enables precise control of shape and function through rheological tuning and external activation, such as US. |
| [121,146,208,209,210,211] | Selective industrial filtration and separation | US and magnetic gradients enhance particle separation and flow control in MRF-based industrial systems. | US combined with MRF enhances efficient, real-time industrial filtration. |
| [212,213,214,215,216] | Smart actuators for soft robotics in hazardous environments | US-controlled soft actuators with self-healing enable safe, precise operation in harsh environments. | US-guided soft actuators enable precise, safe operation in extreme conditions. |
| [217,218,219,220] | Tunable vibration absorption systems in construction | Adaptive vibration absorption with magnetorheological dampers for construction. | MRF-based tunable vibration systems enhance seismic protection in construction. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [221,222,223,224,225] | Cell engineering for organoids-on-a-chip | Advanced technologies improve organoid-on-a-chip growth, control, and automated analysis. | Organoids-on-a-chip offer improved cell function and precision for personalized research and therapy. |
| [226,227,228,229,230] | Magneto-acoustic liquid biopsy | Magneto-US methods improve liquid biopsy sensitivity by isolating tumor biomarkers. | Magneto-acoustic technologies improve liquid biopsy for early cancer detection. |
| [108,231,232,233,234] | Assisted intracranial neuro-transport | Focused US and magnetic agents enable targeted blood–brain barrier crossing. | Focused US and magnetic nanoparticles enable safe, targeted drug delivery across the blood–brain barrier. |
| [235,236,237,238] | Systems for selective biofilm disruption | Magnetic microstructures and US selectively disrupt biofilms, boosting antimicrobial efficacy. | US and magneto-active materials enhance selective biofilm removal and antimicrobial therapy. |
| Symbol | Value | Description |
|---|---|---|
| 3160 kg | Density of solid particles | |
| 2.95–3.15 g | Density of the base fluid | |
| 0.30 | Porosity (particle volume fraction) | |
| c | 1.5 | Structural coefficient |
| 0.112 Pa·s | Off-state dynamic viscosity (at 40°) | |
| Pa | Real part of bulk modulus of particles | |
| Pa | Imaginary part of bulk modulus of particles | |
| Pa | Bulk modulus of the fluid | |
| Pa | Bulk modulus of the porous skeleton | |
| Pa | Shear modulus of the skeleton | |
| Intrinsic permeability | ||
| Dynamic correction function |
| Strengths | The Biot–Stoll model with viscous correction reveals that higher frequencies boost viscosity and energy dissipation in MRFs, improving suspension stability and reducing sedimentation, aided by magnetic field-induced thickening. |
| Weaknesses | The model is analytically complex due to its use of PDEs and matrices, relies on experimentally calibrated variables, assumes MRF homogeneity, and includes empirical corrections that may lack general validity across frequencies or compositions. |
| Opportunities | Integrating US and magnetic fields allows real-time control of suspensions for applications like electronic cooling and drug delivery, with neural networks aiding predictive modeling and adaptability to nanoparticle-based microfluidic systems. |
| Threats | Experimental validation is difficult due to complex measurements, nonlinear field–wave interactions, and sensitivity to material property variations. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [263,264,265,266,267,268,269,270,271] | Optimization of transport in porous pipelines for technical fluids | Advanced poroelastic modeling optimizes fluid transport in porous systems. | Easily implementable computational solutions |
| [272,273,274] | Acoustic monitoring of smart structures coated with MRF materials | US and poroelastic modeling enhance structural monitoring with MRF materials. | MRFs with acoustic sensors enable adaptive US structural monitoring. |
| [275,276,277,278,279,280] | Systems for acoustic printing of gradient composite materials | US enables controlled 3D printing of gradient composite materials. | Acoustic-assisted 3D printing enables precise gradient composites with directional control. |
| Ref. | Domain | Methods | Conclusions |
|---|---|---|---|
| [281,282,283,284,285,286,287,288] | Low-intensity neuro-stimulation in porous environments | Low-intensity US and Biot–Stoll poroelastic models enable noninvasive neural modulation by targeting brain tissue mechanics. | Biot–Stoll theory enhances the safe, precise modulation of brain activity using low-intensity US. |
| [289,290,291,292,293,294,295,296,297,298] | Predictive bio-acoustics in acoustically active prosthetic implants | Smart sensors and predictive acoustics enhance the performance of active prosthetic devices. | Intelligent acoustics improve prosthetic implant performance monitoring. |
| [299,300,301,302] | Poro-acoustic control of hydrogels in intra-articular drug delivery US-activated hydrogels enable controlled drug release in joints through poroelastic and biophysical mechanisms. | US-sensitive poroelastic hydrogels enable targeted, sustained drug delivery for improved osteoarthritis treatment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palumbo, A.; Versaci, M. Controlling Sedimentation in Magnetorheological Fluids Through Ultrasound–Magnetic Field Coupling: Multiscale Analysis and Applications. Mathematics 2025, 13, 2540. https://doi.org/10.3390/math13152540
Palumbo A, Versaci M. Controlling Sedimentation in Magnetorheological Fluids Through Ultrasound–Magnetic Field Coupling: Multiscale Analysis and Applications. Mathematics. 2025; 13(15):2540. https://doi.org/10.3390/math13152540
Chicago/Turabian StylePalumbo, Annunziata, and Mario Versaci. 2025. "Controlling Sedimentation in Magnetorheological Fluids Through Ultrasound–Magnetic Field Coupling: Multiscale Analysis and Applications" Mathematics 13, no. 15: 2540. https://doi.org/10.3390/math13152540
APA StylePalumbo, A., & Versaci, M. (2025). Controlling Sedimentation in Magnetorheological Fluids Through Ultrasound–Magnetic Field Coupling: Multiscale Analysis and Applications. Mathematics, 13(15), 2540. https://doi.org/10.3390/math13152540







