Recovery of Implied Volatility in a Spatial-Fractional Black–Scholes Equation Under a Finite Moment Log Stable Model

Abstract

In this paper, we study direct and inverse problems for a spatial-fractional Black–Scholes equation with space-dependent volatility. For the direct problem, we provide CN-WSGD (Crank–Nicholson and the weighted and shifted Grünwald difference) scheme to solve the initial boundary value problem. The latter aims to recover the implied volatility via observable option prices. Using a linearization technique, we rigorously derive a mathematical formulation of the inverse problem in terms of a Fredholm integral equation of the first kind. Based on an integral equation, an efficient numerical reconstruction algorithm is proposed to recover the coefficient. Numerical results for both problems are provided to illustrate the validity and effectiveness of proposed methods.

1. Introduction

The Black–Scholes (BS) model [1] has achieved remarkable success in option pricing. However, the stochastic behavior in this model is governed by Brownian motion, which underestimates the probability of the underlying price moving significantly over small time steps. To address this limitation, one can assume that the underlying price follows a jump process or Lévy process. Lévy distribution has a fat tail and allows for a long jump, which are often observed in financial markets.

When Brownian motion is replaced by a special Lévy process, the maximally skewed Lévy stable process, Carr and Wu [2] derived the finite moment log-stable (FMLS) model. In addition to capturing the high-frequency empirical probability distributions, this model guarantees the finiteness of option prices at all maturities. However, the FMLS model cannot characterize the non-locality produced by the jumps in the Lévy process. As fractional derivatives [3] provide useful tools for the description of memory and hereditary properties of different materials, some fractional Black–Scholes models (FBSM) governing the option price are introduced. Cartea and Del-Castillo-Negrete [4] successfully connected the FMLS process with the spatial-fractional derivatives, thereby capturing the non-locality information for European-style options.

In this paper, we consider the spatial-fractional Black–Scholes model (SFBSM) for European options under the framework of the FMLS model:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial V}{\partial t}+(r+\frac{1}{2}{\sigma }^{\alpha }\left(x\right)\sec \frac{\alpha \pi }{2})\frac{\partial V}{\partial x}-\frac{1}{2}{\sigma }^{\alpha }\left(x\right)\sec \frac{\alpha \pi }{2}{}_{-\infty }D_x^{\alpha }V-rV=0,}\hfill \\ V(x,T)=\mathrm{\Pi }\left(x\right),\hfill \end{array}\right.$$

(1)

where $V(x,t)$ is the price of European-style options, with x denoting the logaritm of the underlying price S, defined as $x=\ln S$; $\alpha$ is the tail index; r is the risk-free interest rate; $\sigma$ is the volatility, which is a function of x; and T is the maturity date. $\mathrm{\Pi }\left(x\right)$ is the payoff function, which is defined as $\max \left\{e^x-K,0\right\}$ and $\max \left\{K-e^x,0\right\}$ for European call and put options, respectively, with a strike price of K. ${}_{-\infty }D_x^{\alpha }V$ is the one-dimensional Weyl fractional derivative, which is defined as

$${}_{-\infty }D_x^{\alpha }V(x,t)={\displaystyle \frac{1}{\mathrm{\Gamma }(n-\alpha )}}{\displaystyle \frac{{\partial }^n}{\partial x^n}}{\int }_{-\infty }^x{\displaystyle \frac{V(y,t)}{{(x-y)}^{\alpha +1-n}}}dy,n-1\le \Re \left(\alpha \right)<n.$$

(2)

Here, $\mathrm{\Gamma }(·)$ denotes the standard Gamma function. To ensure that the underlying return has the support on the whole real line, the tail index $\alpha$ needs to be restricted to $(1,2]$, which is shown in [2]. If the fractional order $\alpha =2$ and the volatility $\sigma$ is a constant, the system (1) coincides with the classical BS model for European options.

Slightly different from the model in [4], the volatility in model (1) varies with the underlying price. Volatility is a critical parameter in determining the option price. In the real market, volatility is usually observed in a skew curve or smile curve [5]. Rubinstein [6] discovered that short-maturity out of the money calls were priced significantly higher than that predicted by the B-S model when analyzing the 30 most active CBOE options. This finding indicates that implied volatilities are associated with underlying price and time to maturity. For simplicity, we considered in this paper that the volatility depends only on the underlying asset.

The model (1) represents the direct problem: given $\mathrm{\Pi }\left(x\right)$, $\sigma \left(x\right)$, and the corresponding boundary conditions, solve the option price $V(x,t)$ at anytime before the maturity date T. When volatility $\sigma$ is constant in the model (1), Chen et al. [7] managed to derive an explicit closed-form analytical solution for model (1). However, the analytical solution was expressed in integral form with the Fox function, which caused the implementation of the analytical solution to not be as straightforward as the BS formula. Furthermore, when the volatility in the model (1) is variable, there is no analytical solution. Many attempts have been made to find the numerical solution for the fractional BS model. Zhao et al. [8] and Zhang et al. [9] designed implicit difference schemes with second-order accuracy in both temporal and spatial dimensions and analyzed their stability and convergence. Furthermore, An et al. [10] employed the fast biconjugate gradient stabilized method to effectively solve the dense linear system. To improve the accuracy of convergence, the finite difference coupling with the spectral method was also employed for the numerical simulation of SFBSM. Guo and Ling [11] adopted the Gauss–Jacobi sepctral method combined with the first-order finite difference scheme to evaluate SFBSM. Using shifted Chebyshev basis functions of the second kind for spatial dimensions, Xu et al. [12] studied the numerical simulation of a two-asset option equation based on the FMLS process. Based on this, Avazzadeh et al. [13] proposed a hybrid kernel meshless method for the fractional Rayleigh–Stokes problem. Aghdam et al. [14] used a shifted Chebyshev of the fourth kind as a basis function to approximat SFBSM under the CGMY process.

All of the above numerical methods are proposed under the case of constant volatility. To the best of our knowledge, research on the numerical simulation of SPBSM under the FMLS process with variable volatility for European call options is still limited. One contribution of this paper is to construct an efficient numerical scheme with second-order accuracy in time and second-order accuracy in space, as introduced in [15], while establishing rigorous stability and convergence analysis under some conditions.

Assume that

$${\displaystyle \frac{1}{2}}{\sigma }^{\alpha }\sec {\displaystyle \frac{\alpha \pi }{2}}={\displaystyle \frac{1}{2}}{\sigma }_0^{\alpha }\sec {\displaystyle \frac{\alpha \pi }{2}}+f\left(x\right),$$

(3)

where $f\left(x\right)$ is a small perturbation of constant ${\displaystyle \frac{1}{2}{\sigma }_0^{\alpha }\sec \frac{\alpha \pi }{2}}$, $f\in C\left(\overline{\omega }\right)$ and $f=0$ outside $\omega$. We are interested in the inverse problem of recovering $\sigma \left(x\right)$ from the additional observed data

$$V(x,t^{*})=V^{*}\left(x\right),0<t^{*}<T.$$

(4)

This type of problem is referred to as volatility calibration. Extensive research has been conducted on the inverse volatility problem for the classical BS models, as seen in [16,17,18] and the references therein. Bouchouev et al. [19] proposed a reliable numerical algorithm to recover the asset price-dependent volatility for the classical BS model. Deng et al. [20] studied the inverse time-dependent volatility problem using the Landweber iteration approach for the classical BS model. Recently, the inverse volatility problem of the time-fractional BS equation for double barrier options was investigated in [21]. However, to the best knowledge of the authors, there are no results on recovering the volatility of the spatial-fractional BS equation under the FMLS model. In this paper, we present an efficient reconstruction algorithm based on the linearization technique [19] to determine unknown volatility parameters and validate the feasibility of the proposed method through numerical experiments.

The rest of this paper is organized as follows. In Section 2, we show the analytical solution for the direct problem with constant volatility and the numerical method for the case of space-dependent volatility using the CN-WSGD scheme. Additionally, the error analysis of the proposed numerical method is also presented. Subsequently, the linearization technique is applied for recovering the implied volatility in Section 3. Afterwards, in Section 4, numerical examples are presented to validate the efficiency of our proposed algorithms. Finally, concluding remarks are given in Section 5.

2. Direct Problem

2.1. Analytical Solution for Constant Volatility

We first present the analytical solution of the SFBSM (1) for constant volatility as it will be used in Section 3. When the volatility $\sigma ={\sigma }_0$ (${\sigma }_0$ is a constant), we let ${\displaystyle \tau =-\frac{1}{2}{\sigma }_0^{\alpha }\left(\sec \frac{\alpha \pi }{2}\right)(T-t)}$ and ${\displaystyle \gamma =\frac{-2r}{{\sigma }_0^{\alpha }\sec \left(\frac{\alpha \pi }{2}\right)}}$. The SFBSM (1) can be transformed into

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial V}{\partial \tau }=(\gamma -1)\frac{\partial V}{\partial x}{+}_{-\infty }{D}_x^{\alpha }V-\gamma V,}\hfill \\ V(x,0)=\mathrm{\Pi }\left(x\right).\hfill \end{array}\right.$$

(5)

To solve the above Equation (5) analytically, we take the expression of V in Fourier space, i.e., $\tilde{V}(\xi ,\tau )=F\left[V(x,\tau )\right]$. Therefore, $\tilde{V}(\xi ,\tau )$ satisfies

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \tilde{V}}{\partial \tau }=(\gamma -1)i\xi \tilde{V}+{\left|\xi \right|}^{\alpha }\tilde{V}-\gamma \tilde{V},}\hfill \\ \tilde{V}(\xi ,0)=\widetilde{\mathrm{\Pi }\left(\xi \right)},\hfill \end{array}\right.$$

(6)

Then, the option price in the Fourier space can be written as

$$\tilde{V}(\xi ,\tau )=e^{-\gamma \tau }\tilde{\mathrm{\Pi }}\left(\xi \right)e^{-(1-\gamma )\tau i\xi -{\left|\xi \right|}^{\alpha }\tau }.$$

(7)

To obtain the option price $V(x,\tau )$ in the original x-space, we need to carry out the Fourier inversion on the above equation. According to the convolution theorem of the Fourier transform, the European option price is given by $V(x,\tau )=e^{-\gamma \tau }V(x,0)\ast F^{-1}\left[e^{-(1-\gamma )\tau i\xi -{\left|\xi \right|}^{\alpha }\tau }\right]$, which can be further reduced to

$$V(x,\tau )=e^{-\gamma \tau }V(x,0)\ast P(x-(1-\gamma )\tau ;\alpha ),$$

(8)

where $P(x;\alpha )=F^{-1}\left[e^{-{\left|\xi \right|}^{\alpha }\tau }\right]$. Referring to [22], the Fourier inversion of $e^{-{\left|\xi \right|}^{\alpha }\tau }$ is equal to multiples of the closed-form representation of the Lévy stable density $f_{\alpha ,0}$, which is expressed in terms of the Fox function, i.e.,

$$P(x;\alpha )={\displaystyle \frac{1}{{\tau }^{\frac{1}{\alpha }}}}{f}_{\alpha ,0}({\displaystyle \frac{\left|x\right|}{{\tau }^{\frac{1}{\alpha }}}})={\displaystyle \frac{1}{\alpha {\tau }^{\frac{1}{\alpha }}}}{H}_{2,2}^{1,1}({\displaystyle \frac{\left|x\right|}{{\tau }^{\frac{1}{\alpha }}}})={\displaystyle \frac{1}{\alpha {\tau }^{\frac{1}{\alpha }}}}{H}_{2,2}^{1,1}\left[{\displaystyle \frac{\left|x\right|}{{\tau }^{\frac{1}{\alpha }}}}|\begin{array}{cc}(1-{\displaystyle \frac{1}{\alpha }},{\displaystyle \frac{1}{\alpha }})& ({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\\ (0,1)& ({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})\end{array}\right],$$

(9)

where the definition of the H-function $H_{2,2}^{1,1}({\displaystyle \frac{\left|x\right|}{{\tau }^{\frac{1}{\alpha }}}})$ can be referred to in [3] (p. 58) Combining (8) and (9), we have

$$V(x,\tau )={\int }_{-\infty }^{+\infty }{e}^{-\gamma \tau }\mathrm{\Pi }\left(\xi \right){\displaystyle \frac{1}{{\tau }^{\frac{1}{\alpha }}}}{f}_{\alpha ,0}({\displaystyle \frac{|x-\xi -(1-\gamma \left)\tau \right|}{{\tau }^{\frac{1}{\alpha }}}})d\xi .$$

(10)

By changing the integral variable, the above equation can be further written as

$$V(x,\tau )={\int }_{-\infty }^{+\infty }{e}^{-\gamma \tau }\mathrm{\Pi }(x-(1-\gamma )\tau -{\tau }^{{\displaystyle \frac{1}{\alpha }}}m)f_{\alpha ,0}\left(\right|m\left|\right)dm.$$

(11)

2.2. Numerical Method for Variable Volatility

When the volatility $\sigma$ depends on the log underlying price x, there is no explicit analytical solution to the SFBSM (1). Thus, we seek a numerical method. Let ${\tau }^{\prime }=T-t$. Then, we simplify the SFBSM (1) as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial V}{\partial {\tau }^{\prime }}=(r+\frac{1}{2}{\sigma }^{\alpha }\left(x\right)\sec \frac{\alpha \pi }{2})\frac{\partial V}{\partial x}-\frac{1}{2}{\sigma }^{\alpha }\left(x\right)\sec \frac{\alpha \pi }{2}{}_{-\infty }D_x^{\alpha }V-rV,}\hfill \\ V(x,0)=\mathrm{\Pi }\left(x\right).\hfill \end{array}\right.$$

(12)

We denote $V_p(x,{\tau }^{\prime })$ as the price of the European put option. According to [7] (Theorem 3.2), $V_p(x,{\tau }^{\prime })$ presents suitable growth conditions at $x=\pm \infty$, i.e.,

$$\underset{x\to -\infty }{\lim }{V}_p(x,{\tau }^{\prime })=K{e}^{-r{\tau }^{\prime }}\mathrm{and}\underset{x\to +\infty }{\lim }{V}_p(x,{\tau }^{\prime })=0.$$

(13)

Further, $V_p$ approaches 0 exponentially as $x\to +\infty$.

Next, we let $V_c(x,{\tau }^{\prime })$ represent the price of the European call option. In light of put–call parity [7] (Theorem 3.3), which reveals the relationship between the prices of European put and call options when they have the same maturity date and strike price, we have

$$V_c(x,{\tau }^{\prime })-V_p(x,{\tau }^{\prime })=e^x-K{e}^{-r{\tau }^{\prime }},$$

(14)

Based on the growth conditions (13) and the put–call parity formula (14), we consider the interval $\omega =(a,b)$, such that

$$V_c(a,{\tau }^{\prime })=0\mathrm{and}{V}_c(b,{\tau }^{\prime })=e^b-K{e}^{-r{\tau }^{\prime }}.$$

(15)

Assuming that $V(x,{\tau }^{\prime })$ has compact support on $\omega \times (0,T)$, we have ${}_{-\infty }D_x^{\alpha }V(x,{\tau }^{\prime })={}_{a}D_x^{\alpha }(x,{\tau }^{\prime })$, where ${}_{a}D_x^{\alpha }(x,{\tau }^{\prime })$ is the left-sided Riemann–Liouville fractional derivative, defined as

$${}_{a}D_x^{\alpha }V(x,{\tau }^{\prime })={\displaystyle \frac{1}{\mathrm{\Gamma }(n-\alpha )}}{\displaystyle \frac{{\partial }^n}{\partial x^n}}{\int }_a^x{\displaystyle \frac{V(y,{\tau }^{\prime })}{{(x-y)}^{\alpha +1-n}}}dy,n-1\le \Re \left(\alpha \right)<n.$$

In view of the fact that $V_c\to 0$ when $x\to -\infty$, we mainly discuss the numerical solutions of SFBSM (12) for European call options. The prices of European put options can be solved accordingly using put–call parity. We numerically solve the model (12) using the Crank–Nicholson (CN) scheme and the weighted and shifted Grünwald difference (WSGD) operator [15].

Given a numerical approximation scheme, we define that h is the grid size in space, $M=(b-a)/h$, $x_i=a+ih$ for $i=0,\dots ,M$ so that $a\le x_i\le b$, ${\tau }_n^{\prime }=n\Delta {\tau }^{\prime }$ is the integration time $0\le t_n\le T$ for $n=0,\dots ,N$, $l=T/N$, and $v_i^n=V(x_i,{\tau }_n^{\prime })$. Similarly, ${\sigma }_i=\sigma \left(x_i\right),{\mathrm{\Pi }}_i=\mathrm{\Pi }\left(x_i\right)$.

Referring to [15] (Remark 2.6), ${}_{a}D_x^{\alpha }(x,{\tau }^{\prime })$ at each point of x can be approximated by the WSGD operator with second-order accuracy

$$\begin{array}{cc}\hfill {}_{a}D_x^{\alpha }V(x,{\tau }^{\prime })=& {\displaystyle \frac{{\lambda }_1}{h^{\alpha }}}\sum _{k=0}^{\left[{\displaystyle \frac{x-a}{h}}\right]+p}{g}_k^{\left(\alpha \right)}V(x-(k-p)h,{\tau }^{\prime })+{\displaystyle \frac{{\lambda }_2}{h^{\alpha }}}\sum _{k=0}^{\left[{\displaystyle \frac{x-a}{h}}\right]+q}{g}_k^{\left(\alpha \right)}V(x-(k-q)h,{\tau }^{\prime })+O\left(h^2\right),\hfill \end{array}$$

(16)

where ${\lambda }_1={\displaystyle \frac{\alpha -2q}{2(p-q)}},{\lambda }_2={\displaystyle \frac{2p-\alpha }{2(p-q)}}$; p and q are integers, with $p\ne q$; and $g_k^{\left(\alpha \right)}={(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)$. Moreover, $g_k^{\left(\alpha \right)}$ can be evaluated recursively:

$$g_0^{\left(\alpha \right)}=1,g_k^{\left(\alpha \right)}=\left(1-{\displaystyle \frac{\alpha +1}{k}}\right)g_{k-1}^{\left(\alpha \right)},k=1,2,\cdots .$$

(17)

In this paper, we choose $(p,q)=(1,0)$ and plug it into Equation (16). The simplified form of the discrete approximations (16) for ${}_{a}D_x^{\alpha }V$ at the point $x_i$ is

$$\begin{array}{cc}\hfill & {}_{a}D_x^{\alpha }V\left(x_i,{\tau }^{\prime }\right)={\displaystyle \frac{1}{h^{\alpha }}}\sum _{k=0}^{i+1}{w}_k^{\left(\alpha \right)}V\left(x_{i-k+1},{\tau }^{\prime }\right)+O\left(h^2\right),\hfill \end{array}$$

(18)

where $w_0^{\left(\alpha \right)}={\displaystyle \frac{\alpha }{2}}{g}_0^{\left(\alpha \right)},w_k^{\left(\alpha \right)}={\displaystyle \frac{\alpha }{2}}{g}_k^{\left(\alpha \right)}+{\displaystyle \frac{2-\alpha }{2}}{g}_{k-1}^{\left(\alpha \right)},k\ge 1.$

Denote ${\mathcal{D}}_h^{\alpha }{v}_i^n={\displaystyle \frac{1}{h^{\alpha }}}{\displaystyle \sum _{k=0}^{i+1}}{w}_k^{\left(\alpha \right)}V\left(x_{i-k+1},{\tau }_n^{\prime }\right)$, ${\delta }_t{v}_i^n={\displaystyle \frac{v_i^{n+1}-v_i^n}{l}}$, and ${\delta }_x{v}_i^n={\displaystyle \frac{v_{i+1}^n-v_{i-1}^n}{2h}}.$ Using the Crank–Nicolson technique for the time discretization of (12) leads to

$${\delta }_t{v}_i^n={\displaystyle \frac{1}{2}}(r+c_i)({\delta }_x{v}_i^{n+1}+{\delta }_x{v}_i^n)-{\displaystyle \frac{1}{2}}{c}_i({\mathcal{D}}_h^{\alpha }{v}_i^{n+1}+{\mathcal{D}}_h^{\alpha }{v}_i^n)-{\displaystyle \frac{r}{2}}(v_i^{n+1}+v_i^n)+{\epsilon }_i^n,$$

(19)

where $c_i={\displaystyle \frac{1}{2}}{\sigma }_i^{\alpha }\sec {\displaystyle \frac{\alpha \pi }{2}}$, and $|{\epsilon }_i^n|\le C(l^2+h^2)$. Denote $V_i^n$ as the numerical approximation of $u_i^n$. Let

$$L_i{V}_i^n={\displaystyle \frac{lr}{2}}{V}_i^n-{\displaystyle \frac{l}{4h}}(r+c_i)(V_{i+1}^n-V_{i-1}^n)+{\displaystyle \frac{l}{2}}{h}^{-\alpha }{c}_i\sum _{k=0}^{i+1}{w}_k^{\left(\alpha \right)}{V}_{i-k+1}^n.$$

(20)

Then, our scheme of model (12) for European call options reads: find $v_i^{n+1}$ with

$$\left\{\begin{array}{cc}{\displaystyle (I+L_i)V_i^{n+1}=(I-L_i)V_i^n,}\hfill & 1\le i\le M-1,1\le n\le N,\hfill \\ V_i^0={\mathrm{\Pi }}_i,\hfill & 0\le i\le M,\hfill \\ v_0^n=0,\hfill & 0\le n\le N,\hfill \\ v_M^n=e^{x_M}-K{e}^{-r{\tau }_n^{\prime }},\hfill & 0\le n\le N-1,\hfill \end{array}\right.$$

(21)

where I is the identity operator. The CN-WSGD scheme, definedy by (21), gives a local truncation error of $O(l^2+h^2)$.

For the convenience of implementation, we take the matrix form of the grid functions

$${\mathbf{V}}^n=(V_1^n,V_2^n,\dots ,V_{M-1}^n)$$

makes the finite difference scheme (21), which can be described as

$$\begin{array}{c}\hfill \left[\left(1+{\displaystyle \frac{lr}{2}}\right)\mathbf{I}-{\displaystyle \frac{l}{4h}}(r\mathbf{I}-\mathbf{C})\mathbf{A}-{\displaystyle \frac{l}{2h^{\alpha }}}\mathbf{CB}\right]{\mathbf{V}}^{n+1}=\left[\left(1-{\displaystyle \frac{lr}{2}}\right)\mathbf{I}+{\displaystyle \frac{l}{4h}}(r\mathbf{I}-\mathbf{C})\mathbf{A}+{\displaystyle \frac{l}{2h^{\alpha }}}\mathbf{CB}\right]{\mathbf{V}}^n+{\mathbf{H}}^n,\end{array}$$

(22)

where $\mathbf{I}$ is a unit matrix, $\mathbf{C}=\mathrm{diag}(c_1,c_2,\dots ,c_{M-1})$,

$$\begin{array}{c}\hfill \mathbf{A}={\left(\begin{array}{cccc}0& 1& & \\ -1& 0& 1& \\ & \ddots & \ddots & \ddots \\ & & \ddots & \ddots & -1\\ & & -1& 0\end{array}\right)}_{(M-1)\times (M-1)},\end{array}$$

(23)

$$\mathbf{B}=\left(\begin{array}{ccc}{w}_1^{\left(\alpha \right)}& w_0^{\left(\alpha \right)}& \\ w_2^{\left(\alpha \right)}& w_1^{\left(\alpha \right)}& w_0^{\left(\alpha \right)}& \\ ⋮& w_2^{\left(\alpha \right)}& w_1^{\left(\alpha \right)}& \ddots \\ w_{M-2}^{\left(\alpha \right)}& \dots & \ddots & \ddots & w_0^{\left(\alpha \right)}\\ w_{M-1}^{\left(\alpha \right)}& w_{M-2}^{\left(\alpha \right)}& \dots & w_2^{\left(\alpha \right)}& w_1^{\left(\alpha \right)}\end{array}\right),$$

(24)

and

$$\begin{array}{cc}\hfill {\mathbf{H}}^n=& {\displaystyle \frac{l}{2h^{\alpha }}}\left(\begin{array}{c}{c}_1{w}_2^{\left(\alpha \right)}\\ c_2{w}_3^{\left(\alpha \right)}\\ ⋮\\ c_{M-1}{w}_M^{\left(\alpha \right)}\end{array}\right)(V_0^n+V_0^{n+1})+{\displaystyle \frac{l}{2h^{\alpha }}}\left(\begin{array}{c}0\\ ⋮\\ 0\\ c_{M-1}{w}_0^{\left(\alpha \right)}\end{array}\right)(V_M^n+V_M^{n+1})\hfill \\ \hfill & -{\displaystyle \frac{lr{c}_1}{4}}\left(\begin{array}{c}1\\ ⋮\\ 0\\ 0\end{array}\right)(V_0^n+V_0^{n+1})+{\displaystyle \frac{lr}{4}}\left(\begin{array}{c}0\\ ⋮\\ 0\\ 1\end{array}\right)(V_M^n+V_M^{n+1}).\hfill \end{array}$$

(25)

2.3. Stability and Convergence Analyses

Prior to conducting the stability and convergence analysis, we performed a simplification of the CN-WSGD scheme (22). Let $\mu ={\displaystyle \frac{lr}{2}},\mathbf{W}={\displaystyle \frac{l}{4h}}(r\mathbf{I}-\mathbf{C})\mathbf{A}+{\displaystyle \frac{l}{2h^{\alpha }}}\mathbf{CB}$, then the numerical scheme (22) can be written as

$$\left[(1+\mu )\mathbf{I}-\mathbf{W}\right]v^{n+1}=\left[(1-\mu )\mathbf{I}+\mathbf{W}\right]{\mathbf{V}}^n+{\mathbf{H}}^n.$$

(26)

Theorem 1. 

If the fractional order α and volatility $\sigma \left(x\right)$ are chosen such that the eigenvalues of matrix W are negative, i.e., $\mathrm{Re}\left(\lambda \right(\mathit{W}\left)\right)<0$, the CN-WSGD scheme (26) is stable.

Proof. 

It is clear that ${\displaystyle \frac{(1-\xi )+\lambda \left(\mathbf{W}\right)}{(1+\xi )-\lambda \left(\mathbf{W}\right)}}$ is the eigenvalues of the matrix ${\left[(1+\xi )\mathbf{I}-\mathbf{W}\right]}^{-1}$$\left[(1-\xi )\mathbf{I}+\mathbf{W}\right].$ As $\mu ={\displaystyle \frac{lr}{2}}>0$ and $\mathrm{Re}\left(\lambda \right(\mathbf{W}\left)\right)<0$, we have

$${\displaystyle \frac{(1-\mu )+\lambda \left(\mathbf{W}\right)}{(1+\mu )-\lambda \left(\mathbf{W}\right)}}<1,$$

which completes the proof. □

Let $V_h=\left\{v\right|v=v_i,v_i\mathrm{is}\mathrm{the}\mathrm{discrete}\mathrm{function}\mathrm{defined}\mathrm{on}\mathrm{the}\mathrm{grid}{\{x_i=ih\}}_{i=0}^M\}.$ Denote the discrete norm $\parallel v\parallel =\sqrt{h{\displaystyle \sum _{i=0}^N}{v}_i^2}$ for any $v\in V_h$ and ${\mathbf{V}}_e^n={(v_1^n,v_2^n,\cdots ,v_{N-1}^n)}^T$. Suppose $v_i^n$ is the exact solution of the model (1), $V_i^n$ is the numerical solution of the model (12) computed by the numerical discrete format (26) at grid points $(x_i,{\tau }_n^{\prime })$, and ${\mathbf{V}}^n={(V_1^n,V_2^n,\cdots ,V_{M-1}^n)}^T$. Let $e_i^n=v_i^n-V_i^n,i=0,1,2,\cdots ,M$ and ${\mathbf{E}}^n=(e_1^n,e_2^n,\cdots ,e_{N-1}^n),n=1,2,\cdots ,N$. According to the initial value condition and boundary condition, it is easy to see that ${\mathbf{E}}^0=0$ and $e_0^n=e_N^n=0,n=0,1,2,\cdots ,N$.

Theorem 2. 

If the fractional order α and volatility $\sigma \left(x\right)$ are chosen such that the eigenvalues of matrix W are negative, i.e., $\mathrm{Re}\left(\lambda \right(\mathit{W}\left)\right)<0$, then, we have

$$\parallel {\mathit{E}}^n\parallel =\parallel {\mathit{V}}_e^n-{\mathit{V}}^n\parallel \le C(h^2+l^2),n=1,2,\cdots ,N,$$

where C is a positive constant.

Proof. 

It is clear that

$$\left[\left(1+\mu \right)\mathbf{I}-\mathbf{W}\right]{\mathbf{E}}^{n+1}=\left[\left(1-\mu \right)\mathbf{I}+\mathbf{W}\right]{\mathbf{E}}^n+l{\epsilon }^n,$$

(27)

where ${\epsilon }^n={({\epsilon }_1^n,{\epsilon }_2^n,\dots ,{\epsilon }_{M-1}^n)}^T.$ and ${\epsilon }_i^n=O(h^2+l^2),(i=1,2,\cdots ,M-1;n=1,2,\cdots ,N).$ Rearranging the above equation yields

$$({\mathbf{E}}^{n+1}-{\mathbf{E}}^n)+\mu ({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)-\mathbf{W}({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)=l{\epsilon }^n.$$

(28)

By multiplying ${({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T$ on both sides of the above equation, we obtain

$$\begin{array}{c}\hfill {({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T({\mathbf{E}}^{n+1}-{\mathbf{E}}^n)+\mu {({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T\mathbf{I}({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)\\ \hfill -{({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T\mathbf{W}({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)=l{({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T{\epsilon }^n.\end{array}$$

(29)

Since the matrix $\mathbf{W}$ is a negative definite and the identity unit $\mathbf{I}$ is a positive definite matrix, we obtain

$${({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T\mathbf{I}({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)>0,{({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T\mathbf{W}({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)<0,$$

(30)

and from (29) and (30), it yields that

$$\parallel {\mathbf{E}}^{n+1}{\parallel }^2-\parallel {\mathbf{E}}^n{\parallel }^2\le l{({\mathbf{E}}^{n+1}+{\mathbf{E}}^n)}^T{\epsilon }^n\le l(\parallel {\mathbf{E}}^{n+1}\parallel +\parallel {\mathbf{E}}^n\parallel )·\parallel {\epsilon }^n\parallel .$$

(31)

Then, we have

$$\parallel {\mathbf{E}}^{n+1}\parallel -\parallel {\mathbf{E}}^n\parallel \le l\parallel {\epsilon }^n\parallel ,n\ge 0.$$

(32)

Accumulating both sides of the above inequalities for all $0\le k\le n-1$, we obtain

$$\parallel {\mathbf{E}}^n\parallel \le l\sum _{k=1}^n\parallel {\epsilon }^k\parallel \le C(h^2+l^2),n\ge 1,$$

(33)

which is the result we need. □

3. Inverse Problem

In this section, we use the standard linearization procedure to seek the coefficient $f\left(x\right)$ in (3), such that the solution of model (1) fits the option price $V^{*}\left(x\right)$ at the current time $t^{*}$.

Linearization at Constant Volatility

The option price V in (1) can be decomposed into

$$V=U_0+U+u,$$

where $U_0$ solves (1) with $\sigma ={\sigma }_0$,

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial U_0}{\partial t}+(r+\frac{1}{2}{\sigma }_0^{\alpha }\sec \frac{\alpha \pi }{2})\frac{\partial U_0}{\partial x}-\frac{1}{2}{\sigma }_0^{\alpha }\sec \frac{\alpha \pi }{2}{}_{-\infty }D_x^{\alpha }{U}_0-r{U}_0=0,}\hfill \\ U_0(x,T)=\mathrm{\Pi }\left(x\right),\hfill \end{array}\right.$$

(34)

u is quadratically small with respect to f, and the principal linear term U satisfies the following equations:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial U}{\partial t}+(r+\frac{1}{2}{\sigma }_0^{\alpha }\sec \frac{\alpha \pi }{2})\frac{\partial U}{\partial x}-\frac{1}{2}{\sigma }_0^{\alpha }\sec \frac{\alpha \pi }{2}{}_{-\infty }D_x^{\alpha }U-rU=f\left(x\right){(}_{-\infty }{D}_x^{\alpha }{U}_0-\frac{\partial U_0}{\partial x}),}\hfill \\ U(x,T)=0.\hfill \end{array}\right.$$

(35)

with observed data $U(x,t^{*})=V^{*}\left(x\right)-U_0(x,t^{*}),0<t^{*}<T.$ After variable substitution ${\displaystyle \tau =-\frac{1}{2}{\sigma }_0^{\alpha }\left(\sec \frac{\alpha \pi }{2}\right)(T-t)}$, $U_0$ satisfies

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial U_0}{\partial \tau }=(\gamma -1)\frac{\partial U_0}{\partial x}{+}_{-\infty }{D}_x^{\alpha }{U}_0-\gamma U_0,}\hfill \\ U(x,0)=\mathrm{\Pi }\left(x\right),\hfill \end{array}\right.$$

(36)

where ${\displaystyle \gamma =\frac{-2r}{{\sigma }_0^{\alpha }\sec \left(\frac{\alpha \pi }{2}\right)}}$. When we consider the case of European put options, i.e., $\mathrm{\Pi }\left(x\right)=\{K-e^x,0\}$, according to the results in Section 2.1, we have

$$U_0(x,\tau )=K{e}^{-\gamma \tau }{\int }_{d_1}^{+\infty }{f}_{\alpha ,0}\left(\right|m\left|\right)dm-e^x{\int }_{d_1}^{+\infty }{e}^{-\tau -{\tau }^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm,$$

(37)

where ${\displaystyle d_1=\frac{x-\ln K-(1-\gamma )\tau }{{\tau }^{1/\alpha }}}$. Further, we obtain

$${\displaystyle \frac{\partial U_0}{\partial x}}=-e^x{\int }_{d_1}^{+\infty }{e}^{-\tau -{\tau }^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm$$

(38)

and

$${\displaystyle \frac{\partial U_0}{\partial \tau }}=-\gamma U_0+e^x{\int }_{d_1}^{+\infty }\left(1-\gamma +{\displaystyle \frac{1}{\alpha }}{\tau }^{{\displaystyle \frac{1-\alpha }{\alpha }}}m\right)e^{-\tau -{\tau }^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm.$$

(39)

Similarly, we can rewrite (35) as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial U}{\partial \tau }=(\gamma -1)\frac{\partial U}{\partial x}{+}_{-\infty }{D}_x^{\alpha }U-\gamma U+\lambda W(x,\tau )f\left(x\right),}\hfill \\ U(x,0)=0,\hfill \end{array}\right.$$

(40)

with

$$U(x,{\tau }^{*})=U^{*}\left(x\right)$$

(41)

where ${\displaystyle \lambda =\frac{\gamma }{r}=\frac{-2}{{{\sigma }_0}^{\alpha }\sec \left(\frac{\alpha \pi }{2}\right)}}$, ${\displaystyle {\tau }^{*}=-\frac{1}{2}{\sigma }_0^{\alpha }\left(\sec \frac{\alpha \pi }{2}\right)(T-t^{*})}$, and ${\displaystyle W(x,\tau )=\frac{\partial U_0}{\partial x}{-}_{-\infty }{D}_x^{\alpha }{U}_0}$. As $U_0$ is the solution of the model (36), $W(x,\tau )$ is given by

$$W(x,\tau )=\gamma {\displaystyle \frac{\partial U_0}{\partial x}}-\gamma U_0-{\displaystyle \frac{\partial U_0}{\partial \tau }}.$$

Combining Equation (38) with Equation (39), we further obtain

$$W(x,\tau )=-{\int }_{d_1}^{+\infty }\left(1+{\displaystyle \frac{1}{\alpha }}{\tau }^{{\displaystyle \frac{1-\alpha }{\alpha }}}m\right)e^{-\tau -{\tau }^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm.$$

(42)

Next, we start to discuss the analytical solution of U in model (40). Taking the Fourier transform of U in the space direction, i.e., $\tilde{U}(\xi ,\tau )=F\left[U(x,\tau )\right]$, we can derive that

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \tilde{U}}{\partial \tau }=(\gamma -1)i\xi \tilde{U}-{\left|\xi \right|}^{\alpha }\tilde{U}-\gamma \tilde{U}-\lambda g(\xi ,\tau ),}\hfill \\ \tilde{U}(\xi ,0)=0,\hfill \end{array}\right.$$

(43)

where $g(\xi ,\tau )=F\left[f\left(x\right)W(x,\tau )\right]$. Notice that (43) is actually a first-order linear ordinary differential equation of $\tilde{U}$ with respect to $\tau$. Denote $p\left(\xi \right)=-\left[(\gamma -1)i\xi -{\left|\xi \right|}^{\alpha }-\gamma \right],h(\xi ,\tau )=-\lambda g(\xi ,\tau )$. Then, (43) becomes

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \tilde{U}}{\partial \tau }+p\left(\xi \right)\tilde{U}=h(\xi ,\tau ),}\hfill \\ \tilde{U}(\xi ,0)=0.\hfill \end{array}\right.$$

(44)

According to the solution formula of first-order linear ODE, the option price in the Fourier space can be written as

$$\tilde{U}(\xi ,\tau )={\int }_0^{\tau }h(\xi ,t)e^{-p\left(\xi \right)(\tau -t)}dt.$$

(45)

Let $s=\tau -t$. We have

$$\tilde{U}(\xi ,\tau )={\int }_0^{\tau }h(\xi ,\tau -s)e^{-p\left(\xi \right)s}ds.$$

(46)

In light of the convolution theorem of the Fourier transform, it is clear that

$$U(\xi ,\tau )={\int }_0^{\tau }{F}^{-1}\left[h(\xi ,\tau -s)\right]\ast F^{-1}\left[e^{-p\left(\xi \right)s}\right]ds.$$

(47)

Notice that

$$F^{-1}\left[e^{-p\left(\xi \right)s}\right]=e^{-\gamma s}Q(x-(1-\gamma )s;\alpha ),$$

(48)

and

$$F^{-1}\left[h(\xi ,\tau -s)\right]=F^{-1}\left[F\left[-\lambda f\left(\xi \right)W(\xi ,\tau -s)\right]\right]=-\lambda f\left(x\right)W(x,\tau -s),$$

(49)

where $Q(x;\alpha )=F^{-1}\left[e^{-{\left|\xi \right|}^{\alpha }s}\right]={\displaystyle \frac{1}{s^{1/\alpha }}}{f}_{\alpha ,0}\left({\displaystyle \frac{\left|x\right|}{s^{1/\alpha }}}\right)$. Substituting Equations (48) and (49) into Equation (47), we obtain

$$U(x,\tau )=-\lambda {\int }_0^{\tau }{\int }_{-\infty }^{+\infty }f\left(z\right)W(z,\tau -s)e^{-\gamma s}{\displaystyle \frac{1}{s^{1/\alpha }}}{f}_{\alpha ,0}\left({\displaystyle \frac{|x-z-(1-\gamma \left)s\right|}{s^{1/\alpha }}}\right)dzds.$$

(50)

Denote $U^{*}\left(x\right)=U(x,{\tau }^{*})$. A simple calculation gives the following integral equation for $f\left(x\right)$:

$${\int }_{-\infty }^{+\infty }f\left(z\right)K(x,z)dz=U^{*}\left(x\right),$$

(51)

where

$$K(x,z)=-\lambda {\int }_0^{{\tau }^{*}}W(z,{\tau }^{*}-s)e^{-\gamma s}{\displaystyle \frac{1}{s^{1/\alpha }}}{f}_{\alpha ,0}\left({\displaystyle \frac{|x-z-(1-\gamma \left)s\right|}{s^{1/\alpha }}}\right)ds,$$

(52)

$$W(x,{\tau }^{*}-s)=-{\int }_{d_2}^{+\infty }\left[1+{\displaystyle \frac{1}{\alpha }}{\left({\tau }^{*}-s\right)}^{{\displaystyle \frac{1-\alpha }{\alpha }}}m\right]e^{-\left({\tau }^{*}-s\right)-{\left({\tau }^{*}-s\right)}^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm.$$

(53)

Here, ${\displaystyle d_2=\frac{x-lnK-(1-\gamma )\left({\tau }^{*}-s\right)}{{\left({\tau }^{*}-s\right)}^{1/\alpha }}}$. As $f\left(x\right)=0$ outside $\omega$, the Fredholm integral Equation (51) is equivalent to

$${\int }_{\omega }f\left(z\right)K(x,z)dz=U^{*}\left(x\right).$$

(54)

Therefore, the inverse volatility problem comes down to solving a Fredholm integral equation.

4. Numerical Examples

There are two issues of concern in this part. Firstly, we try to study the accuracy and the convergence order of the CN-WSGD scheme. Secondly, we discuss the effect of the reconstruction algorithm in Section 3. It is worth mentioning that these parts are both studied under the following parameter settings, i.e., ${\sigma }_0=0.2,$$r=0.02$$,K=10,$$\alpha =1.9,T=1$. The numerical simulations were performed on a computer with an Intel Core i5-1135G7 processor, 16 GB RAM, running on the Windows 11 operating system. All computations were implemented using MATLAB R2020a.

4.1. Numerical Results for Direct Problem

For the purpose of testing the reliability of the proposed CN-WSGD scheme, one of the most efficient metthods is to calculate our solution to the spatial-fractional BS model without perturbation, i.e., $f\left(x\right)=0$, and to compare it with the corresponding analytical solution. Displayed in Figure 1a is the comparison between our numerical solution and the corresponding closed-form solution. The absolute errors between numerical solutions and analytical solutions at each node are sketched in Figure 1b.

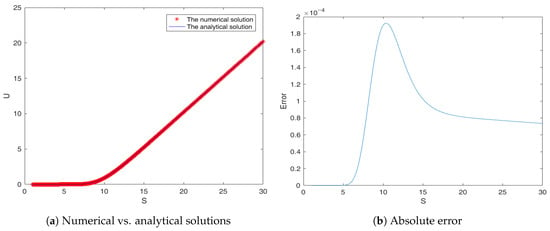
Figure 1. Numerical vs. anlytical solutions compared with $M=1024, N=1600$ discretization.

From Figure 1, we can conclude that the numerical and analytical solutions agree well and the absolute error is quite small, which confirms the correctness of our numerical approach.

Next, we verify the convergence order of the CN-WSGD scheme numerical examples. We replace the exact solution with a very fine numerical solution in time and space $V^{ref}(x,{\tau }^{\prime })$ for the convenience of calculation. It should be noticed that the difference here is measured by absolute errors, which are defined as

$$err=\parallel V(x,{\tau }^{\prime })-V^{ref}(x,{\tau }^{\prime }){\parallel }_2,$$

(55)

where $V^{ref}(x,{\tau }^{\prime })$ is the solution computed with extremely fine grid sizes, while $Orde{r}_{\tau }^{\prime }$ and $Orde{r}_x$ are the so-called EOC (Experimental Order of Convergence), defined as

$$Orde{r}_{{\tau }^{\prime }}={\displaystyle \frac{\ln er{r}_{i+1}-\ln er{r}_i}{\ln \Delta {\tau }_i^{\prime }-\ln \Delta {\tau }_{i+1}^{\prime }}},$$

(56)

$$Orde{r}_x={\displaystyle \frac{\ln er{r}_{i+1}-\ln er{r}_i}{\ln \Delta x_i-\ln \Delta x_{i+1}}}.$$

(57)

We set $f\left(x\right)=0.01x$. As shown in Table 1, the number of grid points in the time direction is fixed, and the number of grid points in the spatial direction is gradually increased. We can see that the order of convergence in the x direction remains close to 2. Meanwhile, we fix the number of grid points in the spatial direction. The EOCs for ${\tau }^{\prime }$ direction are close to 2 when the size of the time step is increasingly accumulated, as shown in Table 2.

Table 1. Convergence order in the x direction of the CN-WSGD scheme.

No. of Time Steps	No. of Spatial Steps	Err	${\mathit{Order}}_{\mathit{x}}$
1001	17	0.1029
1001	33	0.0302	1.7686
1001	65	0.0098	1.6237
1001	129	0.0036	1.4448
1001	257	0.0012	1.5850
1001	513	$3.5907\times {10}^{-4}$	1.7407

Table 2. Order of convergence in ${\tau }^{\prime }$ direction of second-order precision in the CN-WSGD scheme.

No. of Time Steps	No. of Spatial Steps	Err	${\mathit{Order}}_{{\mathit{\tau }}^{\prime }}$
201	1024	0.0880
401	1024	0.0421	1.0599
801	1024	0.0191	1.1423
1601	1024	0.0077	1.3106
3201	1024	0.0019	2.0189

4.2. Numerical Simulation for Inverse Problem

Whether the scheme can be efficiently computed is one of the main criteria for assessing its practical usefulness. Therefore, in this part, we turn to investigate the effect of the reconstruction algorithm.

We first discretize the kernel function $K(x,z)$ in (52) and the function $W(x,{\tau }^{*}-s)$ in the kernel function. For the function $W(x,{\tau }^{*}-s)$, we denote $\tilde{s}={\tau }^{*}-s$ for convenience. For the integral on the semi-infinite domain $[d_2,+\infty )$ in $W(x,\tilde{s})$, we shift the integral region to $[0,+\infty )$ through the integral transformation, and then use Gauss–Laguerre quadrature formula to solve the integral, i.e.,

$$\begin{array}{cc}\hfill W(x,\tilde{s})& =-{\int }_{d_2}^{+\infty }\left[1+{\displaystyle \frac{1}{\alpha }}{\tilde{s}}^{{\displaystyle \frac{1-\alpha }{\alpha }}}m\right]e^{-\tilde{s}-{\tilde{s}}^{{\displaystyle \frac{1}{\alpha }}}m}{f}_{\alpha ,0}\left(\right|m\left|\right)dm\hfill \\ \hfill & =-{\int }_0^{+\infty }{e}^{-m}{e}^m\left[1+{\displaystyle \frac{1}{\alpha }}{\tilde{s}}^{{\displaystyle \frac{1-\alpha }{\alpha }}}(m+d_2)\right]e^{-\tilde{s}-{\tilde{s}}^{{\displaystyle \frac{1}{\alpha }}}(m+d_2)}{f}_{\alpha ,0}\left(\right|m+d_2\left|\right)dm\hfill \\ \hfill & =-\sum _{k=1}^K{e}^{m_k}\left[1+{\displaystyle \frac{1}{\alpha }}{\tilde{s}}^{{\displaystyle \frac{1-\alpha }{\alpha }}}(m_k+d_2)\right]e^{-\tilde{s}-{\tilde{s}}^{{\displaystyle \frac{1}{\alpha }}}(m_k+d_2)}{f}_{\alpha ,0}\left(\right|m+d_2\left|\right)A_k,\hfill \end{array}$$

(58)

where K is the number of Laguerre points used to approximate the integral, ${\left\{m_k\right\}}_{k=0}^K$ is $K+1$ zeros of the Laguerre polynomial $L_{K+1}\left(x\right)$, and $A_k$ is the quadrature coefficient, which is defined as: ${\displaystyle A_k=\frac{{(n!)}^2}{m_k{\left[L_{K+1}^{\prime }\left(m_k\right)\right]}^2}.}$

From the expression of the kernel function $K(x,z)$ in (52), we know that it is singular at $s=0$. In order to deal with the singularity of the kernel function, we first apply the integral transformation to s: $s={\displaystyle \frac{{\tau }^{*}}{2}}\nu +{\displaystyle \frac{{\tau }^{*}}{2}}$, $\nu \in (-1,1)$. Following this, we discretize the interval $(-1,1)$ with Legendre–Gauss–Lobatto points without boundary points. Using the Gaussian quadrantile formula of $M_1$ points corresponding to the Legendre weight $\left\{w_i\right\}$, we obtain the kernel function $K(x,z)$ discrete scheme as follows:

$$\begin{array}{cc}\hfill K(x,z)& =-\lambda {\int }_0^{{\tau }^{*}}W(z,{\tau }^{*}-s)e^{-\gamma s}{\displaystyle \frac{1}{s^{1/\alpha }}}{f}_{\alpha ,0}\left({\displaystyle \frac{|x-z-(1-\gamma \left)s\right|}{s^{1/\alpha }}}\right)ds\hfill \\ \hfill & =-{\displaystyle \frac{{\tau }^{*}\lambda }{2}}\sum _{i=1}^{M_1}G(x,z,{\displaystyle \frac{{\tau }^{*}}{2}}{\nu }_i+{\displaystyle \frac{{\tau }^{*}}{2}})w_i,\hfill \end{array}$$

(59)

where $G(x,z,s)=W(z,{\tau }^{*}-s)e^{-\gamma s}{\displaystyle \frac{1}{s^{1/\alpha }}}{f}_{\alpha ,0}\left({\displaystyle \frac{|x-z-(1-\gamma \left)s\right|}{s^{1/\alpha }}}\right).$

We consider a quadratic function $f\left(x\right)=0.004x^2$ and a cubic $f\left(x\right)=0.005x^3$ as perturbed functions, respectively. In view of the serious deterioration near the boundary, we cut out the middle part of the reconstructed image. We can see that the effect of reconstruction is quite good for the whole space interval, except on both sides of the endpoint, as shown in Figure 2.

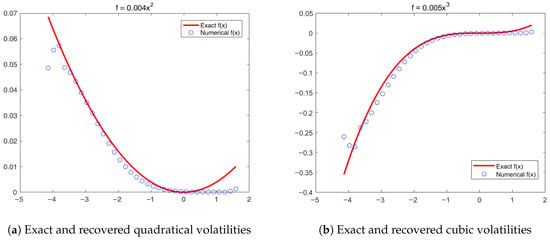
Figure 2. Numerical vs. anlytical solutions compared with $M=40, N=1000$ discretization.

By fixing the term $f\left(x\right)=0.005x^3$ while varying the fractional derivative order $\alpha$ (from 1.4 to 1.9), we quantitatively analyzed the influence of the fractional derivative order on inversion accuracy. The computational results presented in Table 3 demonstrate that as $\alpha$ increases, the $L_2$-norm errors between the reconstructed solutions and exact solutions exhibit a distinct monotonic decreasing trend, except for the case of $\alpha$ = 1.5. This phenomenon suggests that higher-order fractional derivatives provide superior numerical stability in inverse problems, which may be attributed to their enhanced smoothness constraints.

Table 3. $L_2$-norm errors between the numerical inversion solutions and exact solutions with different fractional derivative orders.

$\mathit{\alpha }$	1.4	1.5	1.6	1.7	1.8	1.9
errors	0.7329	0.2192	0.2647	0.2323	0.1559	0.1168

5. Conclusions

The inverse problem for recovering implied volatility under SFBSM is solved for the first time. Using the linearization technique introduced in [19], we transformed the inverse coefficient problem of determining the implied volatility into an inverse source problem. Subsequently, we obtained a Fredholm integral equation of the first kind based on Fourier transform and the results in [7]. The numerical method for solving the integral equation is also given. To numerically tackle the direct problem with variable volatility, we applied the WSGD formula [15] to approximate the spatial-fractional derivative and combined it with Crank–Nicolson scheme for time direction. Numerical examples confirmed the validity of the derived integral equation and the reliability of the proposed numerical implementation algorithms. For simplicity, we only considered space-dependent volatility. We aim to recover more complicated volatilities that are closer to the real market conditions in the near future.