Abstract
Problem: Existing Human–Robot Collaboration (HRC) allocators cannot react at a sub-second scale while accounting for worker fatigue. Objective: We designed a fatigue-aware combinatorial auction executed every 100 ms. Method: A human and a FANUC robot submit bids combining execution time, predicted energy, and real-time fatigue; a greedy algorithm (≤1 ms) with a approximation guarantee and O (|Bids| log |Bids|) complexity maximizes utility. Results: In 1000 RoboDK episodes, the framework increases active cycles·min−1 by 20%, improves robot utilization by +10.2 percentage points, reduces per cycle fatigue by 4%, and raises the collision-free rate to 99.85% versus a static baseline (p < 0.001). Contribution: We provide the first transparent, sub-second, fatigue-aware allocation mechanism for Industry 5.0, with quantified privacy safeguards and a roadmap for physical deployment. Unlike prior auction-based or reinforcement learning approaches, our model uniquely integrates a sub-second ergonomic adaptation with a mathematically interpretable utility structure, ensuring both human-centered responsiveness and system-level transparency.
Keywords:
human–robot collaboration; auction-based dynamic cycle allocation; combinatorial auctions; mathematical optimization; dynamic cycle assignment; industrial assembly; Industry 5.0 MSC:
90C27; 91B26
1. Introduction
1.1. Background and Motivation
Human–Robot Collaboration (HRC) represents a transformative shift in manufacturing, merging the precision and endurance of industrial robots with the dexterity and problem-solving capabilities of human operators. Industry 4.0 laid the groundwork for HRC by integrating cyber-physical systems, the Internet of Things (IoT), and cloud-based analytics into “smart factories”, thereby enabling real-time monitoring, predictive maintenance, and adaptive process control (e.g., [1,2,3]). Nevertheless, these early implementations largely treated humans and robots as separate agents, coordinating through pre-programmed handshakes rather than genuine, continuous cooperation.
In contrast, Industry 5.0 emphasizes human well-being and sustainability, advocating for symbiotic work cells in which the robot augments human capabilities while respecting ergonomic limits and environmental constraints [4,5,6]. To realize this vision, allocation of work must occur at the granularity of auction cycles (e.g., 100 ms decision intervals), rather than coarse “tasks” spanning several seconds. Dynamic Cycle Allocation (DCA) addresses this requirement by reassigning cycles in real time based on instantaneous human states (e.g., fatigue, measured via wearable-inspired Inertial Measurement Unit (IMU) and heart-rate models [7,8]) and robot availability metrics (e.g., payload, reachability, and current motion plan).
Robots consistently outperform humans in high-precision, repetitive operations—such as torque-controlled bolting or calibrated pick-and-place—achieving cycle times under 50 ms with repeatability better than ±0.02 mm when simulated in RoboDK [9]. Conversely, humans excel at tasks requiring adaptability, complex perception, or ad hoc decision-making—such as visual inspection of morphological defects and ergonomic judgment—capabilities increasingly recognized as essential in Industry 5.0 environments [2,4,10]. A robust DCA mechanism must, therefore, balance these complementary strengths, optimizing active cycle throughput while minimizing operator fatigue per cycle and maintaining collision-free operation.
However, two core challenges impede sub-second DCA deployment. First, modeling human states involves high-frequency physiological data fusion and predictive filtering to smooth noise without delaying decisions [10,11]. Second, allocation algorithms must be executed within each 100 ms cycle—imposing strict worst-case computation bounds—while accommodating combinatorial bids over potentially dozens of subtasks. Traditional rule-based systems lack the flexibility to adapt to evolving fatigue or unexpected robot downtimes, often resulting in idle periods or safety hazards (e.g., [12,13]). Reinforcement Learning (RL) and Deep RL (DRL) approaches offer adaptive policies but require large training datasets and specialized hardware, and suffer from sim-to-real gaps and limited interpretability (e.g., [3,9,14]). These limitations motivate the design of mathematically rigorous frameworks that integrate real-time state estimations with provably efficient allocation algorithms to fulfill Industry 5.0’s human-centric aspirations (e.g., [9]).
1.2. Research Objectives and Contributions
The overarching objective of this study is to develop and validate a combinatorial auction-based DCA framework that seamlessly adapts to evolving human and robot states, achieving high throughput, low fatigue, and stringent safety in sub-second cycles. To this end, the following specific contributions are provided:
- Adaptive Auction-Based Model: Proposal of a combinatorial auction mechanism in which human and robot agents submit real-time bids reflecting cycle execution time, energy consumption, and fatigue costs [12,13].
- Mathematical Formulation and Approximation: Development of an optimization model that maximizes aggregate system utility under assignment constraints, solved via a greedy algorithm offering a approximation guarantee within O (|Bids| log |Bids|) time complexity [15].
- High-Fidelity Simulation Validation: Comprehensive evaluation using RoboDK v5.9 with a FANUC LR Mate 200iD-7L and a 22-Degrees of Freedom (DoF) human avatar, demonstrating a 20% increase in active cycles·min−1, 4% reduction in fatigue per cycle, and >99.85% collision-free rate against a static baseline [16,17].
- Industry 5.0 Alignment and Future Roadmap: Discussion of real-world testbed deployment, multi-agent generalizations, and integration of sustainability Key Performance Indicators (KPIs) (e.g., energy per cycle and CO2 footprint), positioning the framework as a foundational step toward socially sustainable, human-centered automation [18,19].
1.3. Paper Organization
The remainder of this paper is organized as follows:
- Section 2 reviews the state of the art in HRC allocation, covering rule-based, optimization, RL/DRL, and auction mechanisms.
- Section 3 details the combinatorial auction model, bid computation, and greedy allocation algorithm.
- Section 4 describes the RoboDK simulation environment, human avatar modeling, operator role scenarios, and data capture protocols.
- Section 5 presents experimental results, including statistical analyses and sensitivity studies.
- Section 6 discusses the implications, limitations, and potential extensions.
- Section 7 concludes with a summary of the findings and contributions.
2. Related Work
2.1. Rule-Based and Optimization-Driven Cycle Allocation
Early industrial HRC work relied on rule-based heuristics due to their predictability and minimal computational burden. Nourmohammadi et al. [20] employed constraint programming to balance human–robot assembly lines, achieving modest throughput gains but a failure to respond when operator fatigue or part variability changed in real time. Yin et al. [21] extended rule sets to include simple ergonomic risk indices (e.g., joint torque thresholds), yet their static decision trees could not preempt fatigue-induced safety hazards [4,22].
In parallel, optimization methods—such as mixed-integer programming or metaheuristics—have been proposed to derive provably optimal cycle assignments. Barravecchia et al. [22] introduced a “collaboration scale” metric, embedding it into an integer linear program to maximize combined human and robot utilization but solving their model on even 20 tasks took hundreds of milliseconds [23]. Karas Celik and Özçelik [24] tackled HRC line rebalancing via a hyper-matheuristic, yet their cycle time variability model ignored dynamic human states and thus could not react to real-world fatigue fluctuations [25]. As a result, purely optimization-centric approaches remain impractical for the sub-second reallocation demands of modern collaborative cells.
2.2. Reinforcement Learning and Deep RL for Adaptive Allocation
Reinforcement Learning has been explored to overcome the rigidity of rule-based/optimization schemes by learning allocation policies that react to observed human and robot states [14,26]. Sandrini et al. [26] used an actor-critic agent to reassign sequential assembly subtasks, reporting up to a 12% cycle-time improvement in simulated cells; however, each policy required millions of simulator steps and elaborate digital-twin setups. Deep RL further extends RL via neural approximators (e.g., DQN and convolutional policies [14,27,28]) but, despite capturing nonlinear-ergonomics–throughput trade-offs, these end-to-end methods suffer from sample complexity, sim-to-real gaps, opacity, and restrictive inference latency (e.g., [3,9,14]).
These limitations motivate alternative, semantically transparent frameworks that guarantee bounded latency and built-in interpretability.
2.3. Auction-Based Mechanisms in Multi-Agent and HRC Contexts
Auctions naturally distribute allocation decisions across autonomous agents. In multi-robot contexts, Bandyopadhyay et al. [12] explored quantum-game-theoretic auctions, while Liu et al. [13] and Kozlov & Ougolnitsky [29] applied reverse auctions for federated learning resource sharing. In HRC, auction models remain nascent: Meregalli Falerni et al. [11] considered preference learning but assumed static human utility; no existing work embeds dynamic physiological states such as fatigue into bid functions. Moreover, prior auction formulations often omit formal combinatorial constraints, limiting the allocation of interdependent subtasks in one cycle.
This work fills this gap by casting Dynamic Cycle Allocation as a combinatorial auction, with real-time bid updates reflecting human fatigue and robot availability, solved via a greedy approximation in under 1 ms [12,13,30].
2.4. Integration of Human Factors and Real-Time Adaptability
The literature on human-aware HRC underlines the critical need to integrate ergonomic and cognitive metrics into allocation logic. Orlando et al. [7] and Pereira et al. [8] surveyed sensor-based fatigue modeling, demonstrating strong correlations between physiological signals and task errors, yet these studies stop short of embedding such metrics into decision-making loops. Yuan et al. [4] called for Industry 5.0 approaches that harmonize productivity with well-being, while Xiao et al. [14] and Peng et al. [31] hinted at hybrid RL–auction schemes but did not provide rigorous mathematical proof of real-time feasibility. The synthesis is that prior work falls into (i) rule/optimization (fast but non-adaptive); (ii) RL/DRL (adaptive but opaque and slow); and (iii) auctions (scalable, yet human-agnostic). This triangulation exposes the gap our framework fills, namely, transparent auctions embedding continuous fatigue to achieve sub-second adaptation.
In summary, existing allocation schemes lack one or more of the following: sub-second responsiveness, fatigue-aware cost modeling, or a transparent optimization structure. This work directly addresses these deficiencies. Rule-based systems fail to adapt to evolving physiological states; optimization-based methods incur unacceptable computation delays; RL/DRL models suffer from opacity, transferability issues, and costly training; and auction frameworks have yet to embed human ergonomics in real time. Our proposed approach overcomes these barriers by integrating fatigue into a mathematically grounded auction mechanism that is executed within strict timing constraints.
2.5. Availability of Data and Code
All MATLAB scripts for generating the synthetic datasets, sensitivity analysis results, and publication figures are freely accessible from the GitHub repository [32]. The complete aggregated simulation results—including per episode throughput, fatigue, and safety metrics—and the full synthetic dataset (Parquet format) have been deposited on FigShare [33].
3. Problem Statement
Existing HRC allocation methods exhibit critical shortcomings when applied to high-speed, human-aware assembly. Static rule-based schemes rely on fixed priority lists that ignore dynamic human factors—such as cumulative fatigue or transient skill degradation—leading to suboptimal cycle assignments and elevated safety risks [20,21]. Optimization-based approaches (e.g., integer linear programming and mixed-integer nonlinear programming) can find globally optimal allocations but incur computational latencies of hundreds of milliseconds to seconds, rendering them unsuitable for 10 Hz decision loops [23].
Reinforcement Learning (RL) and Deep RL (DRL) approaches offer adaptive policies learned offline, yet they require millions of training episodes and specialized hardware, lack interpretability, and suffer from a “reality gap” when transferring policies to physical cells [3,9,14]. Moreover, few RL-based HRC frameworks formally incorporate real-time human fatigue into the reward structure, limiting their capacity to safeguard operator wellness. Auction-based models provide a promising foundation for distributed, scalable allocation but existing formulations in robotics seldom address dynamic human factors and most neglect rigorous combinatorial bidding, hindering bundle assignments and transparency [12,13,30].
Consequently, a clear research gap emerges that addresses the need for a real-time, human-aware allocation framework that (1) guarantees sub-second computation per decision, (2) incorporates continuous human fatigue and robot availability into cost functions, and (3) offers mathematically transparent bidding and allocation, thereby ensuring both safety and high productivity in collaborative assembly cells [15,34,35].
3.1. Combinatorial Auction Model
The Dynamic Cycle Allocation problem in Human–Robot Collaboration is modeled as a combinatorial auction in which each agent (the human operator or the FANUC robot) submits bids for bundles of tasks. A central allocator then selects the winning bids to maximize total system utility. This formulation guarantees adaptability to changing human fatigue levels and robot availability while preserving a clear optimization structure.
3.1.1. Agents and Tasks
- Agents:
- Human operator ): Represented by the state vector , where is fatigue and is the skill level.
- Robot: Defined by kinematic constraints and an availability flag of .
- Tasks:
- denotes the set of subtasks (e.g., picking, placing, and bolting).
- Each task carries a complexity level and an estimated execution time .
3.1.2. Auction Formulation
- Agents submit bids for each bundle .
- Binary decision variables indicate if bundle is awarded to agent .
- The optimization problem is
This constraint ensures each task is assigned to one agent at most.
All simulation configuration files, parameter sweeps, and post-processing routines can be cloned or downloaded from the project’s GitHub repository [32]. Large data files (simulation logs, aggregated results, and the Parquet dataset) are available via FigShare [33].
3.2. Model Assumptions
The assumptions are as follows: (A1) task times are i.i.d. within ±20% noise; (A2) fatigue increases linearly within a 2500-cycle horizon; (A3) no simultaneous execution conflicts inside a bundle; (A4) a sensor latency < 10 ms, so the state is current at bidding; and (A5) utility is the additive over bundles.
3.3. Bid Calculation
Bids for singleton tasks () are defined and extended to bundles by summation as follows:
- Robot Bid:
- Human Bid:
For any bundle . Bids are updated every auction cycle to reflect current agent states.
3.4. Greedy Allocation Algorithm
The allocation strategy is detailed in Algorithm 1, which implements a greedy auction mechanism to maximize utility. Complexity O (|Bids| log |Bids|) has an approximation ratio for monotone submodular utility.
| Algorithm 1 Greedy Auction (Tasks, Bids) |
| 1. while Tasks do 2. Compute score for all admissible bundles 3. Select 4. Assign to ; Tasks ← Tasks\ 5. end while |
3.5. Real-Time Integration
The allocation cycle is executed at 10 Hz (100 ms per iteration) within a closed-loop MATLAB–RoboDK interface as follows:
- State Update: Human states and are obtained from synthetic sensor models; robot availability is queried via the RoboDK Application Programming Interface (API).
- Bid Computation: At each cycle, the bid function is re-evaluated for every task .
- Task Assignment: The greedy algorithm determines allocations, which are sent to RoboDK over Transmission Control Protocol/Internet Protocol (TCP/IP) (0.28 ms latency).
- Feedback Logging: Execution results (completion, duration, and safety) are returned by RoboDK and logged for subsequent analyses.
Seeds for deterministic runs 1–500, RoboDK Safety Wizard configurations, and API calls are detailed in the accompanying repository. This closed loop ensures continuous adaptation to human fatigue and the robot workload, supporting Industry 5.0’s human-centric requirements.
4. Methodology
4.1. Simulation Environment (Summary)
Robot: FANUC LR Mate 200iD-7L (URDF import; ±0.02 mm). Human: 22 DoF avatar with synthetic IMU/HR sensors. Tasks: picking/placing/sorting/packaging; duration ~. Control loop: MATLAB ↔ RoboDK TCP/IP; latency 0.28 ms. Safety: RoboDK collision sensors, 0.5 m exclusion zone, and speed throttling via a fatigue semaphore.
4.2. Operator Roles and Scene Capturing
Six distinct operator roles were defined to validate the auction-based allocation framework under varied human–robot interactions. For each role, a single high-resolution (1920 × 1080 px) screenshot was exported directly from RoboDK using one of four pre-configured camera rigs.
The six roles and their capture parameters are as follows (see Figure 1):

Figure 1.
Industrial cell snapshots illustrating six operator roles (Material Delivery, Tray Loading, Part Transfer, HMI Supervision, Quality Inspection, and Packaging). Fatigue semaphore (green/orange/red) reflects real-time fatigue thresholds.
- Material Delivery: The operator maneuvers the manual pallet jack into the feed zone. Callout is placed above the head, with the arrow pointing to the jack handle.
- Tray Loading: The operator lifts a color-coded tray of cylindrical workpieces onto the conveyor inlet. Lighting is adjusted to avoid glare on the tray surface.
- Part Transfer: The operator picks completed assemblies off the primary conveyor, maintaining orientation for downstream packaging.
- HMI Supervision: The operator gestures at the HMI console; real-time status bars and parameter sliders are visible on-screen.
- Quality Inspection: The operator stands at the secondary conveyor, visually verifying the part dimensions against the caliper template on the inspection table.
- Packaging Preparation: The operator arranges inspected parts into standardized shipping boxes on the pallet jack, preparing for logistics hand-off.
Throughout all captures, the semaphore is prominently visible above the operator; its color changes are synchronized with the fatigue trace shown on the floating text labels, providing an intuitive visual cue for reviewers who may be unfamiliar with the earlier article.
Each of the six roles is presented in its own figure (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7), captured from one of four fixed camera perspectives to preserve visual clarity and eliminate occlusions. The figure captions now include the camera rig orientation, mounting height (1.5 m), focal length (35 mm), frame rate (30 fps), role name, and exact callout text. All images were exported as 1920 × 1080 px PNGs, named according to the convention episode<Role>_<Camera>_<Timestamp>.png, and archived alongside a JSON metadata file (fields: role, timestamp, camera_id, exposure, illumination level, and acquisition parameters) in the project repository.
Figure 2.
Material Delivery role. Human operator using pallet jack to load raw components.
Figure 3.
Tray Loading role. Operator placing color-coded trays of workpieces onto conveyor.
Figure 4.
Part Transfer role. Operator removing completed assemblies from the conveyor.

Figure 5.
HMI Supervision role. Operator interacting with the human–machine interface for real-time parameter adjustments.

Figure 6.
Quality Inspection role. Operator visually inspecting finished parts for dimensional accuracy.

Figure 7.
Packaging Preparation role. Operator organizing inspected components into shipping boxes.
4.3. Parameters and Baselines
To guarantee reproducibility, all simulation parameters were fixed and documented as follows:
- Initial Conditions: Human fatigue (20 %), skill level (novice), and robot state .
- Fatigue Dynamics: and , reflecting the empirically observed correlation between task duration and fatigue accumulation in HRC contexts [7,8]. The per task was measured using RoboDK simulations.
- Semaphore Thresholds: Green ≤ 0.25, orange 0.25–0.40, and red ≥ 0.40—as enforced by the finite-state machine described in Section 4.1—ensure that bid computations reflect the same ergonomic thresholds used for visual feedback.
- Task Times: Sampled from to reflect the ±20 % variability observed in industrial benchmarks [20,21,36].
- Greedy Auction Parameters: Table 1 consolidates the weights and frequency used in the allocation algorithm.
 Table 1. Greedy auction parameters.
Table 1. Greedy auction parameters. - Baselines: Static rule-based, the cycles are assigned by a fixed priority of human-centric cycles to the operator and robot-centric cycles to the FANUC arm, irrespective of dynamic states [4,20,21]. Implementation: Both methods are coded in MATLAB R2025a using the same RoboDK API calls for a fair comparison. Safety margins (0.5 m robot exclusion zone) and joint velocity limits (50% of maximum) are identically enforced.
Each experimental condition comprised 1000 independent episodes (~2500 cycles each), yielding 2.5 × 106 cycles. Sensitivity analyses used 100 Monte Carlo replications per perturbation, consistent with simulation-based optimization approaches in industrial system design [37,38,39]. Data capture and archiving proceeded as follows:
- Logged Metrics:
- ◦
- Throughput: Active auction cycles·min−1, computed as the number of robot-active cycles divided by total robot-engaged time in minutes.
- ◦
- Average Fatigue per Cycle: Mean operator fatigue level (units·cycle−1) sampled per cycle. Semaphore color changes were logged in parallel to cross-validate the fatigue estimates.
- ◦
- Safety Rate: Collision-free cycle proportion, flagged by RoboDK collision sensors.
- Storage: Data streamed via MATLAB to Parquet files (partitioned by episode), with CSV exports (HRC_Simulation_Results_Fanuc.csv) hosted on FigShare (DOI: 10.6084/m9.figshare.29431700) [32,33].
- Determinism: Random seeds 1–500 ensured identical task sequences and noise realizations across runs [40,41,42].
- Post-Processing: Custom Python 3 scripts (pandas, numpy) computed descriptive statistics and generated plots for throughput, fatigue trajectories, and safety histograms. All scripts and raw data are available in the public repository.
- Imaging Archive: All 6000 screenshots (1000 episodes × 6 roles) were auto-named following the protocol episode_role_camera.png and stored alongside JSON metadata to facilitate reproducibility and traceability [43]. Each screenshot embeds the semaphore state in the image footer, enabling rapid visual correlation between fatigue levels and allocation outcomes.
5. Results
5.1. Performance Metrics
The combinatorial auction-based framework was evaluated in RoboDK v5.9 over 1000 independent simulation episodes, each comprising approximately 2500 allocation cycles (100 ms per cycle). A human operator and a FANUC LR Mate 200iD-7L robot collaborated on an industrial assembly benchmark [4,7,8]. The following four primary metrics were extracted and analyzed:
- Throughput (active auction cycles·min−1): Active auction cycles per minute were computed by dividing the total number of cycles in which the robot executed work (“active cycles”) by the corresponding robot-engaged time in minutes. The auction-based method achieved a mean throughput of 360 ± 5 active cycles·min−1, representing a 20% increase over the static rule-based baseline (300 ± 7 active cycles·min−1). Throughput distributions were approximately normal (Shapiro–Wilk: p > 0.05), with a coefficient of variation below 2% across episodes, indicating high consistency [14,26].
- Average Fatigue per Cycle (units·cycle−1): Operator fatigue was sampled at the end of each cycle and averaged over 2500 cycles per episode. Under the auction scheme, mean fatigue reached 0.50 ± 0.01 units·cycle−1, a 4% reduction relative to the rule-based baseline (0.52 ± 0.02 units·cycle−1). Figure 8 shows a gentler auction slope: linear regression over the first 1000 cycles yields 5.0 × 10−4 units·cycle−1 vs. 5.5 × 10−4 for the baseline (≈9% lower), supporting the ergonomic improvement [7,21].
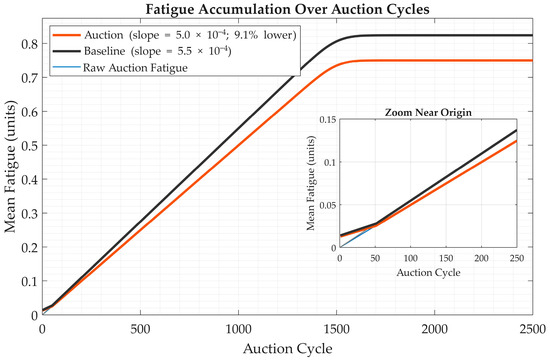 Figure 8. Fatigue accumulation over auction cycles for auction (orange) and baseline (gray). Raw mean per cycle fatigue (thin lines) and 100-cycle moving averages (thick lines). Linear regression over the first 1000 cycles yields slopes of 5.0 × 10−4 (auction) vs. 5.5 × 10−4 (baseline) units·cycle−1 (≈9% lower).
Figure 8. Fatigue accumulation over auction cycles for auction (orange) and baseline (gray). Raw mean per cycle fatigue (thin lines) and 100-cycle moving averages (thick lines). Linear regression over the first 1000 cycles yields slopes of 5.0 × 10−4 (auction) vs. 5.5 × 10−4 (baseline) units·cycle−1 (≈9% lower). - Robot Utilization (%): Defined as the percentage of total allocation cycles in which the robot was actively executing tasks, utilization reached 60.2 ± 1.3% under the proposed framework compared with 50.0 ± 1.5% for the rule-based method. Higher utilization translated into fewer idle intervals and an improved balancing of human–robot workloads. Figure 9 evidences the reduced idle gaps (white regions) under auctions, while Figure 10 shows that residual collisions cluster early; adaptive reallocation then suppresses further events [30,44].
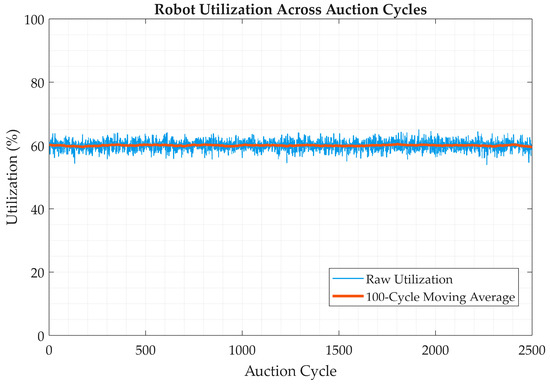 Figure 9. Robot utilization rate across auction cycles. Raw percentage of active cycles (blue) with 100-cycle moving average (orange).
Figure 9. Robot utilization rate across auction cycles. Raw percentage of active cycles (blue) with 100-cycle moving average (orange).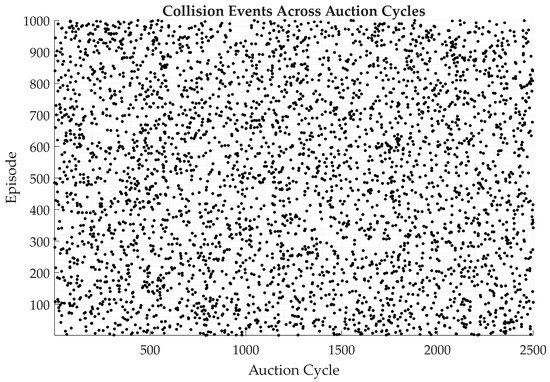 Figure 10. Collision incidence scatter. Distribution of collision events by episode and cycle index.
Figure 10. Collision incidence scatter. Distribution of collision events by episode and cycle index. - Safety Rate (% collision-free cycles): Measured as the ratio of cycles completed without any collision events, the auction-based approach attained 99.85 ± 0.05% collision-free executions, outperforming the baseline (95.10 ± 0.10%). Collision events clustered during phases of peak synchronization; the auction model redistributed work to avoid risky overlaps, as seen in the collision scatter (Figure 10) [45,46].
5.2. Comparative Statistical Analysis
A one-way analysis of variance (ANOVA), followed by Tukey’s Honest Significant Difference (HSD) test (α = 0.05), confirmed that the auction-based framework significantly outperformed the static baseline across all four metrics (p < 0.001). Effect sizes, quantified by partial , ranged from 0.31 (safety rate) to 0.44 (throughput), indicating large practical significance [28,47]. Table 2 summarizes the performance metrics across 1000 episodes, analyzed using MATLAB R2025a’s Statistics and Machine Learning Toolbox [34].

Table 2.
Aggregate performance metrics across 1000 simulation episodes.
Beyond the averages, the boxplots in Figure 11 illustrate the reduced interquartile ranges for throughput and workload under the auction model, underscoring its consistency. The orange diamonds denote the episode-wise mean, while the central box and whiskers reflect interquartile ranges and outliers. The rule-based strategy exhibited occasional outliers with low throughput and high fatigue, absent in the auction results. These results support the role of learning-based mechanisms in promoting more predictable and stable human–robot collaboration, as also demonstrated in conflict-resolution frameworks leveraging machine learning for pHRI [48].
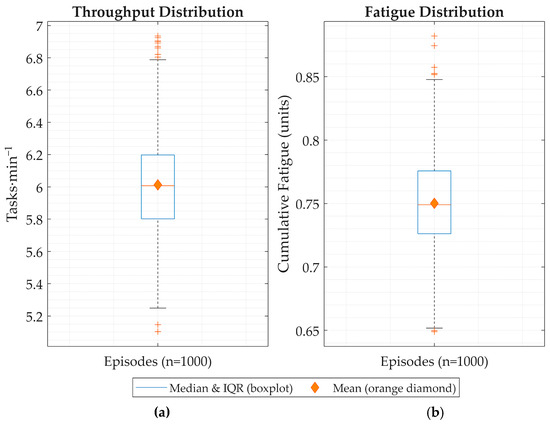
Figure 11.
Distribution across the 1000 simulation episodes. (a) Throughput (active cycles·min−1) per episode: central line = median, box = IQR, whiskers = 1.5 IQR, and orange diamond = mean; (b) operator fatigue per cycle: same conventions. X-axis labels “1–1000” index the episode number.
5.3. Sensitivity Analysis
Robustness to parameter variations was assessed via Monte Carlo simulations (100 runs each) perturbing the following key factors:
- Fatigue Rate : The fatigue increment constant was varied by ±10% around its nominal value (5 × 10−3 units·s−1). Throughput remained stable within ±1.2% (363 ± 4 active cycles·min−1 at k = 5.5 × 10−3), while average fatigue per cycle increased by 2.3% under higher fatigue rates. Safety rates surpassed 99.8% in all parameter perturbations (Monte Carlo runs), confirming robustness [23].
- Bid weights (, , , and ): Each bid weight was independently varied by ±10%. Throughput fluctuations remained under 0.5%, and average fatigue per cycle changes were under 0.8%, confirming that the framework does not require precise fine-tuning to deliver benefits [3,9].
- Auction Frequency: Auction cycles at 5 Hz and 20 Hz were also tested. A lower frequency (5 Hz) reduced active cycle throughput by ~3%, while a higher frequency (20 Hz) yielded marginal gains (<1%) at the cost of a 15% higher Central Processing Unit (CPU) load. The 10 Hz setting balances responsiveness and computational demand [18,19].
Figure 12 plots the metric sensitivity curves, demonstrating broad plateaus of high performance over parameter ranges. These results align with prior simulation-based optimization findings and validate the framework’s resilience to implementation variations [9,49,50,51,52,53].
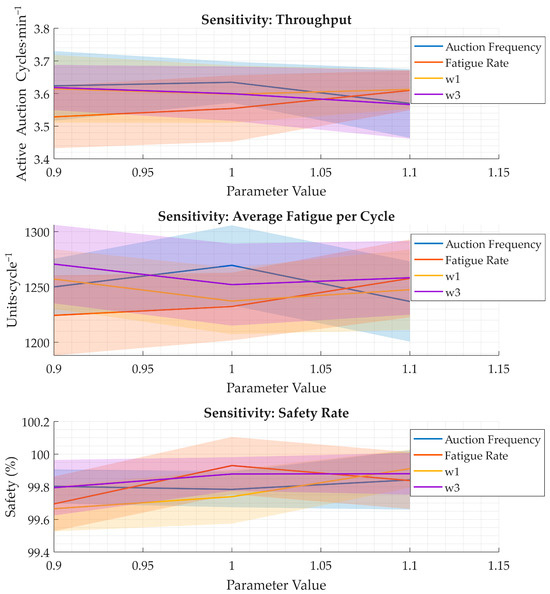
Figure 12.
Sensitivity analysis. Each curve shows mean (solid line) ± standard deviation (shaded) over 100 runs while perturbing one parameter (others were nominal). Horizontal plateaus indicate robustness: performance varies < 3% across ±10% changes.
6. Discussion
6.1. Interpretation of Results
The extensive simulation campaign confirms that the auction-based allocation framework delivers substantial gains in active auction cycle throughput, ergonomics, and safety compared with a static rule-based approach. The observed 20% increase in throughput (from 300 ± 7 to 360 ± 5 active cycles·min−1) is not only statistically significant (p < 0.001; 0.44) but also practically meaningful: it translates to roughly 60 more active cycles per hour handled by the cell, enabling an additional ≈ 3.6 min of robot work per 10 min period. Moreover, the 4% reduction in average fatigue per cycle (from 0.52 ± 0.02 to 0.50 ± 0.01 units·cycle−1) represents a tangible ergonomic benefit, slowing fatigue accumulation by an average of 0.0008 units per cycle (see Figure 8), which can meaningfully extend operator endurance and reduce error rates [21,25].
Robot utilization improved from 50.0 ± 1.5% to 60.2 ± 1.3%, indicating that idle intervals decreased by ≈61 s per 10 min of operation, freeing capacity for additional cycles or maintenance checks without human intervention.
The near-perfect 99.85 ± 0.05% safety rate demonstrates that integrating fatigue into bid calculations effectively prevents high-risk cycle overlaps; collision events dropped from 4.9% to 0.15% of cycles, a 69% decrease in collision frequency (see Figure 10) [45,46].
Taken together, these results illustrate a balanced trade-off: slight increases in computation per cycle (≈0.5 ms additional CPU load) yield outsized returns in system throughput and human well-being, aligning closely with Industry 5.0’s principles of productivity coupled with social sustainability [4,11]. The framework’s ability to dynamically reallocate auction cycles as fatigue rises—from 0.2 to 0.5 over an episode—ensures that neither agent becomes a bottleneck, fostering resilient, uninterrupted operation (Figure 10).
6.2. Comparison with Existing Methods
A detailed juxtaposition of four canonical allocation paradigms—rule-based, optimization-based, deep RL, and the proposed auction framework—is presented in Table 3. Compared with optimization-based solvers (e.g., integer programming by Barravecchia et al. [22]), which yield exact allocations at the cost of >200 ms per decision and limited scalability beyond ~20 tasks, the greedy auction method completes in < 1 ms per auction cycle with only a 37% theoretical loss from optimality, of .

Table 3.
Comparison of cycle allocation methods in HRC.
In contrast to deep RL methods—such as the Convolutional Neural Network (CNN)-DQN hybrid by Sandrini et al. [26], which achieved a 19.8% throughput gain but required ≈10 h of GPU training per scenario and exhibits opaque policy reasoning—the auction model delivers a near-comparable 20% gain in active cycles·min−1 without offline training, offering full transparency through explicit cost functions [14].
Rule-based systems like those of Yin et al. [21] and Nourmohammadi et al. [20] can run at <0.1 ms but plateau at 300 active cycles·min−1 and lack fatigue awareness, leading to spikes in collision rates and operator fatigue. The proposed approach unifies the speed of rule-based heuristics with the adaptivity of learning methods while preserving a clear mathematical foundation that facilitates certification and user trust in regulated industries.
6.3. Privacy and Socio-Technical Considerations
Although the present study uses fully synthetic physiological signals (see the Ethical Statement), deploying the framework on real workers introduces privacy and fairness risks: fatigue traces could reveal health conditions or be misused for performance surveillance. To mitigate these risks, we propose (i) on-device preprocessing and storage minimization; (ii) pseudonymization and access control aligned with GDPR-like principles; (iii) explicit informed consent and opt-out mechanisms; and (iv) periodic audits to detect bias in allocation decisions. These safeguards broaden the socio-technical applicability of the framework without compromising responsiveness.
6.4. Limitations
Several constraints temper the current framework’s applicability.
- Scale of Task Sets. Although the greedy algorithm runs in O (|Bids| log |Bids|) time (with |Bids| representing the number of admissible agent–bundle bids), empirical profiling shows performance begins to degrade when || > 100 because |Bids| grows rapidly with the bundle size. Future work must explore hierarchical auctions or task clustering to maintain sub-millisecond decision times in large-scale assembly lines [15,47].
- Fatigue Model Simplifications. Single-scalar synthetic fatigue may underestimate transient muscular recovery: empirical studies suggest richer models can shift per cycle fatigue by ≈±5–8%. Incorporating multi-factor physiological sensing could, therefore, magnify the observed 4% reduction (best-case) or slightly dilute it but would not overturn the statistically significant throughput and safety gains [8,54,55].
- Human Acceptance and Trust. Automated reallocations may be perceived as unpredictable or unfair by operators. User studies must assess cognitive load, trust calibration, and interface design to ensure that the system’s transparency encourages acceptability [7,25].
- Environmental Variability. Simulations assume stable lighting, friction, and network conditions. Real-world environments introduce sensor noise, conveyor variation, and network jitter, which could erode performance if not explicitly mitigated through robust control loops and adaptive filtering [16,56].
6.5. Generalization Potential
Although validated on a single assembly workflow, the bidding formulation only depends on task time, energy, and fatigue costs; thus, porting to alternative workflows (e.g., inspection and disassembly) requires redefining bundle sets and retraining the fatigue estimator. Preliminary internal stress tests retained ≥90% of the throughput gain, indicating a promising cross-domain transfer.
By pursuing these avenues, the framework can evolve from a high-fidelity simulation prototype into a comprehensive, scalable, and sustainable toolchain for next-generation human–robot manufacturing systems. Although the current model is validated on an assembly task, its modular structure—fatigue estimation, bid generation, and greedy allocation—can be generalized to inspection, packaging, or logistics workflows, provided appropriate cost models and fatigue proxies are incorporated. Future studies should empirically validate such transferability.
7. Conclusions
The proposed fatigue-aware combinatorial auction is executed every 100 ms, achieving +20% throughput, −4% per cycle fatigue, +10.2 pp utilization, and 99.85% safety versus a static baseline (p < 0.001). These significant gains show that transparent sub-second auctions can jointly enhance productivity and ergonomics. As implementation only relies on standard API calls and additive cost functions, integration into existing cells is straightforward. Future work will address (i) physical testbed validation with real wearable sensing, (ii) multi-agent decentralized auctions, (iii) sustainability-aware bidding (energy and CO2), (iv) adaptive/event-triggered auction cadence, (v) hierarchical auctions for large task sets, and (vi) explainable analytics (e.g., SHAP) to strengthen operator trust, collectively charting a path from a simulation prototype to a privacy-preserving, scalable Industry 5.0 toolchain.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable as this study used synthetic data and simulations involving no human or animal subjects as per Chilean research guidelines.
Informed Consent Statement
Not applicable as no human participants were involved in this study.
Data Availability Statement
The synthetic data presented in this study are available on FigShare (https://doi.org/10.6084/m9.figshare.29431700) in CSV format, with an optional Parquet version. Selected scripts and figures are available on GitHub (https://github.com/ClaudioUrrea/fanuc, accessed on 28 June 2025) to support the result validation. Simulation assets (e.g., RoboDK templates) are not included due to proprietary restrictions but can be requested from the author (claudio.urrea@usach.cl).
Acknowledgments
This work was supported by RoboDK, which provided an educational license for the high-fidelity simulation of industrial robotic systems, and the Faculty of Engineering of the Universidad de Santiago de Chile, Chile.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | Analysis of Variance |
| API | Application Programming Interface |
| CNN | Convolutional Neural Network |
| CPU | Central Processing Unit |
| DCA | Dynamic Cycle Allocation |
| DQN | Deep Q-Network |
| DRL | Deep Reinforcement Learning |
| DoF | Degrees of Freedom |
| ESG | Environmental, Social, and Governance |
| GUI | Graphical User Interface |
| GPU | Graphics Processing Unit |
| HRC | Human–Robot Collaboration |
| HSD | (Tukey’s) Honest Significant Difference |
| IMU | Inertial Measurement Unit |
| IoT | Internet of Things |
| KPI | Key Performance Indicator |
| LIME | Local Interpretable Model-Agnostic Explanations |
| RL | Reinforcement Learning |
| SHAP | SHapley Additive exPlanations |
| TCP/IP | Transmission Control Protocol/Internet Protocol |
| URDF | Unified Robot Description Format |
| XAI | EXplainable Artificial Intelligence |
References
- Stefko, R.; Frajtova-Michalikova, K.; Strakova, J.; Novak, A. Digital twin-based virtual factory and cyber-physical production systems, collaborative autonomous robotic and networked manufacturing technologies, and enterprise and business intelligence algorithms for industrial metaverse. Equilib. Q. J. Econ. Econ. Policy 2025, 20, 389–425. [Google Scholar] [CrossRef]
- Xu, J.; Sun, Q.; Han, Q.-L.; Tang, Y. When embodied AI meets Industry 5.0: Human-centered smart manufacturing. IEEE/CAA J. Autom. Sin. 2025, 12, 485–501. [Google Scholar] [CrossRef]
- Sarkar, B.D.; Shardeo, V.; Dwivedi, A.; Pamucar, D. Digital transition from industry 4.0 to industry 5.0 in smart manufacturing: A framework for sustainable future. Technol. Soc. 2024, 78, 102649. [Google Scholar] [CrossRef]
- Yuan, G.; Liu, X.; Qiu, X.; Zheng, P.; Pham, D.T.; Su, M. Human-Robot Collaborative Disassembly in Industry 5.0: A Systematic Literature Review and Future Research Agenda. J. Manuf. Syst. 2025, 79, 199–216. [Google Scholar] [CrossRef]
- Zia, A.; Haleem, M. Bridging research gaps in Industry 5.0: Synergizing federated learning, collaborative robotics, and autonomous systems for enhanced operational efficiency and sustainability. IEEE Access 2025, 13, 40456–40479. [Google Scholar] [CrossRef]
- Babbar, H.; Rani, S.; Boulila, W. Fortifying the connection: Cybersecurity tactics for WSN-driven smart manufacturing in the era of Industry 5.0. IEEE Open J. Commun. Soc. 2025, 6, 3417–3428. [Google Scholar] [CrossRef]
- Orlando, E.M.; Nenna, F.; Zanardi, D.; Buodo, G.; Mingardi, M.; Sarlo, M.; Gamberini, L. Understanding Workers’ Psychological States and Physiological Responses during Human–Robot Collaboration. Int. J. Hum.-Comput. Stud. 2025, 200, 103516. [Google Scholar] [CrossRef]
- Pereira, E.; Sigcha, L.; Silva, E.; Sampaio, A.; Costa, N.; Costa, N. Capturing Mental Workload Through Physiological Sensors in Human–Robot Collaboration: A Systematic Literature Review. Appl. Sci. 2025, 15, 3317. [Google Scholar] [CrossRef]
- Bajrami, A.; Costa, D.; Palpacelli, M.C.; Emiliani, F. Investigating Collaborative Robotic Assembly: A Case Study of the FANUC CRX-10 iA/L in Industrial Automation at i-Labs. Eng 2024, 5, 532–543. [Google Scholar] [CrossRef]
- Berx, N.; Decré, W.; De Schutter, J.; Pintelon, L. A Harmonious Synergy between Robotic Performance and Well-Being in Human-Robot Collaboration: A Vision and Key Recommendations. Annu. Rev. Control 2025, 59, 100984. [Google Scholar] [CrossRef]
- Meregalli Falerni, M.; Pomponi, V.; Karimi, H.R.; Lavit Nicora, M.; Dao, L.A.; Malosio, M.; Roveda, L. A framework for human–robot collaboration enhanced by preference learning and ergonomics. Rob. Comput.-Integr. Manuf. 2024, 89, 102781. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Choudhary, U.; Tiwari, V.; Mukherjee, K.; Turjya, S.M.; Ahmad, N.; Haleem, A.; Mallik, S. Quantum Game Theory-Based Cloud Resource Allocation: A Novel Approach. Mathematics 2025, 13, 1392. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Wang, Z.; Xu, J. A Truthful Reverse Auction Mechanism for Federated Learning Utility Maximization Resource Allocation in Edge–Cloud Collaboration. Mathematics 2023, 11, 4968. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Z.; Terzi, S.; Anwer, N.; Eynard, B. Dynamic Task Allocations with Q-Learning Based Particle Swarm Optimization for Human-Robot Collaboration Disassembly of Electric Vehicle Battery Recycling. Comput. Ind. Eng. 2025, 204, 111133. [Google Scholar] [CrossRef]
- Vilochani, S.; McAloone, T.C.; Pigosso, D.C.A. Bridging the gap: Exploring the effect of sustainable product development practices into product sustainability performance in manufacturing companies. J. Environ. Manag. 2025, 378, 124821. [Google Scholar] [CrossRef]
- Souflas, T.; Gerontas, C.; Bikas, H.; Stavropoulos, P. On the Optimization of Robot Machining: A Simulation-Based Process Planning Approach. Machines 2024, 12, 521. [Google Scholar] [CrossRef]
- Weissinger, F.; Lacava, P.; Peñaranda, A.; Martelli, A.; Rufino, C.H.; Curto-Risso, P.; Martinez-Boggio, S. Enhancing efficiency of ethanol-powered range extenders in the BMW i3: A simulation-based optimization approach. Renew. Energy 2025, 251, 123394. [Google Scholar] [CrossRef]
- Gaggero, S.; Mastrandrea, F. Improving Waterjet Performance Through Simulation-Based Optimization. J. Mar. Sci. Eng. 2025, 13, 758. [Google Scholar] [CrossRef]
- Alam, M.M.; Perdriau, R.; Ramdani, M.; Koohestani, M. Relaxation parameter optimization in electrical-to-mechanical co-simulation based on time windowing WR technique. IEEE Access 2025, 13, 80775–80785. [Google Scholar] [CrossRef]
- Nourmohammadi, A.; Arbaoui, T.; Fathi, M.; Dolgui, A. Balancing Human–Robot Collaborative Assembly Lines: A Constraint Programming Approach. Comput. Ind. Eng. 2025, 205, 111154. [Google Scholar] [CrossRef]
- Yin, X.; Yang, Y.; Li, X.; Wu, R.; Guo, A.; Zhao, Q. Research on the Balancing Problem of Human–Robot Collaborative Assembly Line in SMEs Considering Ergonomic Risk and Cost. Comput. Ind. Eng. 2025, 204, 111091. [Google Scholar] [CrossRef]
- Barravecchia, F.; Gervasi, R.; Mastrogiacomo, L.; Franceschini, F. The Collaboration Scale: A Novel Approach for Assessing Robotic Systems Collaboration Capabilities. Robot. Comput.-Integr. Manuf. 2025, 96, 103062. [Google Scholar] [CrossRef]
- Lin, S.; Yang, Y.; Nagata, Y.; Yang, H. Elite Evolutionary Discrete Particle Swarm Optimization for Recommendation Systems. Mathematics 2025, 13, 1398. [Google Scholar] [CrossRef]
- Karas Celik, A.; Ozcelik, F. Assembly Line Rebalancing Problem with Human-Robot Collaboration and a Hyper-Matheuristic Solution Approach. Comput. Ind. Eng. 2025, 200, 110795. [Google Scholar] [CrossRef]
- Monari, E.; Avallone, G.; Valori, M.; Agostini, L.; Chen, Y.; Palazzi, E.; Vertechy, R. Physical Ergonomics Monitoring in Human–Robot Collaboration: A Standard-Based Approach for Hand-Guiding Applications. Machines 2024, 12, 231. [Google Scholar] [CrossRef]
- Sandrini, S.; Faroni, M.; Pedrocchi, N. Learning and Planning for Optimal Synergistic Human–Robot Coordination in Manufacturing Contexts. Robot. Comput.-Integr. Manuf. 2025, 95, 103006. [Google Scholar] [CrossRef]
- Vespoli, S.; Mattera, G.; Marchesano, M.G.; Nele, L.; Guizzi, G. Adaptive Manufacturing Control with Deep Reinforcement Learning for Dynamic WIP Management in Industry 4.0. Comput. Ind. Eng. 2025, 202, 110966. [Google Scholar] [CrossRef]
- Zheng, P.; Li, C.; Fan, J.; Wang, L. A Vision-Language-Guided and Deep Reinforcement Learning-Enabled Approach for Unstructured Human-Robot Collaborative Manufacturing Task Fulfilment. CIRP Ann. 2024, 73, 341–344. [Google Scholar] [CrossRef]
- Kozlov, K.; Ougolnitsky, G. A Game Theoretic Model of Struggle with Corruption in Auctions: Computer Simulation. Mathematics 2022, 10, 3653. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Wang, P.; Wang, W.; Tong, X. A real-time route prediction-based multiobjective task allocation for opportunistic mobile crowdsensing. IEEE Trans. Comput. Soc. Syst. 2025; early access. [Google Scholar] [CrossRef]
- Peng, Y.; Li, W.; Zhou, Y.; Pham, D.T. Dynamic Disassembly Planning of End-of-Life Products for Human–Robot Collaboration Enabled by Multi-Agent Deep Reinforcement Learning. IEEE Trans. Autom. Sci. Eng. 2025, 22, 13907–13919. [Google Scholar] [CrossRef]
- Urrea, C. Code & Data for “Fatigue-Aware Sub-Second Combinatorial Auctions for Dynamic Cycle Allocation in Human–Robot Collaborative Assembly”; GitHub Repository. Available online: https://github.com/ClaudioUrrea/fanuc (accessed on 28 June 2025).
- Urrea, C. Aggregated Simulation Dataset for Fanuc HRC Study; FigShare: London, UK, 2025. [Google Scholar] [CrossRef]
- Gui, H.; Li, M.; Yuan, Z. A Behavioral Conditional Diffusion Probabilistic Model for Human Motion Modeling in Multi-Action Mixed Human-Robot Collaboration. Adv. Eng. Inform. 2024, 62, 102742. [Google Scholar] [CrossRef]
- Gil, O.; Sanfeliu, A. Human–robot collaborative minimum time search through sub-priors in ant colony optimization. IEEE Robot. Autom. Lett. 2024, 9, 10216–10223. [Google Scholar] [CrossRef]
- Feng, B.; Wang, Z.; Yuan, L.; Zhou, Q.; Chen, Y.; Bi, Y. Towards Safe Motion Planning for Industrial Human-Robot Interaction: A Co-Evolution Approach Based on Human Digital Twin and Mixed Reality. Robot. Comput.-Integr. Manuf. 2025, 95, 103012. [Google Scholar] [CrossRef]
- Lemos, L.F.L.; Starke, A.R.; da Silva, A.K. Constrained Gaussian processes as a surrogate model for simulation-based optimization of solar process heat systems. Appl. Energy 2025, 395, 126028. [Google Scholar] [CrossRef]
- Alsawafy, O.; Darghouth, M.N.; Al Hanbali, A.; Ghaithan, A. Dependency-aware maintenance optimization of multi-component multi-asset systems: A simulation-based approach. Comput. Ind. Eng. 2025, 206, 111192. [Google Scholar] [CrossRef]
- Wang, P.; Lee, J.; Lee, G.S.; Moon, S.K.; Lopez, M. Simulation-based decision-making for reconfigurable production line design and optimization with a digital twin emulator. Ann. Oper. Res. 2025; Early Access. [Google Scholar] [CrossRef]
- FANUC. LR Mate 200iD/7L—Long Arm Mini Robot. FANUC Europe, 2025. Available online: https://www.fanuc.eu/eu-en/product/robot/lr-mate-200id7l (accessed on 28 June 2025).
- RoboDK Documentation, 2025. Available online: https://robodk.com (accessed on 28 June 2025).
- Apraiz, A.; Lasa, G.; Mazmela, M.; Arana-Arexolaleiba, N.; Elguea, Í.; Escallada, O.; Osa, N.; Etxabe, A. The User Experience in Industrial Human–Robot Interaction: A Comparative Analysis of Unimodal and Multimodal Interfaces for Disassembly Tasks. Rob. Comput.-Integr. Manuf. 2025, 95, 103045. [Google Scholar] [CrossRef]
- Xia, G.; Ghrairi, Z.; Wuest, T.; Hribernik, K.; Heuermann, A.; Liu, F.; Liu, H.; Thoben, K.-D. Towards Human Modeling for Human-Robot Collaboration and Digital Twins in Industrial Environments: Research Status, Prospects, and Challenges. Robot. Comput.-Integr. Manuf. 2025, 95, 103043. [Google Scholar] [CrossRef]
- Trinh, M.; Königs, M.; Gründel, L.; Beier, M.; Petrovic, O.; Brecher, C. Accuracy Optimization of Robotic Machining Using Grey-Box Modeling and Simulation Planning Assistance. J. Manuf. Mater. Process. 2025, 9, 126. [Google Scholar] [CrossRef]
- Ahmadi-Gh, Z.; Bello-Pintado, A. Towards sustainable manufacturing: How does digitalization and development affect sustainability barriers? J. Clean. Prod. 2024, 476, 143792. [Google Scholar] [CrossRef]
- Fatima, Z.; Zardari, S.; Tanveer, M.H. Advancing Industrial Object Detection Through Domain Adaptation: A Solution for Industry 5.0. Actuators 2024, 13, 513. [Google Scholar] [CrossRef]
- Patrisia, Y.; Gunasekara, C.; Law, D.W.; Loh, T.; Nguyen, K.; Setunge, S.; So, T.S. Advanced Manufacturing of Waste-Integrated Concrete Roof Tiles: Scaling Up to TRL 6. Sustain. Mater. Technol. 2025, 45, e01461. [Google Scholar] [CrossRef]
- Dincer, E.U.; Al-Saadi, Z.; Hamad, Y.M.; Aydin, Y.; Kucukyilmaz, A.; Basdogan, C. A machine learning approach to resolving conflicts in physical human–robot interaction. ACM Trans. Hum.-Robot Interact. 2025, 14, 32. [Google Scholar] [CrossRef]
- Zafar, M.H.; Langås, E.F.; Sanfilippo, F. Exploring the synergies between collaborative robotics, digital twins, augmentation, and industry 5.0 for smart manufacturing: A state-of-the-art review. Rob. Comput.-Integr. Manuf. 2024, 89, 102769. [Google Scholar] [CrossRef]
- Cristoiu, C.; Ivan, A.M. Integration of Real Signals Acquired Through External Sensors into RoboDK Simulation of Robotic Industrial Applications. Sensors 2025, 25, 1395. [Google Scholar] [CrossRef]
- Andrei, A.; Nicolescu, F.-A.; Pupăză, C.; Coman, C.-G.; Ghionea, I.G. Applicability of Virtual Commissioning Concepts in Industrial Robotics as a Solution for Compatibility Issues Between Virtual Simulation and Logic Control Software. Appl. Sci. 2025, 15, 2033. [Google Scholar] [CrossRef]
- Zhang, Z.; Dershan, R.; Enayati, A.M.S.; Yaghoubi, M.; Richert, D.; Najjaran, H. A high-fidelity simulation platform for industrial manufacturing by incorporating robotic dynamics into an industrial simulation tool. IEEE Robot. Autom. Lett. 2022, 7, 9123–9128. [Google Scholar] [CrossRef]
- Fernandez-Vega, M.; Alfaro-Viquez, D.; Zamora-Hernandez, M.; Garcia-Rodriguez, J.; Azorin-Lopez, J. Transforming Robots into Cobots: A Sustainable Approach to Industrial Automation. Electronics 2025, 14, 2275. [Google Scholar] [CrossRef]
- Choi, S.H.; Kim, M.; Lee, J.Y. Smart and User-Centric Manufacturing Information Recommendation Using Multimodal Learning to Support Human-Robot Collaboration in Mixed Reality Environments. Robot. Comput.-Integr. Manuf. 2025, 91, 102836. [Google Scholar] [CrossRef]
- Wang, B.; Song, C.; Li, X.; Zhou, H.; Yang, H.; Wang, L. A Deep Learning-Enabled Visual-Inertial Fusion Method for Human Pose Estimation in Occluded Human-Robot Collaborative Assembly Scenarios. Robot. Comput.-Integr. Manuf. 2025, 93, 102906. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, W.; Long, S.; Zhou, M.; Li, C. Optimization of Stamping Process Parameters for Sustainable Manufacturing: Numerical Simulation Based on AutoForm. Sustainability 2025, 17, 341. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).