Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects
Abstract
1. Introduction
2. Dataset of Rough Surfaces
3. Methodology
3.1. Calculation of Entropy-Based Complexity
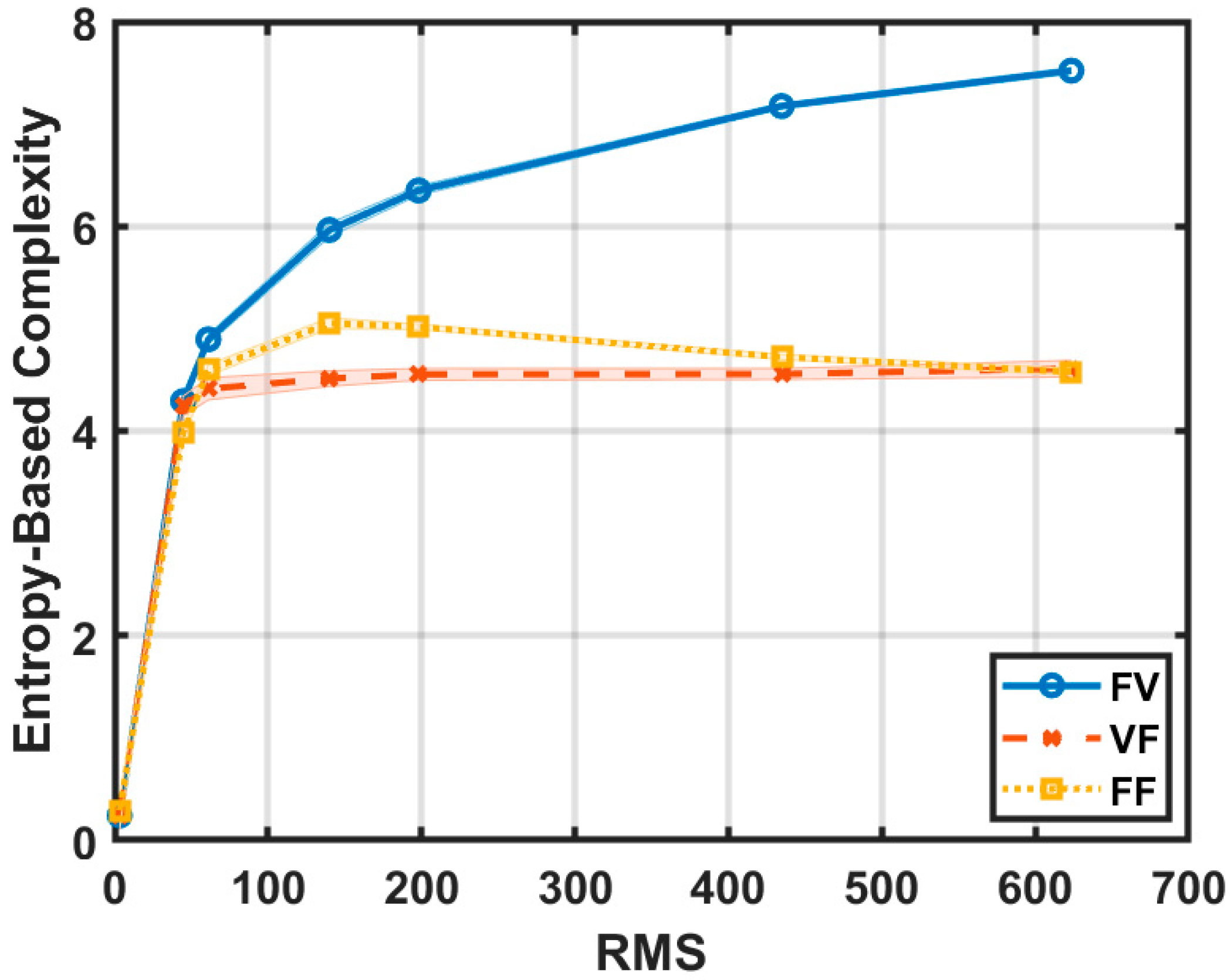
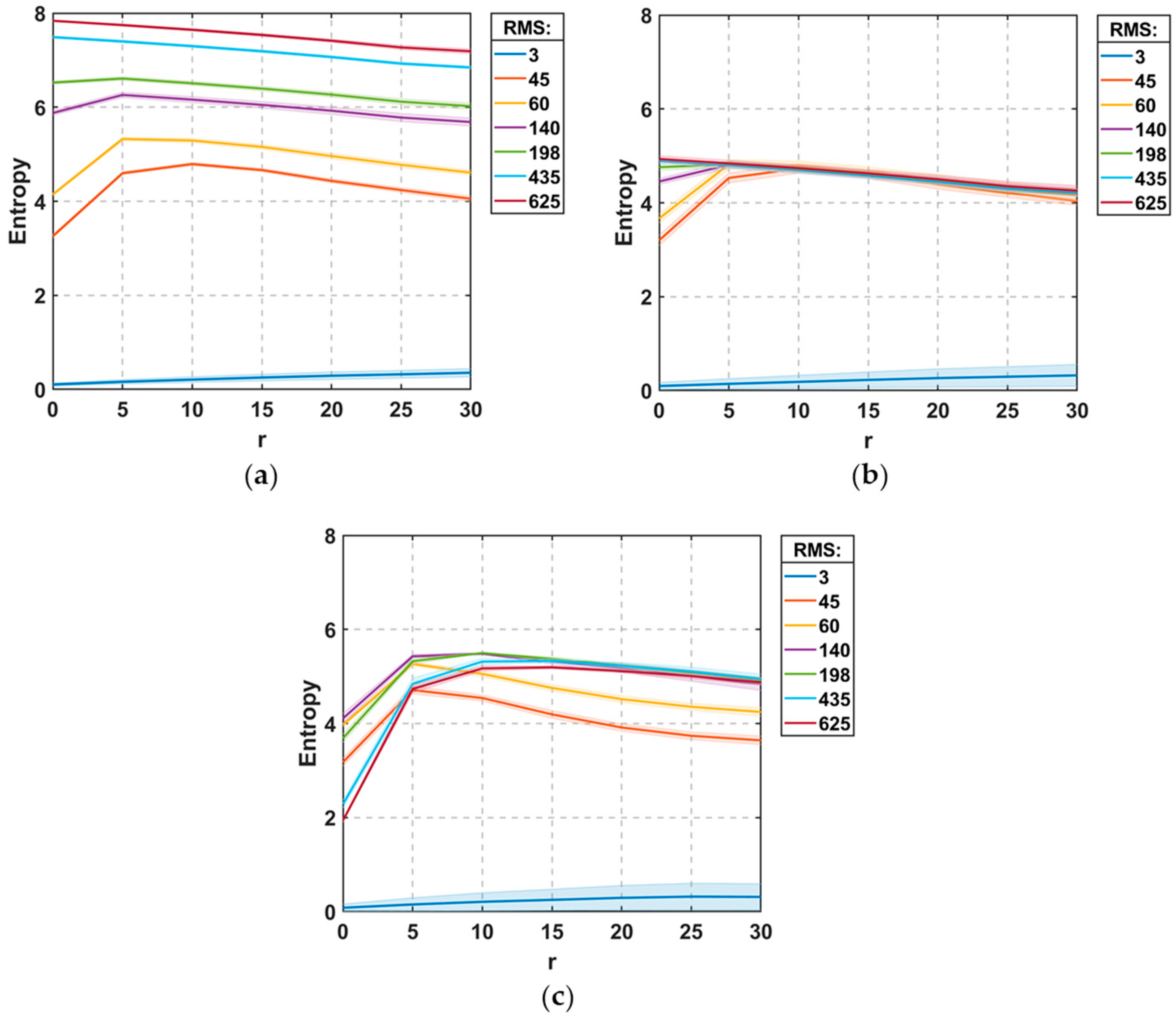
3.2. Binning Schemes
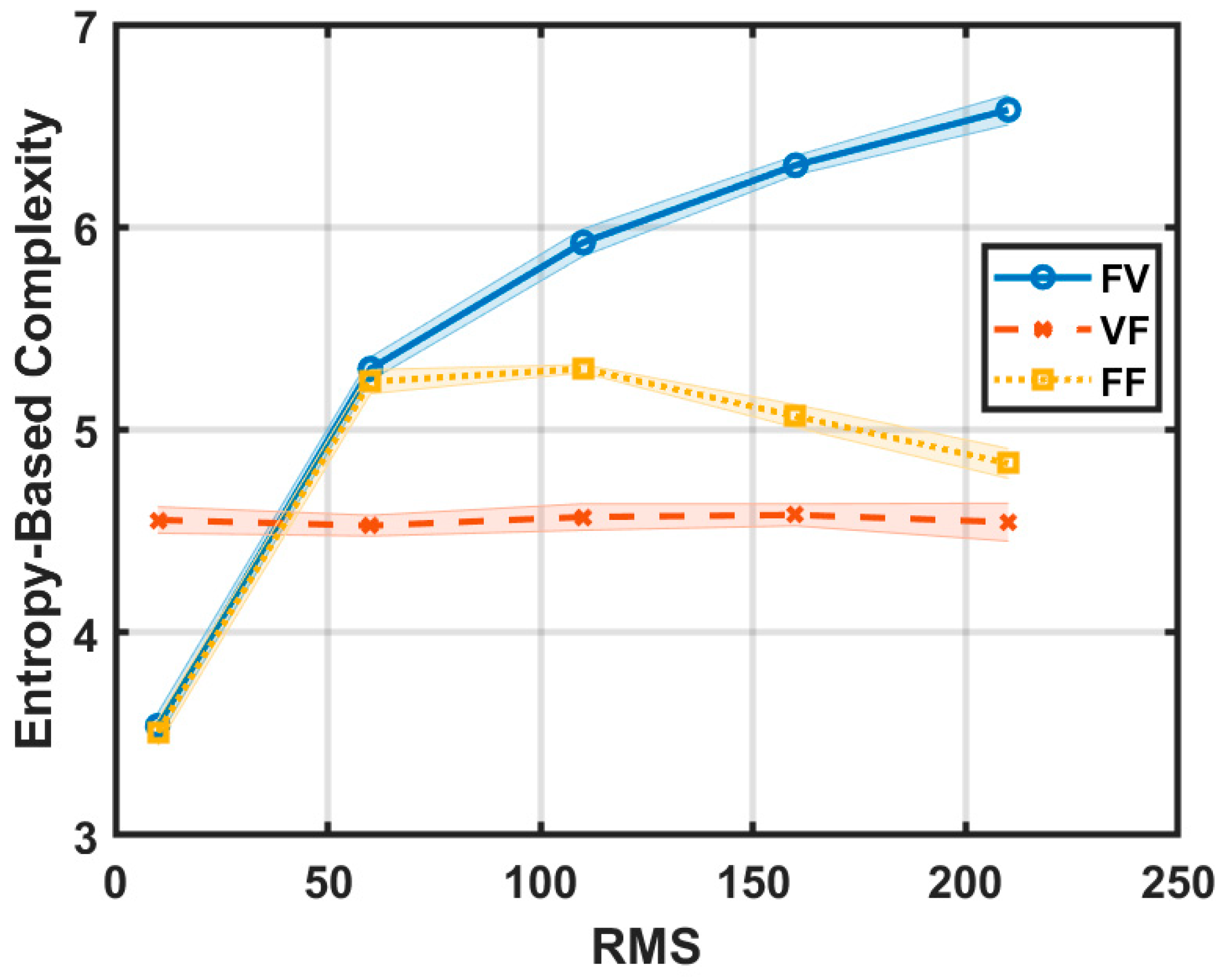
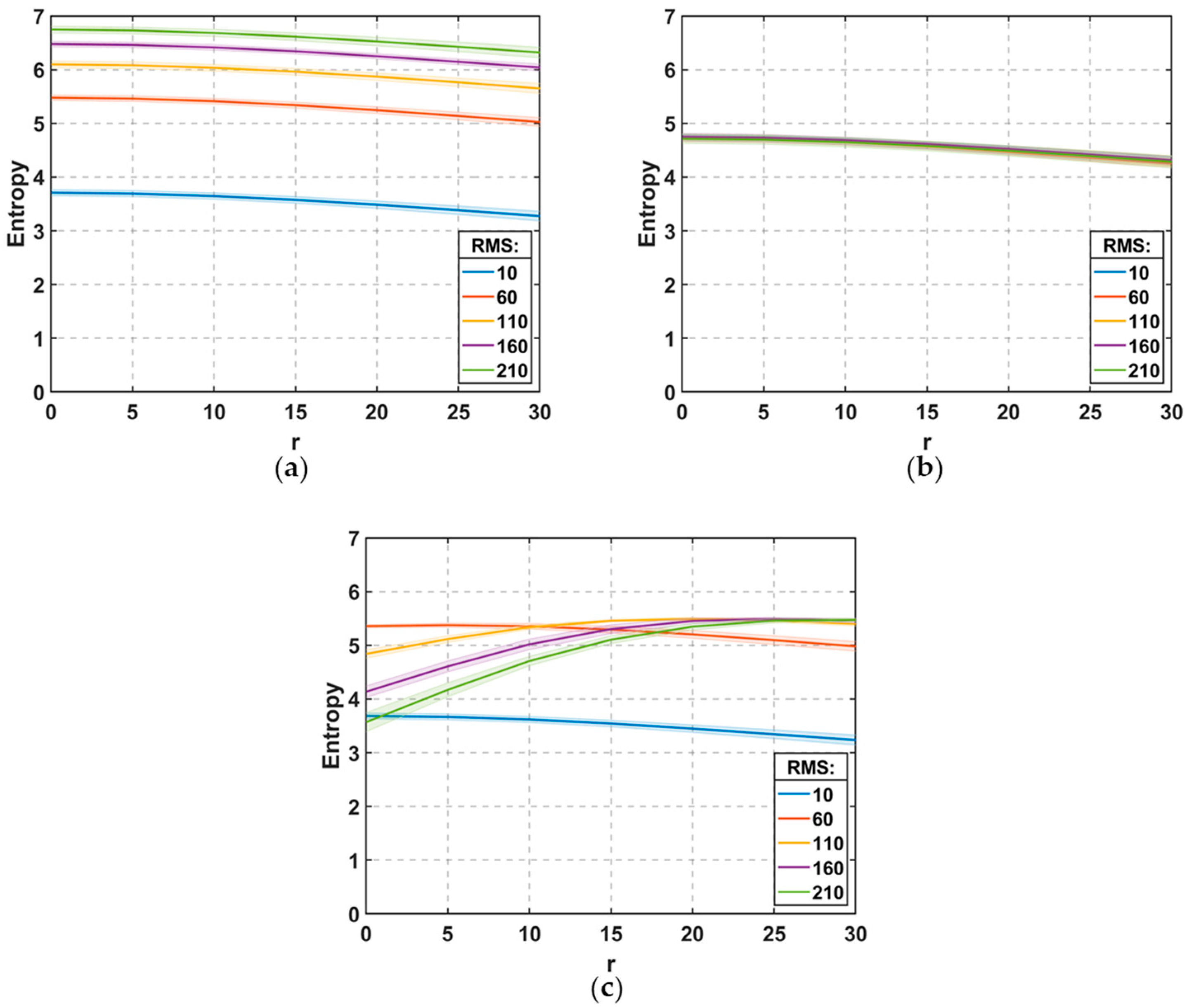
4. Results and Discussion
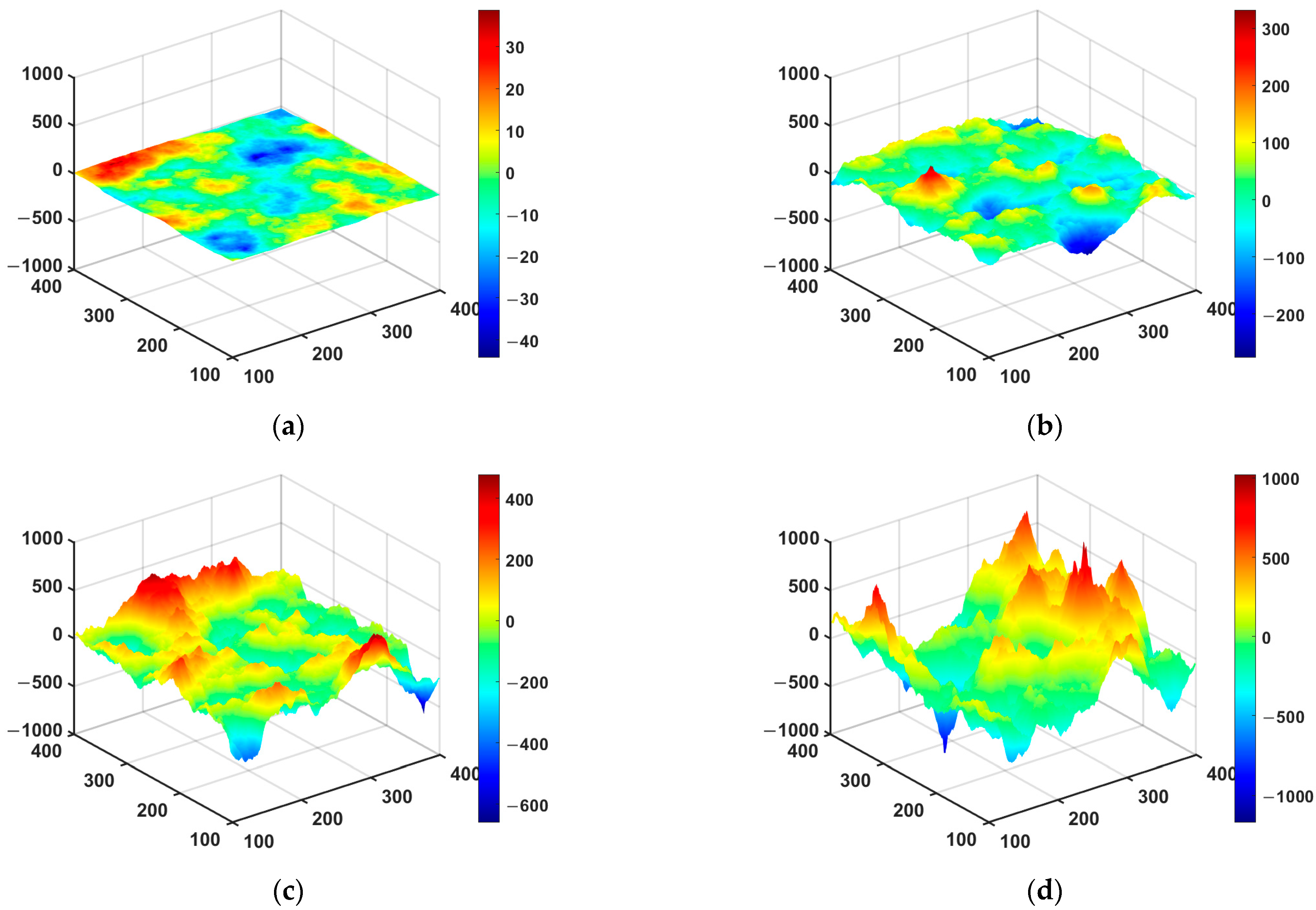
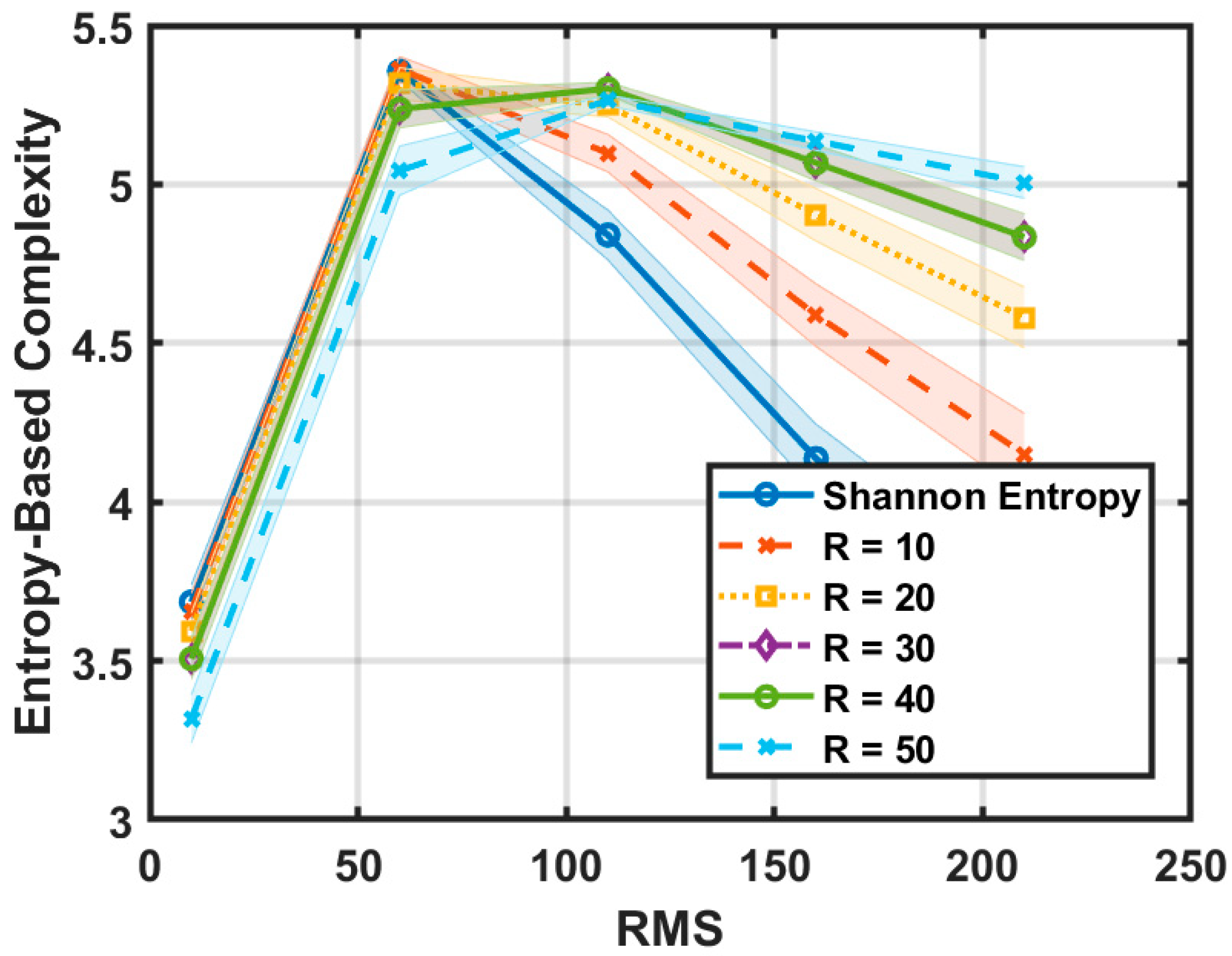
4.1. Self-Affine Surfaces
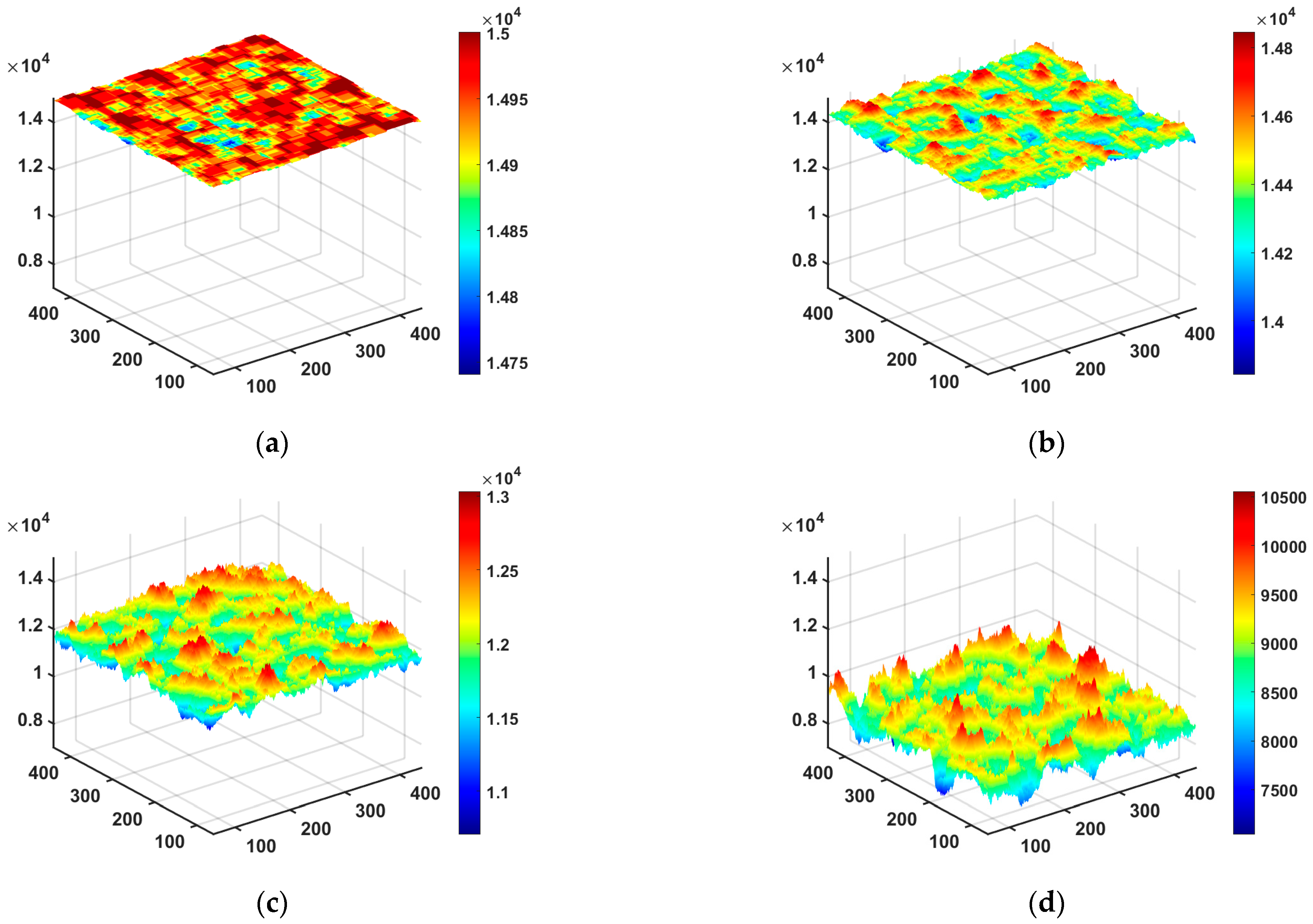
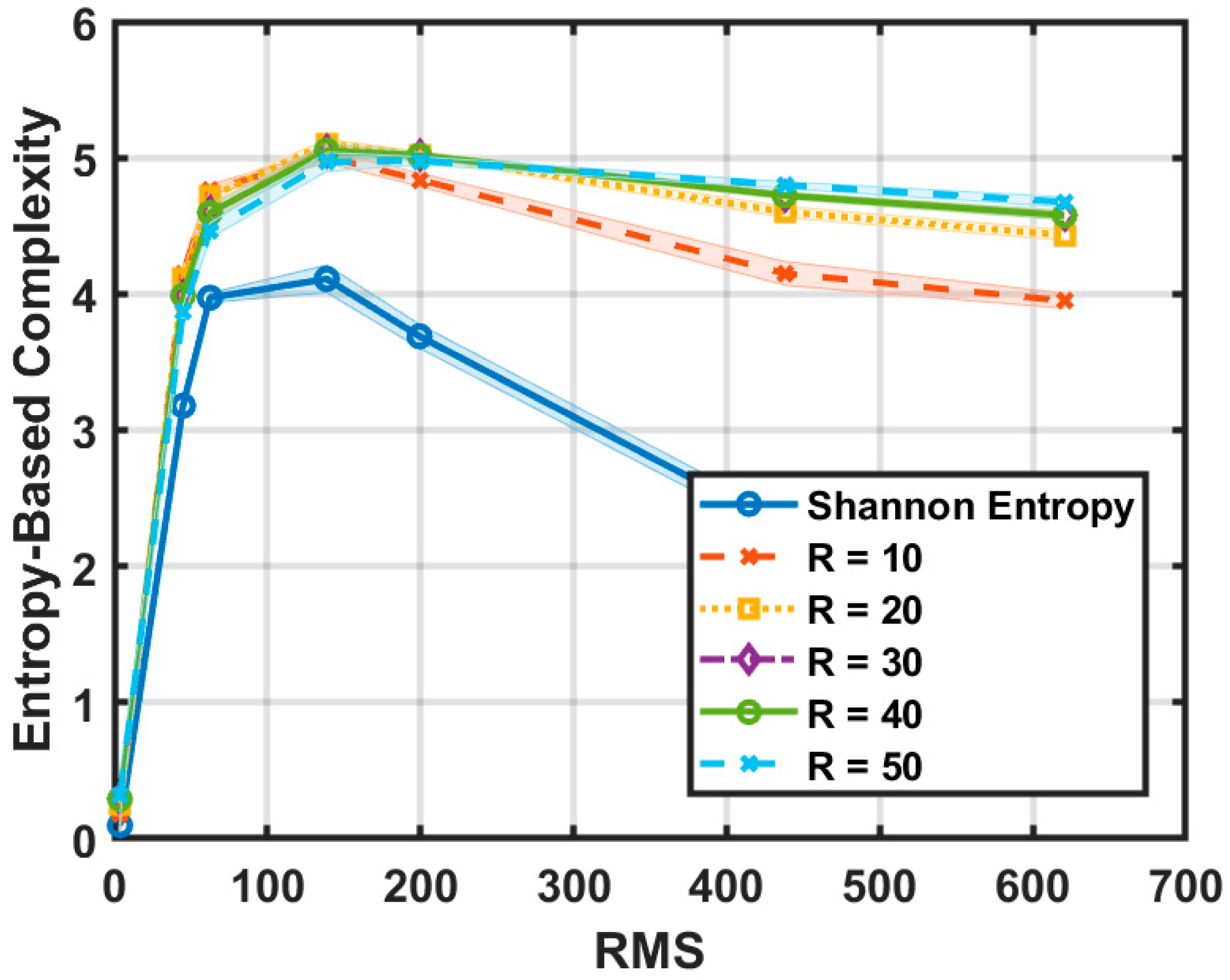
4.2. Stepwise Surfaces
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RMS | Root Mean Square |
| SEM | Scanning Electron Microscopy |
| FV | Fixed–Variable |
| VF | Variable–Fixed |
| FF | Fixed–Fixed |
| r | Neighborhood radius |
| R | Maximum scale used for entropy averaging |
| E(r) | Shannon entropy at neighborhood radius r |
| Cen(R) | Entropy-based spatial complexity averaged over all scales |
| ACF | Autocorrelation Function |
| FFT | Fast Fourier Transform |
| SW | Stepwise |
| SA | Self-affine |
References
- Zhao, Y.; Wang, G.C.; Lu, T.M. Characterization of Amorphous and Crystalline Rough Surface—Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2000; Volume 37. [Google Scholar]
- Almqvist, A. On the Effects of Surface Roughness in Lubrication; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2009. [Google Scholar]
- Vander Voort, G.F. Metallography, Principles and Practice; ASM International: Materials Park, OH, USA, 1999. [Google Scholar]
- Zhou, W.; Apkarian, R.; Wang, Z.L.; Joy, D. Fundamentals of scanning electron microscopy (SEM). In Scanning Microscopy for Nanotechnology: Techniques and Applications; Springer: New York, NY, USA, 2007; pp. 1–40. [Google Scholar]
- Vernon-Parry, K.D. Scanning electron microscopy: An introduction. III-Vs Rev. 2000, 13, 40–44. [Google Scholar] [CrossRef]
- Barabási, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Sarkar, N.; Chaudhuri, B.B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef]
- Florindo, J.B.; Sikora, M.S.; Pereira, E.C.; Bruno, O.M. Characterization of nanostructured material images using fractal descriptors. Phys. A Stat. Mech. Its Appl. 2013, 392, 1694–1701. [Google Scholar] [CrossRef]
- Liu, Y.U.; Chen, L.; Wang, H.; Jiang, L.; Zhang, Y.; Zhao, J.; Wang, D.; Zhao, Y.; Song, Y. An improved differential box-counting method to estimate fractal dimensions of gray-level images. J. Vis. Commun. Image Represent. 2014, 25, 1102–1111. [Google Scholar] [CrossRef]
- Kondi, A.; Papia, E.M.; Stai, E.; Constantoudis, V. Computational methods in nanometrology: The challenges of resolution and stochasticity. Front. Nanotechnol. 2025, 7, 1559523. [Google Scholar] [CrossRef]
- Kondi, A.; Constantoudis, V.; Sarkiris, P.; Ellinas, K.; Gogolides, E. Using chaotic dynamics to characterize the complexity of rough surfaces. Phys. Rev. E 2023, 107, 014206. [Google Scholar] [CrossRef] [PubMed]
- Arapis, A.; Constantoudis, V.; Kontziampasis, D.; Milionis, A.; Lam, C.W.E.; Tripathy, A.; Poulikakos, D.; Gogolides, E. Measuring the complexity of micro and nanostructured surfaces. Mater. Today Proc. 2022, 54, 63–72. [Google Scholar] [CrossRef]
- Bagrov, A.A.; Iakovlev, I.A.; Iliasov, A.A.; Katsnelson, M.I.; Mazurenko, V.V. Multiscale structural complexity of natural patterns. Proc. Natl. Acad. Sci. USA 2020, 117, 30241–30251. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Gu, C.; Yang, H.; Wang, H.; Moore, J.M. Characterizing systems by multi-scale structural complexity. Phys. A Stat. Mech. Its Appl. 2023, 609, 128358. [Google Scholar] [CrossRef]
- Srenevas, S.; Poutous, M.K. Shannon’s entropy and structural complexity of random antireflective nanostructures on fused silica surfaces. In Nanoengineering: Fabrication, Properties, Optics, Thin Films, and Devices XX; SPIE: San Diego, CA, USA, 2023; Volume 12653, pp. 70–79. [Google Scholar]
- Kim, D.; Choi, J.; Nam, J. Entropy-assisted image segmentation for nano-and micro-sized networks. J. Microsc. 2016, 262, 274–294. [Google Scholar] [CrossRef] [PubMed]
- Srenevas, S.; Poutous, M.K. Complexity Imbalance of Nanostructured Antireflective Surfaces. In Proceedings of the 2024 Conference on Lasers and Electro-Optics (CLEO), Charlotte, NC, USA, 5–10 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–2. [Google Scholar]
- Lakhal, S.; Darmon, A.; Bouchaud, J.P.; Benzaquen, M. Beauty and structural complexity. Phys. Rev. Res. 2020, 2, 022058. [Google Scholar] [CrossRef]
- Andraud, C.; Beghdadi, A.; Haslund, E.; Hilfer, R.; Lafait, J.; Virgin, B. Local entropy characterization of correlated random microstructures. Phys. A Stat. Mech. Its Appl. 1997, 235, 307–318. [Google Scholar] [CrossRef]
- Van Siclen, C.D. Information entropy of complex structures. Phys. Rev. E 1997, 56, 5211. [Google Scholar] [CrossRef]
- Ruiz, R.L.; Mancini, H.; Calbet, X. A statistical measure of complexity. In Concepts and Recent Advances in Generalized Information Measures and Statistics; Bentham Science Publishers: Sharjah, United Arab Emirates, 2013; pp. 147–168. [Google Scholar]
- Alamino, R.C. Measuring complexity through average symmetry. J. Phys. A Math. Theor. 2015, 48, 275101. [Google Scholar] [CrossRef]
- Zanette, D.H. Quantifying the complexity of black-and-white images. PLoS ONE 2018, 13, e0207879. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, G.; Nicolis, C. Foundations of Complex Systems: Emergence, Information and Predicition; World Scientific: Singapore, 2012. [Google Scholar]
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Gell-Mann, M. What is complexity? In Complexity and Industrial Clusters: Dynamics and Models in Theory and Practice; Physica-Verlag HD: Heidelberg, Germany, 2002; pp. 13–24. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, Berkeley, CA, USA, 20–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Gray, R.M. Entropy and Information Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L 2 theory. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: London, UK, 2018. [Google Scholar]
- Yang, G.; Li, B.; Wang, Y.; Hong, J. Numerical simulation of 3D rough surfaces and analysis of interfacial contact characteristics. CMES 2014, 103, 251–279. [Google Scholar]
- Wang, Y.; Azam, A.; Wilson, M.C.; Neville, A.; Morina, A. Generating fractal rough surfaces with the spectral representation method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2640–2653. [Google Scholar] [CrossRef]
- Sarkiris, P.; Constantoudis, V.; Ellinas, K.; Lam, C.W.E.; Milionis, A.; Anagnostopoulos, J.; Poulikakos, D.; Gogolides, E. Topography optimization for sustainable dropwise condensation: The critical role of correlation length. Adv. Funct. Mater. 2024, 34, 2306756. [Google Scholar] [CrossRef]
- Papia, E.M.; Kondi, A.; Constantoudis, V. Entropy and complexity analysis of AI-generated and human-made paintings. Chaos Solitons Fractals 2023, 170, 113385. [Google Scholar] [CrossRef]
- Veinidis, C.N.; Akriotou, M.; Kondi, A.; Papia, E.M.; Constantoudis, V.; Syvridis, D. Complexity analysis of challenges and speckle patterns in an Optical Physical Unclonable Function. Chaos Solitons Fractals 2025, 191, 115938. [Google Scholar] [CrossRef]
- Available online: https://gregorygundersen.com/blog/2020/09/01/gaussian-entropy/ (accessed on 21 July 2025).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondi, A.; Constantoudis, V.; Sarkiris, P.; Gogolides, E. Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects. Mathematics 2025, 13, 2325. https://doi.org/10.3390/math13152325
Kondi A, Constantoudis V, Sarkiris P, Gogolides E. Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects. Mathematics. 2025; 13(15):2325. https://doi.org/10.3390/math13152325
Chicago/Turabian StyleKondi, Alex, Vassilios Constantoudis, Panagiotis Sarkiris, and Evangelos Gogolides. 2025. "Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects" Mathematics 13, no. 15: 2325. https://doi.org/10.3390/math13152325
APA StyleKondi, A., Constantoudis, V., Sarkiris, P., & Gogolides, E. (2025). Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects. Mathematics, 13(15), 2325. https://doi.org/10.3390/math13152325







