Using Transformers and Reinforcement Learning for the Team Orienteering Problem Under Dynamic Conditions
Abstract
1. Introduction
2. Related Work on TOP
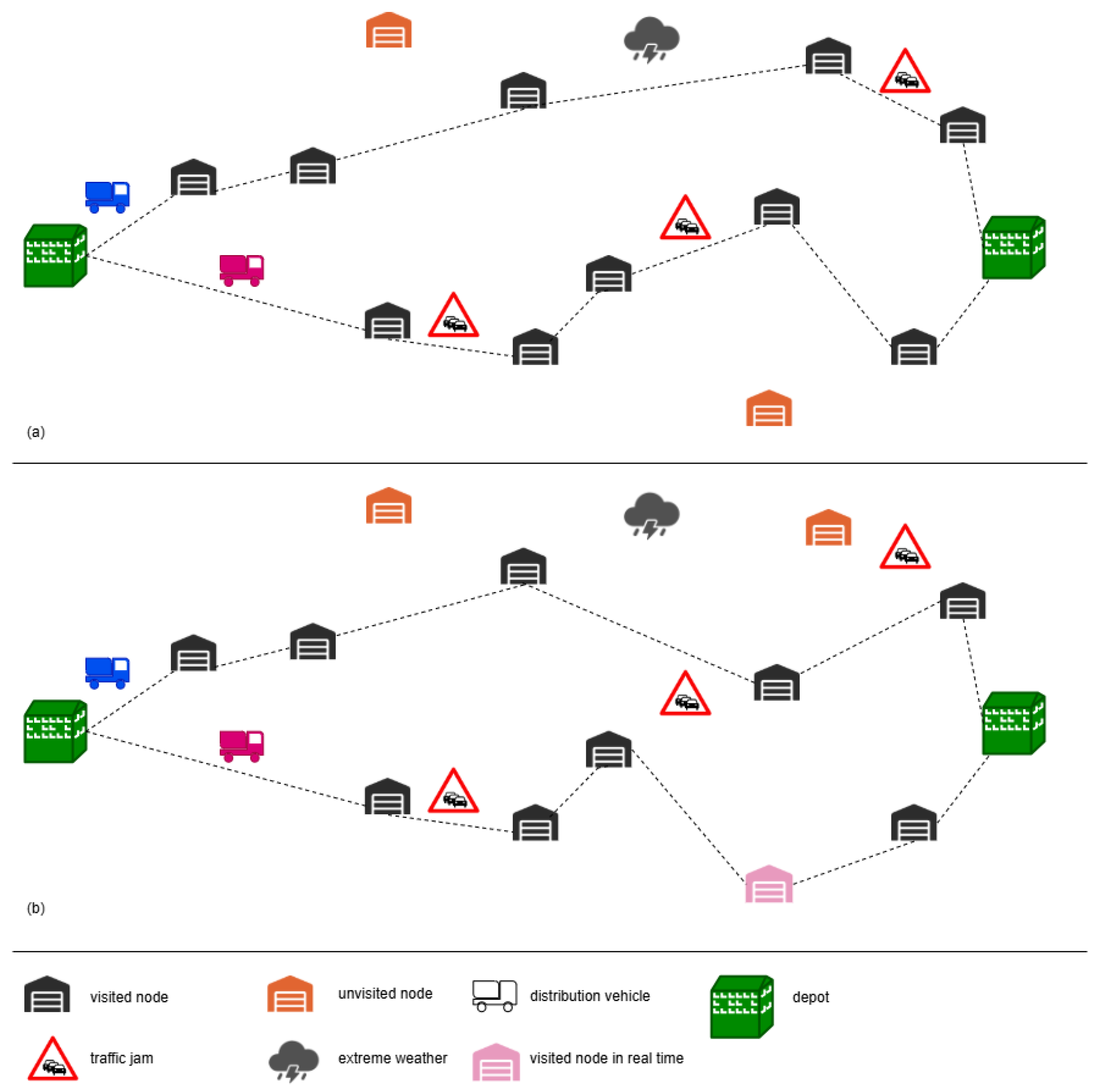
3. Modeling the TOP with Dynamic Travel Times
4. A Numerical Case Study
5. Solving Approaches
5.1. Reinforcement Learning Model
- Greedy decoding: At each timestep, the model selects the node with the highest probability, constructing the solution in a deterministic, greedy manner.
- Reflexion-based augmentation: A set of symmetry-preserving transformations (e.g., horizontal or vertical reflections) are applied to the input problem instance. Each augmented version is then solved using greedy decoding, and the best solution among them is selected as the final output. These augmentations preserve pairwise distances and therefore maintain solution validity in the square. The transformations are illustrated in Figure 3:
- Reflexion and rotation-based augmentation: In addition to previous transformations, rotational transformations of the problem instance are introduced. As with augmentation, each transformed instance is solved greedily, and the best overall solution is retained. This strategy increases the diversity of explored solutions while preserving the structure of the problem and thus the validity of the solution. In the experiments, 32 rotational transformations are applied to each instance. Combined with the 8 reflexion-based transformations, this results in a total of 256 distinct variations for each original problem instance.
5.2. Training Approach
5.3. Learning Rate Scheduling
5.4. VNS Heuristic Used for Evaluation
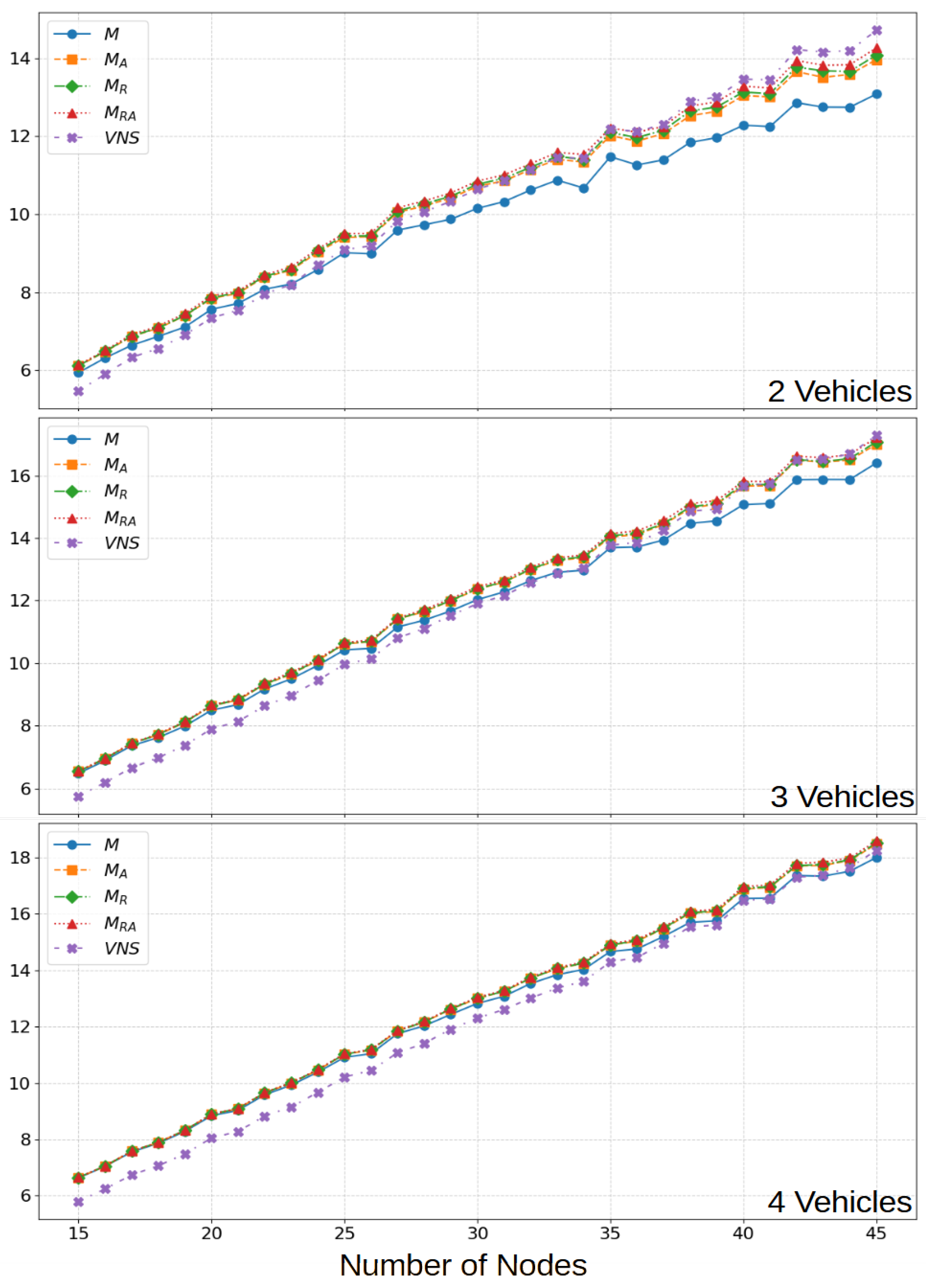
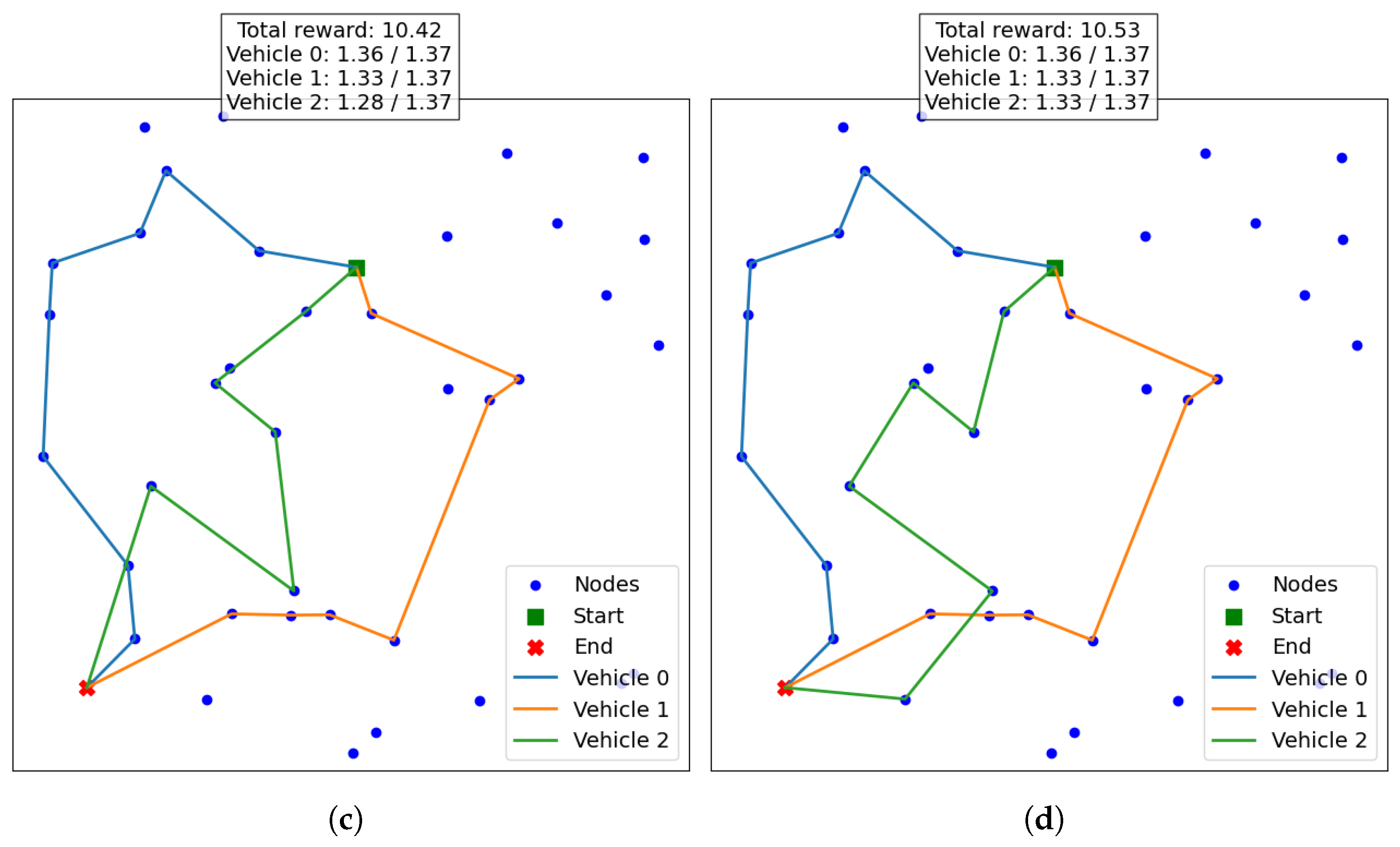
6. Computational Experiments and Results
6.1. Deterministic Problem
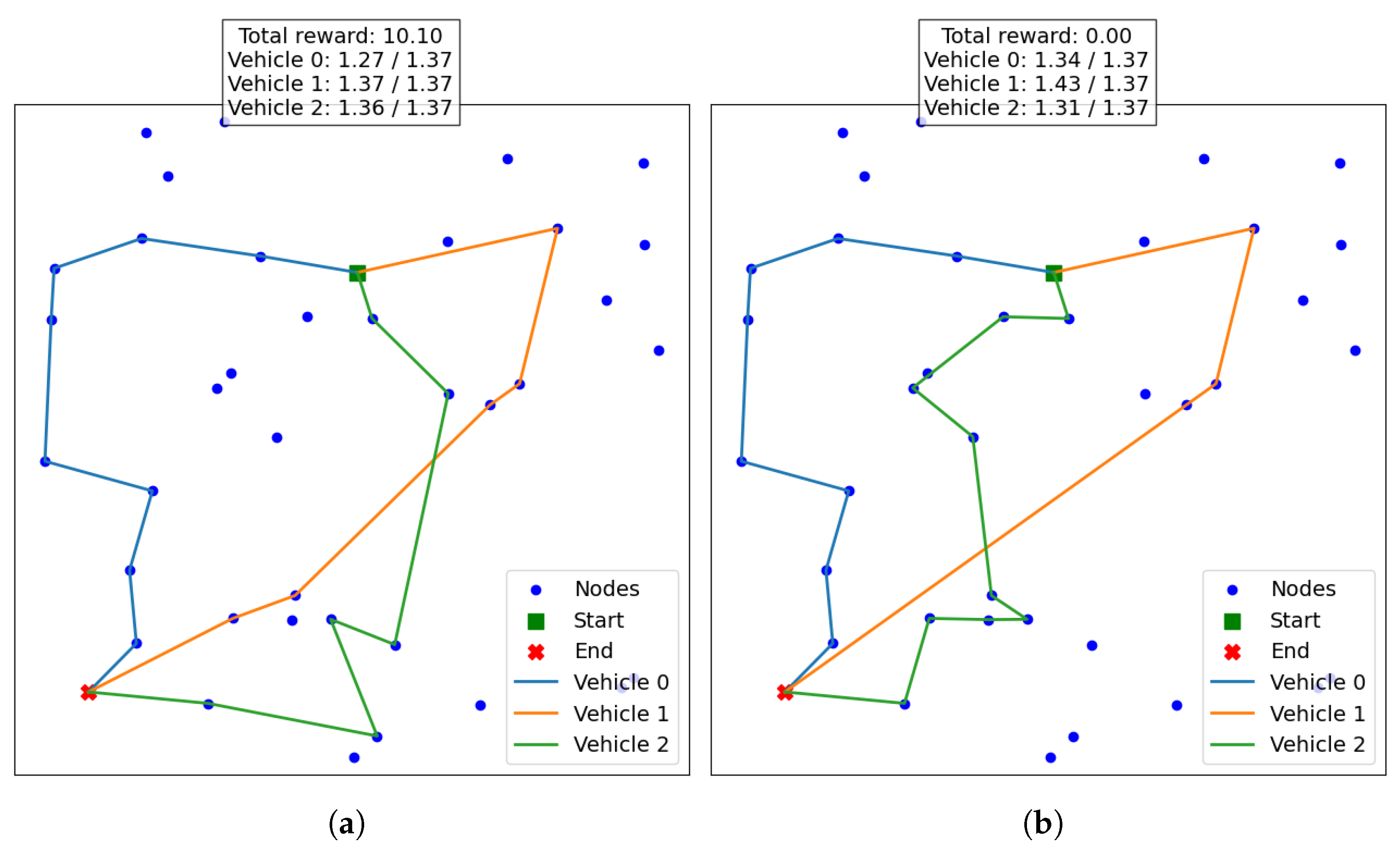
6.2. Dynamic Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Turan, B.; Hemmelmayr, V.; Larsen, A.; Puchinger, J. Transition towards sustainable mobility: The role of transport optimization. Cent. Eur. J. Oper. Res. 2024, 32, 435–456. [Google Scholar] [CrossRef]
- Jnr, B.A. Developing a decentralized community of practice-based model for on-demand electric car-pooling towards sustainable shared mobility. Case Stud. Transp. Policy 2024, 15, 101136. [Google Scholar]
- Puzicha, A.; Buchholz, P. Dynamic mission control for decentralized mobile robot swarms. In Proceedings of the 2022 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Sevilla, Spain, 8–10 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 257–263. [Google Scholar]
- Patil, G.; Pode, G.; Diouf, B.; Pode, R. Sustainable decarbonization of road transport: Policies, current status, and challenges of electric vehicles. Sustainability 2024, 16, 8058. [Google Scholar] [CrossRef]
- Mekky, M.F.; Collins, A.R. The impact of state policies on electric vehicle adoption—A panel data analysis. Renew. Sustain. Energy Rev. 2024, 191, 114014. [Google Scholar] [CrossRef]
- Toraman, Y.; Bayirli, M.; Ramadani, V. New technologies in small business models: Use of electric vehicles in last-mile delivery for fast-moving consumer goods. J. Small Bus. Enterp. Dev. 2024, 31, 515–531. [Google Scholar] [CrossRef]
- Song, L.; Wang, B.; Bian, Q.; Shao, L. Environmental benefits of using new last-mile solutions and using electric vehicles in China. Transp. Res. Rec. 2024, 2678, 473–489. [Google Scholar] [CrossRef]
- Yang, D.; Hyland, M.F. Electric vehicles in urban delivery fleets: How far can they go? Transp. Res. Part D Transp. Environ. 2024, 129, 104127. [Google Scholar] [CrossRef]
- Moradi, N.; Wang, C.; Mafakheri, F. Urban air mobility for last-mile transportation: A review. Vehicles 2024, 6, 1383–1414. [Google Scholar] [CrossRef]
- Mogire, E.; Kilbourn, P.; Luke, R. Electric vehicles in last-mile delivery: A bibliometric review. World Electr. Veh. J. 2025, 16, 52. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, S.; Zheng, Y.; Xie, S.; Yang, Q.; Wang, Y.; Hu, Q. Coordinated optimization of logistics scheduling and electricity dispatch for electric logistics vehicles considering uncertain electricity prices and renewable generation. Appl. Energy 2024, 364, 123147. [Google Scholar] [CrossRef]
- Poeting, M.; Prell, B.; Rabe, M.; Uhlig, T.; Wenzel, S. Considering energy-related factors in the simulation of logistics systems. In Proceedings of the 2019 Winter Simulation Conference (WSC), National Harbor, MD, USA, 8–11 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1849–1858. [Google Scholar]
- Mansour, S.; Raeesi, M. Performance assessment of fuel cell and electric vehicles taking into account the fuel cell degradation, battery lifetime, and heating, ventilation, and air conditioning system. Int. J. Hydrogen Energy 2024, 52, 834–855. [Google Scholar] [CrossRef]
- Lee, G.; Song, J.; Lim, Y.; Park, S. Energy consumption evaluation of passenger electric vehicle based on ambient temperature under Real-World driving conditions. Energy Convers. Manag. 2024, 306, 118289. [Google Scholar] [CrossRef]
- Martins, L.d.C.; Tordecilla, R.D.; Castaneda, J.; Juan, A.A.; Faulin, J. Electric vehicle routing, arc routing, and team orienteering problems in sustainable transportation. Energies 2021, 14, 5131. [Google Scholar] [CrossRef]
- Poeting, M.; Schaudt, S.; Clausen, U. A comprehensive case study in last-mile delivery concepts for parcel robots. In Proceedings of the 2019 Winter Simulation Conference (WSC), National Harbor, MD, USA, 8–11 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1779–1788. [Google Scholar]
- Golden, B.L.; Levy, L.; Vohra, R. The orienteering problem. Nav. Res. Logist. (NRL) 1987, 34, 307–318. [Google Scholar] [CrossRef]
- Marcucci, E.; Gatta, V.; Le Pira, M.; Hansson, L.; Bråthen, S. Digital twins: A critical discussion on their potential for supporting policy-making and planning in urban logistics. Sustainability 2020, 12, 10623. [Google Scholar] [CrossRef]
- Mardešić, N.; Erdelić, T.; Carić, T.; Đurasević, M. Review of stochastic dynamic vehicle routing in the evolving urban logistics environment. Mathematics 2023, 12, 28. [Google Scholar] [CrossRef]
- Grahn, R.; Qian, S.; Hendrickson, C. Improving the performance of first-and last-mile mobility services through transit coordination, real-time demand prediction, advanced reservations, and trip prioritization. Transp. Res. Part C Emerg. Technol. 2021, 133, 103430. [Google Scholar] [CrossRef]
- Ammouriova, M.; Guerrero, A.; Tsertsvadze, V.; Schumacher, C.; Juan, A.A. Using reinforcement learning in a dynamic team orienteering problem with electric batteries. Batteries 2024, 10, 411. [Google Scholar] [CrossRef]
- Abdollahi, M.; Yang, X.; Nasri, M.I.; Fairbank, M. Demand management in time-slotted last-mile delivery via dynamic routing with forecast orders. Eur. J. Oper. Res. 2023, 309, 704–718. [Google Scholar] [CrossRef]
- Butt, S.E.; Ryan, D.M. An optimal solution procedure for the multiple tour maximum collection problem using column generation. Comput. Oper. Res. 1999, 26, 427–441. [Google Scholar] [CrossRef]
- Boussier, S.; Feillet, D.; Gendreau, M. An exact algorithm for team orienteering problems. 4OR 2007, 5, 211–230. [Google Scholar] [CrossRef]
- El-Hajj, R.; Dang, D.C.; Moukrim, A. Solving the team orienteering problem with cutting planes. Comput. Oper. Res. 2016, 74, 21–30. [Google Scholar] [CrossRef]
- Poggi, M.; Viana, H.; Uchoa, E. The team orienteering problem: Formulations and branch-cut and price. In Proceedings of the 10th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems (ATMOS’10) (ATMOS 2010), Liverpool, UK, 9 September 2010; Schloss-Dagstuhl-Leibniz Zentrum für Informatik: Wadern, Germany, 2010. [Google Scholar]
- Li, J.; Zhu, J.; Peng, G.; Wang, J.; Zhen, L.; Demeulemeester, E. Branch-price-and-cut algorithms for the team orienteering problem with interval-varying profits. Eur. J. Oper. Res. 2024, 319, 793–807. [Google Scholar] [CrossRef]
- Archetti, C.; Hertz, A.; Speranza, M.G. Metaheuristics for the team orienteering problem. J. Heuristics 2007, 13, 49–76. [Google Scholar] [CrossRef]
- Gavalas, D.; Konstantopoulos, C.; Mastakas, K.; Pantziou, G. Efficient cluster-based heuristics for the team orienteering problem with time windows. Asia-Pac. J. Oper. Res. 2019, 36, 1950001. [Google Scholar] [CrossRef]
- Ferreira, J.; Quintas, A.; Oliveira, J.A.; Pereira, G.A.; Dias, L. Solving the team orienteering problem: Developing a solution tool using a genetic algorithm approach. In Soft Computing in Industrial Applications, Proceedings of the 17th Online World Conference on Soft Computing in Industrial Applications, Online, 3–14 December 2012; Springer: Berlin/Heidelberg, Germany, 2014; pp. 365–375. [Google Scholar]
- Wu, D.M.; Duan, D.T.; Yang, Q.; Liu, X.F.; Zhou, C.J.; Zhao, J.M. Adapted Ant colony optimization for team orienteering problem. In Proceedings of the 2024 11th International Conference on Machine Intelligence Theory and Applications (MiTA), Melbourne, Australia, 14–23 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Vansteenwegen, P.; Souffriau, W.; Vanden Berghe, G.; Van Oudheusden, D. A guided local search metaheuristic for the team orienteering problem. Eur. J. Oper. Res. 2009, 196, 118–127. [Google Scholar] [CrossRef]
- Panadero, J.; Juan, A.A.; Bayliss, C.; Currie, C. Maximising reward from a team of surveillance drones: A simheuristic approach to the stochastic team orienteering problem. Eur. J. Ind. Eng. 2020, 14, 485–516. [Google Scholar] [CrossRef]
- Labadie, N.; Mansini, R.; Melechovskỳ, J.; Calvo, R.W. The team orienteering problem with time windows: An lp-based granular variable neighborhood search. Eur. J. Oper. Res. 2012, 220, 15–27. [Google Scholar] [CrossRef]
- Vincent, F.Y.; Salsabila, N.Y.; Lin, S.W.; Gunawan, A. Simulated annealing with reinforcement learning for the set team orienteering problem with time windows. Expert Syst. Appl. 2024, 238, 121996. [Google Scholar]
- Li, Y.; Archetti, C.; Ljubić, I. Reinforcement learning approaches for the orienteering problem with stochastic and dynamic release dates. Transp. Sci. 2024, 58, 1143–1165. [Google Scholar] [CrossRef]
- Kool, W.; Van Hoof, H.; Welling, M. Attention, learn to solve routing problems! arXiv 2018, arXiv:1803.08475. [Google Scholar]
- Lee, D.H.; Ahn, J. Multi-start team orienteering problem for UAS mission re-planning with data-efficient deep reinforcement learning. Appl. Intell. 2024, 54, 4467–4489. [Google Scholar] [CrossRef]
- Wang, R.; Liu, W.; Li, K.; Zhang, T.; Wang, L.; Xu, X. Solving orienteering problems by hybridizing evolutionary algorithm and deep reinforcement learning. IEEE Trans. Artif. Intell. 2024, 5, 5493–5508. [Google Scholar] [CrossRef]
- Arnau, Q.; Juan, A.A.; Serra, I. On the use of learnheuristics in vehicle routing optimization problems with dynamic inputs. Algorithms 2018, 11, 208. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Ruthotto, L.; Haber, E. An introduction to deep generative modeling. GAMM-Mitteilungen 2021, 44, e202100008. [Google Scholar] [CrossRef]

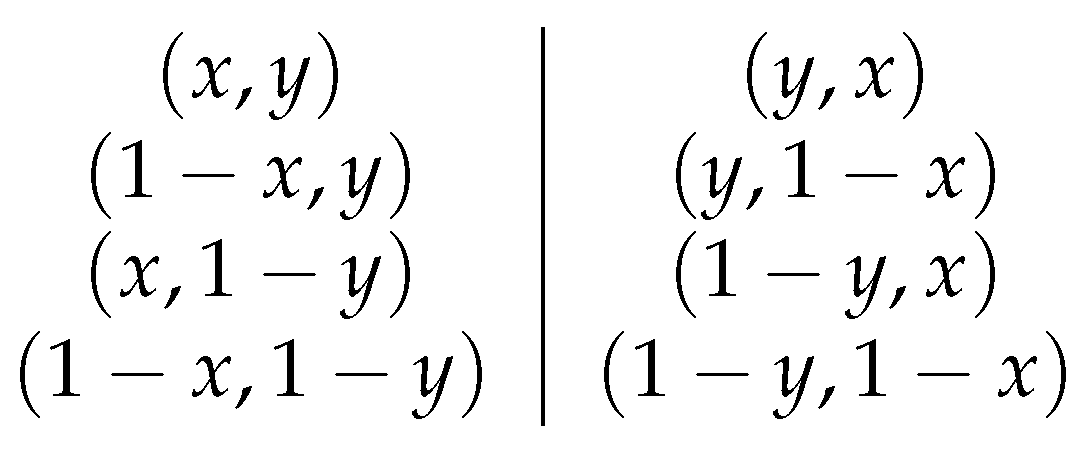

| Number of Vehicles | VNS | M | |||
|---|---|---|---|---|---|
| 2 | 10.38 | 9.90 | 10.41 | 10.46 | 10.56 |
| 3 | 11.69 | 11.76 | 12.09 | 12.11 | 12.16 |
| 4 | 12.12 | 12.58 | 12.77 | 12.78 | 12.81 |
| Mean | 11.40 | 11.41 | 11.76 | 11.78 | 11.84 |
| Number of Vehicles | M | MD | |||
|---|---|---|---|---|---|
| 2 | 3.45 | 9.21 | 9.76 | 9.84 | 9.95 |
| 3 | 2.32 | 11.09 | 11.48 | 11.51 | 11.58 |
| 4 | 1.86 | 11.94 | 12.18 | 12.20 | 12.24 |
| Mean | 2.54 | 10.74 | 11.14 | 11.18 | 11.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, A.; Escoto, M.; Ammouriova, M.; Men, Y.; Juan, A.A. Using Transformers and Reinforcement Learning for the Team Orienteering Problem Under Dynamic Conditions. Mathematics 2025, 13, 2313. https://doi.org/10.3390/math13142313
Guerrero A, Escoto M, Ammouriova M, Men Y, Juan AA. Using Transformers and Reinforcement Learning for the Team Orienteering Problem Under Dynamic Conditions. Mathematics. 2025; 13(14):2313. https://doi.org/10.3390/math13142313
Chicago/Turabian StyleGuerrero, Antoni, Marc Escoto, Majsa Ammouriova, Yangchongyi Men, and Angel A. Juan. 2025. "Using Transformers and Reinforcement Learning for the Team Orienteering Problem Under Dynamic Conditions" Mathematics 13, no. 14: 2313. https://doi.org/10.3390/math13142313
APA StyleGuerrero, A., Escoto, M., Ammouriova, M., Men, Y., & Juan, A. A. (2025). Using Transformers and Reinforcement Learning for the Team Orienteering Problem Under Dynamic Conditions. Mathematics, 13(14), 2313. https://doi.org/10.3390/math13142313








