Abstract
In the real world, most data are unlabeled, which drives the development of semi-supervised learning (SSL). Among SSL methods, least squares regression (LSR) has attracted attention for its simplicity and efficiency. However, existing semi-supervised LSR approaches suffer from challenges such as the insufficient use of unlabeled data, low pseudo-label accuracy, and inefficient label propagation. To address these issues, this paper proposes dual label propagation-driven least squares regression with feature selection, named DLPLSR, which is a pseudo-label-free SSL framework. DLPLSR employs a fuzzy-graph-based clustering strategy to capture global relationships among all samples, and manifold regularization preserves local geometric consistency, so that it implements the dual label propagation mechanism for comprehensive utilization of unlabeled data. Meanwhile, a dual-feature selection mechanism is established by integrating orthogonal projection for maximizing feature information with an ℓ2,1-norm regularization for eliminating redundancy, thereby jointly enhancing the discriminative power. Benefiting from these two designs, DLPLSR boosts learning performance without pseudo-labeling. Finally, the objective function admits an efficient closed-form solution solvable via an alternating optimization strategy. Extensive experiments on multiple benchmark datasets show the superiority of DLPLSR compared to state-of-the-art LSR-based SSL methods.
Keywords:
semi-supervised classification; least squares regression; dual label propagation; fuzzy graph clustering; pseudo-label-free MSC:
62H30
1. Introduction
Supervised learning is a cornerstone of machine learning and has been successfully applied in various domains such as computer vision, natural language processing, and biomedical analysis [1,2,3]. Classic models including K-nearest neighbor (KNN) [4,5], support vector machine (SVM) [6,7], ResNet [8,9], and vision transformer (ViT) [10,11] have shown impressive performance when trained with sufficient labeled data [12]. However, in real-world applications, acquiring labeled data are often costly and time-consuming, whereas unlabeled data are abundant and easily accessible. This has motivated the development of semi-supervised learning (SSL) approaches [13,14,15], which aim to exploit both labeled and unlabeled data for learning.
Pioneering representative methods include semi-supervised support vector machines [7,16], semi-supervised graph models [17,18,19], and non-negative matrix factorization [20,21]. Although these methods often deliver strong performance, their reliance on complex graph construction and iterative optimization incurs high computational costs, particularly on large-scale datasets. As a more efficient alternative, least squares regression (LSR) has gained traction in SSL due to its simplicity and convexity. By modeling label inference as a regression problem with manifold or graph regularization, LSR-based methods provide closed-form solutions and competitive performance with substantially lower computational overhead.
Least squares regression (LSR) aims to learn a projection that maps features to labels via least-squares minimization. In semi-supervised scenarios, where labeled data are limited, existing LSR-based methods typically enhance either feature selection (FS) or label propagation (LP) to improve performance. For FS, ℓ2,1-norm regularization [22], redundancy minimization [23], and discriminant-guided projections [24,25,26] have been explored to promote sparsity and class separability. For LP, early representative works such as flexible manifold embedding (FME) [27] and its acceleration [28] jointly learn graphs and classifiers. Recent advances include binary hash-based propagation [29], adaptive graph learning [30,31], and clustering-guided LSRs [32,33,34] that eliminate manual graphs.
While recent advances have enhanced feature selection in semi-supervised LSR frameworks, challenges remain in designing effective label propagation mechanisms. Existing methods either rely on adaptive graphs built from self-expression or local manifolds, which may overlook intrinsic sample similarity, or on pseudo-labels derived from clustering, whose quality is often unreliable. To overcome these issues, we propose a dual label propagation framework that integrates fuzzy graph-based clustering and adaptive manifold regularization, eliminating the need for pseudo-labels. Meanwhile, a dual feature selection strategy combining orthogonal projection and ℓ2,1-norm regularization is introduced to improve the quality and compactness of the learned representations. The proposed method admits a closed-form solution and achieves superior performance across diverse benchmarks.
The major contributions of this paper are summarized as follows:
- Dual label propagation mechanism: The global structure is preserved via the fuzzy graph, while the adaptive manifold regularization captures local geometric relationships among samples. Benefiting from this design, a dual label propagation mechanism is established to enable effective and consistent knowledge transfer from labeled to unlabeled data.
- Dual feature selection mechanism: An orthogonal projection is employed to preserve feature diversity and maximize information retention, while an ℓ2,1-norm regularization imposes structured sparsity to eliminate irrelevant dimensions. This dual feature selection mechanism enhances the robustness and discriminant capability of the learned representations under limited supervision.
- Pseudo-labels free framework: The proposed framework discards the use of pseudo-labels typically required in semi-supervised LSR models, thereby avoiding performance degradation caused by low-quality supervision. Instead, it transfers supervision from labeled to unlabeled data solely based on structural relationships, which are fully captured through fuzzy graph similarity and manifold regularization.
- End-to-end unified optimization: The model eliminates manual intervention and integrates all components into a single unified objective. It supports fully end-to-end optimization, allowing all modules to be jointly trained via an alternating strategy with closed-form solutions and guaranteed convergence.
Compared with the state-of-the-art (SOTA) semi-LSR, such as DRLSR [34], which performs a single label propagation path by generating pseudo-labels via fuzzy clustering, the proposed pseudo-label-free framework DLPLSR eliminates the need for membership estimation or explicit label assignment. Instead, it directly learns a fuzzy similarity matrix derived from a global clustering partition, enabling label propagation without relying on potentially inaccurate pseudo-labels. At the same time, a manifold similarity matrix based on local geometric structure is incorporated, establishing a dual label propagation mechanism that jointly captures both global and local relationships within a unified optimization framework. Moreover, the designed orthogonal sparse dual feature extraction mechanism enables DLPLSR to capture sample features more accurately and effectively than DRLSR, despite the latter lacking any specialized structural design.
The remainder of this paper is organized as follows. The next section provides the necessary preliminaries and a review of related works. In Section 3, we present the proposed model in detail. Section 4 elaborates on the optimization procedure. Experimental results and comparisons are reported in Section 5 to validate the effectiveness of our method. Finally, the last section concludes the paper and discusses potential directions for future research.
2. Preliminaries and Related Works
2.1. Notations and Definitions
To ensure consistent notation and improve readability, we specify the symbol conventions used throughout this paper. Matrices are denoted by bold, uppercase, upright letters such as . Vectors are denoted by lowercase, italic, bold letters, where represents the vector of the i-th column and may be used to indicate the i-th column vector as well. Scalars are denoted by lowercase, regular (non-bold, nonitalic) letters; for example, represents the -th element of a matrix.
With the notation clarified, we now formally define the semi-supervised classification problem considered in this paper. Given a training dataset consisting of N samples, where each column denotes a d-dimensional sample. Assume that the first samples are labeled and the remaining samples are unlabeled. The labeled samples are associated with label matrix , where K is the number of classes and each is a one-hot vector indicating the class membership of the i-th labeled sample. The unlabeled samples do not have associated ground-truth labels. The objective of semi-supervised classification is to leverage both the labeled data and the unlabeled data to learn an effective classifier that can accurately predict the labels of the unlabeled samples as well as unseen test data.
2.2. Least Squares Regression
LSR serves as one of the most fundamental models for supervised learning, which is commonly solved by least squares methods, shown in Figure 1. By learning a linear transformation, it projects the input data from the feature space into the label space , aiming to minimize the discrepancy between the predicted outputs and the true labels:
where is the projection matrix, denotes the regularization term, and is the regularization coefficient. The choice of plays a key role in controlling the complexity of the model and improving generalization. Common strategies include the Frobenius norm , the ℓ1-norm , and a combination of both, corresponding to ridge regression [35,36], Lasso regression [37,38], and elastic net regression [39,40], respectively. Ridge regression encourages smoothness and prevents overfitting through ℓ2-norm regularization, while Lasso regression promotes sparsity and enables feature selection via ℓ1-norm regularization. Elastic net integrates both penalties, balancing sparsity and stability, and is particularly effective for handling correlated features.
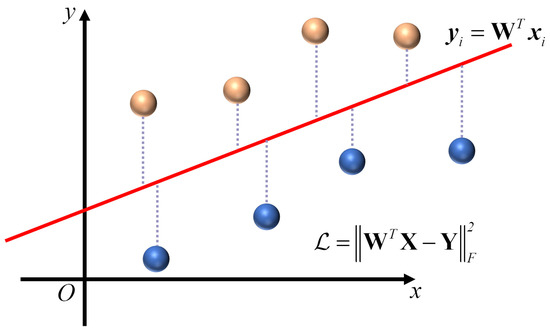
Figure 1.
The demonstration of least squares regression.
By solving for , a linear regression classifier can be obtained, which enables label prediction for unseen test samples. However, it is important to note that LR can only utilize the labeled samples, that is, and , while ignoring the abundant unlabeled training data commonly available in semi-supervised scenarios. This limitation significantly restricts the applicability of LSR in semi-supervised classification tasks, where leveraging both labeled and unlabeled data is essential for improving learning performance.
2.3. Semi-Supervised LSR
SSL fundamentally relies on the construction of an effective bridge between labeled and unlabeled data, with the core objective of propagating label information from the labeled subset to the larger unlabeled portion, a process commonly referred to as the label propagation (LP) mechanism. Typical approaches adopt graph-based perspectives that assume that neighboring or clustered samples are likely to share the same label. Representative works include Gaussian fields and harmonic functions (GFHF) [41], learning with local and global consistency (LGC) [42], and the manifold regularization geometric framework (MRGF) [17], which construct affinity graphs and enforce smoothness over the data manifold to effectively guide label diffusion.
To extend LSR to SSL scenarios, it is essential to incorporate unlabeled data into the whole learning framework. Using abundant unlabeled samples to improve the feature selection performance is an intuitive approach. The representative is rescaled linear square regression (RLSR) [22]:
where is a feature selection vector and is the bias term.
Similarly, Wang et al. [26] extend the RLSR framework by introducing an -drag matrix, leading to the sparse discriminative semi-supervised feature selection (SDSSFS) method. Meanwhile, sparse rescaled linear square regression (SRLSR) [43] improves RLSR by enforcing stronger sparsity on the learned projection matrix .
In addition to feature selection, customized label propagation is also vital to model performance. To overcome the drawbacks of two-stage graph-based methods, Bao et al. [30] proposed robust embedding regression (RER), which jointly learns the classifier and the self-expression matrix of all training samples.
where is the Laplacian matrix of . Complementary to global self-expression-based approaches, local manifold structure-based graph construction is also an effective strategy. Liao et al. [31] proposed the AGLSOFS framework, which was further enhanced with entropy regularization and sparsity regularization for adaptive graph learning.
Moreover, treating pseudo-labels as a soft assignment matrix offers a flexible LP strategy for semi-supervised learning. For example, unified dual label learning model for semi-supervised feature aelection (UDM-SFS) [32] formulates the pseudo-label assignment as:
where denotes an identity matrix representing class prototypes and C denotes a constant. Building upon UDM-SFS, Qi et al. [44] formally proposed the class-credible pseudo-label learning (CPL) framework, which provides a general optimization framework for pseudo-label-based learning. In addition, the introduction of anchor graph structures [34] has been shown to further improve the efficiency of such methods.
2.4. Fuzzy Graph and Its Derived Clustering
For a large number of unlabeled samples, clustering remains one of the most intuitive and widely adopted strategies. As discussed earlier, it is typically integrated into semi-supervised LSR frameworks via pseudo-labels. However, their quality is often unreliable and may degrade performance. Fuzzy graph theory [45] provides an alternative perspective by interpreting the fuzzy membership matrix as an anchor graph, yielding a complete similarity matrix .
Under this formulation, [45] revisited the fuzzy K-means (FKM) clustering objective and derived the following expression:
where is the abstract constraints of . This formulation provides a principled way to embed clustering structure into similarity learning without relying on pseudo-labels.
3. Model Description
In this section, we present a novel semi-supervised classification framework that avoids pseudo-label learning and instead performs dual-path label propagation through both manifold structure and fuzzy clustering. The core idea is to learn a discriminative linear classifier based on labeled data, while simultaneously leveraging the geometric structure and unsupervised clustering patterns of the entire dataset.
3.1. Pseudo-Label-Free Semi-LSR with LP Based on Manifold
We begin with the basic classification objective of semi-supervised least squares regression, which utilizes only the labeled samples to construct the supervised loss. To further enhance the utilization of the unlabeled data, we introduce a manifold regularization term that captures the local geometric structure among all training samples, including both labeled and unlabeled data. The resulting formulation is as follows:
where and denote the labeled data and labels, and is the graph Laplacian matrix derived from a similarity matrix constructed on all training data. This term enables label propagation over the manifold structure, thereby guiding the learning process with both labeled and unlabeled information.
Note that we do not assign pseudo-labels to the unlabeled data. Instead, the unlabeled samples influence the model through the structural constraint encoded by the graph Laplacian, forming the first label propagation path without explicit label learning.
3.2. Dual Label Propagation
While the previous subsection leverages local geometric structure via manifold regularization, this part complements it by introducing a global perspective of label propagation. Specifically, we employ fuzzy clustering to construct a task-adaptive similarity matrix , inspired by fuzzy graph theory [45]. This formulation avoids the need for pseudo-labels, enabling global propagation based on soft cluster assignments over the entire dataset.
The similarity matrix not only provides a new propagation path through global relationships but also replaces the fixed graph used in manifold regularization, allowing joint adaptation. As a result, a unified dual label propagation mechanism is established: the local path relies on the Laplacian , while the global path utilizes the learned directly.
Based on this formulation, we jointly optimize the classifier and the fuzzy graph via the following objective function:
The Frobenius regularization on helps prevent overfitting by controlling the scale and complexity of the similarity matrix. It avoids dense structures that may encode noise or spurious patterns, which is especially important when labeled data are limited. A larger value of encourages a sparser and more stable similarity structure that better captures the intrinsic relationships among samples. The fuzzy graph further enables adaptive connection strengths between samples, resulting in more flexible and informative propagation paths.
3.3. Dual Feature Selection
While the previous sections focus on label propagation and the utilization of unlabeled data, this subsection shifts attention to the features themselves. Under limited supervision, learning compact and discriminative features is crucial for model generalization. To achieve this, we introduce a dual feature selection mechanism.
First, an orthogonality constraint is imposed on the projection matrix, which eliminates feature redundancy and maximizes variance preservation in the projected space. This constraint complements the adaptive dual label propagation by ensuring that the learned features are uncorrelated and carry maximal information.
To further enhance discriminability, we incorporate an ℓ2,1 regularization term on . It enforces structured sparsity by shrinking entire rows of towards 0. This operation effectively removes globally irrelevant features across all classes, leading to a compact, robust, and interpretable model.
Together, these two terms construct a dual feature selection mechanism: orthogonality ensures feature diversity, while sparsity enforces discriminative power by eliminating redundant dimensions. The overall optimization integrates dual propagation and dual feature selection into a unified framework:
This formulation not only facilitates label propagation through both manifold and clustering structures, but also ensures that the selected features are simultaneously informative, uncorrelated, and discriminative. The illustration of the proposed DLPLSR is shown in Figure 2.
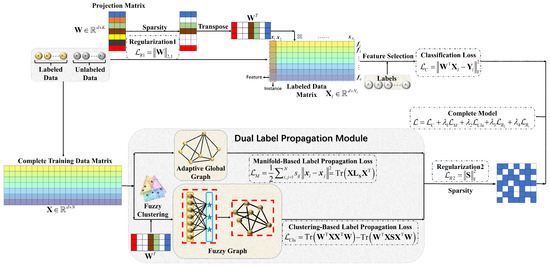
Figure 2.
The illustration of the proposed DLPLSR.
4. Optimization Strategy
The objective function in Equation (8) involves two coupled variables and . To solve the problem efficiently, we adopt an alternating optimization strategy, where we iteratively update one variable while keeping the other fixed until convergence.
4.1. Algorithm Implementation
With fixed, the objective reduces to:
To facilitate unified optimization, we reformulate the ℓ2,1 norm in matrix form. Specifically, it is defined as:
where is a diagonal matrix with
and is a small constant added for numerical stability. This reformulation enables efficient gradient-based optimization in the alternating update framework.
The optimization problem Equation (12) mentioned above with the orthogonality constraint can be effectively solved using the generalized power iteration (GPI) method proposed by Nie et al. [46]. GPI provides a theoretically sound and computationally efficient solution for trace minimization problems under orthogonality constraints, whose complete alternating optimization procedure is summarized in Algorithm 1.
| Algorithm 1 Generalized power iteration (GPI) [46] for Equation (12). |
| Input: Symmetric matrix , matrix . Output: Orthogonal matrix . 1: Initialize . 2: repeat 3: Compute , 4: Perform SVD: , 5: Update . 6: until convergence 7: return |
When is fixed, the objective with respect to is
which is equal to
where
Equation (16) is a constrained quadratic programming problem for which each row of can be computed independently via the linear-time complexity analytical solution proposed by Huang et al. [47].
The algorithm iterates between the -step and the -step until convergence. The general procedure is summarized in Algorithm 2.
| Algorithm 2 DLPLSR: Dual label propagation-driven with feature selection regression for semi-supervised classification. |
| Input: Labeled data , unlabeled data , hyperparameters . Output: Final classifier . 1: Initialize . 2: Calculate . 3: repeat 4: Compute by Equation (17). 5: Update by Equation (16) according to [47]. 6: Calculate and by Equations (13) and (14). 7: Update according to Algorithm 1. 8: until convergence |
4.2. Complexity Analysis
The time complexity of Algorithm 2 is primarily determined by the major matrix operations within each iteration. The pairwise squared distance matrix is computed only once, with a cost of . In the iterative phase, computing via Equation (17) costs . Updating the similarity matrix involves solving Equation (16) for each of the N rows, each with complexity , resulting in a total cost of . The matrix in Equation (13) requires , while the computation in Equation (14) costs . The projection matrix is updated using Algorithm 1, with a complexity of , where denotes the number of inner GPI iterations. Assuming that Algorithm 2 converges after epochs, the total time complexity of DLPR is .
The space complexity of the proposed DLPR algorithm mainly arises from storing the input data and several intermediate matrices. The data matrix requires space. The pairwise distance matrix , similarity matrix , and propagation matrix are all of size , contributing space in total. The projection matrix requires space, and the auxiliary matrices require . The labeled label matrix adds a negligible cost. Therefore, the overall space complexity of DLPR is .
4.3. Convergence Analysis
The proposed DLPR algorithm adopts an alternating optimization strategy to update the variables and . Each subproblem has a closed-form or guaranteed-convergent solution, and the total objective function value strictly decreases at every step. Therefore, the total objective function is monotonically decreasing and bounded below, ensuring that the DLPR algorithm converges to a local optimum.
5. Experiments
In this section, we evaluate the proposed DLPLSR on 14 benchmark datasets against 6 representative SOTA semi-supervised LSR models to demonstrate its effectiveness. We also present comprehensive experimental results, implementation details, parameter settings, sensitivity analyses, an ablation study, and real-world applications experiments.
5.1. Datasets
To provide a comprehensive and systematic evaluation, we select 14 representative benchmark datasets from various domains. These include two UCI datasets (Iris (https://www.kaggle.com/datasets/uciml/iris, accessed on 1 June 2025) and Wine (https://www.kaggle.com/datasets/sgus1318/winedata), accessed on 1 June 2025), handwritten digit datasets (USPS (https://www.kaggle.com/datasets/bistaumanga/usps-dataset, accessed on 1 June 2025), MNIST-2k2k (https://www.kaggle.com/datasets/hojjatk/mnist-dataset/code, accessed on 1 June 2025), MNIST-10k (https://www.kaggle.com/datasets/hojjatk/mnist-dataset/code, accessed on 1 June 2025), and Semeion (https://www.kaggle.com/datasets/ibrahimalizade/semeion/data, accessed on 1 June 2025)), object image datasets (COIL20 (https://git-disl.github.io/GTDLBench/datasets/coil20, accessed on 1 June 2025) and COIL100 (https://www.kaggle.com/datasets/jessicali9530/coil100, accessed on 1 June 2025)), and facial image datasets (ORL (https://cam-orl.co.uk/facedatabase.html, accessed on 1 June 2025), JAFFE (https://zenodo.org/records/3451524, accessed on 1 June 2025), PIX10 (https://www.kaggle.com/datasets/shivamvyasiitm/extended-yale-face-b, accessed on 1 June 2025), Yale (http://cvc.cs.yale.edu/cvc/projects/yalefaces/yalefaces.html, accessed on 1 June 2025), YaleB (https://vision.ucsd.edu/datasets/extended-yale-face-database-b-b, accessed on 1 June 2025), and AR (https://personalpages.manchester.ac.uk/staff/timothy.f.cootes/data/tarfd_markup/tarfd_markup.html, accessed on 1 June 2025)). This diverse selection ensures a fair comparison of data characteristics in semi-supervised learning. The detail information of the employed datasets shown in Table 1, where ‘Capacity’ indicates the range of samples per class. Meanwhile, some example images are shown in Figure 3.

Table 1.
Statistics of the benchmark datasets adopted in the experiments.

Figure 3.
Visual examples of the datasets used in experiments.
5.2. Baseline Methods
To comprehensively evaluate the effectiveness of the proposed DLPLSR framework, we compare it with seven representative semi-supervised LSR-based methods, which cover a wide range of design philosophies, including manifold regularization, graph learning, and label propagation:
- RSSLSR (robust semi-supervised least squares regression using ℓ2,p-norm minimization) [33]: A biased regression model in which each training sample is associated with a learnable weight. It adopts the ℓ2,p-norm to compute the classification loss, thereby enhancing robustness against outliers and label noise.
- SFS_BLL (semi-supervised feature selection with binary label learning) [29]: Performs discriminative feature selection in a binary hashing code space, enhancing class separability. However, its two-stage manual graph construction process may limit adaptability and increase sensitivity to noise.
- DSLSR (discriminative sparse least squares regression) [24]: Enhances the discriminability of the regression space by employing a coordinate relaxation matrix to enlarge the distance between inter-class samples, while imposing sparsity constraints on regression features for more compact representation.
- RER (robust embedding regression) [30]: Constructs an adaptive graph based on self-expressiveness, and evaluates the regression error using the nuclear norm, which captures the global low-rank structure of the error matrix from a holistic perspective. This enhances the model’s robustness against noise and outliers.
- DRLSR (discriminative and robust least squares regression) [34]: Constructs an adaptive anchor-based graph and performs label propagation via the fuzzy membership matrix derived from classical fuzzy clustering, so enhances the model’s robustness and discriminability under semi-supervised scenarios.
- AGLSOFS_N (adaptive orthogonal semi-supervised feature selection with reliable label matrix learning_norm) [31]: Incorporates confidence-based label learning to control inter-class overlap, employs orthogonal projection to enhance feature discriminability, and introduces a Frobenius norm regularization term to facilitate adaptive graph construction.
- AGLSOFS_E (adaptive orthogonal semi-supervised feature selection with reliable label matrix learning_entropy) [31]: Similar in overall structure to AGLSOFS_N, but replaces the Frobenius norm with an entropy regularization term to achieve adaptive graph construction, resulting in a denser similarity structure.
Table 2 provides a detailed comparison of the characteristics and differences among these baseline methods and the proposed DLPLSR.

Table 2.
Comparison of the proposed DLPLSR and Baseline Methods.
In Table 2, it should be clear that Feature Selection refers to the regularization imposed on the projection matrix , rather than the transformed features . Regularizing directly enforces sparsity or discriminative structure, guiding the model to suppress irrelevant features during learning, which is more fundamental than post-hoc analysis of projected outputs. Meanwhile, for pre-KNN methods, the count includes neighborhood size and Gaussian kernel bandwidth.
5.3. Evaluation Metrics
In the comparison experiments, we adopt two commonly used evaluation metrics to assess classification performance: Accuracy (ACC) and the F1-score. These metrics are briefly introduced as follows.
Starting from the binary classification setting, given a trained classifier applied to unlabeled samples (including both training and testing data), each prediction falls into one of the following four categories:
- TP (True Positive): Positive samples correctly predicted as positive.
- FP (False Positive): Negative samples incorrectly predicted as positive.
- TN (True Negative): Negative samples correctly predicted as negative.
- FN (False Negative): Positive samples incorrectly predicted as negative.
Based on these definitions, the ACC is calculated as
which measures the overall proportion of correctly classified samples. ACC is particularly informative when class distributions are relatively balanced.
However, in imbalanced scenarios—such as anomaly detection, where the number of negative samples far exceeds the number of positives—predicting all samples as negative can still yield a deceptively high ACC, despite the classifier’s failure to detect anomalies. To better assess such cases, two additional metrics are introduced:
In the above example, both Recall and Precision would approach zero, indicating poor predictive performance. To balance the trade-off between these two metrics, the F1-score is defined as their harmonic mean:
For multi-class classification problems with K classes, each class can be treated as the positive class while the others are considered negative (one-vs-all strategy). The final macro-average ACC and F1-score are computed by averaging the individual metrics across all classes:
In multi-class scenarios, where class imbalance is common, the F1-score becomes especially important as it better captures per-class performance.
5.4. Configurations
5.4.1. Testing Configuration
To ensure fairness and comparability, we adopt a unified prediction strategy for all testing samples across methods. Specifically, once the final projection matrix is obtained, all testing samples are projected via (plus bias if applicable), and a standard 1-nearest neighbor (1-NN) classifier is employed to assign labels. Each testing sample is classified by finding its nearest labeled training sample in the transformed feature space.
Different methods handle prediction differently for the unlabeled training samples . All evaluated methods are capable of generating pseudo-labels except to our DLPLSR, and we adopt the following rule to determine the prediction of :
- If a method explicitly uses pseudo-labels for unlabeled samples in its original paper, we follow that design, such as RER [30,34].
- If the original paper does not specify the prediction approach for unlabeled data, including RSSLSR [33], SFS_BLL [29], DSLSR [24], AGLSOFS_N [31], and AGLSOFS_E [31], we select the strategy that achieves better performance, either pseudo-labels or 1-NN.
When pseudo-labeling is applied, the predicted label for each unlabeled sample is assigned as
where is the predicted label matrix, and and N denote the number of labeled and total training samples, respectively.
For our proposed DLPLSR with the pseudo-label-free framework, the unlabeled training samples are directly predicted using the same 1-NN classifier as test samples. The detailed prediction strategies of all methods are summarized in Table 3, where, ‘Unlabeled Specified’ indicates whether there is a specific prediction strategy for unlabeled training samples in the original paper.

Table 3.
The detailed prediction strategies of all methods.
5.4.2. Semi-Supervised Configuration
In semi-supervised learning scenarios, the proportion of labeled samples in the training set should remain low. However, it is also important to ensure that each class is represented by at least a few labeled instances, particularly for datasets with a small number of samples but a large number of classes. To balance these requirements, we uniformly set the labeled sample ratio to 10% of the total training set.
Furthermore, to guarantee fairness across all methods, we adopt the standard 50–50% split between training and testing data. For each dataset, the labeled/unlabeled and training/testing splits are pre-determined based on the above ratios via random sampling. These fixed splits are consistently applied throughout all experiments to ensure reproducibility and fair comparison.
5.4.3. Hyperparameters Configurations
The proposed DLPLSR method involves four hyperparameters, namely , , , and , each selected from the range . This leads to a total of unique hyperparameter combinations. To mitigate randomness, the model avoids random initialization. As outlined in Algorithm 2, the projection matrix is initialized with the first K columns of the identity matrix . If the feature dimension d is smaller than K, then the first d rows of are used instead. Under this initialization scheme, each parameter group only requires a single training run. To support reproducibility, the optimal settings for DLPLSR on each dataset are reported in Table 4, and the corresponding relationship between the number and the data can be found in Table 1.

Table 4.
The optimal hyperparameters ( to ) of DLPLSR in the benchmarks.
In comparison methods, regularization coefficients, such as , , or terms like are also chosen from the same candidate set . Additionally, specialized hyperparameters, including the p value in the ℓ2,p-norm [33], the scaling factor in reliable label learning [31], and the fuzzifier r used in membership functions [34], as well as other task-specific settings, are configured according to their respective original papers. For fairness, all methods use the same initialization for as DLPLSR, and biases in biased models are uniformly initialized to zero.
5.5. Comparison Experiments
This section presents the most critical part of the experimental evaluation. The comparison results in terms of ACC and F1-score are reported in Table 5 and Table 6, where the results are presented in Value(Rank) format. The best results are highlighted in bold, and the second-best results are underlined. The last row reports the average ranks across all datasets, respectively. As can be observed, the proposed method achieves a significant lead compared to 7 SOTA semi-supervised LSR models across 14 diverse benchmark datasets. Meanwhile, it is worth noting that compared with other types of semi-supervised learning methods, approaches based on LSR are particularly advantageous in terms of computational efficiency. Therefore, training time (Since the testing stage involves only simple pseudo-label assignment or 1-NN classification, its time consumption is negligible) is also considered an important evaluation metric. So, we report the training time of each method in Table 7, in which the results are reported in Time (Rank) format. AveT denotes the mean training time of each model averaged over all training datasets, while AveR represents the average rank of training time across all datasets.

Table 5.
Classification accuracy (%) and ranks on unlabeled and testing data.

Table 6.
Classification F1-score (%) and ranks on unlabeled and testing data.

Table 7.
Average training time (Seconds) across all hyper-parameter groups for each dataset.
To determine whether the average rank differences between DLPLSR and the baseline methods are statistically significant on multiple datasets, we adopt the Nemenyi post-hoc test at a 0.05 significance level. Specifically, the critical difference (CD) is calculated as:
Here, denotes the total number of compared methods (including DLPLSR), is the number of datasets, and is the critical value at the 0.05 significance level. Accordingly, the critical difference (CD) is calculated to be 2.81. The significance boundaries and relative rankings under all metrics are illustrated in the critical difference diagrams in Figure 4.

Figure 4.
Post-hoc Nemenyi test results at significance level 0.05.
As shown in Table 5 and Table 6, and Figure 4, DLPLSR exhibits consistently competitive performance across the four metrics (ACC_U, ACC_T, F1_U, and F1_T). For instance, in ACC_U, it ranks within the top three on 11 out of 14 datasets, with only USPS, Jaffe, and Yale falling outside. Its average rank is 2.64, slightly behind RER (2.21); however, the difference is not statistically significant, as it lies within the critical difference (CD = 2.81).
In ACC_T, DLPLSR demonstrates even stronger dominance, ranking within the top three on 13 out of 14 datasets, with only USPS falling outside. It achieves the best average rank of 1.79, significantly outperforming the second-best method (RER at 3.79) with a statistically significant margin, indicating superior generalization ability to unseen data.
The results for F1_U and F1_T follow similar trends. On the unlabeled data, DLPLSR ranks second, slightly behind RER, but the difference is not statistically significant. On the testing data, it achieves the best overall performance with a statistically significant lead. The number of datasets where DLPLSR ranks in the top three is also comparable to that in ACC, further confirming its robust generalization capability.
Taking specific datasets for closer inspection, on the Yale dataset, which is the most challenging overall, DLPLSR still ranks first on testing data in both Acc and F1. Similarly, in datasets such as PIX10, COIL100, and AR, our method consistently maintains the top 2 ranks. These results demonstrate that DLPLSR not only performs well on average but also avoids catastrophic failures in difficult cases, reflecting a stable and balanced generalization capability.
Moreover, compared to the other three pseudo-label-based methods, including RSSLSR, DRLSR, and AGLSOFS_E, our method shows a clear advantage in the unlabeled evaluation, outperforming them by large margins. This strongly supports the effectiveness of our pseudo-label-free framework, which reduces optimization variables, improves stability, and avoids overfitting issues caused by overly confident pseudo-labels.
With respect to the efficiency, as shown in Table 7, the proposed DLPLSR model demonstrates strong computational efficiency. It ranks in the top half among all methods, both in terms of AveT and AveR across datasets. Notably, DLPLSR achieves the third-lowest AveT (20.97 s) among all competing methods. Importantly, the time gap between DLPLSR and the fastest method (AGLSOFS_E) (11.63 s) is only 9.34 s, which is even smaller than the gap between DLPLSR and the fourth-fastest method (RSSLSR) (35.25 s). This indicates that DLPLSR sits much closer to the efficiency frontier than to slower alternatives, highlighting its advantage in terms of practical usability, especially in large-scale settings.
Moreover, DLPLSR shows consistently low training times across almost all datasets, ranking 1st or 2nd on 7 out of 14 datasets, including complex and large-scale ones such as 10k, YaleB, COIL100, and USPS. This further demonstrates that the efficiency advantage of DLPLSR becomes even more pronounced as dataset size and complexity increase. In summary, DLPLSR not only achieves competitive learning performance but also maintains a low computational cost across diverse data scenarios, confirming its practicality for efficient large-scale semi-supervised learning tasks.
5.6. Parameter Sensitivity
The proposed DLPLSR model includes four key hyperparameters: controls manifold-based label propagation, governs clustering-based label propagation, imposes graph sparsity regularization, and enforces projection sparsity via the ℓ21 norm.
To evaluate the model’s robustness to hyperparameter selection, we perform a sensitivity analysis by fixing two parameters at their optimal values and varying the other two across a logarithmic range. We select three representative datasets from different application domains, including Wine (UCI tabular), YaleB (face images), and Semeion (handwritten digits), and conduct the analysis under both the Testing and Unlabeled prediction. The results are shown in Figure 5, where each row fixes two hyper-parameters at their optima referred to Table 4 and varies the other two. For example, Wine-U12 represents the impact of varying and on the ACC of unlabeled data on the Wine dataset.
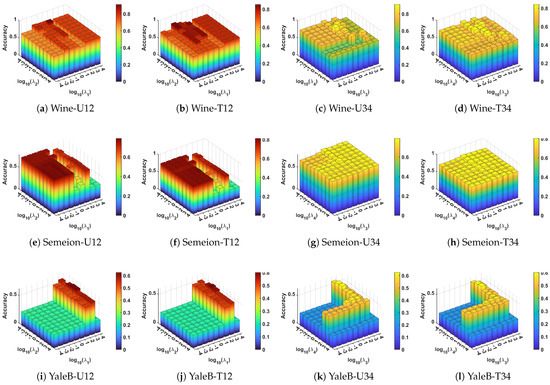
Figure 5.
Parameter sensitivity 3D bar chart of DLPLSR on Wine, Semeion, and YaleB.
Figure 5 illustrates the parameter sensitivity of DLPLSR. We observe that the model is more sensitive to and , particularly on complex datasets such as Semeion and YaleB (e.g., Figure 5e,f,i,j). Performance may vary significantly across different combinations, showing peaks and valleys rather than a flat plateau. In contrast, when and are varied with and fixed, the model generally maintains more stable accuracy, as observed in Figure 5c,d,g,h. This indicates that the regularization terms contribute to stability but are less sensitive overall. Moreover, on relatively simpler datasets such as Wine (Figure 5a–d), DLPLSR achieves consistently high accuracy across a wide range of parameters, demonstrating robustness in low-dimensional settings. These results suggest that proper tuning of and is more critical for complex tasks, while the model remains generally tolerant to variations in and .
5.7. Ablation Study
In the proposed DLPLSR, four hyperparameters are introduced in the objective function, each corresponding to a distinct model component. Specifically, and control the dual label propagation processes based on the local manifold and the global fuzzy graph, respectively, regularizes the Frobenius norm of the similarity matrix , and imposes an ℓ2,1 norm on the projection matrix to promote structured sparsity. Among them, plays a pivotal role in preventing overfitting by stabilizing the learned similarity structure. Moreover, it is a core component of the model formulation and directly influences the optimization procedure. Therefore, is retained in all configurations.
To further verify the necessity of the other three terms, we have added an ablation study in the revised manuscript. By individually setting , , and to zero, we observe consistent performance degradation across various datasets, as detailed in Table 8, in which caption ‘w’ means the complete model and ‘’ means fix . These results validate the contribution of each term to the overall effectiveness and robustness of the proposed framework.

Table 8.
Ablation results on the impact of regularization terms.
From the ablation results in Table 8, it is clear that removing any of the regularization terms leads to noticeable performance degradation on most datasets and evaluation metrics. For instance, when (corresponding to the ℓ2,1-norm constraint) is removed, the ACC and F1-score on datasets (both unlabeled and testing) such as Wine, YaleB, and AR drop significantly, indicating the importance of feature sparsity in enhancing robustness. Likewise, setting or to zero weakens the dual label propagation process, particularly on more complex datasets like YaleB and AR, where both ACC and F1-score degrade by more than 2%. These observations demonstrate that each regularization term plays a distinct and indispensable role in maintaining stable and high-performing model behavior. The ablation study, therefore, confirms the necessity and effectiveness of these components in the overall framework.
5.8. Visualization Analysis
To further validate the proposed DLPLSR, we present a visualization study from two aspects: numerical convergence and confusion matrix.
Although the theoretical convergence of DLPLSR has been established in Section 4.3, we additionally provide empirical evidence of its numerical stability. We select six representative datasets from various domains and scales: Iris, Wine, Yale, YaleB, 10k, and AR. The convergence curves of the loss function over iterations are illustrated in Figure 6. Despite different data characteristics and magnitudes, DLPLSR consistently converges within a small number of iterations (mostly less than 10), showing stable decreasing behavior or bounded oscillation after a sharp descent, which confirms that the optimization procedure of DLPLSR is numerically stable and efficient across different datasets.

Figure 6.
Loss convergence curves of DLPLSR on six representative datasets.
Then, we visualize the confusion matrices on three representative datasets: COIL100, AR, and 10k, as shown in Figure 7. The COIL100 and AR datasets involve 100 classes each, presenting significant classification challenges due to high inter-class similarity. For better visualization, the confusion matrices are grouped by class intervals of 10. Although the absolute accuracy values on COIL100 and AR are moderate, DLPLSR achieves top-tier rank positions among all compared methods (Table 5). This indicates that while fine-grained recognition remains difficult due to limited labels, DLPLSR still captures essential class structures more effectively than others. The 10k dataset, characterized by a larger scale and more complex class distribution, further demonstrates the generalization strength of DLPLSR. As shown in the confusion matrices, most diagonal blocks remain prominent in both unlabeled and testing settings, indicating consistent and robust discrimination ability even with limited supervision.

Figure 7.
Confusion matrix visualization of DLPLSR on COIL100, AR, and 10k.
These visual results reaffirm that DLPLSR maintains reliable classification quality across diverse and challenging scenarios, with strong generalization in large-scale and high-class-count conditions.
5.9. Real-World Applications Experiments
To validate the real-world applicability of the proposed method, we evaluate it on two widely used industrial fault diagnosis datasets, CWRU (https://engineering.case.edu/bearingdatacenter, accessed on 1 June 2025) and SEU (https://github.com/cathysiyu/Mechanical-datasets, accessed on 1 June 2025), both involving vibration signals collected under various fault types and operating conditions. The raw time-series signals are transformed into time-frequency representations using continuous wavelet transform (CWT), with a sliding window of length 1024, an overlap ratio of 0.5, a frequency scale of 128, and the wavelet basis function set to ‘cmor100-1’. From each frequency scale of the CWT matrix, we extract eleven statistical features, including mean, standard deviation, maximum, minimum, energy, skewness, kurtosis, average absolute value, peak value, shape factor, and Shannon entropy. These features are concatenated across all scales to form the final sample-level representation. For dataset splitting, both the CWRU and SEU datasets are divided into training and testing sets with a 1:19 ratio, using a fixed random seed to ensure reproducibility. Specifically, CWRU contains 1635 training samples and 31,065 test samples, while SEU includes 2047 training samples and 38,893 test samples. Furthermore, 50% of the training samples are labeled. The results are shown in the Table 9.

Table 9.
Fault diagnosis performance comparison.
From Table 9, the best overall performer is DSLRSR with an average rank of 1.50, while DLPLSR also demonstrates strong performance, ranking second with an average rank of 2.75 across all metrics. On the SEU dataset, DLPLSR achieves top-2 results in all four metrics (ACC_U, ACC_T, F1_U, F1_T). Although it slightly lags behind the best method on the CWRU dataset, it still ranks within the top four across all metrics, reflecting stable generalization. While its current accuracy may not yet meet the stringent demands of critical fault diagnosis applications, it is notable that DLPLSR achieves over 90% accuracy on both widely used datasets without any task-specific adaptation, indicating considerable potential for further development in the fault diagnosis field.
6. Discussion
In this paper, we proposed DLPLSR, a dual label propagation-driven least squares regression framework without pseudo label learning. By jointly leveraging manifold-based local geometry and fuzzy graph clustering-based global structure, the model enables effective label propagation across all training samples. In addition, a dual feature selection mechanism combining orthogonal projection and ℓ2,1 regularization is integrated to extract compact and discriminative features under limited supervision. Extensive experiments on 14 benchmark datasets against 7 SOTA baselines demonstrate the robustness and effectiveness of DLPLSR across various natural image classification tasks such as faces, objects, and handwritten digits. Moreover, without any domain-specific design, DLPLSR achieves over 90% accuracy on two real-world fault diagnosis datasets, showing strong potential for broader applications beyond standard vision tasks.
With the widespread adoption of multi-view data over single-view data, future work may first consider extending the proposed framework to multi-view semi-supervised classification [48,49], enabling more effective exploration of inter-view relationships to improve accuracy. Meanwhile, in the current model, label information is incorporated solely through the loss function. Exploring coarser-granularity label [50] representations and embeddings may offer a promising direction for enhancing label utilization and further improving model performance. Finally, while DLPLSR exhibits promise in fault diagnosis, its accuracy is not yet adequate for industrial use. Future research will aim to optimize the model for task-specific industrial applications.
Author Contributions
Conceptualization, S.Z. and Z.S.; methodology, Z.Y.; software, Z.Y.; writing—original draft preparation, S.Z.; writing—review and editing, Z.S.; supervision, Z.S.; project administration, Z.S.; funding acquisition, S.Z. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Guangdong Province Youth Innovation Talent Project for Colleges and Universities under Grant 2023KQNCX069 and the Scientific Foundation for Youth Scholars of Shenzhen University under Grant 868-000001032407.
Data Availability Statement
To facilitate academic exchange and reproducibility, the source code of this work is available at: https://github.com/ShiZhaoyin/DLPLSR (accessed on 1 June 2025).
Acknowledgments
The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kotsiantis, S.B.; Zaharakis, I.D.; Pintelas, P.E. Machine learning: A review of classification and combining techniques. Artif. Intell. Rev. 2006, 26, 159–190. [Google Scholar] [CrossRef]
- Sen, P.C.; Hajra, M.; Ghosh, M. Supervised classification algorithms in machine learning: A survey and review. In Emerging Technology in Modelling and Graphics: Proceedings of IEM Graph 2018; Springer Nature: Singapore, 2020; pp. 99–111. [Google Scholar]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of image classification algorithms based on convolutional neural networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Zhang, S. Challenges in KNN classification. IEEE Trans. Knowl. Data Eng. 2021, 34, 4663–4675. [Google Scholar] [CrossRef]
- Xie, J.; Xiang, X.; Xia, S.; Jiang, L.; Wang, G.; Gao, X. Mgnr: A multi-granularity neighbor relationship and its application in knn classification and clustering methods. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 7956–7972. [Google Scholar] [CrossRef] [PubMed]
- Chandra, M.A.; Bedi, S. Survey on SVM and their application in image classification. Int. J. Inf. Technol. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Qiao, Q.; Li, F. A Lie group Laplacian Support Vector Machine for semi-supervised learning. Neurocomputing 2025, 630, 129728. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shafiq, M.; Gu, Z. Deep residual learning for image recognition: A survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10012–10022. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Patel, H.; Nagalapatti, L.; Gupta, N.; Mehta, S.; Guttula, S.; Mujumdar, S.; Afzal, S.; Sharma Mittal, R.; Munigala, V. Overview and importance of data quality for machine learning tasks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD), Virtual, 6–10 July 2020; pp. 3561–3562. [Google Scholar]
- Van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Han, K.; Sheng, V.S.; Song, Y.; Liu, Y.; Qiu, C.; Ma, S.; Liu, Z. Deep semi-supervised learning for medical image segmentation: A review. Expert Syst. Appl. 2024, 245, 123052. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Zhou, Z.H. Semi-supervised learning. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 2021; Chapter 13; pp. 315–341. [Google Scholar]
- Bennett, K.; Demiriz, A. Semi-supervised support vector machines. Adv. Neural Inf. Process. Syst. NIPS 1998, 11, 368–374. [Google Scholar]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Nie, F.; Shi, S.; Li, X. Semi-supervised learning with auto-weighting feature and adaptive graph. IEEE Trans. Knowl. Data Eng. 2019, 32, 1167–1178. [Google Scholar] [CrossRef]
- Qiao, X.; Chen, C.; Wang, W.; Peng, Q.; Ghafar, A. Efficient ℓ2,1-norm graph for robust semi-supervised classification. Pattern Recognit. 2025, 169, 111890. [Google Scholar] [CrossRef]
- Jia, Y.; Kwong, S.; Hou, J.; Wu, W. Semi-supervised non-negative matrix factorization with dissimilarity and similarity regularization. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2510–2521. [Google Scholar] [CrossRef] [PubMed]
- Yuan, A.; You, M.; He, D.; Li, X. Convex non-negative matrix factorization with adaptive graph for unsupervised feature selection. IEEE Trans. Cybern. 2020, 52, 5522–5534. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yuan, G.; Nie, F.; Huang, J.Z. Semi-supervised Feature Selection via Rescaled Linear Regression. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Melbourne, Australia, 19–25 August 2017; Volume 2017, pp. 1525–1531. [Google Scholar]
- Xu, S.; Dai, J.; Shi, H. Semi-supervised feature selection based on least square regression with redundancy minimization. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Liu, Z.; Lai, Z.; Ou, W.; Zhang, K.; Huo, H. Discriminative sparse least square regression for semi-supervised learning. Inf. Sci. 2023, 636, 118903. [Google Scholar] [CrossRef]
- Zhong, W.; Chen, X.; Yuan, G.; Li, Y.; Nie, F. Semi-supervised feature selection with adaptive discriminant analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 10083–10084. [Google Scholar]
- Wang, C.; Chen, X.; Yuan, G.; Nie, F.; Yang, M. Semisupervised feature selection with sparse discriminative least squares regression. IEEE Trans. Cybern. 2021, 52, 8413–8424. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Xu, D.; Tsang, I.W.H.; Zhang, C. Flexible manifold embedding: A framework for semi-supervised and unsupervised dimension reduction. IEEE Trans. Image Process. 2010, 19, 1921–1932. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Nie, F.; Xu, X.; Qing, C.; Xu, D. Accelerating flexible manifold embedding for scalable semi-supervised learning. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2786–2795. [Google Scholar] [CrossRef]
- Shi, D.; Zhu, L.; Li, J.; Cheng, Z.; Liu, Z. Binary label learning for semi-supervised feature selection. IEEE Trans. Knowl. Data Eng. 2023, 35, 2299–2312. [Google Scholar] [CrossRef]
- Bao, J.; Kudo, M.; Kimura, K.; Sun, L. Robust embedding regression for semi-supervised learning. Pattern Recognit. 2024, 145, 109894. [Google Scholar] [CrossRef]
- Liao, H.; Chen, H.; Yin, T.; Horng, S.J.; Li, T. Adaptive orthogonal semi-supervised feature selection with reliable label matrix learning. Inf. Process. Manag. 2024, 61, 103727. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, M.; Nie, F.; Li, X. Unified dual-label semi-supervised learning with top-k feature selection. Neurocomputing 2022, 501, 875–888. [Google Scholar] [CrossRef]
- Wang, J.; Xie, F.; Nie, F.; Li, X. Robust supervised and semisupervised least squares regression using ℓ2,p-norm minimization. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8389–8403. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, C.; Nie, F.; Li, X. Discriminative and robust least squares regression for semi-supervised image classification. Neurocomputing 2024, 575, 127316. [Google Scholar] [CrossRef]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Varaprasad, S.; Goel, T.; Tanveer, M.; Murugan, R. An effective diagnosis of schizophrenia using kernel ridge regression-based optimized RVFL classifier. Appl. Soft Comput. 2024, 157, 111457. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J.A. LASSO regression. J. Br. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Y.; Cui, Z.; Lin, L.; Zong, Y. Diabetes risk analysis based on machine learning LASSO regression model. J. Theory Pract. Eng. Sci. 2024, 4, 58–64. [Google Scholar]
- Zhang, Z.; Lai, Z.; Xu, Y.; Shao, L.; Wu, J.; Xie, G.S. Discriminative elastic-net regularized linear regression. IEEE Trans. Image Process. 2017, 26, 1466–1481. [Google Scholar] [CrossRef] [PubMed]
- Amini, F.; Hu, G. A two-layer feature selection method using genetic algorithm and elastic net. Expert Syst. Appl. 2021, 166, 114072. [Google Scholar] [CrossRef]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on MACHINE Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.; Weston, J.; Schölkopf, B. Learning with local and global consistency. Adv. Neural Inf. Process. Syst. NIPS 2003, 16, 1–8. [Google Scholar]
- Chen, X.; Yuan, G.; Nie, F.; Ming, Z. Semi-supervised feature selection via sparse rescaled linear square regression. IEEE Trans. Knowl. Data Eng. 2018, 32, 165–176. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, H.; Nie, F. Discriminative Semi-Supervised Feature Selection Via a Class-Credible Pseudo-Label Learning Framework. In Proceedings of the ICASSP 2024-2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 6895–6899. [Google Scholar]
- Shi, Z.; Chen, L.; Ding, W.; Zhong, X.; Wu, Z.; Chen, G.Y.; Zhang, C.; Wang, Y.; Chen, C.L.P. IFKMHC: Implicit Fuzzy K-Means Model for High-Dimensional Data Clustering. IEEE Trans. Cybern. 2024, 54, 7955–7968. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Zhang, R.; Li, X. A generalized power iteration method for solving quadratic problem on the stiefel manifold. Sci. China Inf. Sci. 2017, 60, 1–10. [Google Scholar] [CrossRef]
- Huang, J.; Nie, F.; Huang, H. A new simplex sparse learning model to measure data similarity for clustering. In Proceedings of the IJCAI, Buenos Aires, Argentina, 25–31 July 2015; pp. 3569–3575. [Google Scholar]
- Xu, C.; Si, J.; Guan, Z.; Zhao, W.; Wu, Y.; Gao, X. Reliable conflictive multi-view learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 16129–16137. [Google Scholar]
- Shi, Z.; Chen, L.; Ding, W.; Zhang, C.; Wang, Y. Parameter-free robust ensemble framework of fuzzy clustering. IEEE Trans. Fuzzy Syst. 2023, 31, 4205–4219. [Google Scholar] [CrossRef]
- Shi, Z.; Luo, Y.; Liu, X.; Chen, L.; Ding, W.; Zhong, X.; Wu, Z.; Philip Chen, C.L. MGL-FBLS: Multi-Granularity Label-Driven Feature Enhanced Broad Learning System for Semi-Supervised Classification. IEEE Trans. Emerg. Top. Comput. Intell. 2025; early access. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).